Двоичное умножение: Умножение двоичных чисел онлайн

Умножение двоичных чисел онлайн

Примеры решенийПеревод дробных чисел Формат с плавающей точкой Перевести в 2 систему Перевод в 8 систему Перевод в 10 систему Дополнительный код Сложение двоичных чиселУмножение двоичных чисел

Назначение сервиса. Онлайн-калькулятор предназначен для умножения двоичных чисел.

• Решение онлайн
• Видеоинструкция

Число №1

Число №2

Пример №1. Умножить двоичные числа 111 и 101.
Решение.

		1	1	1
		1	0	1
=	=	=	=	=
		1	1	1
	0	0	0
1	1	1
=	=	=	=	=
0	0	0	1	1

При суммировании в разрядах 2, 3, 4 возникло переполнение. Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100011
В десятичной системе счисления данное число имеет следующий вид:
Для перевода необходимо умножить разряд числа на соответствующую ему степень разряда.
100011 = 2⁵*1 + 2⁴*0 + 2³*0 + 2²*0 + 2¹*1 + 2⁰*1 = 32 + 0 + 0 + 0 + 2 + 1 = 35
Проверим результат умножения в десятичной системе счисления. Для этого переводим числа 111 и 101 в десятичное представление.
111₂ = 2²*1 + 2¹*1 + 2⁰*1 = 4 + 2 + 1 = 7
101₂ = 2²*1 + 2¹*0 + 2⁰*1 = 4 + 0 + 1 = 5
7 x 5 = 35

Пример №2. Найти двоичное произведение 11011*1100. Перевести ответ в десятичную систему.
Решение. Умножение начинаем с младших разрядов: если текущий разряд второго числа равен 0, то везде записываем нули, если 1 — то переписываем первое число.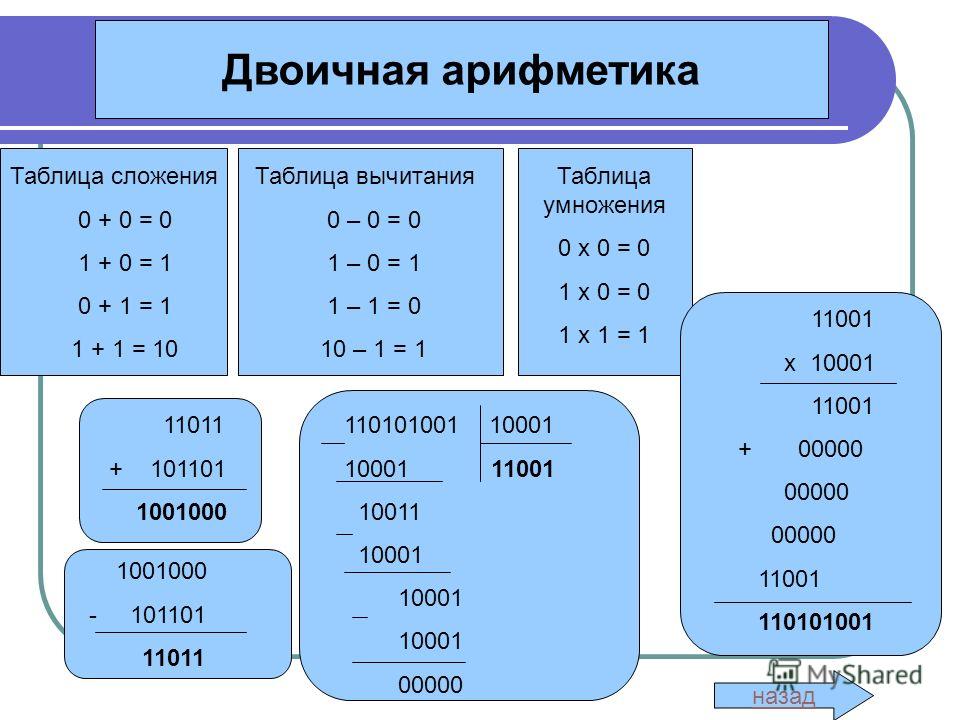

			1	1	0	1	1
				1	1	0	0
=	=	=	=	=	=	=	=
			0	0	0	0	0
		0	0	0	0	0
	1	1	0	1	1
1	1	0	1	1
=	=	=	=	=	=	=	=
0	1	0	0	0	1	0	0

При суммировании в разрядах 3, 4, 5, 6, 7 возникло переполнение. Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 101000100
В десятичной системе счисления данное число имеет следующий вид:
101000100 = 2⁸*1 + 2⁷*0 + 2⁶*1 + 2⁵*0 + 2⁴*0 + 2³*0 + 2²*1 + 2¹*0 + 2⁰*0 = 256 + 0 + 64 + 0 + 0 + 0 + 4 + 0 + 0 = 324
Проверим результат умножения в десятичной системе счисления. Для этого переводим числа 11011 и 1100 в десятичное представление.
11011 = 2⁴*1 + 2³*1 + 2²*0 + 2¹*1 + 2⁰*1 = 16 + 8 + 0 + 2 + 1 = 27
1100 = 2³*1 + 2² *1 + 2¹*0 + 2⁰*0 = 8 + 4 + 0 + 0 = 12
27 x 12 = 324

Пример №3. 1101.11*101
Будем умножать числа без учета плавающей точки: 110111 x 101
Умножение начинаем с младших разрядов: если текущий разряд второго числа равен 0, то везде записываем нули, если 1 — то переписываем первое число.

		1	1	0	1	1	1
					1	0	1
=	=	=	=	=	=	=	=
		1	1	0	1	1	1
	0	0	0	0	0	0
1	1	0	1	1	1
=	=	=	=	=	=	=	=
0	0	0	1	0	0	1	1

При суммировании в разрядах 2, 3, 4, 5, 6, 7 возникло переполнение. Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100010011
Поскольку умножали без учета плавающей запятой, то окончательный результат запишем как: 1000100.11
В десятичной системе счисления данное число имеет следующий вид:
1000100 = 2⁶*1 + 2⁵*0 + 2⁴*0 + 2³*0 + 2²*1 + 2¹*0 + 2⁰*0 = 64 + 0 + 0 + 0 + 4 + 0 + 0 = 68
Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда.
11 = 2^-1*1 + 2^-2*1 = 0.75
В итоге получаем число 68.75
Проверим результат умножения в десятичной системе счисления. Для этого переводим числа 1101.11 и 101 в десятичное представление.
1101 = 2³*1 + 2²*1 + 2¹*0 + 2⁰*1 = 8 + 4 + 0 + 1 = 13
11 = 2^-1*1 + 2^-2*1 = 0.75
В итоге получаем число 13.75
Переводим число: 101₂ = 2²*1 + 2¹*0 + 2⁰*1 = 4 + 0 + 1 = 5
13. 75 x 5 = 68.75

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Как умножать двоичные числа

На прошлом уроке мы научились складывать и вычитать двоичные числа. Сейчас мы с Вами рассмотрим их умножение и деление. Так же, как и в предыдущих уроках, правильность полученного результата мы будем проверять в десятичной системе счисления. Итак, начнем с умножения двоичных чисел. Для начала рассмотрим следующую простую таблицу, которая используется для этого. Как и в случае сложения, умножать двоичные числа будем в столбик.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Двоичная арифметика
• 11 Умножение двоичных чисел
• Арифметические операции в двоичной системе счисления
• Арифметические операции в двоичной системе
• Сложение двоичных чисел онлайн
• Двоичная система счисления
• 11 Умножение двоичных чисел
• Сложение двоичных чисел онлайн

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Умножение двоичных чисел

Двоичная арифметика

Компьютерные сети Системное программное обеспечение Информационные технологии Программирование. Все о программировании Обучение Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации Главная Тексты статей Добавить статьи Контакты Арифметические операции в двоичной системе.

Арифметические действия в двоичной системе производится по тем же правилам что и в десятичной системе счисления. Однако так как в двоичной системе счисления используются только две цифры 0 и 1, то арифметические действия выполняются проще, чем десятичной системе.

Пример 3. Сложить два числа:. Найти разность двух чисел:. Найти произведение двух чисел :. Как видно из приведенных примеров, операция умножения может быть представлена как операции сдвига и суммирования. Деление в двоичной системе производится вычитанием делителя со сдвигом вправо, если остаток больше нуля. Делимое больше делителя:. Как видно из приведенных примеров, операция деления может быть представлена как операции сравнения, сдвига и суммирования.

Вернуться в оглавление: Алгоритмические языки. Поделись: Не нашли то, что искали? Google вам в помощь! Сложение двоичных чисел. Умножение двоичных чисел. Деление двоичных чисел. Карта сайта Карта сайта укр Видео Уроки php mysql Программирование Онлайн сервисы Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские Полезное Аппаратное и программное обеспечение Графика и компьютерная сфера Интегрированная геоинформационная система Интернет Компьютер Комплектующие компьютера Лекции Методы и средства измерений неэлектрических величин Обслуживание компьютерных и периферийных устройств Операционные системы Параллельное программирование Проектирование электронных средств Периферийные устройства Полезные ресурсы для программистов Программы для программистов Статьи для программистов Cтруктура и организация данных.

Полезен материал?

11 Умножение двоичных чисел

Используя наш сайт, вы подтверждаете, что прочитали и поняли политику о куки , политику конфиденциальности и пользовательское соглашение. Stack Overflow на русском — это сайт вопросов и ответов для программистов. Регистрация займёт не больше минуты. Не могли бы вы мне подсказать как написать код для умножения двух двоичных чисел? Нужно именно их умножить, поэтому через перевод в 10 сс не получится. Подобный вопрос задавали ранее и на него уже получен ответ.

умножения и деления столбиком дробных чисел, записанных в двоичной, Причем числа могут быть введены в разных системах счисления.

Арифметические операции в двоичной системе счисления

Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения. Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд.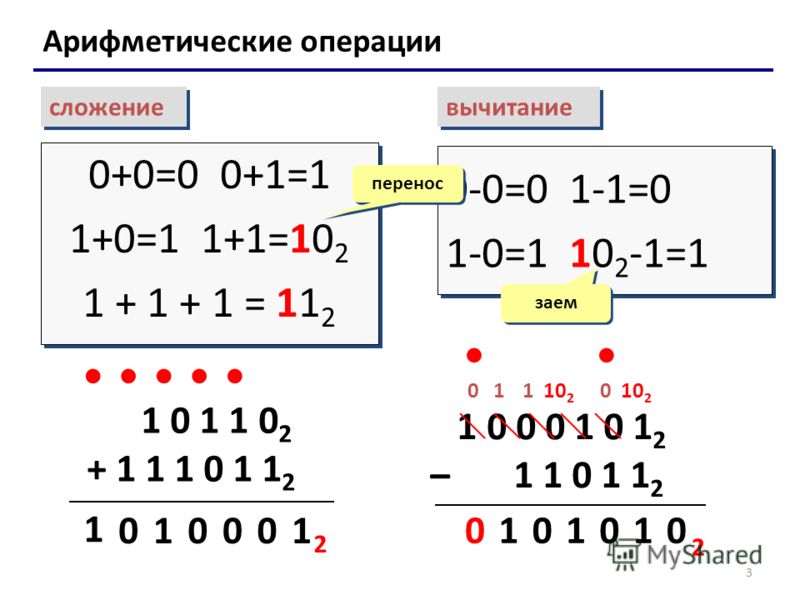 При вычитании, если необходимо, делают заем. Пример 1. Сложить двоичные числа. Пример 2. Вычесть двоичные числа. Пример 3. Умножить двоичные числа. Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления.

Арифметические операции в двоичной системе

Система базовой позицией-2 представляет собой позиционные обозначения с поразрядной равным 2. Каждая цифра упоминается как бит. Из — за своей простой реализации в цифровых электронных схем , с использованием логических вентилей , двоичная система используется практически во всех современных компьютеров и компьютерных устройств. Современная двоичная система счисления была изучена в Европе в 16 — м и 17 — го веков Томас Харриет , Хуан Карамуэль и Готфрида Лейбница.

Компьютерные сети Системное программное обеспечение Информационные технологии Программирование.

Сложение двоичных чисел онлайн

Темы: математика числа двоичное счисление наука история арифметика. Создан бионический программируемый белок. Электричество без проводов. Забытые уроки российского дефолта года. Органическая химия и органический синтез.

Двоичная система счисления

Думаю самое простое решение, это написать 2 функции: 1. Переводит двоичную строку в 10чную 2. Переводит десятичную в двоичную. Нужно перемножить не переводя ни в какую другую систему счисления Visual Basic только изучаю Ну, тут могу посоветовать лиш учить его дальше. Алгоритм умножения понятен, надо только написать его в коде.

Сложим числа 15 и 6 в различных системах счисления. Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится.

11 Умножение двоичных чисел

Я правильно понимаю, что описано вот это, просто по-русски и другими словами? Войдите , пожалуйста. Хабр Geektimes Тостер Мой круг Фрилансим. Войти Регистрация.

Сложение двоичных чисел онлайн

ВИДЕО ПО ТЕМЕ: Умножение в разных системах счисления. Урок 7

Под двоичной системой счисления понимается такая система, в которой для изображения чисел используются два символа, а веса разрядов меняются по закону где k — произвольное целое Таблица 2. Классической двоичной системой является система с символами. Ее двоичные цифры часто называют битами. Чтобы овладеть любой системой счисления, надо уметь складывать и умножать в ней любые цифры.

Рассмотрим основные способы выполнения операции умножения для различных систем cчисления. Самым распространенным способом умножения чисел является способ поразрядного умножения множимого на множитель, начиная с младшего разряда — 1-й способ, начиная со старшего разряда — 2-способ.

Числа которыми мы привыкли пользоваться называются десятичными и арифметика которой мы пользуемся также называется десятичной. Это потому, что каждое число можно составить из набора цифр содержащего 10 символов — цифр — «». Так шло развитие математики, что именно этот набор стал главным, но десятичная арифметика не единственная. Если мы возьмём только пять цифр, то на их основе можно построить пятиричную арифметику, из семи цифр — семиричную. В областях знаний связанных с компьютерной техникой часто используют арифметику в которой числа составляются из шестнадцати цифр, соответственно эта арифметика называется шестнадцатиричной. Чтобы понять, что такое число в не десятичной арифметике сначала выясним, что такое число в десятичной арифметике.

Иногда возникает потребность быстро прочитать или записать числа в двоичной или шестнадцатеричной системе счисления, например, работая с различными байтовыми редакторами,при расчете формул с побитовыми операциями или работе с цветом. Часто в таких ситуациях нет возможности долго переводить числа с помощью формул или калькулятора. О быстрых способах перехода между системами счисления пойдет речь в данной статье.

Вопрос 4. Двоичное умножение

Поскольку построение цифровых автоматов будет рассматриваться на примере реализации алгоритмов машинной арифметики, имеет смысл рассмотреть основные подобнее алгоритмы.

1. Умножение двоичных чисел – это циклическая операция (если используется косвенный алгоритм умножения). Количество шагов зависит от разрядности множителя. На каждом шаге выполняется сдвиг операндов и возможное сложение.

A – множимое

В – множитель

С – сумма частичных произведений

Р(С) – произведение

Данный алгоритм соответствует известному алгоритму «умножение в столбик»

A = 5

В = 6

А2 = 0101 В₂ = 0110

В зависимости от направления сдвига и направления анализа разряда множителя, различают 4 схемы косвенного умножения

1) умножение с младших разрядов со сдвигом вправо СЧП

2) умножение со старших разрядов со сдвигом влево СЧП

3) умножение с младших разрядов со сдвигом влево СЧП

4) умножение со старших разрядов со сдвигом вправо СЧП

Каждый из вариантов соответствует определённому варианту раскрытия скобок в произведении

— 1-ая схема умножения

Вопрос 5.

Умножение в инверсных кодах

При умножении чисел в инверсных кодах, появляются интересные особенности (при умножении в прямых кодах, не отличается от примера, только дополнительно вычисляется знак ):

1. все операции сложения и сдвига выполняются по правила соответствующего инверсного кода

Сложение в обратном коде происходит с циклическим переносом.

Сдвиг вправо происходит с размножением знака.

Сдвиг влево в ОК происходит циклически.

2. При умножении на отрицательный множитель в инверсном коде, необходимо выполнить коррекцию произведения (после завершения основного цикла).

Коррекция в дополнительном коде: P=P’-A

Коррекция в ОК: P=P’-A+A*2^—n

Коррекций №1: С=А (перед циклом)

Коррекций №2: P=P’-A (после цикла)

Все операции с инверсным кодом лучше выполнять в модифицированном коде, т.е. с двумя знаковыми разрядами. 11. – «+», 00. – «-»

Пример: (-5)x(-6)

А_пк=11. 0101

А_дк=11.1011

В_пк=11.0110

В_дк=11.1010

-А_дк=00.1011

Регистр С	Регистр В	В(0)	Комментарий
00.0000	11101	0	CNT=4, CNT0 B(0)=0 => C-> и B->
00.0000 + 11.1011	01110	1	CNT=3, CNT0 B(0)=1 => C=C+A
11.1011	01110	1	C-> и B->
11.1101	10111	0	CNT=2, CNT0 B(0)=0 => C-> и B->
11. 1110 + 11.1011	11011	1	CNT=1, CNT0 B(0)=1 => C=C+A
11.1001	11011	1	C-> и B->
11.1100	11101	1	CNT=0 – конец

В(0)=1 => B<0 => коррекция C:=C+[-A]

P=00.00011110

Вопрос 6. Деление

Деление двоичных чисел – циклическая операция, но в отличие от умножения, деление может выполняться бесконечно. На практике деление останавливается при определении требуемого разряда частного (n+1 разряда частного, затем округляется).

В цикле деления выполняется сдвиг текущего остатка влево и вычитание делителя.

Выделяют два основных алгаритма деления:

а) с восстановлением остатка.

б) без восстановления остатка.

С восстановлением остатка:

1) выполняется пробное вычитание делимого из делителя

Делимое – А, делитель – В, R – остаток, R_i – текущий остаток, R_i+1 – следующий остаток, С – частное.

Если R>0, то деление останавливается (рассматривается деление правильных дробей).

Если R<0, то выполняется восстановление (R+B)

2) удвоение остатка

3) вычитание делителя из остатка

Если R_i+1>0, то очередная цифра частного равна 1, иначе – равна 0. в последнем случае выполняется восстановление остатка.

4) действия 2) и 3) выполняются n раз и результат округляется до n разрядов

При восстановлении остатка, очередной остаток вычисляется так:

R_i+1=2(R_i+B) — B=2R_i+B

В алгоритме без восстановления остатка в случае, когда очередная цифра частного равна 0, восстановление не производят, зато на следующем шаге не вычитают, а прибавляют делитель к R.

Двоичное умножение — правила, метод умножения двоичных чисел, примеры.

LearnPracticeDownload

Двоичное умножение — это процесс умножения двоичных чисел. Процесс умножения двоичных чисел такой же, как и при арифметическом умножении десятичных чисел. Единственное отличие состоит в том, что двоичное умножение включает в себя числа, состоящие из 0 и 1, тогда как десятичное умножение включает числа, состоящие из цифр от 0 до 9. Давайте шаг за шагом изучим процесс двоичного умножения.

1.	Двоичные правила умножения
2.	Как умножать двоичные числа?
3.	Примеры двоичного умножения
4.	Практические вопросы по двоичному умножению
5.	Часто задаваемые вопросы о двоичном умножении

Правила двоичного умножения

Двоичное умножение похоже на умножение десятичных чисел. У нас есть множитель и множимое. В результате умножения получается произведение. Поскольку в двоичном умножении участвуют только двоичные цифры, мы можем умножать только 0 и 1. Правила двоичного умножения следующие.

Множимое	Множитель	Продукт
0	0	0 × 0 = 0
0	1	0 × 1 = 0
1	0	1 × 0 = 0
1	1	1 × 1 = 1

Как умножать двоичные числа?

Процесс умножения двоичных чисел аналогичен и более прост в выполнении, чем десятичное умножение, поскольку двоичные числа состоят только из двух цифр: 0 и 1. Метод умножения двоичных чисел приведен ниже. Тот же набор правил применим и к двоичным числам с десятичной точкой. Возьмем пример умножения (\(11101)_{2}\) и (\(1001)_{2}\). Десятичный эквивалент (\(11101)_{2}\) равен 29, а десятичный эквивалент (\(1001)_{2}\) равен 9. Теперь давайте перемножим эти числа.
Шаг 1: Запишите множимое (\(11101)_{2}\) и множитель (\(1001)_{2}\) один под другим на соответствующих позициях.
Шаг 2: Умножьте самую правую цифру или младший значащий бит (LSB) множителя (1) на все цифры множимого (\(11101)_{2}\).
Шаг 3: Добавьте заполнитель «0» или «X» перед умножением следующего старшего разряда множителя& на множимое.
Шаг 4: Повторите тот же процесс для всех следующих цифр более высокого порядка, пока мы не достигнем самого старшего бита (MSB), который является самой левой цифрой множимого с множителем.
Шаг 5: Произведение, полученное в каждой строке, называется частичным произведением. Наконец, добавьте все частичные продукты. Чтобы сложить все двоичные числа, используйте правила двоичного сложения.

(Правила двоичного сложения перечислены ниже: 0 + 0 = 0, 0 + 1 = 1 и 1 + 1 = 0 с переносом 1. Таким образом, 1 + 1 = 10 и 1 + 1 + 1 = 11 в двоичной системе счисления)

Давайте рассмотрим следующий процесс двоичного умножения, описанный выше.

Следовательно, произведение (\(11101)_{2}\) и (\(1001)_{2}\) равно (\(100000101)_{2}\).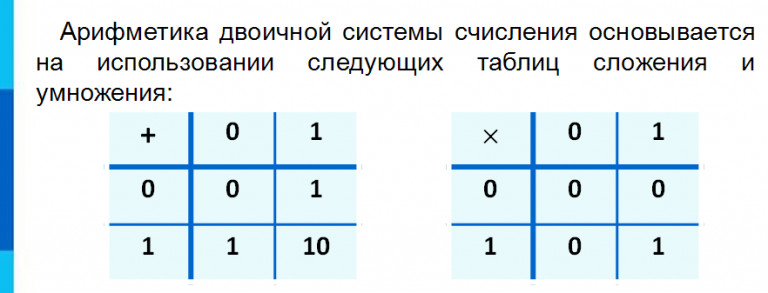 Проверим наш ответ. Десятичный эквивалент (\(100000101)_{2}\) равен 261. Чтобы узнать, как преобразовать двоичное число в десятичное, нажмите здесь. Десятичный эквивалент & (\(11101)_{2}\) равен 29, а десятичный эквивалент (\(1001)_{2}\) равен 9. Когда мы умножаем 29 на 9, произведение равно 261. Десятичный эквивалент of (\(100000101)_{2}\) равно 261. Следовательно, произведение правильное.

Темы, относящиеся к двоичному умножению

Ознакомьтесь с некоторыми интересными темами, связанными с двоичным умножением.

• Двоичная система счисления
• Двоичное вычитание
• Двоичный раздел
• Двоичный код в десятичный
• Системы счисления

 

Примеры двоичного умножения

1. Пример 1. Используя правила двоичного умножения, умножьте ( \(110)_{2}\) и ( \(11)_{2}\).

   Решение:

   Правила двоичного умножения:
   0 × 0 = 0
   0 × 1 = 0
   1 × 0 = 0
   1 × 1 = 1
   Давайте воспользуемся приведенными выше правилами для умножения двоичных чисел.

   GIven, множимое = \(110_{2}\), множитель = \(11_{2}\). Мы умножаем два числа, как показано ниже.

   
   Следовательно, произведение (\(110)_{2}\) и (\(11)_{2}\) равно (\(10010)_{2}\).

2. Пример 2. Используя правила двоичного умножения, найдите произведение (\(11011)_{2}\) и (\(101)_{2}\).
   Решение:

   Множитель GIven = (\(11011)_{2}\) и множитель = (\(101)_{2}\)
   При умножении получаем

   Следовательно, произведение (\(11011)_{2}\) и (\(101)_{2}\) равно (\(10000111)_{2}\).

3. Пример 3. Используя правила двоичного умножения, умножьте двоичные числа (\(1011.1)_{2}\) и (\(10.1)_{2}\).

   Решение:

   Учитывая множимое = (\(1011.1)_{2}\) и множитель = (\(10.1)_{2}\).

   Следовательно, произведение (\(1011.1)_{2}\) и (\(10.1)_{2}\) равно (\(11100.11)_{2}\)

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по двоичному умножению

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о двоичном умножении

Что такое двоичное умножение?

Двоичное умножение — это процесс умножения двоичных чисел. Двоичные числа образуют систему счисления с основанием 2. Данные хранятся в компьютере в виде нулей и единиц. Процесс умножения двоичных чисел такой же, как и арифметическая операция умножения, которая выполняется над десятичными числами или числами с основанием 10. Единственное отличие состоит в том, что двоичные числа состоят из нулей и единиц.

Каковы правила двоичного умножения?

Двоичное умножение также похоже на умножение десятичных чисел (от 0 до 9). Двоичные числа состоят только из 0 и 1. Следовательно, нам нужно знать произведение, когда 0 умножается на 0 и 1, а 1 умножается на 0 и 1. Правила двоичного умножения следующие.

• 0 × 0 = 0
• 0 × 1 = 0
• 1 × 0 = 0
• 1 × 1 = 1

Каков результат двоичного умножения (\(111)_{2}\) и (\(111)_{2}\)?

Произведение (\(111)_{2}\) и (\(111)_{2}\) равно (\(110001)_{2}\).

Как выполнить двоичное умножение?

Двоичное умножение двух чисел можно выполнить, выполнив шаги, указанные ниже.

Шаг 1: Расположите множитель и множимое в нужных местах. Например, мы можем перемножить трехзначное число и двузначное число. В этом случае 2-значное число должно быть правильно размещено под 3-значным числом, например,
110
× 10
———
_____

Шаг 2: Следующим шагом является умножение каждой цифры множимого на каждую цифру множителя, начиная с самой правой цифры или младшего значащего бита (LSB). Произведение, полученное после умножения каждой цифры множимого на множитель, называется частичным произведением. Наконец, мы складываем частичные продукты, полученные на каждом шаге, используя правило бинарного сложения.

Чему равно произведение (\(1111)_{2}\) и (\(1111)_{2}\) с помощью двоичного умножения?

Произведение (\(1111)_{2}\) и (\(1111)_{2}\) с использованием двоичного умножения равно (\(11100001)_{2}\). В этом двоичном умножении множитель и множимое являются одними и теми же двоичными числами. Мы используем правила двоичного умножения, а именно «0 × 0 = 0, 1 × 0 = 0, 0 × 1 = 0& и 1 × 1 = 1», и умножаем числа в соответствии с обычным методом арифметического умножения.

Что такое двоичное умножение отрицательных чисел?

В десятичной системе счисления или системе счисления с основанием 10 есть отрицательные числа, такие как -1, -2, -3 и так далее. Также можно умножать отрицательное число на положительное число или отрицательное число на отрицательное число в двоичном формате. Для этого мы представляем каждое число с помощью 8 бит. Здесь мы используем 4 бита для представления числа в дополнении до 2 и 4 бита для представления знака. Если знак числа положительный, то мы используем четыре нуля, а если число отрицательное, мы используем четыре единицы. Дополнение до 2 двоичного числа получается путем добавления 1 к дополнению до единицы двоичного числа. Дополнение до 1 означает замену каждого 0 на 1 и каждой 1 на 0.

Каков результат двоичного умножения чисел (\(10100)_{2}\) и (\(01011)_{2}\)?

Произведение (\(10100)_{2}\) и (\(01011)_{2}\) равно (\(011011100)_{2}\).

Скачать бесплатные материалы для исследования

Связанный рабочий лист

Математические листы и
Визуальная учебная программа

Двоичный мультипликационный калькулятор

Создан Филиппом Маусом

Обзор Стивена Вудинг

Последний0131

Как умножать двоичные числа?

Каковы правила двоичного умножения?

Как пользоваться калькулятором двоичного умножения?

Часто задаваемые вопросы

Калькулятор двоичного умножения описывает как умножать двоичные числа (которые вы можете получить с помощью двоичного преобразователя). В этой статье вы также узнаете о сходствах и различиях между двоичной и десятичной системами счисления и увидите пошаговые инструкции по умножению двоичных чисел .

🔎 Не ограничивайтесь умножением. Вы можете вычитать, умножать и делить эти типы чисел с помощью нашего двоичного калькулятора.

Как умножать двоичные числа?

В то время как десятичная система счисления, с которой мы все знакомы, основана на степенях 10, двоичная система имеет основание 2 . Это означает, что каждая цифра двоичного числа, так называемый бит, может представлять только два логических значения: 0 или 1 9.0051 . Поэтому двоичные числа обычно используются в цифровой электронике и связи, представляя два состояния «включено» и «выключено». Мы можем преобразовать двоичные числа в десятичную систему. Они также позволяют применять арифметические операции, такие как сложение, вычитание, деление и, как мы увидим в этом двоичном калькуляторе, умножение. Кроме того, двоичные числа позволяют выполнять операции, уникальные для двоичной системы, такие как сдвиг битов и побитовые операции AND, OR и XOR.

Эти операции также могут быть выполнены с отрицательными двоичными числами, как показано в нашем калькулятор дополнения до двух, в котором первая цифра указывает на знак числа . Этот калькулятор двоичного деления использует представление со знаком, что означает, что первый бит ваших входных чисел будет считаться битом со знаком. Будьте осторожны, чтобы не получить ложные результаты из-за этого , и при необходимости увеличьте битовое представление.

Каковы правила двоичного умножения?

Двоичное умножение имеет 4 основных правила :

• 0 × 0 = 0
• 0 × 1 = 0
• 1 × 0 = 0
• 1 × 1 = 1

На основе этих правил двоичное умножение очень похоже на десятичное длинное умножение . Мы можем даже считать это немного проще, так как нам нужно иметь дело только с цифрами 0 и 1 .

Умножение — это коммутативная операция , что означает, что произведение не зависит от порядка множителей. Тем не менее, рекомендуется для длинного деления устанавливать более длинное число в качестве множителя (множитель 1), а более короткое число — в качестве множимого (множитель 2), чтобы уменьшить количество шагов. Умножьте множитель на каждую цифру множимого, чтобы получить промежуточные продукты, последняя цифра которых находится на позиции соответствующей цифры множимого. Конечный продукт представляет собой сумму этих промежуточных продуктов.

В качестве примера рассмотрим умножение 1011 и 0101 (13 и 5 в десятичной системе):

Пошаговая процедура умножения этих двоичных чисел:

1. Установите большее число в качестве множителя . 1011 имеет четыре значащих бита и поэтому имеет коэффициент 1.
2. Умножить множитель на последнюю цифру множимого :

• Следуя основным правилам, указанным выше, 1011 × 1 = 1011 . Это первый промежуточный продукт, начиная с позиции последней цифры множимого.

3. Умножить множитель на предпоследнюю цифру множимого :

• 1011 × 0 = 0000 . Это второй промежуточный продукт, начиная со второй до последней цифры множимого.

4. Умножить множитель на третью до последней цифры множимого :

• 1011 × 1 = 1011 . Это третий промежуточный продукт, начиная с позиции третьей до последней цифры множимого.

5. Умножьте множитель на четвертую до последней (первую) цифру множимого :

• 1011 × 0 = 0000 . Это четвертый промежуточный продукт, начиная с позиции четвертой и заканчивая последней цифрой множимого.

6. Конечный продукт представляет собой сумму промежуточных продуктов :

• 1011 + 00000 + 101100 + 0000000 = 0110111

Как использовать калькулятор двоичного умножения?

Теперь вы знаете, как выполнять умножение двоичных чисел, так что давайте научиться пользоваться калькулятором двоичного умножения . В качестве примера, давайте проверим правильность нашей пошаговой процедуры выше и умножим 1011 и 101 :

1. . представлен в.

• Как мы уже знаем, максимальное число битов произведения равно 6, поэтому 8 битов вполне достаточно.

2. Введите коэффициенты. Поскольку операция умножения коммутативна, порядок не имеет значения.

• 1011 и 101

3. Калькулятор двоичного умножения представляет произведение в двоичной и десятичной системе . Это результат вашего умножения двоичных чисел:
.

• Двоичный: 0011 0111
• Десятичный: 13

Если ваш двоичный результат имеет значение 1 в старшем разряде и может быть понят как положительный результат в записи без знака или отрицательный результат в записи со знаком, будут отображаться оба результата .

Часто задаваемые вопросы

Как умножать двоичные числа?

Для умножения двоичных чисел выполните следующие действия:

1. Установите более длинное число в качестве множителя и более короткое число как множимое .
2. Умножьте множитель на каждую цифру множимого , чтобы получить промежуточные произведения, последняя цифра которых находится на позиции соответствующей цифры множимого.
3. Суммируйте промежуточные продукты , чтобы получить конечный продукт.

Как умножать двоичные числа с помощью битового сдвига?

Двоичное умножение, особенно с коэффициентами, равными степени двойки, можно выполнить с помощью сдвига битов влево . Умножение на 2 — это сдвиг на один бит, 4 — 2 бита, 8 — 3-битный сдвиг и т. д. Благодаря своей математической эффективности этот метод обычно используется в цифровых приложениях.

Как умножить двоичные числа 101 и 11?

на Умножьте двоичные номера 101 и 11 , выполните следующие шаги:

1. SET 101 В качестве множества и 9 3323 как увеличение и 9 33323.
2. Умножьте 101 на последнюю цифру 11 : 101 × 1 = 101 . Это первый промежуточный продукт .
3. Умножьте 101 на первую цифру 11 : 101 × 1 = 101 . Добавьте 0 в конце, чтобы представить позицию цифры множимого: 1010 . Это второй промежуточный продукт .
4. Суммируйте промежуточные продукты , чтобы получить конечный продукт: 101 + 1010 = 1111 .

Филип Маус

Двоичное представление

Вы можете записывать двоичные числа, содержащие не более 8 цифр. Вам не нужно вводить лидирующие нули.

Фактор 1

Фактор 2

Посмотреть 10 похожих бинарных калькуляторов 1️0️

Двоичное сложениеДвоичное делениеДвоичная дробь… 7 еще

Почему двоичное умножение может быть не таким сложным, как вы думаете

You are here: Home / Computer Science / Почему двоичное умножение может быть не таким сложным, как вы думаете

Добро пожаловать в следующий пост в моей серии о двоичных числах и двоичной арифметике. В сегодняшнем посте мы снова собираемся опираться на то, что мы узнали из моих предыдущих постов о двоичном сложении и двоичном вычитании, и посмотрим, как мы можем выполнять умножение в двоичном виде.

Терминология

Прежде чем мы углубимся в тему, я хотел бы воспользоваться моментом, чтобы установить некоторую терминологию. Будет намного проще объяснять вещи по мере продвижения вперед, если у нас обоих будет общий язык.

Пример того, как мы пишем задачу на умножение, показан ниже.

Сверху у нас есть множимое. Это число, которое мы хотим умножить. Внизу у нас есть множитель. Это число мы будем использовать для умножения множимого. По мере того, как мы будем рассматривать примеры далее в этом посте, я буду использовать эти термины для объяснения шагов, которые необходимо предпринять для выполнения умножения.

Четыре этапа умножения

Процесс умножения состоит из нескольких этапов:

• Фаза выравнивания: В фазе выравнивания первое, что мы делаем, это выравниваем числа, которые мы хотим умножить, так, чтобы их правые цифры совпадали. В случаях, когда числа имеют разное количество цифр после точки счисления (помните, что точка счисления отделяет целые части числа от дробной части), это означает, что точки счисления двух чисел не будут совмещены. Не беспокойтесь об этом. Мы решим это на более позднем этапе.

• Фаза умножения: На этой фазе мы производим набор частичных произведений, комбинируя ряд однозначных умножений. Начиная с правой стороны, мы берем каждую цифру множителя и, в свою очередь, используем эту цифру для умножения каждой из цифр множимого. Затем результаты этих отдельных умножений объединяются для создания частичного произведения. Если результат отдельного умножения состоит из нескольких цифр, записывается младшая значащая цифра, а старшая значащая цифра переносится и добавляется к результату следующего одноразрядного умножения. После умножения всех цифр и вычисления частичного произведения берется следующая цифра множителя и повторяются вышеописанные шаги. Каждый раз, когда вычисляется последующий частичный продукт, частичный продукт сдвигается на один столбец влево по сравнению с последним частичным продуктом. Все свободные столбцы справа заполняются нулями. (Это может стать немного яснее, когда мы посмотрим на наш пример.) Как только это будет сделано для всех цифр в множителе, и все цифры будут умножены на все цифры в множимом, у нас должно быть одно частичное произведение для каждой из цифр. в нашем множителе. На этом этапе мы переходим к следующему этапу.

• Фаза сложения: На фазе сложения мы вычисляем результат, складывая все частичные произведения, вычисленные на этапе 1.

• Размещение точки счисления и добавление знака: Последним шагом в этом процессе является размещение точки счисления и вычисление знака числа. Как мы узнали ранее, точка счисления отделяет целые числа от дробных чисел и в десятичном виде также известна как десятичная точка. Главное, что следует помнить при размещении точки счисления в нашем окончательном результате, заключается в том, что наш результат будет иметь такое же количество цифр после точки счисления, сколько после точки счисления в каждом из чисел, которые мы пытаемся умножить вместе. Например, если бы мы умножали 23,6 x 27,564, у нас было бы 4 цифры справа от точки счисления в нашем ответе, поскольку есть 1 цифра после точки счисления в нашем первом числе и еще 3 после точки счисления в нашем втором числе.

Десятичное умножение

Теперь, когда основные этапы понятны, давайте рассмотрим пример.

Для начала рассмотрим пример в десятичном формате. Это может быть для вас переподготовкой, но помогает проиллюстрировать шаги, предпринятые для выполнения умножения в системе счисления, к которой вы привыкли, прежде чем мы представим сложность выполнения его в двоичном формате.

Чтобы успешно выполнить умножение любых двух десятичных чисел, главное, что вам нужно запомнить, это ваши таблицы умножения. Все десятичные умножения основаны на ряде простых однозначных умножений, которые затем складываются вместе.

Для нашего примера представьте, что мы пытаемся вычислить, во сколько нам обходится эксплуатация нашего компьютера в неделю, и мы выяснили, что он потребляет 23,4 единицы электроэнергии в неделю, а каждая единица стоит нам 6,7 цента (Да… я знаете… только представьте…)

	Этап 1: Выровняйте два числа
	Как я указал выше, первый этап процесса заключается в том, чтобы выровнять наши два числа и записать нашу задачу на умножение. Поскольку 23,4 (наш множитель) и 6,7 (наш множитель) имеют одну цифру справа от десятичной точки, в данном случае это довольно простая задача.
	Этап 2: Расчет частичных произведений
	Этап 2 включает в себя вычисление частичных произведений. Поскольку у нас есть две цифры в нашем множителе, у нас будет два частичных продукта.
	Расчет первого частичного произведения
	Давайте начнем вычислять наш первый частичный продукт. Для начала возьмем крайнюю правую цифру множителя (7 из 6,7) и умножим ее на первую цифру множимого (4 из 23,4). 4 x 7 = 28. Мы ставим 8 в качестве первой цифры нашего частичного произведения, а затем переносим 2.
	Затем мы умножаем крайнюю правую цифру множителя (7 из 6,7) на вторую цифру множимого (3 из 23,4), а затем добавляем любые числа, которые у нас есть. 3 x 7 = 21, добавьте 2, которые мы перенесли из предыдущего шага = 23. Мы ставим 3 в качестве второй цифры в нашем частичном произведении, а затем переносим 2.
	Затем мы умножаем крайнюю правую цифру множителя (7 из 6,7) на третью цифру множимого (2 из 23,4) и снова складываем любые числа, которые у нас есть. 2 x 7 = 14, добавьте 2, которые мы перенесли из предыдущего шага, = 16. Мы ставим 6 в качестве следующей цифры нашего частичного произведения, и, поскольку у нас больше нет цифр для умножения, мы помещаем перенесенную 1 в следующий столбец. В результате наш первый частичный продукт 1638 г.
	Расчет второго частичного произведения
	Умножив первую цифру нашего множителя, мы теперь переходим ко второй цифре. Поскольку эта вторая цифра на порядок больше, чем первая цифра, которую мы умножили, мы ставим ноль в качестве первой цифры нашего второго частичного произведения.
	Настроившись, мы теперь берем вторую цифру множителя (6 из 6,7) и умножаем ее на первую цифру множимого (4 из 23,4). 4 x 6 = 24. Мы ставим 4 как вторую цифру в частичном произведении и переносим 2.
	Затем мы умножаем вторую цифру множителя (6 из 6,7) и умножаем ее на вторую цифру множимого (3 из 23,4) перед добавлением того, что мы перенесли из предыдущего шага. 3 x 6 = 18, добавьте 2, которые мы перенесли, = 20. Мы ставим 0 в качестве третьей цифры в нашем частичном произведении и снова переносим 2.
	Затем мы умножаем вторую цифру множителя (6 из 6,7) на третью цифру множимого (2 из 23,4) и снова добавляем все, что у нас есть. 2 x 6 = 12, добавьте 2, которые мы перенесли, = 14. Мы поместим 4 в качестве следующей цифры в нашем частичном произведении, и, поскольку больше нет цифр для умножения, поместите 1 в следующий столбец. Результатом является наш второй частичный продукт числа 14040.
	Этап 3. Добавление частичных произведений
	Следующий этап заключается в сложении двух частичных произведений. Начиная с крайнего правого столбца, мы добавляем 8 первого частичного произведения к 0 второго частичного произведения и получаем 8, которые помещаем в первый столбец нашего результата.
	Затем мы переходим ко второму столбцу, добавляя 3 первого частичного произведения к 4 второго частичного произведения, чтобы получить 7. Это добавляется как вторая цифра нашего результата.
	В третьем столбце показано, как мы добавляем 6 первого частичного произведения к 0 второго частичного произведения, чтобы получить 6, которое занимает третью цифру в нашем результате.
	В четвертом столбце мы добавляем 1 из первого частичного произведения к 4 из второго частичного произведения, чтобы получить 5, которое мы записываем как четвертую цифру результата.
	Наконец, мы берем единицу второго частичного произведения и перемещаем ее вниз как пятую цифру в нашем результате. Это дает нам результат 15678.
	Этап 4. Поиск места для основания корня
	Следующим шагом является установка системы счисления или десятичного разряда. Правило состоит в том, что в нашем результате будет столько же разрядов, сколько во всех числах, которые мы перемножали вместе. Наше множимое 23,4 имеет только одно место, и наш множитель также имеет одно место, что дает нам в сумме 2. Начиная справа от самой правой цифры в нашем результате, мы перемещаем десятичный разряд на 2 знака влево, чтобы получить окончательный результат 156,78.

Двоичное умножение

Двоичное умножение обычно проще десятичного умножения. Вместо того, чтобы знать таблицу умножения, вам действительно нужно знать только три вещи:

• 1 х 1 = 1

• 0 х 1 = 0

• 1 х 0 = 0

Когда вы выполняете умножение с двоичным числом, вы заметите, что никаких переносов никогда не бывает, а частичные произведения будут либо нулевыми, либо сдвинутой версией множимого. Давайте посмотрим на другой пример. Представьте, что мы пытаемся умножить следующее: 1,01 x 10,10 (это несколько натянутая аналогия, если предположить, что это также ваш счет за электроэнергию!). Мы снова пройдем те же этапы, что и с десятичным умножением.

	Этап 1: Выравнивание
	Как мы уже знаем, этап 1 заключается в сопоставлении двух наших чисел. Опять же, каждое из наших чисел в этом случае имеет две цифры справа от точки счисления, поэтому мы выравниваем их и записываем нашу проблему.
	Этап 2: Расчет частичных произведений
	На первом этапе вычисляются частичные произведения. Поскольку наш множитель имеет четыре цифры, у нас будет четыре частичных продукта.
	Расчет первого частичного произведения
	Сначала мы берем первую цифру множителя (правый 0 из 10,10) и умножаем ее на другие цифры множимого. Как мы знаем, все, что умножается на 0, равно нулю, поэтому наш первый частичный продукт равен 0 (или, точнее, 000).
	Расчет второго частичного произведения
	По мере того, как мы переходим ко второй цифре нашего множителя (правая 1 из 10,10), первое, что мы делаем, — это ставим 0 в первый столбец частичного произведения. Затем мы умножаем каждую отдельную цифру множимого на единицу нашего множителя, заполняя цифры столбцов с возрастающим значением. Результат — частичный продукт 1010. (Обратите внимание, как первые три цифры — это наше множимое, сдвинутое на одну позицию.)
	Расчет третьего частичного произведения
	Когда мы переходим к третьей цифре (левый 0 в 10.10), первое, что мы делаем, это добавляем два нуля в первые два столбца частичного произведения. Затем мы умножаем 0 из нашего множителя на каждую цифру множимого. Поскольку 0, умноженный на что-либо, равен 0, третье частичное произведение равно 0 (или, точнее, 00000).
	Расчет четвертого частичного произведения
	Переходя к последней цифре в нашем множителе (левая единица из 10,10), мы сначала помещаем три нуля в первые три столбца частичного произведения, чтобы представить увеличенное значение цифры, которую мы умножаем. Затем мы берем единицу нашего множителя и умножаем ее на каждую цифру множимого. Результатом является частичное произведение 101000.
	Этап 3. Добавление частичных произведений
	Следующим этапом будет добавление всех наших частичных продуктов. Сложение выполняется с помощью бинарного сложения, о котором мы узнали в моем предыдущем посте. Это дает нам результат 110010.
	Этап 4. Поиск места для основания корня
	Заключительный этап — определение места счисления. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт