Двоичная и десятичная система счисления таблица: Таблица соответствия десятеричного от 1 до 255 (decimal), двоичного (binary) и шестнадцатеричного (hexadecimal) представлений чисел. Шестнадцатиричная система счисления, двоичное счисление.

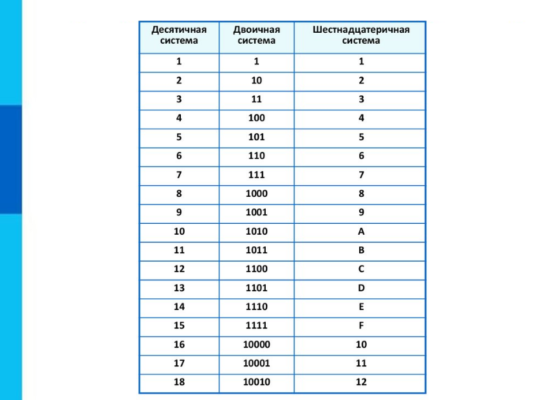
Двоичная система счисления – таблица последовательности, примеры (8 класс, информатика)

4.7

Средняя оценка: 4.7

Всего получено оценок: 226.

4.7

Средняя оценка: 4.7

Всего получено оценок: 226.

Информация в компьютере обрабатывается в цифровом формате, в виде набора нулей и единиц, поэтому все числа переводятся в двоичный вид. Система счисления, в которой для обозначения чисел применяется всего два знака, называется двоичной. Метод представления чисел в двоичном формате изучается в курсе информатики 8 класса.

Двоичная система

Система счисления, которая в своем арсенале использует только две цифры, то есть имеющая основание два, называется двоичной или бинарной. В такой системе числа заменяются последовательностью нулей и единиц. Например, десятичное число 134 в двоичном формате выглядит как 10000110. Для того чтобы понять, как это работает, следует придерживаться правил перевода чисел из одной системы счисления в другую.

Рис. 1. Двоичная система счисления.

Перевод чисел из десятичной системы счисления в двоичную

Перевод целой части десятичного числа производится путем поочередного деления частного на основание двоичной системы, то есть на два. В остатке от деления останется либо ноль, либо единица. Эти остатки записываются, начиная с последнего частного в направлении слева направо. Это и будет двоичным представлением десятичного числа.

Рассмотрим примеры.

Для перевода десятичного числа 29 в двоичный формат:

Делят 29 на два, получают 14 и в остатке 1. Остаток следует запомнить.

Затем частное от деления, то есть число 14 снова делят на два, получено 7 и в остатке 0 (ноль).

Разделим 7 на два, получим частное 3 и остаток 1.

Три делят на два, получено в частном 1 и остаток 1.

Так как последнее частное 1 меньше основания системы счисления, то есть числа 2, то последовательное деление прекращают.

Затем записывают остатки, начиная с последнего частного, и получают последовательность чисел: 11101.

Таким образом, десятичное число 29 в двоичной системе счисления равно 11101.

Еще один пример: перевод числа 37 в двоичный формат.

37 / 2 = 18 (1)

18 / 2 = 9 (0)

9 / 2 = 4 (1)

4 / 2 = 2 (0)

2 / 2 = 1 (0)

Получен результат: 100101.

Если десятичные числа расположить последовательно и сопоставить с их двоичными эквивалентами, то можно увидеть некоторую закономерность.

Таблица двоичной системы счисления

0	0	8	1000
1	01	9	1001
2	10	10	1010
3	11	11	1011
4	100	12	1100
5	101	13	1101
6	110	14	1110
7	111	15	1111

Как видно из таблицы, после 11 в числовом ряду двоичных чисел идет число 100. Так как в двоичной системе счисления только два знака 0 и 1 для обозначения числа, то происходит сдвиг разрядной сетки влево. После двузначного числа 11 идет трехзначное число 100.

Таблицей двоичной системы удобно пользоваться для перевода только небольших десятичных чисел. Ее даже рекомендуется запомнить, как таблицу умножения в математике. Но ни в коем случае нельзя по таблице переводить отдельные цифры числа в десятичный формат. Это приведет к ошибке. Например, десятичное число 15 это не 1 и 101, (вместе 1101), а все-таки 1111.

Перевод двоичных чисел в десятичную систему счисления

Обратный перевод двоичного числа в десятичную систему производится также строго по правилу перевода.

Рис. 2. Портрет Г. В. Лейбница.

Сначала нумеруются разряды двоичного числа справа налево, начиная с нулевого, а затем каждая цифра двоичного числа умножается на основание двоичной системы, то есть на два, возведенной в степень соответствующего разряда. Полученные произведения суммируются, и получается десятичное число.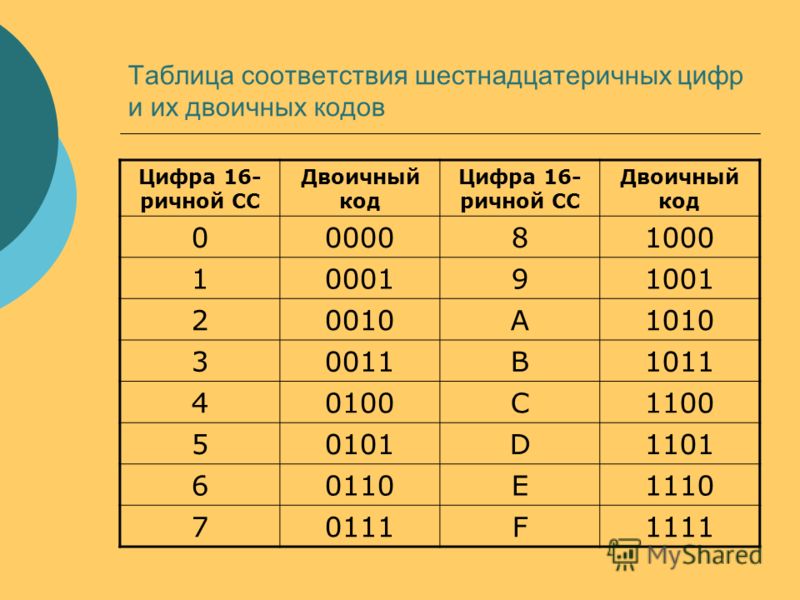

Например: двоичное число 1110001 в десятичной системе равно 113.

Нумеруем разряды числа, начиная с нуля: 1(6) 1(5) 1(4) 0(3) 0(2) 0(1) 1(0).

Каждую цифру двоичного числа умножаем на два в степени разряда и суммируем:

1*2⁶ + 1*2⁵ + 1*2⁴ +0*2³ + 0*2² + 0*2¹ + 1*2⁰ = 64 + 32 + 16 + 0 + 0 + 0 +1 = 113

Следует помнить, что любое число в степени ноль равно единице.

Двоичная система счисления была описана Готфридом Вильгельмом Лейбницем в 18 веке. На это его вдохновили гексограммы из китайской книги Перемен, которые соответствовали двоичным числам от 0 до 111111.

Рис. 3. Гексаграммы книги перемен.

Что мы узнали?

Данные в ЭВМ представляются в двоичном формате. Двоичная система счисления оперирует для записи чисел только двумя символами 0 и 1. Перевод десятичных чисел в двоичную систему и обратно производится строго по правилам.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.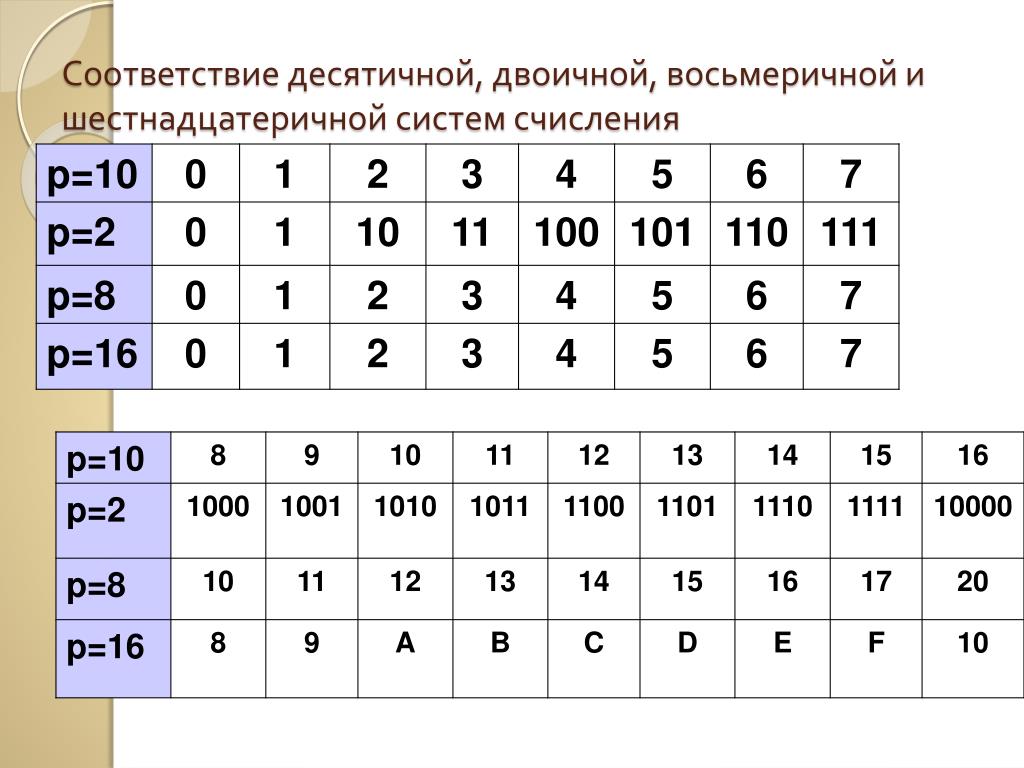

• Альбина Авезова

  5/10

Оценка статьи

4.7

Средняя оценка: 4.7

Всего получено оценок: 226.

---

А какая ваша оценка?

6.Двоичная система счисления. Двоичные таблицы сложения и умножения.

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления, числа записываются с помощью двух символов (0 и 1).

Таблица сложения

+	0	1
0	0	1
1	1	10

Пример сложения «столбиком»:

		1	↖
+		1	1	1	0
			1	0	1
	1	0	0	1	1

Таблица умножения

×	0	1
0	0	0
1	0	1

7.

Перевод числа (целого и дробного) из десятичной системы в двоичную систему. Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9 с остатком 1

9 /2 = 4 c остатком 1

4 /2 = 2 без остатка 0

2 /2 = 1 без остатка 0

1 /2 = 0 с остатком 1

Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справо налево. Т.е. нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.

Преобразование дробных десятичных чисел в двоичные

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

• Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

• Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

• В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

• Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа: .116 • 2 = 0.232 .232 • 2 = 0.464 .464 • 2 = 0.928 .928 • 2 = 1.856 .856 • 2 = 1.712 .712 • 2 = 1.424 .424 • 2 = 0.848 .848 • 2 = 1.696 .696 • 2 = 1.392 .392 • 2 = 0.784 и т. д. Получим: 206,116₁₀=11001110,0001110110₂

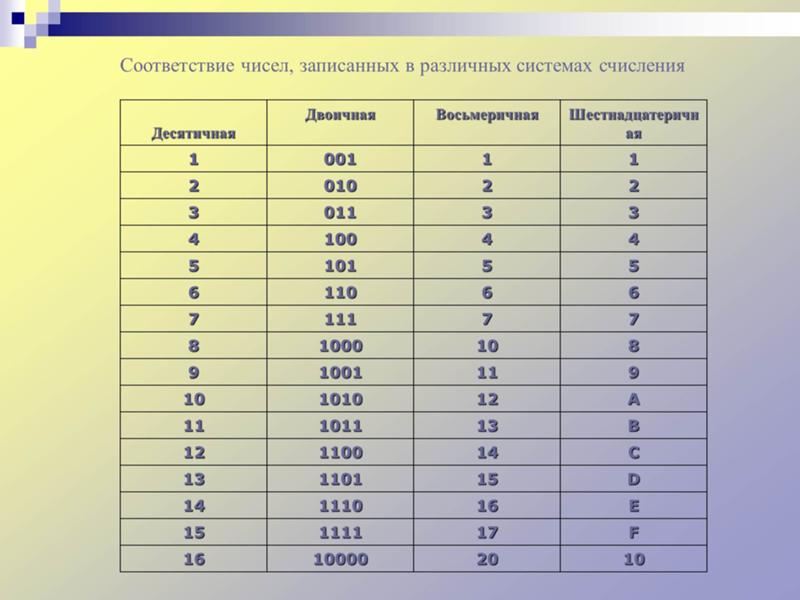
8. Восьмеричная и шестнадцатеричная системы счисления.

Шестнадцатеричная система счисления — это позиционная система счисления с основанием 16. Для записи чисел в шестнадцатеричной системе используется 10 цифр от нуля до девяти (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и латинские буквы A, B, C, D, E, F, обозначающие числа от 10 до 15.

Таким образом, все символы шестнадцатеричной системы:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Применение: шестнадцатеричная система используется в цифровой электронике и компьютерной технике, в частности в низкоуровневом программировании на языке ассемблера для различных ЭВМ.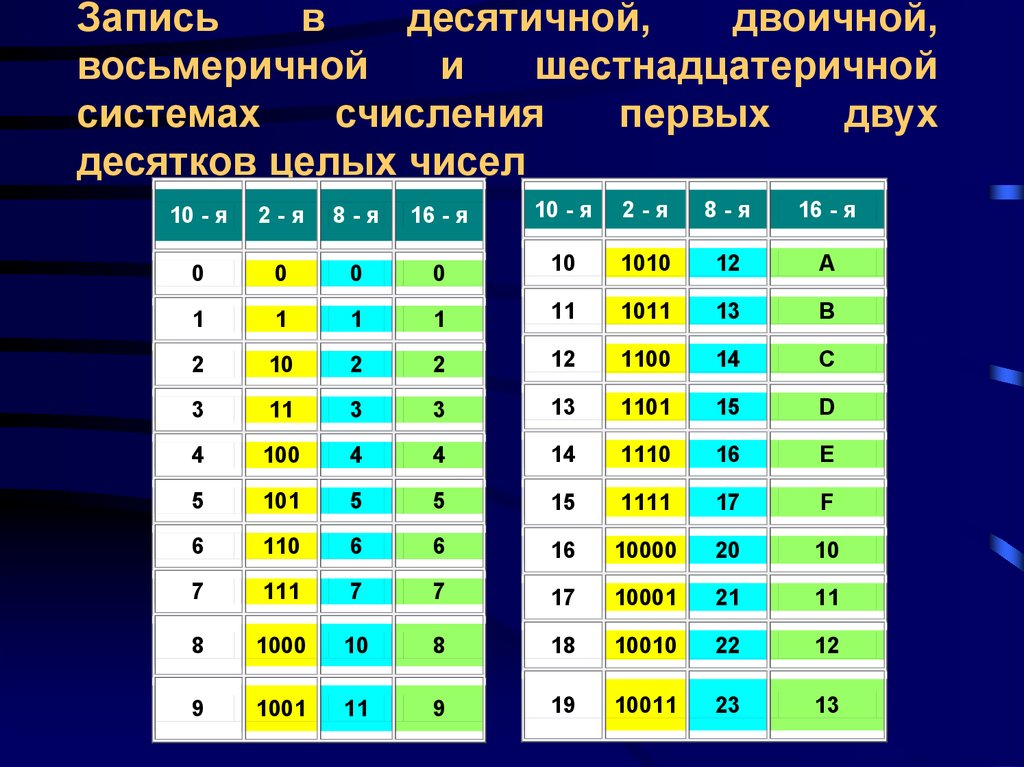

Восьмеричная система счисления — это позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе используется 8 цифр от нуля до семи (0,1,2,3,4,5,6,7). Применение: восьмеричная система наряду с двоичной и шестнадцатеричной используется в цифровой электронике и компьютерной технике, однако в настоящее время применяется редко (ранее использовалась в низкоуровневом программировании, вытеснена шестнадцатеричной).

Таблица преобразования десятичных и двоичных чисел — Исследование двоичных чисел

Автор: Rick Regan 30 июня 2009 г.

Вот таблица, которую вы можете использовать для преобразования небольших целых чисел — целых чисел от 0 до 255 — непосредственно между десятичными и двоичными числами (в качестве альтернативы использованию десятичного/двоичного преобразователя):

Целые числа от 0 до 255, в Двоичный

Декабрь	Двоичный		Декабрь	Двоичный		Декабрь	Двоичный		Декабрь	Двоичный
0	0		64	1000000		128	10000000		192	11000000
1	1		65	1000001		129	10000001		193	11000001
2	10		66	1000010		130	10000010		194	11000010
3	11		67	1000011		131	10000011		195	11000011
4	100		68	1000100		132	10000100		196	11000100
5	101		69	1000101		133	10000101		197	11000101
6	110		70	1000110		134	10000110		198	11000110
7	111		71	1000111		135	10000111		199	11000111
8	1000		72	1001000		136	10001000		200	11001000
9	1001		73	1001001		137	10001001		201	11001001
10	1010		74	1001010		138	10001010		202	11001010
11	1011		75	1001011		139	10001011		203	11001011
12	1100		76	1001100		140	10001100		204	11001100
13	1101		77	1001101		141	10001101		205	11001101
14	1110		78	1001110		142	10001110		206	11001110
15	1111		79	1001111		143	10001111		207	11001111
16	10000		80	1010000		144	10010000		208	11010000
17	10001		81	1010001		145	10010001		209	11010001
18	10010		82	1010010		146	10010010		210	11010010
19	10011		83	1010011		147	10010011		211	11010011
20	10100		84	1010100		148	10010100		212	11010100
21	10101		85	1010101		149	10010101		213	11010101
22	10110		86	1010110		150	10010110		214	11010110
23	10111		87	1010111		151	10010111		215	11010111
24	11000		88	1011000		152	10011000		216	11011000
25	11001		89	1011001		153	10011001		217	11011001
26	11010		90	1011010		154	10011010		218	11011010
27	11011		91	1011011		155	10011011		219	11011011
28	11100		92	1011100		156	10011100		220	11011100
29	11101		93	1011101		157	10011101		221	11011101
30	11110		94	1011110		158	10011110		222	11011110
31	11111		95	1011111		159	10011111		223	11011111
32	100000		96	1100000		160	10100000		224	11100000
33	100001		97	1100001		161	10100001		225	11100001
34	100010		98	1100010		162	10100010		226	11100010
35	100011		99	1100011		163	10100011		227	11100011
36	100100		100	1100100		164	10100100		228	11100100
37	100101		101	1100101		165	10100101		229	11100101
38	100110		102	1100110		166	10100110		230	11100110
39	100111		103	1100111		167	10100111		231	11100111
40	101000		104	1101000		168	10101000		232	11101000
41	101001		105	1101001		169	10101001		233	11101001
42	101010		106	1101010		170	10101010		234	11101010
43	101011		107	1101011		171	10101011		235	11101011
44	101100		108	1101100		172	10101100		236	11101100
45	101101		109	1101101		173	10101101		237	11101101
46	101110		110	1101110		174	10101110		238	11101110
47	101111		111	1101111		175	10101111		239	11101111
48	110000		112	1110000		176	10110000		240	11110000
49	110001		113	1110001		177	10110001		241	11110001
50	110010		114	1110010		178	10110010		242	11110010
51	110011		115	1110011		179	10110011		243	11110011
52	110100		116	1110100		180	10110100		244	11110100
53	110101		117	1110101		181	10110101		245	11110101
54	110110		118	1110110		182	10110110		246	11110110
55	110111		119	1110111		183	10110111		247	11110111
56	111000		120	1111000		184	10111000		248	11111000
57	111001		121	1111001		185	10111001		249	11111001
58	111010		122	1111010		186	10111010		250	11111010
59	111011		123	1111011		187	10111011		251	11111011
60	111100		124	1111100		188	10111100		252	11111100
61	111101		125	1111101		189	10111101		253	11111101
62	111110		126	1111110		190	10111110		254	11111110
63	111111		127	1111111		191	10111111		255	11111111

Имеется четыре столбца по 64 записи в каждой, всего 256 записей.

Если вы используете эти значения для хранения в компьютерном слове — например, в байте — не забудьте дополнить их начальными нулями, если это необходимо.

Категории Двоичные числа

Изучение двоичных преобразований — Учебное пособие по двоичным преобразованиям

Двоичные преобразования!

Теория чисел и принцип работы двоичных чисел.

Введение

В этом разделе учебника по двоичному коду мы рассмотрим, как легко преобразовать двоичные, десятичные, шестнадцатеричные и восьмеричные числа.

Важно уметь переводить значение из одной системы счисления в другую. Нам нужно уметь определять, когда два значения представляют одну и ту же сумму. Иногда нам становятся доступны ярлыки. Например, восьмеричные и шестнадцатеричные числа часто используются как сокращение для двоичных (ниже мы увидим, почему). Некоторые системы также будут принимать значения только в определенной базе. К счастью, переключение между системами счисления не представляет особой сложности.

В настоящее время существует множество калькуляторов, которые могут выполнять преобразования за вас. Почти каждая настольная операционная система, смартфон и планшет имеют встроенный или легко приобретаемый модуль. Совершенно нормально использовать калькулятор, но мы также должны знать, как делать это вручную. Это даст нам гораздо лучшее понимание того, что происходит на самом деле. Это понимание важно для понимания того, как работают определенные механизмы (особенно в вычислительной технике). Я рекомендую попрактиковаться на бумаге от руки, но использовать калькулятор для проверки своей работы.

Двоичный код в десятичный

Мы кратко коснулись преобразования двоичного кода в десятичный в предыдущем разделе. Мы рассмотрим это снова здесь. Процесс довольно прост.

• Каждая цифра может быть только 1 или 0.
• Если это 0, то ничего не добавляется.
• Если это 1, то мы добавляем 2 к степени этой позиции.

Самая правая цифра двоичного числа умножается на 2 в степени 0 (что равно 1). Следующая цифра умножается на 2 в степени 1 (что равно 2) и так далее.

Я считаю, что проще всего начать с крайней правой двоичной цифры, так как она всегда будет в степени 0. Если вы начнете с крайней левой цифры, вам придется выяснить, какой должна быть начальная степень (сколько цифры там минус 1) и легко ошибиться. Начиная с крайнего правого угла, наши расчеты также упрощаются, поскольку каждый раз, когда мы увеличиваем степень, мы просто удваиваем результат предыдущей степени.

• 2 ⁰ = 1
• 2 ¹ = 2
• 2 ² = 4
• 2 ³ = 8
• 2 ⁴ = 16
• ну вы поняли.

Вот простая демонстрация, которая должна прояснить процесс. Вы можете ввести свой собственный номер или нажать кнопку, чтобы сгенерировать случайное число.

Промежуточный итог в десятичной системе:

Десятичное число в двоичное

Преобразование десятичного числа в двоичное немного сложнее. Как только вы освоитесь, это будет довольно прямолинейно. Есть несколько способов преобразования десятичного числа в двоичное, но метод, который я считаю наиболее удобным, это 9.1454 повторное деление на 2 .

При повторном делении на 2 многократно делим число на 2 и записываем остаток. После того, как вы сделали это, вплоть до 0, вы читаете оставшиеся цифры снизу вверх, и у вас есть двоичное число. Нижеприведенный пример проиллюстрирует это. Результат деления на 2 указан слева, а остаток — справа.

Результат в двоичном формате:

Распространенной ошибкой является чтение остатков в неправильном направлении. Помните: разделить на , затем прочитать .

Еще одна распространенная ошибка — делить до 1, а затем не выполнить окончательное деление. Не забывайте всегда делить до 0.

Помните, что двоичное число может быть нечетным только в том случае, если самая правая цифра равна 1. Эту характеристику можно использовать для быстрой проверки того, сделали ли вы глупая ошибка (для преобразования в любом случае).

Приведенный выше совет не гарантирует, что ответ правильный, но если он не подходит, вы точно знаете, что допустили ошибку.

Шестнадцатеричное в двоичное

Преобразование из двоичного в шестнадцатеричное и из шестнадцатеричного в двоичное на самом деле очень просто. Это связано с тем, что шестнадцатеричное число — это основание 16, которое на самом деле равно 2 ⁴ .

Таким образом, чтобы преобразовать шестнадцатеричное число в двоичное, все, что нам нужно сделать, это заменить каждую шестнадцатеричную цифру эквивалентной ей двоичной. В следующих примерах может помочь обращение к справочной таблице ниже по странице.

Например, если у нас есть шестнадцатеричное значение 75C , затем он может быть преобразован в двоичный файл следующим образом:
(см. Справочную таблицу, если это необходимо, при необходимости.)

7
0111

5
0101

C
1100

РЕЗУЛЬТАТ: 111011100

. Каждая шестнадцатеричная цифра (кроме крайней левой) должна быть заменена 4 двоичными цифрами. Если для цифры (например, 5 выше) обычно требуется только 3 двоичных разряда, мы должны соответственно дополнить ее нулями. Распространенная ошибка — забывать об этом.

Двоичный код в шестнадцатеричный

Чтобы преобразовать двоичный код в шестнадцатеричный, достаточно выполнить описанный выше процесс в обратном порядке. Разделите двоичное число на части по 4 (начиная с крайнего правого угла), затем замените каждую часть соответствующим шестнадцатеричным значением.

Восьмеричное число в двоичное

Преобразование восьмеричного числа в двоичное аналогично процессу преобразования шестнадцатеричного. Восьмеричное число — это основание 8, которое равно 2 ³ , поэтому вместо того, чтобы разбивать двоичное число на части по 4, мы разбиваем на части по 3.

В этом примере мы сведем восьмиугольное число 3625 в двоичный файл:

3
011

6
110

2
010

5
101

Результат: 1111001011011

. Подобно шестнадцатеричному, преобразование из двоичного в восьмеричное — это просто обратный процесс. Опять же, не забудьте разделить на части по 3, начиная с крайнего правого.

Шестнадцатеричное и восьмеричное в десятичное

Если вам нужно преобразовать десятичное в шестнадцатеричное или восьмеричное, можно использовать методы, перечисленные для двоичного, но заменив 2 на 16 или 8. Это будет работать, но если вы похожи на меня, вы не слишком хорошо, когда дело доходит до ваших таблиц умножения на 16. Лучшим подходом является использование двоичного кода в качестве промежуточного звена. Легко преобразовать шестнадцатеричное или восьмеричное число в двоичное, а затем несложно перейти от двоичного к десятичному.

Это немного больше работает, но 2 простых шага, как правило, намного лучше, чем 1 сложный шаг.

Справочная таблица

Вот справочная таблица для различных систем счисления. Это полезно для преобразования между двоичным и шестнадцатеричным или восьмеричным (и наоборот).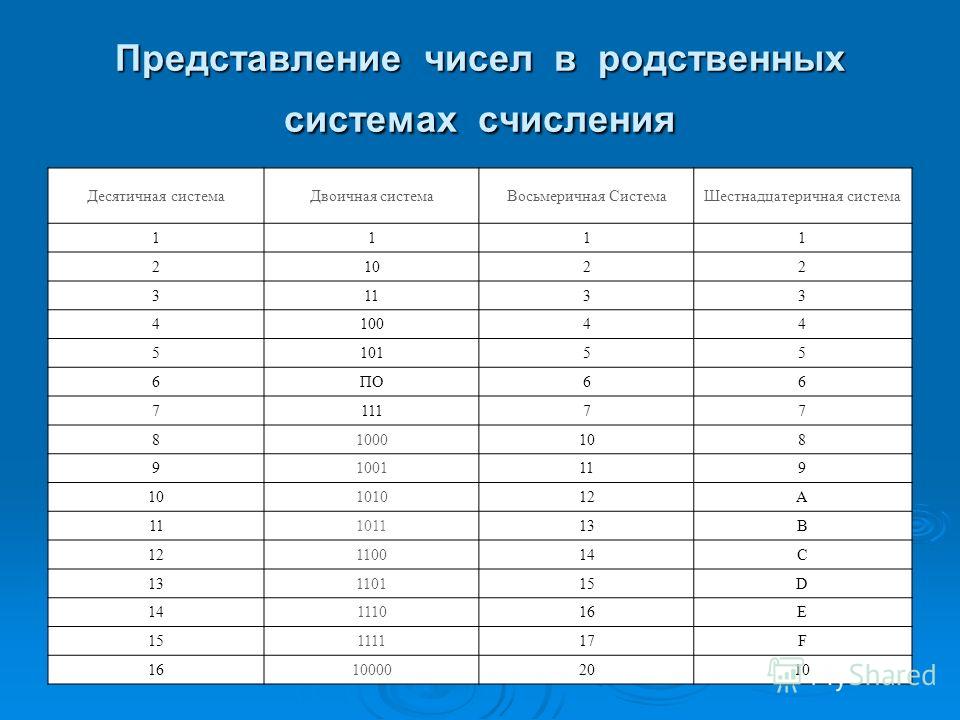

Десятичный	Двоичный	Окталь	Шестнадцатеричный
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	А
11	1011	13	Б
12	1100	14	С
13	1101	15	Д
14	1110	16	Е
15	1111	17	Ф

Вы заметите, что в двоичном файле есть шаблон.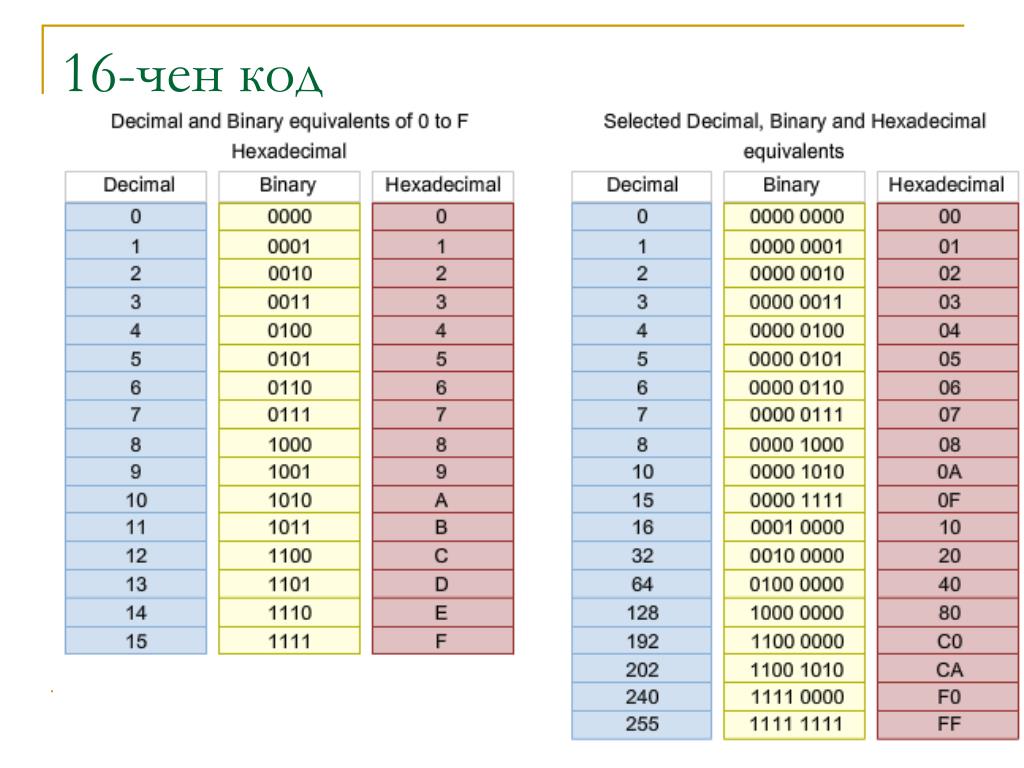 Крайний правый столбец чередуется между 0 и единицей. Следующий столбец делает то же самое, но по 2 за раз. Третий столбец делает то же самое, но по 4 за раз. Крайний левый столбец делает то же самое, но по 8 за раз. Этот шаблон упрощает проверку правильности написания.

Если вы сдаете экзамен по двоичному коду, вам часто не разрешают сдавать материал, но ничто не мешает вам самостоятельно нарисовать эту таблицу после начала экзамена. Это может быть хорошим справочным материалом, особенно для конверсий, которые мы рассмотрим в следующем разделе.

Совет

Это может быть немного сложно уложить в голове. Если вы обнаружите, что чтение материала немного утомляет вашу голову, вот что я предлагаю:

• Выполните несколько заданий, приведенных ниже, на бумаге. Изучение двоичного кода похоже на езду на велосипеде. Лучший способ — просто сделать это.
• Оставьте это на день или два, затем вернитесь и попробуйте еще раз.

Занятия

Итак, лучший способ изучить этот материал — это попрактиковаться, и сейчас мы научим вас делать именно это.