Электродинамика и MATLAB
Электродинамика и MATLABДля правильного отражения решений задач, сделанных с помощью пакета Mathematica НЕОБХОДИМО:
- Установить на своем локальном компьютере бесплатный проигрыватель CDF-файлов, который можно скачать здесь.
- Для правильного выполнения задач, подготовленных с помощью пакета Mathematica, необходимо войти на этот сайт с помощью браузера Internet Explorer и запустить выбранную задачу.
- Если используется другой браузер, то после запуска задачи система предложит сохранить соответствующий файл модели *.CDF на своем компьютере, а потом запустить его off-line.
Скин
Магнитное поле в полом цилиндре параллельно оси.
Демонстрация: «Магнитное поле в полом цилиндре параллельно оси»Магнитное поле в цилиндре перпендикулярно оси.
Демонстрация: «Магнитное поле в цилиндре перпендикулярно оси»Нестационарный скин-эффект.

Демонстрация: «Нестационарный скин-эффект»Магнитное поле в пластине.
Демонстрация: «Магнитное поле в пластине»
Математика
ЭПР и ЯМР
Электростатика
Генерация излучения
Излучение антенн
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача о распределении излучения антенн. Задача рисует трехмерное изображение диаграммы направленности.Излучение вектора Герца
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача об излучении электромагнитных волн точечным диполем.Излучение релятивистской частицы
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача об излучении релятивисткой частицы. Задача рисует трехмерное изображение диаграммы направленности.
Другие задачи
Измерение искажений магнитного поля эллипсоидом
Задача об искажении магнитного поля Земли эллипсоидом.
Использование Matlab Web сервера для расчетов на удаленном сервере.
Движение электрона в электромагнитной волне
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача о движении электрона в поле сильной электромагнитной волны.Trivelpiece-Gould mode
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача о Распространении TG волны с нулевым азимутальным числом в длинном облаке заряженной плазмы.
Математика
График функции «синус»
Построение движущегося графика функции «синус», зависящей от временной и пространственной координаты.График функции «Присоединенные полиномы Лежандра»
Построение зависимости полинома и его квадрата от угла.
Электростатика и магнитостатика
Электростатическое поле двух зарядов
Использование Matlab Web сервера для расчетов на удаленном сервере. Карта электростатического поля (силовые линии) 2-х зарядов.
Электростатическое поле точечных зарядов
Использование Matlab Web сервера для расчетов на удаленном сервере. Карта электростатических полей произвольного числа точечных зарядов.
Квазистационарные явления
Поля и токи прямоугольного резонатора
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача о распределении зарядов и токов в стенках прямоугольного резонатора. Программа создает трехмерное изображение, в котором стрелками показано направление токов в стенках разонатора, а цветом — изолинии плотности заряда.Скин-эффект в полом цилиндре
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача о скин-эффекте в полом цилиндре.Плоский нестационарный скин-слой.
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача о проникновении импульса поля произвольной формы в металл.Скин-эффект в полупространстве
Анимированный график проникновения магнитного гармонического поля в полупространствоДвижение волнового пакета в среде с дисперсией
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача о движении волнового пакета в среде с дисперсией.
Задача о движении волнового пакета в среде с дисперсией.
Задачи дифракции
Дифракция волны на круглой таблетке
Использование Matlab Web сервера для расчетов на удаленном сервере. Задача о дифракции плоской волны на круглой таблетке, изменяющей фазу и частично поглощающей падающее излучение.
См. также
Руководство для преподавателей, желающих создать свои задачи-демонстрации
Во всех задачах web-интерфейс сгенерирован из XML-описателя задачи,
используется кэширование сгенерированных рисунков для ускорения работы.
© 2002—2022 ФизФак НГУ
Байесовский ниндзя / Хабр
Coderik однажды отметил: «Фильтра Калмана много не бывает». Так же можно сказать и о теореме Байеса, ведь это с одной стороны так просто, но с другой стороны так сложно осмыслить её глубину.
На просторах YouTube есть замечательный канал Student Dave, однако последнее видео опубликовано шесть лет назад. На канале представлены обучающие видео, в которых автор рассказывает очень простым языком сложные вещи: теорему Байеса, фильтр Калмана и пр. Свой рассказ студент Дейв дополняет примером расчета в matlab.
Однажды мне очень помог его видео урок под названием “Итеративная байесовская оценка” (на канале ему соответствует плейлист “Iterative bayesian estimation: with MATLAB”). Я захотел, чтобы каждый мог познакомиться с объяснениями Дейва, но к сожалению проект не поддерживается. Сам Дейв не выходит на связь. Добавить перевод к видео нельзя, так как это должен инициировать сам автор. Обращение в youtube не дало результата, поэтому я решил описать материал в статье на русском языке и опубликовать там, где его больше всего оценят. Материал очень сильно переработан и дополнен, так как он прошёл через мое субъективное восприятие, поэтому выложить его как перевод было бы неуместно.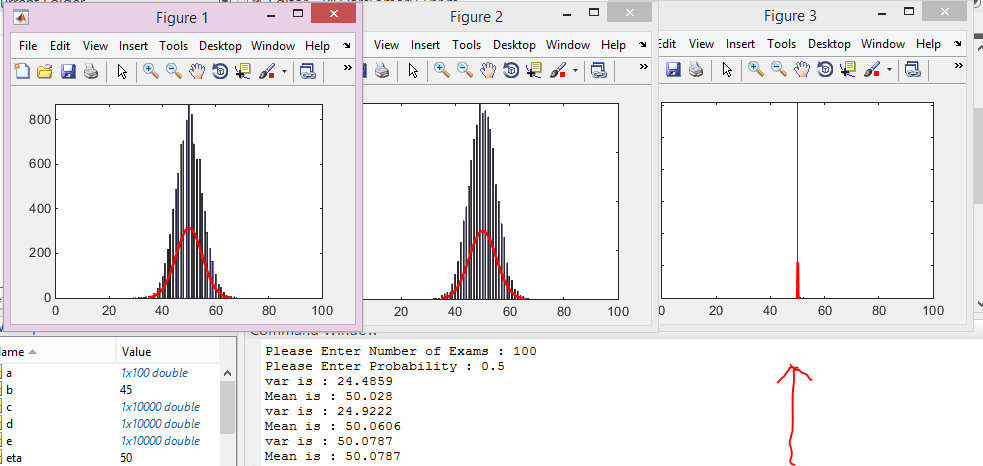
Итак, если вы хотите глубже осмыслить тему теоремы Байеса, добро пожаловать.
Для того чтобы проиллюстрировать мощь теоремы Байеса для непрерывных случайных величин, Дейв предлагает рассмотреть задачу “байесовского ниндзя”. Суть задачи в следующем.
Есть ниндзя-математик, который очень не любит перепелов. Перепел прячется в кустах, а ниндзя сидит на дереве рядом. Ниндзя может одним решительным прыжком на перепела сразить его, но он не знает где точно находится перепел. При этом перепел и издает время от времени звук. По звуку ниндзя может определить местоположение перепела, но очень неточно. Теорема Байеса позволяет ниндзя по серии криков перепела определить местоположение перепела все точнее и точнее. И в какой-то момент количество криков позволит ниндзя нанести сокрушительный удар.
Спойлер
Если вы ознакомитесь с видео на канале, то узнаете, что ниндзя так и не удалось удачно спрыгнуть на перепела, но это уже другая история.
Ниндзя-математик видит кусты как ограниченную область по оси . Истинное положение перепелки пока неизвестно. Вероятность в каждой точке области поиска одна и та же. Априорное распределение равномерное.
В процессе наблюдения (ниндзя славились своей выдержкой) были получены замеров (гипотез) местонахождения.
К тому же ниндзя знал дисперсию измерения положения перепелки по крику .
Благодаря теореме Байеса есть возможность из равномерного распределения получить нормальное, да и с дисперсией куда меньшей чем дисперсия измерения.
где — уточненное распределение;
— распределение известное до опыта;
— распределение модели измерения (правдоподобие ).
Дисперсия распределения модели измерения известна ниндзя заранее. За математическое ожидание принимается точка пространства, а за случайную величину замер (вероятность гипотезы о том, что в этой точке пространства сидит перепелка при получении замера):
где — функция плотности нормального распределения;
— стандартное отклонение измерения;
— измеренная величина.

Данную формулу необходимо повторить для серии опытов (), каждый раз подставляя вместо априорного распределение апостериорное, которое было получено при предыдущем опыте.
На анимации ниже видно как меняется распределение от оценки к оценке.
Код по ссылке.
Как только шесть уменьшатся до размера ноги ниндзя, он сможет нанести свой сокрушительный удар с вероятностью успеха в 99,7 %.
Можно не читать
Так-то именно двумерный случай рассмотрен Дейвом, в отличие от одномерного случая.
Рассмотрим более реальную задачу. Ведь ниндзя всё таки смотрит на кусты сверху-вниз.
Истинное положение перепелки . Дисперсии (ковариационная матрица) и количество криков те же.
До опыта (априори) вероятность того, что перепелка будет в любом месте кустов одинакова. Априорное распределение равномерное.
Формула Байеса для непрерывных многомерных случайных величин примет вид:
где — вектор координат вида ;
— уточненное распределение;
— распределение известное до опыта;
— распределение модели измерения.
Распределение модели измерения:
где — ковариационная матрица;
— результат замера вида .
На анимации ниже видно, как меняется распределение от опыта к опыту.
Код по ссылке.
Таким образом видно, как результаты опыта влияют на априорное распределение. Если правильно пользоваться измерениями, можно получать хорошую точность.
Но не проще ли просто найти среднее из всех замеров и таким образом сделать оценку местоположения перепела? Конечно. Данный пример лишь наглядный пример теоремы Байеса для непрерывных случайных величин. Цель статьи в том, чтобы утрясти теорию.
Заходите на канал Дейва в течении этих недель самоизоляции. Всем добра.
Среднее значениеF и дисперсия — MathWorks 中国
Перейти к содержимомуОсновное содержание
F среднее значение и дисперсия
Синтаксис
[M,V] = fstat(V1,V2)
Описание
9000 2 [М,В] = fстат(В1,В2) возвращает среднее значение и
дисперсия распределения F со степенями свободы в числителе V1 и знаменатель степеней свободы V2 .
V1 и V2 могут быть векторами, матрицами или
многомерные массивы, которые имеют одинаковый размер, который также является размером М и В . Скалярный ввод для V1 или V2 расширяется до константных массивов
с теми же размерами, что и другой вход. В1 и V2 Параметры должны содержать действительные положительные значения.Среднее значение распределения F для значений из ν 2 больше чем 2 равно
ν2ν2−2
Дисперсия распределения F для значений из ν 2 больше чем 4 равно
2ν22(ν1+ν2−2)ν1(ν2−2)2(ν2−4)
Среднее значение распределения F не определено если ν 2 меньше 3. Дисперсия не определена для ν 2 меньше чем 5.
Примеры
fstat возвращает NaN , когда
среднее значение и дисперсия не определены.
[м, об] = fstat(1:5,1:5)
м =
NaN NaN 3,0000 2,0000 1,6667
v =
NaN NaN NaN NaN 8.8889 Расширенные возможности
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Массивы графических процессоров
Ускорьте код, запустив его на графическом процессоре (GPU) с помощью Parallel Computing Toolbox™.
Эта функция полностью поддерживает массивы GPU. Для получения дополнительной информации см. Запуск функций MATLAB на графическом процессоре (Parallel Computing Toolbox).
История версий
Представлено до R2006a
См. также
fpdf | ФКДФ | финв | frnd
Темы
- F Распространение
Выберите веб-сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Америка
- Америка Латина (Испания)
- Канада (английский)
- США (английский)
Европа
- Бельгия (английский)
- Дания (английский)
- Германия (немецкий)
- Испания (Испания)
- Финляндия (английский)
- Франция (французский)
- Ирландия (английский)
- Италия (итальяно)
- Люксембург (английский)
- Нидерланды (английский)
- Норвегия (английский)
- Австрия (Германия)
- Португалия (английский)
- Швеция (английский)
- Швейцария
- Немецкий
- Английский
- Французский
- Великобритания (английский)
Азиатско-Тихоокеанский регион
- Австралия (английский)
- Индия (английский)
- Новая Зеландия (английский)
- 中国
- 简体中文
- Английский
- 日本 (日本語)
- 한국 (한국어)
Обратитесь в местный офис
- 用版
- 用版
- 产品更新
- 产品更新
| $F_X(x)$ | $=P(X \leq x)$ |
| $=P( \sigma Z+\mu \leq x) \hspace{20pt} \big(\textrm{где}Z \sim N(0,1)\big)$ | |
| $=P\left(Z \leq \frac{x-\mu}{\sigma}\right)$ | |
$=\Phi\left(\frac{x-\mu}{\sigma}\right). |

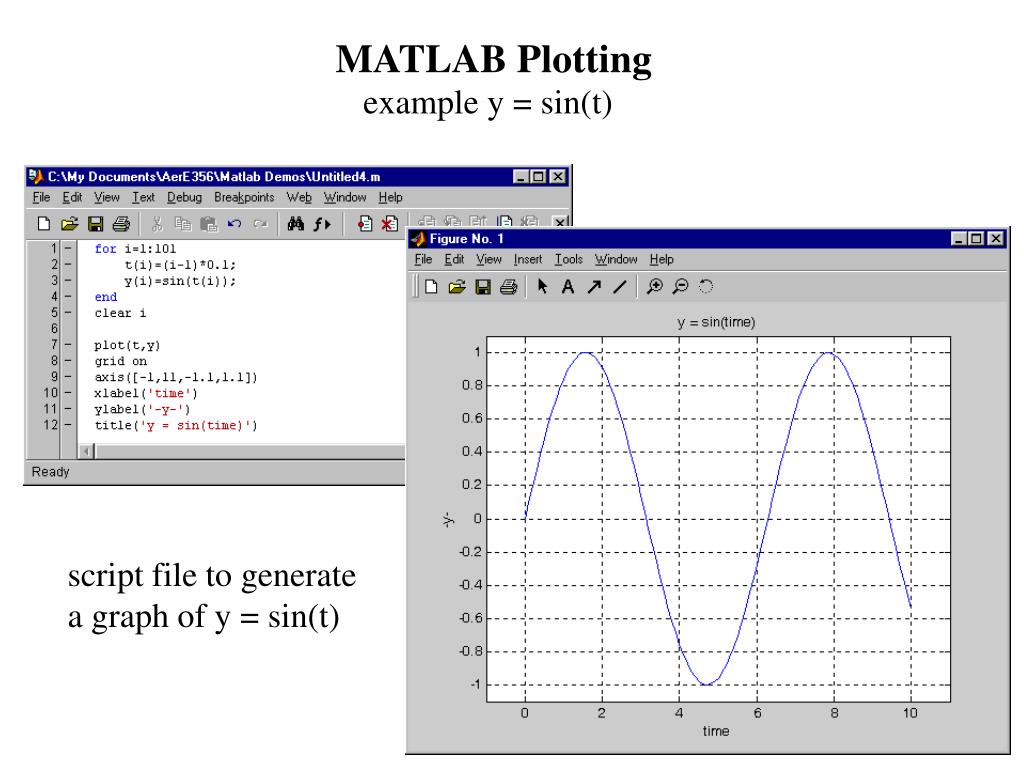 Одна из главных причин
ибо это Центральная предельная теорема (ЦПТ), которую мы обсудим позже в этой книге. Чтобы дать вам
идея, CLT утверждает, что если вы добавите большое количество случайных величин, распределение суммы
будет примерно нормальным при определенных условиях. Важность этого результата состоит в том, что
что многие случайные величины в реальной жизни могут быть выражены как сумма большого числа случайных величин
и, согласно CLT, мы можем утверждать, что распределение суммы должно быть нормальным. CLT является одним из самых
важные результаты в вероятности, и мы обсудим это позже. Здесь мы введем обычный случайный
переменные. 92}{2}\right\}, \hspace{20pt} \textrm{for all } z \in \mathbb{R}.$$
Одна из главных причин
ибо это Центральная предельная теорема (ЦПТ), которую мы обсудим позже в этой книге. Чтобы дать вам
идея, CLT утверждает, что если вы добавите большое количество случайных величин, распределение суммы
будет примерно нормальным при определенных условиях. Важность этого результата состоит в том, что
что многие случайные величины в реальной жизни могут быть выражены как сумма большого числа случайных величин
и, согласно CLT, мы можем утверждать, что распределение суммы должно быть нормальным. CLT является одним из самых
важные результаты в вероятности, и мы обсудим это позже. Здесь мы введем обычный случайный
переменные. 92}{2}\right\}, \hspace{20pt} \textrm{for all } z \in \mathbb{R}.$$