Дифференциальные уравнения matlab: Решение систем обыкновенных дифференциальных уравнений в среде MATLAB. Часть 1

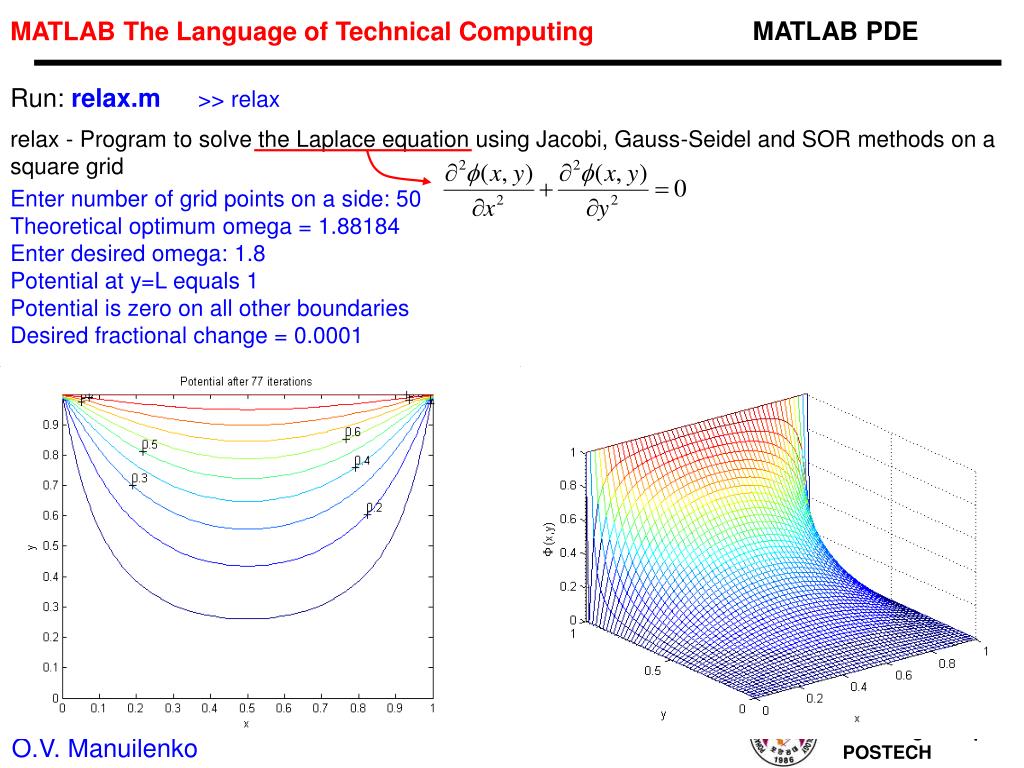
Решение систем обыкновенных дифференциальных уравнений в среде MATLAB. Часть 1

В среде MATLAB можно решать системы диффуров с начальными условиями, краевые задачи, а также решать дифференциальные уравнения в частных производных с помощью инструмента PDE toolbox.

В данном обзоре речь пойдет лишь о системах дифференциальных уравнений с начальными условиями, то есть о задаче Коши. В англоязычной литературе это называется Initial Value Problem.

Рассмотрим:

• каким образом записывать системы диффуров
• как задать начальные условия
• временной интервал
• какой получать результат решения для дальнего использования

Решать системы обыкновенных дифференциальных уравнений можно как в MATLAB, так и в Simulink. 

В первую очередь, следует определиться, использовать для решения Matlab и его текстовый редактор, или Simulink, где те же системы дифференциальных уравнений могут быть записаны в виде функциональных блоков.

Выбор ваш должен зависеть от задачи. Если Вы, например, хотите смоделировать какой-либо объект управления, описываемый системой диффуров, то в данном случае имеет смысл использовать именно Simulink, так как Вам, впоследствии, понадобиться синтез, например, системы управления, и Simulink подойдет здесь как нельзя лучше.

А вот если у Вас, например, есть необходимость решать системы диффуров с большим количеством уравнений и неизвестных, или специфика Вашей задачи требует особой и специальной настройки численного метода, а также если вы хотите использовать решение диффура в составе других скриптов MATLAB, то Вам имеет смысл решать дифференциальные уравнения способом, о котором пойдёт речь в этом обзоре.

Рассмотрим синтаксис решателей matlab.В качестве аргументов следует подать правую часть системы в виде MATLAB-функции.

На рисунке показан требуемый вид системы, когда выражены старшие производные.

 

Системы, чей вид отличается от требуемого, следует преобразовать к таковому.

Если функция простая, то её можно записать прямо в поле аргумента, однако, когда речь идёт о системах уравнений, имеет смысл записывать систему уравнений в виде отдельной функции, в том числе и в виде отдельного м-файла.

Об этом мы поговорим чуть позже и на конкретном примере. 

Также подается интервал времени, на котором будет найдено решение. Интервал задаётся строкой из двух чисел: начальной величины независимого аргумента t и его конечного значения.

Далее задаются начальные условия. Значения всех неизвестных искомых переменных в начале расчёта задаются в виде столбца соответствующей размерности.

Далее, при необходимости, задаются опции. Вот тут и раскрываются широкие возможности MATLAB по настройке решателя. Помимо управления точностью и величиной шага, имеется возможность обрабатывать данные в процессе вычисления, а также выполнять скрипты по завершению вычисления. Но ещё более полезным является опция отслеживания событий по условию, более подробно поговорим об этом дальше. Также есть другие специальные опции, которые могут быть использованы при решении определённых типов систем.

Вы могли заметить, что название функции — odeXY – это обозначение для всех решателей, которых всего 8 штук. В данном ролике мы пользоваться решателем ode45, соответствующего численному по методу Дормана-Принса 4(5). Этого решателя достаточно для подавляющего большинства задач. Остальные решатели будут подробно рассмотрены в приложении к задачам соответствующих типов позже.

Перейдем к примерам.

Рассмотрим 2 примера:

• решение дифференциального уравнения первого порядка.
• решение системы двух дифференциальных уравнений второго порядка.

В качестве уравнение первого порядка рассмотрим логистическое уравнение Ферхюльста, которое описывает динамику численности популяции. Суть уравнения такова: скорость прироста населения y пропорциональна количеству населения, однако лимитирована максимальной численностью популяции.

Забавный факт: Ферхюльст назвал это уравнение логистическим, и никто до сих пор не знает почему, ибо сам Ферхюльст об этом никому не рассказал.

Решение этого дифференциального уравнения выглядит следующим образом.

Пишем функцию в явном виде, задаём интервал расчёта и записываем начальное условие.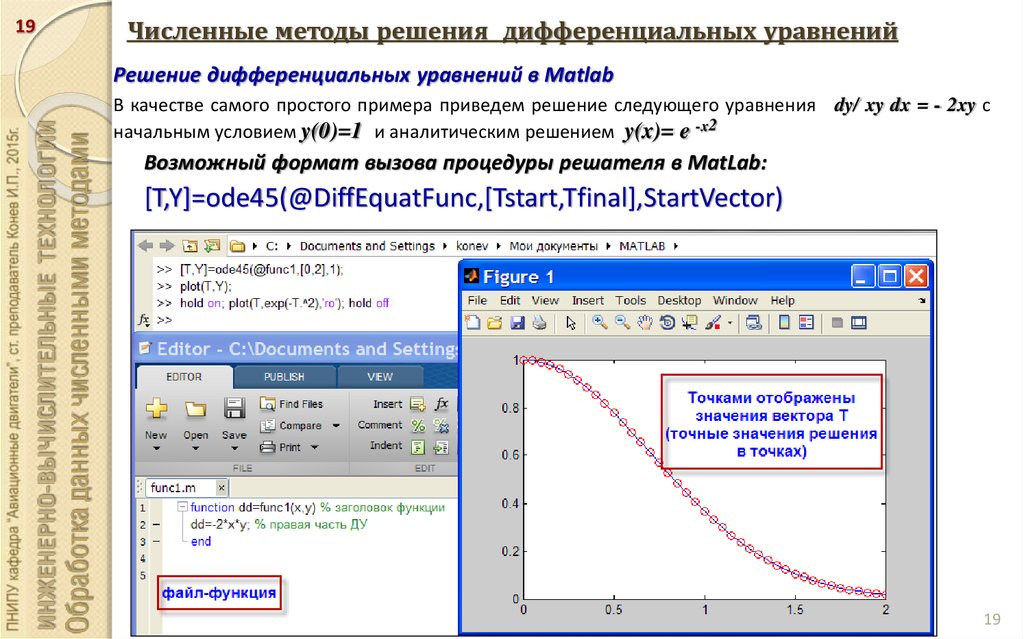 Пару слов о записи функции подобным образом. Знак собаки в матлабе является оператором создания функции соответствующих переменных. Вы задаёте аргументы функции и саму функцию через пробел, как показано на рисунке.

Перейдем в окно MATLABа и посмотрим, как это выглядит.

Так выглядит скрипт:

Так выглядит график решения дифференциального уравнения:

В качестве примера решения системы, состоящей из двух дифференциальных уравнений второго порядка, рассмотрим шарик, подвешенный на пружине, который ещё и тормозит о воздух.

Уравнения показаны на рисунке. Но вид системы отличается от требуемого, в том числе потому, что в нём присутствуют вторые производные. Для приведения системы в требуемый вид выполним 2 простых шага:

Первое: следует заменить переменные соответствующим образом. Теперь у нас 4 неизвестных. Далее следует преобразовать уравнение с учетом замены. Таким образом, мы имеем систему из четырёх дифференциальных уравнений первого порядка.

Настало время её записать.

Итак, мы имеем систему, параметры, интервал времени и начальные условия. Решим же эту задачу скорее.

В отличие от предыдущего примера, систему четырех уравнений проблематично записать в поле аргумента. Поэтому всю систему будем записывать в отдельную функцию.

Эту функцию можно располагать как в самом скрипте решения в самом его конце, так и в виде отдельного m-файла.

На выходе функция должна представлять собой вектор-столбец, который записывается перечислением компонент через точку запятой как показано на рисунке.

Теперь рассмотрим скрипт самого решения.

На этот раз запишем интервал и начальные условия в виде переменных MATLAB. Интервал, соответственно, в виде строки, а начальные условия – в виде столбца длинной 4.

Сообразно с уже разобранным ранее синтаксисом укажем функцию pendulum_np, интервал времени и начальные условия.

Перейдем теперь в окно MATLAB и посмотрим решение.

Так выглядит скрипт:

Часть 2

Запускаем скрипт и получаем графики:

Зачастую хочется, чтобы одну и ту же систему можно было бы решать с разными параметрами, и при этом не менять их в теле самой функции.

И это можно, и даже нужно осуществлять.

На рисунке показана функция MATLAB, которая соответствует движению подвешенного на пружине шара, однако можно заметить, что эта функция теперь имеет на 5 аргументов больше.

Параметры задаются в скрипте, а при вызове функции мы обращаемся к уже известному оператору-собаке, которая превращает функцию семи переменных pendulum_n в функцию двух переменных t и X. Вот и всё.

Я вам очень рекомендую разобраться с тем, как работает оператор-собака. В хелпе он называется function-handle. Разобравшись с ним Вам будет работать в среде MATLAB ещё проще и ещё приятнее.

Вывод: не так страшно решать диффуры

Под конец стоит сказать какие вообще системы дифференциальных уравнений матлаб может решать, а может он решать системы практически любых типов. 

Их можно, с одной стороны, разделить по степени жёсткости, а с другой стороны, по структуре самой системы.

Когда уравнения представляют поведение системы, которая содержит ряд быстрых и медленных реакций, то такую систему уравнения можно назвать жесткой.   Для жестких задач явные численные методы работают плохо, или не работают вовсе. Примером жесткой задачи может являться протекание тока через клеточную мембрану. На самом деле, чёткого разделения между жесткими и нежёсткими системами не существует. Степень жесткости системы формально определяется через собственные значения матрицы Якоби, но давайте не будем закапываться. 

Видеообзор по теме решения систем Д/У доступен по ссылке.  

7.2.6. Средства Matlab для решения систем обыкновенных дифференциальных уравнений

Рассмотренные в работе 6 программы ode34 и ode45 имеют векторную реализацию, т.е. предназначены для решения систем обыкновенных дифференциальных уравнений 1-го порядка (7.1). Уточним описания этих программ с учетом их векторного использования. При этом будем использовать обобщенное имя

solver (решатель), понимая под ним ode34 или ode45.

[T,y]=solver(‘f’, tspan, y0) интегрирует векторное уравнение вида

от t0 до tfinal с начальными условиями y0. Здесь ‘f’ – строка, содержащая имя

m-файла-функции, реализующей правую часть уравнения – функцию

оформленную в виде function v=f(t,y).

Функция f(t,y) должна возвращать вектор-столбец v. tspan – массив из двух

элементов, tspan=[t0, tfinal]. T – вектор значений аргумента t , при которых

вычисляются значения функции y(t) . y – матрица значений функции y(t), каждая строка которой содержит значения функций

в фиксированный момент времени. Для получения решения в конкретных точках

t0, t1,…, tfinal (расположенных в порядке увеличения или уменьшения значений) можно использовать

tspan=[t0, t1, …, tfinal].

[T,y]=solver(‘f’, tspan, y0, options) дает решение, подобное описанному выше, но с параметрами, определяемыми значениями аргумента options, созданного функцией odeset. Обычно используемые опции включают допустимое значение относительной погрешности RelTol (10^–3 по умолчанию) и допустимое значение абсолютной погрешности AbsTol (10^–6 по умолчанию).

В данном пособии использование функции odeset не рассматривается, и она не

описывается.

[T,y]=solver(‘f‘, tspan, y0, options, p1, p2,…) дает решение, подобное описанному выше, помещая дополнительные параметры p1, p2,…

в m-файл f всякий раз, когда он используется. При этом файл f должен быть оформлен в виде

function v=f(t, y, flag, p1, p2,…).

Если никакие опции не установлены, то необходимо использовать options=[].

При обращении к функции solver без указания выходных параметров по умолчанию вызывается выходная функция odeplot для построения графиков

полученного решения.

Пример. Пусть требуется найти решение дифференциального уравнения

удовлетворяющее начальным условиям

Обозначив вместо этого уравнения 2-го порядка

мы получим следующую систему из двух уравнений 1-го порядка:

с начальными условиями

Для численного решения этой системы дифференциальных уравнений составим m-файл-функцию, реализующую правую часть системы:

и m-файл-сценарий

7. 3.1. Из табл. 7.1 в соответствии с номером своей бригады взять дифференциальное уравнение и представить его в виде системы дифференциальных уравнений 1-го порядка.

7.3.2. Написать m-файл-сценарий для решения данного дифференциального

уравнения изложенными выше методами. Получить также решение с помощью

функций ode34 и ode45. Вывести графики полученных решений.

Таблица 7.1

Дифференциальные уравнения 2-го порядка для индивидуальных заданий

Дифференциальные уравнения с Matlab, 3-е издание

Выбранный тип: Электронная книга

112,50 $

Брайан Р. Хант, Рональд Л. Липсман, Джон Э. Осборн, Джонатан М. Розенберг

ISBN: 978-1-119-23114-1 январь 2019 г. 304 страницы

• Электронная книга

  Всего от 39 долларов США

• Печать

  Всего от 53,95 долл. США

Электронная книга com are delivered on the VitalSource platform. To download and read them, users must install the VitalSource Bookshelf Software.</li><li>E-books have DRM protection on them, which means only the person who purchases and downloads the e-book can access it.</li><li>E-books are non-returnable and non-refundable.</li><li>To learn more about our e-books, please refer to our&nbsp;<a href="https://www.wiley.com/wiley-ebooks" target="_blank">FAQ</a>.</li></ul>» data-original-title=»» title=»»/>

112,50 $

Мягкая обложка

$53,95

Загрузить рекламный проспект

Загрузить рекламный проспект

Загрузить флаер продукта для загрузки PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание.

Предпочитаете электронные версии своих учебников?

Получите мгновенный доступ к электронной книге Wiley. Купить или взять напрокат электронные книги на срок до 150 дней.

Описание

Дополнительный текст, который может обогатить и улучшить любой первый курс по обыкновенным дифференциальным уравнениям

Это дополнение помогает преподавателям перейти к более раннему использованию численных и геометрических методов, уделять больше внимания системам (включая нелинейные) и активизировать обсуждение как преимущества, так и возможные ловушки в численном решении ОДУ. Предоставляя введение в программное обеспечение, интегрированное с соответствующей математикой, Дифференциальные уравнения с MATLAB могут прекрасно дополнять и улучшать другие тексты от Wiley.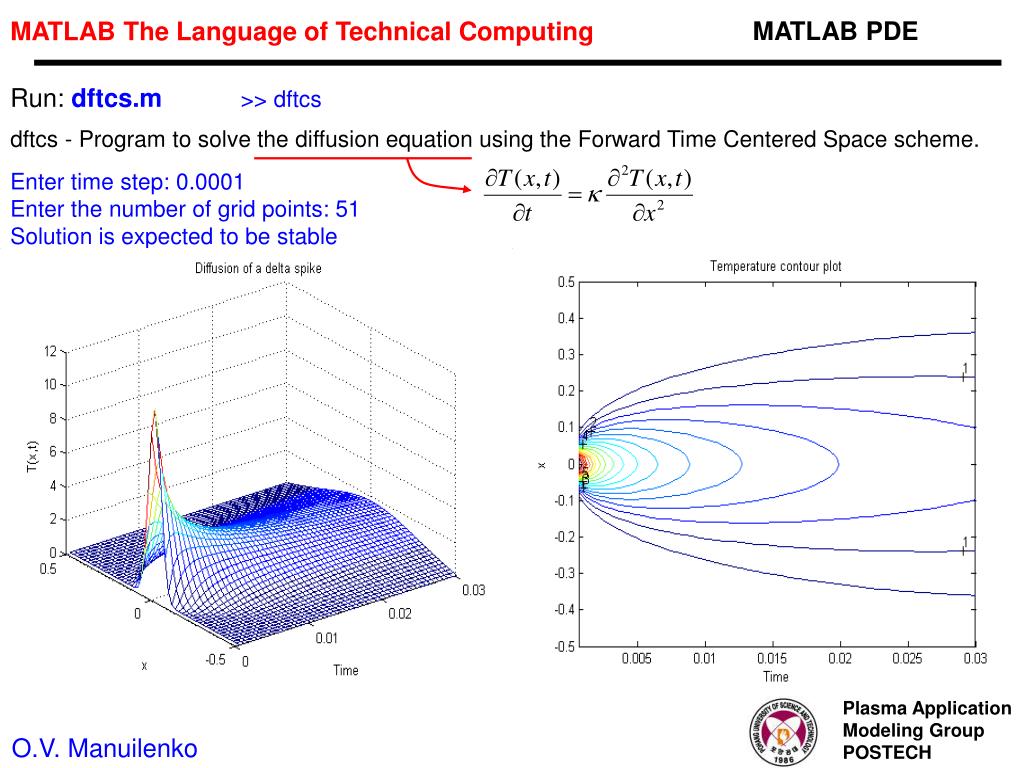

С тех пор как в 2012 году впервые появилось третье издание дифференциальных уравнений с MATLAB , в MATLAB и Simulink было внесено множество изменений и улучшений. К ним относятся добавление живых сценариев, новые команды построения графиков и серьезные изменения в Symbolic Math Toolbox. В этой исправленной версии текст полностью обновлен до версии MATLAB 2019a.

 

Об авторе

Брайан Хант и Рональд Липсман являются почетными профессорами математики, а Джонатан Розенберг является профессором математики Рут М. Дэвис в Университете Мэриленда.

Джон Э. Осборн был почетным профессором математики в Университете Мэриленда до своей смерти в 2011 году.

Содержание

Предисловие v

1 ВВЕДЕНИЕ 1

1.1 ПРАВДА ПЕРЕДАЧА 1

1. 2 РУКОВОДСТВО СТУДЕНТА 3

1.3 6

1,4 Слова о версиях программного обеспечения 7

2 Начало работы с MATLAB 9

2.1 Платформы и версии 9

2.2 Установка 10

2,3 Запуск MATLAB 10

2,4 Типинг В окне команды 11

2,3.0005

2,5 онлайн -справка 11

2.6 Matlab Windows 13

2.7. Завершение сеанса 14

3 Выполнение математики с MATLAB 15

3.1 Арифметика 15

3,2 Символические вычисления 16

3.2.1.

3.2.2 Символьные выражения и арифметика переменной точности 17

3.3 Векторы 18

3.3.1 Подавление вывода 19

3.4 Восстановление после проблем 19

9 Ошибки ввода

3.4.2 Расчеты об аборте 20

3.5 Функции 20

3.5.1 Встроенные функции 20

3.5.2 Указанные пользователи функции 21

3.6 Управление переменные 21

3,7 Уравнения 23

3.8.

3.8.1 График с FPLOT 25

3.8.2 Модифицируя графики 26

3. 8.3 График с График 26

3,8,4 График множества кривых 28

3.8.5 Параметрические участки 28 99.4.0005

3.8.6 Неявные участки и контурные графики 29

3,9 Calculus 31

3.10 Некоторые советы и напоминания 32

4 Использование настольных и скриптов 33

4.1.

4.1.2 Текущая папка и путь поиска 34

4.1.3 История команд 35

4.2 Сценарии и функции 36 Функции 39

4.3 Петли 40

4.4 Представление ваших результатов 41

4.4.1 Представление графики 42

4.4.2 Прекрасная печать 44

4.4.3 «Публикация». Скрипт 44

4.4.4 4.4.5 Экспорт Live Script 46

4.5 Отладка ваших скриптов 48

Набор задач A: Практика с MATLAB 51

5 Решения дифференциальных уравнений 55

5.1 Поиск 5 Символьных решений 50005

5.2 Существование и уникальность 58

5.3 Стабильность дифференциальных уравнений 60

5.4 Различные типы символических решений 63

6 Точные точки символического математического инструментального ящика 69

70003 7 Качественный подход к дифференциальным соглашениям 75

7 Актативный

7. 1 Поле направления для линейного уравнения первого порядка 75

7.2 Поле направления для нелинейного уравнения 77

7.3 Автономные уравнения 79

7.3.1 Примеры автономных уравнений 81

Набор задач B: Уравнения первого порядка 85

8 Численные методы 97

8.1 Численные растворы с использованием MATLAB 98

8.2 Некоторые численные методы 101

8.2.1 Метод EULER 102

8.2.2 Метод 105

8.2.3 Метод Runge-Kutta 106

8.2.4 Внутри ODE45 107

8.2.5 Ошибка округа 108

8.3. Управление ошибкой в ​​ ODE45 108

8.4 Обращение численности Методы 109

9 Особенности MATLAB 113

9.1 Классы данных 113

9.1.1 Символические и плавучивые номера 114

9.1.2 Структуры 115

9.1.3. 9.3 Подробнее о сценариях и функциях 118

9.3.1 Переменные и ввод/вывод в сценариях 118

9.3.2 Переменные в функциях 118

9.3.3 Структура функций 119

9. 4 Матрицы 1200005

9.4.1 Решение линейных систем 121

9.4.2 Расчет собственных значений и собственных векторов Численные решения ОДУ 125

9.6.1 Оценка численных решений с помощью deval 125

9.6.2 Построение графиков семейств численных решений ОДУ 126

9.6.3 Обнаружение событий 127

0002 9.7 Устранение неполадок 129

9.7.1 Наиболее распространенные ошибки 129

9.7.2 Ошибка и предупреждающие сообщения 130

10 Использование Simulink 133

. 10.1 Конструирование и запуск модели Simulink 133

10.2 Выходные к Рабочке и Рабочая площадка и Рабочий класс Как работает Simulink 138

Набор задач C: численные решения 143

11 Решение и анализ линейных уравнений второго порядка 151

11.1 Уравнения второго порядка с помощью MATLAB 153

11,2 Уравнения второго порядка с Simulink 157

11,3 Методы сравнения 159

11.3.1. Включение нулей 160

11. 3.2 Доказательство теоремы сравнения Штурма 161

11,4 A Geometric Method 162

11.4.11 Случай постоянного коэффициента 163

11.4.2. Случай коэффициента переменного коэффициента 164

11.4.3 Уравнение Эйри 165

11.4.4 Уравнение Бесселя 166

12 серийных решений 183

12.1 Решения серии 184

12,2 Один и единственные точки 186

12.3 Другие линейные и нелинейные уравнения 187

13 преобразования LAPLACE 189

13.1 Дифференциальные экведита и преобразования LAPLACE 1915

13.1 Дифференциальные экведита и LAPLACE Transforms 1919295.1000 210002 13.1 Дифференциальные экв. Функции 194

13.3 Дифференциальные уравнения с разрывными воздействиями 196

Набор задач E: Решение ряда и преобразование Лапласа 199

14 Уравнения и системы более высокого порядка уравнений первого порядка 213

14.1 Линейные уравнения более высокого порядка 214

14. 2 Системы уравнений первого порядка 215

14.2.1. Собственные пары 218

14.3 Фазовые портреты 222

14.3.1 Построение одной траектории 222

14.3.2 Построение нескольких траекторий 223

14.3.3 Численные решения систем первого порядка 2250005

14.3.4 Нелинейная система 227

15 Качественная теория систем дифференциальных уравнений 229

Набор задач F: Системы дифференциальных уравнений 237

Примеры решений 250 6

5 Индекс

Исчисление и дифференциальные уравнения с MATLAB в каталоге SearchWorks

Ответственность

Прамоте Дешомфай.

Публикация

Оксфорд: Alpha Science International; Бангкок: Чулалонгкорн, University Press, [2016]

Уведомление об авторских правах

© 2016

Физическое описание

xii, 441 стр.: иллюстрации; 25 см

Доступно онлайн

В библиотеке

Научная библиотека (Ли и Ма)

Стеки

Предметы в стопках

Номер телефона	Статус
QA371 . D33 2016	Неизвестный

Описание

Создатели/Соавторы

Автор/Создатель

Дешамфаи, Прамоте, автор.

Содержание/Резюме

Библиография

Включает библиографические ссылки (страницы 433-436) и предметный указатель.

Содержимое

• Preface / Symbolic Mathematics by MATLAB / Исчисление / Дифференциальные уравнения / Дифференциальные уравнения первого порядка / Линейные дифференциальные уравнения второго порядка / Линейные дифференциальные уравнения высшего порядка / Преобразования Лапласа / Преобразования Фурье / Краевые задачи / Дифференциальные уравнения в частных производных / Специальные функции / Библиография / Указатель.
• (источник: данные книги Нильсена)

Резюме издателя

Книга «Исчисление и дифференциальные уравнения с MATLAB» представляет собой ясное и понятное руководство по использованию MATLAB для решения задач исчисления и дифференциальных уравнений. Книга содержит одиннадцать глав с основными материалами, которые преподаются в курсах исчисления и дифференциальных уравнений. К ним относятся: * Пределы, дифференцирование и интегрирование * Тейлор, Маклорен и другие бесконечные ряды * Обыкновенные дифференциальные уравнения * Преобразования Лапласа и Фурье * Уравнения в частных производных * Численные методы и методы конечных элементов * Специальные функции (погрешность, гамма, бета, Бесселя, Эйри, Лежандр и т.