Диаграммы вороного: Диаграмма Вороного и её применения / Хабр

Построение диаграммы Вороного методом ‘разделяй и властвуй’. Релаксация Ллойда / Хабр

Недавно, на хабрахабре была опубликована статья, целиком и полностью посвященная диаграммам Вороного. В статье автор подробно описывает алгоритм Форчуна, применяемый для построения Диаграммы Вороного за O(n*log(n)). Стоит отметить, что описание этого алгоритма не раз появлялось в рунете, в то время как о других алгоритмах (с той же асимптотикой) рассказано ровным счетом ничего. Данная статья исправляет это недоразумение, а также является отличным дополнением к уже опубликованному ранее материалу.

Ниже я расскажу о алгоритме ‘разделяй и властвуй’ построения диаграммы Вороного за O(n*log(n)), а также, основываясь на своем практическом опыте, о по-настоящему крутых штуках, в которых это применимо. Вообще, алгоритмы типа ‘разделяй и властвуй’ являются своего рода классикой программирования (думаю, про сортировку данным методом слышал каждый программист), хорошо параллелятся и легко читаются (если, конечно, знать основную идею алгоритма).

Описание алгоритма

‘разделяй и властвуй’ построения диаграммы Вороного

Исходное множество точек сортируется по одной из координат(положим, x) и делится на два, примерно равных множества. Каждое из полученных множеств снова делится на два и так происходит до тех пор, пока в каждом из множеств останется не более двух точек. Легко видеть, что таких разбиений будет не более чем log(n). Далее, для каждого полученного множества строятся диаграммы Вороного, после чего, в порядке обратном делению, эти диаграммы объединяются в одну. Полученная диаграмма Вороного и будет конечным результатом.

Чтобы описанный алгоритм имел сложность порядка O(n*log(n)), необходимо выполнять процесс объединения двух диаграмм Вороного за O(N). Отмечу, что для множества из двух точек, диаграммой Вороного будет являться серединный перпендикуляр отрезка образованного этими двумя точками.

Положим, что все точки отсортированы по X координате, а исходное множество разделено на два и для каждого построена диаграмма Вороного.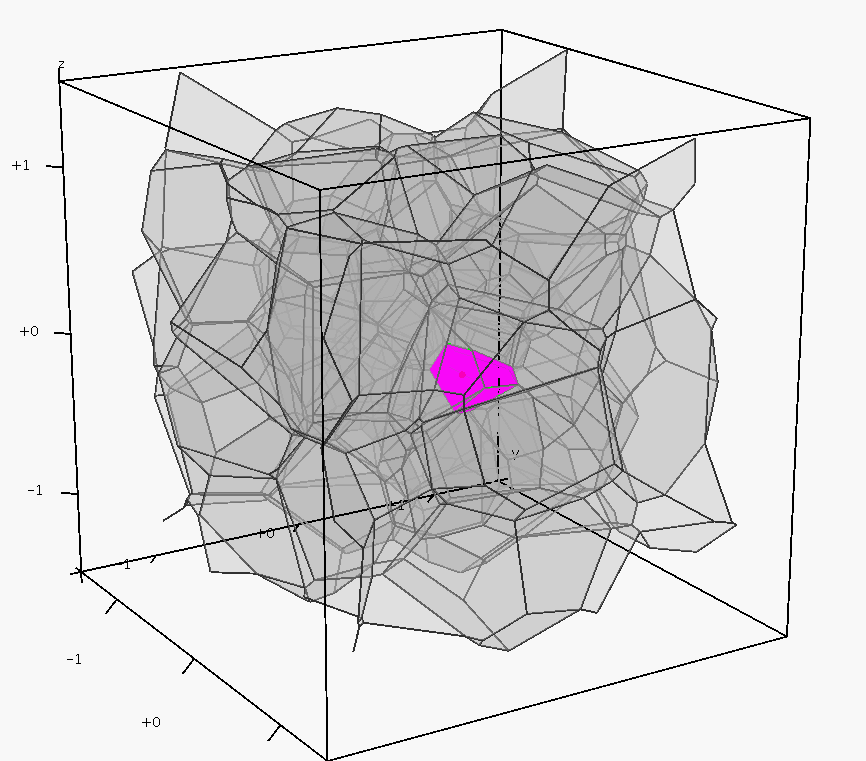

Выполним объединение данных множеств и их диаграмм следующим образом:

⦁ 1. Для каждого из подмножеств найдем выпуклую оболочку (заметим, что построение выпуклой оболочки для каждого из множеств можно выполнять все тем же ‘разделяй и властвуй’: то есть, на каждом шаге объединения диаграмм Вороного мы объединяем и выпуклые оболочки данных множеств за O(N)).

⦁ 2. Теперь, когда у нас есть две выпуклые оболочки исходных множеств, найдем ‘верхнюю и нижнюю’ границы данных множеств: то есть, мы должны найти два таких отрезка, которые объединяют две данные выпуклые оболочки в одну (естественно, выпуклую). Таким образом мы выполним условия шага 1, а также получим инициализирующие значения для шага 3. Данный шаг, как я и писал, можно выполнить за

O(N).

⦁ 3. Из полученных отрезков на шаге 2, выберем любой и обозначим за L (оставшийся обозначим за Q), и через его середину, перпендикулярно пускаем бесконечный луч.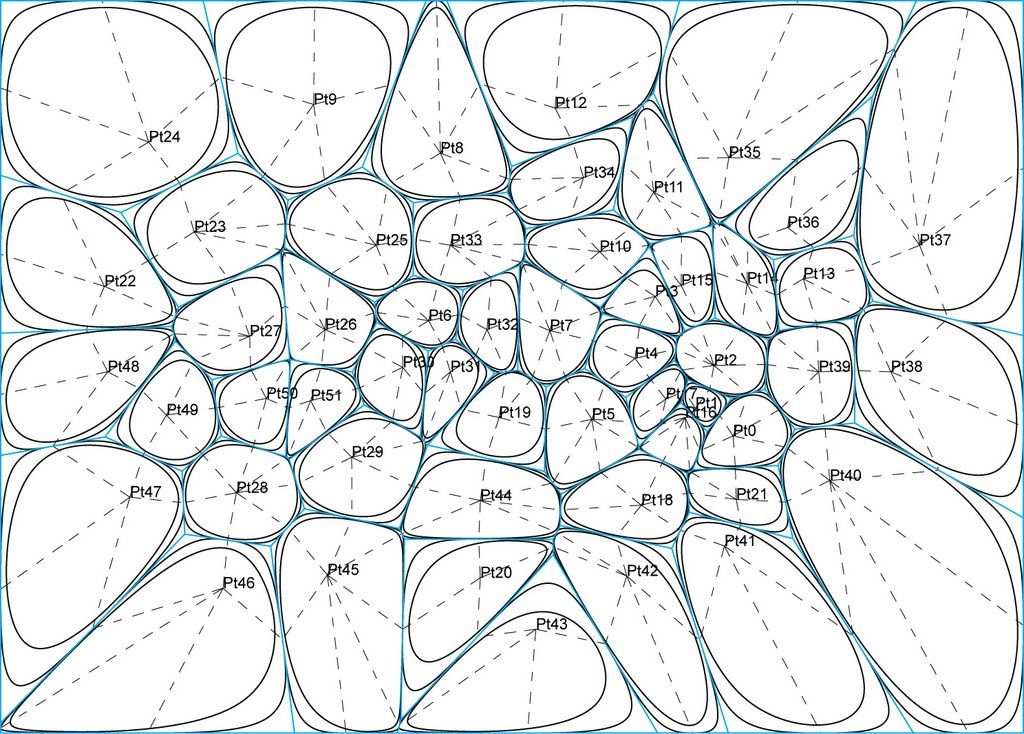 Представим, что данный луч только входит в исходное множество, и найдем его пересечения с ячейками диаграмм Вороного исходных множеств (считается, что луч простирается вперед, то есть у него есть направление). Мы пересекаем луч только с теми ячейками Вороного, центрами которых являются концы отрезка, перпендикулярно которому мы пускаем луч. Нам нужно найти точки пересечения данного луча с соответствующими ячейками Вороного и выбрать среди них ту, что пересекается раньше. Обозначим эту точку за M, а ячейку которую мы пересекли запомним и обозначим V. Далее, сделаем следующее: тот конец отрезка L, что является центром для не пересеченной ячейки Вороного оставляем в покое, а вот тот, что был центром ячейки которую мы пересекли — обновляем: мы пересекли одну из сторон ячейки Вороного, тогда новым концом отрезка

L станет центр ячейки Вороного, смежной по этой стороне с пересеченной ячейкой. В специальное множество S (в нем хранится граница двух Диаграмм Вороного) надо добавить ту часть луча, которая простирается до пересечения со стороной ячейки. Повторяем шаг 3 до тех пор, пока значения концов отрезка L, не станут равны значениям концов отрезка Q. В итоге, в множестве S окажется непрерывный ломаный луч. Доказательство многих фактов, приведенных здесь (например, непрерывность луча в множестве S), можно найти в [1].

⦁ 4. Мы получили множество S, которое представляет собой непрерывный ломаный луч. Этот луч является границей, соединяющей диаграммы Вороного двух множеств. Для получения финального результата, нужно для диаграммы Вороного левого множества ‘затереть’ те отрезки что находятся справа от полученного луча, а для диаграммы Вороного правого множества ‘затереть’ те что слева. Сделать это быстро не проблема: когда мы пересекаем ячейку лучом, то очевидно, что сначала луч будет в неё входить, а затем, в какой-то определенный момент-выйдет. Нам нужно ‘отловить’ эти события, и в зависимости от того с диаграммой какого множества мы работаем(левого или правого), удалить левую или правую цепочки ребер ячейки Вороного, которую мы пересекли лучом, и добавить туда нужную часть из множества

S.

Описанный выше алгоритм сложно понять без хорошей иллюстрации(картинки были взяты здесь):

Ну и закончу этот подраздел публикации на том, что если точки имеют одинаковую координату X, то стоит их сортировать по координате Y, таким образом, чтобы равномерно и последовательно их разделить.

Применение Диаграммы Вороного — релаксация Ллойда

Релаксация Ллойда — один из удивительных и ‘залипательных’ алгоритмов, в котором активно используется построение диаграмм Вороного. Опишу сам алгоритм:

⦁ 1. Строим диаграмму Вороного для исходного множества точек, формируем ячейки Вороного.
⦁ 2. Находим «Центр Масс» каждой ячейки Вороного (сумма координат вершин ячейки Вороного, деленная на их количество).
⦁ 3. Сдвигаем центр каждой ячейки Вороного в позицию рассчитанного «Центра Масс».
⦁ 4. Повторяем данную процедуру N раз: до тех пор, пока расстояние сдвига не станет близким к нулю.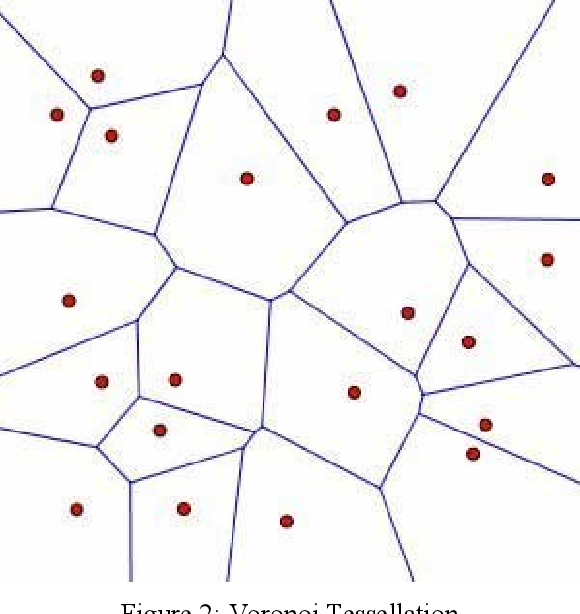

Что же мы получаем в итоге? Результат можно увидеть на этих двух коротких видео:

Выглядит красиво, но немного бесполезно!? Далеко нет! На моем практическом опыте, релаксация Ллойда применялась в 3D моделировании: в так называемом

«ремешинге сетки». То есть, дана сетка (обычно после обработки дешевеньким китайским сканером) и стоит задача полученную ‘мешанину’ треугольников превратить в нечто красивое и живое: в то, на чем можно производить более-менее точные вычисления(расчет ‘кривизны сетки’, аппроксимация точек триангуляционной сетки бесконечно гладкими поверхностями и т.п), стараясь не сильно отклониться в точности от оригинальной ‘сканерной’ сетки (более того, эта точность задается пользователем, а такой ‘ремешинг’ называется адаптивным (adaptive). Существует еще ‘ремешинг’ униформный (uniform) — здесь, задается не отклонение, а желаемая длина ребра в треугольнике). Я немного заговорился и забыл объяснить, что же мы понимаем под словом ‘красивая’ сетка. Сетку назовем ‘красивой’, если по своей структуре она состоит преимущественно из равносторонних треугольников, а валентность каждой вершины у такой сетки 6 (если вершина внутренняя, ну т. е 360. / 6. = 60 deg. — градус угла равностороннего треугольника) или 4 (если вершина лежит на открытом ребре, то есть треугольников с данной вершиной 3). Ну, и одним из важных этапов получения такой сетки является построение диаграммы Вороного и использование релаксации Ллойда. Собственно, получаем что-то в этом духе(аккуратно, картинки большие!):

Картиночки результата работы ‘ремешинга’, закодированного мною

До:

После:

А теперь и до и после на одном изображении:

Кстати, можно заметить что оригинал был получен с помощью алгоритма Марширующих Кубов.

Ну и картинки поменьше, но уже из интернета:

И… (куда ж без нее то) — статуя Давида:

Красота, да и только!

Завершить хотел бы на том, что использование алгоритма Ллойда, дело затратное. И для получения более быстрого результата, без особой потери в качестве были разработаны так называемые методы ‘Минимизации Энергии’.

Почитать можно в [2]

Полезные ссылки и литература

[0] Крутая статья на Хабрахабр-е о диаграммах Вороного
[1] Оригинал описания алгоритма, со всеми доказательствами
[2] Сравнение методов ‘Минимизации Энергии’
[3] Небольшая статья о ‘Разделяй и властвуй’ алгоритме построения диаграммы Вороного

Построение диаграммы Вороного в Python для задач визуализации

Время прочтения: 5 мин.

Диаграмма Вороного представляет собой множество точек и регионов на плоскости.

Рисунок 1 – Диаграмма Вороного

Для точек (seed points) и регионов (Voronoi cells) диаграммы Вороного на плоскости действуют следующие правила:

1. В каждом из регионов находится только одна точка p_i.
2. Расстояние от любой точки одного региона ближе к seed точке p
   i этого региона, чем к любой другой seed точке.

Диаграмма Вороного может быть использована для решения широкого спектра задач — геометрических, картографических, задач построения логики искусственного интеллекта, а также применяется в машинном обучении и computer vision.

Построение диаграммы на простом примере

Существует множество различных способов построения диаграммы Вороного. В статье приведён способ построения диаграммы упрощённым методом, по своему исполнению более всего напоминающим 3-d Convex Hull.

Суть алгоритма:

1. Каждая точка p_i с 2д плоскости последовательно проецируется на 3д параболоид с центром в этой точке.
2. Для первой точки p₁ массив с исходной матрицей fields заполненной значениями, заведомо превышающими значения массива paraboloid, таким образом матрица colors заполняется одним кодом, соответствующим одному цвету (рис. 1).
3. Следующим шагом матрица значений paraboloid перетирается новыми данными для следующей точки p_i, для дальнейшего сравнения с матрицей fields, обновляя, таким образом, массив colors в точках, соответствующих новой цветовой зоне (рис. 2).
4. Массив field обновляется с учетом вершины нового параболоида, а алгоритм снова переходит к пункту 3 (дальнейшее построение представлено на рис. 3 и рис. 4).

Для упрощения восприятия можно привести пример построения диаграммы для 4 точек и код программы ниже:

Рисунок 2Рисунок 3Рисунок 4Рисунок 5

shape = 10,10
dot_x = [2,5,7,2]                               
dot_y = [2,5,2,7]
points = ([2,2], [5,5],
          [7,2], [2,7])  
def Z(X,Y):                     #матрица значений Z параболоида
    return (X-x)**2 + (Y-y)**2
for i,(x,y) in enumerate(points):    #кол-во циклов определяется числом точек
    paraboloid = numpy.fromfunction(Z,(shape))  #создается массив Z для отдельной точки
    colors = numpy.where(paraboloid < field,i+1,colors) #заполняется цветовая матрица
    field = numpy.where(paraboloid < field,paraboloid,field) №
    fig = plt.figure(figsize=plt.figaspect(0.5))   
    ax = fig.add_subplot(1, 2, 1, projection='3d')
    X = np.arange(0, 10, 1)
    Y = np.arange(0, 10, 1)
    X, Y = np.meshgrid(X, Y)
    surf = ax.plot_surface(X, Y, paraboloid,rstride=1, cstride=1, cmap=cm.magma,
                       linewidth=0, antialiased=False)
    ax. set_zlim(0, 100)
    fig.colorbar(surf, shrink=0.5, aspect=10)
    ax = fig.add_subplot(1, 2, 2)
    C = numpy.transpose(colors)
    ax.imshow(C, cmap=cm.magma, alpha = 1)
    ax.scatter(dot_x, dot_y , c = 'Red')
    ax.scatter(dot_x[i], dot_y[i] , c = 'Blue')
    plt.show()

Ввиду того что границы зон отрисовываются по пикселям, практическое применение описанного метода целесообразно для задач визуализации, не требующих абсолютно точного определения границ.

Решение прикладной задачи при помощи диаграммы Вороного

Примером решаемой задачи является определение «зон покрытия» остановок общественного транспорта в рамках одного населенного пункта. В данном примере будут рассмотрены только некоторые из остановок во избежание излишнего нагромождения.

Входными данными в данной ситуации служат карта местности (г. Новосибирск) и нанесенные на неё координаты остановок (рис. 5).

Рисунок 6 – Карта Новосибирска с отмеченными на ней остановками общественного транспорта

Данная задача является более масштабной, чем рассмотренная в примере, но всё же практически полностью повторяет её, за исключением необходимости переопределить входные данные и построить графики в новом формате.

 А именно:

shape = 1244,767 #размер карты
dot_x = [390,440,423,403,377,355,337,331,541,572,611,605,499,531,567,592,458,439,422,460,471,479,497,435]
dot_y = [533,557,573,607,592,542,550,597,416,437,511,429,289,271,283,259,284,302,329,343,351,327,379,365]
points = ([390, 533], [440,557], [423, 573], [403, 607], [377, 592], [355, 542],
        [337, 550], [331, 597], [541, 416],[572,437],[611,511],[605,429],[499,289],[531,271],
        [567,283],[592,259],[458,284],[439,302],[422,329],[460,343],[471,351],[479,327],[497,379],[435,365])
#--------------------------- визуализция ---------------------------
C = numpy.transpose(colormap)
plt.figure(figsize=(40,20))
imgplot = plt.imshow(img, alpha=1)
plt.imshow(C, alpha = 0.2, cmap = cm.prism)   #, cmap = cm.prism
plt.scatter(dot_x, dot_y , c = 'Red')
plt.savefig('voronoi_map.png')
plt.show()

Результатом работы программы в данном случае является карта, поделённая на сегменты.

Рисунок 7 – Карта «зон покрытия» остановок общественного транспорта в г. Новосибирск

Таким образом, выбор ближайшей остановки (или больницы, или магазина, или отделения банка), для человека, находящегося в любой точке города, оказывается решен. А тот факт, что код, использованный для объяснения принципа, и код для решения задачи практически ничем не отличаются друг от друга, делает данный метод готовым инструментом для решения любых аналогичных задачах визуализации.

Как диаграммы Вороного помогают нам понять наш мир – The Irish Times

Нам часто нужно найти ближайшую больницу, хирургию или супермаркет. Карта, разделенная на ячейки, каждая из которых охватывает район, ближайший к определенному центру, может помочь нам в наших поисках. Такая карта называется диаграммой Вороного, названной в честь Георгия Вороного, математика, родившегося в Украине в 1868 году. Сегодня его помнят в основном по этой диаграмме, также известной как мозаика Вороного, разложение или разбиение.

Еще одна практическая проблема заключается в выборе места для новой службы, например школы, максимально удаленной от существующих школ и в то же время обслуживающей максимальное количество семей.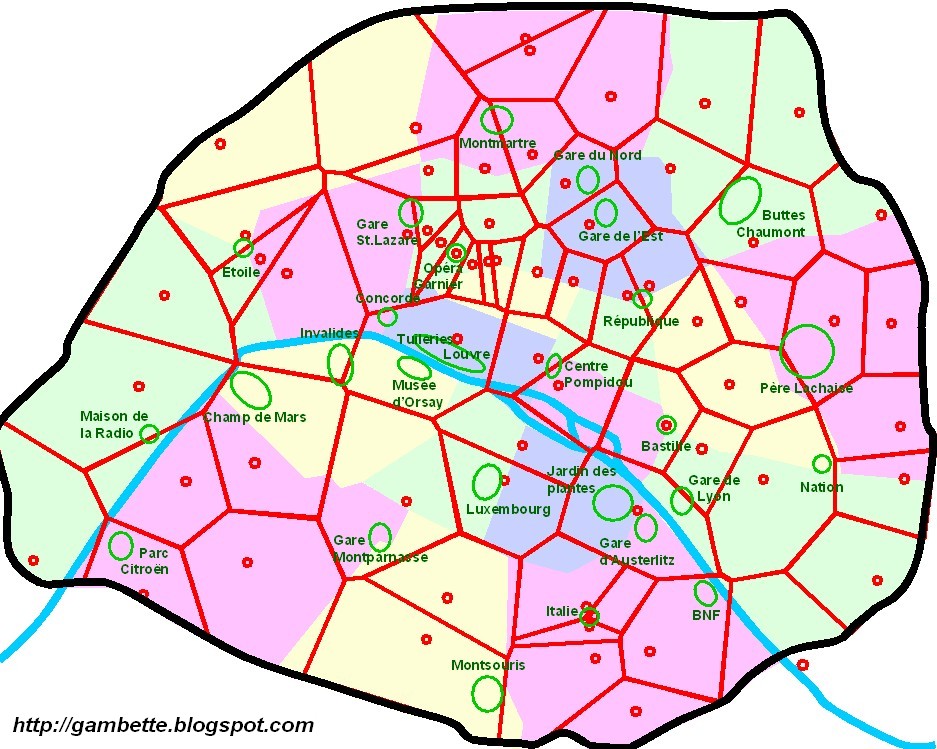 Диаграмму Вороного можно использовать для поиска наибольшего пустого круга среди набора точек, что дает идеальное место для новой школы. Конечно, необходимо учитывать множество других параметров, кроме расстояния, но время доступа часто является критическим фактором.

Говоря математическим языком, нам дан конечный набор точек на плоскости, и для каждой точки соответствующая ячейка Вороного состоит из всех точек, расположенных ближе к ней, чем к любой другой точке. Все ячейки представляют собой выпуклые многоугольники; то есть они имеют границы, состоящие из отрезков прямых линий, и все углы имеют внутренние углы менее 180 градусов.

Диаграммы Вороного легко построить и с помощью компьютерного программного обеспечения можно изобразить в виде цветных диаграмм, указывающих регион, связанный с каждым пунктом обслуживания или сайтом. Для любого местоположения ближайший сервис можно сразу увидеть на схеме (см. прилагаемый рисунок). Диаграммы близости использовались многими математиками, начиная с Декарта в середине 17 века, но их теория была развита Вороным, который в 1908 году определил и изучил диаграммы этого типа в общем контексте n-мерного пространства, где n является количество измерений.

ПОДРОБНЕЕ

Биологические структуры

Диаграммы Вороного находят применение почти во всех областях науки и техники. С их помощью можно описать биологические структуры. В авиации они используются для определения ближайшего аэропорта в случае отклонений. В горнодобывающей промышленности они могут помочь в оценке общих минеральных ресурсов на основе разведочных скважин. В эпидемиологии они могут помочь в выявлении источника инфекций.

Одним из первых применений диаграммы Вороного был доктор Джон Сноу, известный лондонский врач. Холера, получившая широкое распространение в 19 в.ХХ века унесла жизни десятков миллионов человек. До того, как была выделена бактерия холеры, подозревались перенаселенность, плохое питание, плохие санитарные условия и вредные миазмы, исходящие от гниющих органических веществ. Сноу считал, что холера вызывается зараженной питьевой водой.

Серьезная вспышка холеры в 1854 году унесла жизни 500 человек за пять дней. Сноу собрал статистику по количеству жертв и местам вспышек. Он разделил внутренний Лондон на кварталы, каждый из которых имел отдельный водопровод. Он нанес свои данные на график, эффективно построив диаграмму Вороного. Это показало, что почти все смертельные случаи произошли в домах, снабженных одним насосом на Брод-стрит, Сохо. Когда ручку насоса сняли, уровень смертности значительно снизился, и эпидемия быстро прекратилась. Позже инженерное обследование показало, что плохо сконструированный дренаж загрязнял воду насоса.

Существует множество других применений диаграмм Вороного. К ним относятся сетевой анализ, компьютерная графика, медицинская диагностика, астрофизика, гидрология, робототехника и вычислительная гидродинамика. Удивительно, как простая концепция тесселяции области с точки зрения расстояния до заданного набора точек может быть настолько мощной.

Питер Линч — заслуженный профессор школы математики и статистики Университетского колледжа Дублина. Он ведет блог по адресу thatsmaths. com

Математика за минуту: диаграммы Вороного

Поделиться этой страницей

Представлено Marianne 30 марта 2020 г.

Представьте себе город с несколькими больницами. Когда у кого-то возникает неотложная ситуация, вы бы хотели, чтобы он всегда шел или был доставлен в больницу, ближайшую к тому месту, где он сейчас находится. Что вам нужно, так это карта, показывающая зону обслуживания каждой больницы: для любого человека в этом регионе эта больница ближе, чем любая другая. Как ты это делаешь?

Это не сложно, только немного утомительно, если делать это вручную. Начните с двух больниц в точках A и B на карте. Нарисуйте отрезок, который их соединяет, найдите середину этого отрезка, а затем нарисуйте линию, проходящую через эту среднюю точку и перпендикулярную отрезку от A до B. Эта линия делит город на две области. Одна из них, содержащая A, содержит все точки ближе к A, чем к B. Другая содержит все точки ближе к B, чем к A. Точки на прямой находятся на одинаковом расстоянии от A и B.

Теперь посмотрите на третью больницу, в точку C. Повторяя то, что мы делали выше, вы определяете область точек, которые ближе к A, чем к C, и область точек, которые ближе к B, чем к C. Область точек, которая ближе к A, чем к B и C, теперь является пересечением области точек, расположенных ближе к A, чем к B, и области точек, расположенных ближе к A, чем к C.

Продолжайте в том же духе, пересекая области, пока вы не учли все больницы. Картина, которую вы получите в конце, деление карты на области точек, которые ближе к одной из заданных точек, чем к любой другой, называется 9.0023 Диаграмма Вороного . Он назван в честь русского математика Григория Вороного (1868-1908).

Диаграмма Вороного (создана Балу Эртлом, CC BY-SA 4.0.

Как вы понимаете, диаграммы Вороного полезны во всех областях. Например, их можно использовать для изучения закономерностей роста лесов или помощи в Роботы находят четкие маршруты через множество препятствий. В Википедии перечислены многие другие приложения.

Карта Джона Сноу. Каждая полоса представляет собой смерть по адресу. Кривая отмечает точки на равном расстоянии от насоса на Брод-стрит и другого насоса.

Но мы выбрали аналогию с медициной не просто так. В 1850-х годах вспышка холеры опустошила Сохо в Лондоне, убив 10% населения и уничтожив целые семьи за несколько дней. В то время считалось, что болезнь вызвана «плохим воздухом», но у врача Джона Сноу была другая идея: он думал, что холера возникает из-за зараженной воды, которая в те дни поступала из насосов, расположенных по всему городу.

Он смог убедить других в своей теории, сначала отметив количество смертей по каждому адресу на карте Сохо. Затем он также определил «зону водосбора» конкретного водяного насоса на Брод-стрит, 40 (ныне Бродвик-стрит). Точки в этой области охвата были ближе к насосу на Брод-стрит, чем к любому другому насосу — только то, что, в отличие от нашего примера выше, Сноу использовал не прямое расстояние, на котором пролетит ворона, а расстояние, пройденное пешком по улицам и переулкам.