Деление с остатком | это… Что такое Деление с остатком?
Деление c остатком (деление по модулю, нахождение остатка от деления, остаток от деления) — арифметическая операция, результатом которой является два целых числа: неполное частное и остаток от деления целого числа на другое целое число.
Содержание
|
Определение
Разделить целое число на натуральное число с остатком означает представить его в виде:
При этом называется неполным частным, а — остатком от деления на
Например, при делении с остатком на получаем неполное частное и остаток
В программировании
| Язык | Оператор | Знак результата |
|---|---|---|
| ActionScript | % | Делимое |
| Ada | mod | Делитель |
| rem | Делимое | |
| ASP | Mod | Не определено |
| Си (ISO 1990) | % | Не определено |
| Си (ISO 1999) | % | Делимое[источник не указан 316 дней] |
| C++ | % | Не определено[1] |
| C# | % | Делимое |
| ColdFusion | MOD | Делимое |
| Common Lisp | mod | Делитель |
rem | Делимое | |
| Delphi | mod | Делимое |
| Microsoft Excel | =MOD() (англ.=ОСТАТ() (рус. версия) | Делитель |
| Euphoria | remainder | Делимое |
| FileMaker | Mod | Делитель |
| Fortran | mod | Делимое |
modulo | Делитель | |
| GML (Game Maker) | mod | Делимое |
div | Делитель | |
| J | |~ | Делитель |
| Java | % | Делимое[2] |
| JavaScript | % | Делимое |
| Lua | % | Делитель |
| Mathematica | Mod | Делитель |
| MATLAB | mod | Делитель |
rem | Делимое | |
MOD% | Делимое | |
| Objective Caml | mod | Не определено |
| Pascal | mod | Делимое |
| Perl | % | Делитель |
| PHP | % | Делимое |
| PL/I | mod | Делитель (ANSI PL/I) |
| Prolog (ISO 1995) | mod | Делитель |
| Python | % | Делитель |
| QBasic | MOD | Делимое |
| R | %% | Делитель |
| RPG | %REM | Делимое |
| Ruby | % | Делитель |
| Scheme | modulo | Делитель |
| SenseTalk | modulo | Делитель |
| rem | Делимое | |
| Tcl | % | Делитель |
| Verilog (2001) | % | Делимое |
| VHDL | mod | Делитель |
| rem | Делимое | |
| Visual Basic | Mod | Делимое |
версия)Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получении случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.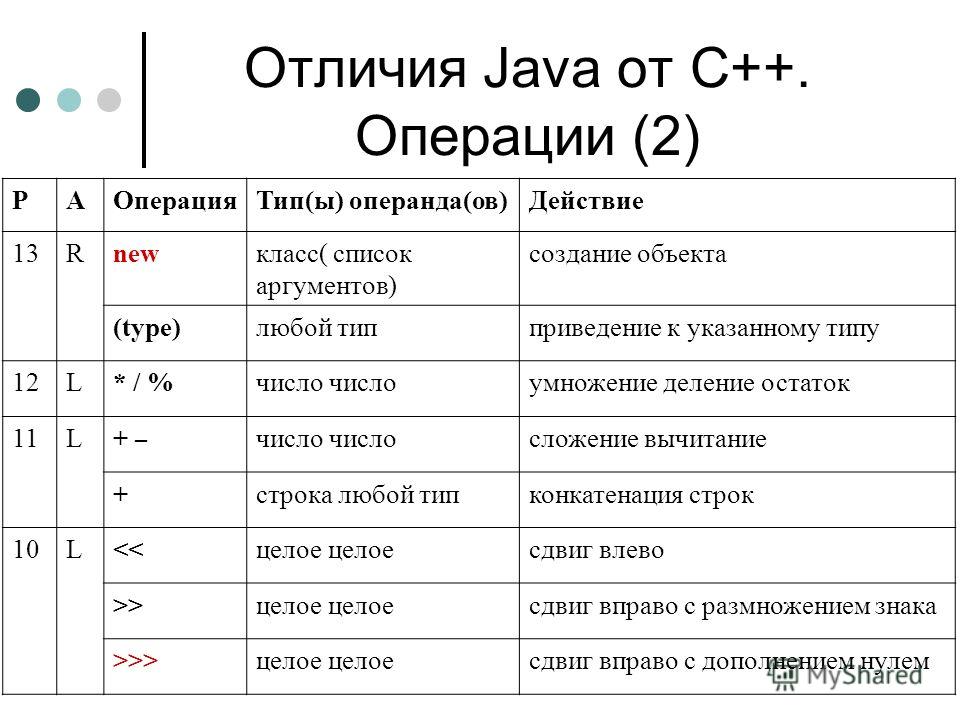
Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа. Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:
78 mod 33 = 12 78 div 33 = 2
Важно отметить, что операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Для нахождения минимального неотрицательного остатка от деления числа b, где a может принимать как положительные, так и отрицательные значения, можно воспользоваться следующей формулой:
(b+(a mod b)) mod b
См. также
- Делимость
- Деление (математика)
- Сравнение по модулю
- Остаток от деления
Целочисленное деление указано простейшей операцией, приносящей системные сбои, не выполнимой правильно в свойствах деления меньшего на большее.
A\B = 0 при A<B (A mod B) = A
Проверка:
B*0 + A = A
Примечания
- ↑ ««ISO/IEC 14882:2003 : Programming languages — C++»», 5.6.4: International Organization for Standardization , International Electrotechnical Commission, 2003 . «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
- ↑ К. Арнолд, Дж. Гослинг, Д. Холмс Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0
Алгоритм Евклида — нахождение наибольшего общего делителя
Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел.
Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.
Решение задачи на языке программирования Python
Алгоритм нахождения НОД делением
- Большее число делим на меньшее.
- Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
- Если есть остаток, то большее число заменяем на остаток от деления.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6
a = int(input())
b = int(input())
while a != 0 and b != 0:
if a > b:
a = a % b
else:
b = b % a
print(a + b)В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД.
Если условием завершения цикла является равенство хотя бы одной из переменных нулю (a == 0 or b == 0), то условием продолжения его работы является обратное этому условие — обе переменные должны иметь отличные от нуля значения (a != 0 and b != 0).
Для того, чтобы вышеприведенная программа могла обрабатывать отрицательные числа, в логическом выражении при if должны сравниваться модули значений переменных: if abs(a) > abs(b):. Иначе большим числом может оказаться меньшее по модулю. В этом случае интерпретатор Питона в качестве остатка от деления выдает вещественное число. В результате это приводит к зацикливанию, так как низвести переменные до нуля становится как минимум маловероятным.
Алгоритм нахождения НОД вычитанием
- Из большего числа вычитаем меньшее.
- Если получается 0, значит, числа равны друг другу и являются НОД (следует выйти из цикла).
- Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
- Переходим к пункту 1.
Пример:
Найти НОД для 30 и 18.
30 — 18 = 12
18 — 12 = 6
12 — 6 = 6
6 — 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6
a = int(input())
b = int(input())
while a != b:
if a > b:
a = a - b
else:
b = b - a
print(a)Функция, вычисляющая НОД
def gcd(m, n):
while m != n:
if m > n:
m = m - n
else:
n = n - m
return n
a = int(input())
b = int(input())
print(gcd(a, b))Функция
gcd модуля math В модуле math языка программирования Python есть функция gcd, вычисляющая наибольший общий делитель двух чисел.>>> import math >>> math.
gcd(30, 18)
6Больше задач в PDF
Калькулятор модуля
Базовый калькулятор
Поделись этим калькулятором и страницей
Использование калькулятора
Вычислить a mod b , что для положительных чисел является остатком от деления a на b в задаче на деление. Операция по модулю находит остаток, поэтому, если вы делите
Как выполнить расчет по модулю
Операция по модулю находит остаток от деления a на b .
Чтобы сделать это вручную, просто разделите два числа и запишите остаток. Если вам нужно найти 27 по модулю 6, разделите 27 на 6.
- 27 мод 6 = ?
- 27 ÷ 6 = 4 с остатком 3
- 27 модуль 6 = 3
Пример расчета по модулю
Вам нужно написать программу, которая сообщает пользователю, является ли введенное им число кратным 4. Для этого можно использовать вычисление по модулю.
Если число кратно 4, то при делении его на 4 в остатке будет 0. Таким образом, вы создадите логику для ввода и использования мод 4 операция на нем. Если результат равен 0, число кратно 4, в противном случае число не кратно 4.
Логика этой части вашей программы будет следующей:
- x число, введенное пользователем
- Если x mod 4 = 0, то x кратно 4
- Иначе x не кратен 4
Если бы вы не использовали оператор мода, вам пришлось бы выполнять математические операции в коде.
Например, вам нужно будет вычислить «равно 496 кратно 4?». Вы должны разделить 496 на 4, так что 496 / 4 = 124 без остатка. С точки зрения модуса, 496 по модулю 4 = 0, так что да, 496 кратно 4.
Является ли число 226 кратным 4? Разделите 226 на 4, так что 226/4 = 56 с остатком 2. 226 mod 4 = 2, так что нет, 226 не кратно 4.
В некоторых калькуляторах и языках компьютерного программирования a % b совпадает с mod b совпадает с modulo b, где % или mod используются в качестве операторов по модулю.
Пример: 1 мод 2
1 mod 2 — это ситуация, когда делитель 2 больше делимого 1, поэтому полученный остаток равен делимому 1.
При делении 1 на 2 2 превращается в 1 ноль раз с остатком 1. Таким образом, 1 mod 2 = 1 .
Аналогично, 5 mod 10 = 5 , так как 10 делится на 5 нулевых умножений, а 5 остается в остатке.
Для положительных чисел всякий раз, когда делитель (модуль) больше делимого, остаток равен делимому.
Дополнительное чтение
Дальнейшее изучение модульной арифметики и операций по модулю, включая a mod b для отрицательных чисел.
Академия Кана, Что такое модульная арифметика?
Лучшее объяснение, развлечение с модульной арифметикой
Википедия, Приложения модульной арифметики
Мир Математики, Конгруэнтность
Академия Кана, сравнение по модулю
Теорема о частном остатке и алгоритм Евклида
Теорема о частном остатке и алгоритм ЕвклидаТеорема о частном остатке и алгоритм Евклида
Теорема 3.4.1 Теорема о частном остатке
Для любого целого числа n и положительного целого числа d существуют уникальные
целые числа q и r такие, что
n = dq + r и 0 < r < d .
Если вы разделите одно число, n , на другое, d , вы получить частное, q , и остаток, r , и что остаток меньше делителя, d . Для случаев, когда r = 0, мы говорим d . делит n или d | п . Здесь мы называем d делителем n или коэффициент n . Символически
д | п тогда и только тогда, когда $ k Z такое, что n = k d.
Чтобы восстановить частное с помощью целочисленного деления, используйте n .
div d в Паскале; n / d в C, C++, Java и Ada. Чтобы восстановить
остаток с использованием целочисленного деления использует n mod d в Паскале; п % d в C, C++ и Java; н рем д в Аде. див это сокращение от
«делится на», а мод — это сокращение от «по модулю». В Java, когда деление выполняется с использованием двух целых чисел, результат
представляет собой целое частное ( n / d = q ).
Когда модуль
выполненный с двумя целыми числами, результатом будет остаток ( n % d = r ).
Чтобы не выполнять целочисленное деление в Java, нужно привести одно из
целые числа в вещественное число или использовать действительный литерал в качестве одного из операндов. Рассмотрим эти
два присваивания с использованием соглашения Java
анс1 = 5/10*2;
анс2 = (двойной) 5 / 10 * 2
Решение первой задачи равно 0, а решение второй вторая 1.0.
Чему равен наибольший общий делитель двух чисел? Это просто наибольшее число, которое делит оба числа точно, не оставляя остатка. Например, делители 4 = {1, 2, 4} и делители 12 = {1, 2, 3, 4, 6, 12}, поэтому НОД числа 4 а 12 — это самое большое число, которое встречается в обоих списках: 4. Таким же образом вы можно проверить, что НОД чисел 36 и 210 равен 6, а НОД чисел 15 и 4 1,
Евклида
Алгоритм деления: Чтобы найти НОД двух чисел, разделите одно из них
в другой, и обратите внимание, что НОД также точно разделит остаток.
Например, 210 = 5*36 + 30, НОД 210 и 36 равен 6, а 6 действительно делит 30.
ровно (30 = 5*6). Теперь разделите старый остаток на старый делитель и
НОД старого делителя и старого остатка точно разделит новый
остаток. Продолжайте делать это, пока не получите остаток от 0. Последний ненулевой
остаток, который вы получите, будет НОД двух чисел, с которых вы начали.
Как это так? Сначала обратите внимание, что gcd( n, d ) = gcd( d, r ). Итак задача нахождения НОД n и d сводится к нахождению НОД d и r после деления n на d , чтобы получить r .
| НОД(330, 156) = | гкд(156, 18) | 330 = 156*2 + 18 |
| = | гкд(18, 12) | 156 = 18*8 + 12 |
| = | НОД(12, 6) | 18 = 12*1 + 6 |
| = | НОД(6, 0) | 12 = 6*2 + 0 |
| = | 6 | нулевой остаток, поэтому НОД является последним ненулевым остатком |
Вот простое итеративное решение для нахождения наибольшего общего делителя
два целых числа в Java.