Деление java: Java | Арифметические операции

Pro Java: Примитивные целочисленные типы Java

Особенности типа char мы рассмотрели в предыдущей статье. Здесь же мы рассмотрим все целочисленные примитивные типы Java оптом, так как они отличаются друг от друга только размером, а следовательно, только максимальным и минимальным значениями, которые могут содержать. Все типы за исключением char являются знаковыми, char, как уже объяснялось без знаковый. Повторим таблицу размеров и значений для этих типов тут еще раз:

Тип	Содержит	По умолчанию	Размер	Диапазон	Обертки
char	целое беззнаковое	\u0000	16 bits	от \u0000  до \uFFFF (от 0 до 65535 десятичное)	Charaster
byte	целое знаковое	0	8 bits	от -128 до 127	Byte
short	целое знаковое	0	16 bits	от -32768 до 32767	Short
int	целое знаковое	0	32 bits	от -2147483648 до 2147483647	Integer
long	целое знаковое	0	64 bits	от -9223372036854775808 до 9223372036854775807	Long

Целочисленные литералы

Значения целочисленным переменным и константам задаются при помощи следующих литералов:

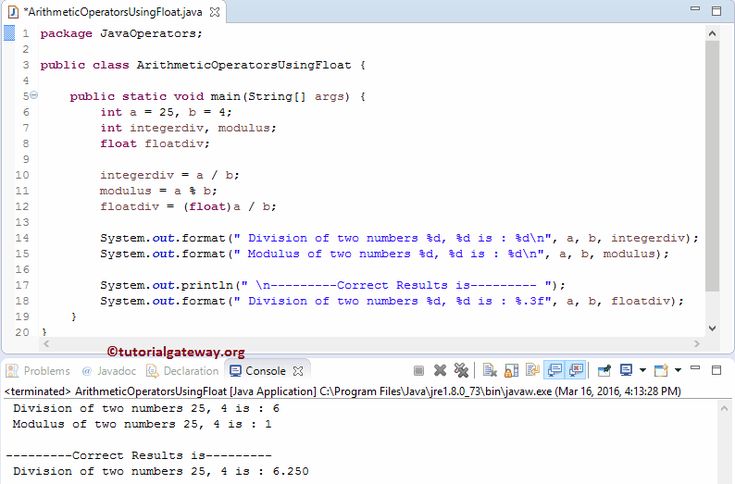
108 – десятичный литерал
0154 – восьмеричный литерал (в начале стоит ноль)
0x6c – шестнадцатеричный литерал
0b01101100 – двоичный литерал (с Java 7)

Так же в числовых литералах можно использовать символ подчеркивания _ для разграничения разрядов, это сделано только для удобства написания и понимания и ни как не влияет на значение (с Java 7). Например:

0110_1100, 0x7fff_ffff, 0177_7777_7777

Для обозначения литерала типа long можно использовать суффикс L (можно использовать и маленькую l, но ее легко попутать с единицей 1). Например:

3_000_000_000L

В связи с этим есть один интересный момент, что переменной типа long не возможно задать значения больше 2147483647 следующим оператором присваивания:

long

iLong = 2147483648;

Хотя значение 2147483648 является допустимым для типа long, но компилятор считает это число 2147483648 литералом типа int, поскольку у него нет суффикса L, а для типа int число 2147483648 является не допустимым значением и поэтому компилятор выдаст ошибку. Чтобы этого не было надо использовать суффикс L. Например:

long

iLong = 2147483648L;

Такое выражение компилятор уже примет как правильное.

Над целочисленными типами можно совершать различные операции при помощи операторов сравнения, математических операторов и операторов побитового сдвига.

Операции сравнения для примитивных типов вообще и для целочисленных в частности сравнивают их значения. Операторы сравнения мы уже рассматривали при изучении типа boolean. Результатом этих операций может быть только значение типа boolean.

Арифметические операции

Тут впрочем все просто. На что только надо обратить внимание это то, что деление над целочисленными типами тоже целочисленное и в результате этих операций можно получить как целое число или целую или дробную часть от операции совершенной соответствующими операторами. Инкремент и декремент (увеличение или уменьшение на единицу) может быть как префиксным, так и постфиксным. При использовании префиксного оператора сперва происходит инкремент иди декремент переменной,  а затем используется ее значение, при постфиксной наоборот – сперва используется текущее значение переменной, а затем происходит ее декремент или инкремент.

 

Результат арифметической операции имеет тип int, кроме того случая, когда один из
операндов типа long. В этом случае результат будет типа long. Перед выполнением арифметической операции всегда происходит повышение (promotion) типов byte, short, char. Они преобразуются в тип int, а может быть, и в тип long, если другой операнд типа long. Операнд типа int повышается до типа long, если другой операнд типа long. Конечно, числовое значение операнда при этом не меняется. Это правило приводит иногда к неожиданным результатам.

Все это мы подробно рассмотрим на практических примерах.

Стоит упомянуть, что при делении на ноль возникает исключительная ситуация, которая при отсутствии обработки этой исключительной ситуации (ArithmeticException) приводит к аварийному завершению работы программы.

Так же надо иметь в виду, что переполнение не является исключительной ситуацией, лишние старшие биты просто выкидываются.

Операция деление по модулю (или остаток) определяется так:
a % b = a — (a / b) * b

То есть 5%3=2, потому что 5-(5/3)*3=2, имейте в виду что 5/3 в данном случае это целочисленное деление и результат этой операции равен 1.

Все операции кроме инкремента и декремента имеют короткую форму записи, представленную в левой колонке. С подобным мы уже сталкивались в типе boolean.

И еще стоит упомянуть об унарном операторе минус (−). Если «−» используется как унарный оператор перед отдельным операндом, он выполняет унарную инверсию знака. Другими словами, он переводит положительное значение в эквивалентное ему отрицательное, и наоборот.

Ну а теперь, чтобы не было скучно, простенький пример на пройденную тему.

Программа очень простая, единственное что может потребовать объяснение это пример переполнения, хотя в полном смысле этого слова, это нельзя назвать переполнением, так как значение не вышло за пределы байта, а просто произошло инвертирование числа в отрицательное значение. Можно было бы создать цикл чтобы догнать значение до реального переполнения, но во первых циклы мы еще не проходили, а во вторых и так понятно, даже на этом примере что происходит.

Если не понятно то в двух словах объясню. Максимальное положительное значение переменной типа byte равно 127. Что мы и задали в строке 32. Затем чтобы обмануть компилятор мы два раза сделали инкремент этого значения, то есть по идее должны были получить число 129. Если бы мы просто попытались сделать c=c+2, то компилятор и IDE показали бы нам ошибку приведения типов (можете попробовать и убедиться).  Далее мы вывели получившиеся значение, которое стало равно –127. Это произошло потому, что в старший разряд (первый слева) была помещена единица. Числу 129 соответствует двоичное значение 1000 0001.

Но для типа byte, максимальным положительным значением является 127, что соответствует двоичному числу 0111 1111. Когда в старший разряд помещается единица, то это число начинает интерпретироваться как отрицательное.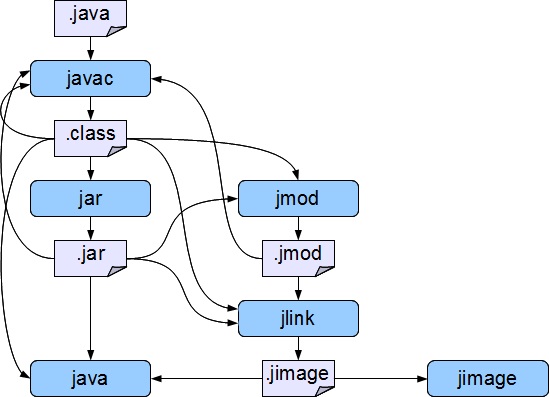 То есть если двоичное число 1000 0001 интерпретировать как отрицательное, то его десятичное значение будет равно –127. Почему так?

А потому-что надо было учить информатику

Теперь приведу вывод этой программы:

Если вдруг не понятно с двоичными числами, то очень рекомендую подтянуть информатику, так как далее будем обсуждать побитовые операции, а там без этого ни куда просто.

Побитовые операции в ряде случаев вещь чрезвычайно полезная и нужная.

В данном примере я рассмотрел из совмещенных операций только операции совмещенного сложения и присвоения, а так же вычитания и присвоения (строки 28 и 30), умножение, деление и деление по модулю уже не стал кодить, так как там все аналогично.

Про операцию деления по модулю еще стоит отметить одно правило:

a == (a / b) * b + (a % b)

Это так на заметку. Ну и поперли дальше!

Побитовые операции

Побитовые операторы и операторы сдвига манипулируют отдельными битами целого числа. Чаще всего побитовые операторы применяются для проверки и установки отдельных флаговых битов. Чтобы понять их поведение, необходимо понимать двоичные числа и формат дополнения, используемый для представления отрицательных чисел. Эти операторы нельзя использовать с массивами, объектами или с плавающей точкой. Операторы побитового сдвига и оператор NOT (~) так же нельзя использовать с операндами типа boolean. Все побитовые операторы за NOT, имеют совмещенные операторы присваивания. Если один из аргументов побитового оператора имеет значение long, то в результате тоже получится long. Если нет, то результат получается int. Если левый операнд оператора сдвига имеет значение long, то в результате тоже будет long. Если нет, то в результате получится int.

Арифметический сдвиг вправо это сдвиг с сохранением знака числа, то есть все освободившиеся старшие биты заполняются единицами. В логическом сдвиге вправо все немного сложнее.

Арифметический сдвиг влево бывает только один, так как там только один вариант чем заполнять младшие освободившиеся биты – это ноль.

Побитовые операции выполняются поразрядно, после того как оба операнда будут приведены к одному типу int или long, так же как и для арифметических операций. Это обстоятельство надо учитывать, если вы применяете побитовые операции к типам byte, short и возможно char, поскольку тут тоже могут быть неожиданные эффекты.

Особенно осторожным надо быть с логическим сдвигом вправо >>>.

 

Теперь рассмотрим все эти операторы более подробно.

Побитовое НЕ (~)

Унарный оператор ~ является оператором побитового отрицания, или побитового НЕ. Он инвертирует каждый бит своего единственного операнда, преобразовывая единицы в нули и нули в единицы. Например:

Побитовое И (&)

Этот оператор объединяет два целых операнда посредством логической операции И с их отдельными битами. В результате биты устанавливаются в единицу только там, где соответствующие биты установлены в единицу в обоих операндах. )

Этот оператор объединяет два целых операнда посредством логической операции
исключающего ИЛИ с их отдельными битами. В результате биты установлены в единицу только там, где соответствующие биты в двух операндах различны. Если оба бита – нули или единицы, то результат будет содержать нулевой бит. Например:

Побитовый сдвиг влево (<<)

Оператор << сдвигает биты левого операнда влево на количество позиций, обозначенное правым операндом. Старшие биты левого операнда теряются, а справа добавляются нулевые биты. Сдвиг целого числа влево на n позиций равносилен умножению этого числа на 2ⁿ. Например:

Если левый операнд представляет тип long, то значение правого операнда должно находиться в диапазоне между 0 и 63. В противном случае левый операнд считается int, а значение правого операнда должно располагаться между 0 и 31.

Побитовый арифметический сдвиг вправо со знаком (>>)

Оператор >> сдвигает биты левого операнда вправо на количество позиций, обозначенное правым операндом. Младшие биты левого операнда сдвигаются «наружу» и теряются. Старшие биты, сдвигаемые «внутрь», идентичны изначальному старшему биту левого операнда, то есть если в старшем бите была единица, то освободившиеся старшие биты заполняются единицами, а если ноль, то нолями.  Данный прием называется расширением знака. Он применяется для сохранения знака левого операнда. Если левый операнд положительный, а правый имеет значение n, то оператор >> равносилен целочисленному делению на 2ⁿ.
Например:

Побитовый логический сдвиг вправо без знака (>>>)

Этот оператор аналогичен оператору >>, но он всегда заполняет нулями старшие биты, каким бы ни был знак левого операнда. Данный прием называется дополнением нулями. Его применяют, если левый операнд интерпретируется как значение без знака (несмотря на то что в Java все типы со знаком). Например:

Как я уже говорил, с этим оператором надо быть очень осторожным, так как надо учитывать, что его операнды автоматически приводятся к типу int (или long), то есть их разрядность увеличивается. Приведенный пример справедлив для типа данных int, а вот для byte и short, он уже может подглючить. Поэтому пример с логическим сдвигом вправо мы рассмотрим более подробно, отдельно от остальных.

И еще несколько небольших замечаний:

• В побитовых операциях используется по умолчанию тип int, то есть компилятор java всегда воспринимает правый операнд как int, поэтому при операциях с byte и short необходимо пользоваться операцией приведения типов. Мы это еще пока не проходили, но скоро пройдем, а пока мотаем на ус.
• Это же справедливо и для арифметических операций, как я уже говорил, происходит автоматическое приведение всех операндов к типу int или long.

Ну а теперь немножко практики.

В библиотеку ProJava.jar я добавил еще парочку статических методов printlnByte и printByte для вывода значений типа byte в двоичном виде как строку.

И далее то что это программа выводит

Тут все более или менее просто и понятно. Далее будем разбираться с оператором логического сдвига вправо.

Теперь посмотрим на вывод этой программы:

Как видим для типа int все идет так как написано, то есть старшие биты заполняются нужным количеством нулей. А вот для типа byte, уже начинаются глюки.
Строка 32 выводит нам десятичное значение переменной типа byte b1. И это значение равно 1073741811. Не хило так для типа byte, у которого максимальное положительное значение это 127. Это произошло потому, что, как уже говорилось, при арифметических и побитовых операциях происходит автоматическое приведение типов byte и short до типа int (или long). Вот на это мы и напоролись в 32 строке.

39 строка, которая выводит двоичное значение переменной типа byte b1 тоже преподнесла нам сюрприз. По идее в двух старших битах должны быть два нуля, но мы их там не наблюдаем. Там пара единиц. Это опять же произошло все по той же причине автоматического расширение byte и short до int или long, если long присутствует в выражении.

Приведение типов, явное и неявное мы рассмотрим чуток позже, а пока полезно знать о граблях неявного приведения типов.

И так в строке 39 мы просто получили обрубок значения int, старшие разряды которого были выкинуты, вместе с двумя нулями в начале (смотрите внимательно скриншот вывода).

Теперь поправим эту ситуацию, чтобы все работало правильно. Для этого надо применить маску 0xff, которая превратит все старшие 24 разряда типа int в нули.

Исправленный вариант:

и далее вывод программы (только новая часть):

Ну и напоследок приведу табличку побитовых операций (не сдвиговых, т.к. это не имеет смысла)

В принципе это тема весьма нужная и полезная и развлекаться с примерами здесь можно очень долго, но нам надо двигаться вперед.

Хотя про еще одни грабли все таки стоит упомянуть. Это опять же касается операций сдвига. Перед тем как совершать любой побитовый сдвиг (например, x>>y) виртуальная машина java вычисляет остаток от деления y на ширину типа данных (для int 32 (y%32), для long 64 (y%64) и т. д.) и производит сдвиг на величину этого остатка. Поэтому, например, если мы задумаем сдвинуть значение типа int на 32 бита или 64 бита и т.п., каким либо оператором сдвига, то значение x останется прежним, потому что 32%32=0 (64%32=0).

А теперь, чтобы стало понятнее рассмотрим это на примере:

И вывод этой программы на консоль:

Как видим, там где мы сдвигали на 32 разряда, ни какого сдвига на самом деле не произошло по описанной выше причине.

Кроме того, при сдвиге на 48 позиций вправо, сдвиг на самом деле произошел на 16 позиций, по той же причине.

То есть можно заключить, что двигать переменную на количество бит равное или большее ее ширине в битах просто не имеет смысла, так как в этом случае сдвига или вовсе не будет или же будет на количество бит равное делению по модулю количества сдвигаемых бит, на ширину сдвигаемого типа.

Как получить остаток от деления в java

Арифметические операторы

В следующей таблице перечислены основные арифметические операторы (или операции), применяемые в языке Java:

Операция	Описание
+	Сложение (а также унарный плюс)
—	Вычитание (а также унарный минус)
*	Умножение
/	Деление
%	Деление по модулю

Рассмотрим некоторые правила работы с арифметическими операторами:

• Выражения вычисляются слева направо, если не добавлены круглые скобки или одни операции имеют более высокий приоритет.
• Операции * , / , и % имеют более высокий приоритет чем + и — .

Арифметические операторы над целочисленными значениями

Например, в этом коде, переменные a и b будут иметь разные значения:

Унарные операции сложения и вычитания

• Операция унарного вычитания изменяет знак своего единственного операнда.
• Операция унарного сложения просто возвращает значение своего операнда. Она в принципе не является необходимой, но возможна.

Деление целочисленных чисел в Java

Когда операция деления выполняется над целочисленным типом данных, ее результат не будет содержать дробный компонент. Это деление без остатка в Java:

Результат выполнения этой программы:

Арифметические операторы над переменными типа char

Операнды арифметических операторов должны иметь числовой тип. Арифметические операторы нельзя выполнять над логическими типами данных, но допускается над типами данных char , поскольку в Java этот тип, по существу, является разновидностью типа int .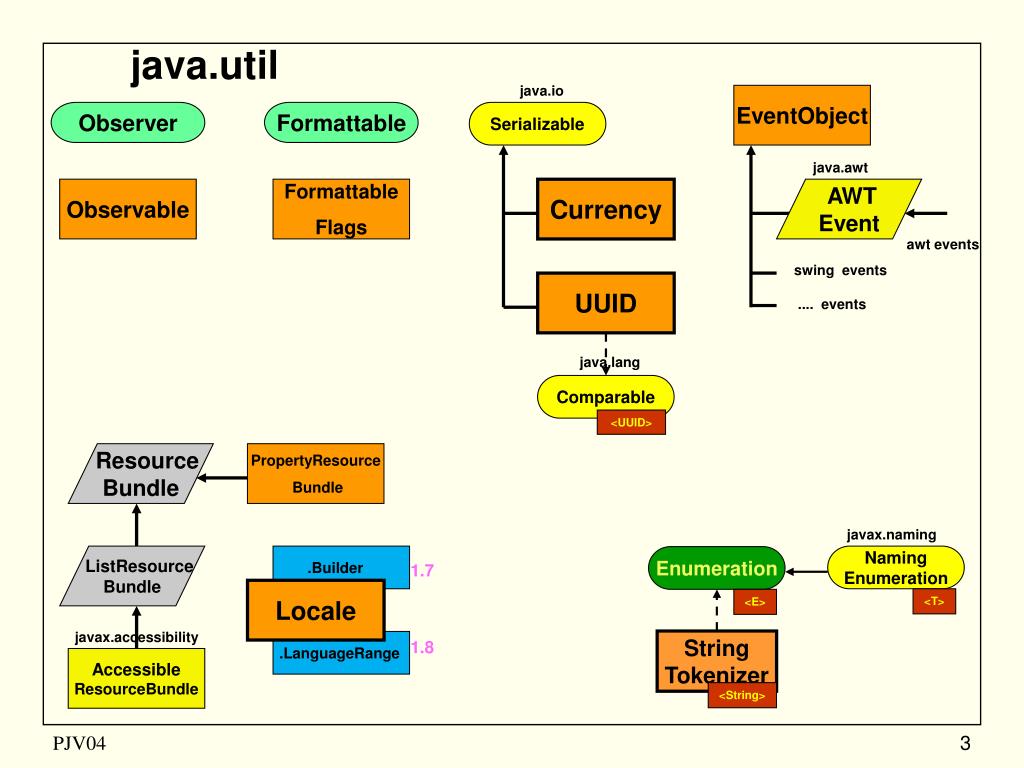 Например:

Или как в следующем примере:

Деление по модулю в Java

Оператор деления по модулю — обозначается символом % . Этот оператор возвращает остаток от деления первого числа на второй в Java. При делении целого числа результатом будет так же целое число:

2. Составные арифметические операции с присваиванием

Операция	Описание
+=	Сложение с присваиванием
-=	Вычитание с присваиванием
*=	Умножение с присваиванием
/=	Деление с присваиванием
%=	Деление по модулю с присваиванием

В Java имеются специальные операции, объединяющие арифметические операторы с операцией присваивания. Рассмотрим следующее выражение:

B Java эту операцию можно записать следующим образом:

Составные операции с присваиванием позволяют не только уменьшить объем кода, но и позволяют выполнять автоматическое преобразование чего не делают обычные операции:

Основы

Как и в любом языке программирования, в языке Java резервируются определенные слова, которые компилятор распознает как особые. Их нельзя использовать для именования конструкций Java: переменных, методов и т.д. Список ключевых слов не слишком велик:

abstract	assert	boolean	break	byte
case	catch	char	class	const
continue	default	do	double	else
enum	extends	final	finally	float
for	goto	if	implements	import
instanceof	int	interface	long	native
new	package	private	protected	public
return	short	static	strictfp	super
switch	synchronized	this	throw	throws
transient	try	void	volatile	while

Формально слова true, false и null не входят в число ключевых слов, но их тоже нельзя использовать в качестве имён переменных. Обратите внимание, что Android Studio выделяет ключевые слова в редакторе кода особым цветом (синтаксическая подсветка).

Переменные

Переменные используются для хранения данных. Переменные сначала должны быть объявлены, и только после этого ими можно пользоваться.

Как следует из названия, переменные могут меняться (точнее их значения). Проведём аналогию с кошачьим приютом. Котов привозят в приют, потом добрые люди забирают котов из него. Получается, что коты постоянно меняются, а приют остаётся.

Переменные могут быть двух видов

• примитивные типы: int, float, double, char и другие, которые представляют собой числа, символы
• объекты, которые представляют классы

Список переменных примитивных типов рассматривается в следующей статье.

Переменной можно присвоить начальное значение (инициализировать) через знак равенства и указанием значения. Указываемое значение должно подходить типу, который вы указали для переменной. Для объявления нескольких переменных одного типа можно использовать запятые:

Также возможна динамическая инициализация. Вам нужно только проследить, чтобы вычисляемое выражение соответствовало переменной.

В некоторых случаях нужно, чтобы переменная не менялась, в этом случае переменная называется константой и имеет ключевое слово final.

Переменные имеют свою область видимости. Она может быть доступна только внутри метода, цикла, класса. Подобная защита уменьшает риск ошибок от несанкционированного доступа или изменений от чужого кода. Также следует помнить, что внутри блока переменные можно объявить в любом месте, но они становятся допустимыми только после объявления. Если ситуация будет обратной, то конструкция будет бессмысленной и вам не разрешат так делать:

Переменные создаются при входе в их область видимости и уничтожаются при выходе из неё. Иными словами, переменная утратит своё значение сразу после выхода из области видимости. Поэтому, переменные, которые объявлены внутри метода, не будут хранить свои значения между обращениями к этому методу.

Если объявление переменной содержит инициализацию, то инициализация будет повторяться при каждом вхождении в блок, в котором она объявлена. Допустим, у нас есть блок:

При каждом вхождении в цикл переменной присваивается снова и снова значение 42. И хотя потом переменной присваивается значение 54, оно теряется при повторном вхождении в блок.

Блоки бывают вложенными, но тем не менее во внутреннем блоке нельзя объявлять переменные с тем же именем, что и во внешней области:

Оператор присваивания

Оператором присваивания является одиночный знак равенства (=):

Тип переменная должен соответствовать типу выражение. Оператор присваивания можно использовать в виде цепочки присваивания:

Оператор присваивания берёт значение правого выражения. Поэтому выражение z = 9 будет равно 9, после чего оно присваивается переменной y, а затем — переменной x.

Помните, что в сравнении используется другой оператор ==, а не оператор присваивания.

Комментарии

В Java используются три вида комментариев. Многострочные комментарии начинаются с символов /* и заканчиваются символами */. Однострочные комментарии начинаются с комбинации символов //. Причем, однострочный комментарий можно использовать не только на отдельной строке, но и после оператора.

Начинающим программистам необходимо писать комментариев как можно больше, так как, вернувшись к своему коду через месяц-другой, вы с трудом вспомните, что вы тут нашкодили накодили.

Существует ещё третий тип комментариев для создания самодокументирующего кода (комментарий документации). Но это отдельная тема для разговора.

В студии создание и управление комментариями можно упростить через меню Code. Там вы найдёте такие команды как Comment With Line Comment, Comment With Block Comment. Попробуйте самостоятельно разобраться с ними.

Backdoor!

С помощью комментария злобные программисты могут внедрить закладку в разрабатываемый софт. Если в комментариях программы использовать Unicode для переноса строки и после нее написать свой код, то IDE (Android Studio) будет отображать это как комментарий, но код будет выполняться.

На первый взгляд, код не должен выполняться. Но это не так. Можете проверить.

\u000a — это Unicode-символ переноса строки (он же \n). Сначала производится декодирование, а потом уже разбор самого кода. Получается, что сначала произойдёт перенос, а потом будет напечатан рабочий код. Следующий пример тоже рабочий.

Стиль оформления кода

Существует негласные правила оформления стиля при написании кода. Старайтесь их придерживаться. Также запоминайте оформление кода в документации и справочниках. Например, принято записывать имена классов с большой буквы (class JavaQuickCourseActivity). Если имя состоит из нескольких слов, то каждое слово в имени также начинается с большой буквы. Использовать символы подчеркивания или тире нежелательно (Java_Quick_Course_Activity или Java-Quick-Course-Activity).

Для методов и переменных используется такой же формат, только первый символ записывается с маленькой буквы, например, resultButton.

Константы принято писать только большими буквами — IDD_LIST_NAMES. В этом случае одного взгляда достаточно, чтобы сразу определить, что перед вами константа.

На первых порах вам этого достаточно.

Операторы

Как и везде, в Java есть операторы сложения (+), вычитания (-), умножения (*), деления (/), которые применимы к числам.

Оператор	Пример использования	Описание
+	a + b	Сложение а и b (также унарный плюс)
+	+a	Преобразование a в переменную типа int, если это переменная типа byte, short или char
—	a – b	Вычитание b из а (также унарный минус)
—	-a	Арифметическая инверсия а
*	a * b	Умножение а на b
/	a / b	Деление a на b
%	a % b	Вычисление остатка от деления а на b (деление по модулю)
++	a++	Приращение а на 1 с предварительным вычислением значения а (инкремент)
++	++a	Приращение а на 1 с последующим вычислением значения а
—	a—	Уменьшение а на 1 с предварительным вычислением значения а (декремент)
—	—a	Уменьшение а на 1 с последующим вычислением значения а
+=	a += b	Краткая форма записи a = a + b (сложение с присваиванием)
-=	a -= b	Краткая форма записи a = a – b (вычитание с присваиванием)
*=	a *= b	Краткая форма записи a = a * b (умножение с присваиванием)
/=	a /= b	Краткая форма записи a = a / b (деление с присваиванием)
%=	a %= b	Краткая форма записи a = a % b (деление по модулю с присваиванием)

Операнды арифметических операторов должны иметь числовой тип.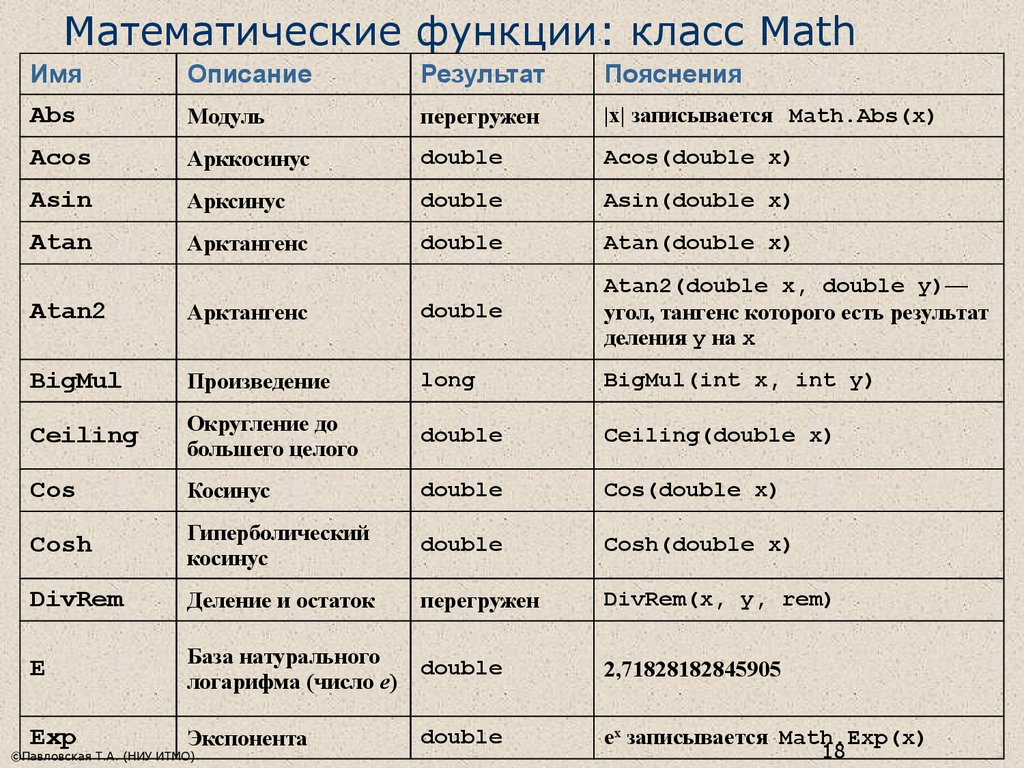 Нельзя использовать их к логическим типам. Можно применять к типам char, который по сути можно представлять как тип int.

Для строк можно использовать только операции + и +=. Умножать, вычитать и делить слова нельзя. Обратите внимание, что при сложении слов «мышь»+»мышь» получается не «мыши», как предположил мой кот Рыжик, а «мышьмышь». На самом деле символ + при работе со строками называется не сложением, а конкатенацией.

Оператор деления по модулю

Существует оператор, вычисляющий остаток от деления нацело (%). Чтобы запомнить данный знак, обратите внимание на наклонную черту, как в обычном делении, которую окружают два нолика. Деление нацело обрезает, а не округляет результат.

Если 42 разделить по модулю на 10, то получим значение 2, а если 42.56 разделить по модулю на 10, то получим 2.5600000000000023:

Деление по модулю очень удобно использовать для разбивки числа на части. Предположим вам надо получить последние две цифры 2013 года. Вот как можно это сделать:

Вот и другой пример. Предположим, у вас есть фильм «Кот в сапогах», продолжительность которого равна 135 минутам. Чтобы разбить это число на часы и минуты, нужно применить такой код:

В результате получим ответ: Кот в сапогах идёт 2 часа 15 минут.

Обратите внимание, что переменная minutes всегда будет содержать числа в диапазоне от 0 до 59.

Стоит запомнить одну особенность. При делении большого числа на меньшее, например (5 % 4), понятно, что остаток будет 1. При делении по модулю меньших чисел 0, 1, 2, 3 на число 4 получатся те же значения 0, 1, 2, 3.

Напоследок, остаётся сказать, что делить на 0 нельзя. У вас будет выводиться сообщение об ошибке либо на этапе компиляции, либо во время работы программы.

В задачнике есть упражнения с применением данного оператора: 1, 2

Приоритет

Если вы не прогуливали уроки математики, то знаете, что в сложных выражениях скобки позволяют определить порядок вычислений. Например, в выражении 2 + 3 * 4 сначала идет умножение, а потом сложение. Расставив скобки, мы можем сначала сложить два числа, а потом умножить:

Кстати, использование скобок не влияет на производительность программы. Поэтому можете не стесняться и расставлять их побольше.

Укороченная форма записи

В Java также можно использовать укороченную форму записи, чтобы одновременно произвести операцию и присвоение. Для укороченной записи используется оператор с последующим знаком равенства. Например, чтобы прибавить число 7 к переменной x и присвоить результат этой же переменной, используйте команду x += 7. Это справедливо и для других операторов:

Укороченная форма записи не только сокращает объём и время написания кода, но и работает более эффективно (хотя доказательств не знаю).

Автоувеличение и автоуменьшение на единицу

Очень часто вам придется увеличивать или уменьшать значение переменной на единицу. Поэтому существует специальные операторы увеличения (инкремента) и уменьшения (декремента).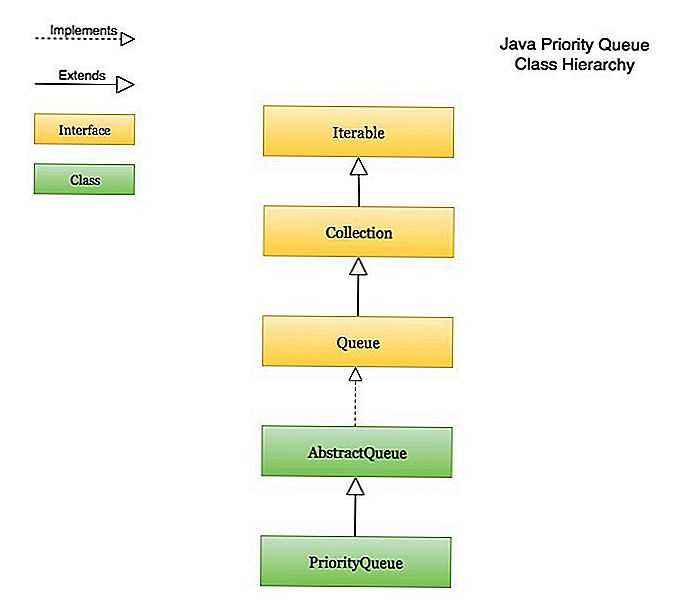 Для инкремента используются два плюса (++), а для декремента два минуса (—).

Данные операторы существуют в двух версиях — префиксной и постфиксной. Префиксный инкремент или декремент значит, что ++ или — записываются перед переменной или выражением.

В этом случае сначала выполняется операция, а затем выдается результат.

При постфиксном инкременте или декременте оператор записывается после переменной или выражения:

Здесь сначала выдается значение, и лишь затем выполняется операция.

Например, мы хотим ежегодно увеличивать возраст кота в анкете:

Данный код аналогичен более длинному варианту:

В простых выражениях особой разницы в постфиксной и префиксной формами нет, но в сложных выражениях может играть существенную роль. Поэтому не рекомендую использовать этот способ в выражениях, чтобы не запутаться самому. Пишите код проще.

Инкремент и декремент применяется только к значениям переменных, к числу применять этот способ нельзя.

По ссылке или по значению

У нас есть класс Cat

Попробуем, используя этот класс, передать объект Cat в метод и посмотреть, что получится:

Как получить остаток от деления в java

6 сентября 2014 Мария (admin)

В уроке 8 мы затронули логические операторы, они нам были необходимы для формирования логического выражения в условиях if. Этот урок будет посвящен математике в Java, и поэтому мы рассмотрим подробнее арифметические операторы и частично возможности класса Math.

Но для начала, выясним, что же такое операторы. Операторы это специальные символы, отвечающие за ту или иную операцию, например сложение, умножение, сравнение. Все операторы в Java можно разбить на 4 класса &#8212; арифметические, битовые, операторы сравнения и логические.

Арифметические операторы в Java

Для стандартных арифметических операций, таких как сложение, вычитание, умножение, деление в Java используются традиционные символы, к которым мы привыкли со школы:

Примечание: при операции деления, если оба аргумента являются целыми числами, то в результате получим целое число. Дробная часть, если такая имеется, отбросится. Если хотим получить число с дробной частью, то нужно, чтобы один из аргументов был типа double. Это можно указать в самом выражении при помощи добавления после числа . 0 или .d. Пример:

В Java также имеется специальный оператор %, обозначающий остаток от делния.

Пример использования: дан массив целых чисел, вывести на консоль только те числа, которые делятся на 3.

Операции с присваиванием

Рассмотрим задачу вывода на экран 10 первых четных чисел чисел

мы можем записать сокращенно

+= это оператор сложения с присваиванием. Подобные операторы есть для всех основных 5 операций, рассмотренных выше

Пример использования: Найти факториал числа 7.

Инкрементирование и декрементирование

Инкремент, обозначается ++ и увеличивает значение переменной на единицу. Декремент обозначается &#8212; и уменьшает значение на единицу. С инкрементом и декрементом мы часто встречаемся в цикле for.

Инкремент и декремент бывают двух форм

Различие префиксной и постфиксной формы проявляется только тогда, когда эти операции присутствуют в выражениях. Если форма префиксная, то сначала произойдет увеличение (или уменьшение) переменной на единицу, а потом с новым значением будет произведены дальнейшие вычисления. Если форма постфиксная, то расчет выражения будет происходить со старым значением переменной, а переменная увеличится (или уменьшится) на единицу после вычисления выражения. Пример

В первом случае сначала переменная a увеличится на 1, потом произойдет вычисление всего выражения. Во втором случае произойдет вычисление выражения при старом значении b = 3, и после вычисления b увеличится на 1, на результат в postfix это уже не повлияет.

Если вы поняли принцип работы постфиксного и префиксного инкремента/декремента, то предлагаю решить в уме такую задачу:

Вопрос: чему в итоге равны x и y? После того, как вы сделали предположение, проверьте его в java.

Задача со зведочкой. Дан код:

Какие числа будут выведены на экран? Почему? Разобраться самостоятельно.

Примечание: инкремент и декремент применяются только к переменной. Выражение вида 7++ считается недопустимым.

Математические функции и константы (класс Math)

Для решения задач нередко требуется использование математических функций.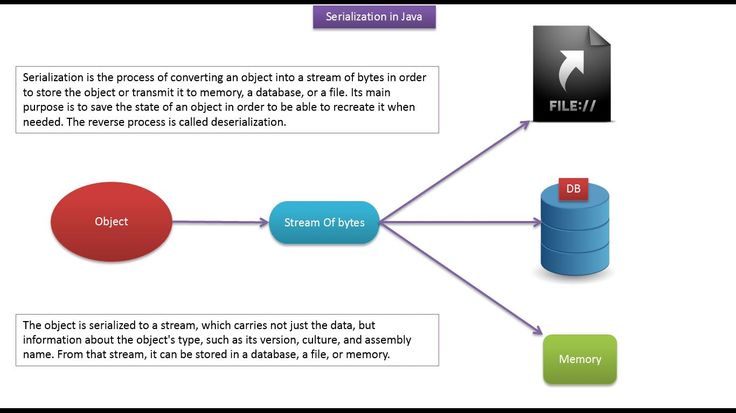 В Java такие функции включены в класс Math. Для того, чтобы использовать методы класса Math, нужно подключить его в начале .java файла с вашим кодом.

Часто используемые математические функции

• sqrt(a) &#8212; извлекает квадратный корень из числа а.
• pow(a, n) &#8212; a возводится в степень n.
• sin(a), cos(a), tan(a) &#8212; тригонометрические функции sin, cos и tg угла a указанного в радианах.
• asin(n), acos(n), atan(n) — обратные тригонометрические функции, возвращают угол в радианах.
• exp(a) &#8212; возвращает значение экспоненты, возведенной в степень a.
• log(a) &#8212; возвращает значение натурального логарифма числа a.
• log10(a) &#8212; возвращает значение десятичного логарифма числа a.
• abs(a) &#8212; возвращает модуль числа a.
• round(a) &#8212; округляет вещественное число до ближайшего целого.

Константы

• PI — число «пи», с точностью в 15 десятичных знаков.
• E — число «e»(основание экспоненциальной функции), с точностью в 15 десятичных знаков.

Упражнения

1. Дан массив целых чисел, найти среди элементов массива числа, которые делятся на 3 и на 6
2. Посчитать среднее арифметическое чисел в массиве
3. Известны катеты прямоугольного треугольника, найти его площадь и периметр
4. Даны два целых числа, найти их наибольший общий делитель и наименьшее общее кратное
5. Даны радиус вращения и высота конуса, вычислить объем конуса.

Категория: Уроки Java

Быстрый ввод адресов по ФИАС (ГАР), компаний по ЕГРЮЛ, банков, ФИО и email

Быстрый ввод адресов, компаний, банков, ФИО, email и ещё много чего

Адрес

мск сухонская 11 89

Квартира найдена в ГАР

Выберите вариант или продолжите ввод

г Москва, ул Сухонская, д 11, кв 89

г Москва, ул Сухонская, д 11А, кв 89

Нажмите, чтобы попробовать вживую

Индекс

127642

Регион

г Москва

Населенный пункт

Улица

ул Сухонская

Корпус

Квартира

89 34.

6 м²

«Подсказки» разложат адрес по полям
и расскажут другие полезные сведения

Дополнительная информация

Код ФИАС (ГАР)
f26b876b-6857-4951-b060-ec6559f04a9a

Часовой пояс
Московское время (UTC+3)

Район
Северное Медведково

Ближайшее метро
Бабушкинская (1.1 км)

Кадастровый номер
77:02:0004008:4143

Уровень по ФИАС
9 (квартира)

Геокоординаты
55.87826, 37.65372, внутри МКАД

Компания

моторика мос

Найдена в ЕГРЮЛ

Выберите вариант или продолжите ввод

ООО «МОТОРИКА»

77 19 40204 7 г Москва, г Троицк, Сиреневый б-р, д 1

ООО «МОТОРИКА»

40 28 05110 8 г Калуга ул Московская, д 328

Нажмите, чтобы попробовать вживую

Наименование

ООО «МОТОРИКА»

ИНН

7719402047

КПП

775101001

ОГРН

1157746078984

Адрес

108840, г Москва, г Троицк, Сиреневый б-р, д 1

Дата регистрации

05. 02.2015

Статус

Действующая

«Подсказки» заполнят реквизиты
и расскажут другие полезные сведения

Дополнительная информация

Генеральный директор
Чех Илья Игоревич

Учредители
Андрей Давидюк, Илья Чех,
Руслан Бабинцев, Василий Хлебников

ОКВЭД
72.19 (2014)
Научные исследования и разработки в области естественных и технических наук прочие

Налоговая инспекция
№ 46 по г. Москве (проезд Походный, д 3 стр 2)
код 7746

Финансы
Доходы 40 млн ₽, расходы 20 млн ₽, долгов и штрафов нет.

Количество сотрудников
18

Город, улица, дом, квартира

иностранные города

подсказки латиницей

муниципальное деление

[[ validationMessage ]]

Индекс

по данным Почты от 23 июня

Все поля заполняются
автоматически

Регион

[[ historyValues ]]

[[ address.

federal_district ]] фед. округ

Район

[[ centralArea ]]

[[ historyValues ]]

Город / н.п.

[[ capitalMarker ]]

[[ historyValues ]]

Улица

[[ historyValues ]]

Квартира

Площадь [[ address.flat_area ]] м², стоимость [[ flatPrice ]] ₽

кадастровый номер [[ address.flat_cadnum ]]

Зем. участок

кадастровый номер [[ address.stead_cadnum ]]

 копировать ссылку на адрес  ✓

OpenStreetMap ID

[[ address.fias_id ]]

Geoname ID

[[ address.geoname_id ]]

Геокоординаты

[[ geoLinkLabel ]] [[geoLinkDescription]]

Часовой пояс

[[ address.timezone ]]

ISO-код

[[ isoCodes ]]

Ближайшее метро

Геокоординаты

[[ geoLinkLabel ]] [[geoLinkDescription]]

Часовой пояс

[[ address.timezone ]]

ISO-код

[[ isoCodes ]]

Уровень по ФИАС

[[ fiasLevel ]]

Код ФИАС (ГАР)

Кадастровый номер

Код КЛАДР

[[ address. kladr_id ]]

Код ОКАТО

[[ address.okato ]]

Код ОКТМО

[[ address.oktmo ]]

Код ИФНС

[[ address.tax_office ]]

СДЭК

[[delivery.cdek_id]]

Boxberry

[[delivery.boxberry_id]]

DPD

[[delivery.dpd_id]]

запросить

Сведения актуальны на 11.10.2022

Индекс

Регион / район

Город / н.п.

От региона до дома
работают подсказки

Квартира

Площадь [[ address.flat_area ]] м², стоимость [[ address.flat_price ]] ₽

Сведения актуальны на 11.10.2022

Организация или ИП

[[ name ]]

[[ fullname ]]

Основной вид деятельности

[[ okved ]]

Юридический адрес

Город

[[ address ]]

на карте

Учредители

[[ founder | formatFounderName ]]

ИНН [[ founder.inn ]]

[[ founder.share | formatFounderShare ]] доля

Правопредшественники

[[ party.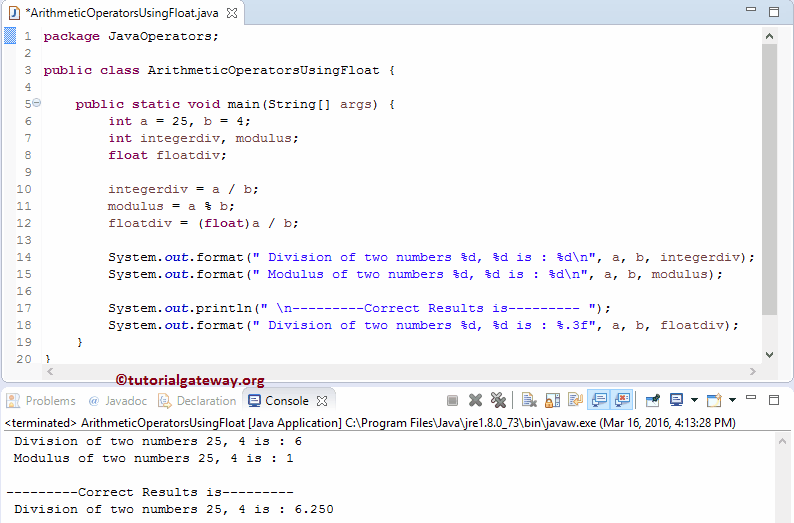 name ]]

ИНН [[ party.inn ]]

Правопреемники

[[ party.name ]]

ИНН [[ party.inn ]]

Реестр МСП

Коды статистики

ОКАТО: [[ party.okato ]]

ОКТМО: [[ party.oktmo ]]

ОКПО: [[ party.okpo ]]

ОКОГУ: [[ party.okogu ]]

ОКФС: [[ party.okfs ]]

[[ managerTitle ]]

[[ managerName ]]

[[ managerInn ]]

⚠️ дисквалифицирован

ОГРН

[[ party.ogrn ]]

от [[ registrationDate ]]

ИНН / КПП

[[ party.inn ]]

[[ party.kpp ]]

Статус

[[ status ]]

Реестр МСП

Коды статистики

ОКАТО: [[ party.okato ]]

ОКТМО: [[ party.oktmo ]]

ОКПО: [[ party.okpo ]]

ОКОГУ: [[ party.okogu ]]

ОКФС: [[ party.okfs ]]

Уставной капитал

Спец. налоговый режим

Доходы • [[ party. finance.year ]]

Расходы • [[ party.finance.year ]]

Недоимки

Штрафы

Телефон

[[ phone.value ]]

—

Email

[[ email.value.toLowerCase() ]]

—

Среднесписочная численность

[[ employeeCount ]]

Налоговая инспекция

Свидетельство о регистрации

[[ registration ]]

на сайте налоговой

Пенсионный фонд

Фонд соц. страхования

 копировать ссылку на организацию  ✓

Сведения актуальны на 17.10.2022

Банк

Наименование

[[ fullname ]]

БИК / SWIFT

ИНН / КПП

Корсчет

Казначейские счета

Рег. номер

Дата регистрации

 копировать ссылку на банк  ✓

Сведения актуальны на 15.10.2022

ФИО

[[ validationMessage ]]

Фамилия

Имя

Эти поля заполняются
автоматически

Отчество

Пол

И пол тоже!

Именительный:

[[ fio. result ]]

Родительный: кого?

[[ fio.result_genitive ]]

Дательный: кому? 

[[ fio.result_dative ]]

Творительный: кем?

[[ fio.result_ablative ]]

Падежи подключаются отдельно, через API стандартизации.

Фамилия

Имя

Для каждого из полей
работают подсказки

Отчество

[[ validationMessage ]]

Именительный:

[[ fio.result ]]

Родительный: кого?

[[ fio.result_genitive ]]

Дательный: кому? 

[[ fio.result_dative ]]

Творительный: кем?

[[ fio.result_ablative ]]

Падежи подключаются отдельно, через API стандартизации.

Справочник

Кем выдан паспортПочтовые отделенияНалоговые инспекцииТаможниМировые судыСтанции метроМарки автомобилейТовары и услугиСтраныВалютыДоменыОКВЭДОКПДОКТМО

Выбранная запись:

• [[ key ]]: [[ value ]]

Подключить бесплатно

10 тысяч запросов в день
≈ 300 введенных адресов

ввести один адрес	10–30 запросов
ФИО, email, компанию или банк	10–20 запросов

«Подсказки» помогут ввести

Почтовый адрес

По России и всему миру. Без опечаток, с почтовым индексом, привязкой к ФИАС (ГАР), районом города, метро и координатами.

Реквизиты компании и ИП

Название организации, адрес, ИНН, КПП, ОГРН, ОКВЭД, руководитель и прочее от налоговой

ФИО

Без опечаток и с полом

Email

Без опечаток

Банк

Название, ИНН, БИК, SWIFT, адрес и корр. счёт

И любые другие справочники

Кем выдан паспорт, почтовые отделения, метро, автомобили, страны, валюты и много других. Можно подключать собственные!

С чем работают «Подсказки»

• Битрикс24
• 1С
• Opencart
• WordPress
• Drupal
• amoCRM
• jQuery-плагин
• HTTP API

и ещё 80 готовых модулей

и ещё 80 готовых модулей

Если вы разработчик — сделайте свой модуль по гайдлайну, чтобы получить бесплатный пиар в рассылке и соцсетях Дадаты

Уже на 34 000 сайтов

«Подсказки» используют QIWI, OZON, KUPIVIP. RU, JOOM, METRO, ВсеИнструменты, ИЛЬ ДЕ БОТЭ, ЮМани, Росбанк и другие крупнейшие сайты Рунета.

До Дадаты было две проблемы:

1. Адреса написаны всегда по-разному, приходилось переспрашивать сам адрес и индекс.
2. Расчёт доставки вручную, клиент общался с менеджером по телефону.

Дадата помогла решить обе:

1. Адреса теперь стандартизированы — если человек не ввел адрес с точностью до дома, то заказ не оформляется. Это снимает нагрузку с менеджеров, и снижает вероятность ошибки.
2. Мы точно знаем код ФИАС каждого адреса и смогли интегрировать сайт с курьерской службой. Клиент сам выбирает способ доставки на сайте, а не по телефону с менеджером. Удобнее всем — и клиенту, и менеджерам.

Подключили Подсказки. Раньше на ручную обработку отправлялась до 35% адресов по Москве и МО, теперь не более 15%.

Удобное, современное и настраиваемое API и подсказки, «живой» контакт с разработчиками.

На форме заказа оставили одно поле для адреса и подключили подсказки «Дадаты». Конверсия в заказ выросла на 20%.

[[plan.header]]

50 тыс. запросов в день

Все поля по ФИО, email и банку

Базовые сведения по адресу и компании

Геокоординаты

Все города мира

Публичные справочники

100 тыс. запросов в день

Всё, что в «Лёгком», плюс:

Геокоординаты и расстояние до кольцевой

Все ОКВЭДы компании

Реквизиты налоговой и пенсионного фонда

Численность сотрудников и система налогообложения

is_active»>[[subscription.limit/1000]] тыс. запросов в день

[[option.description]] запросов в день

Всё, что в «Расширенном», плюс:

Площадь, стоимость и кадастровый номер квартиры

Ближайшее метро

Финансы, документы и лицензии компании

Учредители, руководители, правопреемники, контакты

Приватные справочники

Продлить или изменить

Счет для юрлиц — после регистрации

действует [[ subscription.end_date ]]

Бесплатный тариф

Как «Легкий», но с ограничением 10 тыс. запросов в день.

Инструкция по настройке

Что такое «запрос»

×

На каждый символ, который вводит человек, виджет «подсказок» отправляет отдельный запрос к «Дадате».

• Ввести один адрес: 10–30 запросов
• ФИО, email, компанию или банк: 10–20 запросов

При работе через API вы сами контролируете, сколько и каких запросов отправлять.

Базовые сведения по адресу

×

Почтовый индекс.

Адрес одной строкой, от региона до квартиры (Россия).

Отдельные поля адреса: регион, город, улица, дом, квартира (Россия).

Адрес одной строкой и отдельными полями от страны до города (остальные страны).

Геокоординаты.

Код ФИАС (ГАР), КЛАДР-код, ОКАТО, ОКТМО и ИФНС.

Базовые сведения по компании

×

Краткое и полное название, организационно-правовая форма.

Адрес одной строкой и гранулярный.

ОГРН, ИНН, КПП, основной ОКВЭД.

ФИО и должность руководителя.

Статус организации: действующая или ликвидирована.

Ваши собственные справочники

×

Вы можете подключить к «Дадате» собственный справочник:

• На бесплатном тарифе, а также тарифах «Лёгкий» и «Расширенный» он будет доступен всем остальным пользователям.
• На тарифе «Максимальный» можно загружать приватные справочники, скрытые от остальных.

API-сервисы

Все тарифы

Обратное геокодирование

Находит ближайший адрес по географическим координатам.

Город по IP-адресу

Определяет город с почтовым индексом по IP-адресу в России.

Адрес по коду

Возвращает всю информацию об адресе коду КЛАДР / ФИАС (ГАР) или кадастровому номеру.

Ближайшее почтовое отделение

Находит точное отделение по индексу или ближайшее — по координатам.

Идентификатор города в службе доставки

Для интеграции со СДЭК, Boxberry и DPD.

Организация по ИНН

Определяет реквизиты компании или ИП по ИНН или ОГРН.

«Максимальный»

Аффилированные компании

Находит организации по ИНН учредителей и руководителей.

Коробочная версия

Устанавливается на ваш сервер.

Подходит, если больше 1 млн запросов в день, или отдел безопасности запрещает использовать «облака».

Включает виджет для пользователей и API для программ.

Подключается к любым корпоративным справочникам.

Стоимость

825 тыс. ₽ за адреса или 1500 тыс. ₽ за все компоненты. Включает лицензию и обновления на 3 года для одного экземпляра «Подсказок».

Запросить договор

Прочие условия

Раздел

: Глоссарий Java Раздел

: Глоссарий Java

* 0-9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z (все) 900

• Вы здесь :
• дом
• Глоссарий Java
• Д-слова
• отдел
•  

© 1996-2017 2008-04-15 Roedy Green of Canadian Mind Products

отдел

В Java существует два вида деления: целочисленное и с плавающей запятой. Оба они используют оператор / для обеспечения вы их запутаете. Это зависит от того, являются ли окружающие его операнды int/long или float/double, какая форма используется. Целочисленное деление всегда дает целочисленный результат, без дробей, усеченный в сторону 0. Деление с плавающей запятой дает дробный ответ с точностью до Формат IEEE (Институт инженеров по электротехнике и электронике) позволяет.

Целое деление

Разделение с плавающей запятой

Деление с плавающей запятой всегда кажется немного от того, что вы ожидаете. Это потому, что многие общие десятичные дроби являются повторителями, когда они выражены в двоичном формате, который Java использует внутри.

Остаток

В Java вы берете остаток с помощью оператора % . В Java знак остатка следует за делимым, а не за делителем. Подразделение Java имеет Евклидово свойство. Когда вы умножаете частное на делитель и прибавьте полученный остаток к делимому. С другой стороны, когда вы просите % 3 в Java, вы можете быть поражены, иногда получая ответ снаружи диапазон 0..2. См. остаток/модуль правила подписи. Будьте особенно осторожны при объединении случайных чисел в меньшую группу. диапазон с помощью оператора %. У подразделения Java есть Евклидово свойство. Когда вы умножаете частное на делитель и прибавляете остаток вы получите обратно на дивиденды. Ява дивизия усеченный разделение.

Напольное отделение

Floored дивизия — это то, что вы обычно требуется при попытке выяснить, к какой ячейке принадлежит элемент. Вы можете вычислить округление в меньшую сторону несколько.

Коэффициент покрытия

Для вычисления количества ячеек фиксированного размера вам нужно содержать N элементов, вам нужно потолочное деление, также известное как покрыл частное . Вы можете вычислить покрытое частное как: округление до следующего большего кратного.

Оттачивая свою интуицию

Изучив закономерности в следующие таблицы / целочисленного деления, у вас будет лучшая интуиция того, как это работает.

	Целочисленное деление: столбец/ряд
	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10
-10	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	-1	-10
-9	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	-1	-1	-9
-8	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	-1	-1	-1	-8
-7	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	-1	-1	-1	-1	-7
-6	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	-1	-1	-1	-1	-1	-6
-5	2	1	1	1	1	1	0	0	0	0	0	0	0	0	0	-1	-1	-1	-1	-1	-2	-5
-4	2	2	2	1	1	1	1	0	0	0	0	0	0	0	-1	-1	-1	-1	-2	-2	-2	-4
-3	3	3	2	2	2	1	1	1	0	0	0	0	0	-1	-1	-1	-2	-2	-2	-3	-3	-3
-2	5	4	4	3	3	2	2	1	1	0	0	0	-1	-1	-2	-2	-3	-3	-4	-4	-5	-2
-1	10	9	8	7	6	5	4	3	2	1	0	-1	-2	-3	-4	-5	-6	-7	-8	-9	-10	-1
0	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	0
1	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10	1
2	-5	-4	-4	-3	-3	-2	-2	-1	-1	0	0	0	1	1	2	2	3	3	4	4	5	2
3	-3	-3	-2	-2	-2	-1	-1	-1	0	0	0	0	0	1	1	1	2	2	2	3	3	3
4	-2	-2	-2	-1	-1	-1	-1	0	0	0	0	0	0	0	1	1	1	1	2	2	2	4
5	-2	-1	-1	-1	-1	-1	0	0	0	0	0	0	0	0	0	1	1	1	1	1	2	5
6	-1	-1	-1	-1	-1	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	6
7	-1	-1	-1	-1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	7
8	-1	-1	-1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	8
9	-1	-1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	9
10	-1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	10
	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10

Узнать больше

JLS (спецификация языка Java): порядок оценки выражения

JLS : подразделение

*
+
++
—
—
оператор присваивания
ceil
плавающая запятая
пол
смешанная база
модуль: % оператор
умножение
оператор
приоритет

остаток

---

стандартный нижний колонтитул

	Эта страница размещена в Интернете по адресу:	http://mindprod.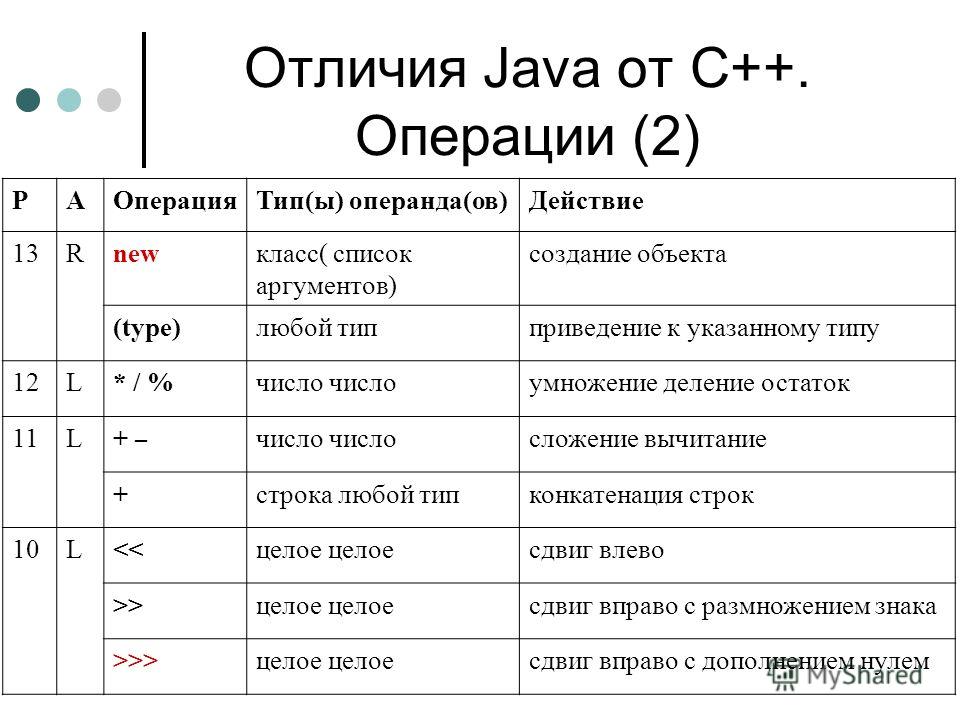 com/jgloss/division.html
	Дополнительное зеркало репликатора сайта mindprod.com на локальном жестком диске J:	J:\mindprod\jgloss\division.html
	Пожалуйста, ознакомьтесь с отзывами других посетителей, или отправить свой отзыв о сайте. Связаться с Роуди. Пожалуйста, не стесняйтесь ссылаться на эту страницу без явного разрешения.
	канадский Разум Товары IP: [65.110.21.43] IP вашего лица: [161.97.168.212]
Обратная связь	Вы посетитель номер

Документация JDK 19 — Домашняя

1. Домашняя
2. Ява
3. Ява SE
4. 19

Обзор

• Прочтите меня
Примечания к выпуску
• Что нового
• Руководство по миграции
• Загрузить JDK
• Руководство по установке
• Формат строки версии

9Инструменты 1257

• Спецификации инструментов JDK
• Руководство пользователя JShell
• Руководство по JavaDoc
• Руководство пользователя средства упаковки

Язык и библиотеки

• Обновления языка
• основных библиотек
• HTTP-клиент JDK
• Учебники по Java
• Модульный JDK
• Руководство программиста API бортового регистратора
• Руководство по интернационализации

Технические характеристики

• Документация API
• Язык и ВМ
• Имена стандартных алгоритмов безопасности Java
• банок
• Собственный интерфейс Java (JNI)
• Инструментальный интерфейс JVM (JVM TI)
• Сериализация
• Проводной протокол отладки Java (JDWP)
• Спецификация комментариев к документации для стандартного доклета
• Прочие характеристики

Безопасность

• Руководство по безопасному кодированию
• Руководство по безопасности

Виртуальная машина HotSpot

• Руководство по виртуальной машине Java
• Настройка сборки мусора

Управление и устранение неполадок

• Руководство по устранению неполадок
• Руководство по мониторингу и управлению
• Руководство по JMX

Client Technologies

• Руководство по специальным возможностям Java

Деление с помощью побитовых операций

Получить эту книгу -> Задачи на массив: для интервью и конкурентного программирования

В этой статье мы увидим, как разделить число с помощью побитового оператора 9. 1368 >> вместо обычного оператора деления / или оператора умножения * или оператора по модулю % .

Содержание :

1. Введение в раздел
2. Резюме необходимых побитовых операций
3. Деление с помощью оператора сдвига влево
4. Сложность времени и пространства
5. Заключение

Теперь мы рассмотрим алгоритм побитового алгоритма.

Таким образом, задача здесь состоит в том, чтобы разделить данное число на другое число и вернуть минимальное значение, то есть просто десятичное частное, но мы должны использовать побитовые операторы, а не обычные операторы, такие как * / % , для деления числа.

давайте посмотрим на это на примере, рассмотрим 96 и 7
96 / 7 = 13,71 и его минимальное значение равно 13

Итак, нам нужно написать функцию, используя функцию, чтобы сделать это побитовые операторы.

Прежде чем мы перейдем к проблеме, давайте быстро вспомним об операторах побитового сдвига, потому что именно их мы собираемся использовать для решения этой проблемы.

Оператор побитового сдвига влево

Оператор сдвига влево используется для сдвига заданного числа влево на определенное количество битов, как показано ниже.

Но что происходит, когда мы оставляем смену? давайте посмотрим поближе.

Мы знаем, что двоичная система счисления основана на степени двойки. Взглянув на таблицу, мы видим, что позиционный вес каждого из следующих битов в два раза больше предыдущего бита, т.е. его мощность увеличивается на 1. Как В результате, когда мы сдвигаем число влево на 1 бит, все число умножается на 2 в степени 1. Точно так же, когда число сдвигается влево на n бит, это означает, что число умножается на 2 в степени n.

Например. 25 << 1 = 50 (25 * 2 в степени 1)
25 << 3 = 200 (25 * 2 в степени 3)

Таким образом, в общем случае, если вы сдвинете число влево на n бит, оно умножается n раз на 2.

Оператор побитового сдвига вправо

Оператор сдвига вправо сдвигает биты вправо. Это означает, что он делает прямо противоположное оператору сдвига влево, т. е. каждый раз, когда мы сдвигаем число вправо на 1 бит, оно делит это число на 2.

Например. 96 >> 1 = 48

Теперь, когда мы получили достаточное представление об операторах сдвига, давайте воспользуемся ими для деления числа на другое число.

Возьмем два числа a = 96 и b = 7 . Когда мы делим на на на , мы вычисляем, сколько раз на равно на или сколько на может поместиться внутри на . В этом случае мы можем поместить 13 b в a т.е. a / b = 13 (Примечание: здесь мы вычисляем только минимальное значение)

Мы знаем, что каждое число может быть представлено как сумма степеней двойки, а также когда мы сдвигаем число влево на n бит умножается на 2 степень n . Таким образом, мы сдвигаем делитель b влево и проверяем, меньше ли он делимого a или равен ему. Если он меньше или равен дивиденду, мы вычитаем его из дивиденда и прибавляем значение 9.1368 2 power n на наш ответ. Сделав это, мы получим наш ответ в виде суммы степеней двойки, что даст нам требуемое частное.

И мы повторяем этот процесс для степеней двойки от 31 до 0. Здесь мы выбрали 31, потому что обычно размер целочисленного типа данных составляет 32 бита, т.е. он начинается с 0 и продолжается до 31.

Шаги

1. Первоначально установите переменную ответа, т. е. частное, равным 0 .

2. Проверить, является ли какое-либо из чисел отрицательным, и сохранить его в отдельной переменной.

3. Сделайте оба числа положительными.

4. Начать с n = 31 старшего бита и выполнить цикл до n = 0 младшего значащего бита.

5. И, наконец, верните частное после проверки, должно ли оно быть положительным или отрицательным с результатом шага 2.

 по определению bit_div(a,b):
    ans = 0 # инициализируется частное
    neg = a < 0 или b < 0 # Проверка, является ли одно из чисел отрицательным
    a = abs(a) # убедитесь, что оба числа
    b = abs(b) # положительны
    for i in range(31,-1,-1): # запуск нашего цикла
        if b << i <= a : # проверка того, что b, умноженное на 2**i, равно <= a
            a -= b << i # вычитание b << i из a
            ans += 1 << i # добавление 2 степени i к ответу
    # и, наконец, проверка, должен ли вывод быть отрицательным, и возвращение его
    вернуть ответ, если отрицательный == 0 иначе -1 * ответ
 

.
Теперь давайте разберем этот код.

Мы получаем два числа a и b в качестве входных данных, а затем инициируем переменную и для хранения нашего окончательного ответа, то есть частного. Затем мы проверяем, является ли одно из чисел отрицательным, но зачем мы это делаем? Потому что, если одно из чисел отрицательное, частное также будет отрицательным, но если оба числа положительные или оба отрицательные, ответ будет положительным.

Затем мы берем абсолютное значение обоих чисел, что делает их оба положительными. Затем мы начинаем нашу петлю. Мы начинаем с 31 старший значащий бит , потому что, как было сказано ранее, размер целого числа составляет 32 бита, и переходим к 0 младшему значащему биту . И во время каждой итерации мы проверяем, является ли b << i , то есть b, умноженное на 2 в степени i , меньше или равно a дивиденда. Если это правда, мы вычитаем b << i из делимого a и обновляем его, а затем добавляем 1 << i , что равно 2 степени i к переменной ответа и . мы делаем это, пока цикл не достигнет 0 .

И, наконец, мы проверяем, должен ли ответ быть отрицательным или положительным, используя значение переменной neg , и возвращаем его в правильном виде.

Давайте рассмотрим это на примере, чтобы лучше понять,

рассмотрим a = 96 и b = 7

Итак, поток управления выглядит следующим образом,

1. инс = 0
2. neg = 0 т. е. False (поскольку и 96, и 7 положительны)
3. Поскольку оба числа положительные, абсолютное значение совпадает с числом.
4. Тогда цикл начинается с i = 31
5. До i = 4 , если оператор не выполняется, так как 7 << i больше, чем 96 .
6. Когда i = 3 значение 7 << i — это 56 , что меньше, чем 96 , поэтому оно входит в оператор if.
   • а = 40 ( а = а - b << i т. е. а = 96 - 56 )
   • анс = 8 ( анс += 1 << i т.е. анс = 0 + 8 )
7. Теперь, i = 2 значение 7 << i равно 28 , что меньше 40 текущее a
   • а = 12
   • анс = 12 т. е. 8 + 4
8. Теперь i = 1 снова 7< (14) больше, чем a , т. е. 12 , поэтому не выполняется.
9. И тогда i становится 0
   • а = 5
   • анс = 13 т. е. 12 + 1
10. И цикл заканчивается, и мы остаемся без напоминания 5 92) , где а — делимое.

    Это связано с тем, что каждая операция сдвига влево занимает время O(log a). Короче говоря, деление основано на операции умножения, а временная сложность базового алгоритма умножения — это временная сложность операции деления.