Цилиндр с вырезом в трех проекциях: Построение фигуры-цилиндр с вырезом

Содержание

Построить три проекции тела с вырезом — Dudom

Пример 1. Вырез на конусе (рис.142).

Рис.142

Вырез произведен двумя плоскостями. Одна проходит через вершину конуса и рассечет его поверхность по образующим. Вторая плоскость — фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей.

1. Отметим фронтальные проекции характерных точек для построения выреза — А», В», С», M»,N» (рис. 143).

2. Точки D и Е выбраны произвольно для построения эллипса, т.к. линия среза от А до СN представляет собой часть эллипса.

3. Найдем горизонтальные проекции точек А, В, С, D, Е, N. Точки лежат на поверхности конуса, а значит, они лежат на линиях, принадлежащих поверхности конуса. Горизонтальные проекции точек М и В, D и E найдены на окружностях, принадлежащих поверхности конуса. Точки

С и N — на образующих S₁ и S₂.

4. Соединяем полученные горизонтальные проекции. S’С’ и S’N‘ – прямые, C’, B’, D’, A’, E’, M’, N’ – кривая линия — часть эллипса (рис. 142).

Рис.143

Рис.144

Строим профильную проекцию конуса и профильные проекции точек. Соединяем их (рис.145).

Пример 2. Вырез на цилиндре (рис.146).

Вырез произведен тремя плоскостями. Наклонные фронтально-проецирующие плоскости рассекут цилиндр по части эллипса, ограниченного прямой. Плоскость, параллельная оси вращения, пересекает поверхность цилиндра по образующим.

1. Отметим на фронтальной проекции выреза фронтальные проекции A»,F»,G»,K»,L»,P». Характерные точки D»,E» ,M»,N» — на оси симметрии цилиндра, B»,C»,T»,V » — отмечены произвольно на линии, принадлежащей поверхности цилиндра. Все точки принадлежат боковой поверхности цилиндра, которая проецируется в окружность на горизонтальной плоскости проекций.

Поэтому все горизонтальные проекции точек принадлежат этой окружности (рис.147).

Рис.147

Найдем профильные проекции всех точек. Затем полученные точки соединяем. Линия GECABDF — часть эллипса, FK и GL отрезки прямых, GF и KL-отрезки прямых, LNVPTMK — часть эллипса (рис. 148).

Рис.148

Пример 3. Вырез на призме (рис.149).

Рис.149 Hbc

Пример 4. Вырез на пирамиде (рис.150).

Пример 5. Вырез на сфере (рис. 151

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9122 —

| 7289 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Пошаговое руководство решения задачи №6 — построение линии пересечения сферической поверхности от сквозного призматического выреза.

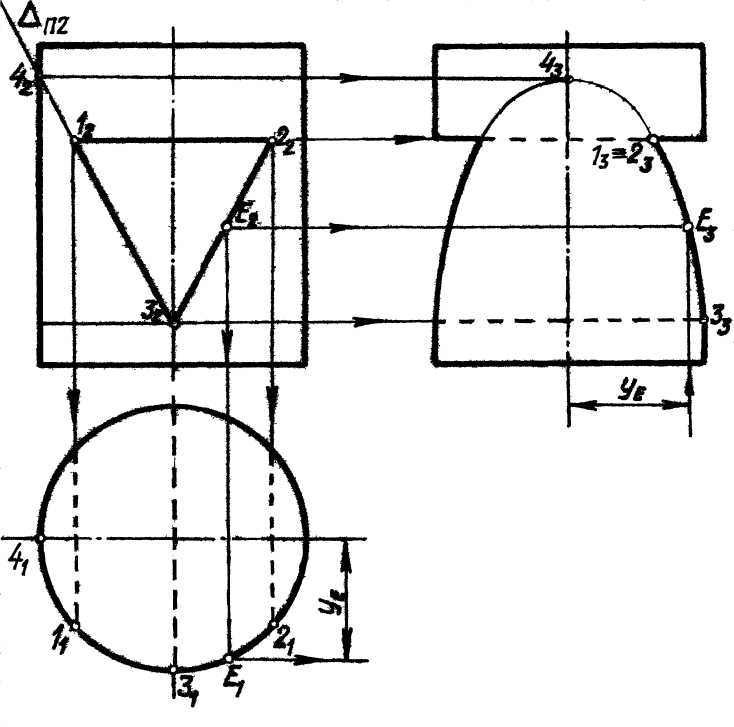
Необходимо построить линию пересечения сферической поверхности (шара) от сквозного призматического выреза, состоящего из четырех граней (проецирующих плоскостей). Фронтальная проекция линии пересечения заданных поверхностей (шара и многогранника) задана исходным чертежом, требуется построить ее в горизонтальную и профильную проекции.

Для решения такой задачи по начертательной геометрии необходимо знать:

— построение трех проекций сферической поверхности (шара) по заданным координатам, на комплексном чертеже;

— построение линии пересечения шаровой поверхности с гранным телом;

— частные случаи построения линии пересечения шаровой поверхности с проецирующей плоскостью.

Порядок решения Задачи

Рис.6.1

1. В правой части листа формата A3 наносятся оси координат и согласно варианту задания строится фронтальная, горизонтальная и профильная проекции сферы (шара) заданного радиуса.

По координатам точек, взятым из таблицы по своему варианту, наносятся вершины сквозного четырехгранного выреза во фронтальной проекции (рис.6.1).

2. Решение задачи заключается в построении горизонтальной и профильной проекции линии пересечения данного выреза.

Прежде чем приступить к построению этих проекций, необходимо вспомнить некоторые частные случаи сечений шаровой поверхности от проецирующей плоскости (сквозное отверстие можно рассматривать как гранное тело, образованное четырьмя плоскостями), а именно:

(а) если плоскость во фронтальной проекции рассекает шаровую поверхность параллельно экватору, то в горизонтальной проекции это сечение проецируется в виде окружности с радиусом, взятым в этом сечении от оси вращения шара до очерка, а в профильной проекции это сечение проецируется в виде прямой линии;

(b) если плоскость во фронтальной проекции рассекает шаровую поверхность перпендикулярно экватору, то в горизонтальной проекции это сечение проецируется в виде прямой линии, а в профильной — в виде окружности с радиусом, взятым тем же способом что и в первом случае;

(c) если плоскость во фронтальной проекции рассекает шаровую поверхность под некоторым (отличным от 0 и 90 градусов) углом к экватору, то в горизонтальной и фронтальной проекциях это сечение будет проецироваться в виде эллипса. Построение эллипса осуществляется по опорным (характерным) и некоторым промежуточным, взятым произвольно, точкам;

(d) все точки фронтальной проекции сферы, расположенные на очерке, в горизонтальной проекции будут проецироваться на экваторе, а в профильной — на главном меридиане;

(e) все точки фронтальной проекции сферы, расположенные на экваторе, в горизонтальной проекции будут проецироваться на очерке, а в профильной — на экваторе;

(f) все точки фронтальной проекции сферы, расположенные на главном меридиане, в горизонтальной проекции будут проецироваться также на главном меридиане, а в профильной — на очерке сферы.

Рис.6.2

3. С учетом приведенных частных случаев сечений построение выреза в горизонтальной и профильной проекциях не вызывает особых затруднений и начинается с определения характерных (опорных) точек сквозного выреза во фронтальной проекции. Этими точками являются А, В, С, D. Тогда берем проекцию стороны призмы B’C’ и рассматриваем ее как проецирующую плоскость ’, рассекающую шар параллельно экватору, — строим в горизонтальной проекции окружность с радиусом r₁ взятым в этой плоскости, от оси шара до очерка. Проецируем на эту окружность точки B’ и C’, получаем B и C — их горизонтальные проекции. Вполне очевидно, что этих точек будет по две (точки входа и выхода), т.к. отверстие сквозное.

Аналогичным способом строится проекция сечения плоскости А’D’. Берется радиус от оси сферы до очерка (разумеется не до точки A’) и в горизонтальной проекции проводится окружность этим радиусом.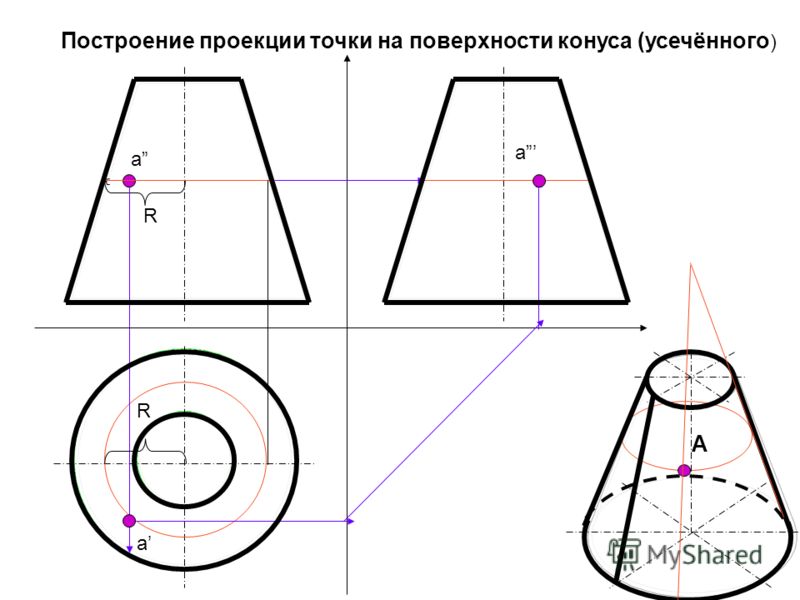 Проецированием находятся проекции точек D (их будет две — точка входа и точка выхода) — D и D₁ и промежуточной точки, расположенной на экваторе.

Рис.6.3

Сторона четырехугольника СD горизонтальной проекции проецируется в прямую линию, причем эта линия должна начинаться от очерка, т.к. во фронтальной проекции
она пересекает экватор шара и продолжается до точек С и D.

Рис.6.4

Горизонтальной проекцией сторон четырехугольника АВ будет эллипс, строим его по характерным (опорным) точкам. Проецируем точки, расположенные на меридиане, экваторе и очерке фронтальной проекции соответственно на меридиан, очерк и экватор горизонтальной проекции. Соединяя их по лекалу с уже имеющимися
проекциями точек B и B₁, и получаем искомую проекцию эллипса.

4. Аналогичным способом строится третья профильная проекция данного выреза (вид слева), поэтому нет надобности в подробном изложении четырехугольника ВС и АD будут проецироваться в прямые линии, СD – в окружность, AB – в эллипс.

Рис.6.5

5. Заключительным этапом в решении задачи является определение видимости сторон сквозного выреза, которая определяется из расположения их на сопряженной плоскости проекций. Тогда видимыми точками и линиями в горизонтальной плоскости будут точки и линии, которые во фронтальной — расположены выше экватора и на профильной проекции видимыми будут точки и линии которые на фронтальной плоскости расположены левее меридианы.

Экватор и меридиан являются границами видимости. Точки и линии, расположенные ниже экватора и правее меридиана во фронтальной проекции, в горизонтальной и профильной проекциях будут невидимыми.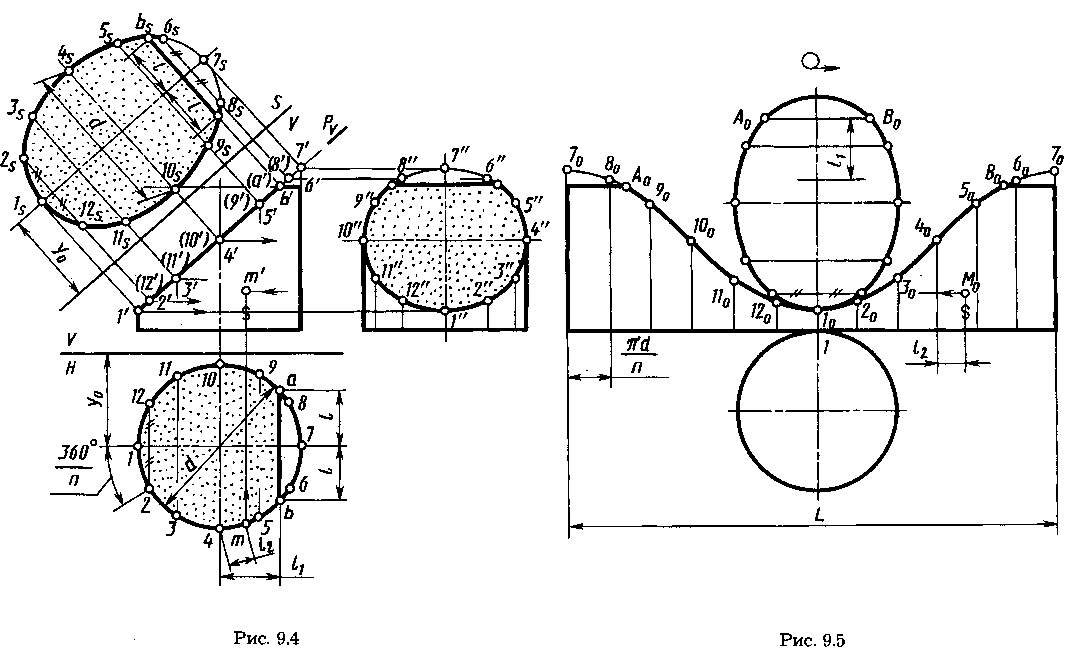

Пример 1. Построить три проекции цилиндра с вырезом (рис. 147).

Отмечаем характерные точки выреза А, В, С, Д, Е, F, а также произвольную точку к для построения профильной проекции части эллипса. Горизонтальные проекции точек отмечаем на горизонтальном очерке цилиндра, так как горизонтальная проекция боковой поверхности цилиндра совпадает с горизонтальным очерком (рис .148)

Построение профильной проекции выреза показано на рис. 149. Для этого целесообразно ось x ₁₂ провести через ось симметрии горизонтальной проекции,а ось x ₂₃ через профильную ось симметрии.

Пример 2. Построить три проекции конуса с вырезом (рис. 150).

Отмечаем характерные точки вареза А, В, С, Е, K, а также произвольную точку D для построения части эллипса. Горизонтальные проекции точек отмечаем на образующих конуса и вспомогательных окружностях (рис. 151).

На рис. 152 показано построение профильной проекции конуса с вырезом.Для этого целесообразно ось x ₁₂ провести через ось симметрии горизонтальной проекции, а ось x ₂₃ через профильную ось симметрии.

Пример 3. Построить три проекции вырезе на призме (рис. 153).

Решение показано на рис. 154

Пример 4. Построить три проекции выреза на пирамиде (рис. 155).

Отмечаем фронтальные проекции характерных точек выреза – это точки 1₂, 2₂, 3₂, 4₂, 5₂, 6₂. Для нахождения горизонтальных проекций точек 4 и 5 проводим по поверхности пирамиды две вспомогательные линии, параллельные основанию пирамиды ABC. Горизонтальные проекции этих линий являются треугольниками, параллельными горизонтальной проекции основания А₁В₁С₁.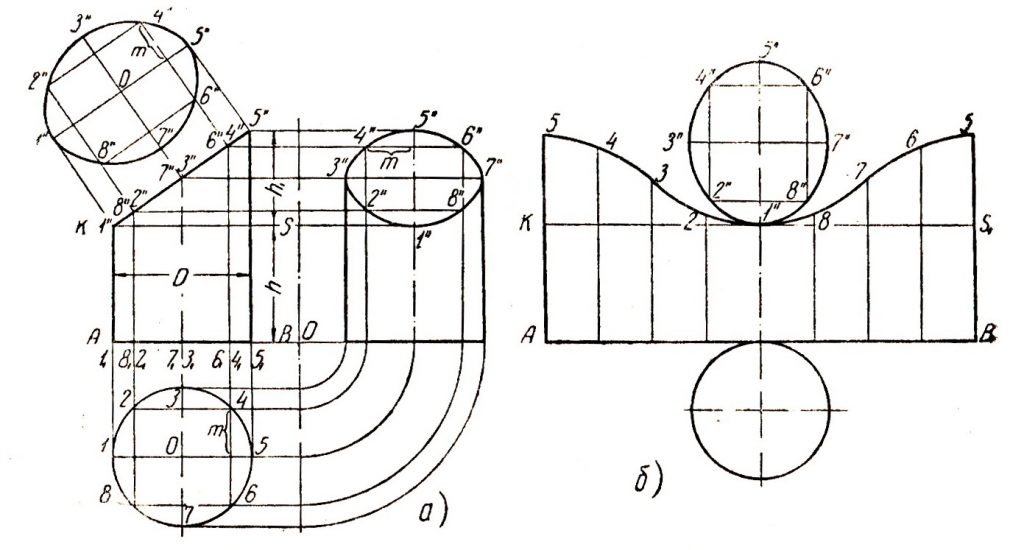 На этих треугольниках отмечаем горизонтальные проекции точек 4 и 5 (рис. 156).

Затем строим профильную проекцию пирамиды и точек выреза. Для этого оси целесообразно провести как показано на рис. 157.

Пример 5. Построить три проекции выреза на сфере (рис. 158).

Вырез образован двумя фронтально-проецирующими плоскостями α и τ, горизонтальной плоскостью φ, двумя профильными плоскостями β и γ. Горизонтальная плоскость пересекает поверхность сферы по части окружности, ограниченной прямой. Фронтально-проецирующая плоскость пересекают поверхность сферы по окрухностям, которые на горизонтальной и профильной плоскости проецируются как части эллипсов. Профильная плоскость пересечет поверхность сферы по части окружности, которая на профильной плоскости спроецируется как часть окружности (рис. 159).

Построение профильной проекции показано на рис. 160

Метрические задачи

Дата добавления: 2018-10-15 ; просмотров: 1914 | Нарушение авторских прав

Образование и изображение поверхностей вращения.

Алгоритм построения выреза на поверхностях, страница 3

Математика \ Начертательная геометрия и инженерная графика

2. На фронтальной проекции очерк выреза представляет собой треугольник, а опорные точки выреза являются его вершинами.

3. С помощью линий связи и дополнительных секущих плоскостей определяем горизонтальные проекции точек, принадлежащих очерку выреза. Точки находятся на пересечении линий связи, проведенных с фронтальной проекции и контуров фигур сечения, образованных от дополнительных секущих плоскостей.

Рис. 68

4. Строится профильная проекция выреза с помощью линий связи, проведенных из фронтальных и горизонтальных проекций опорных точек.

5. Найденные проекции точек, принадлежащие очерку выреза, соединяются между собой прямыми линиями.

6. Так как вырез представляет собой трехгранную призму, штриховыми линиями изображаются ее невидимые ребра (рис. 68).

Пример. Построить ортогональные проекции цилиндра со сквозным вырезом (рис. 69).

Алгоритм решения задачи

1. Форма выреза представляет собой цилиндр, опорными точками которого являются точки, находящиеся на пересечении очерка выреза и осевых линий (на фронтальной проекции).

Рис.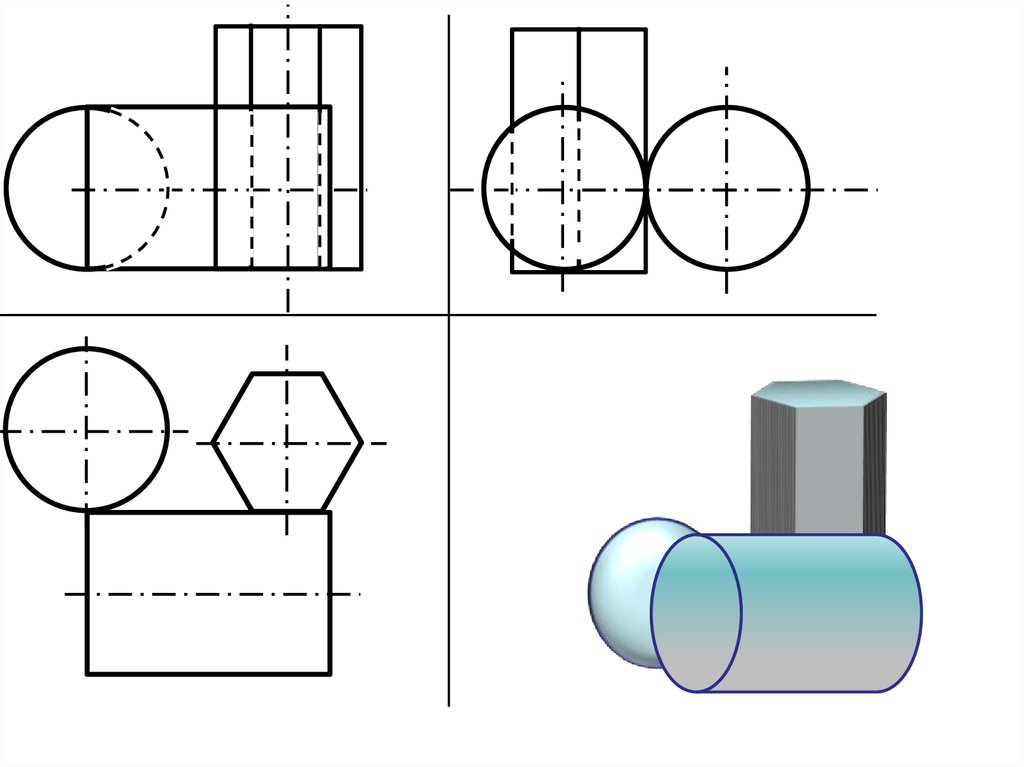 69

2. С помощью линий связи достраиваются проекции опорных точек. Так как самая высокая и низкая точки выреза лежат на вертикальной оси симметрии, то на профильной проекции они будут находиться на очерке. Точки, располагающиеся на горизонтальной оси симметрии, будут лежать на горизонтальной проекции цилиндра на очерке.

3. Вырез представлен отверстием цилиндрической формы. В связи с этим на горизонтальной проекции его очерк будет отображен дугой.

4. Так как вырез в цилиндре является сквозным отверстием, то на горизонтальной и профильной проекциях он изображается прямой линией невидимого контура (штриховой).

Пример. Построить три проекции конуса с вырезом (рис. 70).

Построение осуществляется по указанному алгоритму (табл. 6). Опорными точками на фронтальной проекции будут точки, располагающиеся на пересечении очерка выреза с контуром фигуры и осевых линий (рис. 70).

Рис.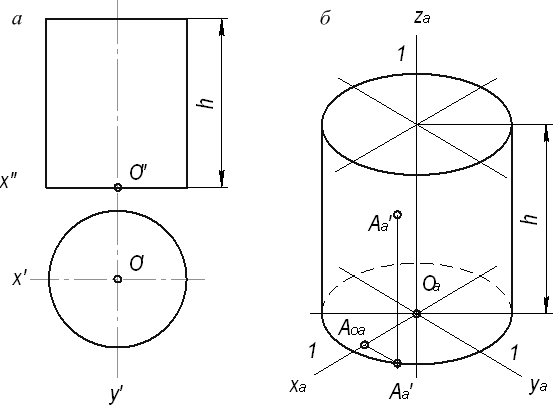

9. ПОСТРОЕНИЕ ПРОЕКЦИЙ ГЕОМЕТРИЧЕСКИХ ТЕЛ, УСЕЧЕННЫХ ПЛОСКОСТЬЮ

На практике часто приходится выполнять чертежи объектов, форма которых представляет собой геометрические тела, усеченные одной или несколькими секущими плоскостями.

Построение проекций геометрических тел, усеченных плоскостью, сводится к построению точек, принадлежащих как секущей плоскости, так и самой поверхности. Секущие плоскости, перпендикулярные одной из плоскостей проекций, отображаются на ней в виде прямой линии. На других проекциях видно изображение плоской фигуры сечения.

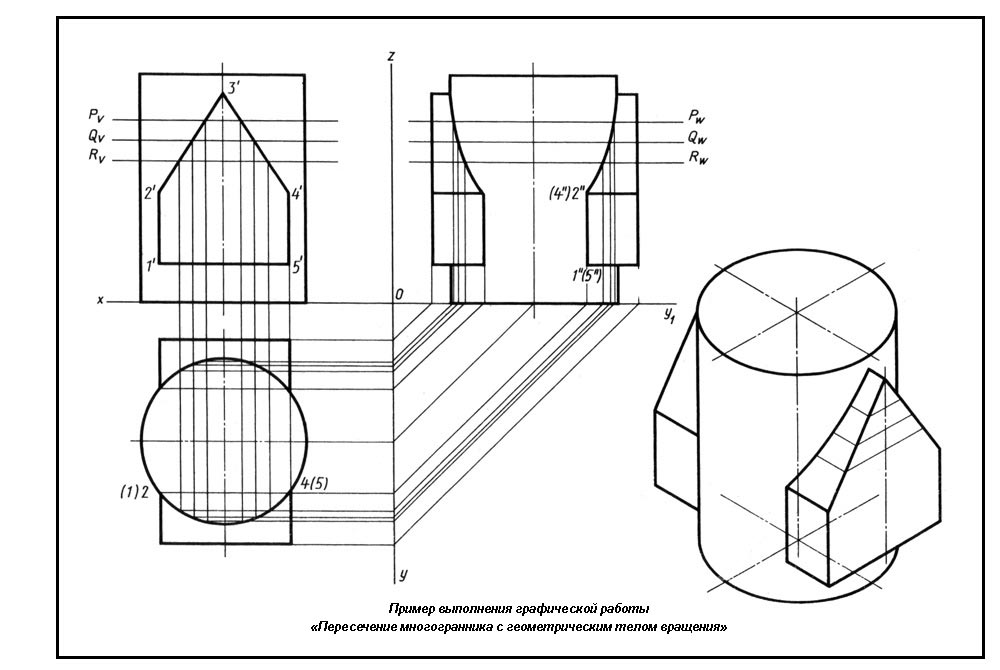
Следует отметить, что при пересечении плоскостью многогранников (призм, пирамид) получаемая фигура сечения всегда является многоугольником, число сторон которого равно числу пересекаемых плоскостью граней (рис. 71, а).

Скачать файл

5. Картографические проекции

Урок 6:
Картографические проекции

Концепты:

Картографические проекции включают перенос данных из трехмерной модели земли, земного шара, в двухмерный поверхность, лист бумаги. Причина этого в том, что глобус трудно носить в кармане, а глобусы слишком маленького размера, чтобы показывать отличная деталь. Где земной шар, по-видимому, является идеальной моделью Земли, это означает, что расстояние, местоположение, направление, размер (площадь), форма и все в остальном верны, карта НЕ идеальна. Процесс проецирования вызывает различный формы искажения. Если проекция вызывает искажение, то почему мы должны проект?

Почему проект?

Причина, по которой проекция необходимый заключается в том, что земной шар или любая другая сфера не может лежать плоско без искажение. Представьте, что вы пытаетесь завернуть баскетбольный мяч в подарочную бумагу. Если вы пробовали это, ты обнаружит, что бумага будет сгибаться в некоторых местах и, возможно, порвется другие. Любой трехмерный объект, который нельзя заставить лежать плоско в два измерения без искажений типа складок и разрывов называется Неразвиваемый Геометрическая поверхность или форма . Итак, чтобы составить карту, данные на глобус должен быть переведен в развёртываемую геометрическую форму. Два таких формы показаны ниже.

Используемые три развертывающиеся поверхности в картографии — это цилиндр, конус и уже плоский кусок бумага или самолет. Эти три поверхности составляют три основных класса проекции, Цилиндрический, конический и азимутальный (который также можно назвать зенитным). или Планар). Они показаны на следующем рисунке.

Как проецировать:

Хотя современная проекция требует в математическое преобразование данных на земном шаре в разрабатываемую поверхность, мы можем понять процесс, представив себе буквальное процесс проекции с использованием света. Представьте себе глобусы на предыдущей диаграмме. к быть из плексигласа и что очертания континентов мира нарисованный черным цветом на поверхности глобусов. Если бы свет был помещен в центр каждого земного шара, тени континентов будут отбрасываться на каждый развертывающаяся поверхность земного шара. Если бы конус и цилиндр были затем разрезаны и разрабатывали, то есть кладут плашмя, были бы карты.

Аспект проекции:

Аспект касается ориентации развертки поверхности относительно земного шара. Есть три аспекта, Нормальный, поперечный и наклонный. На диаграммах ниже показаны эти три аспекты для азимутальной, конической и цилиндрической проекций.

Футляр для проектора:

Дело касается способа, которым земной шар и разворачиваемая поверхность касаются. Важно помнить, что везде, где шар и поверхность соприкасаются, НИКАКИХ искажений не происходит. Есть два проекционные случаи, тангенс и секанс. Касательный случай означает, что развиваемый поверхность соприкасается только с поверхностью земного шара (см. ниже). Для азимутального класса касательный случай означает, что бумага касается глобус в одной точке. Для конических и цилиндрических классов бумага касается линии. В случае секущей бумага проходит через глобус (очевидно, это должна быть математическая форма проекции). результат заключается в том, что азимутальные карты будут иметь круг касания и конусы и цилиндры будет иметь две линии контакта (см. ниже).

Пример искажения:

Помните, что всякий раз, когда проекция берет место, должно произойти какое-то искажение. На приведенной ниже диаграмме показан простой форма искажения.

Это простой азимутальный/зенитальный/планарный Пример класса проекции. Свет исходит от источника в середине излучается наружу во всех направлениях, но блокируется точками A и В на поверхности. А и В отбрасывают тени на плоскую поверхность, удерживаемую касательная на экваторе земного шара. Это был бы касательный случай, экваториальный (или поперечный) аспект, азимутальная проекция. Обратите внимание, что отрезок AB не в той же длины, что и отрезок линии A’ B’. Расстояние, очевидно, было искаженный.

Управление искажениями:

Контроль искажений всегда компромисс. Очень важно отметить, что местоположение, расстояние, направление, форма, и площадь не может быть верна на одной и той же карте. Форма и площадь в наименее совместимые характеристики. Карты, сохраняющие территорию, называются картами равной площади. В то время как области будут точными на таких картах, формы будет искажено. Карты, сохраняющие форму, называются конформными. Конформный карты, однако, сильно искажают местность.

На схеме слева изображена голова человека, нарисованная с истинной формой и площадью на одной карте, а затем то, что происходит с изображением проецируется на конформную и на равновеликую карту. первый спроецированная карта — это карта Меркатора , которая является конформной картой (мы более подробно рассмотрим Меркатор позже). Обратите внимание, что БАЗОВЫЙ форма головы сохранена, но область сильно искажена. В второй экземпляр проекции показывает карту равной площади. Площадь Голова теперь правильная, но форма сильно искажена.

Плюсы и минусы карты:

Вам необходимо ознакомиться с ОСНОВНЫЕ плюсы и минусы для каждого из основных классов проекций. Что показано вот результат большого упрощения, но достаточный для нашего целей.

Азимутальный/Зенитальный/Планарный Проекции: Плюсы: Эти карты полезны для навигации если читатель карт знает, как это сделать. Вот факты. 1) расстояния от или через центр карты верен; 2) направления от центра карты до любого другого точки также считаются верными. Любая другая мера расстояния или направления воля не быть правдой. Минусы: Если используется буквальная проекция, то эти карты не могут показать всю землю. Обычно эти прогнозы показывают о половину земли за раз, поэтому они не годятся для карт мира. Конический Проекции: Плюсы: Эти карты очень хороши для составления карт. регионы которые в первую очередь являются Запад-Восток в измерении, подобно Соединенным Штатам. Что это потому, что конус, когда он развит, сам в ширину больше, чем в высоту.

Минусы: Основной минус в том, что один конус не могу показать весь земной шар. Обычно они показывают немного больше, чем полушарие. Кроме того, конические карты показывают только сектор полного круга… они не развивать в полный круг.

Цилиндрический Проекции: Плюсы: Цилиндр, обернутый вокруг земного шара, покрыть большую часть земного шара, чем плоскость или конус. Это означает что они, как правило, лучше всего подходят для карт мира.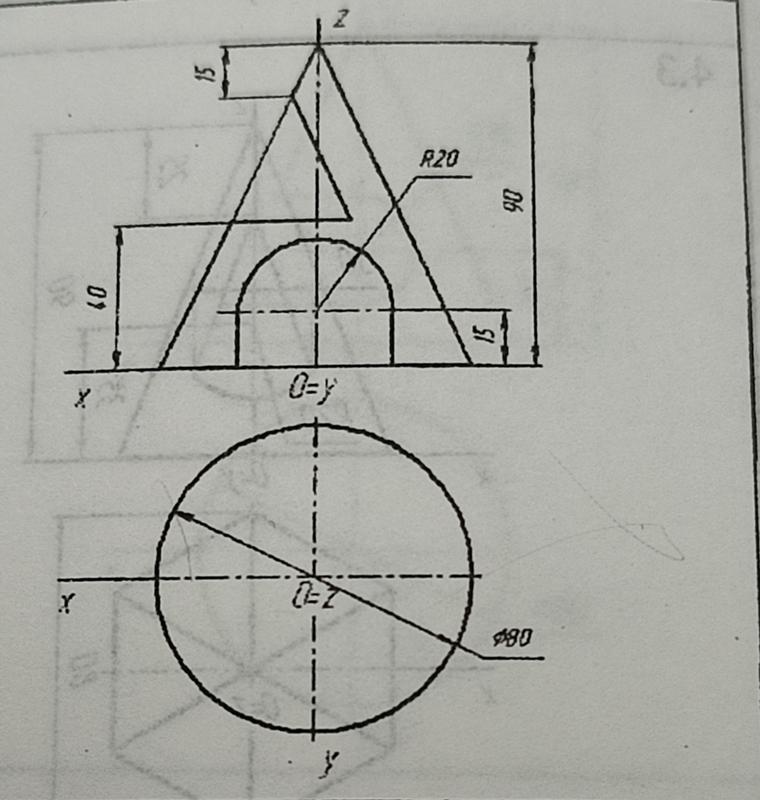

Минусы: Они по-прежнему не могут отображать ВСЕ земной поверхность.

Фокус на Меркатор:

Проекция Меркатора конформный, цилиндрическая проекция. Эта конкретная проекция датируется 1569 годом.и был представлен фламандским математиком/картографом Герардусом. Меркатор. Цель Меркатора состояла в том, чтобы создать карту мира, пригодную для навигации. Чтобы понять, почему эта карта хороша для навигации, мы должны сначала получить контроль над над набором понятий.
Концепты:
Локсодромия или Локсодром: Это линии постоянного пеленга по компасу. Если линия имеет постоянный компасный азимут, линия будет пересекать меридианы под постоянным углом, как показано на следующий диаграмма. На схеме показано Локсодромная кривая , которая курс, постоянного направления по компасу. По этой кривой нельзя было ориентироваться с потребуется постоянная коррекция курса. Позже мы увидим, как этот Проблема решается с помощью Меркатора.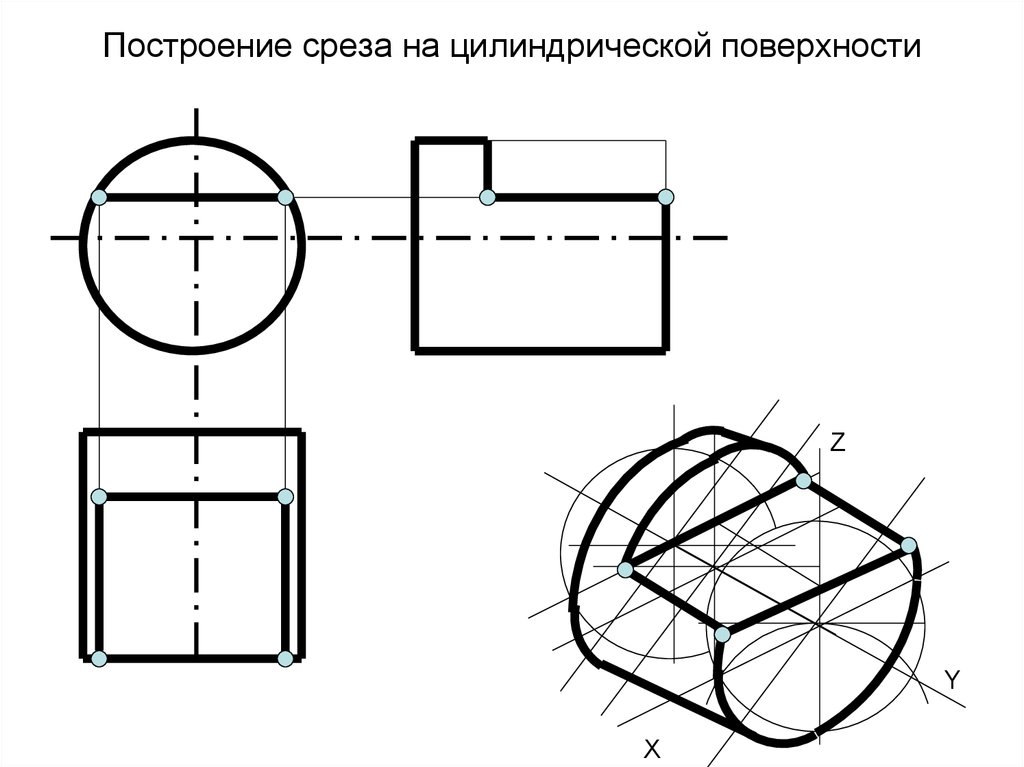
Большие круги и Большой круг Маршруты. Большой круг — это наименьший возможный «обруч», который поместится полностью вокруг света. Таких «обручей» бесконечное множество, и они может быть ориентирован как угодно, как только можно вообразить. Это означает, что любые два точки на поверхности земного шара может быть связано перемещением одного из этих «обручи» пока не пройдет через обе точки. Важным фактом является то, что самый короткий расстояние между любыми двумя точками на поверхности земного шара велико круг маршрут. Маршрут большого круга может быть определен для любых двух точек на глобус, просто соединив точки кратчайшим кусочком строки, как показано на следующей диаграмме.
В идеале навигатор должен нравиться следовать по маршруту большого круга, потому что это сведет к минимуму путешествие расстояние, время и стоимость. Однако мы обнаружим, что маршруты большого круга редко прямые судоходные линии! Нам понадобится трюк, чтобы сделать Меркатора работа.

Теперь наше внимание обратим на работу с проекцией Меркатора. Работа с Меркатором Проекция: Мы будем использовать следующие диаграммы, чтобы проиллюстрировать, как перемещаться с помощью Меркатора, а также плюсы и минусы, связанные с этим проекция. Прежде чем мы продолжим, необходимо ввести некоторые дополнительные факты.

1. Любая прямая линия, проведенная на меркаторской локсодромия или локсодромия. Это означает, что любая прямая может быть ориентировался на.

2. Не все прямые будут самыми короткими расстояние между любыми двумя точками на земном шаре.

3. Только меридианы и экватор также являются кратчайшее расстояние между любыми двумя точками, поскольку все они эквивалентны в большие круги.

4. Все пути кратчайшего расстояния, кроме меридианы и экватор изогнуты, поэтому они несудоходны.

Теперь рабочий пример. Мы хотим путешествовать от Портленда, штат Орегон (на северо-западе США) до Каир, Египет (в устье реки Нил на северо-востоке Африки).

Обратите внимание, что между Портленд и Каир. Поскольку это прямая линия, это румб и, следовательно, судоходный. Однако этот путь не был бы кратчайшим расстоянием между двумя города. Если бы перед вами был глобус, вы могли бы проследить этот путь и увидеть, что вам придется путешествовать по «более толстой» части глобус… что находится ближе к экватору. На диаграмме есть вторая линия, кривая. На самом деле это кратчайшее расстояние между Портлендом и Каиром. большой кольцевой маршрут. Если вы попытаетесь соединить эти два города на земной шар со строкой, этот путь потребует наименьшего количества. Изогнутый Путь не Румб и не Локсодром, поэтому по нему нельзя было пройти. Почему тогда Меркатор такая хорошая карта для навигации?

Следующая диаграмма показывает, как перемещаться с использованием Меркатор. Если криволинейный путь является кратчайшим расстоянием, но не может быть навигация, потому что она изогнута, то почему бы не приблизиться к кривой с серией прямых, судоходных, отрезков? навигатор взял бы курс по первому участку и летать определенное время а затем скорректировать курс, чтобы следовать второму сегменту и так далее.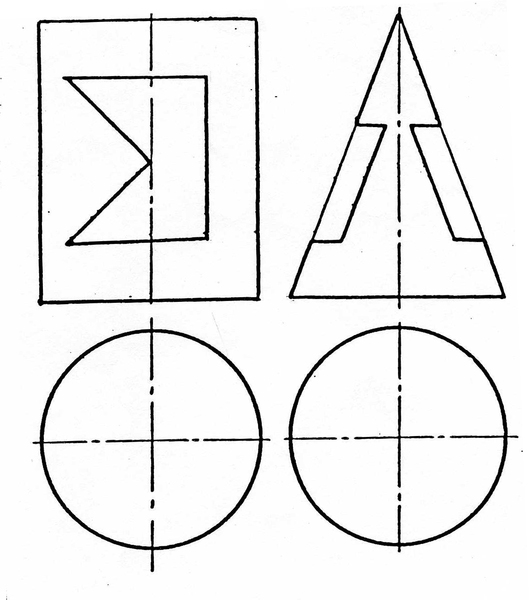 Это как ориентироваться по меркатору.

Меркатор Плюсы и минусы:

Плюсы: 1. Будучи цилиндрическим выступом, Меркатор показывает большую часть земного шара и поэтому очень удобен для мир карты. 2. Меркатор также конформен, поэтому формы сохраняются. Эти поэтому карты хороши для изучения континентов, океанов и наций. 3. В нормальном аспекте, касательный случай находит экватор как стандарт (линия ноль искажений). Если секанс, есть две параллели нулевого искажения и они могут располагаться там, где выберет картограф. 4. И, как мы только что видели, Меркатор хорош для навигации.

Минусы:1. Если вы посмотрите на предыдущую схему, ты увидите, что полюсов не видно. Это означает, что Меркатор все еще не может показать ВЕСЬ земной шар. 2. Хотя это карта у вас есть работал с большинством в вашей школьной карьере, это солгало вам!! Один из в Худшие характеристики карты Меркатора, являющейся конформной картой, заключаются в том, что это сильно искажает площадь. Обратите внимание на кажущиеся размеры Гренландии и Южной Америка. Если вы только изучали Меркатора и не смотрели на глобус, вы бы пришли к выводу, что Гренландия такая же большая или больше чем Южная Америка. Это не так в действительности. Южная Америка на самом деле В 8 раз больше Гренландии!! Взгляните на следующую диаграмму. карта слева — Меркатор… выглядит знакомо, не так ли? Это карта вы видели большую часть своей жизни, и это ответственно за то, что дало вам в впечатление, что Гренландия такая большая. Теперь посмотрите на карту равной площади на право. Форма Гренландии выглядит странно, но ее площадь сейчас правильный.

Универсальный поперечный Меркатор (UTM): Ранее мы говорили, что конический класс проекция хорошо подходит для картографирования регионов, которые преимущественно расположены с запада на восток в измерение так как шишки развиваются больше горизонтально, чем вертикально. Так что насчет отображение такие регионы, как Чили, очень узкие? Возможно, особая форма Меркатор мог это осуществить. Если цилиндр, на который земной шар информация должен быть спроецирован, помещается в поперечный аспект (вспомним из ранее), тогда линия соприкосновения шара и цилиндра будет меридиан по выбору картографа. Эта ориентация является универсальной Поперечный Меркатор (UTM). UTM может быть либо касательной, что дает один меридиан без искажения или секущей, что дает минимизированную центральную область карты искажение (см. ниже). Оба случая отлично подходят для картографирования узких полос земной поверхности.

Математика за три минуты: Картографические проекции

Когда вы думаете о Земле в географических терминах, первое, что, вероятно, приходит на ум, — это проекция Меркатора , названная в честь 16-го века фламандским картографом Герардусом Меркатором.

Проекция Меркатора. Изображение: Daniel R. Strebe, CC BY-SA 3.0

Основная идея этой проекции состоит в том, чтобы поместить Землю (или, лучше, уменьшенную версию Земли) в вертикальный цилиндр, касающийся экватора и с северным полюсом.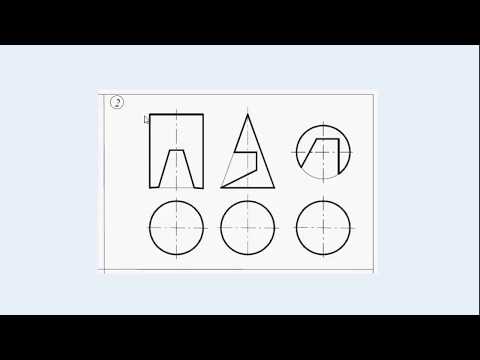 прямо вверх. Учитывая любую точку x на Земле, затем вы рисуете линию, соединяющую x с центром Земли. Продлите эту линию, пока она не коснется цилиндра в какой-то точке y — эта точка y является проекцией вашей точки x . Используя эту технику, вы можете проследить очертания континентов и стран на цилиндре, который затем можно разрезать и развернуть в плоский лист.

Цилиндрический выступ. Представьте себе лампочку в центре Земли. Континенты и острова будут отбрасывать тени на цилиндр, который затем можно разрезать и развернуть в плоский лист. Изображение предоставлено НОАА.

Проблема возникает, когда вы приближаетесь к полюсам. Спроецированные точки перемещаются все выше и выше вверх по цилиндру по мере того, как вы сходитесь к Северному полюсу, и все дальше и дальше вниз по цилиндру по мере приближения к Южному полюсу. Чтобы спроецировать всю Землю, вам понадобится цилиндр бесконечной длины. Сами два полюса вообще не появляются на цилиндре: линия, соединяющая их с центром Земли, параллельна сторонам цилиндра и поэтому никогда не пересекается с ним.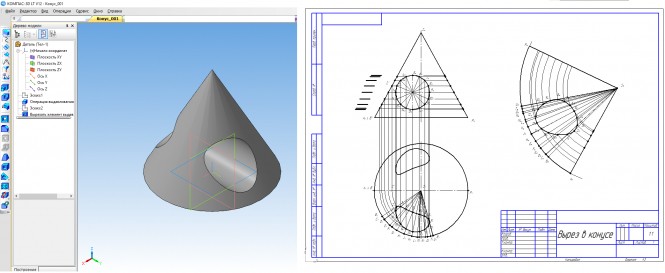

Точки вблизи Северного полюса (например, две точки справа) проецируются намного выше, чем точки вблизи экватора (например, две точки слева). Эта диаграмма также показывает искажение, которое происходит, когда вы приближаетесь к полюсам.

Проекция Меркатора — это разновидность этой цилиндрической проекции, которая обеспечивает точное представление углов на карте (подробнее о математических расчетах проекции см. здесь). Однако проблема с полюсами все еще актуальна, и именно по этой причине проекция Меркатора не содержит их и их непосредственное окружение.

Большое преимущество проекции Меркатора состоит в том, что линии постоянного компаса (например, линия, проведенная при движении строго на восток) соответствуют прямым линиям на карте. Это означает, что если вы хотите плыть из пункта А в пункт Б, вам нужно всего лишь провести прямую линию между ними на карте. Угол, который линия образует с экватором (или любой линией широты), говорит вам о вашем направлении север-юг, а ее отношение к меридиану Гринвича говорит вам о вашем направлении восток-запад. Затем вы направляетесь в указанном направлении, используя свой компас в качестве ориентира. Пока вы держите стрелку компаса неподвижной и не сталкиваетесь ни с какими островами и континентами по пути, вы доберетесь туда.

Несправедливое искажение

Недостаток проекции Меркатора заключается в том, что, как прямой результат техники цилиндра, расстояния вблизи полюсов растягиваются, в результате чего места вблизи полюсов кажутся намного больше, чем они есть на самом деле. В стандартной проекции Гренландия кажется больше Африки, хотя на самом деле Африка больше в 14 раз! Политически это имеет неловкие последствия. Европа и Северная Америка расположены достаточно далеко к северу от экватора, чтобы извлечь выгоду из искажения. Они кажутся намного больше по отношению к поясу, окружающему экватор, чем они есть на самом деле, таким образом добавляя картографическую дискриминацию к расовой, культурной и экономической дискриминации.

Как правило, никакая проекция Земли на 2D-карту не является точной на 100%. Единственный способ представить поверхность сферической Земли на плоском листе бумаги — это ввести искажение. Вы можете убедиться в этом сами, выдернув апельсин из кожуры, сохранив при этом кожуру единым куском. Когда вы положите кожу вниз, она естественным образом сохранит свою округлую форму. Любая попытка сплющить его либо сломает, либо растянет и сожмет в каком-то направлении.

Еще один хороший пример неизбежного искажения исходит от Стереографическая проекция : представьте, что вы балансируете на жестком листе бумаги на Северном полюсе так, чтобы он был перпендикулярен оси Север-Юг Земли.

Стереографическая проекция сферы на двумерную плоскость.

Затем вы можете провести прямые линии от Южного полюса через любую точку x на Земле, и проекция этой точки x будет точкой y , в которой прямая линия встречается с бумагой. Эта проекция сохраняет углы и отлично подходит для изучения Арктики, но становится все более и более искаженной по мере продвижения к Южному полюсу. (Вы также можете прикоснуться бумагой к Земле в любой другой точке, чтобы получить карту региона, окружающего эту точку.)

Стереографическая проекция. Изображение: Strebe, CC BY-SA 3.0

Есть также проекции, которые пытаются минимизировать искажения. Одна из них — тройная проекция Винкеля. Он усредняет координаты из двух других проекций, проекции Айтоффа и равнопрямоугольной проекции с целью минимизации искажений расстояния, направления и площади.

Тройная проекция Винкеля. Изображение: Strebe, CC BY-SA 3.0

Еще одна известная карта, которая часто используется в отличие от карты Меркатора, — это проекция Галла-Питерса. Он точно отражает относительный размер территорий — вы удивитесь, насколько на самом деле маленькая Европа, — но сильно искажает формы. Вблизи экватора формы сжимаются по горизонтали и растягиваются по вертикали, а вблизи полюсов происходит обратное. Континенты, пересекающие экватор, кажутся длинными и тонкими, поэтому проекцию сравнивают с веревкой для стирки, на которой сушится страны.

Цилиндр с вырезом в трех проекциях: Построение фигуры-цилиндр с вырезом — Чертежик