Разное

Цикл в матлаб: Циклы и условия matlab: теория и примеры

Содержание

Циклы и условия matlab: теория и примеры

Доброго времени суток. Сегодня речь пойдёт о циклах и условиях в Matlab. Материал, который взят за основу — это help в Matlab и несколько простых примеров, которые мы с вами и разберем.

Условия в MATLAB

Ни один язык программирования не обходится без таких конструкций как условия, именно об этом мы с вами и поговорим:
Начнём с синтаксиса условия if и посмотрим на формальный вариант записи в справке:

if expression, statements, end

Что значит:

if Условие, Действие, end

Теперь примеры:

x = 1;
y = 61;
if ((x >= 0.90) && (y >= 60))
   disp('ok');
end;

&& — логически оператор умножения (логическая «И»).
И вот пример с else:

x = 1;
y = 50;
if ((x >= 0.90) && (y >= 60))
   disp('ok');
else 
   disp('not right')
end;

В отличие от 1 примера, здесь выведется «not right».
Пару слов теперь о switch.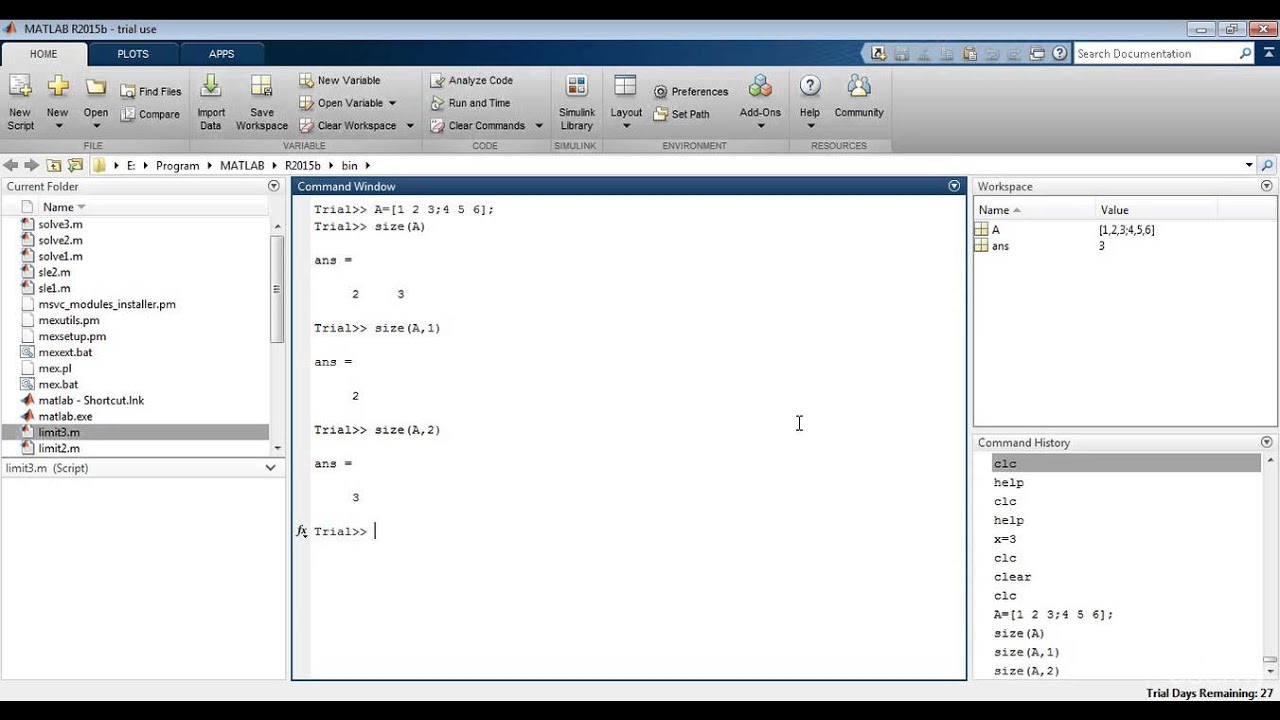 Формально в справке:

Syntax
switch switch_expr
 case case_expr
    statement, ..., statement
  case {case_expr1, case_expr2, case_expr3, ...}
    statement, ..., statement
  otherwise
    statement, ..., statement
end

Более приземлённо:

Syntax
switch switch_expr
 case Значение - 1
    Действие
  case {Зачение - 2, Знчение - 3, Значение - 4, ...}
    Действие
  В остальных случиях
    Действие
end

Это значит, что если заданная переменная равна значению в case Значение — 1, то выполняется действие при case Значение — 1 и так далее. Если ни один из case не подошёл выполняется действие при otherwise.
Вот пример:

method = 'Bilinear';
switch lower(method)
   case {'linear','bilinear'}
      disp('Method is linear')
   case 'cubic'
      disp('Method is cubic')
   case 'nearest'
      disp('Method is nearest')
   otherwise
      disp('Unknown method.')
end

Циклы в MATLAB

Теперь перейдём к циклам, начнём с for.

В справке это записано в виде

Syntax
for index = values
   program statements
          :
end

В приземлённом виде это значит:

Syntax
for переменная = значению
   действие
end

Не будем задерживаться на официальных формулировках, лучше к понятным и любимым примерам

for m = 1:10
    m
end

Вот так выглядит самый распространённый способ использования for. В этом цикле мы просто выводим значение m.
Второй способ с использованием шага (step)

for s = 1.0: -0.1: 0.0
   disp(s)
end

В данном случае цикл for идёт от 1 до 0 с шагом -0.1.
Ещё один вариант:

for s = [1,5,8,17]
   disp(s)
end

В данном случае переменная s будет последовательно приравниваться 1, 5 ,8 , 17 и, соответственно, выводиться.
А также с for очень удобно выводить вектора. Вот:

for e = eye(5)
  disp('Current value of e:')
  disp(e)
end

В данном примере идёт последовательное обращение к элементам вектора e.

Цикл while:
Формально в справке:

Syntax
while expression
   program statements
          :
end

Приземлённо:

Syntax
while Условие
   Действие
end

И давайте сразу к примеру (как это в реальной жизни используется).

eps = 10;
while eps > 1
    eps = eps - 1
end

Пока в условие (eps > 1) выполняется, цикл выполняет действие
(eps = eps-1).
Также в условии while можно использовать логические операторы И — && и ИЛИ — ||, записывая несколько логических выражений в условие.

Если есть вопросы по статье, пишите в комментариях.

Поделиться ссылкой:

Похожее

Циклы for, while в Матлаб(Matlab)

Оператор for предназначен для выполнения заданного числа повторяющихся действий. Самое простое использование оператора for осуществляется следующим образом:

for count = start:step:final  команды MatLab  end

Здесь count — переменная цикла, start — ее начальное значение, final — конечное значение, а  step   — шаг, на который увеличивается count при каждом следующем заходе в цикл. Цикл заканчивается, как только значение count становится больше final. Переменная цикла может принимать не только целые, но и вещественные значения любого знака

Цикл  for  оказывается полезным при выполнении повторяющихся похожих действий в том случае, когда их число заранее определено. Обойти это ограничение позволяет более гибкий цикл  while.

while  условие цикла команды MatLab  end

62. Какой командой создается М-книга в текстовом редакторе Word, связанном сMatLab?

Начало новой М-книги Чтобы приступить к написанию новой М-книги, нужно: 1) запустить редактор Word; 2) выбрать в диалоговом окне WordопциюNewиз менюFile; 3) в окне, которое появится на экране, выбрать шаблон M-book. В результате этих действий будет запущена системаMatLAB, и вид глав- ного меню редактора Word несколько изменится — в нем появится новое менюNotebook. Это и будет свидетельствовать, что кWordприсоединена системаMatLAB. Если теперь с помощью мыши активизировать менюNotebookокнаWord, на экране появится дополнительное меню

63. Какая команда в текстовом редакторе Word преобразует текст в ячейку ввода MatLab?

выбрать команду Define Input Cell(Определить Входную Ячейку) в ме- нюNotebook(см. рис. 3.20), или нажать клавиши ; после этого вид стро- ки команды должен измениться — символы команды приобретают темно-зеленый цвет, а команда становится отороченной квадратными скобками темно-серого цвета;@

64. Какая команда в текстовом редакторе Word обеспечивает в ячейке выполнение команды MatLab?

выбрать мышкой команду Evaluate Cell (Вычислить ячейку), или нажать комбинацию клавиш ; результатом этих действий должно стать появ- ление сразу после текста команды результатов ее выполнения системой MatLAB. Результаты выполнения команды выводятся, синим цветом и взяты в квад- ратные скобки

65. Какая команда в текстовом редакторе Word обеспечивает выполнение команд MatLab во всей М-книге?

Выполнение команд всех ячеек или групп ячеек ввода раздела произ- водится при помощи пункта Evaluate Calc Zone, а сразу всей М-книги – Evaluate М-book

66. Какая команда в текстовом редакторе Word обеспечивает выполнение команд MatLab во всех ячейках автоматически при открытии М-книги?

Команды ячеек, имею- щих стиль Autolnit, запускаются сразу после открытия М-книги. Полезно включить в первую такую ячейку команду clear для очистки рабочей среды. Для установки стиля Autolnit служит пункт Define Autoinit Cell меню Notebook

67. Какие кнопки содержит панель Excel Link в электронной таблице Excel при их связи с MatLab?

68. Что обеспечивает команда putmatrix?

Функция MLPutMatrix служит для по- мещения данных из ячеек рабочего листа Excel в массив рабочей среды Matlab. Аргументами данной функции являются имя переменной, заключен- ное в кавычки, и диапазон ячеек Excel, относящихся к этой переменной

68. Что обеспечивает команда getmatrix?

Об- ратную операцию осуществляет функция MLGetMatrix, при этом аргу- ментами этой функции являются имя переменной рабочей среды MatLab с 22 данными, заключенной в кавычки, и диапазон ячеек Excel, где будут разме- щены данные этой переменной, также заключенный в кавычки.

70. Для чего предназначен пакет Simulink?

В состав системы Matlab входит пакет моделирования динамических систем – Simulink. Данный пакет является ядром интерактивного программ- ного комплекса, предназначенного для математического моделирования ли- нейных и нелинейных динамических систем, представленных своей функ- циональной блок-схемой, именуемой S –моделью или просто моделью

71. Какая библиотека Simulink содержит источники сигналов?

Построим простейшую модель источника синусоидального сигнала, который подается на вход виртуального осциллографа. Для этого щелкнем на кнопке открытия браузера библиотек и в левой части появившегося окна браузера щелкнем на разделе Sources(Источники), при этом в правой части окна отображаются пиктограммы блоков, входящих в данный раздел

72. Какая библиотека Simulink содержит регистрирующие виртуальные приборы?

осциллограф Scope из раздела Sinks.

73. Какая библиотека Simulink содержит блоки дифференцирования и интегрирования?

Continuous содержит непрерывные блоки. К числу важнейших относятся блоки дифференцирования Derivative и интегрирова- ния Integrator. Первый блок осуществляет численное дифференцирование входного сигнала, для данного блока никакие параметры не вводятся. Вто- рой блок в окне параметров содержит несколько полей, в котором можно задать постоянную интегрирования на выходе блока в поле Initial condition

74. Какая библиотека Simulink содержит блоки вычисления элементарных функций?

Окно библиотеки Mathсодержит блоки выполнения математических операций

К блокам вычисления элементарных функций относятся три блока: блок математических функций MathFunction, блок тригонометрических функцийTrigonometricFunctionи блок функций округленияRounding Function.

75. Сколько значений параметров шага устанавливается в Simulink при переменном шаге моделирования?

Большое значение имеют две опции решателя в поле Solver options: тип решения и метод решения. Возможны два варианта первой опции:

• Variable-step solvers – решение с переменным шагом;

• Fixed-step solvers – решение с фиксированным шагом. По умолчанию установлена опция решения с переменным шагом, ко- гда шаг автоматически уменьшается при увеличении скорости изменения результатов и наоборот. Обычно этот метод дает лучшие результаты, чем моделирование с фиксированным шагом, исключая в большинстве случаев расхождение результатов. Применение моделирования с фиксированным шагом применяется обычно в том случае, если это обусловлено спецификой решаемой задачи

для цикла в python в 10 раз медленнее, чем matlab Ru Python

Причина, по которой это происходит, связана с компилятором JIT , который оптимизирует цикл MATLAB for. Вы можете отключить / включить ускоритель JIT, используя feature accel off ускорения, и включить ускорение feature accel off . Когда вы отключите акселератор, времена резко меняются.

MATLAB с ускорением: Elapsed time is 0.009407 seconds.

MATLAB с ускорением: Elapsed time is 0.287955 seconds.

python: time cost = 0.0511920452118

Таким образом, ускоритель JIT напрямую вызывает ускорение, которое вы замечаете. Есть еще одна вещь, которую вы должны рассмотреть, что связано с тем, как вы определили итерационные индексы.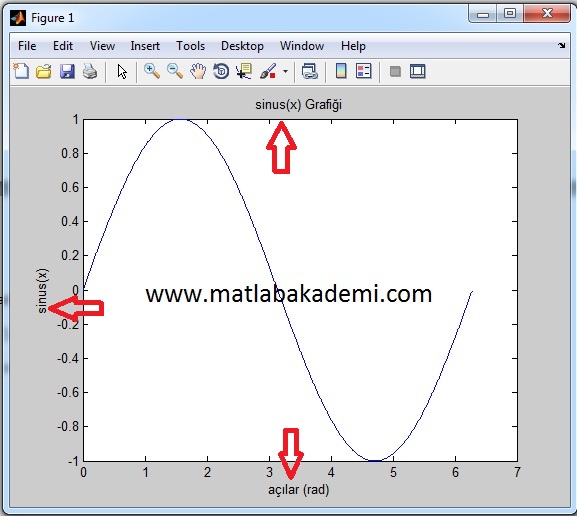 В обоих случаях, MATLAB и python, вы использовали Итераторы для определения ваших циклов. В MATLAB вы создаете фактические значения, добавляя квадратные скобки ( [] ), а в python вы используете range вместо xrange . Когда вы делаете эти изменения

 % MATLAB for i = [1:1000] for j = [1:1000] # python for r in range(1000): for c in range(1000):

Время становится

MATLAB с ускорением: Elapsed time is 0.338701 seconds.

MATLAB с ускорением: Elapsed time is 0.289220 seconds.

python: time cost = 0.0606048107147

Одно последнее соображение заключается в том, чтобы добавить быстрый цикл в цикл. т. е. t=t+1 . Тогда время становится

MATLAB с ускорением: Elapsed time is 1.340830 seconds.

MATLAB с ускорением: Elapsed time is 0.905956 seconds. (Да, было быстрее)

python: time cost = 0. 147221088409

Я думаю, что мораль здесь заключается в том, что скорости вычислений для петель, из коробки, сопоставимы для чрезвычайно простых циклов, в зависимости от ситуации. Тем не менее, в python есть и другие, численные инструменты, которые могут значительно ускорить процесс, numpy и PyPy были доведены до сих пор.

Основная реализация Python, CPython, не должна быть сверхскоростной. Если вам нужна эффективная численная манипуляция в стиле Matlab, используйте пакет numpy или реализацию Python, предназначенную для быстрой работы, например PyPy или даже Cython. (Написание расширения Python на C, которое, конечно же, будет довольно быстрым, также является возможным решением, но в этом случае вы можете просто использовать numpy и сэкономить усилия).

Если производительность исполнения Python действительно важна для вас, вы можете взглянуть на PyPy

Я сделал ваш тест:

 import time for a in range(10): start_time = time. time() for r in xrange(1000): for c in xrange(1000): continue elapsed_time = time.time()-start_time print elapsed_time

со стандартным Python 2.7.3, я получаю:

 0.0311839580536 0.0310959815979 0.0309510231018 0.0306520462036 0.0302460193634 0.0324130058289 0.0308878421783 0.0307397842407 0.0304911136627 0.0307500362396

тогда как, используя PyPy 1.9.0 (что соответствует Python 2.7.2), я получаю:

 0.00921821594238 0.0115230083466 0.00851202011108 0.00808095932007 0.00496387481689 0.00499391555786 0.00508499145508 0.00618195533752 0.005126953125 0.00482988357544

Ускорение PyPy действительно потрясающе и действительно становится видимым, когда его оптимизация компилятора JIT перевешивает их стоимость. Вот почему я представил дополнительный цикл. Для этого примера абсолютно не требуется модификация кода.

Оператор break — Операторы — Учебник по MQL4

В ряде случаев, например, при программировании циклических операций, возникает необходимость прервать выполнение цикла ещё до того, когда условие оператора цикла станет ложным. Для решения подобных задач необходимо использовать оператор break.

Формат оператора break

Оператор break состоит из одного слова, заканчивается знаком ; (точка с запятой).

   break;                                         // Оператор break

Правило исполнения оператора break


Оператор break прекращает исполнение ближайшего внешнего оператора while, for или switch. Исполнением оператора break является передача управления за пределы составного оператора while, for или switch, ближайшему следующему оператору. Оператор break может использоваться только для прерывания выполнения указанных операторов.

Исполнение оператора break можно проиллюстрировать на следующем примере.

Задача 14. Дана нить длиной 1 метр. Требуется сложить нить в форме прямоугольника, имеющего максимально возможную площадь. Путём последовательного перебора вариантов найти площадь этого прямоугольника и длины сторон с точностью до 1 мм.

Из цельного отрезка нити можно сложить бесконечное количество прямоугольников различных размеров. Учитывая, что по условиям задачи точность вычислений составляет 1 мм, мы можем рассмотреть всего 499 вариантов. Первый, самый «тонкий», прямоугольник будет иметь размеры 1 х 499 мм, второй — 2 х 498 мм и так далее, а размеры последнего будут составлять 499 х 1 мм. Нам необходимо перебрать все эти прямоугольники и выбрать из них один, имеющий максимальную площадь.

Легко заметить, что в рассматриваемом наборе прямоугольников встречаются повторяющиеся размеры. Например, первый и последний прямоугольники имеют одинаковый размер: 1 х 499 (то же, что 499 х 1). Аналогично этому, размер второго прямоугольника совпадает с размером предпоследнего и т. д. Нам необходимо составить алгоритм перебора всех оригинальных вариантов, но перебирать повторяющиеся нет необходимости.

Для начала проведём предварительную оценку: определим, как площадь прямоугольника будет зависеть от его размеров. Легко понять, что у первого прямоугольника, с размерами сторон 1 х 499, будет самая маленькая площадь. Далее, по мере увеличения малой стороны, площадь прямоугольников будет увеличиваться. По достижении некоторого значения площади прямоугольников начнут снижаться. Эта зависимость отражена на рис. 44:


Рис. 44. Зависимость размера площади прямоугольника от размера одной стороны.

Глядя на рис. 44, несложно прийти к выводу, что искать максимальную площадь, перебирая варианты, начиная с первого, необходимо лишь до тех пор, пока площадь в процессе вычислений увеличивается. Как только она начнёт снижаться, необходимо закончить перебор и выйти из цикла перебора вариантов. Ниже представлен скрипт rectangle. mq4, в котором реализован такой алгоритм.


int start()                         
{
int
L=1000,                          
A,                               
B,                               
S,                               
a,b,s;                           
for(a=1; a<L/2; a++)             
{                              
b=(L/2) - a;                  
s=a * b;                      
if (s<=S)                     
break;                     
A=a;                          
B=b;                          
S=s;                          
}                              
Alert("Максимальная площадь = ",S,"  A=",A,"  B=",B);
return;                             
}

Проследим, как эта программа работает. В начале программы объявлены и прокомментированы переменные. В пределах цикла for реализуется собственно алгоритм решения задачи. В Выражении_1 задано начальное значение размера стороны а прямоугольника, равное 1. В соответствии с Условием, перебор ведётся до тех пор, пока размер стороны прямоугольника а остаётся меньше половины длины нити. Выражение_2 предписывает увеличивать размер стороны прямоугольника а на каждом шаге итерации.

Переменные a, b и s — текущие переменные, значения которых перебираются. Переменные A, B и S — искомые значения. В начале цикла вычисляется вторая сторона b и площадь s текущего прямоугольника.

      b = (L/2) - a;                   
s = a * b;

В операторе if проверяется условие выхода из цикла:

      if (s <= S )                     
break;

Если только что вычисленная площадь текущего прямоугольника s оказывается больше площади S, вычисленной на предыдущей итерации, то это новое значение s и становится лучшим достигнутым результатом. В этом случае Условие оператора if не выполняется, а управление передаётся ближайшему оператору, следующему за оператором if. В этих строках запоминаются лучшие достигнутые результаты:

      A = a;                           
B = b;                           
S = s;

При достижении ближайшей закрывающей фигурной скобки итерация заканчивается, и управление передаётся в заголовок оператора for для выполнения Выражения_2 и проверки Условия. Если на момент проверки размер стороны а ещё не вырос до указанных пределов, то выполнение цикла продолжится.

Повторяющиеся циклические вычисления будут продолжаться до тех пор, пока не произойдёт одно из событий: либо размер стороны а превысит допустимые пределы (в соответствии с Условием оператора for), либо размер вычисленной площади s окажется меньше ранее достигнутого значения, хранящегося в переменной S. У нас есть все основания считать, что раньше произойдёт выход из цикла по условию оператора if:

     if (s <= S )                     
break;

Действительно, оператор цикла for составлен так, что перебирает все возможные варианты без исключения (половина длины нити L/2 — это сумма двух сторон). В то же время максимальная площадь прямоугольника будет достигнута где-то в середине перебираемого набора вариантов. И как только это событие произойдёт (площадь текущего прямоугольника s окажется меньше или равной ранее достигнутого значения S), в рамках исполнения оператора if управление будет передано оператору break, который, в свою очередь, передаст управление за пределы оператора for в строку:

     Alert("Максимальная площадь = ",S,"  A=",A,"  B=",B);

В результате исполнения встроенной функции Alert() будет напечатана следующая строка:

Максимальная площадь = 62500 А=250 В=250

После этого управление будет передано оператору return, в результате чего специальная функция start() завершит свою работу. Это, в свою очередь, приведёт к окончанию работы скрипта и выгрузке его клиентским терминалом из окна финансового инструмента.

В данном примере оператор break прекращает работу (передаёт управление за пределы) оператора цикла for, а именно того оператора цикла, внутри которого он находится. Ниже приведена функциональная схема цикла for, в котором используется специальный выход:


Рис. 45. Функциональная схема цикла for с использованием оператора break (rectangle.mq4).

На схеме видно, что из цикла имеется два выхода: нормальный выход (выход из цикла в результате срабатывания условия, заключённого в заголовке оператора цикла) и специальный выход из цикла (выход из тела цикла по дополнительному условию с помощью оператора break).

Возможность специального выхода из цикла в языке MQL4 трудно переоценить. В нашем примере использование оператора break позволило составить алгоритм, при котором выполняются только необходимые вычисления. Алгоритм, составленный без специального выхода из цикла, был бы неэффективным — в этом случае производились бы повторяющиеся вычисления, что привело бы к необоснованной трате вычислительных ресурсов и времени. Заштрихованная область на рис. 44 наглядно показывает область параметров, которые не обрабатывались в рассматриваемой программе (почти половина всех вычислений!), что не помешало получить правильный результат.

Необходимость использования эффективных алгоритмов становится особенно очевидна, когда время работы программы растягивается на секунды и даже минуты, что может оказаться больше, чем промежуток времени между тиками. В этом случае сохраняется риск пропустить обработку некоторых содержательных тиков и как результат — потерять инициативу в управлении торговлей. Кроме этого, снижение времени вычислений особенно остро ощущается при выполнении тестирования программ на тестере стратегий. Тестирование сложных программ на большом промежутке исторических данных может занимать часы и дни. Снижение времени тестирования наполовину в этой ситуации оказывается очень важной возможностью.

В правиле указано, что оператор break прекращает действие ближайшего внешнего оператора. Посмотрим, как работает программа, в которой используются вложенные циклы.

Задача 15. Используя алгоритм Задачи 14, подобрать наименьшую нить, кратную 1 метру, достаточную, чтобы образовать прямоугольник площадью 1.5 м ².

В этой задаче необходимо последовательно перебирать имеющиеся длины нитей, для каждой из которых нужно вычислить максимально достижимую площадь. Решение задачи 15 реализовано в скрипте area.mq4. Варианты решения перебираются в двух циклах — во внешнем и во внутреннем. Внешний цикл перебирает длину нити с шагом 1000 мм, а внутренний находит максимальную площадь для текущей длины нити. В данном случае оператор break используется для выхода из внешнего и внутреннего циклов.


int start()                             
{
int
L,                                  
S_etalon=1500000,                   
S,                                  
a,b,s;                              
while(true)                         
{                                 
L=L+1000;                        
S=0;                             
for(a=1; a<L/2; a++)             
{                              
b=(L/2) - a;                  
s=a * b;                      
if (s<=S)                     
break;                     
S=s;                          
}                              
if (S>=S_etalon)                 
{
Alert("Подходит нить длиной ",L/1000," м. ");
break;                         
}
}                                 
return;                              
}

Здесь внутренний цикл работает подобно тому, как и в решении предыдущей задачи. Оператор break используется для выхода из цикла for, когда достигнуто максимальное значение площади для нити заданной длины. Необходимо особо подчеркнуть, что оператор break, указанный во внутреннем цикле for, передаёт управление оператору, следующему за закрывающей фигурной скобкой цикла for, прекращая таким образом работу цикла. Это явление не оказывает никакого влияния на исполнение внешнего оператора цикла while.

В момент, когда срабатывает оператор break во внутреннем цикле for, управление передаётся оператору if:

   if (S >= S_etalon)                
{
Alert("Подходит нить длиной ",L/1000," м.");
break;                         
}

В операторе if производится проверка: является ли найденная площадь больше или равной заданному по условию задачи минимально допустимому значению 1.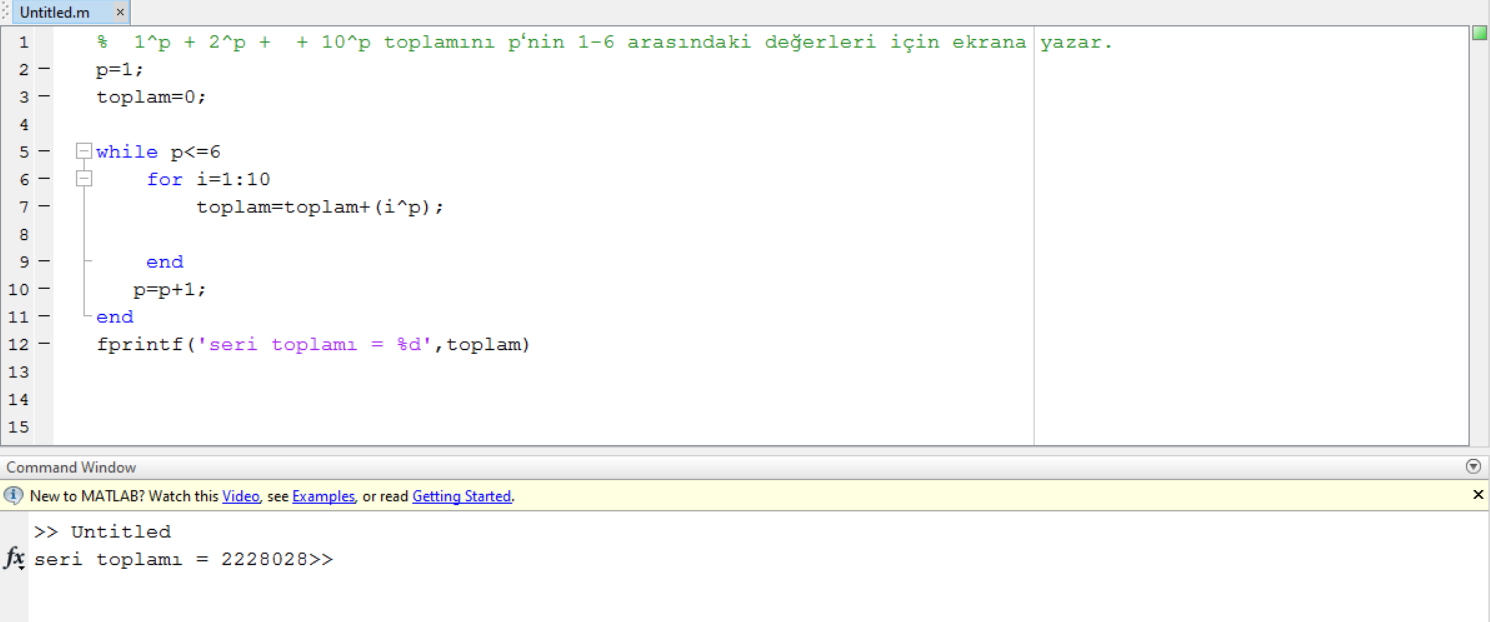 5 м 2? Если это так, то решение найдено, и продолжать вычисления нет смысла; управление передаётся в тело оператора if. Исполняемую часть оператора if составляют всего два оператора, первый из которых выводит на экран сообщение о найденном решении:

Подходит нить длиной 5 м.

С помощью второго оператора — break — осуществляется выход из внешнего цикла while и последующий выход из программы. Ниже представлена функциональная схема алгоритма, реализованного в программе area.mq4.


Рис. 46. Функциональная схема программы, в которой реализуется возможность специального выхода из внутреннего и внешнего цикла (area.mq4).

На схеме видно, что из каждого цикла имеется нормальный и специальный выход. Каждый из операторов break прекращает работу своего цикла и никак не отражается на работе другого; каждому специальному выходу соответствует свой оператор break. Один и тот же оператор break не может использоваться для специального выхода из обоих циклов. В данном случае каждый из циклов имеет только один специальный выход, но в общем случае допускается использование нескольких операторов break, образующих несколько специальных выходов из одного цикла.

Обратите внимание, Условием в заголовке внешнего цикла while является (true), т. е. запись, не содержащая переменной, значение которой в процессе выполнения программы могло бы измениться. Это значит, что выход из цикла while по Условию, указанному в заголовке, никогда не произойдёт. В этом случае использование оператора break является единственной возможностью для выхода из цикла.

В этом примере алгоритм построен так, что фактически используется только специальный выход как из внутреннего, так и из внешнего цикла. Однако не следует полагать, что использование оператора break обязательно приводит к построению алгоритмов, предполагающих только специальный выход. В алгоритмах других программ вполне возможно достижение условий, при которых происходит нормальный выход из цикла.

Использование оператора break для передачи управления за пределы оператора switch рассматривается в разделе Переключатель switch.


MATLAB — Типы петель — CoderLessons.com

Может возникнуть ситуация, когда вам нужно выполнить блок кода несколько раз. Как правило, операторы выполняются последовательно. Первый оператор в функции выполняется первым, затем следует второй и так далее.

Языки программирования предоставляют различные управляющие структуры, которые допускают более сложные пути выполнения.

Оператор цикла позволяет нам выполнять оператор или группу операторов несколько раз, и в большинстве языков программирования ниже приводится общая форма инструкции цикла.

MATLAB предоставляет следующие типы циклов для обработки требований циклов. Нажмите на следующие ссылки, чтобы проверить их детали —

Sr.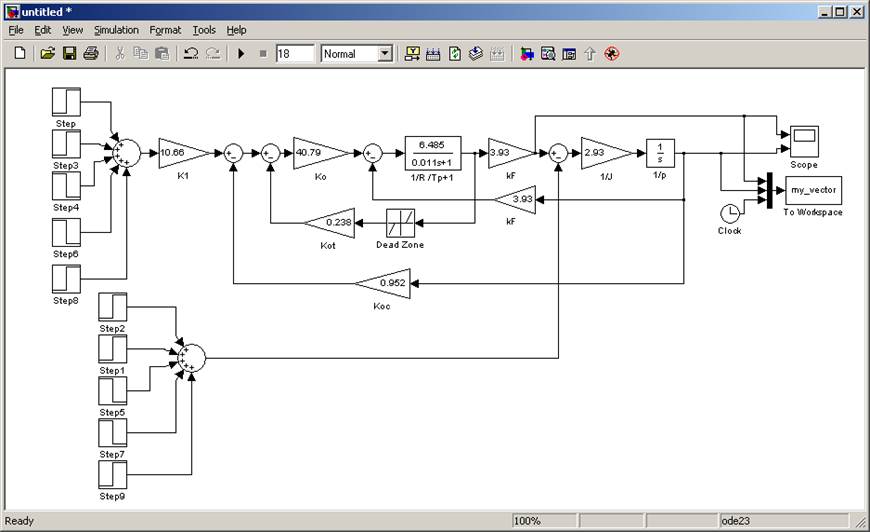 No. Тип и описание петли
1 в то время как цикл

Повторяет оператор или группу операторов, пока данное условие выполняется. Он проверяет условие перед выполнением тела цикла.

2 для цикла

Выполняет последовательность операторов несколько раз и сокращает код, который управляет переменной цикла.

3 вложенные циклы

Вы можете использовать один или несколько циклов внутри любого другого цикла.

Повторяет оператор или группу операторов, пока данное условие выполняется. Он проверяет условие перед выполнением тела цикла.

Выполняет последовательность операторов несколько раз и сокращает код, который управляет переменной цикла.

Вы можете использовать один или несколько циклов внутри любого другого цикла.

Заявления о контроле цикла

Операторы управления циклом изменяют выполнение от его нормальной последовательности. Когда выполнение покидает область действия, все автоматические объекты, созданные в этой области, уничтожаются.

MATLAB поддерживает следующие управляющие операторы. Нажмите на следующие ссылки, чтобы проверить их детали.

Завершает оператор цикла и передает выполнение в оператор, следующий сразу за циклом.

Заставляет петлю пропускать оставшуюся часть своего тела и немедленно проверять свое состояние перед повторением.

от скуки Matlab в руки ))

 

Ну в общем это случилось..)) мое знакомство с Matlab))))) все время откладывала это мероприятие на какое-то заоблачное завтра вместо того чтобы уже просто садиться и ковыряться с ним))) 

Начала с чтения книжечки и тыкания разных примитивных командочек в Command Window. Надоело быстро, ничего интерсного. Основной вывод — интерфейс ужасен!!! (ну может дело привычки, или просто с маткада, такого любимого и удобного, так сложно на что-то более заморочистое перелезать. .). Решила не тратить время на ерунду, а разбираться с ним уже в процессе решения конкретной задачи — за  задачей в карман лезть не стала — свою маткадовскую модель хочу перевести на матлаб.

Итак, задаем константы — тут все просто, буква=значение;, то есть никакого там пока что описания типов переменных (+ матлабу, но пока ниче нового по сравнению с маткадом).

Идем дальше, генераторы случайных чисел и формирование матриц и массивов… Читать про это было лень, так что методом научного тыка и остаточных воспоминаний вкурила как задаются циклы и матрицы соответственно. Встроенного генератора случайных чисел, распределенных экспоненциально здесь кажется нет («-«), зато пришлось пошевелить башкой и вспомнить как числа из простого random (rnd) превращаются в экспоненциально распределенные)) («+» — думать головой — всегда плюс). Развлечения ради вывела их plot-ом на график:

Чудненько, в настройках еще не ковырялась, как там подписи и условные обозначения выводить. Но смысл ясен — эта фигня работает. Следующим пунктом моего алгоритма было собственно создать матрицу моментов поступления пакетов у каждой станции, упорядоченных в порядке возрстания (да здравствует рекурсия канеш!), короче в матлабе это выглядит так:

N=10 % число станций
K=25;
G=0.9 % интенсивность входной нагрузки
r=G/N; % интенсивность нагрузки у каждой станции
for n=1:N, %цикл по станциям
t(n,1)=-1/r*log(rand(1)), %нулевые, экспоненциально распределенные моменты поступления пакетов у каждой станции
for k=2:K, % цикл по запросам
K0(n,k)=-1/r*log(rand(1)), % интервалы между моментами появления соседних заявок
t(n,k)=t(n,k-1)+K0(n,k), % собственно, матрица моментов поступления пакетов
end;
end;
for n=1:N, %цикл для вывода моментов поступления пакетов у каждой станции
hold on %не стирает предыдущий график, в итоге выводится столько графиков. сколько прогоняешь цикл
plot(t(n,1:K)), %функция построения графиков.
end;
 

И в итоге получается вот такая уже упорядоченная красотисча:

Ну и все бы ничего, НО!!!! он считал эти жалкие 10 кривых, в которых всего по 25 точек около минуты!!!!!! это ж какой-то кошмар!!!! а мне ж надо не десять станций, а 128 хотя бы , да и пакетов у них чтобы штук по 50 было для статистики.. может я чего-то не понимаю, но после маткадушки, у которого подобные плевые вычисления заняли бы не более полусекунды, эта хрень мне кажется тупостью полной! и что будет дальше, когда мне надо будет около 10 циклов внутри одного прогонять, когда будет миллион условий, он что просто повесится?! в общем надо почтать как тут у него с организацией памяти и че это за фигня. но это явно не дело((( огромный МИНУС матлабу….
Потом правда выяснилось, что с матлабом все в порядке, эт я просто лошара в цикле запятые вместо «;»  поставила))) как только поменяла — все залетало! (Леше пасиба!!)))) Так что можно двигаться дальше)

Операторы и операции Matlab | Piter Melnikov

Оператор – это символ или символическая конструкция, который указывает компилятору выполнять определенную операцию. MATLAB допускает следующие виды элементарных операций:
— Арифметические операторы.
— Операторы отношений.
— Логические операторы.
— Операторы управления.
Арифметические операторы Matlab рассмотрены в статье.
Заметим, что каждому оператору Matlab соответствует определенная функция. Далее приведены различные операторы, соответствующие им функции и описания.

Операторы отношений

Логические операторы

MATLAB имеет два типа логических операторов и функций:
— Поэлементный. Такие операторы работают с соответствующими элементами логических массивов.
— Короткое замыкание. Такие операторы работают со скалярными и логическими выражениями.

Приоритет операций
При одновременном использовании в выражении логических, арифметических операций и операций сравнения следует учитывать приоритет операций. Он следующий:
1. Логические операторы.
2. Логическая операция ~ .
3. Арифметические операции в соответствии со своим приоритетом.
4. Операции отношения.
5. Логическая операция «И» – &.
6. Логическая операция «ИЛИ» – |.

Операторы управления

Оператор условия

Для записи условий в М-языке MATLAB используется оператор If. Существуют две разновидности оператора If обычная и расширенная. Обычная форма If имеет синтаксис подобный оператору If в языке Basic:

If условие
блок инструкций_1
else
блок инструкций_2
end

Синтаксис расширенного оператора If:
If условие_1
блок инструкций_1
elseif условие_2
блок инструкций_2
elseif условие n
блок инструкций_n
else
блок инструкций
end

Оператор выбора SWITCH (переключатель)

Оператор SWITCH
Этот оператор выполняет роль переключателя. При получении некоторой переменной какого -либо значения, равного значению определенной константы, он совершает переключение на выполнение нужного блока инструкций. Оператор имеет следующий синтаксис:
switch expr case
case_expr,
<операторы_1>
case {case_expr1, case_expr2, case_expr3,…}
<операторы_2>
…
otherwise,
<операторы>
end
где :
expr – переменная, значение которой проверяется на равенство тем или иным константам;
case_expr – константы, с которым сравнивается значение переменной; otherwise – ключевое слово, для выполнения операторов, при всех ложных условиях.

Пример. Требуется создать программу, которая выводит оценку по итогам набранного количества баллов. Для решения таких задач удобнее пользоваться условным оператором switch.
Код скрипта М-файла может быть записан как на рис. 1.

Рис 1.

Рис 1.

Операторы цикла

Оператор for … end

Цикл for … end применяют в тех случаях, когда заранее известно число повторений цикла. Синтаксис:

for x = xn: hx: xk
операторы
end

где:
— х – имя переменной – счетчика цикла;
— xn – начальное значение счетчика цикла;
— xk – конечное значение счетчика цикла;
— hx – шаг приращения счетчика цикла. Если шаг цикла равен 1, то hx можно опустить.
Для досрочного выхода из цикла служит оператор break.
Пример. Требуется вычислить четвертый член геометрической прогрессии. Код скрипта М-файла для решения задачи может быть записан как на рис. 2.

Рис. 2.

Рис. 2.

Когда количество циклов заранее не известно, но известно условие завершения цикла применяется цикл while.
Синтаксис оператора while:
while условие
<операторы>
end
Пример. Требуется вычислить четвертый член геометрической прогрессии.
Код скрипта М-файла для решения задачи может быть записан как на рис. 3.

Рис. 3.

Рис. 3.

(PDF) Численное продолжение бифуркаций предельных циклов в MATLAB

22 В. Говертс, Ю.А. Кузнецов, А. Дхоге

СПИСОК ЛИТЕРАТУРЫ

[1] Э. Л. Аллгауэр, К. Георг, Методы численного продолжения: Введение, Springer-

Verlag (1990).

[2] У. Ашер, Дж. Кристиансен и Р. Д. Рассел, Программное обеспечение для сопоставления граничных значений

ODE, ACM TOMS 7 (2) (1981), стр. 209–222.

[3] У. Ашер, Р. Д. Рассел, Преобразование краевых задач в стандартную форму,

SIAM Review 23 (2) (1981), стр.238–254.

[4] W. J. Beyn, A. Champneys, E. Doedel, W. Govaerts, Yu. А. Кузнецов, Б. Сандстеде,

Численное продолжение и вычисление нормальных форм. В: B. Fiedler, G. Iooss, and N.

Kopell (eds.) «Handbook of Dynamical Systems: Vol 2», Elsevier (2002), pp. 149–219.

[5] К. Де Бур и Б. Шварц, Коллокация в точках Гаусса, SIAM Journal on Numerical

Analysis 10 (1973), стр. 582–606.

[6] A. Dhooge, W. Govaerts, Yu. А.Кузнецов, matcont: Пакет Matlab для численного бифуркационного анализа

ОДУ, ACM TOMS 29 (2) (2003), стр. 141–164.

[7] A. Dhooge, W. Govaerts, Yu. А. Кузнецов, В. Местром и А. М. Рит, cl matcont:

Набор инструментов продолжения в matlab, Материалы симпозиума ACM 2003 г. по прикладным вычислениям

, Мельбурн, Флорида (2003), стр. 161–166.

[8] E. J. Doedel, H. B. Keller и J. P. Kernevez, Численный анализ и управление бифуркационными задачами I, Бифуркация в бесконечных измерениях, Int.J. Bifurcation and Chaos, 1 (1991),

pp. 493 — 520.

[9] EJ Doedel, HB Келлер и JP Kernevez, Численный анализ и управление катионными проблемами bifur-

II, Бифуркация в бесконечных измерениях , Int. J. Bifurcation and Chaos, 1

(1991), pp. 745 — 772.

[10] E. J. Doedel, A. R. Champneys, T. F. Fairgrieve, Yu. А. Кузнецов, Б. Сандстеде,

X. Дж. Ван, auto97-auto2000: Программа продолжения и бифуркации для обыкновенных дифференциальных уравнений

(с HomCont), Руководство пользователя, Университет Конкордия, Монреаль,

Канада (1997-2000).(http://indy.cs.concordia.ca).

[11] E. J. Doedel и R. F. Heinemann, Численный расчет ветвей периодического решения

и колебательной динамики реактора с мешалкой при A → B → Creactions, Chemical

Engineering Science, Vol. 38 (9) (1983), стр. 1493–1499.

[12] E. J. Doedel, W. Govaerts, Yu. А. Кузнецов, Вычисление бифуркации периодических решений в ОДУ с использованием систем с границами, SIAM J. Numer. Анализ 41 (2003), стр. 401–435.

[13] E.Фрейре, А. Родригес-Луис, Э. Гамеро и Э. Понсе, Пример гомоклинического хаоса

в автономной электронной схеме: поездка от Такенса-Богданова до Хопфа-Шильникова,

Physica D 62 (1993), С. 230–253.

[14] Р. Генезио, А. Теси, Методы гармонического баланса для анализа хаотической динамики в нелинейных системах

. Automatica 28 (1992), стр. 531–548.

[15] Р. Генезио, А. Тези, Ф. Виллорези, Модели сложной динамики в нелинейных системах.

Systems Control Lett. 25 (1995), стр. 185–192.

[16] Г. Г. Голуб, К. Ф. Ван Лоан, Матричные вычисления, Джон Хопкинс, Балтимор, 3-е изд.

(1996).

[17] W. Govaerts, Yu. А. Кузнецов, Б. Сийнаве, Численные методы для обобщенной бифуркации Хопфа

. SIAM J. Numer Anal. 38 (2000), стр. 329–346.

[18] В. Говертс, Численные методы бифуркаций динамических равновесий, SIAM, Philadel-

phia (2000).

[19] Дж.Guckenheimer и B. Meloon, Вычисление периодических орбит и их бифуркаций с помощью автоматического дифференцирования

, SIAM J. Sci. Comput. 22 (2000), стр. 951–985.

[20] Х. Б. Келлер, Численные методы в задачах бифуркации, Springer Verlag, Берлин, Нью-Йорк,

1987.

[21] Ю. А. Кузнецов, Элементы прикладной теории бифуркаций, 2-е издание, Springer-Verlag, New

York (1998).

[22] Ю. А. Кузнецов, В. В. Левитин, содержание: Интегрированная среда анализа динамических систем

.CWI, Амстердам (1997): ftp://ftp.cwi.nl/pub/CONTENT

[23] Д. Руз Д. и др., Аспекты программного обеспечения продолжения, в: Продолжение и бифуркации:

. Applications, (ред. Roose, D., De Dier, B., Spence, A.), NATO

ASI series, Series C, Vol. 313, Kluwer (1990), стр. 261–268.

[24] С. Стейнмец и Р. Лартер, Квазипериодический путь к хаосу в модели пероксидазной реакции

— оксидаз, J. Chem. Phys. 74 (1991), стр.1388–1396.

[25] А. Теси, Э. Х. Абед, Р. Дженезио и Х. О Ван, Анализ гармонического баланса периода

— бифуркации удвоения с последствиями для управления нелинейной динамикой, Automatica

32 (9) (1996), С. 1255–1271.

программ Matlab

программ Matlab

Эта страница содержит ссылки на программы Matlab

В тексте использованы программы: «Двигатели внутреннего сгорания: Прикладные науки о теплоте «, К. Фергюсон и А.Киркпатрик, Третье издание, Джон Вили и сыновья, 2016.

  • Объем, м Программа вычисляет и строит точный и приблизительный цилиндр объем в зависимости от угла поворота коленчатого вала.
  • Скорость.м Программа вычисляет и строит график зависимости скорости поршня от кривошипа. угол.
  • BurnFraction.m Программа вычисляет и строит график зависимости доли выгорания от кривошипа. угол.
  • FiniteHeatRelease.m Программа вычисляет профиль давления, работу, эффективность и imep для данного профиля ожога.
  • FiniteHeatMassLoss.m Программа вычисляет профиль давления, работу, КПД и imep, включая потерю тепла и массы.
  • FourStrokeOtto.m Программа вычисляет объемный и тепловой КПД, остаточную дробь и состояния для четырехтактного двигателя Отто.
  • RunFarg.m Файл ввода / вывода для программы смеси топливо — воздух — остаточный газ farg.m.
  • farg.m Программа вычисляет мольные доли и термодинамические свойства топливо — воздух — остаточный газ смесь.
  • топливо.м Топливо файл свойств.
  • RunEcp.m Файл ввода / вывода для программы ecp.m.
  • экп.м. Программа вычисляет мольные доли и термодинамические Свойства равновесного горения топливовоздушной смеси
  • AdiabaticFlameTemp.m Программа вычисляет адиабатическую температуру пламени при постоянном давлении топлива — воздуха смесь.
  • OttoFuel.m Программа вычисляет состояния, работу, имеп, эффективность топливно-воздушного цикла Отто.
  • FourStrokeFuelAir.м Программа вычисляет состояния, работа, имеп, эффективность для четырехтактного двигателя Отто топливно-воздушный цикл.
  • Однородный.м Программа вычисляет состояния, работу, имеп, КПД и NO двухзонного тепловыделения топливовоздушного цикла.
  • Friction.m Программа вычисляет компонент и общее трение означают эффективное давление.
  • WoschniHeatTransfer.m Программа вычисляет профиль давления, работу, КПД и imep, включая тепло Woschni и потеря массы.

Моделирование и имитация гибридного электромобиля с использованием MATLAB / Simulink и ADAMS

dc.description.abstract Поскольку мировая экономика стремится к экологически чистой энергии перед лицом изменения климата, автомобильная промышленность изучает возможности повышения эффективности автомобили. Были предложены системы гибридных транспортных средств, которые продемонстрировали способность снижать расход топлива при сохранении рабочих характеристик транспортного средства. Производителями различных транспортных средств были произведены различные гибридные автомобили в форме параллельных и последовательных гибридов.Целью данной диссертации является создание модели гибридного транспортного средства в MATLAB и ADAMS, чтобы продемонстрировать улучшение экономии топлива по сравнению с традиционной системой транспортного средства. Модель гибридного автомобиля использует архитектуру Honda IMA (Integrated Motor Assist), в которой электродвигатель действует как дополнение к крутящему моменту двигателя. Блок двигателя также действует как генератор во время рекуперативного торможения, чтобы восстановить потерянную кинетическую энергию. Расчет выходной мощности компонентов трансмиссии и логика управления моделировались в MATLAB / Simulink, а механические инерционные компоненты моделировались в ADAMS.Модель использует имитацию действий водителя, при которой модуль управления водителем сравнивает фактическую и желаемую скорости и применяет дроссельную заслонку или процент торможения к компонентам трансмиссии, которые, в свою очередь, прикладывают ведущий или тормозной момент к колесам. Связь между MATLAB и ADAMS была установлена ​​ADAMS / Controls. Чтобы оценить точность модели гибридного автомобиля MATLAB / ADAMS, результаты моделирования сравнивали с опубликованными данными ADVISOR. Для сравнения двух программных моделей использовался ездовой цикл Университета Западной Вирджинии «5 пиков».Результаты, полученные из MATLAB / ADAMS и ADVISOR для двигателя и двигателя / генератора, хорошо коррелировали. Существовали незначительные расхождения, но они были сочтены несущественными. Это подтверждает соответствие модели гибридного транспортного средства MATLAB / ADAMS опубликованным результатам ADVISOR. Экономия топлива гибридных и обычных моделей автомобилей сравнивалась с использованием цикла EPA New York City Cycle (NYCC) и цикла экономии топлива шоссе (HWFET). Гибридный автомобиль продемонстрировал улучшение экономии топлива на 8,9% и 14,3% по сравнению с традиционной моделью транспортного средства для ездовых циклов NYCC и HWFET соответственно.Кроме того, двигатель потреблял 83,6 кДж электроэнергии в режиме помощи, в то время как рекуперативное торможение рекуперировало 105,5 кДж электроэнергии во время движения по городу. Для цикла движения по шоссе двигатель потреблял 213,6 кДж электроэнергии во время вспомогательного режима, в то время как рекуперативное торможение восстанавливало 172,0 кДж энергии. Модель транспортного средства MATLAB / ADAMS предлагает платформу моделирования, которая является модульной, гибкой и может быть удобно модифицирована для создания различных типов моделей транспортных средств.Кроме того, результаты моделирования ясно продемонстрировали преимущество гибридного транспортного средства в экономии топлива над традиционной моделью транспортного средства. Рекомендуется реализовать в модели более сложный алгоритм управления мощностью, чтобы оптимизировать КПД двигателя и двигателя / генератора. Кроме того, предлагается проверить модель транспортного средства ADAMS на реальном транспортном средстве, чтобы в полной мере использовать динамические возможности многофюзеляжного транспортного средства, которые может предложить ADAMS. и

Моделирование и имитация электромобиля с использованием Matlab и его проверка с помощью ездовых циклов | Maaz Mufti

[1] ICCT, «Движение электрификации», ICCT — Int. Counc. Чистый трансп., Нет. May, 2014.

[2] Д. Дайн, М. Хоули и М. Холланд, «Энергия на транспорте», Sustain. Energy Auth. Irel., 2014.

[3] DFOR Science, CFOR Information, C. Policy, R. Applications и C. Initiatives, «DSTI / ICCP / IE (2007) 13 / FINAL Unclassified Working Party on the Information Economy», нет.2007, pp. 1–29, 2008.

[4] GM Mufti, M. Jamil, D. Naeem, MU Mukhtiar и AT Al-Awami, «Анализ производительности параболических коллекторов желоба для Пакистана с использованием математических и вычислительных моделей. ”Clemson Univ. Power Syst. Конф. PSC 2016, 2016.

[5] М.С. Азиз, С. Ахмед, У. Салим и Г.М. Муфти, «Ветрогибридные системы выработки энергии с использованием возобновляемых источников энергии — Обзор ветро-гибридных систем выработки энергии с использованием возобновляемых источников энергии». Обзор », т. 7, вып.Март, 2017.

[6] С.З. Хассан, Х. Ли, С. Кагриенер, Т. Камаль, Г.М. Муфти, М.Х. Васим и Х. Гохар, «Интеграция и моделирование ветра с гибридной системой хранения водорода / суперконденсатора», 2017 г. Конф. Электр. Англ. ICEE 2017, стр. 1–6, 2017.

[7] A. Küçüker, T. Kamal, SZ Hassan, H. Li, GM Mufti и MH Waseem, «Проектирование и управление микросетями на основе фотоэлектрических / ветряных / аккумуляторных батарей. Система », стр. 1–6, 2017.

[8] Г. Мааз Муфти, М. Джамиль, М. Наваз, Мобин-ур-Рехман, С.Зулкадар Хасан и Т. Камаль, «Оценка проблем и вызовов в контексте энергетического кризиса Пакистана», Indian J. Sci. Technol., Т. 9, вып. 36, 2016.

[9] iea, «Дорожная карта технологий», SpringerReference, стр. 81, 2015.

[10] МЭА, «Отчет о рынке энергоэффективности 2016», Публикация МЭА, 2016.

[11] Международное энергетическое агентство, «Инициатива по электромобилям Global EV Outlook 2016», Iea, p. 51, 2016.

[12] МЭА, «Перспективы энергетических технологий 2016 — Краткое изложение», Iea, p.14, 2016.

[13] Международное энергетическое агентство, «Global EV Outlook 2016 Beyond одного миллиона электромобилей», Iea, p. 51, 2016.

[14] С. Мунникс, «Электронная мобильность в Нидерландах и Нидерландах», нет. Май, 2015 г.

[15] Дж. Лармини и Дж. Лоури, Разъяснение технологии электромобилей. 2003.

[16] «Характеристики зоны E (электромобиль)». [В сети]. Доступно: http://cttev.com/e-zone/. [Доступ: 24 июля 2017 г.].

% PDF-1.4 % 34 0 объект > эндобдж xref 34 86 0000000016 00000 н. 0000002587 00000 н. 0000002668 00000 н. 0000002798 00000 н. 0000002933 00000 н. 0000003964 00000 н. 0000004135 00000 п. 0000004212 00000 н. 0000004394 00000 н. 0000007081 00000 п. 0000007369 00000 н. 0000007700 00000 н. 0000007926 00000 н. 0000008437 00000 н. 0000008740 00000 н. 0000008782 00000 н. 0000008981 00000 п. 0000009307 00000 н. 0000009580 00000 н. 0000009872 00000 н. 0000010198 00000 п. 0000010377 00000 п. 0000010592 00000 п. 0000010775 00000 п. 0000011034 00000 п. 0000011240 00000 п. 0000011526 00000 п. 0000011709 00000 п. 0000011892 00000 п. 0000012107 00000 п. 0000012396 00000 п. 0000012593 00000 п. 0000012834 00000 п. 0000013121 00000 п. 0000013361 00000 п. 0000013635 00000 п. 0000013932 00000 п. 0000014199 00000 п. 0000014489 00000 н. 0000014790 00000 п. 0000015028 00000 п. 0000015324 00000 п. 0000015563 00000 п. 0000015911 00000 п. 0000016159 00000 п. 0000016450 00000 п. 0000016692 00000 п. 0000016902 00000 п. 0000017133 00000 п. 0000017435 00000 п. 0000017707 00000 п. 0000017972 00000 п. 0000018268 00000 п. 0000018582 00000 п. 0000018831 00000 п. 0000019051 00000 п. 0000019256 00000 п. 0000019532 00000 п. 0000019803 00000 п. 0000020058 00000 н. 0000020266 00000 н. 0000020432 00000 п. 0000020597 00000 п. 0000020985 00000 п. 0000021172 00000 п. 0000021373 00000 п. 0000021565 00000 п. 0000021757 00000 п. 0000021800 00000 п. 0000021868 00000 п. 0000022048 00000 н. 0000022214 00000 п. 0000022385 00000 п. 0000022670 00000 п. 0000022953 00000 п. 0000023030 00000 н. 0000023089 00000 п. 0000023253 00000 п. 0000023463 00000 п. 0000023507 00000 п. 0000023550 00000 п. 0000023609 00000 п. 0000023778 00000 п. 0000024071 00000 п. 0000024115 00000 п. 0000002016 00000 н. трейлер ] >> startxref 0 %% EOF 119 0 объект > поток xb«f`0d`g`icg @

Код и данные — Сильвия Миранда-Агриппино 

  В этом разделе собраны данные и коды MatLab, которые я использовал в своих статьях.Контент организован по темам. Репликационный материал для отдельных статей отмечен в каждой теме.

ИНСТРУМЕНТЫ ДЛЯ УДАРОВ ДЕНЕЖНОЙ ПОЛИТИКИ

  1. Высокочастотный

    Информационно надежный сюрпризы денежно-кредитной политики при ежемесячных и встречах FOMC 2018). Контроль всех серий для информационных эффектов центрального банка; ежемесячные ряды также контролируют автокорреляцию денежных неожиданностей.Подробная информация о построении ряда содержится в Miranda-Agrippino & Ricco (2016) «Передача шоков денежно-кредитной политики»

    🔸скачать инструмент MPI


    Ежемесячная денежно-кредитная политика сюрприза с поправкой на внутренние прогнозы Центрального банка для US и UK , используемых в Miranda-Agrippino (2016). Подробная информация о конструкции серии находится в Miranda-Agrippino (2016) “ Неудивительно, что потрясения: информация, премия и денежная трансмиссия ”

    сюрпризов 🔸загрузить онлайн-приложение

  2. Рассказ (расширение Romer & Romer 2004)

    Ежемесячные и квартальные сюрпризы денежно-кредитной политики для США, построенные на основе описательных отчетов заседаний FOMC с 1960 года.Серии заканчиваются при наступлении ЗЛБ. В папке содержатся данные и документация по конструкции, а также сравнение с оригинальной серией R&R. Используется в Miranda-Agrippino and Rey (2015), Miranda-Agrippino & Ricco (2016), Miranda-Agrippino, Hacioglu-Hoke & Bluwstein (2018)

    🔸загрузить повествовательную серию и документацию

    FSEC


IMPUL : BVAR, LP, & BLP

Папка содержит файла репликации для Miranda-Agrippino & Ricco (2016) «Передача шоков денежно-кредитной политики» .Код оценивает функции импульсной характеристики для байесовской векторной авторегрессии со стандартными априорными значениями NIW , локальными проекциями и байесовскими локальными проекциями . Идентификация может быть одним из Cholesky или внешних инструментов ( BSVAR-IV и BLP-IV )

🔸загрузить файлы репликации BLP (1,1 МБ)

PROXY SVAR / SVAR-IV

Папка содержит код MatLab для оценка функций импульсного отклика (IRF) в структурных OLS VAR, идентифицированных с внешними инструментами, и сравнение его со стандартным упорядочением Холецкого.В SVAR-IV двухэтапный алгоритм оценки и идентификации позволяет использовать различные выборки в нововведениях VAR и выбранных IV. Стандартные ошибки рассчитываются с использованием Wild Bootstrap . Код воспроизводит рисунок IV из Miranda-Agrippino (2016) “ Неудивительные шоки: информация, премия и денежная трансмиссия ”

🔸загрузить 450

ГЛОБАЛЬНЫЙ ФИНАНСОВЫЙ ЦИКЛ

Исследования — Личный веб-сайт Матиаса Трабандта

с M.Эйхенбаум и С. Ребело

Обзор финансовых исследований (готовится к печати)

Этот документ был представлен, например, New York Times (титульный лист), Washington Post, Frankfurter Allgemeine Zeitung, Science, Forbes, Bloomberg, International Business Times, BBC Brazil, NZZ am Sonntag, The Academic Times и др.

с Л. Кристиано и М. Эйхенбаумом

Обзор экономической динамики (готовится к печати)

с М. Эйхенбаумом и С. Ребело

Эта версия: 18 декабря 2020 г.

с М.Эйхенбаум, М. Годиньо де Матос, Ф. Лима и С. Ребело

Эта версия: 21 октября 2020 г.

Статья была представлена, например, NZZ am Sonntag.

с М. Эйхенбаумом и С. Ребело

Эта версия: 1 апреля 2021 г.

Газета была представлена, например, Frankfurter Allgemeine Zeitung.

с М. Эйхенбаумом и С. Ребело

Эта версия: 19 июня 2020 г.

с Л. Кристиано и К. Валентином

Review of Economic Dynamics (готовится к печати)

с J.Линде

Эта версия: 23 сентября 2019 г.

с Л. Кристиано и М. Эйхенбаумом

Journal of Economic Perspectives , Vol. 32, No. 3, Summer 2018, pp. 113-140

с Ф. Сметсом

Эта версия: 20 июля 2018 г.

с J. Lindé

Journal of Applied Econometrics , 2018, Vol. 33, выпуск 7, стр. 937-965

* Предыдущая версия документа называлась «Фискальные мультипликаторы в нелинейном мире».

с Л. Кристиано и М. Эйхенбаумом

Econometrica , июль 2016 г., 84 (4), стр. 1523-1569

с Дж. Ариасом и К. Эрцегом

European Economic Review, Volume 88 , Сентябрь 2016 г., стр. 88-107

с Л. Кристиано и М. Эйхенбаумом

American Economic Journal: Macroeconomics , 7 (1), январь 2015 г., стр. 110-167

Денежно-кредитная политика, суверенный долг и финансовая стабильность: Новая трилемма, редактор Д.Моханти, 2014, стр. 332-363, ISBN: 978-93-82993-20-9, Cambridge University Press, Индия.

с Г. Коененом и Р. Штраубом

Journal of Economic Dynamics and Control , 37 (2), февраль 2013 г., стр. 367-386.

с Х. Улиг

NBER Главы: Фискальная политика после финансового кризиса , редакторы А. Алесина и Ф. Джавацци, 2013, стр. 211-249, ISBN: 9780226018447, University of Chicago Press.

с Г. Коененом и Р.Straub

American Economic Review , Papers and Proceedings, 102 (3), май 2012 г., стр. 71-76.

с Коененом, де Резенде, Эрцегом, Фридманом, Фурчери, ин ‘т Вельд, Кумхоф, Лалонд,
Лакстон, Линде, Моуруган, Мьюир, Мурсула, Робертс, Роджер и Снудден

American Economic Journal: Macroeconomics, 1), январь 2012 г., стр. 22–68.

Журнал денежно-кредитной экономики , том 58, выпуск 4, май 2011 г., страницы 305–327.

с Л. Кристиано и К. Валентином.

Journal of Economic Dynamics and Control , 35 (12), декабрь 2011 г., стр. 1999–2041.

Справочник по монетарной экономике , 2010, редакторы Б. М. Фридман и М. Вудфорд, том 3а, глава 7, страницы 285-367, ISBN: 978-0-444-53238-1, Elsevier B.V., Северная Голландия.

Налогово-бюджетная политика зоны евро и кризис
с Афонсу, Аттинаси, Катц, Чечерита, Никель, Лейнер-Киллингер, Маурер, Ротер, Славик, Валента, Рит и Вармедингер

Периодическая статья ЕЦБ , No.109, под редакцией А. ван Рита

Исследовательский бюллетень ЕЦБ , № 10

Важная информация против липких цен: скачки в рамках DSGE

Эта версия: 29 января 2009 г.

Предыдущая версия : Рабочий документ Sveriges Riksbank № 209

Эта версия: 29 января 2009 г.

Предыдущая версия: Рабочий документ EUI ECO 2007/52

Следует ли координировать валютную политику США и Европы? Подход «липкой информации»

Дипломная работа , Университет Гумбольдта в Берлине, август 2001 г.

с J.Scheide

Эта версия: декабрь 2000 г .

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *