Простой и эффективный расчёт Modbus CRC16 в ПЛК и МК без побитового сдвига и таблиц / Хабр
Сакральный алгоритм расчёта CRC16, описанный в литературе и связанный с побитовым сдвигом, плохо вписывается в формат вычислительных возможностей ПЛК и МК. Во-первых, постольку, поскольку его реализация отнимает изрядный объем вычислительных ресурсов вышеозначенных устройств, во-вторых, потому что в ходе такого расчета существенно растягивается время скана программы. Рост скана программы обусловлен тем, что, вследствие словной или байтовой организации аккумулятора арифметико-логического устройства, результирующие битовые операции со словами/байтами в нём выполняются гораздо дольше операций со словами/байтами целиком. В отдельных устройствах операции побитового сдвига и вовсе не поддерживаются, тогда как алгоритм подразумевает выполнение восьми циклов с такими операциями.
В целях сокращения объема вычислений и, как следствие, времени сканирования при обработке CRC, часто применяется иной алгоритм — табличный, когда таблица масок рассчитывается и заполняется единожды в первом скане программы.
А можно ли видоизменить алгоритм расчёта CRC таким образом, чтобы отказаться от применения побитовых сдвигов и таблиц? Безусловно, да. Достаточно лишь внимательно приглядеться к алгоритму с побитовым сдвигом.
Напомню его суть:
- осуществляется сложение по модулю 2 очередного байта массива посылки с младшим байтом двухбайтной CRC;
- осуществляется ациклический сдвиг CRC на один бит от старшего 15-го разряда к младшему, нулевому, с выдвижением младшего бита, при этом старший разряд обнуляется;
- если значение выдвинутого бита единичное, выполняется сложение CRC по модулю 2 c полиномом 16#A001.
- шаги 2 и 3 повторяются ещё 7 раз.
Почему это реализовано так, а не иначе? Да потому, что такая алгоритмизация представлялась наиболее подходящей для реализации посредством аппаратной логики.
Внимательно взглянув на этот алгоритм, нетрудно обнаружить, что фактически мы имеем дело с циклическим побитовым сдвигом слова. За его цикличность отвечает старший бит полинома. В результате, значение старшего битового разряда CRC после каждого сдвига идентично значению выдвинутого младшего. Таким образом, при осуществлении циклического побитового сдвига, полином, с которым затем необходимо производить сложение по модулю 2, трансформируется в 16#2001.
Подобных сдвигов выполняется восемь… Проще говоря, в глобальном плане речь идёт о перемене местами младшего байта CRC со старшим её байтом. А это наводит на мысль, что, после сложения по модулю 2 очередного байта массива посылки с младшим байтом CRC, достаточно поменять местами младший и старший байт CRC, а затем, последовательно проанализировав восемь бит старшего её байта, начав с младшего его разряда, восьмого, произвести сложение СRC по модулю 2 c известными константами, предопределёнными значением полинома, значение которого для Modbus CRC16, как уже указано выше, эквивалентно 16#2001.
Итоговый алгоритм для учёта в CRC очередного байта массива посылки выглядит следующим образом:
Осуществляется сложение по модулю 2 очередного байта массива посылки с младшим байтом двухбайтовой CRC, после чего младший и старший байт CRC меняются местами;
- Если значение 8-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#0240;
- Если значение 9-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#0480;
- Если значение 10-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#0900;
- Если значение 11-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#1200;
- Если значение 12-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#2400;
- Если значение 13-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#4800;
- Если значение 14-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#9000;
- Если значение 15-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#2001, расчёт окончен.
Преимущества такого способа расчёта:
1) По сравнению с алгоритмом побитового сдвига:
а) предложенный алгоритм позволяет избавиться от команд вложенного цикла FOR-NEXT и команд побитового сдвига в таком цикле, при том, число количество исполняемых команд сложения по модулю 2 сохраняется неизменным;
б) в контроллерах c поддержкой команды SWAP, восьмикратный побитовый сдвиг CRC заменяется единственной командой, а в контроллерах, такую команду не поддерживающих, — одной или двумя командами пересылки, входящими в число базовых команд контроллера и отнимающими минимальное время;
2) По сравнению с табличным методом расчёта, этот метод не нуждается в выделении места в памяти данных под таблицу, в её предварительном заполнении, в выборке соответствующей маски из таблицы с последующим ее наложением на байт CRC.
Проработка предложенного алгоритма расчёта СRC16 изначально велась для ПЛК Mitsubishi моделей FX3S/3G, не поддерживающих инструкций расчёта СRC и перемены местами байт в слове, между тем, предельное суммарное время расчета СRC с применением указанного алгоритма для массива посылки, состоящего из 128 байт, не превышает 2,4мс.
Прямой табличный алгоритм crc16
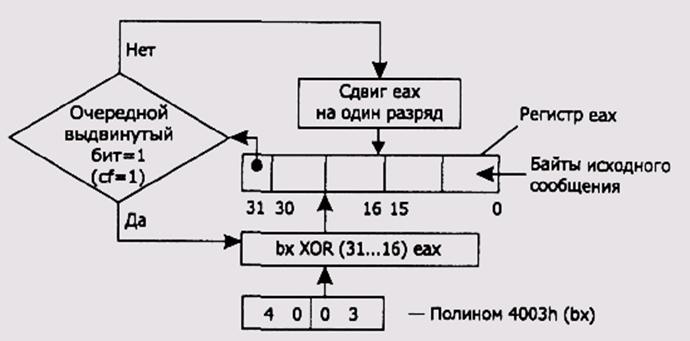
Необходимость дополнения исходной строки завершающими нулевыми байтами представляет большое неудобство при реализации общей схемы табличного алгоритма. Поэтому на практике используют другую схему вычисления CRC, не требующую завершения исходного сообщения нулевыми байтами. В этой схеме очередной байт исходной строки объединяется операцией XOR со старшим байтом регистра, выдвинутым с левой стороны этого регистра.
Полученное в результате объединения значение используется в качестве индекса для доступа к CRC-таблице. Извлекаемое из CRC-таблицы значение объединяется операцией XOR с содержимым регистра. Описанный алгоритм называют прямым табличным алгоритмом.
Рис. 12.6
На схеме вычислений CRC с использованием
прямого табличного алгоритма цифрами
обозначена последовательность шагов
вычисления CRC.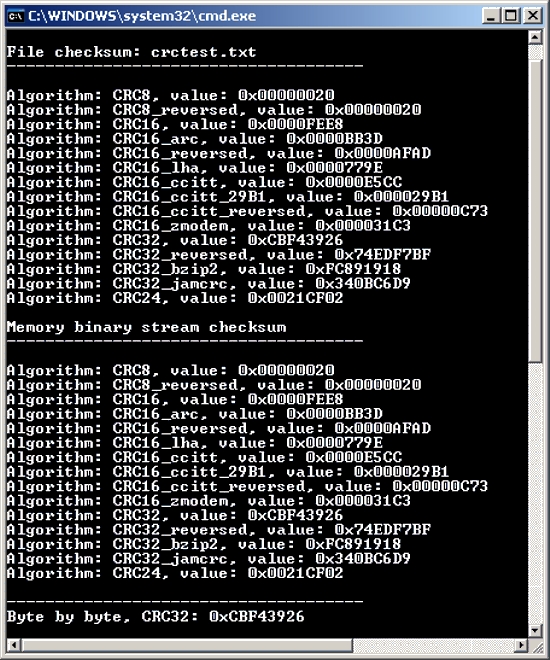
Выдвижение старшего байта регистра АХ в байтовую ячейку.
Выполнение операции XOR над выдвинутым на шаге 1 в байтовую ячейку старшим байтом регистра АХ и очередным байтом исходной строки.
Полученное на шаге 2 значение используется в качестве индекса для доступа к элементу CRC-таблицы.
Извлеченное из CRC-таблицы значение объединяется по XOR со значением в регистре АХ.
Результат выполнения на шаге 4 операции XOR помещается обратно в регистр АХ.
После обработки последнего байта исходной строки регистр АХ содержит значение CRC.
Все существующие алгоритмы вычисления CRC являются, по сути, различными модификациями описанного выше табличного алгоритма. Эти модификации преследуют разные цели, перечислим некоторые из них:
переход от цикла по всем битам к циклу по большим порциям данных – байтам, словам и т. д.;
повышение разрядности порождающего полинома;
отражение особенностей функционирования аппаратуры передачи данных (наличие этой цели обусловлено тем, что микросхемы, поддерживающие работу последовательного порта компьютера, передачу байта начинают с его младших битов, поэтому описанные ниже алгоритмы расчета CRC, учитывающие эту особенность, называются зеркальными).
Алгоритмы вычисления CRC получили свое закрепление в некоторых стандартах. Перечислим отличительные особенности основных алгоритмов вычисления CRC. Итак, основные алгоритмы вычисления CRC различаются:
по значению и степени порождающего полинома, при этом значение полинома обычно указывается без ведущей единицы в старшем разряде;
по начальному содержимому регистра, в котором формируется значение CRC;
по тому, производится ли обращение битов каждого байта перед его обработкой;
по способу прохода байтов через регистр – способ может быть косвенным или прямым;
по тому, производится ли обращение конечного результата;
по конечному значению, с которым производится объединение по XOR результата вычисления CRC.
После появления 32-разрядных микропроцессоров
наибольшей популярностью стали
пользоваться 32-разрядные алгоритмы
вычисления CRC.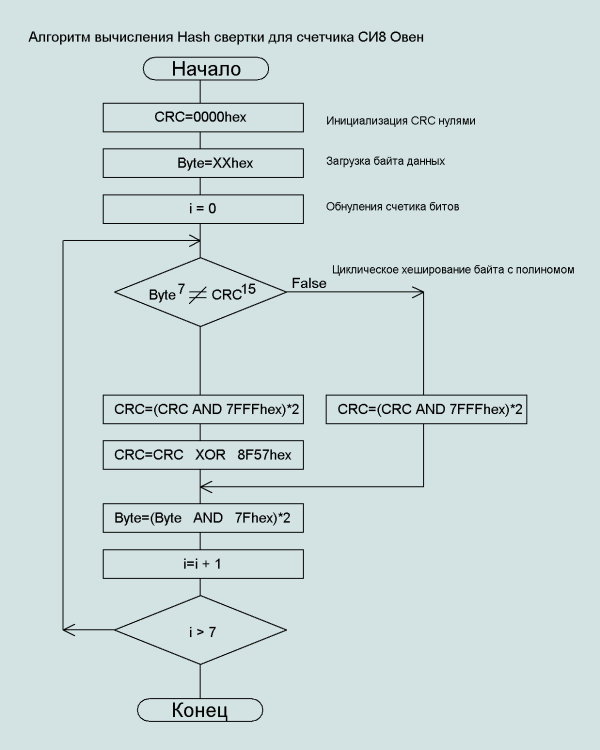
В различных источниках
рассматривают два типа таких алгоритмов
– прямой и зеркальный. Рассмотрим их
конкретные реализации, рекомендуемые
стандартами.
Как и любой табличный алгоритм, табличный алгоритм вычисления CRC32 требует задания CRC-таблицы. Ее можно задать в программе статически, явно прописав значения элементов таблицы в сегменте кода, или динамически, вычислив значения элементов таблицы перед началом расчета CRC.
В заключение обсудим «зеркальный» вариант табличного алгоритма – алгоритм CRC32 (V.42 МККТТ). Этот вариант вычисления CRC обязан своим возникновением существованию последовательного интерфейса, который посылает биты, начиная с наименее значимого (бит 0) и заканчивая самым старшим (бит 7), то есть в обратном порядке. В «зеркальном» регистре все биты отражены относительно центра. Например, 10111011001 есть отражение значения 10011011101.
Вместо того чтобы менять
местами биты перед их обработкой, можно
зеркально отразить все значения и
действия, участвующие в прямом алгоритме.
Рис. 12.7. Схема «Зеркального» табличного алгоритма
Для зеркального алгоритма вычисления CRC32 процесс вычисления такой же, за исключением порядка – сдвиги и заполнение регистра осуществляются вправо.
Этот вариант работы алгоритма вычисления
CRC32 удобен тем, что не нужно знать длину
собственно исходной последовательности
(без значения CRC). Достаточно просто
обработать весь входной поток, не
различая в строке завершающую ее
подстроку с CRC. Далее необходимо сравнить
содержимое регистра ЕАХ с 6b202ca2h. Если
эти значения равны, значит, исходная
последовательность нарушена не была.
Для получения собственно строки
достаточно отбросить последние 4 байта
сообщения, полученного приемником.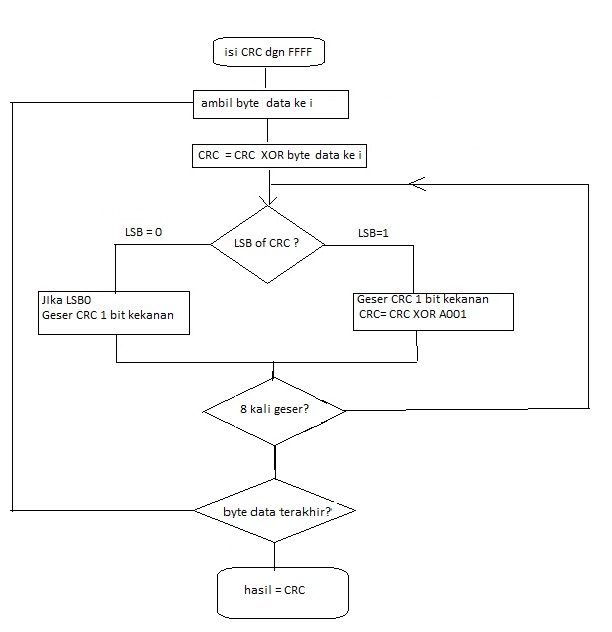
CRC16 (ModBus) — алгоритм вычисления
Я использую ModBus RTU и пытаюсь выяснить, как вычислить CRC16. Мне не нужен пример кода. Мне просто интересен механизм. Я узнал, что базовая CRC представляет собой полиномиальное деление слова данных, которое дополняется нулями в зависимости от длины полинома. Следующий тестовый пример должен проверить правильность моего основного понимания:
- слово данных: 0100 1011 Полином
- : 1001 (x 3 +1)
- дополнено 3 битами из-за наибольшего показателя степени x 3
- расчет: 0100 1011 000 / 1001 -> остаток: 011
Расчет.
01001011000
1001
0000011000
1001
01010
1001
0011
Edit1: до сих пор проверено Марком Адлером в предыдущих комментариях/ответах.
В поисках ответа Я видел много разных подходов с реверсированием, зависимостью от прямого или прямого порядка байтов и т.д., которые изменяют результат от заданного 011 .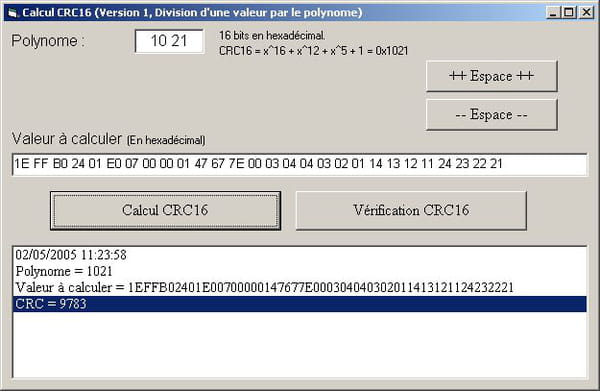
Modbus RTU CRC16
Конечно, мне хотелось бы понять, как работают различные версии CRC, но мой основной интерес состоит в том, чтобы просто понять, какой механизм здесь применяется. Насколько я знаю:
- x 16 +x 15 +x 2 +1 это многочлен: 0x18005 или 0b11000000000000101
- начальное значение 0xFFFF
- пример сообщения в шестнадцатеричном формате: 01 10 C0 03 00 01
- CRC16 вышеуказанного сообщения в шестнадцатеричном виде: C9CD
Я рассчитал это вручную, как в примере выше, но я бы не хотел записывать это в двоичном формате в этом вопросе. Я предполагаю, что мое преобразование в двоичный файл правильно. Чего я не знаю, так это того, как включить начальное значение — используется ли оно для заполнения им слова данных вместо нулей? Или мне нужно изменить ответ? Что-то другое?
1-я попытка: Дополнение нулями на 16 бит. Вычисленный остаток в двоичном формате будет
1111 1111 1001 1011, что соответствуетFF9Bв шестнадцатеричном формате и неверно для CrC16/Modbus, но правильно для CRC16/байпаса2-я попытка: заполнение 16 бит единицами из-за начального значения.
Вычисленный остаток в двоичном формате будет 0000 0000 0110 0100, что равно0064в шестнадцатеричном формате и неверно.
Вычисленный остаток в двоичном формате будет Было бы здорово, если бы кто-нибудь объяснил или прояснил мои предположения. Честно говоря, я потратил много часов на поиск ответа, но каждое объяснение основано на примерах кода на C/C++ или других языках, которые я не понимаю. Заранее спасибо.
EDIT1: Согласно этому сайту, «1-я попытка» указывает на другой метод CRC16 с тем же полиномом, но с другим начальным значением (0x0000), что говорит мне о том, что расчет должен быть правильным. Как включить начальное значение?
EDIT2: Марк Адлерс Ответ делает свое дело. Однако теперь, когда я могу вычислить CRC16/Modbus, осталось прояснить некоторые вопросы. Не нужно, но ценится.
A) Порядок вычисления будет следующим: … ?
- 1-е применение RefIn для полного ввода (включая дополненные биты)
- 2-й
xorInitValue с (в CRC16) для первых 16 бит - 3-е применение RefOut для полного вывода/оставшейся части (остаток максимум 16 бит в CRC16)
B) Ссылаясь на RefIn и RefOut: Всегда ли он отражает 8 бит для ввода и все биты для вывода, несмотря на то, что я использую CRC8, CRC16 или CRC32?
C) Что означают 3-й (check) и 8-й (XorOut) столбцы на веб-сайте, о котором я говорю? Последнее кажется довольно простым, я предполагаю, что оно применяется путем вычисления значения xor после RefOut, как и InitValue?
Выяснить, какой алгоритм CRC16 использовался
спросил
Изменено 4 года, 4 месяца назад
Просмотрено 2к раз
У меня есть протокол последовательной связи, и у меня возникли проблемы с определением используемого алгоритма контрольной суммы.
я пробовал несколько CRC16 алгоритмы и ни один из них не работает.
сообщения выглядят так (в шестнадцатеричном формате):
55 13 04 03 09 f1 01 00 00 06 50 08 00 02 00 00 00 cc 1a 55 13 04 03 09 f1 01 00 00 06 50 00 00 02 00 00 00 94 3b 55 13 04 03 09 f1 02 00 00 06 50 08 00 02 00 00 00 7f e4 55 13 04 03 09 f1 02 00 00 06 50 00 00 02 00 00 00 27 c5 55 13 04 03 09 f1 03 00 00 06 50 08 00 02 00 00 00 ее b1 55 13 04 03 09 f1 03 00 00 06 50 00 00 02 00 00 00 b6 90
Я знаю, что начальный байт равен 0x55 и 2-й байт это длина сообщения
При необходимости могу предоставить больше данных. Будем признательны за любую помощь или подсказку 😉
С уважением, Амир
1
этот калькулятор CRC поможет вам.
1
Зависит от того, по каким байтам рассчитывается CRC.
Вы можете использовать RevEng, чтобы попытаться извлечь параметры CRC из примеров.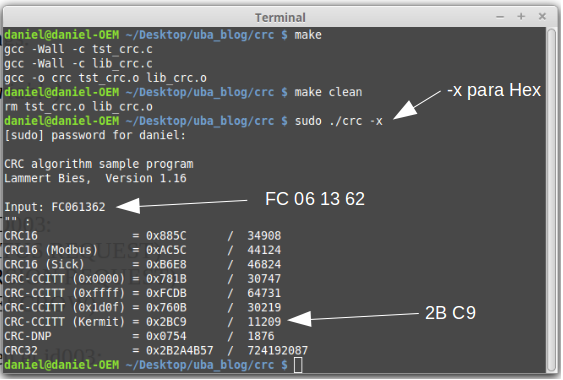
Из ваших примеров видно, что это 16-битная CRC с полиномом 0x1021 , и что CRC отражается (многочлен инвертируется при подаче на вход, а регистр CRC сдвигается вправо, а не влево). Однако начальное значение и конечное исключающее ИЛИ зависят от того, над какими байтами вычисляется CRC. Чтобы действительно разобраться с ними, вам также понадобятся примеры сообщений разной длины.
В каталоге 16-битных CRC RevEng есть несколько стандартных CRC, которые могут быть:
width=16 poly=0x1021 init=0xffff refin=true refout=true xorout=0x0000 check=0x6f91 имя="CRC-16/MCRF4XX" width=16 poly=0x1021 init=0xb2aa refin=true refout=true xorout=0x0000 check=0x63d0 name="CRC-16/RIELLO" width=16 poly=0x1021 init=0x89ec refin=true refout=true xorout=0x0000 check=0x26b1 name="CRC-16/TMS37157" width=16 poly=0x1021 init=0xc6c6 refin=true refout=true xorout=0x0000 check=0xbf05 name="CRC-A" width=16 poly=0x1021 init=0x0000 refin=true refout=true xorout=0x0000 check=0x2189 name="KERMIT" width=16 poly=0x1021 init=0xffff refin=true refout=true xorout=0xffff check=0x906e имя="Х-25"
Я не получаю ни одного из них, предполагая, что все это сообщение, и если я отбрасываю первые один или два байта.+for+CRC.jpg)