Что такое восьмеричная система: Восьмеричная система счисления | это… Что такое Восьмеричная система счисления?

Восьмеричная система — счисление — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Восьмеричная система счисления применяется для записи программы вычислений на ЭВМ благодаря простоте перевода чисел из восьмеричной в двоичную систему и обратно.  [1]

Восьмеричная система счисления играет в ЭВМ вспомогательную роль и используется для компактной записи двоичных кодов чисел и машинных команд ЭВМ, в различных периферийных устройствах и устройствах подготовки данных. Разбиение двоичного числа на триады осуществляется влево и вправо от запятой, отделяющей целую часть числа от дробной. Если крайние триады получаются неполными, то они дополняются нулями.  [2]

Восьмеричная система счисления способствует компактности записи двоичного числа во внешней форме. Двоичный код, подлежащий переводу в восьмеричный, разбивают по триадам, начиная с младших разрядов, и каждой триаде ставят в соответствие разряд восьмеричного числа.  [3]

Восьмеричная система счисления удобна тем, что от нее легко можно перейти к двоичной системе счисления. После того как данные записаны в восьмеричной системе, их в процессе ввода в машину чисто механическим путем переводят в двоичную систему счисления.  [4]

Восьмеричная система счисления является наиболее распространенной для кодирования команд машины.  [5]

Восьмеричная система счисления применяется программистами для записи вручную программы, а именно для кодирования команд и адресов. Для этой цели восьмеричная система удобна в том отношении, что она более экономична ( требует меньшего числа разрядов, чем двоичная) и в то же время перевод из восьмеричной системы в двоичную очень прост. Одному разряду восьмеричной системы соответствуют три разряда двоичной системы. Поэтому каждый разряд восьмеричной системы переводится в двоичную систему в отдельности.  [6]

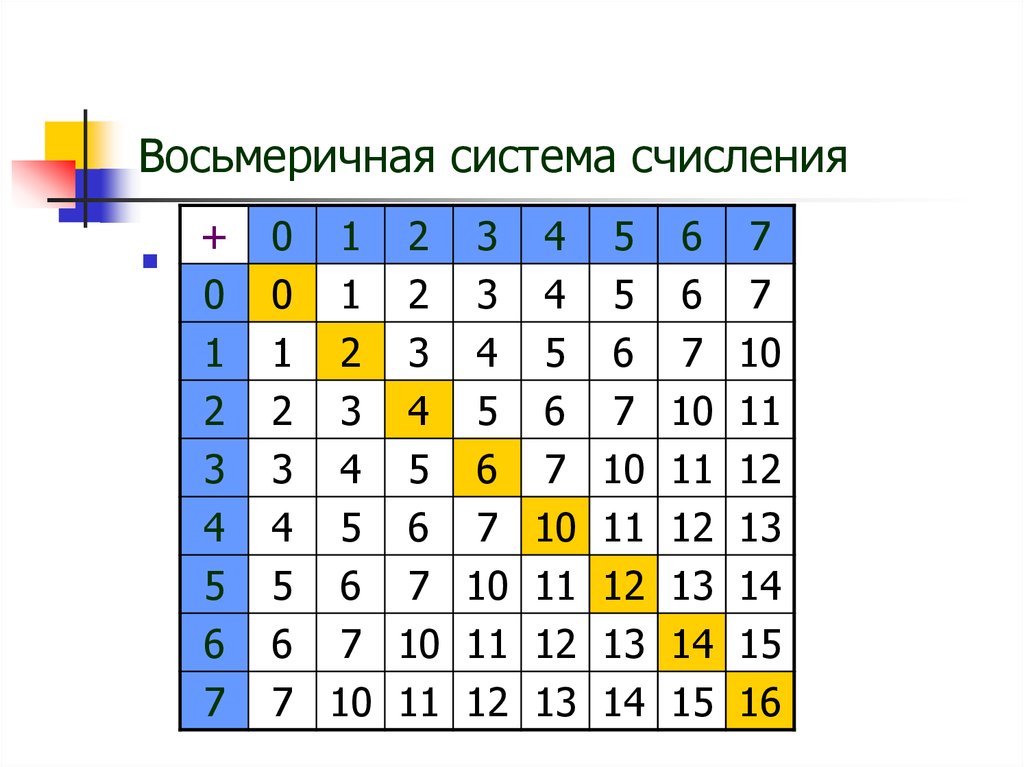
Восьмеричная система счисления

, так же как и шестнадцатеричная, вследствие простоты перевода в двоичную систему широко применяется для представления команд в программе при подготовке задач.  [7]

Восьмеричная система счисления имеет основанием число восемь.  [8]

Восьмеричная система счисления удобна при выполнении вручную перевода чисел из десятичной системы счисления в двоичную. При этом перевод выполняется в следующем порядке: десятичное число — восьмеричное число — двоичное число.  [9]

Восьмеричная система счисления является наиболее распространенной для кодирования команд машины.  [10]

Восьмеричная система счисления используется для кодирования операций, нумерации ячеек оперативной и внешней памяти.  [11]

Восьмеричная система счисления применяется в ЭВМ в основном для составления программ, так как позволяет производить более короткую и удобную запись двоичных чисел.  [12]

Восьмеричную систему счисления используют при подготовке задачи к решению ( программировании), для записи на бланках порядковых номеров команд, кодов операций и адресов в командах. Данная система удобна тем, что в ней запись числа короче в три раза, чем в двоичной системе счисления. Перевод из восьмеричной системы счисления в двоичную и обратно несложен, поскольку он может выполняться при помощи простых электронных и электромеханических схем.  [13]

Однако восьмеричная система счисления ( так же как двоичная) не используется ни в экономике, ни в технике, и поэтому исходные данные в этой системе не задаются. Тем не менее преимущества восьмеричной системы используются при работе ЭВМ для задания машине программы обработки данных и ряда констант. Команды, образующие программу, кодируются в восьмеричной системе.  [14]

Основание восьмеричной системы счисления записывается как 10 ( восемь), оно больше единицы в восемь раз.  [15]

Страницы:      1    2    3    4

Перевод из восьмеричной в двоичную систему счисления, калькулятор

Осуществить перевод числа из восьмеричной системы счисления в двоичную можно тремя способами.

Способ 1:

Перевести сначала в десятичную систему счисления, затем из нее в конечную.

Способ 2:

1. Высший разряд восьмеричного числа делим на 2, записываем остаток и делим снова до тех пор, пока в результате не будет нуля. Каждый раз записываем остаток.
2. Записываем полученные остатки в обратном порядке, получая двоичное число.
3. Если полученное двоичное число имеет менее трех разрядов (то есть на если предыдущем шаге получили менее трех остатков), то дополняем нулями слева до трех разрядов.
4. Повторяем предыдущие шаги для каждого следующего разряда восьмеричного числа, таким образом получаем несколько групп по 3 разряда двоичного числа.
5. Записываем все вместе по порядку, отбрасываем нули слева при их наличии, получаем искомую двоичную запись числа.

Возьмем число 256₈.

1. Делим высший разряд на 2, получаем остатки:

   2 / 2 = 1, остаток 0

   1 / 2 = 0, остаток 1

2. Записываем остатки в обратном порядке: 10
3. Дополняем до трех разрядом нулями слева: 010
4. Повторяем для каждого следующего разряда:

   5 / 2 = 2, остаток 1

   2 / 2 = 1, остаток 0

   1 / 2 = 0, остаток 1

   Получаем 101

   6 / 2 = 3, остаток 0

   3 / 2 = 1, остаток 1

   1 / 2 = 0, остаток 1

   Получаем 110

5. Записываем все вместе (010)(101)(110). Отбрасываем слева ноль, получаем двоичное число 10101110₂

Способ 3:

Используем таблицу триад:

Цифра	0	1	2	3	4	5	6	7
Триада	000	001	010	011	100	101	110	111

Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.

351₈ = (011) (101) (001) = 011101001₂ = 11101001₂

Смотрите также

• Перевод из двоичной в десятичную
• Перевод из двоичной в восьмеричную
• Перевод из двоичной в шестнадцатеричную
• Перевод из десятичной в двоичную
• Перевод из десятичной в восьмеричную
• Перевод из десятичной в шестнадцатеричную
• Перевод из восьмеричной в десятичную
• Перевод из шестнадцатеричной в двоичную
• Перевод из шестнадцатеричной в десятичную

восьмеричных? Что за гекс? | ПЛКдев

«Не беспокойтесь о своих проблемах с математикой, уверяю вас, что мои проблемы намного больше.

» — Альберт Эйнштейн

У вас трещит голова, наверное, уже все готово сказать вам, что двоичные числа читать нелегко. В качестве компромисса между людьми и компьютерами используются восьмеричная (с основанием 8) и шестнадцатеричная (с основанием 16) системы.

Восьмеричный

Хотя восьмеричный не так распространен, как его двоюродный брат шестнадцатеричный, он все еще используется в различных ПЛК, поэтому важно понять концепцию. Например, при программировании ПЛК AutomationDirect адреса памяти являются восьмеричными. Восьмеричное число, как восемь ног осьминога, означает восемь, и поэтому существует восемь чисел, которые можно использовать от нуля до семи. Веса столбцов: 1, 8, 64, 512 и т. д. Веса получаются путем возведения базового числа в степень столбца: 8 ⁰ = 1, 8 ¹ = 8, 8 ² = 64, 8 ³ = 512 и т. д. Теперь мы можем выполнить то же упражнение, что и в предыдущей главе, чтобы преобразовать восьмеричное число в десятичное.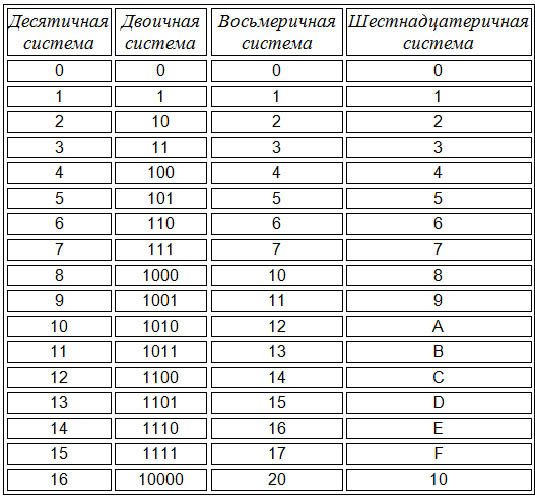

 

 

Я знаю, что пока это бесполезно. Где это действительно удобно, так это в переходе от двоичного к восьмеричному, потому что все, что вам нужно сделать, это разбить двоичное число на части по три. Это потому, что 8 равно 2 ³ .

 

 

Большинство программируемых контроллеров имеют платы ввода и вывода, сгруппированные по 8 или 16 (при высокой плотности 32 и 64). Причина этого в том, что компьютеры любят иметь числа в степени 2, 4, 8, 16 и так далее. Поэтому, если он не в восьмеричном формате, он обычно в шестнадцатеричном формате.

Шестнадцатеричный

Шестнадцатеричный немного сложнее, потому что это основание 16, и поэтому нам нужно что-то большее от 0 до 9 для символов, и это делается с помощью букв от «A» до «F». Шестнадцатеричный используется по тем же причинам, что и восьмеричный, чтобы мы могли представить двоичный код в сжатой форме и упростить преобразование. Там, где в восьмеричной системе используются 3 бита, в шестнадцатеричной системе используются 4 бита для представления одного числа.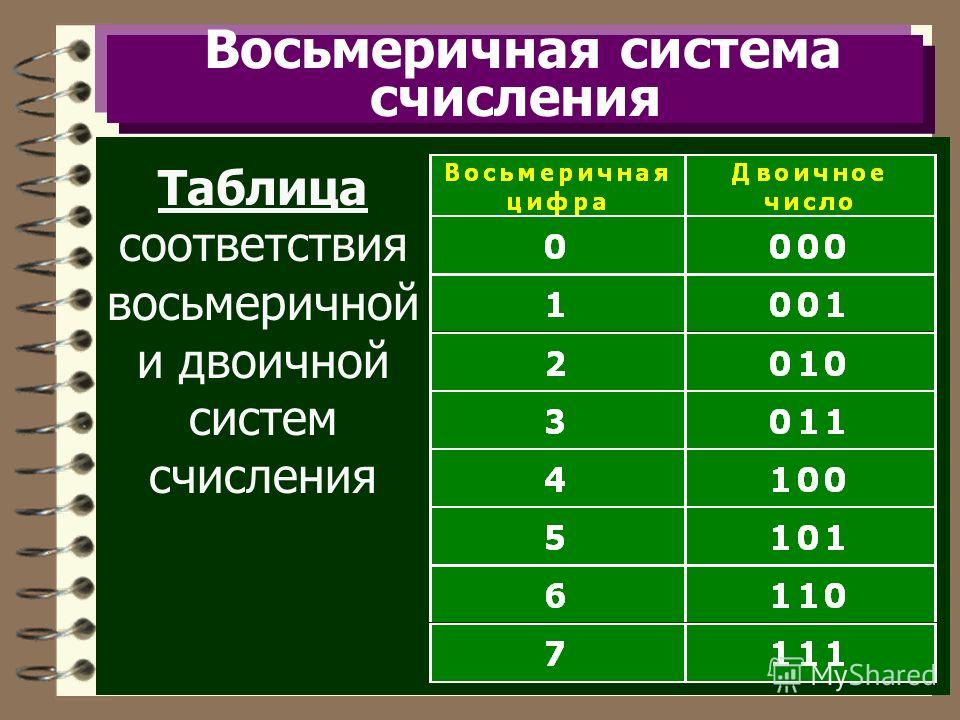

 

 

Если вы собираетесь программировать что-то вроде ПЛК Mitsubishi, вам лучше привыкнуть к шестнадцатеричной системе счисления.

Заключение 

В заключение приведем таблицу ниже, в которой показаны эквиваленты для каждой системы нумерации.
 

Десятичный	Бинарные люди: изучение единиц и нулей.»>Двоичные	Восьмеричный	Шестигранник
0	00000	0	0
1	00001	1	1
2	00010	2	2
3	00011	3	3
4	00100	4	4
5	00101	5	5
6	00110	6	6
7	00111	7	7
8	01000	10	8
9	01001	11	9
10	01010	12	А
11	01011	13	В
12	01100	14	С
13	01101	15	Д
14	01110	16	Е
15	01111	17	Ф
16	10000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	13

 

и так далее и тому подобное. . .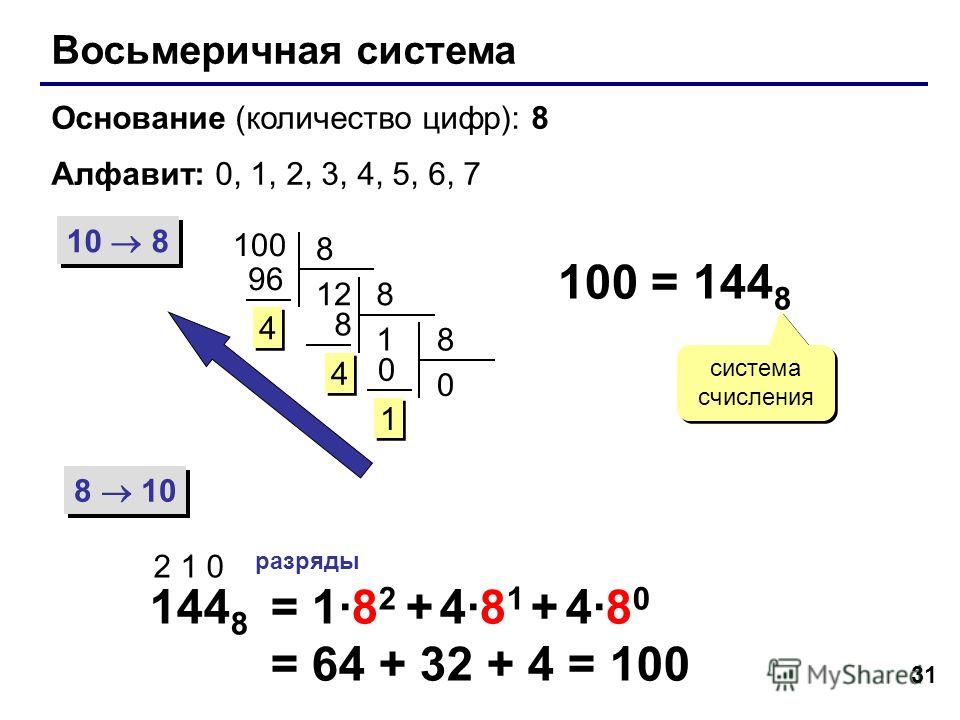

‹ Бинарные люди: изучение единиц и нулей. Когда отрицательное отношение является дополнением ›

Краткая информация о восьмеричной и шестнадцатеричной системах счисления

Компьютеры созданы человеком, но они работают на языке чисел. Когда мы набираем на компьютере букву, цифру или специальный символ, операционная система преобразует ввод в числа. Это связано с тем, что компьютер может понимать только позиционную систему счисления, в которой есть некоторые символы, называемые цифрами. Символы, используемые в системе счисления, отображают различные значения.

Величина каждой цифры в числе определяется с помощью цифры, места цифры в числе и основания системы счисления. Существует несколько типов систем счисления, таких как десятичная система счисления, двоичная система счисления и т. д.

В этой статье мы обсудим восьмеричную и шестнадцатеричную системы счисления. Сначала мы поговорим о том, что такое восьмеричная система счисления и ее представление. Затем мы перейдем к обсуждению шестнадцатеричной системы счисления и ее представления.

Восьмеричная система счисления

Восьмеричная система счисления, также известная как октальная, представляет собой систему счисления с основанием 8. В системе используются цифры от 0 до 7. Поэтому, если мы пишем восьмеричное число 10, оно изображает 8, а если мы записываем восьмеричное число 100, оно представляет 64. Когда мы изучаем десятичную систему счисления, каждый разряд представляется в степени 10. Но когда мы реализуем восьмеричную систему счисления, каждый разряд равен степени 8.

Преобразование восьмеричных чисел довольно просто. Для преобразования восьмеричного числа все, что нам нужно сделать, это сгруппировать двоичные цифры в группу из трех. Примером восьмеричной системы счисления является представление десятичного числа 74. Десятичное представление числа 74 – 1001010. В этой системе перед двоичной цифрой 1 можно поставить два нуля, и теперь мы преобразуем 74 в восьмеричное. Восьмеричное число 112.

Основная характеристика восьмеричной системы счисления состоит в том, что она имеет 8 различных счетных цифр от 0 до 7. На заре вычислительной техники восьмеричные числа и восьмеричная система счисления считали входы и выходы. Восьмеричное число было введено для удобного преобразования больших двоичных чисел. Однако восьмеричная система счисления постепенно вымирает из-за более популярной шестнадцатеричной системы счисления.

Представление восьмеричного числа

Система не использует числа или алфавиты выше 8. Кроме того, преобразование восьмеричных чисел в двоичные числа аналогично шестнадцатеричным числам. Восьмеричные числа представляются следующим образом.

Decimal number	3-bit binary number	Octal number
0	000	0
1	001	1
2	4010	2	44444010	. 0057	2
3	011	3
4	100	4
5	101	5
6	110	6
7	111	7
8	001 000	10 (1+0)
9	001 001	11 (1+1 )

Когда пишете 10 или 20, не путайтесь, потому что числа 10 и числа 20 представляются с использованием (1+0) и (2+0) в восьмеричной системе счисления. Восьмеричное число равно 8octal. Восьмеричное значение варьируется от 0 до 7.

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления — это система счисления, в которой базовое значение равно 16. Это означает, что в шестнадцатеричной системе используется 16 символов. Шестнадцатеричные символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Алфавиты, используемые в шестнадцатеричной системе, представляют собой однобитовое представление десятичные числа 10, 11, 12, 13, 14 и 15. Шестнадцатеричная система требует 4 бита для изображения любой цифры. Поскольку существует так много систем счисления, шестнадцатеричная система счисления обычно обозначается буквой h.

В шестнадцатеричной системе счисления каждая цифра имеет вес, эквивалентный степени 16. Таким образом, в шестнадцатеричной системе счисления каждая цифра в 16 раз ценнее предыдущей. Числовое значение каждой цифры в шестнадцатеричной последовательности получается путем умножения числа в степени 16, которая зависит от положения числа, и последующего прибавления числа к сумме.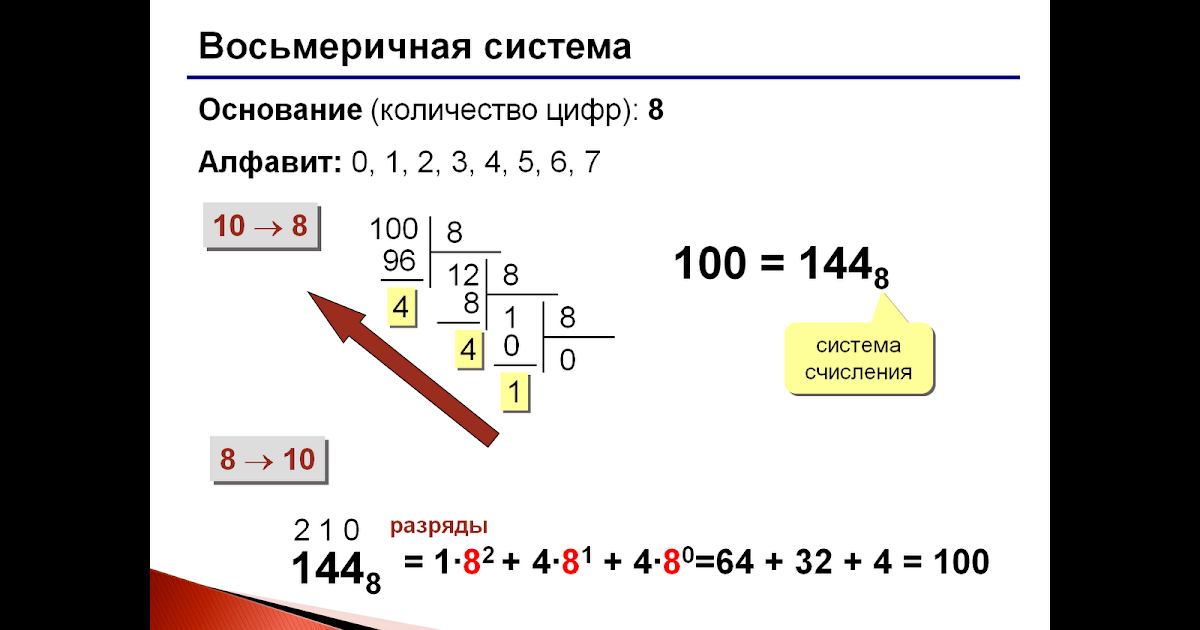

Разработчики программного обеспечения широко используют шестнадцатеричную систему счисления, потому что она удобно представляет значения в двоичном коде.

Представление шестнадцатеричных чисел

Из приведенного выше определения ясно, что шестнадцатеричная система счисления представляет собой набор из 4 битов. Каждый набор битов в шестнадцатеричных числах равен 0 и 15. Шестнадцатеричные числа широко используются в современных компьютерах и цифровых системах, поскольку их удобно интерпретировать.

Представление шестнадцатеричных чисел следующее:

Hex	0	1	2	3	4	5	6	7	8
Binary	0000	0001	0010	0011	0100	0101	0110	0111	1000

0284 14 = E

Hex	9	10 = A	11 = B	12 = C	13 = D		15 = F
Binary	1001	1010	1011	1100	1101	1110	1111

Основной причиной изобретения шестнадцатеричной системы счисления было решение проблемы преобразования больших двоичных чисел.