эпохальное доказательство из сферы компьютерной науки, которое вызвало эффект домино в физике и математике / Хабр
Учёные-информатики вышли на новые рубежи в деле проверки решений задач вычислительными методами. При этом они нашли ответы на важнейшие открытые вопросы квантовой механики и чистой математики.
В 1935 году Альберт Эйнштейн, работая с Борисом Подольским и Натаном Розеном, исследовал возможность, открытую новыми законами квантовой физики: две частицы могут находиться в запутанном состоянии, когда их взаимосвязь не нарушают даже огромные расстояния.
В следующем году Алан Тьюринг сформулировал первую общую теорию вычислений, и доказал, что существуют задачи, которые никогда не смогут быть решены компьютерами.
Эти две идеи произвели революцию в тех областях наук, к которым они относятся. Кроме того, казалось, что они не имеют никакого отношения друг к другу. Но теперь доказательство MIP* = RE их скомбинировало, что привело к решению множества задач в сфере информатики, физики и математики.
Квантовые компьютеры производят вычисления, оперируя запутанными квантовыми битами (кубитами), а не классическими нулями и единицами. Новое доказательство указывает на то, что такие компьютеры, теоретически, могут быть использованы для проверки решений огромного количества задач. Связь между квантовой запутанностью и традиционными вычислениями стала для многих исследователей большой неожиданностью.
Мигель Наваскес (Miguel Navascués) занимается квантовой физикой в Институте квантовой оптики и квантовой информации в Вене. «Это было полным сюрпризом», — сказал он, комментируя доказательство.
Соавторы доказательства поставили перед собой цель определить границы подхода по проверке решений вычислительных задач. Этот подход включает в себя квантовую запутанность. Обнаружив эти границы, исследователи пришли к решению двух других задач, что явилось едва ли не побочным результатом их работы. Речь идёт о гипотезе Цирельсона в физике, касающейся математического моделирования квантовой запутанности, и связанной задачи в чистой математике — проблемы Конна в теории алгебр фон Неймана (проблемы вложения Конна).
В итоге же результаты применения доказательства вызвали в математике и физике нечто вроде эффекта домино.
«Все идеи относятся к одному и тому же периоду. Приятно видеть то, что они снова сошлись столь эффектным образом», — говорит Генри Юэнь (Henry Yuen) из Университета Торонто – один из соавторов доказательства. Помимо него в этой работе участвовали Чжэнфэн Джи (Zhengfeng Ji) из Технологического университета Сиднея, Джон Райт (John Wright) из Техасского университета в Остине, Ананд Натараджан (Anand Natarajan) и Томас Видик (Thomas Vidick) из Калифорнийского технологического института. Все пять учёных работают в сфере компьютерных наук.
Неразрешимые задачи
Тьюринг, ещё до появления компьютеров, заложил фундамент, на котором строятся размышления о вычислениях. И он, в то же время, показал, что существует определённая задача, которую, что доказуемо, компьютеры решить не могут. Это — так называемая проблема останова.
Обычно компьютерные программы получают что-то на вход и генерируют выходные данные.
Но иногда они застревают в бесконечных циклах, а значит — никогда не останавливаются. Когда такое происходит, есть лишь один выход из сложившейся ситуации. По словам Генри Юэня, нужно вручную остановить программу. Нужно просто поставить точку в её работе.
Тьюринг доказал, что не существует универсального алгоритма, способного выяснить, будет ли программа когда-нибудь остановлена. Для того чтобы это узнать, надо запустить программу.
Генри Юэнь, Томас Видик, Чжэнфэн Джи, Ананд Натараджан, Джон Райт
«Вы прождали миллион лет, а программа не остановилась. Может, нужно просто подождать 2 миллиона лет? Нет способа сказать это заранее», — говорит Уильям Слофстра (William Slofstra), математик из Университета Уотерлу.
Тьюринг, с технической точки зрения, доказал, что задача останова неразрешима. Даже самый мощный компьютер, который можно себе представить, не способен с ней справиться.
После Тьюринга учёные-информатики начали классифицировать другие задачи по их сложности.
Для решения более сложных задач требуется больше вычислительной мощности — больше процессорного времени и памяти. Это — исследование вычислительной сложности алгоритмов.
В итоге любая задача ставит перед исследователями два больших вопроса: «Насколько тяжело её решить? Какова сложность проверки того, что полученное решение является правильным?».
Проверка решения с помощью допроса
Если задачи сравнительно просты — их решения можно проверять самостоятельно. Но когда задачи становятся сложнее, даже проверка результатов их решения может оказаться невероятно сложным делом. Несмотря на это, в 1985 году учёные-компьютерщики решили, что можно сформировать уверенность в правильности ответа даже в том случае, если невозможно самостоятельно это подтвердить.
Метод проверки следует логике полицейского допроса.
Если подозреваемый рассказывает тщательно продуманную историю, то следователь, вероятно, не сможет просто взять и найти подтверждение каждой её детали.
Но, задавая правильные вопросы, можно либо подловить подозреваемого на лжи, либо подтвердить правдивость его рассказа.
С точки зрения информатики, две стороны допроса представлены двумя компьютерами. Первый — это мощная вычислительная система, которая предлагает решение задачи. Его называют доказывателем. Второй — это уже не такое мощное устройство, которое задаёт доказывателю вопросы для определения того, правильным ли является предложенный им ответ. Этот компьютер называют верификатором.
Рассмотрим простой пример. Предположим, некто (верификатор) страдает цветовой слепотой. Кто-то другой (доказыватель) утверждает, что два шарика окрашены в разные цвета и ничем больше друг от друга не отличаются. Верификатор не может сам проверить это утверждение. Но, умно построив допрос, он, всё же, может узнать, так ли это на самом деле.
Для этого можно спрятать шарики за спиной и перемешать их. А потом — спросить доказывателя о том, в какой руке находится какой шарик. Если они и правда разные — доказыватель должен всегда отвечать на подобный вопрос правильно.
А если же они имеют один и тот же цвет, то есть — выглядят совершенно одинаково, половина ответов доказывателя окажется неправильной.
Томас Видик говорит, что если гораздо больше половины ответов доказывателя оказываются правильным, то можно быть весьма сильно уверенным в том, что шарики имеют разные цвета.
Задавая доказывателю вопросы, можно проверить решения более широкого класса задач, чем можно проверить самостоятельно.
В 1988 году учёные-информатики рассмотрели ситуацию, в которой имеются два доказывателя, предлагающих решения для одной и той же задачи. В конце концов, если есть два подозреваемых, которых можно допросить, это упростит раскрытие преступления, или — проверку решения, так как их можно заставить играть друг против друга.
По словам Томаса Видика, это даёт верификатору больше влияния. Он проводит допрос, задаёт связанные вопросы, выполняет перекрёстную проверку ответов. Если подозреваемые говорят правду — их ответы должны соответствовать друг другу большую часть времени.
Аналогично, исследователи показали, что допрашивая два доказывателя раздельно, задавая им вопросы о найденных ими решениях, можно быстро верифицировать решения даже более обширного класса задач, чем в том случае, когда работают с одним доказывателем.
Исследования вычислительной сложности алгоритмов могут показаться чисто теоретическими, но они очень тесно связаны с реальным миром. Ресурсы, которые нужны компьютерам для решения задач и проверки решения — время и память — это физические ресурсы. По этой причине новые открытия в физике могут изменить подход к исследованиям вычислительной сложности.
Ананд Натараджан говорит, что если отойти от классической физической базы вычислений и выбрать что-то совсем другое, вроде квантовых механизмов, то в результате мы получим и новую теорию вычислительной сложности.
Новое доказательство — это конечный результат столкновения учёных-компьютерщиков 21 века с одной из самых странных идей физики прошлого века — с идеей квантовой запутанности.
Проблема Конна
Когда две частицы запутаны, они, на самом деле, не влияют друг на друга. Между их действиями нет причинно-следственной связи. Эйнштейн и его соавторы проработали эту идею в статье 1935 года. Впоследствии физики и математики попытались прийти к математическому способу описания того, что, на самом деле, означает квантовая запутанность.
Однако эти усилия привели к неоднозначным результатам. Учёные пришли к двум разным математическим моделям запутанности. При этом не было ясно то, являются ли эти модели эквивалентными друг другу.
Наличие такого вот потенциального диссонанса, кружным путём, привело к появлению важной проблемы в сфере чистой математики. Это — проблема Конна в теории алгебр фон Неймана. В конце концов, это сыграло роль некоей «зацепки», которой пять учёных-компьютерщиков воспользовались при выводе своего доказательства.
Первый способ моделирования квантовой запутанности заключался в восприятии частиц как объектов, пространственно изолированных друг от друга.
Предположим, одна из таких частиц находится на Земле, а другая — на Марсе. Расстояние между ними — это то, что исключает причинную связь между ними (они каузально разделены). Это — то, что называется моделью тензорного произведения.
Но в некоторых ситуациях каузальное разделение сущностей не вполне очевидно. В результате математики пришли ко второму, более общему способу описания каузальной независимости.
Когда порядок, в котором выполняют две операции, не влияет на результат, операцию называют коммутативной: 3×2 — это то же самое, что 2×3. В этой второй модели частицы запутаны в том случае, когда их свойства коррелируют, но порядок, в котором производят измерения, значения не имеет. Можно произвести измерения над частицей A для того, чтобы спрогнозировать импульс частицы B, и наоборот. В любом случае результат будет одним и тем же. Это называют моделью запутанности коммутирующего оператора.
В обоих описаниях запутанности используются массивы чисел, называемые матрицами.
Матрицы состоят из строк и столбцов. Модель тензорного произведения использует матрицы с конечным числом строк и столбцов. Модель коммутирующего оператора использует более общие объекты, которые функционируют как матрицы с бесконечным количеством строк и столбцов.
Со временем математики начали исследовать эти матрицы как объекты, представляющие самостоятельный интерес, никак не связанные с физическим миром. В русле этой работы математик Ален Конн (Alain Connes) высказал в 1976 году предположение, в соответствии с которым должна существовать возможность аппроксимировать множество матриц бесконечной размерности с помощью матриц конечной размерности. Это — одно из следствий проблемы Конна в теории алгебр фон Неймана.
В следующем десятилетии физик Борис Цирельсон сформулировал новую версию этой проблемы, которая вновь вернула её в область физики. Цирельсон предположил, что модели тензорного произведения и коммутирующего оператора примерно эквивалентны друг другу. Это утверждение имеет смысл, так как обе эти модели, теоретически, представляют собой два разных способа описания одного и того же физического явления.
Последующая работа показала, что из-за связи между матрицами и физическими моделями, использующими их, задачи Конна и Цирельсона косвенно связаны: если решить одну, то будет решена и другая.
Но решение обеих этих задач пришло из совершенно неожиданного места.
Физика игр
В 1960-е годы физик Джон Белл придумал тест для определения того, является ли квантовая запутанность реальным физическим явлением, а не теоретическим понятием. В тесте использовалось нечто вроде игры, результаты которой позволяли узнать о том, действуют ли в ходе игры некие механизмы, не относящиеся к обычной физике.
Позже специалисты по информатике поняли, что этот тест, касающийся квантовой запутанности, может быть использован и как инструмент для верификации решений очень сложных задач.
Но, прежде чем двигаться дальше, давайте поговорим об игре. Представим, что есть два игрока: Алиса и Боб, а также — игровое поле размером 3×3. Ведущий назначает Алисе строку и предлагает ей ввести в каждую ячейку 0 или 1, причём так, чтобы их сумма дала бы нечётное число.
Боб получает столбец, который надо заполнить нулями и единицами так, чтобы их сумма дала бы чётное число. Они выиграют в том случае, если поместят одно и то же число в то место, где строка и столбец пересекаются. Общаться им при этом нельзя.
В обычных обстоятельствах лучшее, на что они будут способны — это выигрывать в 89% случаев. Но если учесть фактор квантовой запутанности, то их шансы улучшаются.
Представим, что у Алисы и Боба имеются запутанные квантовые частицы. Они выполняют измерения своих частиц и используют результаты измерений для указания на то, что писать в каждой из ячеек — 0 или 1. Из-за того, что частицы запутаны, результаты измерений будут коррелировать друг с другом. А это означает и то, что и действия игроков будут взаимосвязаны. В результате окажется, что они смогут побеждать в игре всегда.
Если в той ячейке, где строка и столбец пересекаются, будут разные цифры — игра проиграна. Если одинаковые — выиграна
Итак, если оказывается, что два игрока удивительно удачно играют в эту игру, то можно сделать вывод о том, что они используют нечто, отличающееся от того, что способна дать классическая физика.
Подобные «Белловские» эксперименты в наши дни называют «нелокальными» играми, имея в виду разделение игроков. Физики, на самом деле, проводят подобные игры в лабораториях.
Генри Юэнь говорит, что за прошедшие годы учёные провели эксперименты, доказавшие реальность этих пугающих явлений.
Как и при анализе любой игры, тут может понадобиться узнать о том, как часто игроки могут выиграть в нелокальной игре, учитывая то, что они играют так хорошо, как только могут. Например, в случае с пасьянсом, можно вычислить частоту возможных выигрышей того, кто играет идеально.
Но в 2016 году Уильям Слофстра доказал, что не существует общего алгоритма для вычисления точной максимальной вероятности выигрыша для всех нелокальных игр. В результате исследователи задались вопросом: можно ли хотя бы приблизительно подсчитать максимальный процент выигрышей?
Учёные-компьютерщики пришли к ответу, используя две вышеописанные модели квантовой запутанности. Алгоритм, который использует модель тензорного произведения, задаёт минимальное значение при приближённом вычислении максимальной вероятности выигрыша для всех нелокальных игр.
Другой алгоритм, в котором используется модель коммутирующего оператора, задаёт максимальное значение.
Ответ, выдаваемый реализациями этих алгоритмов, тем точнее, чем дольше выполняется программа. Если гипотеза Цирельсона верна, и эти две модели эквивалентны, тогда нижняя и верхняя оценки должны приближаться к друг другу, превращаясь в единственное значение, представляющее приблизительную максимальную вероятность выигрыша.
Но если гипотеза Цирельсона не верна, и две модели не эквивалентны, то, по словам Генри Юэня, верхняя и нижняя оценка всегда будут разделены. И не будет способа рассчитать даже приблизительный процент выигрышей для нелокальных игр.
Пять исследователей в своей новой работе воспользовались рассуждениями о том, сходятся ли верхняя и нижняя оценки, и о том, истинна или ложна гипотеза Цирельсона. Сделали они это ради поиска ответа на вопрос о том, в каких ситуациях можно верифицировать решения вычислительных задач.
Запутанная помощь
В начале двухтысячных учёные-информатики начали задаваться вопросом о том, как изменится диапазон задач, решения которых можно верифицировать, если «допрашивать» два доказывателя, которые обладают запутанными частицами.
Большинство учёных полагало, что запутанность вредит верификации. В конце концов, двум «подозреваемым» будет легче согласовать ложные показания в том случае, если у них будет какой-то способ координировать ответы.
Но в течение следующих нескольких лет стало понятно, что истинным является противоположное утверждение: «допрашивая» доказыватели, у которых имеются запутанные частицы, можно верифицировать гораздо более обширный класс задач, чем при работе с доказывателями, у которых таких частиц нет.
Томас Видик говорит, что запутанность — это способ создания корреляций, которые, как кажется, могут помочь доказывателям лгать. Но, на самом деле, это явление можно использовать в своих интересах.
Для того чтобы понять то, как этим пользоваться, сначала нужно разобраться с почти сверхъестественным масштабом задач, решения которых можно верифицировать благодаря этой интерактивной процедуре.
Представьте себе граф — набор точек (вершин), соединённых линиями (гранями).
Нужно узнать о том, удастся ли, используя три цвета, закрасить вершины так, чтобы в графе не было бы двух вершин, соединённых гранью и при этом окрашенных в один цвет. Если это возможно, то такой граф является «трёхцветным».
Если дать паре доказывателей очень большой граф, и они сообщат, что он является «трёхцветным», то можно задаться вопросом о том, есть ли способ верифицировать их ответ.
В случае с очень большими графами было бы невозможно проверить ответ напрямую. Вместо этого можно спросить у каждого из доказывателей о том, какой цвет имеет одна из двух соединённых вершин. Если каждый из них сообщит о разных цветах, и они будут давать подобные ответы каждый раз, когда их об этом спрашивают, у нас сформируется уверенность в том, что граф, и правда, является «трёхцветным».
Но даже эта стратегия допроса не сработает на огромных графах, в которых больше граней и вершин, чем атомов во вселенной. Даже постановка конкретного вопроса («Сообщи мне цвет вершины XYZ») становится неподъёмной проблемой для того, кто пытается проверить решение задачи.
Объём данных, необходимый для того, чтобы просто задать имя конкретной вершины, больше, чем верификатор может хранить в доступной ему памяти.
Но квантовая запутанность делает возможной схему работы, при применении которой доказыватели сами формулируют вопросы.
«Верификатору не нужно ставить вопросы. Верификатор заставляет доказыватели самостоятельно формулировать эти вопросы и отвечать на них», — говорит Джон Райт.
Верификатору нужно, чтобы доказыватели сообщали бы о цветах соединённых вершин. Если вершины не соединены, тогда ответы на вопросы ничего не сообщат о том, является ли граф «трёхцветным» или нет. Другими словами, верификатору нужно, чтобы доказыватели задавали бы связанные вопросы. Один из доказывателей задаёт вопрос о вершине ABC, а второй — о вершине XYZ. Предполагается, что две вершины соединены, несмотря на то, что ни один из доказывателей не знает о том, о какой именно вершине «думает» другой. (Это похоже на то, как Алиса и Боб надеются записать одно и то же число в одну и ту же ячейку, несмотря на то, что ни один из них не знает о том, с какой строкой или с каким столбцом таблицы работает другой.
)
Если два доказывателя полностью самостоятельно формулировали бы подобные вопросы, тогда не было бы механизма, позволяющего заставить их выбирать соединённые (коррелирующие) вершины, делая это так, чтобы позволить верификатору проверять их ответы. Но подобная корреляция — это именно то, чего позволяет достичь квантовая запутанность.
Томас Видик говорит, что они собираются использовать запутанность для передачи практически всех дел доказывателям. Учёные заставляют доказыватели самостоятельно выбирать вопросы.
В конце выполнения этой процедуры каждый из доказывателей сообщает цвет вершины. Верификатор проверяет — разные это цвета или нет. Если граф действительно является «трёхцветным» — доказыватели никогда не должны сообщать об одном и том же цвете.
По словам Генри Юэня, если граф является «трёхцветным», то доказыватели смогут убедить исследователя в том, что это действительно так.
Как оказалась, эта процедура верификации представляет собой ещё один пример нелокальной игры.
Доказыватели «выигрывают» в том случае, если убеждают исследователя в том, что их решение является верным.
В 2012 году Томас Видик и Цуёси Ито (Tsuyoshi Ito) доказали, что можно играть во множество разнообразных нелокальных игр с использованием запутанных доказывателей для проверки решений. Это относится, как минимум, к тому же числу задач, которые можно проверить, опрашивая два классических компьютера. Таким образом, использование запутанных доказывателей не вредит верификации. В прошлом году Ананд Натараджан и Джон Райт доказали, что взаимодействие с запутанными доказывателями, на самом деле, расширяет класс задач, решения которых могут быть верифицированы.
Но учёные-компьютерщики не знали о полном спектре задач, решения которых могут быть проверены с использованием этого подхода. Сейчас же они об этом знают.
Эффект домино
В своей новой работе пять учёных доказали, что «допрос» запутанных доказывателей делает возможной верификацию решений нерешаемых задач, включая решение задачи останова.
Генри Юэнь говорит, что модели такого типа имеют невообразимые верифицирующие возможности.
Но задача останова нерешаема. И этот факт стал той движущей силой, которая привела к получению итогового доказательства.
Представьте, что вы передали программу паре запутанных доказывателей. Вы задали им вопрос о том, остановится ли когда-нибудь эта программа. Вы готовы верифицировать их ответы посредством некоей нелокальной игры. Доказыватели генерируют вопросы и «выигрывают» на основании скоординированности их ответов.
Если программа на самом деле остановится, то у доказывателей должна быть возможность выиграть в игре в 100% случаев. Это похоже на пример с графом — если он и правда «трёхцветный», то запутанные доказыватели никогда не должны сообщать об одном и том же цвете для связанных вершин. Если программа никогда не остановится, доказыватели должны выигрывать лишь по случайности — в 50% случаев.
Это значит, что если некто попросит вас определить приблизительную максимальную вероятность выигрыша для конкретной нелокальной игры, то вам сначала придётся решить задачу останова.
Но решить эту задачу невозможно. Это означает, что нахождение приблизительного максимального уровня вероятности выигрыша для нелокальных игр так же, как и для задачи останова, невозможно.
А это, в свою очередь, значит, что гипотеза Цирельсона ложна: две модели квантовой запутанности не эквивалентны. Если бы они были эквивалентны, то можно было бы свести нижнюю и верхнюю оценку к одному и тому же значению и вычислить приблизительную максимальную вероятность выигрыша.
Давид Перес-Гарсиа (David Pérez-García) из Мадридского университета Комплутенсе говорит, что не может существовать такого алгоритма, в результате две [модели] должны быть разными.
Новая работа доказывает то, что класс задач, решения которых можно верифицировать с помощью запутанных квантовых доказывателей, класс, называемый MIP*, в точности равен классу задач, которые не сложнее задачи останова — классу RE. В заголовке работы имеется сжатое указание на это: «MIP* = RE».
В ходе вывода доказательства того, что два класса сложности равны, учёные доказали ложность гипотезы Цирельсона, что, благодаря ранее проведённой работе, означает то, что гипотеза Конна также ложна.
Исследователи, работающие в соответствующих областях, были ошеломлены тем, что решения столь масштабных задач были получены благодаря доказательству из сферы компьютерной науки, которое, как кажется, не связано с математикой и с физикой.
Мигель Наваскес говорит, что если бы увидел статью с заголовком MIP* = RE, то не подумал бы о том, что у неё есть что-то общее с его работой. Он был соавтором более ранней работы, связывающей гипотезы Цирельсона и Конна. Для него это стало полным сюрпризом.
Квантовые физики и математики только начинают осваивать новое доказательство. До этого математиков интересовал вопрос о том, могут ли они аппроксимировать матрицы бесконечной размерности, используя вместо них большие матрицы конечной размерности. Теперь, благодаря тому, что доказана ложность гипотезы Конна, они знают о том, что сделать этого нельзя.
«Их результаты указывают на то, что это невозможно», — сказал Уильям Слофстра.
Учёные из сферы компьютерной науки не стремились к анализу гипотезы Конна.
И они, в результате, находятся не в самом лучшем положении для объяснения возможных последствий решения этой задачи.
«Лично я — не математик. Я не очень хорошо понимают исходную формулировку гипотезы Конна», — говорит Ананд Натараджан.
Он с соавторами ожидает, что математики переведут новые результаты на свой язык. В публикации, где сообщается о доказательстве, Томас Видик пишет: «Я не сомневаюсь в том, что в итоге теория сложности вычислений не понадобится для получения чисто математических результатов».
Тем не менее, когда другие исследователи знакомятся с доказательством, путь исследования, благодаря которому удалось на него выйти, подходит к концу. Более трёх десятилетий учёные-компьютерщики просто пытались узнать, как далеко их может завести интерактивная верификация решений задач. Теперь перед ними лежит ответ, в форме длинной статьи с простым заголовком и с отголосками идей Тьюринга.
«Есть множество работ, авторы которых лишь задаются вопросом о том, каковы возможности процедуры верификации, использующей два запутанных квантовых доказывателя.
Теперь мы знаем о том, какой мощью обладает эта процедура. Эта история подошла к концу», — говорит Ананд Натараджан.
Уважаемые читатели! Что значит доказательство MIP* = RE для той сферы, в которой работаете вы?
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
| Справочник по математике | Алгебра | Комплексные числа |
| Алгебраическая форма записи комплексных чисел |
| Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
| Комплексно сопряженные числа |
| Модуль комплексного числа |
| Деление комплексных чисел, записанных в алгебраической форме |
| Изображение комплексных чисел радиус-векторами на координатной плоскости |
| Аргумент комплексного числа |
| Тригонометрическая форма записи комплексного числа |
Формула Эйлера. Экспоненциальная форма записи комплексного числа |
| Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
| Извлечение корня натуральной степени из комплексного числа |
Алгебраическая форма записи комплексных чисел
Пусть x и y — произвольные вещественные числа.
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0).
Комплексные числа, заданные парами (0, y), называют чисто мнимыми числами.
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи.
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y), записывается в виде
| z = x + i y . | (1) |
где использован символ i , называемый мнимой единицей.
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z.
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z.
Комплексные числа, у которых Im z = 0 , являются вещественными числами.
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами.
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Сложение и вычитание комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 осуществляется по правилам сложения и вычитания двучленов (многочленов) x1 + i y1 и x2 + i y2 , т.е. в соответствии с формулами
z1 + z2 =
= x1 + i y1 + x2 + i y2 =
= x1 + x2 + i (y1 + y2) ,
z1 – z2 =
= x1 + i y1– (x2 + i y2) =
= x1– x2 + i (y1– y2) .
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
| i 2 = – 1 . | (2) |
По этой причине
z1z2 = (x1 + i y1) (x2 + i y2) =
= x1x2 + i x1 y2 +
+ i y1x2 + i 2y1 y2 =
= x1x2 + i x1y2 +
+ i y1x2 – y1 y2 =
= x1x2 – y1 y2 +
+ i (x1 y2 + i x2 y1) .
Комплексно сопряженные числа
Два комплексных числа z = x + iy и у которых вещественные части одинаковые, а мнимые части отличаются знаком, называются комплексно сопряжёнными числами.
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения, обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
Замечание.
Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy – мнимой осью.
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z.
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z.
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента, обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ, то мы можем найти вещественную и мнимую части по формулам
| (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.
е. нам известны числа x и y, то модуль этого числа, конечно же, определяется по формуле
| (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось | x > 0 , y = 0 | 0 | φ = 2kπ | |
| Первый квадрант | x > 0 , y > 0 | |||
| Положительная мнимая полуось | x = 0 , y > 0 | |||
| Второй квадрант | x < 0 , y > 0 | |||
| Отрицательная вещественная полуось | x < 0 , y = 0 | π | φ = π + 2kπ | |
| Третий квадрант | x < 0 , y < 0 | |||
| Отрицательная мнимая полуось | x = 0 , y < 0 | |||
| Четвёртый квадрант | x > 0 , y < 0 |
| Расположение числа z | Положительная вещественная полуось |
| Знаки x и y | x > 0 , y = 0 |
| Главное значение аргумента | 0 |
| Аргумент | φ = 2kπ |
| Примеры |
| Расположение числа z | Первый квадрант |
| Знаки x и y | x > 0 , y > 0 |
| Главное значение аргумента | |
| Аргумент | |
| Примеры |
| Расположение числа z | Положительная мнимая полуось |
| Знаки x и y | x = 0 , y > 0 |
| Главное значение аргумента | |
| Аргумент | |
| Примеры |
| Расположение числа z | Второй квадрант |
| Знаки x и y | x < 0 , y > 0 |
| Главное значение аргумента | |
| Аргумент | |
| Примеры |
| Расположение числа z | Отрицательная вещественная полуось |
| Знаки x и y | x < 0 , y = 0 |
| Главное значение аргумента | π |
| Аргумент | φ = π + 2kπ |
| Примеры |
| Расположение числа z | Третий квадрант |
| Знаки x и y | x < 0 , y < 0 |
| Главное значение аргумента | |
| Аргумент | |
| Примеры |
| Расположение числа z | Отрицательная мнимая полуось |
| Знаки x и y | x = 0 , y < 0 |
| Главное значение аргумента | |
| Аргумент | |
| Примеры |
| Расположение числа z | Четвёртый квадрант |
| Знаки x и y | x < 0 , y < 0 |
| Главное значение аргумента | |
| Аргумент | |
| Примеры |
Расположение числа z : Положительная вещественная полуось Знаки x и y : x > 0 , y = 0 Главное значение аргумента: 0 Аргумент: φ = 2kπ Примеры: |
Расположение числа z : Первый квадрант Знаки x и y : x > 0 , y > 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Положительная мнимая полуось Знаки x и y : x = 0 , y > 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Второй квадрант Знаки x и y : x < 0 , y > 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Отрицательная вещественная полуось Знаки x и y : x < 0 , y = 0 Главное значение аргумента: π Аргумент: φ = π + 2kπ Примеры: |
Расположение числа z : Третий квадрант Знаки x и y : x < 0 , y < 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Отрицательная мнимая полуось Знаки x и y : x = 0 , y < 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Четвёртый квадрант Знаки x и y : x < 0 , y < 0 Главное значение аргумента: Аргумент: Примеры: |
Тригонометрическая форма записи комплексного числа
Из формулы (3) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа.
Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера:
| cos φ + i sin φ = e iφ . | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r e iφ , | (7) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа.
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
cos φ + i sin φ,
или, что то же самое, числа e iφ, при любом значении φ равен 1.
Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел и записанных в экспоненциальной форме, осуществляется по формулам
Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Извлечение корня натуральной степени из комплексного числа
Пусть — произвольное комплексное число, отличное от нуля.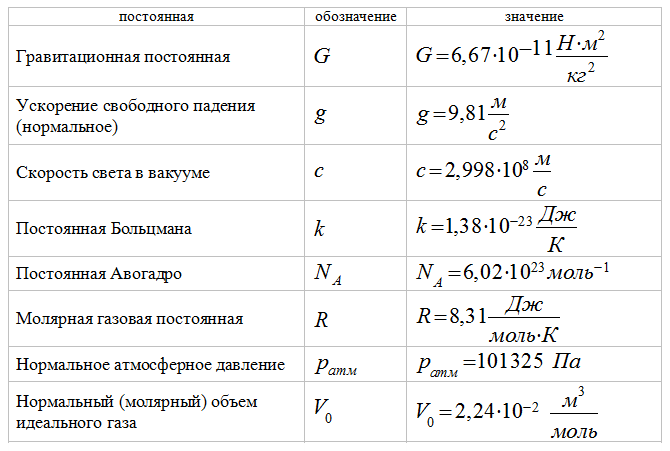
Корнем n — ой степени из числа z0 , где называют такое комплексное число z = r e iφ , которое является решением уравнения
| z n = z0 . | (8) |
Для того, чтобы решить уравнение (8), перепишем его в виде
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна 2kπ , где k — произвольное целое число. По этой причине справедливы равенства
следствием которых являются равенства
| (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
| (10) |
где
причем на комплексной плоскости концы радиус-векторов zk при k = 0 , .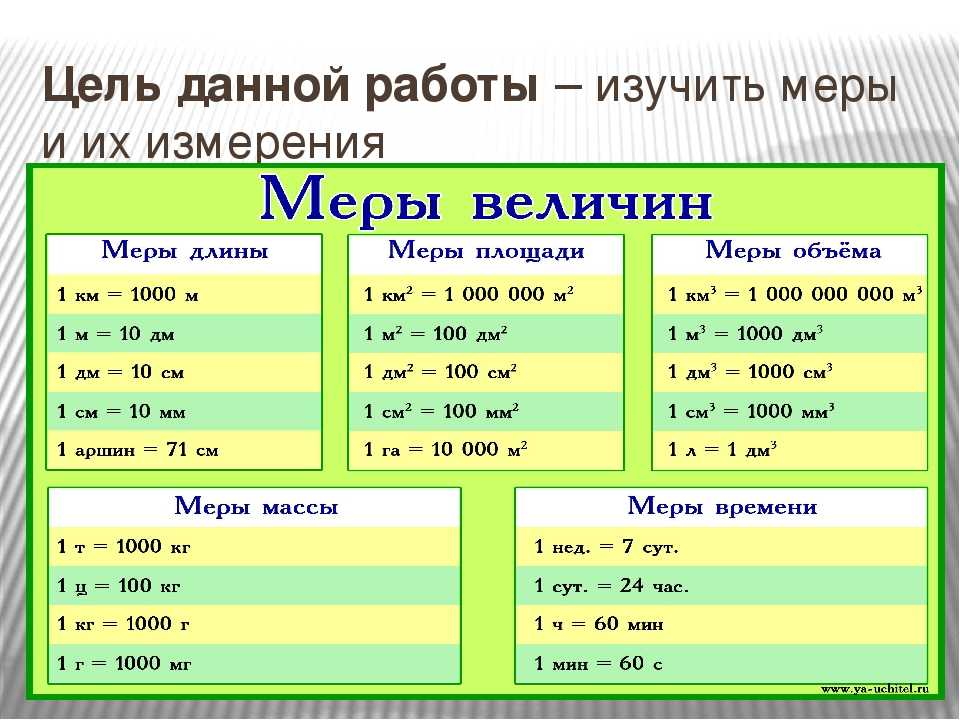
.. , n – 1 располагаются в вершинах правильного n — угольника, вписанного в окружность радиуса с центром в начале координат.
Замечание. В случае n = 2 уравнение (8) имеет два различных корня z1 и z2 , отличающихся знаком:
z2 = – z1 .
Пример 1. Найти все корни уравнения
z3 = – 8i .
Решение. Поскольку
то по формуле (10) получаем:
Следовательно,
Пример 2. Решить уравнение
z2 + 2z + 2 = 0 .
Решение. Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:
Так как
то решения уравнения имеют вид
z1 = – 1 + i , z2 = – 1 – i .
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Обозначение. Что означает :=?
спросил
Изменено 2 года, 4 месяца назад
Просмотрено 141 тысяч раз
$\begingroup$
Что означает := ?
- обозначение
$\endgroup$ 92(\theta)$».
По сути, некоторые люди думают, что должна быть разница в обозначениях между высказыванием «Я определяю бла равным бла » и утверждением « бла равно бла » Таким образом, они используют := для первого и = для второго.
Обычно из контекста ясно, какое из двух применений знака равенства имеет в виду (часто из-за сигнальных слов, таких как «Пусть», «Мы определить» и т.д.)
$\endgroup$
21
$\begingroup$
Я думаю, Бурбаки использовали его первым.. не уверен.. Я знаю, что физики используют $\equiv$
$\endgroup$
11
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
9n$ и $x \in \mathbb R$.