ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ — это… Что такое ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ?
- ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ
способ приближенного вычисления значения функции f(x), основанный на замене функции f(х).линейной функцией
параметры аи b к-рой выбираются таким образом, чтобы значения L(х).совпадали со значениями f(x).в заданных точках х 1 и х 2:
Этим условиям удовлетворяет единственная функция
приближающая заданную функцию f(х)на отрезке [x1 , x2]с погрешностью
Вычисления, необходимые для Л. и., легко реализуются при ручном счете, благодаря чему этот способ широко используется при интерполировании табличных данных.
Лит.:[1] Б а х в а л о в Н. С., Численные методы, 2 изд., М., 1975; [2] Б е р е з и н И. С., Жидков Н. П., Методы вычислений, 3 изд.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
- ЛИНЕЙНАЯ ЗАВИСИМОСТЬ
- ЛИНЕЙНАЯ КЛАССИЧЕСКАЯ ГРУППА
Смотреть что такое «ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ» в других словарях:
линейная интерполяция — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN linear interpolation … Справочник технического переводчика
Линейная интерполяция — Линейная интерполяция интерполяция алгебраическим двучленом P1(x) = ax + b функции f, заданной в двух точках x0 и x1 отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно линейной функцией.… … Википедия
линейная интерполяция — tiesinė interpoliacija statusas T sritis fizika atitikmenys: angl.
 linear interpolation vok. lineare Interpolation, f rus. линейная интерполяция, f pranc. interpolation linéaire, f … Fizikos terminų žodynas
linear interpolation vok. lineare Interpolation, f rus. линейная интерполяция, f pranc. interpolation linéaire, f … Fizikos terminų žodynasинтерполяция — Вычисление промежуточных значений между двумя известными точками. Например: linear линейная интерполяция exponential экспоненциальная интерполяция Процесс вывода цветного изображения, когда пикселы, относящиеся к области между двумя цветными… … Справочник технического переводчика
интерполяция — и, ж. interpolation f. < лат. interpolatio изменение; переделка, искажение. 1. Вставка позднейшего происхождения в каком л. тексте, не принадлежащая оригиналу. БАС 1. В древних рукописях много интерполяций, внесенных переписчиками. Уш. 1934. 2 … Исторический словарь галлицизмов русского языка
Интерполяция — О функции, см.: Интерполянт. Интерполяция, интерполирование в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
 Многим из тех, кто сталкивается с научными и… … Википедия
Многим из тех, кто сталкивается с научными и… … ВикипедияИнтерполяция (матем.) — О функции, см.: Интерполянт. Интерполяция в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто … Википедия
Билинейная интерполяция — Билинейная интерполяция в вычислительной математике расширение линейной интерполяции для функций двух переменных. Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в другом … Википедия
Интерполирование — О функции, см.: Интерполянт. Интерполяция в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто … Википедия
Таблица поиска — (англ.
 lookup table) это структура данных, обычно массив или ассоциативный массив, используемая с целью заменить вычисления на операцию простого поиска. Увеличение скорости может быть значительным, так как получить данные из памяти… … Википедия
lookup table) это структура данных, обычно массив или ассоциативный массив, используемая с целью заменить вычисления на операцию простого поиска. Увеличение скорости может быть значительным, так как получить данные из памяти… … Википедия
Линейная интерполяция онлайн с решением и графиком
- Подробности
-
Калькулятор линейной интерполяции позволяет вычислить значение линейной функции промежуточной переменной, зная значения функции переменных меньше и больше искомого.
Если абсцисса (Х) искомой точки лежит за пределами отрезка интерполяции [X1, X2], то необходимо использовать калькулятор линейной экстраполяции.
Дано:
округление до 12345знаков после запятой
Решение:
Формула линейной интерполяции
расчет линейной интерполяции по двум точкам
Помощь на развитие проекта premierdevelopment. ru
ru
Спасибо, что не прошели мимо!
I. Порядок действий при расчете линейной интерполяции онлайн калькулятором:
- Для проведения интерполяции требуется ввести значения координат 2 точек ([X1, Y1]; [X2, Y2]) и абсциссу (Х) той точки, значение которой необходимо вычислить.
- Точка X1 должна лежать левее точки X2 (X1 < X2), а точка X должна лежать между точками X1 и X2 (X1 < X < X2).
- В случае невыполнения одного из условий пункта 2, будет показано соответствующее предупреждение.
- График справа позволяет визуализировать полученный линейной интерполяцией результат.
II. Для справки:
- интерполяция
- — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

- линейная интерполяция
- — нахождение промежуточного значения функции по двум точкам (условно проведя прямую между ними).
- квадратичная интерполяция
- — нахождение промежуточного значения функции по трем точкам (интерполирующая функция многочлен второго порядка — парабола).
- экстраполяция
- — способ нахождения значений функции по уже известным нескольким ее значениям.
13.1.1. Линейная интерполяция MathCAD 12 руководство
Самый простой вид интерполяции — линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии. Интерполирующая функция А(х) состоит из отрезков прямых, соединяющих точки (рис. 13.2).
Рис. 13.2. Линейная интерполяция (продолжение листинга 13.1)
Для построения линейной интерполяции служит встроенная функция linterp (листинг 13.1):
- linterp(х,у,t) — функция, аппроксимирующая данные векторов х и у кусочно-линейной зависимостью:
- х — вектор действительных данных аргумента;
- у — вектор действительных данных значений того же размера;
- t — значение аргумента, при котором вычисляется интерполирующая функция.
ВНИМАНИЕ!
Элементы вектора х должны быть определены в порядке возрастания, т. е. Xl<X2<X3<. . .<XN.
Листинг 13.1. Линейная интерполяция
Как видно из листинга, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
1. Ввести векторы данных х и у (первые две строки листинга).
2. Определить функцию linterp (х, у, t).
3. Вычислить значения этой функции в требуемых точках, например, linterp(х,у,2.4)=3.52, или linterp(х,у,6)=5.9, или постройте ее График, как показано на рис. 13.2.
ПРИМЕЧАНИЕ
Обратите внимание, что функция A(t) на графике имеет аргумент t, а не х. Это означает, что функция
A(t) вычисляется не только при значениях аргумента (т. е. в семи точках), а при гораздо большем числе аргументов в интервале
(0,6), что автоматически обеспечивает Mathcad. Просто в данном случае эти различия незаметны, т. к. при обычном построении графика функции
А(х) от векторного аргумента х (рис. 13.3) Mathcad по умолчанию соединяет точки графика прямыми линиями (т. е. скрытым образом осуществляет их линейную интерполяцию).
к. при обычном построении графика функции
А(х) от векторного аргумента х (рис. 13.3) Mathcad по умолчанию соединяет точки графика прямыми линиями (т. е. скрытым образом осуществляет их линейную интерполяцию).
Рис. 13.3. Обычное построение графика функции от векторной переменной х (продолжение листинга 13.1)
Линейная интерполяция — онлайн калькулятор, формула
Скачать, сохранить результат
Выберите способ сохранения
Информация
Такие науки, как статистика и математика, используют в своей методологии инструмент «Интерполяция». Он используется инженерии и архитектурном проектировании.
Интерполяция применима в следующих случаях:
- Явление было изучено со всесторонне, а не одним путем определенного исчисления.
- Применение данного инструмента возможно только в случаях, когда допускается изменение погрешности, между проверенными точками, которое также подчиняется конкретному закону.

- Применение может быть оправдано не во всех случаях, так как при эмпирических функциях может возникнуть ряд других нюансов.
Так или иначе, применяя метод линейной интерполяции, допущение ошибок при расчетах недопустимо. Для того, чтобы обезопасить специалистов от возникновения ошибок по причине допущения просчета, мы разработали калькулятор линейной интерполяции онлайн. Благодаря этому инструменту теперь есть возможность избежать допущения каких-либо ошибок, поскольку калькулятор имеет предельную точность в расчетах.
Линейная интерполяция онлайн:
- Обезопасить себя от допущения ошибок, которые в случаях со строительством жилых зданий могут приводить к ужасным последствиям.
- Избавить себя от необходимости самостоятельного расчета формулы и просто ввести необходимые значения в соответствующие поля и получить готовый ответ.
- Метод линейной интерполяции покажется очень простым, благодаря интерфейсу нашего калькулятора.

Наш калькулятор, осуществляя расчет методом линейной интерполяции, использует следующую формулу:
Y = y1+(x-x1)/(x2-x1)*(y2-y1),
где y – показатель линейной интерполяции,
y1, y2, x, x1, x2 – известные значения, которые необходимо вставить в поля калькулятора.
Таким образом, используя наш онлайн калькулятор, Вы получите точный ответ, легко разберетесь в функционале калькулятора, благодаря простому интерфейсу, и никогда не допустите ошибки по причине человеческого фактора.
поделиться и оценить
Смотрите также:
Добавить комментарий
Н.В. Байдакова. Линейная интерполяция на тетраэдре …С. 80-84
Том 24, номер 4, 2018
УДК 517.51
MSC: 65D05
DOI: 10.21538/0134-4889-2018-24-4-80-84
Полный текст статьи (Full text)
Исследование выполнено за счёт гранта Российского научного фонда (проект № 14-11-00702).
Рассмотрен стандартный способ линейной интерполяции функции, имеющей непрерывные и ограниченные заданной константой частные производные второго порядка, на тетраэдре. Получены оценки аппроксимации производных первого порядка, более точные по сравнению с известными.
Ключевые слова: многомерная интерполяция, конечные элементы
СПИСОК ЛИТЕРАТУРЫ
1. Байдакова Н.В. Влияние гладкости на погрешность аппроксимации производных при локальной интерполяции на триангуляциях // Тр. Ин-та математики и механики УрО РАН. 2011. Т. 17, № 3. С. 83–97.
2. Байдакова Н.В. Об оценках П. Жамэ для конечных элементов с интерполяцией в равномерных узлах симплекса // Мат. тр. 2017. Т. 20, № 1. С. 43–74.
3. Клячин В.А. Модифицированное условие пустой сферы Делоне в задаче аппроксимации градиента // Изв. РАН. Сер. математическая. 2016. Т. 80, № 3. С. 95–102.
4. Субботин Ю.Н. Зависимость оценок многомерной кусочно полиномиальной аппроксимации от геометрических характеристик триангуляции // Тр. n$ with applications to finite element methods // Arch. Rational Mech. Anal. 1972. Vol. 46, no. 3. P. 177–199. doi: 10.1007/BF00252458 .
n$ with applications to finite element methods // Arch. Rational Mech. Anal. 1972. Vol. 46, no. 3. P. 177–199. doi: 10.1007/BF00252458 .
6. Hannukainen A., Korotov S., K$\check{\mathrm{r}}$$\acute{\mathrm{i}}$$\check{\mathrm{z}}$ek M. On Synge-type angle condition for d-simplices // Appl. Math. 2017. Vol. 62, no. 1. P. 1–13. doi: 10.21136/AM.2017.0132-16 .
7. Jamet P. Estimation d’erreur pour des $\acute{\mathrm{e}}$l$\acute{\mathrm{e}}$ments finis droits presque d$\acute{\mathrm{e}}$g$\acute{\mathrm{e}}$n$\acute{\mathrm{e}}$r$\acute{\mathrm{e}}$s // RAIRO Anal. Numer. 1976. Vol. 10, no. 1. P. 43–60.
Поступила 18.09.2018
После доработки 18.10.2018
Принята к публикации 22.10.2018
Байдакова Наталия Васильевна
канд. физ.-мат. наук, старший науч. сотрудник
Институт математики и механики им. Н.Н.Красовского УрО РАН,
г. Екатеринбург
e-mail: [email protected]
English
N.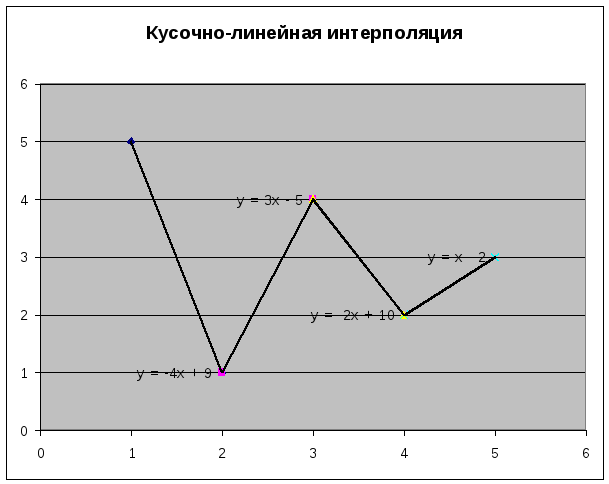 V. Baidakova. Linear interpolation on a tetrahedron
V. Baidakova. Linear interpolation on a tetrahedron
The standard method for the linear interpolation on a tetrahedron of a function with continuous second-order partial derivatives bounded by a given constant is considered. Estimates of the approximation of first-order derivatives that are more exact than the known estimates are derived.
Keywords: multidimensional interpolation, finite elements
Received September 18, 2018
Revised October 18, 2018
Accepted October 22, 2018
Funding Agency: This work was supported by the Russian Science Foundation (project no. 14-11-00702).
Nataliya Vasil’evna Baidakova, Cand. Sci. (Phis.-Math.), Krasovskii Institute of Mathematics and Mechanics, Ural Branch of the Russian Academy of Sciences, Yekaterinburg, 620990 Russia, e-mail: [email protected]
[References -> on the «English» button bottom right]
Линейная интерполяция и столкновение объектов
Явление , которое вы испытываете, называется туннелированием и является проблемой, присущей дискретным архитектурам обнаружения столкновений. Вы правы, полагая, что линейная интерполяция может иметь какое-то отношение к решению, поскольку она может позволить вам в пределах погрешности (обычно) предсказать путь объекта между кадрами, но это всего лишь одна часть гораздо большего решения. Терминология, которую я видел, связанная с этими типами решений, — «Continuous Collision Detection». Эта тема обширна и становится довольно сложной, и есть книги, которые обсуждают ее, такие как обнаружение столкновений в реальном времени и другие онлайн-ресурсы.
Вы правы, полагая, что линейная интерполяция может иметь какое-то отношение к решению, поскольку она может позволить вам в пределах погрешности (обычно) предсказать путь объекта между кадрами, но это всего лишь одна часть гораздо большего решения. Терминология, которую я видел, связанная с этими типами решений, — «Continuous Collision Detection». Эта тема обширна и становится довольно сложной, и есть книги, которые обсуждают ее, такие как обнаружение столкновений в реальном времени и другие онлайн-ресурсы.
Итак, чтобы ответить на ваш вопрос: нет, линейная интерполяция сама по себе не решит ваш problems*., если вы не имеете дело только с кругами или сферами.
О чем начать думать
То, как решения выглядят и ведут себя, зависит от ваших проектных решений и, как правило, является большим. Таким образом, чтобы просто указать направление решения, фундаментальная идея непрерывного обнаружения столкновений состоит в том, чтобы выяснить: Как далеко между ранним кадром и более поздним кадром происходит столкновение, и в каком положении и вращении находятся два объекта в этой точке. Затем вы должны рассчитать конфигурацию, в которой объекты будут находиться в более позднее время кадра в ответ на это. Все становится очень интересным, решая эти проблемы для чего-то другого, кроме кругов в двух измерениях.
Затем вы должны рассчитать конфигурацию, в которой объекты будут находиться в более позднее время кадра в ответ на это. Все становится очень интересным, решая эти проблемы для чего-то другого, кроме кругов в двух измерениях.
Я не реализовал это, но я видел описанное решение, в котором вы маршируете двух кандидатов вперед между кадрами, продвигая их положение с помощью линейной интерполяции и их ориентацию с помощью сферической линейной интерполяции и проверяя с помощью дискретных алгоритмов, пересекаются ли они (алгоритм Gilbert-Johnson-Keerthi). Отсюда вы продолжаете применять дискретные алгоритмы, чтобы получить наименьшую глубину проникновения (алгоритм расширяющегося многогранника) и передать это и оставшееся время между кадрами вместе с решателем, чтобы получить, как объекты выглядят в вашем более позднем времени кадра. Это не дает аналитического ответа, но у меня нет знаний об аналитическом ответе для обобщенных случаев 2 или 3D.
Если вы не хотите идти по этому пути, ваше лучшее оружие в борьбе со сложностью-это предположения: Если вы можете предположить, что ваши высокоскоростные объекты могут быть представлены в виде точки, все становится проще, если вы можете предположить, что ориентация объектов не имеет значения (круги, сферы), все становится проще, и это продолжается и продолжается. Эта тема чрезвычайно интересна, и я все еще нахожусь на пути ее изучения, но она обеспечила некоторые из самых приятных моментов в моем программном периоде. Я надеюсь, что эти идеи приведут вас и на этот путь.
Эта тема чрезвычайно интересна, и я все еще нахожусь на пути ее изучения, но она обеспечила некоторые из самых приятных моментов в моем программном периоде. Я надеюсь, что эти идеи приведут вас и на этот путь.
Правка: поскольку вы указали, что работаете над бильярдной игрой.
Сначала мы проверим, нужен ли дискретный или непрерывный
- Допустимо ли в этой игре какое-либо количество туннелирования? Не в бильярде нет.
- Какова скорость, с которой мы увидим туннелирование? Используя радиус 0.0285m для шара (стандартный американский) и шаг физики 0.01s, мы получаем 2.85m/s как минимальную скорость, с которой столкновения начинают давать плохую реакцию. Я не знаком со скоростью бильярдных шаров, но это число кажется мне слишком низким.
Поэтому просто проверять на каждом кадре, пересекаются ли два шара, недостаточно, но нам не нужно идти полностью непрерывно. Если мы используем интерполяцию для разделения каждого кадра, мы можем увеличить скорость, необходимую для создания неправильного поведения: с 2 подразделениями мы получаем 5. 7m/s, что все еще низко; 3 подразделения дают нам 8.55m/s, что кажется разумным; и 4 дает нам 11.4m/s, который чувствует себя выше, чем я представляю себе, что бильярдные шары движутся. Так как же нам этого добиться?
7m/s, что все еще низко; 3 подразделения дают нам 8.55m/s, что кажется разумным; и 4 дает нам 11.4m/s, который чувствует себя выше, чем я представляю себе, что бильярдные шары движутся. Так как же нам этого добиться?
Дискретные столкновения с подразделениями кадров с использованием линейной интерполяции
Использование подразделений стоит дорого, поэтому стоит потратить время на обнаружение кандидатов, чтобы использовать его только там, где это необходимо. Это еще одна проблема с кучей забавных решений, и, к сожалению, выходящая за рамки вопроса.
Таким образом, у вас есть два круга кандидатов, которые очень вероятно столкнутся между текущим кадром и следующим кадром. Таким образом, в псевдокоде алгоритм выглядит следующим образом:
dt = 0.01
subdivisions = 4
circle1.next_position = circle1.position + (circle1.velocity * dt)
circle2.next_position = circle2.position + (circle2.velocity * dt)
for i from 0 to subdivisions:
temp_c1.position = interpolate(circle1. position, circle1.next_position, (i + 1) / subdivisions)
temp_c2.position = interpolate(circle2.position, circle2.next_position, (i + 1) / subdivisions)
if intersecting(temp_c1, temp_c2):
intersection confirmed
no intersection
position, circle1.next_position, (i + 1) / subdivisions)
temp_c2.position = interpolate(circle2.position, circle2.next_position, (i + 1) / subdivisions)
if intersecting(temp_c1, temp_c2):
intersection confirmed
no intersection
Где интерполируемая сигнатура равна interpolate(start, end, alpha)
Таким образом, здесь у вас есть интерполяция, используемая для «move» кругов вдоль пути, который они будут проходить между текущим и следующим кадром. На подтвержденном пересечении вы можете получить глубину проникновения и передать Дельта-время (dt / подразделения), два круга, глубину проникновения и точки столкновения вместе с шагом разрешения, который определяет, как они должны реагировать на столкновение.
Линейная Интерполяция. Как реализовать этот алгоритм в C? (дана версия Python)
Интерполяция в смысле «signal sample rate increase»
… или я называю его «upsampling» (неправильный термин, вероятно. отказ от ответственности: я не читал Лайонса). Мне просто нужно было понять, что делает код, а затем переписать его для удобства чтения. Как данность у него есть пара проблем:
а) это неэффективно — два цикла-это нормально, но он делает умножение для каждого отдельного выходного элемента; также он использует промежуточные списки (hold ), генерирует результат с append (мелочь)
б) он неправильно интерполирует первый интервал; он генерирует поддельные данные перед первым элементом. Скажем, у нас есть множитель=5 и seq=[20,30] — он будет генерировать [0,4,8,12,16,20,22,24,28,30] вместо [20,22,24,26,28,30].
Итак, вот алгоритм в виде генератора:
def upsampler(seq, multiplier):
if seq:
step = 1.0 / multiplier
y0 = seq[0];
yield y0
for y in seq[1:]:
dY = (y-y0) * step
for i in range(multiplier-1):
y0 += dY;
yield y0
y0 = y;
yield y0
Хорошо а теперь перейдем к некоторым тестам:
>>> list(upsampler([], 3)) # this is just the same as [Y for Y in upsampler([], 3)]
[]
>>> list(upsampler([1], 3))
[1]
>>> list(upsampler([1,2], 3))
[1, 1.3333333333333333, 1.6666666666666665, 2]
>>> from math import sin, pi
>>> seq = [sin(2.0*pi * i/10) for i in range(20)]
>>> seq
[0.0, 0.58778525229247314, 0.95105651629515353, 0.95105651629515364, 0.58778525229247325, 1.2246063538223773e-016, -0.58778525229247303, -0.95105651629515353, -0.95105651629515364, -0.58778525229247336, -2.4492127076447545e-016, 0.58778525229247214, 0.95105651629515353, 0.95105651629515364, 0.58778525229247336, 3.6738190614671318e-016, -0.5877852522924728, -0.95105651629515342, -0.95105651629515375, -0.58778525229247347]
>>> list(upsampler(seq, 2))
[0.0, 0.29389262614623657, 0.58778525229247314, 0.76942088429381328, 0.95105651629515353, 0.95105651629515364, 0.95105651629515364, 0.7694208842938135, 0.58778525229247325, 0.29389262614623668, 1.2246063538223773e-016, -0.29389262614623646, -0.58778525229247303, -0.76942088429381328, -0.95105651629515353, -0.95105651629515364, -0.95105651629515364, -0.7694208842938135, -0.58778525229247336, -0.29389262614623679, -2.4492127076447545e-016, 0.29389262614623596, 0.58778525229247214, 0.76942088429381283, 0.95105651629515353, 0.95105651629515364, 0.95105651629515364, 0.7694208842938135, 0.58778525229247336, 0.29389262614623685, 3.6738190614671318e-016, -0.29389262614623618, -0.5877852522924728, -0.76942088429381306, -0.95105651629515342, -0.95105651629515364, -0.95105651629515375, -0.76942088429381361, -0.58778525229247347]
А вот мой перевод на C, вписывающийся в шаблон Fn Краца:
/**
*
* @param src caller supplied array with data
* @param src_len len of src
* @param steps to interpolate
* @param dst output param will be filled with (src_len - 1) * steps + 1 samples
*/
float* linearInterpolation(float* src, int src_len, int steps, float* dst)
{
float step, y0, dy;
float *src_end;
if (src_len > 0) {
step = 1.0 / steps;
for (src_end = src+src_len; *dst++ = y0 = *src++, src < src_end; ) {
dY = (*src - y0) * step;
for (int i=steps; i>0; i--) {
*dst++ = y0 += dY;
}
}
}
}
Обратите внимание, что фрагмент C «набран, но никогда не компилируется и не запускается», поэтому могут быть синтаксические ошибки, ошибки off-by-1 и т. д. Но в целом идея есть.
Формула линейной интерполяции — Образование
Формула интерполяции: Метод поиска новых значений для любой функции, использующей набор значений, осуществляется путем интерполяции. Неизвестное значение точки находится по этой формуле. Если речь идет о формуле линейной интерполяции, то ее следует использовать для нахождения нового значения из двух заданных точек. По сравнению с формулой интерполяции Лагранжа, должен быть доступен набор чисел «n», и для нахождения нового значения следует использовать метод Лагранжа.
Интерполяция — это процесс нахождения значения между двумя точками на линии или кривой. Чтобы помочь нам запомнить, что это означает, мы должны думать о первой части слова «интер» как о значении «ввод», которое напоминает нам о том, чтобы заглянуть «внутрь» данных, которые у нас были изначально. Этот инструмент, интерполяция, полезен не только в статистике, но также полезен в науке, бизнесе или в любое время, когда необходимо предсказать значения, которые попадают в две существующие точки данных.
Формула линейной интерполяцииФормула линейной интерполяции
Если две известные точки заданы координатами {\ displaystyle (x_ {0}, y_ {0})} и {\ displaystyle (x_ {1}, y_ {1})}, линейный интерполянт является прямая линия между этими точками.Для значения x в интервале {\ displaystyle (x_ {0}, x_ {1})} значение y вдоль прямой линии определяется из уравнения уклонов
.- {\ displaystyle {\ frac {y-y_ {0}} {x-x_ {0}}} = {\ frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}) }},}
который геометрически может быть получен из рисунка справа. Это частный случай полиномиальной интерполяции с n = 1.
Решение этого уравнения для y , которое является неизвестным значением при x , дает
- {\ displaystyle y = y_ {0} + (x-x_ {0}) {\ frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}} = {\ frac {y_ {0} (x_ {1} -x) + y_ {1} (x-x_ {0})} {x_ {1} -x_ {0}}},}
— формула линейной интерполяции в интервале {\ displaystyle (x_ {0}, x_ {1})}.За пределами этого интервала формула идентична линейной экстраполяции.
Эту формулу также можно понимать как средневзвешенное значение. Веса обратно пропорциональны расстоянию от конечных точек до неизвестной точки; более близкая точка имеет большее влияние, чем более удаленная. Таким образом, веса равны {\ textstyle {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}}} и {\ textstyle {\ frac {x_ {1} -x} {x_ { 1} -x_ {0}}}}, которые представляют собой нормализованные расстояния между неизвестной точкой и каждой из конечных точек. Потому что эти суммы равны 1
- {\ displaystyle y = y_ {0} \ left (1 — {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}} \ right) + y_ {1} \ left ( 1 — {\ frac {x_ {1} -x} {x_ {1} -x_ {0}}} \ right) = y_ {0} \ left (1 — {\ frac {x-x_ {0}} { x_ {1} -x_ {0}}} \ right) + y_ {1} \ left ({\ frac {x-x_ {0}} {x_ {1} -x_ {0}}} \ right),}
Калькулятор формул интерполяции
Решенные примеры
Вопрос 1: Используя формулу интерполяции, найти значение y при x = 8 для некоторого набора значений (2, 6), (5, 9)?Решение:
Известные значения: x0 = 8, x1 = 2, x2 = 5, y1 = 6, y2 = 9y = y1 + (x − x1) (x2 − x1) × (y2 − y1)
.у = 6 + ((8−2) (5−2) × (9−6)
у = 6 + 6
г = 12
Что такое метод линейной интерполяции?
Линейная интерполяция — это простейший метод получения значений в положениях между точками данных.Точки просто соединяются отрезками прямых линий.
Как найти интерполяцию между двумя числами?
Знать формулу для процесса линейной интерполяции . Формула : y = y1 + ((x — x1) / (x2 — x1)) * (y2 — y1), где x — известное значение, y — неизвестное значение, x1 и y1 — координаты, которые ниже известного значения x, а x2 и y2 — координаты выше значения x.
Что такое метод интерполяции?
В математической области численного анализа, интерполяция — это метод построения новых точек данных в диапазоне дискретного набора известных точек данных.… Несколько точек данных исходной функции можно интерполировать на , чтобы получить более простую функцию, которая все еще довольно близка к исходной.
Формула интерполяции Excel
Формула интерполяции ExcelВот пример, иллюстрирующий концепцию интерполяции. Садовник посадил помидор, и она измеряла и отслеживала его рост через день. Этот садовник — любопытный человек, и она хотела бы оценить, насколько высоким было ее растение на четвертый день.
Читайте также: Средняя и мгновенная скорость изменения
Ее таблица наблюдений выглядела так:
Исходя из диаграммы, нетрудно понять, что на четвертый день растение было примерно 6 мм в высоту. Это потому, что это дисциплинированное растение томата росло линейно; была линейная зависимость между количеством измеренных дней и ростом растения. Линейный образец означает, что точки образуют прямую линию.Мы могли даже оценить, нанеся данные на график.
А что, если растение росло не по удобной линейной схеме? Что, если бы его рост выглядел примерно так?
Что бы сделал садовник, чтобы сделать оценку на основе приведенной выше кривой? Что ж, вот здесь и пригодится формула интерполяции.
Формула интерполяции Thermo
Линейная интерполяция использовалась с древних времен для заполнения пробелов в таблицах.Предположим, у вас есть таблица, в которой перечислено население какой-либо страны в 1970, 1980, 1990 и 2000 годах, и вы хотите оценить численность населения в 1994 году. Линейная интерполяция — простой способ сделать это. Считалось, что метод использования линейной интерполяции для составления таблиц использовался вавилонскими астрономами и математиками в Месопотамии Селевкидов (последние три века до нашей эры), а также греческим астрономом и математиком Гиппархом (2 век до нашей эры). Описание линейной интерполяции можно найти в Альмагесте (2 век нашей эры) Птолемея.
Основная операция линейной интерполяции между двумя значениями обычно используется в компьютерной графике. На жаргоне этой области его иногда называют lerp . Термин может использоваться как глагол или существительное для операции. например «Алгоритм Брезенхема постепенно перемещается между двумя конечными точками линии».
Lerp-операции встроены в аппаратное обеспечение всех современных графических процессоров. Их часто используют в качестве строительных блоков для более сложных операций: например, билинейную интерполяцию можно выполнить за три лерпа.Поскольку эта операция стоит недорого, это также хороший способ реализовать точные таблицы поиска с быстрым поиском плавных функций без слишком большого количества записей в таблице.
Читайте также: Что такое буквенно-цифровые символы?
Формула интерполяции
Допустим, у нас есть две известные точки x1, y1x1, y1 и x2, y2x2, y2.
Теперь мы хотим оценить, какое значение yy мы получили бы для некоторого значения xx, которое находится между x1x1 и x2x2. Назовите это значение yy оценкой — интерполированное значение .
На ум приходят два простых метода выбора yy. Первый — посмотреть, ближе ли xx к x1x1 или к x2x2. Если xx ближе к x1x1, тогда мы используем y1y1 в качестве оценки, в противном случае мы используем y2y2. Это называется интерполяцией ближайшего соседа .
Второй — провести прямую линию между x1, y1x1, y1 и x2, y2x2, y2. Мы смотрим, чтобы увидеть значение yy в строке для нашего выбранного xx. Это линейная интерполяция .
Можно показать, что формула линии между x1, y1x1, y1 и x2, y2x2, y2:
y = y1 + (x − x1) y2 − y1x2 − x1y = y1 + (x − x1) y2 − y1x2 − x1
Формула двойной интерполяции
Чтобы выполнить линейную интерполяцию в Excel, мы будем использовать приведенное ниже уравнение, где x — независимая переменная, а y — значение, которое мы хотим найти:
Определение интерполяции
Что такое интерполяция?
Интерполяция — это статистический метод, с помощью которого связанные известные значения используются для оценки неизвестной цены или потенциальной доходности ценной бумаги.Интерполяция достигается за счет использования других установленных значений, расположенных в последовательности с неизвестным значением.
Интерполяция — это простая математическая концепция. Если существует в целом согласованная тенденция по набору точек данных, можно разумно оценить значение набора в точках, которые не были рассчитаны. Инвесторы и биржевые аналитики часто создают линейную диаграмму с интерполированными точками данных. Эти графики помогают им визуализировать изменения цен на ценные бумаги и являются важной частью технического анализа.
Ключевые выводы
- Интерполяция — это простой математический метод, используемый инвесторами для оценки неизвестной цены или потенциальной доходности ценной бумаги или актива с использованием связанных известных значений.
- Используя последовательный тренд по набору точек данных, инвесторы могут оценивать неизвестные значения и наносить эти значения на графики, представляющие движение цены акции во времени.
- Одно из критических замечаний по поводу использования интерполяции в инвестиционном анализе заключается в том, что ей не хватает точности и она не всегда точно отражает волатильность публично торгуемых акций.
Общие сведения об интерполяции
Инвесторы используют интерполяцию для создания новых оценочных точек данных между известными точками данных на графике. Графики, представляющие ценовое действие и объем ценной бумаги, являются примерами, где может использоваться интерполяция. Хотя сегодня компьютерные алгоритмы обычно генерируют эти точки данных, концепция интерполяции не нова. Интерполяция использовалась человеческими цивилизациями с древних времен, особенно ранними астрономами в Месопотамии и Малой Азии, пытающимися заполнить пробелы в своих наблюдениях за движением планет.
Существует несколько формальных видов интерполяции, включая линейную интерполяцию, полиномиальную интерполяцию и кусочно-постоянную интерполяцию. Финансовые аналитики используют интерполированную кривую доходности для построения графика, представляющего доходность недавно выпущенных казначейских облигаций США или нот с определенным сроком погашения. Этот тип интерполяции помогает аналитикам понять, в каком направлении могут развиваться рынки облигаций и экономика в будущем.
Интерполяцию не следует путать с экстраполяцией, которая относится к оценке точки данных за пределами наблюдаемого диапазона данных.Экстраполяция имеет более высокий риск получения неточных результатов по сравнению с интерполяцией.
Пример интерполяции
Самый простой и распространенный вид интерполяции — это линейная интерполяция. Этот тип интерполяции полезен, если кто-то пытается оценить стоимость ценной бумаги или процентной ставки для точки, в которой нет данных.
Предположим, например, что мы отслеживаем цену ценной бумаги в течение определенного периода времени. Строку, по которой отслеживается значение ценной бумаги, назовем функцией f (x).Мы построили бы график текущей цены акции по серии точек, представляющих моменты времени. Таким образом, если мы запишем f (x) для августа, октября и декабря, эти точки будут математически представлены как x августа, x октября, и x Dec, или x 1, x 3 и х 5.
По ряду причин мы можем захотеть узнать стоимость безопасности в течение сентября, месяца, по которому у нас нет данных. Мы могли бы использовать алгоритм линейной интерполяции для оценки значения f (x) в точке графика x сентября или x 2 , которая появляется в пределах существующего диапазона данных.
Критика интерполяции
Одна из самых серьезных критических замечаний по поводу интерполяции заключается в том, что, хотя это довольно простая методология, которая существует уже много лет, ей не хватает точности. Интерполяция в Древней Греции и Вавилоне заключалась в первую очередь в том, чтобы делать астрономические прогнозы, которые помогли бы фермерам рассчитать свои стратегии посадки для повышения урожайности.
Хотя движение планетных тел зависит от многих факторов, они все же лучше подходят для неточности интерполяции, чем дико вариативная, непредсказуемая волатильность публично торгуемых акций.Тем не менее, с учетом огромного количества данных, используемых для анализа ценных бумаг, большие интерполяции ценовых движений довольно неизбежны.
Большинство графиков, представляющих историю акций, на самом деле широко интерполированы. Линейная регрессия используется для построения кривых, которые приблизительно представляют колебания цены ценной бумаги. Даже если бы график, измеряющий акции за год, включал точки данных за каждый день года, нельзя было бы с полной уверенностью сказать, где будет оцениваться акция в определенный момент времени.
4.7.6: Линейная интерполяция и экстраполяция
Предположим, что вы нанесли несколько точек данных на координатную плоскость, причем координата x каждой точки данных представляет количество месяцев с момента посадки дерева, и координата y- каждой точки, представляющая высоту дерева в метрах. Если у вас есть данные за 1 месяц, 2 месяца, 3 месяца и 4 месяца, как вы думаете, сможете ли вы угадать, какой будет высота дерева через 5 месяцев? Как насчет того, какой была высота дерева на уровне 2?5 месяцев?
Прогнозирование с помощью линейных уравненийЦифровая информация появляется во всех сферах жизни. Вы можете найти его в газетах, журналах, журналах, по телевидению или в Интернете. В разделе «Подгонка линий к концепции данных» вы увидели, как найти уравнение линии наилучшего соответствия. Использование линии наилучшего соответствия — хороший метод, если взаимосвязь между зависимыми и независимыми переменными является линейной. Однако не все данные укладываются в прямую линию. Эта концепция покажет другие методы, помогающие оценить значения данных.Эти методы полезны как в линейных, так и в нелинейных отношениях.
Линейная интерполяция полезна при поиске значения между заданными точками данных. Это можно рассматривать как «заполнение пробелов» в таблице данных. Стратегия линейной интерполяции заключается в использовании прямой линии для соединения известных точек данных по обе стороны от неизвестной точки. Линейная интерполяция часто не точна для нелинейных данных. Если точки в наборе данных сильно изменяются, линейная интерполяция может не дать хорошей оценки.
Линейная экстраполяция может помочь нам оценить значения, которые либо выше, либо ниже значений в наборе данных. Думайте об этом как о «долгосрочной оценке» данных. Стратегия линейной экстраполяции заключается в использовании подмножества данных вместо всего набора данных. Это особенно верно для нелинейных данных, с которыми вы столкнетесь на более поздних уроках. Для этого типа данных иногда полезно экстраполировать с использованием последних двух или трех точек данных, чтобы оценить значение, превышающее диапазон данных.
Сбор и систематизация данныхДанные можно собирать различными способами, включая опросы или эксперименты. Опрос — это метод сбора данных, используемый для сбора информации об индивидуальных мнениях, убеждениях или привычках, в то время как эксперимент — это контролируемый тест или расследование. Информация, собранная Бюро переписи населения США или Центром по контролю за заболеваниями, является примерами данных, собранных с помощью опросов.Бюро переписи населения США собирает информацию о многих аспектах населения США.
Допустим, нас интересует, как изменился средний возраст вступления в первый брак в течение ХХ века. Перепись населения США предоставляет следующую информацию о среднем возрасте вступления в первый брак для мужчин и женщин. Ниже представлена таблица данных и соответствующий график разброса.
Рисунок 4.7.6.1Средний возраст мужчин и женщин при первом браке по годам
| Год | Средний возраст мужчин | Средний возраст женщин |
|---|---|---|
| 1890 | 26.1 | 22,0 |
| 1900 | 25,9 | 21,9 |
| 1910 | 25,1 | 21,6 |
| 1920 | 24,6 | 21,2 |
| 1930 | 24,3 | 21,3 |
| 1940 | 24.3 | 21,5 |
| 1950 | 22,8 | 20,3 |
| 1960 | 22,8 | 20,3 |
| 1970 | 23,2 | 20,8 |
| 1980 | 24,7 | 22,0 |
| 1990 | 26.1 | 23,9 |
| 2000 | 26,8 | 25,1 |
Сначала мы воспользуемся методом интерполяции, потому что есть «пробел», который необходимо заполнить. 1946 год — это период между 1940 и 1950 годами, поэтому мы будем использовать эти данные.
Рисунок 4.7.6.3Соединяя две точки, можно найти уравнение.
м = (22,8-24,3) / (1950-1940) = — 1,5 / 10 = -0,15 Уклон
y = −0,15x + b
24,3 = -0,15 (1940) + b
б = 315,3
y = −0,15x + 315,3 Уравнение
Чтобы оценить средний возраст вступления в брак мужчин в 1946 году, подставьте в уравнение x = 1946.
y = −0,15 (1946) + 315,3 = 23,4 года
Теперь давайте оценим средний возраст вступления в первый брак женщины в 1968 году:Используйте метод интерполяции, чтобы создать линию, которая аппроксимирует значения между 1960 и 1970 годами, поскольку 1968 год находится между этими годами.Мы будем использовать точки данных (1960, 20.3) и (1970, 20.8) как две точки, определяющие линию.
м = (20,8-20,3) / (1970-1960) = 0,5 / 10 = 0,05 Уклон
y = 0,05x + b
20,3 = 0,05 (1960) + b
б = -77,7
y = 0,05x − 77,7 Уравнение
Чтобы оценить средний возраст вступления в брак женщин в 1968 году, подставьте в уравнение x = 1968.
y = 0,05 (1968) −77,7 = 20,7 года
Прогнозирование с использованием уравненияКогда линейная интерполяция и линейная экстраполяция не дают точных прогнозов, использование линии наилучшего соответствия ( линейная регрессия ) может быть лучшим выбором.В последней Концепции были представлены «ручные» и калькуляционные методы определения линии наилучшего соответствия.
Решим следующую задачу с помощью уравнения:Мировые рекорды в беге на 100 метров среди женщин приведены в следующей таблице. Оцените мировой рекорд времени в 2010 году. Это хорошая оценка?
Мировой рекорд для женщин в беге на 100 метров к
году| Победитель | Ctry. | Год | секунды | Победитель | Ctry. | Год | секунды |
|---|---|---|---|---|---|---|---|
| Мэри Лайнс | UK | 1922 | 12,8 | Крепкина Вера | Сов. | 1958 | 11,3 |
| Лени Шмидт | Germ. | 1925 | 12,4 | Wyomia Tyus | США | 1964 | 11,2 |
| Gertrurd Glasitsch | Germ. | 1927 | 12,1 | Барбара Феррелл | США | 1968 | 11.1 |
| Толлин Шуурман | Neth. | 1930 | 12,0 | Эллен Строфал | E. Germ. | 1972 | 11,0 |
| Хелен Стивенс | США | 1935 | 11,8 | Инге Хелтен | W. Germ. | 1975 | 11,0 |
| Лулу Мэй Хаймс | США | 1939 | 11,5 | Марлиз Гор | E. Germ. | 1982 | 10,9 |
| Fanny Blankers-Koen | Neth. | 1943 | 11,5 | Флоренс Гриффит Джойнер | США | 1988 | 10.5 |
| Марджори Джексон | Austr. | 1952 | 11,4 |
Начните с построения диаграммы разброса данных. Соедините две последние точки на графике и найдите уравнение линии.
Рисунок 4.7.6.4м = (10,5−10,9) / (1988−1982) = — 0,4 / 6 = −0,067 Наклон
у = -0.067x + b
10,5 = -0,067 (1988) + b
б = 143,7
y = −0,067x + 143,7 Уравнение
Мировой рекорд в 2010 году оценивается следующим образом: y = -0,067 (2010) + 143,7 = 9,03 секунды.
Насколько точна эта оценка? Скорее всего, это не очень точно, потому что 2010 год сильно отличается от 1988 года. Этот пример демонстрирует слабость линейной экстраполяции. Оценки, полученные с помощью линейной экстраполяции, никогда не будут так хороши, как использование уравнения из метода линии наилучшего соответствия.В этом конкретном примере последняя точка данных явно не соответствует общей тенденции данных, поэтому наклон линии экстраполяции намного круче, чем должен быть.
В качестве исторической справки, последняя точка данных соответствует мировому рекорду Флоренс Гриффит Джойнер в 1988 году. После гонки ее обвинили в употреблении препаратов, улучшающих работоспособность, но этот факт так и не был доказан. Кроме того, возникает вопрос о точности хронометража, потому что некоторые официальные лица заявили, что попутный ветер не учитывался в этой гонке, даже несмотря на то, что на все другие гонки дня повлиял сильный ветер.
ПримерыПример 4.7.6.1
Ранее вам сказали, что у вас есть данные, нанесенные на координатную плоскость, и что координаты x представляют количество месяцев с момента посадки дерева, а координаты y представляют высоту дерева в метрах. Если у вас есть данные за 1 месяц, 2 месяца, 3 месяца и 4 месяца, можете ли вы угадать, какой будет высота дерева через 5 месяцев? Как насчет того, какой была высота дерева в 2,5 месяца?
Решение
Да, вы можете догадаться, какой высоты будет дерево и в 5, и в 2 месяца.5 месяцев.
Чтобы угадать высоту через 5 месяцев, вы можете использовать линейную экстраполяцию, потому что точка данных выше значений в данном наборе данных. Лучший способ сделать это — использовать точки данных за 1 и 4 месяца, чтобы написать общее уравнение для линии. Затем подключите 5, чтобы найти высоту. Как указано в данной Концепции, эта оценка, вероятно, не очень точна.
Чтобы угадать, какой была высота дерева в 2,5 месяца, вы можете использовать линейную интерполяцию, потому что 2,5 месяца находятся между двумя указанными нами точками данных, 2 месяцами и 3 месяцами.Мы пытаемся восполнить пробел, поэтому это будет интерполяция. Лучший способ сделать это — использовать точки данных за 2 месяца и 3 месяца, чтобы написать уравнение, а затем вставить 2,5, чтобы найти высоту.
Пример 4.7.6.2
Центр по контролю за заболеваниями (CDC) располагает следующей информацией о процентном соотношении курящих беременных женщин по годам. Оцените процент курящих беременных женщин в 1998 году.
Решение
| Год | Процент |
|---|---|
| 1990 | 18.4 |
| 1991 | 17,7 |
| 1992 | 16,9 |
| 1993 | 15,8 |
| 1994 | 14,6 |
| 1995 | 13,9 |
| 1996 | 13,6 |
| 2000 | 12.2 |
| 2002 | 11,4 |
| 2003 | 10,4 |
| 2004 | 10,2 |
Процент курящих беременных женщин по годам
Рисунок 4.7.6.5Мы хотим использовать информацию, близкую к 1998 году, чтобы интерполировать данных. Мы делаем это, соединив точки по обе стороны от 1998 года прямой линией и находим уравнение этой линии.
м = (12,2−13,6) / (2000−1996) = — 1,4 / 4 = −0,35 Наклон
y = −0,35x + b
12,2 = -0,35 (2000) + b
б = 712,2
y = −0,35x + 712,2 Уравнение
Чтобы оценить процент курящих беременных женщин в 1998 году, подставьте в уравнение x = 1998.
y = -0,35 (1998) + 712,2 = 12,9%
Линейная интерполяция
конец группы инверсного парка
Линейная интерполяция — это метод подбора кривой с использованием линейных полиномов.Линейная интерполяция работает, эффективно рисуя прямую линию между двумя соседними выборками и возвращая соответствующую точку вдоль этой линии
Линейная интерполяция
- Функция Linear Interpolate вычисляет выходное значение (y) для входа (x) с использованием линейной интерполяции входных значений x0, x1 (ближайшие входные значения) и выходных значений y0 и y1 (ближайшие выходные значения )
- Алгоритм:
y = y0 + (x - x0) * ((y1 - y0) / (x1-x0)) где x0, x1 - ближайшие значения входа x y0, y1 - ближайшие значения для вывода y
- Этот набор функций реализует процесс линейной интерполяции для типов данных Q7, Q15, Q31 и с плавающей запятой.Функции работают с одним образцом данных, и каждый вызов функции возвращает одно обработанное значение.
Sуказывает на экземпляр структуры данных функции линейной интерполяции.x— это значение входной выборки. Функции возвращают выходное значение.
- , если x находится за пределами границы таблицы, линейная интерполяция возвращает первое значение таблицы, если x ниже диапазона ввода, и возвращает последнее значение таблицы, если x находится выше диапазона.
- Параметры
[вход, выход] S — это экземпляр структуры линейной интерполяции с плавающей запятой [вход] x входной образец для обработки
- Возвращает
- y обработанный выходной образец.
- Примеры:
- arm_linear_interp_example_f32.c.
| __STATIC_FORCEINLINE q15_t arm_linear_interp_q15 | ( | q15_t * | pYData , |
| q31_t | х , | ||
| uint32_t | n Значения | ||
| ) |
- Параметры
[дюйм] pYData указатель на таблицу линейной интерполяции Q15 [дюйм] x входной образец для обработки [дюйм] значений nValues nValues
- Возвращает
- y обработанный выходной образец.12.
| __STATIC_FORCEINLINE q31_t arm_linear_interp_q31 | ( | q31_t * | pYData , |
| q31_t | х , | ||
| uint32_t | n Значения | ||
| ) |
- Параметры
[дюйм] pYData указатель на таблицу линейной интерполяции Q31 [дюйм] x входной образец для обработки [дюйм] значений nValues
- Возвращает
- y обработанный выходной образец.12.
| __STATIC_FORCEINLINE q7_t arm_linear_interp_q7 | ( | q7_t * | pYData , |
| q31_t | х , | ||
| uint32_t | n Значения | ||
| ) |
- Параметры
[дюйм] pYData указатель на таблицу линейной интерполяции Q7 [дюйм] x входной образец для обработки [дюйм] значений nValues nValues
- Возвращает
- y обработанный выходной образец.12.
Линейная интерполяция в Excel | Как выполнить линейную интерполяцию с примерами
Линейная интерполяция в Excel
Линейная интерполяция в Excel означает прогнозирование или угадывание ближайшего следующего значения любой определенной переменной, заданной в текущих данных, здесь мы создаем прямую линию, которая соединяет два значения, и мы оцениваем будущее значение через нее, в Excel мы используем функцию прогноза и функция поиска для линейной интерполяции.
Интерполяция — это математический или статистический инструмент, который используется для прогнозирования значений между двумя точками на кривой или линии.Этот инструмент используется не только в статистике, но и во многих других областях, таких как бизнес, наука и т. Д., Везде, где есть возможность прогнозировать значения между двумя точками данных.
Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. Д. Пожалуйста, предоставьте нам ссылку с указанием авторства Ссылка на статью по гиперссылке
Например:
Источник: Линейная интерполяция в Excel (wallstreetmojo.com)
Как сделать линейную интерполяцию в Excel?
Пример # 1
Выполнение интерполяции для определения температуры погоды в разных часовых поясах
Во-первых, снимите цифры температуры в регионе Бангалор за каждый час, и данные будут следующими: —
Данные показывают, что у нас есть данные о температуре в районе Бангалора на определенную дату.В столбце on-time у нас есть часовые пояса для всего дня и часов, в столбце мы упомянули количество часов с начала дня, например, 12:00 AM будет 0 часов, 1:00 AM будет 1 час, и так на.
Теперь мы собираемся выполнить интерполяцию данных, чтобы получить значение температуры для требуемого часового пояса, которым может быть любое время, а не только точный час.
Чтобы выполнить интерполяцию, мы должны использовать несколько формул в Excel, например ПРОГНОЗ, СМЕЩЕНИЕ, ПОИСКПОЗ.Давайте вкратце рассмотрим эти формулы, прежде чем мы продолжим.
ПРОГНОЗ () — Эта функция Excel для прогноза вычисляет или прогнозирует будущее значение на основе существующих значений вместе с линейным трендом.
- X — это значение, для которого мы хотим спрогнозировать.
- Known_ys — это зависимые значения из данных и обязательное поле для заполнения.
- Known_xs — это независимые значения из данных и обязательное поле для заполнения.
MATCH () — Эта функция Match Excel возвращает относительное положение искомого значения в строке, столбце или таблице, которое соответствует указанному значению в указанном порядке.
- Lookup_value — это значение, которое необходимо сопоставить из lookup_array
- Lookup_array — Это диапазон для поиска
[match_type] — Это может быть 1,0, -1. По умолчанию будет 1. Для 1 — Match найдет наибольшее значение, которое меньше или равно значению look_up, и значение должно быть в порядке возрастания.Для 0 — Match находит первое значение, точно равное lookup_value и не нуждающееся в сортировке. Для -1 — Match найдет наименьшее значение, которое больше или равно значению look_up и должно быть отсортировано в порядке убывания.
OFFSET () — Эта функция Offset возвращает ячейку или диапазон ячеек, в которых указано количество строк и столбцов. Ячейка или диапазон ячеек будет зависеть от высоты и ширины указанных нами строк и столбцов.
- Ссылка — это начальная точка, с которой будет производиться подсчет строк и столбцов.
- Строки — Число строк для смещения ниже начальной опорной ячейки.
- Столбцы — Число столбцов для смещения вправо от начальной опорной ячейки.
- [высота] — высота в строках из возвращенной ссылки. Это необязательно.
- [ширина] — ширина в столбцах из возвращенной ссылки. Это необязательно.
Как мы вкратце видели формулы, которые мы собираемся использовать для выполнения интерполяции.Теперь выполним интерполяцию следующим образом:
Введите формулу в ячейку, которая нам нужна, чтобы увидеть температуру для другого часового пояса. Это говорит о том, что мы должны выбрать ячейку, которую необходимо спрогнозировать, а функция смещения и сопоставления используется для выбора известных_ys и известных_x.
ПРОГНОЗ ($ F $ 5 — Выберите ячейку с часовым поясом для прогнозирования.
OFFSET ($ C $ 3: $ C $ 26, MATCH ($ F $ 5, $ B $ 3: $ B $ 26,1) -1,0,2) — Используется для выбора known_ys, поскольку используется ссылка temp столбец, потому что это зависимые значения.Функция соответствия используется для генерации позиции значения, которое нам нужно спрогнозировать, и вычисления количества строк. Столбцы должны быть равны 0, потому что мы хотим, чтобы зависимое значение было в том же столбце, который выбран, а высота равна 2, поскольку нам нужно выполнить прогноз на основе последних 2 значений.
OFFSET ($ B $ 3: $ B $ 26, MATCH ($ F $ 5, $ B $ 3: $ B $ 26,1) -1,0,2) — Используется для выбора известных_x в качестве эталонного часа. столбец, потому что это независимые значения, а остальные такие же, как и для количества строк.
Теперь укажите часовой пояс в ячейке, которую мы считали прогнозируемой. Здесь введено значение 19,5, что составляет 19:30, и мы получим температуру 30, которая прогнозируется на основе значений температуры, которые указываются на почасовой основе.
Точно так же мы можем увидеть значения температуры для разных часовых поясов из этой формулы.
Пример # 2
Выполнение линейной интерполяции для определения продаж организации в 2018 году
Предположим, что мы получили подробную информацию о продажах организации в 2018 году, как показано ниже.У нас есть данные о днях и их продажах в совокупности. У нас было продано 7844 единицы за первые 15 дней года, 16094 единицы за 50 дней в году и так далее.
Мы можем использовать ту же формулу, которую мы использовали при интерполяции, для прогнозирования стоимости продаж для разных дней, которая не была упомянута в данных, которые мы рассматриваем. Здесь продажи прямолинейны (линейны), как мы взяли кумулятивно.
Если мы хотим увидеть количество продаж, которых мы достигли за 215 дней, мы можем получить прогнозируемое количество продаж на 215 дней, как показано ниже, с учетом данных продаж.
Точно так же мы можем узнать количество продаж в этом году, сделав прогноз между заданными точками.
Что нужно помнить
- Это наименее точный метод, но он будет быстрым и точным, если значения таблицы расположены близко друг к другу.
- Это также можно использовать для оценки значений для точки географических данных, осадков, уровней шума и т. Д.
- Он очень прост в использовании и не очень точен для нелинейных функций.
- Помимо линейной интерполяции в Excel, у нас также есть различные типы методов, такие как полиномиальная интерполяция, сплайн-интерполяция и т. Д.
Рекомендуемые статьи
Это руководство по линейной интерполяции в Excel. Здесь мы увидим, как выполнять интерполяцию и линейную интерполяцию в Excel, а также некоторые примеры и загружаемый шаблон Excel. Вы можете узнать больше об Excel из следующих статей —
Пакет All in One Excel VBA (35 курсов с проектами)- 35+ курсов
- 120+ часов
- Полный пожизненный доступ
- Свидетельство о завершении
Interpolation :: Godot Recipes
Linear Interpolation , или его обычно используемое сокращение lerp , — это термин, который часто используется при разработке игр.Если вы никогда не сталкивались с этим, прежде чем он может показаться загадочным и высокотехнологичным, но, как вы увидите в этом руководстве, на самом деле это простая концепция с широким спектром приложений в программировании игр.
Числовая интерполяция
Основная формула линейной интерполяции:
func lerp (a, b, t):
return (1 - t) * a + t * b
В этой формуле a и b представляют два значения, а t — это величина интерполяции, обычно выражаемая как значение между 0 (которое возвращает a ) и 1 ( который возвращает b ).Функция находит значение заданной суммы между ними. Например:
x = lerp (0, 1, 0,75) # x равно 0,75
x = lerp (0, 100, 0.5) # x равно 50
x = lerp (10, 75, 0,3) # x равно 29,5
x = lerp (30, 2, 0.75) # x равно 9
Это называется линейной интерполяцией , потому что путь между двумя точками представляет собой прямую линию.
Вы можете анимировать свойства узла с помощью lerp () . Например, если вы разделите прошедшее время на желаемую продолжительность, вы получите значение от нуля до единицы, которое можно использовать для плавного изменения свойства с течением времени.Этот скрипт масштабирует спрайт до пятикратного его начального размера при его постепенном исчезновении (используя modulate.a ) в течение двух секунд:
расширяет Sprite
var time = 0
var duration = 2 # длина эффекта
func _process (дельта):
если время <продолжительность:
время + = дельта
modulate.a = lerp (1, 0, время / продолжительность)
scale = Vector2.ONE * lerp (1, 5, время / продолжительность)
Векторная интерполяция
Вы также можете интерполировать между векторами.И Vector2 , и Vector3 предоставляют для этого методы linear_interpolate () .
Например, чтобы найти вектор, который находится на полпути между векторами прямого и левого направления узла Spatial :
var forward = -transform.basis.z
var left = transform.basis.x
var forward_left = forward.linear_interpolate (слева, 0,5)
В следующем примере узел спрайта перемещается к месту щелчка мыши. Каждый кадр узел перемещается на 10% пути к цели.Это приводит к эффекту «приближения», когда скорость объекта уменьшается по мере приближения к цели.
расширяет Sprite
var target
func _input (событие):
если событие InputEventMouseButton и event.pressed:
target = event.position
func _process (дельта):
если цель:
position = position.linear_interpolate (цель, 0,1)
Для более сложных приложений интерполяции см. Tween .
Комментарии
Как интерполировать числа | Sciencing
Интерполяция включает использование значений данных для вычисления числа между ними. Это можно сделать графически или с помощью уравнения. Важно знать, как интерполировать числа, потому что это может помочь вам лучше понять данные, пытаясь определить значения данных, которые не были конкретно указаны в исходном наборе. Для интерполяции вам понадобится всего несколько наборов значений.
Составьте таблицу значений данных, а затем создайте график из этих значений.Например, вам могут быть предоставлены данные о количестве студентов, не сдавших экзамен по математике в 2000, 2002, 2004 и 2006 годах. В 2000 году 100 студентов не прошли. В 2002 году не прошли обучение 90 студентов. В 2004 году 48 студентов не прошли обучение. В 2006 году не прошли обучение 32 студента. Проблема может попросить вас использовать интерполяцию, чтобы найти количество студентов, которые не прошли тест в 2001 году.
Постройте график данных в таблице. Поместите годы на ось абсцисс, а количество студентов, не прошедших обучение, - на ось ординат.Соедините все точки линией.
С помощью линейки проведите вертикальную линию от значения x 2001 года до линии графика. Проведите горизонтальную линию от точки на графике к оси ординат. Выполняя эту графическую интерполяцию, вы можете обнаружить, что около 95 студентов не прошли тест по математике в 2001 году.
Знайте формулу для процесса линейной интерполяции. Формула: y = y1 + ((x - x1) / (x2 - x1)) * (y2 - y1), где x - известное значение, y - неизвестное значение, x1 и y1 - координаты, которые находятся ниже известное значение x, а x2 и y2 - координаты выше значения x.
Запишите числа, которые вы собираетесь ввести в уравнение.
