Графическое счисление пути судна. Сущность графического счисления. Ведение графического счисления и решение задач при отсутствии дрейфа и течения
Графическое счисление пути судна
Сущность графического счисления
Безопасность плавания в навигационном отношении обеспечивается правильным выбором маршрута между пунктами и следованием по выбранному пути.
Выбор пути – одна из важнейших задач в судовождении, решение которой основывается на тщательном анализе всей обстановки в течении перехода.
Выбранный путь
судна наносится на карты – выполняется предварительная прокладка. Предварительная
прокладка выполняется до выхода судна в рейс капитаном. Она является она
является итогом работы по выбору безопасного и наивыгоднейшего пути судна. Для
обеспечения навигационной безопасности плавания на карте намечают места
изменения курсов, для чего выбирают такие точки поворотов, чтобы моменты
приходы судна в эти точки могли быть быстро определены, например моменты
прихода на траверз, на створ и т. д.
д.
Намечают в каком расстоянии будут проходить мысы, маяки, другие ориентиры.
Склонение приводят к году плавания и надписывают его величину карандашом доль всего пути судна..
Над линиями пути надписывают значения истинных курсов.
С карты снимают расстояние в милях по каждому курсу и подсчитывают количество миль всего перехода.
На линии пути отмечают границы дальности видимости маяков и огней для высоты мостика, намечают наиболее целесообразные способы определения места судна на отдельных участках. Учёт времени ведут с оперативного, считая время отхода судна в 00 часов 00 минут.
Перед выполнением предварительной прокладки производится подъём карты (см § 45).
Расчёты выполненные в процессе предварительной прокладки являются ориентировочными и должны корректироваться во время плавания.
Предварительная прокладка выполняется, как правило, на путевых картах.
Вторая
важнейшая задача – обеспечение движения судна по выбранному пути, дл этого
ведут непрерывно учёт движения судна – счисление пути судна.
Основными элементами счисления являются курс (по компасу) и пройденное расстояние (по лагу).
Графическое счисление судна выражается в ведении исполнительной навигационной прокладки. Её начало совпадает с отходом судна от причала (съёмки с якоря), при выходе из порта штурман основное внимание уделяет глазомерной ориентировке в окружающей обстановке, основанной на знании гавани или рейда и правильного использования ТСС, СНО и естественных ориентиров.
С выходом на чистую воду точно определяют место судна и от полученной точки ведут прокладку.
Перед приходом в эту точку включают лаг, около исходной точки записывают в виде дроби в числителе время, в знаменателе отсчёт лага.
От исходной точки прокладывают линию ИК, на которой каждый час или через четыре часа отмечают счислимые точки, т.е. места, полученные без измерения навигационных параметров внешних ориентиров.
Счислимые
точки отмечаются на линии пути короткой поперечной чёрточкой, а толщина самой
линии пути должна быть примерно равна толщине меридианов и параллелей.
Все прокладки и расчёты выполняются мягким тонко заточенным карандашом.
Места положения судна по обсервациям, т.е. по результатам измерения навигационных параметров внешних ориентиров наносятся как можно чаще и обязательно, если есть возможность, при изменении курса.
Обсервованные места обозначаются условными знаками согласно РШС-89.
Несоответствие обсервованной точки со счислимой называется невязкой, обозначается буквой «С». В судовой журнал записывается её направление и величина (С=225º -1,5’)
Направление невязки счисляется от счислимой точки к обсервованной.
Ведение прокладки заканчивается при входе судна на акваторию порта или в точке начала манёвров при постановке судна на якорь.
Таким образом прокладкой называется совокупность измерений, вычислений и графических построений, связанных с выбором пути судна, учётом его движения и определением места судна.
Ведение графического счисления и решение
задач при отсутствии дрейфа и течения
Отсутствие дрейфа
судна и сноса течением упрощает как графические построения на карте, так и
расчёты при решении различных задач.
Во-первых, линия пути судна совпадает с направлением его ДП т.е. с линией ИК.
Во-вторых, расстояние, пройденное судном относительно воды т.е. по показаниям лага, исправленным его ошибкой, одновременно является и действительным расстоянием, пройденным относительно грунта (SЛ=SИ).
Решение прямой задачи
(Задачи по исправлению курса)
При заданном рулевому КК по МК | То же по ГК | ||||||||
+ | КК | → | + | δ | ± | + | ГКК | ||
ΔМК | ± | dПР | ± | ΔМК | ± | ||||
ИК | ΔМК | ± | ИК | ||||||
Решение обратной задачи
(Задачи на перевод курса)
_ | ИК | _ | ИК | ||||||
dПР | ± | ΔГК | ± | ||||||
_ | МК | → | δ’ | ± | ГКК | ||||
δ’ | ± | ||||||||
КК’ | → | + | δ | ± | |||||
dПР | ± | ||||||||
± | |||||||||
_ | ИК | ||||||||
ΔМК | ± | ||||||||
КК |
Решение частных задач
I. Нанесение счислимого места судна на карту.
Нанесение счислимого места судна на карту.
Дано: Т1, ОЛ1, Т2, ОЛ2. Найти: SЛ.
Решение:
_ | ОЛ2 | |
ОЛ1 | ||
× | ||
КЛ | ||
SЛ |
Или по РОЛ и ΔЛ из таблицы МТ-75 прилож 4.
II.Расчёт Т2 и ОЛ2
1. Приход в точку поворота
SЛ | ×60 | |||
+ | ΔТ | VЛ | ||
Т1 | ||||
Т2 |
или по МТ-75 прилож. 3 по S и V. Или по
логарифмической шкале.
3 по S и V. Или по
логарифмической шкале.
SЛ | ×100 | |||
+ | РОЛ | КЛ | ||
ОЛ1 | ||||
ОЛ2 |
Или по прилож.4 к МТ-75 или по логарифмической шкале найдём РОЛ
2. Приход на траверз маяка
Находим точку траверза
+ | ИК | |
КУ┴ | ±90º | |
ИП |
Главная — МТК им.
 адмирала Д.Н. Сенявина Главная — МТК им. адмирала Д.Н. Сенявина
адмирала Д.Н. Сенявина Главная — МТК им. адмирала Д.Н. СенявинаПожалуйста, включите JavaScript! Как?
| Размер шрифта: | Цвет сайта: | Изображения: |
Новости
2024-12-30 14:15:00
2023-08-26 11:49:00
19 августа Комитетом по образованию подписано распоряжение об утверждении устава с новым наименованием.
2023-04-27 14:07:00
Уведомление о завершении реорганизации СПбМТК
Санкт-Петербургское государственное автономное профессиональное образовательное учреждение «Морской технический колледж имени адмирала Д.Н. Сенявина» информирует о завершении реорганизации путем присоединения Санкт-Петербургского государственного бюджетного профессионального образовательного учреждения «Кронштадтский лицей» на основании распоряжения Комитета по образованию от 11.04. 2022 № 755-р «О внесении изменений в сеть государственных образовательных учреждений Санкт-Петербурга». Соответствующая запись внесена в ЕГРЮЛ 29 июля 2022 года.
2022 № 755-р «О внесении изменений в сеть государственных образовательных учреждений Санкт-Петербурга». Соответствующая запись внесена в ЕГРЮЛ 29 июля 2022 года.2022-09-29 14:10:00
Морской совет в МТА
29 сентября в актовом зале второй площадки Морской технической академии имени адмирала Д.Н. Сенявина прошло расширенное совместное заседание секции по морскому образованию и молодёжной политике, постоянной комиссии по взаимодействию с общественными организациями и средствами массовой информации и постоянной комиссии по морскому наследию Морского совета при Правительстве Санкт-Петербурга.2022-09-26 09:46:00
В преддверии Международного дня пожилых людей
26 сентября в Морской технической академии имени адмирала Д.Н. Сенявина снова говорили о важном, а именно о важном, чудесном, душевном, добром празднике – Международном дне пожилых людей, который мы отмечаем 1 октября.2022-09-25 14:09:00
«Навигатор поступления» указал курс
24–25 сентября в Санкт-Петербурге, в гостинице «Park Inn Прибалтийская» (ул. Кораблестроителей, д. 14), прошла профориентационная выставка «Навигатор поступления», в которой приняла участие и Морская техническая академия имени адмирала Д.Н. Сенявина.
Кораблестроителей, д. 14), прошла профориентационная выставка «Навигатор поступления», в которой приняла участие и Морская техническая академия имени адмирала Д.Н. Сенявина.2022-09-22 09:35:00
Синяя птица против наркотиков
22 сентября курсанты Морской технической академии имени адмирала Д.Н. Сенявина в очередной раз приняли участие в городской сетевой акции «Синяя птица – безопасная территория», которая организуется сотрудниками СПб ГБУ «Подростково-молодёжный центр «Невский».2022-09-21 13:50:00
Акция «Колокольчик мира»
21 сентября в группе курсантов судомеханического отделения Морской технической академии имени адмирала Д.Н. Сенявина прошла дискуссия, приуроченная к Международному дню мира.2022-09-20 09:42:00
ХXVI Слёт юных моряков
20 сентября завершился XVI Слёт юных моряков, в котором, начиная с 16 сентября, приняли участие 23 команды из Санкт-Петербурга и ещё одна – из Ярославля. Всего заявились на слёт в этом году почти 200 юношей и девушек трёх возрастных групп от 14 до 19 лет и команды в возрастной группе «Юнга». Слёт был организован Комитетом по молодёжной политике и взаимодействию с общественными организациями.
Слёт был организован Комитетом по молодёжной политике и взаимодействию с общественными организациями.2022-09-19 10:03:00
Разговоры о важном К.Э. Циолковский
Традиционно каждую учебную неделю Морская техническая академия имени адмирала Д.Н. Сенявина начинает с занятий «Разговоры о важном». В понедельник 19 сентября классные часы были посвящены теме 165-летия со дня рождения Константина Эдуардовича Циолковского.2022-09-16 09:59:00
Экспозиция «Пропавшие в кинохронике»
16 сентября курсанты 1 курса отделения техносферной безопасности Морской технической академии имени адмирала Д.Н. Сенявина посетили трёхмерную экспозицию в киноцентре «Ленфильм» на Каменноостровском проспекте. Инсталляция называлась «Пропавшие в кинохронике».2022-09-16 09:56:00
Финал соревнований пожарно-спасательных подразделений
16 сентября в Северной столице прошёл финал 44-х международных соревнований среди пожарно-спасательных подразделений на приз имени Владимира Владимировича Дехтерёва. На мероприятие пригласили и курсантов Морской технической академии имени адмирала Д.Н. Сенявина.
На мероприятие пригласили и курсантов Морской технической академии имени адмирала Д.Н. Сенявина.
2022-09-16 09:51:00
Курсанты МТА познакомились с работой кинологов
16 сентября состоялось выездное занятие курсантов Морской технической академии им. адмирала Д.Н. Сенявина на базе Центра кинологической службы ГУ МВД России по Санкт-Петербургу и Ленинградской области.2022-09-16 08:20:00
МТА принимает участие в выставке OMR 2022
С 13 по 16 сентября в павильоне H конгрессно-выставочного центра «Экспофорум» Морская техническая академия имени адмирала Д.Н. Сенявина в рамках стенда Санкт-Петербурга приняла участие в Международной выставке-конференции по судостроению и разработке высокотехнологичного оборудования для освоения континентального шельфа OMR.2022-09-14 15:42:20
День Лодейного Поля10 сентября курсанты Морской технической академии имени адмирала Д.Н. Сенявина приняли участие в праздновании 320-летия Лодейного поля.
 В этот день в областном центре Ленинградской области прошёл юбилейный Большой Петровский фестиваль.
В этот день в областном центре Ленинградской области прошёл юбилейный Большой Петровский фестиваль. ВСЕ НОВОСТИ
Морские карты дают наглядное представление о навигационных особенностях, изображенных на них водных районах и прилегающих к ним участков суши. Основное назначение морских карт—графическое решение задач судовождения. Совокупность графических работ, производимых па морской карте для обеспечения безопасности судовождения, называется прокладкой, которая является одним из основных видов решения повседневных штурманских задач на морской карте. Выйдя из порта в открытое море, судно ложится на свой курс. Продолжая плавание, судоводитель должен быть уверен в безопасности своего судна, для чего ему необходимо знать точное место судна на карте. При плавании вблизи берегов относительно небольшие глубины и наличие подводных и надводных опасностей требуют от судоводителя особого внимания к ведению прокладки пути судна. Поэтому при плавании в пределах видимости берега необходимо непрерывно следить за перемещением судна и тщательно вести прокладку пути судна.
Прокладка ведется при помощи прокладочного инструмента: транспортира, параллельной линейки, циркуля. При плавании вблизи берегов судоводитель обязан постоянно производить определения, или обсервации1, места судна по береговым предметам. Обсервованное место судна определяется точкой пересечения двух или более линий, которые называются линиями положения2. Линиями положения чаще всего бывают пеленги береговых предметов. Для определения места судна достаточно иметь две линии положения. Однако во всех случаях, когда представляется возможность, следует определять место судна по трем (и более) линиям положения (пеленгам), так как третий пеленг будет как бы контрольным, свидетельствующим о точности определения. Для определения места судна по трем пеленгам следует предварительно выбрать на берегу три хорошо видимых с судна и нанесенных на карту предмета.
При выборе объектов для пеленгования необходимо, чтобы углы между первым и вторым объектами и между вторым и третьим были бы не меньше 30 и не больше 150°, так как чем меньше угол пересечения, тем больше будет ошибка в обсервованном месте, которая увеличивается за счет того, что трудно выделить точку пересечения. Наиболее точными будут определения в случае, если угол между объектами близок к 90°. Начинать пеленговать следует с предмета, который ближе расположен к диаметральной плоскости судна (его пеленг меняется медленнее), а в ночное время первым пеленгуют маяк, огонь которого хуже виден.
Полученные значения пеленгов способом, описанным ранее, прокладывают на карте (рис. 46). Пересечение пеленгов даст точку — место судна. Однако на практике вследствие ошибок при взятии пеленгов и при прокладке их на карте, а также неверной поправки компаса три линии пеленгов в большинстве случаев в одной точке не пересекаются, на а образуют треугольник, называемый треугольником погрешности. При сторонах треугольника погрешности, не превышающих 0,5 мили, место судна принимают в центре треугольника. Полученное обсервованное место судна обозначают кружочком с точкой в центре.
Большие размеры треугольника свидетельствуют о наличии значительных ошибок. Определение места судна по трем пеленгам является наиболее точным способом навигационных определений.
Определение места судна по двум пеленгам производится так же, как и по трем. Однако в этом случае отсутствие третьей линии положения не позволяет проконтролировать надежность полученного обсервованного места судна. Определение места судна по двум расстояниям. С помощью РЛС, дальномера или каким-либо другим способом измеряют расстояние до двух предметов. Затем с боковой рамки карты снимают циркулем измеренные расстояния D1и D2и проводят дуги окружностей с центрами А и В в местах нахождения объектов наблюдения на карте . Определение места судна по пеленгу и расстоянию. Если с судна наблюдается только один предмет, то определение места можно сделать по пеленгу и расстоянию до него. В этом случае по компасу берется пеленг наблюдаемого предмета, который прокладывается на карте. Сразу же измеряют по РЛС расстояние, которое откладывают на линии пеленга . Определение места судна по крюйс-пеленгу. Определение места способом крюйс-пеленга производится тогда, когда с судна виден только один предмет, измерить расстояние до которого невозможно по каким-либо причинам. Сущность этого метода заключается в том, что наблюдаемый предмет пеленгуют несколько раз через определенные промежутки времени. Пусть в какой-то момент взят пеленг П1маяка А, а через некоторый промежуток времени получен пеленг П2того же предмета . За это время судно, следуя каким-то определенным курсом, прошло по лагу расстояние Sл.
Для определения места судна производят следующую прокладку. Из точки В (пересечение линии первого пеленга с линией курса) откладывают пройденное расстояние Sл. Из полученной точки С проводят прямую ПА1, параллельную линии первого пеленга П1А. Пересечение линий ПА1с линией второго пеленга П2А даст точку М, которая и будет местом судна. Дальнейшее счисление пути судна ведут от этой точки. Место судна, определенное по крюйс-пеленгу, называется счислимо-обсервованным, так как обсервацию определяют взятые пеленги, а элементом счисления является отсчет лага. Такое определение, конечно, менее надежно, чем обсервованное. 1 Определение места судна по наблюдениям береговых предметов, радиомаяков, радионавигационных систем или небесных светил. 2 Геометрическое место точек, отвечающих результатам произведенного наблюдения. |
ГРАФИЧЕСКОЕ СЧИСЛЕНИЕ ПУТИ СУДНА ГРАФИЧЕСКОЕ
ГРАФИЧЕСКОЕ СЧИСЛЕНИЕ ПУТИ СУДНА
• ГРАФИЧЕСКОЕ СЧИСЛЕНИЕ ПУТИ СУДНА. Для того чтобы судить о безопасности плавания, ориентироваться в окружающей обстановке и правильно выбирать курсы для дальнейшего перемещения, судоводитель должен в любой момент знать положение своего судна. Для этого он ведет навигационную прокладку. • Перед выходом судна в рейс под руководством капитана по картам и навигационным пособиям изучают условия плавания на всем предстоящем переходе. На основании этих данных выполняют предварительную прокладку. Однако она дает только общее представление об условиях перехода. С момента выхода в рейс окончательный выбор курсов и все принимаемые к учету факторы определяются конкретной обстановкой плавания. Поэтому в рейсе осуществляют исполнительную прокладку. Она включает в себя счисление пути, расчеты и построение на карте, расчеты маневрирования для расхождения с другими судами.
С момента выхода в рейс окончательный выбор курсов и все принимаемые к учету факторы определяются конкретной обстановкой плавания. Поэтому в рейсе осуществляют исполнительную прокладку. Она включает в себя счисление пути, расчеты и построение на карте, расчеты маневрирования для расхождения с другими судами.
• Счислением называется непрерывный учет элементов движения судна (скорости и направления) и воздействий внешних сил с целью определения координат судна (счислимого места) без наблюдений береговых ориентиров и небесных светил (обсерваций). Этот учет осуществляют на основании значений курса, скорости и вектора сноса судна. Исходную точку для счисления на карте определяет капитан. За такую точку могут быть приняты точное место судна, полученное сразу же после выхода за пределы акватории порта, плавучий маяк, приемный буй и т. д. Ее координаты записывают в судовой журнал. К моменту начала исполнительной прокладки следует включить лаг, определить поправку компаса по створам или другим способом.
• ВЕДЕНИЕ СЧИСЛЕНИЯ ПРИ ПЛАВАНИИ БЕЗ ДРЕЙФА И ТЕЧЕНИЯ. При плавании без дрейфа и течения линия пути судна на карте совпадает с линией ИК, поэтому учет перемещения судна на карте производится по линиям ИК, по которым откладывают расстояния, пройденные судном по лагу с учетом его коэффициента Кл. От исходной точки на карте прокладывают линию первого курса. Снятый с карты ИК переводят в КК, на который ложатся по магнитному компасу. На карте над линией ИК надписывают курс по компасу и его поправку. Пройденное по курсу расстояние Sл определяют по лагу: • Sл = Кл (ол 2 — ол 1) ; • (Где ол 2 — отсчёт лага в точке нахождения судна, ол 1 — отсчёт лага в исходной точке, Кл коэффициент лага).
• На линии ИК в указанных ниже случаях наносят счислимое мести судна, т. е. место, рассчитанное по курсу и плаванию. Если плавание совершают вблизи берегов, счислимые точки отмечают каждый час, в открытом море — в конце вахты. Кроме того, счислимое место наносят в точках начала и конца поворотов, при изменении скорости, при получении обсерваций. Рядом с местом судна в виде дроби записывают момент по судовым часам с точностью до 1 мин (Т) и отсчет лага с точностью до 0, 1 мили (ол). (См. рис 31).
Рядом с местом судна в виде дроби записывают момент по судовым часам с точностью до 1 мин (Т) и отсчет лага с точностью до 0, 1 мили (ол). (См. рис 31).
В реальных условиях морского плавания возможны три основных варианта, определяющих соответствующие практические приемы счисления пути яхты: • плавание в условиях устойчивого полного ветра; • плавание в условиях устойчивого противного ветра; • плавание при неустойчивом по силе и направлению ветре.
• В первом случае яхту ведут обычно по линии пути, проложенного при предварительной прокладке. Условия счисления здесь благоприятные. Во втором случае выполняют лавировку относительно генерального курса, при этом прокладываемый фактический путь на каждом галсе не совпадает с предварительной прокладкой. Если лавировочный галс не слишком крутой, то рулевой точно выдерживает заданный курс, что упрощает счисление и повышает его точность. В таких условиях продолжительность галсов зависит от угла лавировки (угол между генеральным курсом и путем яхты). При равенстве углов правого и левого галсов их продолжительность одинакова, а лавировка может быть симметричной. Если нет — счисление и прокладку пути выполняют на каждом частном лавировочном галсе по данным приборов. Если лага нет, скорость рекомендуется оценивать на каждом галсе.
При равенстве углов правого и левого галсов их продолжительность одинакова, а лавировка может быть симметричной. Если нет — счисление и прокладку пути выполняют на каждом частном лавировочном галсе по данным приборов. Если лага нет, скорость рекомендуется оценивать на каждом галсе.
• При лавировке может случиться, что рулевой по указанию капитана яхты, выбираясь на ветер, не обращает внимания на компас. Здесь через небольшие, но равные промежутки времени (15 — 30 мин. ) определяют и записывают средний КК и соответствующий ему ИК, по которому откладывают данные, полученные по лагу или скорости. При неустойчивом ветре курс рулевому не задают, а ставят задачу править по парусу в поисках ветра, придерживаясь по возможности ближе к генеральному курсу. Иногда в такой ситуации в зависимости от местных признаков и прогноза погоды бывает выгодно уклониться от генерального курса, чтобы скорее получить полный устойчивый ветер (например, бриз под берегом). Во всех этих случаях в интересах счисления пути на яхте фиксируют все повороты и на каждом галсе (в начале и конце галса обязательно) с определенной периодичностью (1 -2 раза в час, в зависимости от условий) записывают данные о движении судна (время, курс, скорость, отсчет лага). Эти записи обрабатывают, усредняя курс и скорость каждого галса, а затем прокладывают на карте.
Эти записи обрабатывают, усредняя курс и скорость каждого галса, а затем прокладывают на карте.
• Практика показывает, что точность счисления в таких условиях повышается с увеличением дискретности наблюдений. Ошибки апроксимации криволинейных участков плавания прямолинейными будут незначительны по сравнению с другими ошибками.
• ДРЕЙФ СУДНА. В навигации дрейфом («a») называют снос судна с линии курса под совместным действием ветра и вызванного им волнения. При дрейфе судно перемещается относительно воды под совместным действием судовых машин и ветра. Линия его фактического перемещения (ОВ), называемая линией пути судна при дрейфе, не совпадает с курсом судна (ОА). (См. рис 33). При смещении линии пути вправо от ДП судна (ветер дует в левый борт) a приписывают знак плюс (+), а при смещении влево (ветер дует в правый борт) — знак минус (-). Зависимость между путевым углом с учётом дрейфа (ПУa), ИК и a: • ПУa = ИК + a ; ИК = ПУa — a ; a = ПУa — ИК
• Угол дрейфа может быть определен путем сравнения действительного пути судна, полученного по обсервациям, с ИК. При следовании в виду берегов проводят ряд надежных навигационных наблюдений. Соединив обсервованные точки, получают линию действительного перемещения судна, т. е. линию пути при дрейфе ПУa (рис. 34). Угол между линией пути и проложенной на карте линией ИК соответствует углу дрейфа. Найденный угол дрейфа с его знаком учитывают при дальнейшем счислении. Если в районе плавания имеется течение, то полученный угол сноса будет результатом воздействия на судно не только ветра, но и течения.
При следовании в виду берегов проводят ряд надежных навигационных наблюдений. Соединив обсервованные точки, получают линию действительного перемещения судна, т. е. линию пути при дрейфе ПУa (рис. 34). Угол между линией пути и проложенной на карте линией ИК соответствует углу дрейфа. Найденный угол дрейфа с его знаком учитывают при дальнейшем счислении. Если в районе плавания имеется течение, то полученный угол сноса будет результатом воздействия на судно не только ветра, но и течения.
• УЧЕТ ДРЕЙФА ПРИ СЧИСЛЕНИИ. Если судно испытывает дрейф, то при ведении прокладки на карту наносят линию пути судна при дрейфе. На ней надписывают КК, поправку компаса и принятый к учету угол дрейфа a со своим знаком. По линии пути откладывают пройденные по лагу расстояния Sл. Считается, что при a
• Если судоводитель не уверен в точности угла дрейфа, то для контроля безопасности плавания, кроме линии пути при дрейфе, на карту рекомендуется наносить линию ИК. Обе эти линии должны проходить чисто относительно подводных препятствий. Счисление ведется только по линии пути, по которой и происходит перемещение судна.
Обе эти линии должны проходить чисто относительно подводных препятствий. Счисление ведется только по линии пути, по которой и происходит перемещение судна.
• МОРСКИЕ ТЕЧЕНИЯ. Морскими течениями называют горизонтальные перемещения больших масс воды. Течение характеризуется его элементами: направлением и скоростью. Направление течения Кт указывают в градусах по круговому счету или румбах и задают по той точке горизонта, к которой течение направлено. Скорость течения Vt измеряют в узлах, а небольшие его скорости — в милях в сутки. По характеру течения классифицируют на постоянные, элементы которых из года в год почти не изменяются, периодические, элементы которых меняются по определенному закону, и временные (случайные), элементы которых могут резко меняться. На практике судоводителю чаще всего приходится иметь дело с постоянными и периодическими (приливо-отливными) течениями. Сведения об элементах постоянных и приливо -отливных течений помещают в лоциях, атласах течений и на картах. При этом указывают средние значения элементов течений, которые могут значительно отличаться от действительных. Перемещение судна относительно грунта при плавании на течении определяют следующими факторами (рис. 36).
При этом указывают средние значения элементов течений, которые могут значительно отличаться от действительных. Перемещение судна относительно грунта при плавании на течении определяют следующими факторами (рис. 36).
• Под действием судовых машин судно перемещается относительно воды по направлению его ДП, т. е. линии истинного курса ОА. Скорость судна относительно воды является скоростью Vл показываемой лагом. Одновременно вместе со всей массой воды судно сносится относительно грунта по направлению течения ОД со скоростью течения Vt. В результате относительно грунта судно перемещается по равнодействующей OB со скоростью, называемой истинной скоростью судна V. При этом ДП судна остается параллельной линии ИК. Линия OB, по которой перемещается судно под совместным действием судовых машин и течения, называется линией пути судна на течении. Положение линии пути относительно истинного меридиана определяется углом NOB, который называется путевым углом на течении ПУ. Угол » » , заключенный между линией истинного курса судна ОА и линией пути OB, называется углом сноса течением. При сносе судна вправо от его ДП (течение направлено в левый борт) приписывают знак «+», а при сносе влево — знак «-«. Зависимость между (ПУ ), ИК и :
Угол » » , заключенный между линией истинного курса судна ОА и линией пути OB, называется углом сноса течением. При сносе судна вправо от его ДП (течение направлено в левый борт) приписывают знак «+», а при сносе влево — знак «-«. Зависимость между (ПУ ), ИК и :
• ПУ = ИК + ; ИК = ПУ — ; = ПУ — ИК
• СЧИСЛЕНИЕ ПРИ ПЛАВАНИИ НА ТЕЧЕНИИ. При плавании на постоянном течении на карту наносят линию пути судна, по которой оно фактически перемещается относительно грунта. Над линией пути надписывают КК, поправку компаса и угол сноса со своим знаком. Для вспомогательных расчетов тонкой линией наносят также линию ИК, по которой откладывают расстояния Sл, проходимые судном относительно воды по показаниям лага. Точки, полученные на линии ИК, переносят по направлению течения на линию пути (рис. 37). У счислимых точек на линии пути делают отметку времени и отсчета лага, а у соответствующих точек на линии курса — только отсчета лага. Точки траверза, открытия и скрытия ориентиров наносят на линию пути (рис. 38).
38).
• СЧИСЛЕНИЕ ПРИ СОВМЕСТНОМ УЧЕТЕ ДРЕЙФА И ТЕЧЕНИЯ. Рассмотрим случай, когда судно перемещается относительно грунта под совместным действием судовых машин, ветра и течения. Для ведения счисления на карте прокладывают линию пути судна при дрейфе и течении и надписывают КК, поправку компаса и суммарный угол сноса • с=a+.
• Кроме того, для вспомогательных расчетов на карте прокладывают также линию пути при дрейфе, по которой откладывают плавание судна по лагу Sл. Каждой точке на линии пути при дрейфе соответствует точка на линии действительного перемещения судна. Эти точки связаны между собой вектором течения. Графически задачи, связанные с нахождением на карте линии пути при дрейфе и течении, истинной скорости V и суммарного угла сноса с по заданным КК, Vл, a, и элементам течения, нанесением счислимого места, предвычислением времени и ол на момент прихода в заданную точку, нахождением траверза ориентира, решают так же, как и при плавании на течении, но все вспомогательные построения делают на линии пути при дрейфе, заменяющей линию ИК.
• ОЦЕНКИ ТОЧНОСТИ СЧИСЛЕНИЯ. В результате воздействия неучтенных погрешностей действительный путь судна и пройденное им расстояние (плавание) не будут соответствовать тем, которые учитывались при счислении на карте, а фактическое место судна — счислимому. Для ориентировочного суждения о погрешностях в счислении можно пользоваться следующими данными, которые отражают накопленный обобщённый опыт судовождения и проведенные исследования. Продолжительности плавания (часы) соответствует радиальная средняя квадратическая ошибка счисления, % от S: • До 3 ч — 10%; 3 -6 ч — 9%; 6 -10 ч — 8%; 10 -14 ч — 7%; 14 -18 ч — 6%; 18 -23 ч — 5%; 23 -25 ч — 4%; более 35 ч — 3%. • При прокладке пути судна на карте в том или ином расстоянии от навигационных опасностей необходимо учитывать возможность отклонения судна от линии пути, причем значение отклонения будет возрастать с увеличением пройденного расстояния, в особенности при плавании с дрейфом и течением. Недостаточная точность счисления вызывает необходимость дополнительного контроля за местонахождением судна, т. е. определения его места не только путем счисления, но и по обсервациям: навигационным, астрономическим либо при помощи GPS.
е. определения его места не только путем счисления, но и по обсервациям: навигационным, астрономическим либо при помощи GPS.
СУЩНОСТЬ ГРАФИЧЕСКОГО СЧИСЛЕНИЯ — Студопедия
Поделись
Для обеспечения безопасности плавания судоводитель должен в любой момент знать положение своего судна, чего можно достичь ведением навигационной прокладки. Прокладка включает в себя счисление пути, расчеты и построения на карте для определения места судна и расчеты маневрирования для расхождения с другими судами.
Навигационная прокладка подразделяется на два вида:
— предварительная прокладка выполняется перед выходом в рейс для изучения предстоящего перехода по картам, пособиям и руководствам для плавания:она дает общее представление об условиях перехода.
— исполнительная прокладка выполняется с момента выхода в рейс и вплоть до его окончания. При этом выбор курсов и все принимаемые к учету факторы определяются конкретной обстановкой плавания.
При этом выбор курсов и все принимаемые к учету факторы определяются конкретной обстановкой плавания.
Счислением называется учет движения судна по морской карте. В зависимости от условий плавания этот учет осуществляется двумя методами:
-письменное счисление применяется при океанских плаваниях, когда приходится руководствоваться картами мелкого масштаба. Сущность его состоит в расчете координат судна, который производит судоводитель по формулам с последующим нанесением вычисленного места на карту.
— графическое счисление применяется при плавании вблизи берегов, когда на относительно небольших расстояниях от курса могут располагаться опасные глубины, надводные и подводные препятствия, влияние на судно ветра, создающего дрейф, и течения. В этом случае счисление должно вестись особенно тщательно и непрерывно.
Исходная точка для прокладки пути судна на карте определяется капитаном. Координаты точки начала прокладки записываются в судовой журнал. К моменту начала прокладки следует включить лаг и определить поправку компаса.
К моменту начала прокладки следует включить лаг и определить поправку компаса.
От исходной точки на карте прокладывают линию первого курса. Если плавание совершается вблизи берегов, счислимые точки должны отмечаться каждый час, при плавании в открытом море в конце вахты, в моменты начала и конца поворотов, при изменении скорости, при получении обсерваций. Рядом со счислимым местом в виде дроби записывают момент по судовым часам с точностью до 1 мин и отсчет лага с точностью до 0,1 мили. Для контроля и уточнения счисления место судна в рейсе определяют различными навигационными, радионавигационными и астрономическими методами. Полученные при этом обсервованные точки наносят на карту. При получении обсервованного места дальнейшую прокладку ведут от обсервованной точки, показывая на карте величину и направление отклонения судна от счисления. Кривую линию, соединяющую обсервованную и счислимую точки, называют невязкой.
Графическое счисление без учета дрейфа и течения:
При плавании без дрейфа и течения линия пути судна на карте совпадает с линией ИК, поэтому учет перемещения судна на карте производится по линиям ИК, по которым откладывают расстояния, пройденные судном по лагу с учетом его коэффициента Кл. От исходной точки на карте прокладывают линию первого курса. Снятый с карты ИК переводят в КК (ГКК), на который ложатся по магнитному (гиро) компасу. На карте над линией ИК надписывают курс по компасу и его поправку. Пройденное по курсу расстояние Sопределяют по лагу:
От исходной точки на карте прокладывают линию первого курса. Снятый с карты ИК переводят в КК (ГКК), на который ложатся по магнитному (гиро) компасу. На карте над линией ИК надписывают курс по компасу и его поправку. Пройденное по курсу расстояние Sопределяют по лагу:
S = Кл (ОЛ2 — ОЛ1);
(где ОЛ2 — отсчёт лага в точке нахождения судна, ОЛ1 — отсчёт лага в исходной точке, Кл — коэффициент лага).
На линии ИК в указанных ниже случаях наносят счислимое место судна, т. е. место, рассчитанное по курсу и плаванию. Кроме того, счислимое место наносят в точках начала и конца поворотов, при изменении скорости, при получении обсерваций. Рядом с местом судна в виде дроби записывают момент по судовым часам с точностью до 1 мин (Т) и отсчет лага с точностью до 0,1 мили (ОЛ).
При ведении прокладки возможны два типа задач:
Прямая задача. Известны КК, vл (vоб), исходная точка счисления (φ1, λ1, T1, ОЛ1). Неизвестны ИК, конечная точка счисления (φ2, λ2, T2, ОЛ2).
Известны КК, vл (vоб), исходная точка счисления (φ1, λ1, T1, ОЛ1). Неизвестны ИК, конечная точка счисления (φ2, λ2, T2, ОЛ2).
Решение:
— Рассчитать ИК = КК + ΔК и проложить его линию от начальной точки счисления;
— Рассчитать S = vt (если счислимая точка рассчитывается заблаговременно),
или S = РОЛ kл (если счислимая точка рассчитывается на пройденный момент) и отложить его на линии ИК;
— Снять счислимые координаты φ2, λ2 и определить время прихода в эту точку Т2 = Т1 + S/v, заметить показания лага ОЛ2.
Обратная задача. Известны ИК, vл (vоб), φ1, λ1, T1, ол1.
Неизвестны КК, φ2, λ2, T2, ОЛ2.
Решение:
- Проложить линию ИК от исходной точки счисления;
- Рассчитать КК = ИК — ΔК и задать его рулевому;
- Рассчитать Sл = vл t (если счислимая точка рассчитывается заблаговременно), или S = РОЛ kл (если счислимая точка рассчитывается на пройденный момент) и отложить его на линии ИК;
- Снять φ2, λ2 и определить время прихода в эту точку Т2 = Т1 + S/v, и в этот момент снять показания лага ОЛ2.
Счисление пути судна с учётом ветра, течение
Загрузка…
Заказать написание учебной работы у преподавателя по Судовождению
Имя
1500+ квалифицированных специалистов готовы вам помочь
Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое
ПринимаюПолитику конфиденциальности
Rate this post
Графическое счисление без учета дрейфа и течения:
Прямая задача. Известны КК, vл (vоб), исходная точка счисления (j1, l1, T1, ол1). Неизвестны ИК, конечная точка счисления (j2, l2, T2, ол2).
Известны КК, vл (vоб), исходная точка счисления (j1, l1, T1, ол1). Неизвестны ИК, конечная точка счисления (j2, l2, T2, ол2).
Решение:
- Рассчитать ИК = КК + DК и проложить его линию от начальной точки счисления;
- Рассчитать Sл = vл t или Sоб = vоб t (если счислимая точка рассчитывается заблаговременно), или Sл = рол kл (если счислимая точка рассчитывается на пройденный момент) и отложить его на линии ИК;
- Снять счислимые координаты j2, l2 и определить время прихода в эту точку Т2 = Т1 + S/v, заметить показания лага ол
Обратная задача. Известны ИК, vл (vоб), j1, l1, T1, ол1. Неизвестны КК, j2, l2, T2, ол2.
Решение:
- Проложить линию ИК от исходной точки счисления;
- Рассчитать КК = ИК – DК и задать его рулевому;
- Рассчитать Sл = vл t или Sоб = vоб t (если счислимая точка рассчитывается заблаговременно), или Sл = рол kл (если счислимая точка рассчитывается на пройденный момент) и отложить его на линии ИК;
- Снять j2, l2 и определить время прихода в эту точку Т2 = Т1 + S/v, и в этот момент снять показания лага ол
Ветровой дрейф судна и его учет.
При воздействии на судно ветра фактическое направление движения судна относительно воды происходит по путевому углу ПУa при дрейфе. При ветре в левый борт линия пути судна смещается вправо, в этом случае угол дрейфа a имеет знак плюс, при смещении судна влево (ветер в правый борт) – минус.
Связь между ИК, ПУa и a следующая: ПУ a = ИК ± a л/б ;пр/б
Соединив серию из трёх или четырёх обсерваций, полученных достаточно точными методами, на карте получают линию пути, откуда определяют величину угла a= ПУa – ИК
Учет дрейфа при прокладке.
При наличии угла дрейфа рассчитывается и прокладывается на карте:
ПУa = ГКК + DГК + a
Пройденное по лагу расстояние Sл откладывается по линии пути, так как лаг при a < 100
дрейф учитывает. Если же a >100, то по линии пути откладывается расстояние
Если же a >100, то по линии пути откладывается расстояние
S = Sл sec a
При обратной задаче, когда требуется рассчитать ГКК, направление ПУ снимают с карты, после чего
ГКК = ПУ a – a – DГК
Для нахождения счислимой точки в момент траверза ориентира следует рассчитать ИП = ИК ± 900
и линию пеленга провести до пересечения с линией пути.
Прямая задача. Известны ИК, vл (vоб), направление ветра Км и угол дрейфа a. Неизвестен ПУa.
Решение:
- Рассчитать ПУa = ИК ± aл/бпр/б , проложить линию ПУa от исходной точки счисления;
- Вдоль линии ПУa отложить Sл или Sоб.

Обратная задача. Известны ПУa , vл (vоб), Кu , a. Неизвестен ИК.
Решение:
- Проложить линию ПУa и вдоль неё отложить Sл или Sоб;
- Рассчитать ИК = ПУa m aл/бпр/б , затем ККм.к. (ГКК) и задать последний рулевому.
Счисление при плавании на течении.
Рис. Прямая задача графического счисления пути судна с учётом сноса течением (Обратная задача).
Совместный учёт дрейфа и сноса течением.
Категория : Навигация, Судоводители
- ← ПРОСТОЕ АНАЛИТИЧЕСКОЕ СЧИСЛЕНИЕ
- Счисление пути судна с учётом ветра, течение →
Эй! Моряк, почитай и это:
Реклама
Загрузка. ..
..
Мы в соц. сетях
Читать @SeaspiritRu
Расчетная графика — Дуглас Н. Арнольд
Расчетная графика — Дуглас Н. АрнольдЭто выдержки из коллекции графических демонстраций I разработан для первого года исчисления в середине 1990-х годов. Те, кто интересуется высшей математикой, могут также хочу посетить мою страницу графики для сложных анализ. Эта страница находится в списке самый математические страницы, на которые часто ссылаются, согласно MathSearch.
Просмотр инструкций. Анимации на этой странице используют анимированный формат GIF. Есть
также Java-версия этой страницы. Ява
аниматор позволяет запускать и останавливать анимацию, переходить
кадры вручную и контролировать скорость. Также анимация является
немного плавнее, и кадры качаются (сначала в последний, а затем в обратном направлении). к первому и т. д.), что немного приятнее. К сожалению, версии Java
анимации обычно загружаются гораздо дольше, а Java
Известно, что аниматор приводит к сбою браузеров, особенно на компьютерах без
много памяти. Старая версия этой страницы
использование формата анимации MPEG доступно, но больше не активно
поддерживается, поэтому не рекомендуется.
к первому и т. д.), что немного приятнее. К сожалению, версии Java
анимации обычно загружаются гораздо дольше, а Java
Известно, что аниматор приводит к сбою браузеров, особенно на компьютерах без
много памяти. Старая версия этой страницы
использование формата анимации MPEG доступно, но больше не активно
поддерживается, поэтому не рекомендуется.
Эта анимация
расширяет классическую диаграмму исчисления выше.
диаграмма иллюстрирует локальную точность аппроксимации касательной линии
гладкой кривой, или, иначе говоря, близость дифференциала
функции к разности значений функции за счет малого приращения независимой переменной.
(На диаграмме приращение независимой переменной
показан зеленым цветом, дифференциал, т. е. произведение
производная и приращение — красным цветом, а разность значений функции
как красный сегмент плюс желтый сегмент. Дело в том
что если зеленый сегмент маленький, желтый сегмент очень маленький.) Проблема с диаграммой в том, что когда она
нарисовано достаточно большим, чтобы быть видимым, приращение слишком велико, чтобы сделать
точка. Например, здесь желтый сегмент составляет около 30% зеленого.
сегмент. Эта анимация решает эту проблему, показывая два вида
диаграмма, каждая из которых меняется по мере изменения приращения. В левом представлении
«камера» фиксируется, поэтому диаграмма становится очень маленькой,
в то время как в виде справа «камера» приближается так, что диаграмма
занимает постоянную площадь на экране, и связь между
четко видны длины сегментов. Обратите внимание, как желтый сегмент
становится очень маленьким во втором виде (в то время как зеленый сегмент появляется
иметь постоянную длину из-за масштабирования). Заметьте также, что по мере продвижения
разница между фиолетовой кривой и синей касательной
становится незначительным.
Например, здесь желтый сегмент составляет около 30% зеленого.
сегмент. Эта анимация решает эту проблему, показывая два вида
диаграмма, каждая из которых меняется по мере изменения приращения. В левом представлении
«камера» фиксируется, поэтому диаграмма становится очень маленькой,
в то время как в виде справа «камера» приближается так, что диаграмма
занимает постоянную площадь на экране, и связь между
четко видны длины сегментов. Обратите внимание, как желтый сегмент
становится очень маленьким во втором виде (в то время как зеленый сегмент появляется
иметь постоянную длину из-за масштабирования). Заметьте также, что по мере продвижения
разница между фиолетовой кривой и синей касательной
становится незначительным.
Эти изображения относятся к вычислению объема путем интегрирования
площади поперечного сечения. Первое изображение рассматривает основной принцип.
другие изображения относятся к определенному объему, то есть к клину воды, образованному
когда цилиндрический класс одинаковой высоты и диаметра наклоняется до
линия воды проходит через центр основания. Фотографии
замороженные кадры из AVS, и может передать лишь приблизительное представление о
интерактивная презентация в классе (которая обычно длится около 30
минут).
Фотографии
замороженные кадры из AVS, и может передать лишь приблизительное представление о
интерактивная презентация в классе (которая обычно длится около 30
минут).
- Принцип
- Клин воды, образованный опрокидывание стакана
- Поперечные сечения, перпендикулярные ватерлиния у основания
- Три разных способа нарезать тот же объем
А теперь викторина: подсчитайте процент заполнения стакана воды, используя каждый из трех срезов, изображенных на последнем слайде и убедитесь, что все они приводят к одному и тому же ответу.
В третьем веке до нашей эры Архимед вычислил стоимость с точностью до одной тысячной доли. Его метод основан на вписывании и описании многоугольников в круг, и очень сродни методу нижних и верхних сумм используется для определения интеграла Римана. Его подход представлен в следующую последовательность слайдов.
- Вычисление площади круга
- Вписанный шестигранник
- Триангуляция
- Нижняя граница площади
- Описанный шестиугольник: an верхняя граница площади
- Уточнение границ с помощью додекагоны
- Таблица результатов
Как способ помочь учащимся оценить функции, их приложения,
и их графики, я вовлекаю их в небольшой проект, чтобы описать
функции, определяемые высотой прыгающего мяча. Хотя я начинаю
сбросив настоящий теннисный мяч с высоты одного метра над землей,
количественное представление о функции можно получить с помощью компьютера
анимация, в том числе измерительная линейка и часы. Учащиеся рассматривают
анимацию (в замедленной съемке, с ручной перемоткой кадра и т. д.) и попробуйте
построить график функции. В качестве домашнего задания они
попросили определить функцию алгебраически. это кусочно
квадратичный и помогает учащимся осознать, что кусочно заданное
функции существуют вне учебников по математическому анализу.
Хотя я начинаю
сбросив настоящий теннисный мяч с высоты одного метра над землей,
количественное представление о функции можно получить с помощью компьютера
анимация, в том числе измерительная линейка и часы. Учащиеся рассматривают
анимацию (в замедленной съемке, с ручной перемоткой кадра и т. д.) и попробуйте
построить график функции. В качестве домашнего задания они
попросили определить функцию алгебраически. это кусочно
квадратичный и помогает учащимся осознать, что кусочно заданное
функции существуют вне учебников по математическому анализу.
- Анимация прыгающий мяч
- Анимация мяч с графиком его высоты
- Анимация мяч с графиком его высоты и скорости
- файл Mathematica, используемый для построения анимация
- рабочий лист ученика (файл PostScript)
Это довольно простая анимация, изображающая геометрический
схождение секущих к касательной. Наклон секущей
(которая сходится к производной). я использую различные
вариации этой демонстрации в начале курса исчисления.
- Анимация секущих, приближающихся к касательной
- То же анимация с показанной касательной
- сек. проходящий через точку недифференцируемости
- сек. приближение к вертикальной касательной — еще одна форма недифференцируемости
- Файл Mathematica, используемый для построить анимации.
Эта анимация является версией обычной демонстрации того, что гладкая кривая становится неотличимы от его касательной, если смотреть под достаточно микроскоп с большим увеличением. Студенты могут легко продемонстрировать это сами с помощью графического калькулятора, оснащенного кнопкой масштабирования. В этом анимации, мы обеспечиваем очередь на дополнительное расстояние, показывая сетку и чередование касательной. Вот файл Mathematica, используемый для построить анимации.
Элегантное геометрическое доказательство, доступное начинающий студент, изучающий математику, является доказательством фундаментального тригонометрического лимит
Доказательство основано на диаграмме, изображающей круговой сектор в
единичный круг вместе с вписанным и описанным треугольниками. От того, что сектор имеет площадь, превышающую площадь вписанного
треугольник, но меньший, чем у описанного, приводит к
неравенства
От того, что сектор имеет площадь, превышающую площадь вписанного
треугольник, но меньший, чем у описанного, приводит к
неравенства
Тогда доказательство следует из «теоремы сжатия».
Я обычно трачу около 15 минут на это доказательство, включая много посещение занятий. Диаграмма строится в три этапа: сначала только сектор, то с вписанным треугольником и, наконец, с обоими треугольниками. Вот несколько инструкций по созданию это в классе. Во время презентации я часто прибегаю к рисунку программное обеспечение для проверки различных неравенств. Например это участок, созданный из этого файла MATLAB, убедительно проверяет второй набор неравенств.
Вот несколько простых графиков, которые
полезны при обсуждении пределов. Все первые три функции имеют
предел -5 как x приближается к 1, подчеркивая неуместность значения
функционировать в самой предельной точке. Последняя функция отличается
левое и правое ограничения равны 1, поэтому предела не существует. графики были построены с помощью этого MATLAB
файл.
графики были построены с помощью этого MATLAB
файл.
Краткое графическое исследование непрерывного, нигде дифференцируемая функция очень хорошо вписывается в первый семестр исчисление, например, чтобы дать сильный контрпример к обратная теорема о том, что дифференцируемость влечет непрерывность; или к показать, что только дифференцируемые функции выглядят как прямые линии под микроскопом. Учитывая хорошие графические возможности в классе такое исследование легко, но без них почти безнадежно. Этот график такой функции был производится с помощью нескольких строк кода Matlab по классической конструкции Вейерштрасса. В классе я увеличиваю масштаб этот график несколько раз, чтобы выявить его фрактальную природу. Следовательно, я использовал очень маленькое расстояние между точками. На более медленной машине предпочтительнее используйте меньшее количество точек и уменьшайте расстояние между точками по мере увеличения масштаба.
Студентов часто озадачивает внешний вид числа и ,
который приведен выше (до 35 знаков после запятой). Простое объяснение
его происхождение связано с тем, что e является единственным номером для
касательная к графику y = e x через точку (0,1) имеет наклон ровно 1. Важный результат
что функция е ( х )= д х является собственной производной, легко следует из этого факта и элементарного
законы показателей. Этот
анимация
здесь просто показан график у = a х , но с разными и . Управляя продвижением кадра, вы можете
отрегулируйте a так, чтобы наклон касательной был близок к 1.
второй
анимация похожа на первую, но нарисована на большем
шкале, и по ней можно прочитать первые несколько знаков после запятой и .
Вот файл Mathematica, используемый для
построить анимации.
Простое объяснение
его происхождение связано с тем, что e является единственным номером для
касательная к графику y = e x через точку (0,1) имеет наклон ровно 1. Важный результат
что функция е ( х )= д х является собственной производной, легко следует из этого факта и элементарного
законы показателей. Этот
анимация
здесь просто показан график у = a х , но с разными и . Управляя продвижением кадра, вы можете
отрегулируйте a так, чтобы наклон касательной был близок к 1.
второй
анимация похожа на первую, но нарисована на большем
шкале, и по ней можно прочитать первые несколько знаков после запятой и .
Вот файл Mathematica, используемый для
построить анимации.
Вот демонстрация моей коллега Дэвид Сибли, иллюстрирующий вычисление объема область, образованная двумя пересекающимися цилиндрами.
Этот
работа лицензирована в соответствии с
Лицензия Creative Commons Attribution-Noncommercial-Share Alike 3. 0.
0.
Последнее изменение: 2 июля 1997 г., автор: Дуглас Н. Арнольд
Исчисление I — общие графики
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-10: Общие графики
Цель этого раздела — убедиться, что вы знакомы с графиками многих основных функций, с которыми вы можете столкнуться в классе исчисления.
Пример 1. График \(\displaystyle y = — \frac{2}{5}x + 3\).
Показать решение
Это линия в форме пересечения склона
\[у = мх + б\]
В этом случае линия имеет точку пересечения \(y\) \(\left(0,b\right)\) и наклон \(m\). Напомним, что наклон можно представить как
\[m = \frac{{{\rm{подъем}}}}{{{\rm{run}}}}\]
Обратите внимание, что если наклон отрицательный, мы склонны думать о подъеме как о падении.
Наклон позволяет нам получить вторую точку на линии. Как только у нас есть точка на линии и наклон, мы двигаемся вправо на , пробегаем и вверх/вниз на , поднимаемся на в зависимости от знака. Это будет вторая точка на линии.
Это будет вторая точка на линии.
В этом случае мы знаем, что \(\left(0,3\right)\) — это точка на прямой, а наклон равен \( — \frac{2}{5}\). Итак, начиная с \(\left(0,3\right)\) мы переместим 5 вправо ( т. е. \(0 \to 5\)) и вниз 2 ( т.е. \(3 \to 1\)) чтобы получить \(\left(5,1\right)\) в качестве второй точки на линии . Когда у нас есть две точки на линии, все, что нам нужно сделать, это нанести две точки и соединить их линией.
Вот эскиз этой линии.
Пример 2. График \(f\left( x \right) = \left| x \right|\).
Показать решение
В этой проблеме нет ничего особенного, кроме как напомнить себе, что такое абсолютное значение. Напомним, что функция абсолютного значения определяется как 92} + 2\влево( 1 \вправо) + 3 = 4\конец{выравнивание*}\]
Итак, вершина этой параболы равна \(\left(1,4\right)\).
Мы также можем определить, в каком направлении открывается парабола, по знаку \(a\). Если \(а\) положителен, парабола открывается вверх, а если \(а\) отрицателен, парабола открывается вниз. В нашем случае парабола раскрывается вниз.
Если \(а\) положителен, парабола открывается вверх, а если \(а\) отрицателен, парабола открывается вниз. В нашем случае парабола раскрывается вниз.
Теперь, поскольку вершина находится над осью \(x\) и парабола направлена вниз, мы знаем, что у нас будут пересечения \(x\) ( 92} — 6у + 5\).
Показать решение
Большинство людей выходят из класса алгебры, способного работать с функциями в форме \(y = f(x)\). Однако многие функции, с которыми вам придется иметь дело в классе исчисления, имеют форму \(x = f(y)\), и с ними можно легко работать только в этой форме. Итак, вам нужно привыкнуть работать с функциями в таком виде.
Преимущество таких функций в том, что если вы можете работать с функциями в форме \(y = f(x)\), то вы можете работать и с функциями в форме \(x = f(y)\) даже если вы не так хорошо знакомы с ними. 92} + по + с\]
Это общая форма параболы такого типа, и это будет парабола, открывающаяся влево или вправо в зависимости от знака \(a\). \(y\)-координата вершины задается \(y = — \frac{b}{{2a}}\), и мы находим \(x\)-координату, подставляя ее в уравнение. Итак, вы можете видеть, что это очень похоже на тот тип параболы, с которым вы уже привыкли иметь дело.
\(y\)-координата вершины задается \(y = — \frac{b}{{2a}}\), и мы находим \(x\)-координату, подставляя ее в уравнение. Итак, вы можете видеть, что это очень похоже на тот тип параболы, с которым вы уже привыкли иметь дело.
Теперь вернемся к примеру. Наша функция представляет собой параболу, которая открывается вправо (\(a\) положительна) и имеет вершину в точке \(\left(-4,3\right)\). Вершина находится слева от оси \(y\) и открывается вправо, поэтому нам понадобятся \(y\)-перехваты ( 92}\]
Когда круги имеют такую форму, мы можем легко определить центр \(\left(h, k\right)\) и радиус \(r\). Получив их, мы можем построить круг, просто начав с центра и двигаясь вправо, влево, вверх и вниз с помощью \(r\), чтобы получить крайнюю правую, крайнюю левую, самую верхнюю и самую нижнюю точки соответственно.
Наш круг имеет центр в точке \(\left(-1, 4\right)\) и радиус 3. Вот набросок этого круга.
Пример 6 График \(\displaystyle \frac{{{{\left( {x — 2} \right)}^2}}}{92}}} = 1\]
Это эллипс с центром \(\left(h, k\right)\) и крайняя правая и крайняя левая точки находятся на расстоянии \(a\) от центра, а самая верхняя и самая нижняя точки находятся на расстоянии \(b\) от центра. {2}}}{92}}} = 1\)
{2}}}{92}}} = 1\)
Итак, что все это значит? Во-первых, обратите внимание, что один из членов положительный, а другой отрицательный. Это определит, в каком направлении открываются две части гиперболы. Если член \(x\) положителен, гипербола открывается влево и вправо. Точно так же, если член \(y\) положителен, парабола раскрывается вверх и вниз.
Это определит, в каком направлении открываются две части гиперболы. Если член \(x\) положителен, гипербола открывается влево и вправо. Точно так же, если член \(y\) положителен, парабола раскрывается вверх и вниз.
Оба имеют одинаковый «центр». Обратите внимание, что гиперболы на самом деле не имеют центра в том смысле, что у кругов и эллипсов есть центры. Центр является отправной точкой при построении графика гиперболы. Он говорит нам, как добраться до вершин и как настроить асимптоты.
Асимптоты гиперболы — это две линии, пересекающиеся в центре и имеющие указанные выше наклоны. По мере удаления от центра график будет все ближе и ближе к асимптотам.
9{ — Икс}}\).Показать решение
На самом деле в этой задаче нет ничего особенного, кроме как убедиться, что обе эти экспоненты где-то изображены на графике.
Они оба будут появляться с некоторой регулярностью в последующих разделах, и потребуется их поведение, когда \(x\) достигает плюс и минус бесконечности, и на этом графике мы можем ясно увидеть это поведение. 3}\).
3}\).
Показать решение
Опять же, в этом нет ничего особенного, кроме как убедиться, что это было где-то нарисовано, чтобы мы могли сказать, что сделали это.
Пример 12. График \(y = \cos\left( x \right)\).
Показать решение
В этом нет ничего особенного. Вот график для \( — 4\pi \le x \le 4\pi \).
Здесь также отметим, что мы можем положить все значения \(x\) в косинус (что не будет иметь место для большинства триггерных функций), так что доменом будут все действительные числа. Также обратите внимание, что
\[ — 1 \le \cos \left( x \right) \le 1\]
Важно отметить, что косинус никогда не будет больше 1 или меньше -1. Иногда это будет полезно на уроках математического анализа. В целом можно сказать, что
\[ — R \le R\cos \left( {\omega \,x} \right) \le R\]
Пример 13. График \(y = \sin\left( x \right)\).
График \(y = \sin\left( x \right)\).
Показать решение
Как и в случае с предыдущей задачей, здесь практически нечего делать, кроме как изобразить ее. Вот график для \( — 4\pi \le x \le 4\pi \).
Из этого графика видно, что синус имеет тот же диапазон, что и косинус. В целом
\[ — R \le R\sin \left( {\omega \,x} \right) \le R\]
Как и косинус, сам синус никогда не будет больше 1 и никогда не будет меньше -1. Также областью определения синуса являются все действительные числа.
Пример 14. График \(y = \tan \left( x \right)\).
Показать решение
В случае тангенса мы должны быть осторожны при подстановке \(x\), так как тангенс не существует везде, где косинус равен нулю (помните, что \(\tan x = \frac{{\sin x}} {{\cos х}}\)). Тангенс не будет существовать на
Тангенс не будет существовать на
\[x = \cdots , — \frac{{5\pi}}{2}, — \frac{{3\pi}}{2}, — \frac{\pi }{2},\frac{\ pi }{2},\frac{{3\pi }}{2},\frac{{5\pi }}{2}, \ldots \]
и график будет иметь асимптоты в этих точках. Вот график касательной на диапазоне \( — \frac{{5\pi }}{2} < x < \frac{{5\pi }}{2}\).
Пример 15. График \(y = \sec \left( x \right)\).
Показать решение
Как и в случае с тангенсом, нам придется избегать \(x\), для которых косинус равен нулю (помните, что \(\sec x = \frac{1}{{\cos x}}\)). Секант не будет существовать по адресу
\[x = \cdots , — \frac{{5\pi}}{2}, — \frac{{3\pi}}{2}, — \frac{\pi }{2},\frac{\ pi }{2},\frac{{3\pi }}{2},\frac{{5\pi }}{2}, \ldots \]
9{1}/{}_{\pm 1}=\pm 1\), поэтому мы получаем следующие диапазоны для секущей.
\[\ sec \left( {\omega \,x} \right) \ge 1\hspace{0.5in}{\rm{and}}\hspace{0.5in}\sec \left({\omega \,x } \справа) \le — 1\]
Обратите внимание, что здесь мы не отображали котангенс и косеканс. Тем не менее, они похожи на графики тангенса и секущей, и вы должны быть в состоянии сделать их быстрые наброски, учитывая вышеописанную работу, если это необходимо.
Наконец, обратите внимание, что мы не рассмотрели здесь ни одного из основных преобразований, которые часто используются при графическом отображении функций. В практических задачах этого раздела довольно много задач, разработанных для того, чтобы помочь вам их запомнить. Если вы знаете основные преобразования, это часто значительно упрощает процесс построения графиков, поэтому, если вы не чувствуете себя комфортно с ними, вам следует поработать над практическими задачами для этого раздела.
анализ | математика | Британика
анализ
Посмотреть все СМИ
- Ключевые люди:
- Анри Пуанкаре Бернхард Риманн Леонард Эйлер Норберт Винер Жозеф Фурье
- Связанные темы:
- векторный анализ тензорный анализ гармонический анализ вариационное исчисление теорема о среднем значении
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
анализ , раздел математики, изучающий непрерывные изменения и некоторые общие типы процессов, возникшие в результате изучения непрерывных изменений, таких как пределы, дифференциация и интеграция. С момента открытия дифференциального и интегрального исчисления Исааком Ньютоном и Готфридом Вильгельмом Лейбницем в конце 17 века анализ превратился в огромную и центральную область математических исследований с приложениями во всех науках и в таких областях, как финансы, экономика. и социология.
С момента открытия дифференциального и интегрального исчисления Исааком Ньютоном и Готфридом Вильгельмом Лейбницем в конце 17 века анализ превратился в огромную и центральную область математических исследований с приложениями во всех науках и в таких областях, как финансы, экономика. и социология.
Исторические истоки анализа можно найти в попытках вычислить пространственные величины, такие как длина кривой линии или площадь, ограниченная кривой. Эти проблемы можно сформулировать чисто как вопросы математической техники, но они имеют гораздо большее значение, поскольку в физическом мире имеют большое разнообразие интерпретаций. Площадь внутри кривой, например, представляет непосредственный интерес для измерения земли: сколько акров содержит участок земли неправильной формы? Но та же техника определяет и массу однородного листа материала, ограниченного какой-либо выбранной кривой, или количество краски, необходимое для покрытия поверхности неправильной формы. Менее очевидно, что эти методы можно использовать для определения общего расстояния, пройденного транспортным средством, движущимся с различной скоростью, глубины, на которой будет плавать корабль, когда он находится в море, или общего расхода топлива ракеты.
Точно так же математический метод нахождения касательной к кривой в заданной точке можно также использовать для расчета крутизны изогнутого холма или угла, на который должна повернуться движущаяся лодка, чтобы избежать столкновения. Менее непосредственно это связано с чрезвычайно важным вопросом расчета мгновенной скорости или других мгновенных скоростей изменения, таких как охлаждение теплого объекта в холодной комнате или распространение болезнетворного организма среди людей.
Эта статья начинается с краткого введения в историю анализа и основных понятий, таких как системы счисления, функции, непрерывность, бесконечные ряды и пределы, которые необходимы для понимания анализа. За этим введением следует полный технический обзор, от исчисления до нестандартного анализа, а затем статья завершается полной историей.
Britannica Quiz
Числа и математика
A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.
Историческая справка
Преодоление разрыва между арифметикой и геометрией
Математика делит явления на два широких класса, дискретные и непрерывные, исторически соответствующие разделению между арифметикой и геометрией. Дискретные системы могут быть подразделены только до определенного предела, и их можно описать целыми числами 0, 1, 2, 3, …. Непрерывные системы можно подразделять бесконечно, и для их описания требуются действительные числа, числа, представленные десятичными расширениями, такими как 3,14159.…, возможно, это будет продолжаться вечно. Понимание истинной природы таких бесконечных десятичных дробей лежит в основе анализа.
Различие между дискретной математикой и непрерывной математикой является центральной проблемой математического моделирования, искусства представления свойств природного мира в математической форме. Вселенная не содержит реальных математических объектов и не состоит из них, но многие аспекты вселенной очень похожи на математические понятия. Например, число два не существует как физический объект, но оно описывает важную особенность таких вещей, как человеческие близнецы и двойные звезды. Точно так же действительные числа обеспечивают удовлетворительные модели для различных явлений, хотя никакая физическая величина не может быть точно измерена с точностью более дюжины или около того знаков после запятой. К реальному миру применимы не значения бесконечного числа десятичных разрядов, а дедуктивные структуры, которые они воплощают и обеспечивают.
Например, число два не существует как физический объект, но оно описывает важную особенность таких вещей, как человеческие близнецы и двойные звезды. Точно так же действительные числа обеспечивают удовлетворительные модели для различных явлений, хотя никакая физическая величина не может быть точно измерена с точностью более дюжины или около того знаков после запятой. К реальному миру применимы не значения бесконечного числа десятичных разрядов, а дедуктивные структуры, которые они воплощают и обеспечивают.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Анализ возник потому, что многие аспекты мира природы можно выгодно рассматривать как непрерывные — по крайней мере, с превосходной степенью приближения. Опять же, это вопрос моделирования, а не реальности. Материя на самом деле не непрерывна; если материю разделить на достаточно мелкие кусочки, то появятся неделимые составляющие, или атомы. Но атомы чрезвычайно малы, и для большинства приложений рассмотрение материи как континуума вносит незначительную ошибку и значительно упрощает вычисления. Например, моделирование континуума является стандартной инженерной практикой при изучении течения жидкостей, таких как воздух или вода, изгиба эластичных материалов, распределения или потока электрического тока и потока тепла.
Например, моделирование континуума является стандартной инженерной практикой при изучении течения жидкостей, таких как воздух или вода, изгиба эластичных материалов, распределения или потока электрического тока и потока тепла.
Открытие исчисления и поиск основ
Два основных шага привели к созданию анализа. Первым было открытие удивительной связи, известной как фундаментальная теорема исчисления, между пространственными задачами, включающими вычисление некоторого общего размера или значения, такого как длина, площадь или объем (интеграция), и задачами, связанными со скоростью изменения. такие как наклоны касательных и скорости (дифференциация). Заслуга независимого открытия около 1670 года фундаментальной теоремы исчисления вместе с изобретением методов применения этой теоремы принадлежит Готфриду Вильгельму Лейбницу и Исааку Ньютону.
В то время как полезность исчисления для объяснения физических явлений была очевидна сразу, использование им бесконечности в вычислениях (через разложение кривых, геометрических тел и физических движений на бесконечное множество мелких частей) вызвало широкое беспокойство. В частности, англиканский епископ Джордж Беркли опубликовал известную брошюру «Аналитик»; или «Рассуждение, адресованное неверующему математику» (1734), указывающее на то, что исчисление — по крайней мере, в том виде, в каком оно представлено Ньютоном и Лейбницем — имеет серьезные логические недостатки. Анализ вырос в результате кропотливого тщательного изучения ранее слабо определенных понятий, таких как функция и предел.
В частности, англиканский епископ Джордж Беркли опубликовал известную брошюру «Аналитик»; или «Рассуждение, адресованное неверующему математику» (1734), указывающее на то, что исчисление — по крайней мере, в том виде, в каком оно представлено Ньютоном и Лейбницем — имеет серьезные логические недостатки. Анализ вырос в результате кропотливого тщательного изучения ранее слабо определенных понятий, таких как функция и предел.
Подход Ньютона и Лейбница к исчислению был в основном геометрическим и включал отношения с «почти нулевыми» делителями — ньютоновские «флюксии» и «бесконечно малые» Лейбница. В течение 18 века исчисление становилось все более алгебраическим, поскольку математики, в первую очередь швейцарец Леонард Эйлер и итальянец, француз Жозеф-Луи Лагранж, начали обобщать понятия непрерывности и пределов от геометрических кривых и тел до более абстрактных алгебраических функций и начали расширять эти идеи комплексным числам. Хотя эти разработки не были полностью удовлетворительными с фундаментальной точки зрения, они имели фундаментальное значение для окончательного уточнения строгой основы исчисления французом Огюстеном-Луи Коши, богемцем Бернхардом Больцано и, прежде всего, немцем Карлом Вейерштрассом в XIX веке. век.
век.
Математика для компьютерной графики
Математика для компьютерной графикиГрег Терк, август 1997 г.
«Какую математику мне нужно выучить, чтобы изучать компьютерную графику?» Это пожалуй, самый распространенный общий вопрос, который студенты задают мне о компьютере графика. Ответ зависит от того, насколько глубоко вы хотите войти в поле. Если вы хотите начать использовать готовые графические программы, то ответ заключается в том, что вам, вероятно, вообще не нужно знать очень много математики. Если вы хотите чтобы пройти вводный курс по компьютерной графике, то вам следует прочитать первые два раздела ниже для моих рекомендаций (алгебра, тригонометрия и линейная алгебра). Если вы хотите когда-нибудь стать исследователем в области графики то я считаю, что вы должны рассматривать свое математическое образование как непрерывный процесс на протяжении всей вашей карьеры.
Если вас не особо волнует математика, есть ли еще шанс
работаешь в поле? Да, некоторые области компьютерной графики не
много занимался математическими идеями. Не стоит отказываться от графики
только потому, что ты не волшебник математики. Однако вполне вероятно, что вы
иметь больше свободы в выборе тем исследований, если у вас есть желание
узнавать о новых математических идеях.
Не стоит отказываться от графики
только потому, что ты не волшебник математики. Однако вполне вероятно, что вы
иметь больше свободы в выборе тем исследований, если у вас есть желание
узнавать о новых математических идеях.
Нет абсолютного ответа на вопрос, какая математика важна в компьютере. графика. Различные области внутри поля требуют различных математических методы, и ваши собственные интересы, вероятно, приведут вас к некоторым темам и никогда не может касаться других. Ниже приведены описания ряда областей в математики, которые я считаю полезными в компьютерной графике. Не чувствовать что вам нужно быть экспертом в каждой из этих областей, чтобы стать графическим Исследователь! Я намеренно включил многие области ниже, чтобы дать довольно широкое представление о математических идеях, используемых в графике. Однако многие исследователи, никогда не сочту нужным взглянуть на некоторые из тем, которые я упоминаю ниже.
Наконец, хотя из прочтения этого должно быть ясно, высказанные мнения
в этом документе полностью принадлежат мне. Вполне вероятно, что вы получите
другой список тем или, по крайней мере, разные акценты от других людей
кто занимается компьютерной графикой. Теперь к списку тем.
Вполне вероятно, что вы получите
другой список тем или, по крайней мере, разные акценты от других людей
кто занимается компьютерной графикой. Теперь к списку тем.
Алгебра и тригонометрия
Алгебра и тригонометрия уровня средней школы, вероятно, являются наиболее важными области, которые нужно знать, чтобы начать изучать компьютерную графику. Просто примерно каждый день мне нужно определить одно или несколько неизвестных из простого набора уравнений. Почти так же часто мне нужно выполнить простую тригонометрию, такую как нахождение длины ребра одной геометрической фигуры по другим длины и углы. Алгебра и тригонометрия – предметы, которые решать такие повседневные задачи в компьютерной графике. А как насчет геометрии, которую мы изучаем в средней школе? Это может прийти как
сюрприз, но наша школьная геометрия не очень часто нужна большинству
задачи по компьютерной графике. Причина этого в том, что геометрия как таковая
преподаваемый во многих школах, на самом деле является курсом построения математических
доказательства. Хотя построение доказательства, безусловно, является ценным интеллектуальным
инструмент, фактические теоремы и доказательства из вашего класса геометрии не часто
используется в компьютерной графике. Если вы идете в аспирантуру по математике
смежной области (включая компьютерную графику), то вы вполне можете оказаться
доказывая теоремы, но это не обязательно для того, чтобы начать в
графика.
Хотя построение доказательства, безусловно, является ценным интеллектуальным
инструмент, фактические теоремы и доказательства из вашего класса геометрии не часто
используется в компьютерной графике. Если вы идете в аспирантуру по математике
смежной области (включая компьютерную графику), то вы вполне можете оказаться
доказывая теоремы, но это не обязательно для того, чтобы начать в
графика.
Если вы хорошо разбираетесь в алгебре и тригонометрии, то вы вполне готов приступить к чтению вводной книги по компьютерной графике. Большинство таких книг содержат, по крайней мере, сокращенное введение в следующую важная область математики для компьютерной графики, а именно линейная алгебра.
Рекомендация книги:
- Компьютерная графика: принципы и практика
- Джеймс Фоули, Андрис ван Дам, Стивен Файнер, Джон Хьюз
- Эддисон-Уэсли
- [огромная книга, но все равно моя любимая]
- Джеймс Фоули, Андрис ван Дам, Стивен Файнер, Джон Хьюз
Линейная алгебра
Идеи линейной алгебры используются во всей компьютерной графике. Фактически,
любая область, занимающаяся числовым представлением геометрии
часто собирает числа, такие как позиции x, y, z, в
математические объекты, называемые векторами. Векторы и связанные с ними математические
объект, называемый матрицей, постоянно используется в графике. Язык
векторов и матриц — это элегантный способ описать (среди прочего)
способ, которым объект может быть повернут, сдвинут (перемещен) или увеличен
или меньше (в масштабе). Линейная алгебра обычно предлагается либо в
продвинутый класс средней школы или в колледже. Всем, кто хочет работать в
компьютерная графика должна в конечном итоге получить прочную основу в этом предмете.
Однако, как я упоминал ранее, многие учебники по графике дают
введение в эту тему — достаточно часто, чтобы пройти первый курс
в графике.
Фактически,
любая область, занимающаяся числовым представлением геометрии
часто собирает числа, такие как позиции x, y, z, в
математические объекты, называемые векторами. Векторы и связанные с ними математические
объект, называемый матрицей, постоянно используется в графике. Язык
векторов и матриц — это элегантный способ описать (среди прочего)
способ, которым объект может быть повернут, сдвинут (перемещен) или увеличен
или меньше (в масштабе). Линейная алгебра обычно предлагается либо в
продвинутый класс средней школы или в колледже. Всем, кто хочет работать в
компьютерная графика должна в конечном итоге получить прочную основу в этом предмете.
Однако, как я упоминал ранее, многие учебники по графике дают
введение в эту тему — достаточно часто, чтобы пройти первый курс
в графике.Рекомендация книги:
- Линейная алгебра и ее приложения
- Гилберт Странг
- Академическая пресса
- Гилберт Странг
Исчисление
Знание исчисления является важной частью продвинутой компьютерной графики. Если вы планируете заниматься графикой, я настоятельно рекомендую получить базовый
заземление в исчислении. Это верно не только потому, что это сборник
инструментов, которые часто используются в этой области, но также и потому, что многие исследователи
описывать свои проблемы и решения на языке исчисления. В
Кроме того, ряд важных математических областей требует исчисления в качестве основы.
обязательное условие. Это единственная область математики в дополнение к базовой
алгебра, которая может открыть вам больше всего дверей в компьютерной графике с точки зрения
вашего будущего математического понимания.
Если вы планируете заниматься графикой, я настоятельно рекомендую получить базовый
заземление в исчислении. Это верно не только потому, что это сборник
инструментов, которые часто используются в этой области, но также и потому, что многие исследователи
описывать свои проблемы и решения на языке исчисления. В
Кроме того, ряд важных математических областей требует исчисления в качестве основы.
обязательное условие. Это единственная область математики в дополнение к базовой
алгебра, которая может открыть вам больше всего дверей в компьютерной графике с точки зрения
вашего будущего математического понимания.Исчисление — последняя из тем, которые я буду часто упоминать. вводится в старшей школе. Темы, за которыми следует следить, почти всегда можно найти в курсы колледжа.
Дифференциальная геометрия
Эта область математики изучает уравнения, управляющие геометрией плавные изгибы и поверхности. Если вы пытаетесь выяснить, в каком направлении перпендикулярно (указывает прямо от) гладкой поверхности (т. «нормальный вектор»), то вы используете дифференциальную геометрию. Изготовление автомобиля
движение с определенной скоростью по криволинейному пути также является дифференциальным
геометрия. В графике существует общепринятая техника создания плавных переходов.
поверхность выглядит шероховатой, известной как «рельефное отображение», и этот метод основан на
дифференциальная геометрия. Если вы планируете работать с кривыми и поверхностями для
создание формы (называемое «моделированием» в области графики), то вы должны
изучите хотя бы основы дифференциальной геометрии. Многомерное исчисление
является обязательным условием для этой области.
«нормальный вектор»), то вы используете дифференциальную геометрию. Изготовление автомобиля
движение с определенной скоростью по криволинейному пути также является дифференциальным
геометрия. В графике существует общепринятая техника создания плавных переходов.
поверхность выглядит шероховатой, известной как «рельефное отображение», и этот метод основан на
дифференциальная геометрия. Если вы планируете работать с кривыми и поверхностями для
создание формы (называемое «моделированием» в области графики), то вы должны
изучите хотя бы основы дифференциальной геометрии. Многомерное исчисление
является обязательным условием для этой области.Рекомендация книги:
- Элементарная дифференциальная геометрия
- Барретт О’Нил
- Академическая пресса
- Барретт О’Нил
Численные методы
Почти каждый раз, когда мы представляем и манипулируем числами на компьютере, который мы используем приблизительные, а не точные значения, и поэтому всегда вероятность появления ошибок. Кроме того, часто бывает много
различные подходы к решению данной численной задачи, а также некоторые методы
будет быстрее, точнее или потребует меньше памяти, чем другие. Изучение
из этих проблем имеет ряд названий, включая «численные методы» и
«научные вычисления». Это очень обширная область, и несколько других
области математики, которые я упомяну, можно считать подобластями
под этим зонтом. Эти подобласти включают теорию выборки, матричную
уравнения, численное решение дифференциальных уравнений и оптимизация.
Кроме того, часто бывает много
различные подходы к решению данной численной задачи, а также некоторые методы
будет быстрее, точнее или потребует меньше памяти, чем другие. Изучение
из этих проблем имеет ряд названий, включая «численные методы» и
«научные вычисления». Это очень обширная область, и несколько других
области математики, которые я упомяну, можно считать подобластями
под этим зонтом. Эти подобласти включают теорию выборки, матричную
уравнения, численное решение дифференциальных уравнений и оптимизация.Рекомендация книги:
- Численные рецепты на C: искусство научных вычислений
- Уильям Пресс, Сол Теукольски, Уильям Феттерлинг и Брайан Флэннери
- Издательство Кембриджского университета
- [это очень ценный справочник, но обычно он не используется в качестве учебника]
- Уильям Пресс, Сол Теукольски, Уильям Феттерлинг и Брайан Флэннери
Теория дискретизации и обработка сигналов
Снова и снова в компьютерной графике мы представляем некоторый объект, например изображение. или поверхность как набор чисел, хранящихся в регулярном двумерный массив. Всякий раз, когда мы делаем это, мы создаем «выборку».
представление объекта. Хорошее понимание теории выборки
важно, если мы хотим использовать и контролировать качество таких
представления. Распространенная проблема сэмплирования применительно к графике:
зубчатые края, которые могут появиться на силуэте объекта, когда он
рисуется на экране компьютера. Появление таких зубчатых краев (одна форма
явления, известного как «алиасинг»), очень отвлекает, и это может быть
можно свести к минимуму с помощью хорошо изученных методов теории выборки. В
В основе теории выборки лежат такие понятия, как свертка, Фурье
преобразование, пространственное и частотное представление функций. Эти
идеи также важны в области обработки изображений и звука.
Всякий раз, когда мы делаем это, мы создаем «выборку».
представление объекта. Хорошее понимание теории выборки
важно, если мы хотим использовать и контролировать качество таких
представления. Распространенная проблема сэмплирования применительно к графике:
зубчатые края, которые могут появиться на силуэте объекта, когда он
рисуется на экране компьютера. Появление таких зубчатых краев (одна форма
явления, известного как «алиасинг»), очень отвлекает, и это может быть
можно свести к минимуму с помощью хорошо изученных методов теории выборки. В
В основе теории выборки лежат такие понятия, как свертка, Фурье
преобразование, пространственное и частотное представление функций. Эти
идеи также важны в области обработки изображений и звука.Рекомендация книги:
- Преобразование Фурье и его приложения
- Рональд Н. Брейсуэлл
- Макгроу Хилл
- Рональд Н. Брейсуэлл
Матричные уравнения
В компьютерной графике возникает множество разнообразных задач. которые требуют численного решения матричных уравнений. Некоторые проблемы
которые нуждаются в матричных методах, включают в себя: поиск наилучшего положения и
ориентация для сопоставления одного объекта с другим (один пример «наименее
квадратов»), создавая поверхность, которая драпирует заданный набор
точки с минимальными заломами (тонкопластинчатые сплайны) и имитация
материалов, таких как вода или ткань. Возникают матричные формулировки задач
достаточно часто в графике, поэтому я ставлю эту область очень высоко в свой список
темы, которые нужно знать.
Некоторые проблемы
которые нуждаются в матричных методах, включают в себя: поиск наилучшего положения и
ориентация для сопоставления одного объекта с другим (один пример «наименее
квадратов»), создавая поверхность, которая драпирует заданный набор
точки с минимальными заломами (тонкопластинчатые сплайны) и имитация
материалов, таких как вода или ткань. Возникают матричные формулировки задач
достаточно часто в графике, поэтому я ставлю эту область очень высоко в свой список
темы, которые нужно знать.Рекомендация книги:
- Матричные вычисления
- Джин Голуб и Чарльз Ван Лоан
- Издательство Университета Джона Хопкинса
- Джин Голуб и Чарльз Ван Лоан
Физика
Физика, очевидно, является самостоятельной областью изучения, а не подкатегория математики. Тем не менее, физика и математика тесно связаны друг с другом в нескольких областях компьютерной графики. Примеры графических задач, связанных с физикой, включают в себя то, как свет взаимодействует с поверхностями объектов, как свет отражается в сложная окружающая среда, то, как люди и животные передвигаются, и движение вода и ветер. Знание физики важно для моделирования всех
эти явления. Это тесно связано с решением дифференциальных уравнений,
которые я буду обсуждать далее.
Знание физики важно для моделирования всех
эти явления. Это тесно связано с решением дифференциальных уравнений,
которые я буду обсуждать далее.Численные решения дифференциальных уравнений
Я считаю, что методы решения дифференциальных уравнений крайне важно для компьютерной графики. Как мы только что обсудили, большая часть компьютерная графика посвящена моделированию физических систем из реальных Мир. Как образуются волны в воде и как животное ходит по земле два примера физического моделирования. Моделирование физических систем очень часто приводит к численным решениям дифференциальных уравнений. Примечание что на самом деле это сильно отличается от символических решений дифференциальных уравнения. Символические решения являются точными ответами и обычно могут быть найдены только для очень простых систем уравнений. Иногда курс колледжа под названием «Дифференциальные уравнения» будут исследовать только символические решения, и это не поможет для большинства проблем с компьютерной графикой.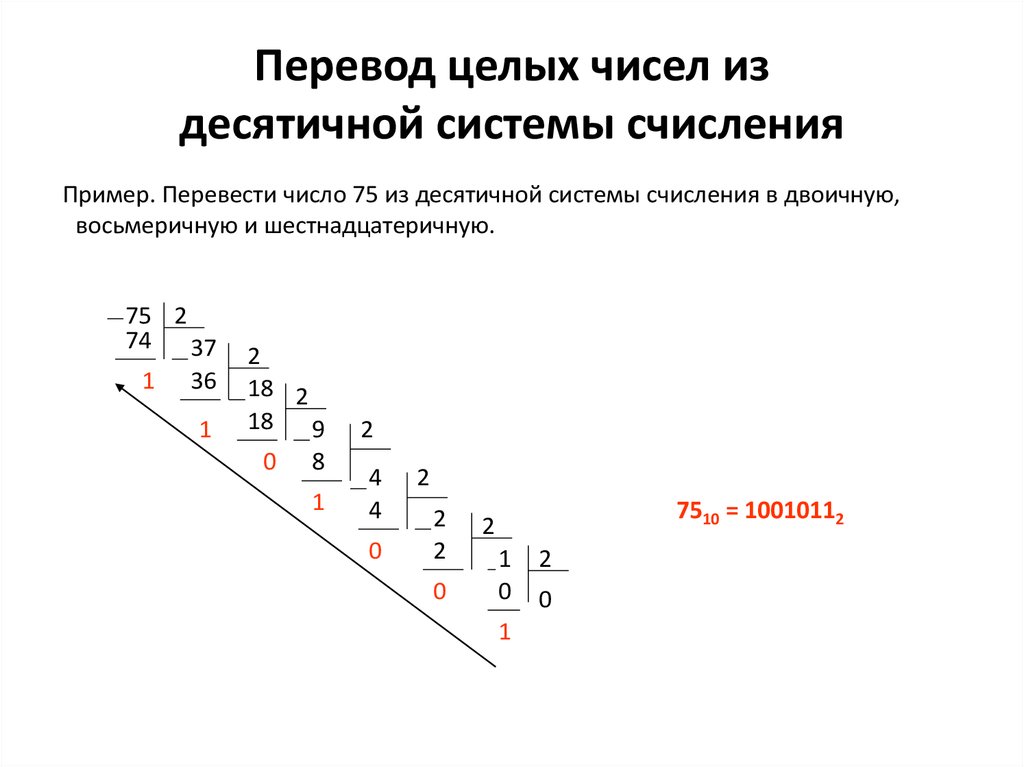
В физическом моделировании мир разбивается на маленькие кусочки, которые представлены в виде больших векторов. Тогда отношения между частями мир запечатлен в записях в матрицах. Решение матрицы уравнения, которые возникают, обычно не выполняется точно, а вместо этого выполняется проведя длинную серию вычислений, которая дает приблизительную решение в виде списка чисел. Это и есть численные решения дифференциальные уравнения о. Заметим, что решение матрицы уравнений является неотъемлемой частью численных решений дифференциальных уравнения.
Оптимизация
Довольно часто в компьютерной графике мы ищем описание объект или совокупность объектов, которые удовлетворяют некоторой желаемой цели. Примеры включают в себя поиск положений огней, которые дают определенное «чувствовать» то, как освещена комната, выясняя, как анимированный персонаж может двигать конечностями для выполнения определенного действия, а также позиционировать формы и текст на странице, чтобы результат не выглядел загроможденным. Каждый из них
примеры можно сформулировать как задачу оптимизации. Десять лет назад был
мало в графической литературе, которая использовала методы оптимизации,
но в последнее время в этой области все больше и больше используется оптимизация. Я думаю
что оптимизация будет продолжать играть все более важную роль в
компьютерная графика.
Каждый из них
примеры можно сформулировать как задачу оптимизации. Десять лет назад был
мало в графической литературе, которая использовала методы оптимизации,
но в последнее время в этой области все больше и больше используется оптимизация. Я думаю
что оптимизация будет продолжать играть все более важную роль в
компьютерная графика.Вероятность и статистика
В компьютерной графике существует ряд областей, в которых используются вероятность и/или статистика. Конечно, когда исследователи проводят исследования используя человека, им требуются статистические методы для выполнения анализ данных. Области, связанные с графикой, которые часто используют человеческие субъекты включают виртуальную реальность и взаимодействие человека с компьютером (HCI). Кроме того, многие компьютерные описания реального мира включают использование различные вероятности того, что данное действие произойдет. Вероятность того, что ветка дерева будет ветвиться во время роста или что синтетическое животное решит идти в определенном направлении — два примера этого. Наконец, некоторые
Методы решения сложных уравнений используют случайные числа для
оценить их решения. Важным примером этого является класс
методы, известные как методы Монте-Карло, которые часто используются для определения того, как
свет распространяется в окружающей среде. Это лишь некоторые из способов, которыми
Вероятность и статистика используются в компьютерной графике.
Наконец, некоторые
Методы решения сложных уравнений используют случайные числа для
оценить их решения. Важным примером этого является класс
методы, известные как методы Монте-Карло, которые часто используются для определения того, как
свет распространяется в окружающей среде. Это лишь некоторые из способов, которыми
Вероятность и статистика используются в компьютерной графике.Вычислительная геометрия
Вычислительная геометрия — это изучение эффективных способов представления и манипулировать геометрией в компьютере. Типичные проблемы включают тестирование сталкиваются ли два объекта, решая, как разбить многоугольник на треугольники и поиск ближайшей точки в группе к заданному местоположению. Эта область представляет собой смесь алгоритмов, структур данных и математики. Исследователи графики, работающие над созданием фигур (моделированием), много рисуют. на этой территории.Рекомендации по книгам:
- Вычислительная геометрия на C
- Джозеф О’Рурк
- Издательство Кембриджского университета
- [текст для студентов]
- Вычислительная геометрия: введение
- Франко Препарата и Майкл Шамос
- Спрингер-Верлаг
- [классический текст, несколько устаревший]
- Джозеф О’Рурк
Заключительные слова: Прикладная и чистая математика
Одна общая нить ко многим математическим темам, которые связаны с графики в том, что они с прикладной стороны, а не с теоретической сторону математики. Это не должно вызывать удивления. Многие из
проблемы компьютерной графики тесно связаны с задачами, которые решают физики.
и инженеры изучали, и математические инструменты физика и
инженера в подавляющем большинстве случаев являются инструментами, которые используют исследователи графики.
Большинство тем, из которых состоит теоретическая («чистая») математика, редко
использовать в компьютерной графике. Это не следует воспринимать как абсолютную
правда однако. Следует обратить внимание на примеры из других областей:
молекулярная биология теперь опирается на теорию узлов для изучения ДНК.
динамика и субатомная физика используют абстрактную теорию групп. Кто может
сказать, когда тема «чистой» математики будет использована в компьютере
графика?
Это не должно вызывать удивления. Многие из
проблемы компьютерной графики тесно связаны с задачами, которые решают физики.
и инженеры изучали, и математические инструменты физика и
инженера в подавляющем большинстве случаев являются инструментами, которые используют исследователи графики.
Большинство тем, из которых состоит теоретическая («чистая») математика, редко
использовать в компьютерной графике. Это не следует воспринимать как абсолютную
правда однако. Следует обратить внимание на примеры из других областей:
молекулярная биология теперь опирается на теорию узлов для изучения ДНК.
динамика и субатомная физика используют абстрактную теорию групп. Кто может
сказать, когда тема «чистой» математики будет использована в компьютере
графика? Есть несколько областей математики, которые, как кажется, должны быть
важны, но никогда не играют большой роли в компьютерной графике.
Пожалуй, наиболее интересной из этих областей является топология. Обычно
описание топологии одним предложением — это изучение того, почему пончик и
кофейная чашка такая же. Ответ состоит в том, что они обе поверхности с одной
отверстие. Здесь мы говорим об идеях из топологии. Разве поверхности не большие
часть компьютерной графики? Да, но оказывается, что большинство идей в
топологию, полезную для графики, можно изучить на первом курсе в
дифференциальная геометрия. Дифференциальная геометрия изучает *формы*
поверхности, в то время как топология изучает такие вещи, как то, какие части поверхности
находятся рядом с другими частями. Я видел очень мало топологии, которая ставится
для использования в графике, и я считаю, что это связано с тем, что большая часть топологии
связаны с довольно абстрактными множествами, и что большая часть топологии далека от
из понятий трехмерного евклидова пространства, которое так важно для
большая часть графики. Бывают времена, когда формализм топологии (т.
символическая запись) — удобный способ графического выражения идей, но
реальные инструменты из абстрактной топологии так редко играют роль в графике.
Изучайте этот прекрасный предмет ради него самого, но не ждите немедленного результата.
Ответ состоит в том, что они обе поверхности с одной
отверстие. Здесь мы говорим об идеях из топологии. Разве поверхности не большие
часть компьютерной графики? Да, но оказывается, что большинство идей в
топологию, полезную для графики, можно изучить на первом курсе в
дифференциальная геометрия. Дифференциальная геометрия изучает *формы*
поверхности, в то время как топология изучает такие вещи, как то, какие части поверхности
находятся рядом с другими частями. Я видел очень мало топологии, которая ставится
для использования в графике, и я считаю, что это связано с тем, что большая часть топологии
связаны с довольно абстрактными множествами, и что большая часть топологии далека от
из понятий трехмерного евклидова пространства, которое так важно для
большая часть графики. Бывают времена, когда формализм топологии (т.
символическая запись) — удобный способ графического выражения идей, но
реальные инструменты из абстрактной топологии так редко играют роль в графике.
Изучайте этот прекрасный предмет ради него самого, но не ждите немедленного результата. расплата за графику!
расплата за графику!
Меня несколько раз спрашивали, является ли абстрактная алгебра (теория групп, кольца и т. д.) или теории чисел играют роль в компьютерной графике. Немного что я видел. Эти предметы, как и топология, являются областями, полными красивые идеи. К сожалению, эти идеи редко находят отражение в компьютерная графика.
Графическое лямбда-исчисление | chorasimilarity
ОБНОВЛЕНИЕ (2020): Если вы ищете историю графического лямбда-исчисления и его связь с хемлямбдой, используйте:
- Переписывание графа, от возникающих алгебр до chemlambda или arXiv:2007.10288 [cs.LO] или (pdf) или (figshare)
Для получения дополнительной информации посетите страницу Chemlambda или arXiv:2003.14332 [cs.AI].
Если вы ищете только графическое лямбда-исчисление, см.
(журнал) (arxiv) — Графическое лямбда-исчисление. Complex Systems 22, 4 (2013), 311-360
ОБНОВЛЕНИЕ (2020 г.): Коллекция анимаций chemlambda, извлеченная из G+, теперь доступна в расширенной форме. Поучительно, много ссылок.
Поучительно, много ссылок.
ОБНОВЛЕНИЕ (2019): Есть три недавних проекта, которые продолжаются после GLC. Вас может больше всего заинтересовать анализатор лямбда-исчисления в chemlambda, главным образом потому, что вы можете играть с ним исключительно в javascript. Я постепенно добавляю гораздо больше информации, чем раньше.
ОБНОВЛЕНИЕ (2019 г.): На этой странице вы можете изучить графики и сокращения в chemlambda и Interaction Combinators. Если вы хотите использовать этот блог для получения дополнительной информации о графическом лямбда-исчислении и хемлямбда, вам следует прочитать более свежие пояснительные сообщения, начиная с этого.
ОБНОВЛЕНИЕ (2017 г.): Графическое лямбда-исчисление (GLC) и chemlambda — это два разных формализма, которые разрабатывались параллельно. На мой взгляд, GLC значительно превосходит chemlambda, а также основной интерес к chemlambda исходит от молекулярных компьютеров, а не от децентрализованных вычислений.
В GLC_computations_examples собраны некоторые конструкции с GLC, более ранние, чем chemlambda.
Это логотип chemlambda:
ОБНОВЛЕНИЕ 11.06.2016: На данный момент лучшей точкой входа в эту вселенную является файл README из активной ветки репозитория chemlambda. Что касается некоторых важных идей, которые можно взять домой, то это:
- Весь алгоритм с его различными частями является моделью, а не только системой перезаписи.
- Модель имеет chemlambda в качестве доказательства концепции.
- Идите как можно дальше без глобальной семантики и контроля
- Все локально и децентрализовано.
- Лямбда-исчисление — это лишь крошечная часть, служащая лишь источником вдохновения для более интересных идей, таких как, например, понимание предшественника и превращение его в первый искусственный живой организм в хемлямбде, а затем для создания понятия хемлямбда-квайн
- Пространство вообще не понимается в других подходах.
 Доказательство вещи не то же самое, что вещь.
Доказательство вещи не то же самое, что вещь. - Space — это плагин того же типа, что и остальная часть модели.
- Природа — самый быстрый компьютер.
_______________________________________
Это учебник по графическому лямбда-исчислению. На данный момент лучшей экспозицией является arXiv:1305.5786 , но некоторые факты там не освещены.
См. также соответствующий учебник по chemlambda, также известному как «машина для химического бетона».
Посетите страницу демонстрации chemlambda, чтобы ПОСМОТРЕТЬ, как это работает.
Прочтите страницу видения, чтобы понять, для чего это нужно.
Часто задаваемые вопросы: chemlambda в реальном и виртуальном мирах
Модель децентрализованных вычислений описана в учебном пособии по распределенному GLC.
Источники:
- М. Булига, Графическое лямбда-исчисление, Комплексные системы 22, 4 (2013), 311-360, arXiv:1305.5784
4
- М.
 Булига, Л. Х. Кауфман, Чемлямбда, универсальность и самоумножение, arXiv:1403.8046, принято в
Булига, Л. Х. Кауфман, Чемлямбда, универсальность и самоумножение, arXiv:1403.8046, принято в
ALIFE 14: Четырнадцатая международная конференция по синтезу и моделированию живых систем, 30 июля – 2 августа 2014 г., Нью-Йорк - Графическое лямбда-исчисление тега из блога хороподобных
- Страница «Эмерджентные алгебры / Вычисления с пространством / Графические исчисления»
- М. Булига, Л.Х. Кауфман, акторы GLC, искусственные химические коннектомы, топологические вопросы и узлы, arXiv:1312.4333
- Распределенный проект GLC.
——————————————
Что такое графическое лямбда-исчисление?
Графическое лямбда-исчисление — это формализм, работающий с набором ориентированных, локально плоских, трехвалентных графов с декорированными узлами (а также проводами, петлями и завершающим вентилем узлом). Набор описан во Введении в графическое лямбда-исчисление.
На таких графах действуют движения, которые могут быть локальными или глобальными.
Графическое лямбда-исчисление содержит дифференциальное исчисление в метрических пространствах, нетипизированное (или просто типизированное) лямбда-исчисление и ту часть теории узлов, которая может быть выражена с помощью диаграмм узлов.
—————————————
Набор ГРАФ.
Это набор графов, которые подвергаются перемещениям. Любая сборка следующих элементарных графов , называемых «воротами» , является графом в .
- График , который соответствует операции лямбда-абстракции из лямбда-исчисления, см. лямбда-термины. Это:
Но подождите! Эти ворота выглядят так, как будто у них есть один вход (стрелка входа) и два выхода (левая и правая стрелки выхода соответственно). Это не может быть граф, представляющий операцию, потому что операция имеет два входа и один выход. Например, операция лямбда-абстракции принимает в качестве входных данных имя переменной и терм и выводит терм.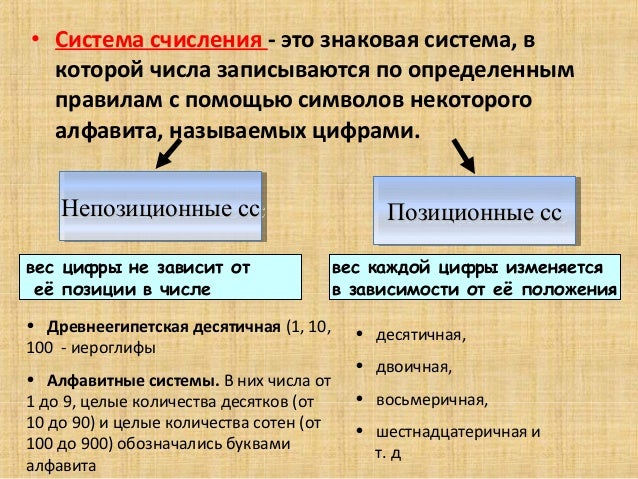
Помните, что графическое лямбда-исчисление не имеет имен переменных. Существует определенный алгоритм, который преобразует лямбда-терм в граф в , так что любой лямбда-абстракции, которая появляется в терме, соответствует вентиль. Алгоритм начинается с представления операции лямбда-абстракции в виде узла с двумя входами и одним выходом, а именно в виде элементарного вентиля, который выглядит как вентиль, но ориентация левой стрелки выхода обратна ориентации вентиля. В какой-то момент алгоритма ориентация меняется на обратную, и мы получаем ворота, как показано здесь. На это есть причина, подождите и увидите. 9. (Он этого не делает, потому что в формализме не будет имен переменных, но все равно круто.)
- Граф , который соответствует операции приложения из лямбда-исчисления, см. лямбда-термины. Это:
Это похоже на график операции, здесь нет никаких хитростей. Знак, который я использую, похож на фигурный знак соединения.
- Граф , который будет использоваться как вентиль FAN-OUT, это:
- Граф. Для любого элемента абелевой группы (представьте, что это или ) есть «ворота исследования» или «ворота расширения», которые выглядят как график операции:
(Поэтому у нас есть семейство операций, называемых «расширениями», индексируемых элементами абелевой группы. Это структура, происходящая из эмерджентных алгебр.)
Мы используем эти элементарные графы для построения графов в . Любая сборка этих ворот в любом количестве, учитывающая ориентацию стрелок, находится в .
Заметим, что мы получаем трехвалентные графы с декорированными узлами, причем каждый узел имеет циклический порядок своих стрелок (отсюда локально планарные графы).
Следует упомянуть небольшую вещь: у нас могут быть стрелки, которые вводят или выводят в ничто. В самом деле, в частности, элементарные графы или элементы находятся внутри, и все стрелки элементарного графа либо входят, либо выходят в ничто.
Технически мы можем представить себе, что мы дополняем граф в , если это необходимо, одновалентными узлами, называемыми «листьями» (они могут быть украшены «ВХОДОМ» или «ВЫВОДОМ», в зависимости от ориентации стрелки, где они сидят на).
- По этой причине мы допускаем в стрелки без узлов, которые являются элементарными графами, называемыми проводами
и петли (без узлов из элементарных графов, без листьев)
- Наконец, мы вводим одновалентный вентиль, завершающий вентиль :
Терминатор имеет входной лист и не имеет выхода.
и теперь любой граф, представляющий собой воссоединение линий, циклов и сборок элементарных графов (включая граф завершения), находится в .
——————————————
Ходы.
- Графический бета-ход с деталями
- Разветвление: CO-COMM, CO-ASSOC, GLOBAL FAN-OUT, LOCAL FAN-OUT
- Подрезные ходы
- Возникающая алгебра перемещает R1a, R1b, R2 и ext2
Все еще в бета-версии:
- Расширенный бета-ход, представленный здесь.

- Производящие ходы, обсуждаемые здесь, здесь и здесь.
Еще больше:
- Движение ext1, если вам нужна экстенсиональность.
Если нет ориентированного пути от «2» к «1» за пределами левой картинки, то можно заменить эту картинку ребром. И наоборот, если нет ориентированного пути, соединяющего «2» с «1», то можно заменить ребро графом из левой части следующего рисунка:
————————————— —
Макросы.
- Пересечения в лямбда-исчислении (графическое бета-правило как плетение)
- Переходы эмерджентной алгебры
- Молния и примеры
- Укладка стрелы (II) и пряди сети сектор
- Наборы, списки и порядок ходов в графическом лямбда-исчислении
——————————————
Секторы.
сектор графического лямбда-исчисления:
- набор графиков, определяемый локальным или глобальным условием,
- набор ходов из списка всех доступных ходов.

Название «графическое лямбда-исчисление» происходит от того, что там оно имеет нетипизированное лямбда-исчисление в качестве сектора. На самом деле существует три четыре важных сектора графического лямбда-исчисления:
- нетипизированный сектор лямбда-исчисления, который содержит все графы, в которых получены из нетипизированных термов лямбда-исчисления по описанному здесь алгоритму. Ходы этого сектора: графический бета-ход, разветвляющийся ход, обрезной ход. Статья arxiv:1207.0332 подробно описывает этот сектор.
- сектор эмерджентной алгебры, который содержит все графы, описанные в статье arxiv:1103.6007, с помощью макросов пересечения эмерджентной алгебры и следующих ходов: двойной графический бета-ход (который вместе с графическим ходом образует расширенный бета-ход), разветвление ходы, обрезные ходы, эмерджентные алгебраические ходы. Подробное описание см. arXiv:1305.5786 в разделе 5, а также пост-эмерджентные алгебры как комбинаторную логику, часть IV (и ознакомьтесь с обратными ссылками).

- сектор диаграмм узлов и клубков, определенный с помощью пересечений в макросе лямбда-исчисления и движений Райдемайстера, как описано в посте Генерация набора движений Райдемайстера для графических лямбда-пересечений, которые являются составными движениями, полученными из графического бета-перемещения и некоторого локального разветвления. движется. Статья arxiv:1211.1604 подробно описывает этот сектор.
- Сектор свободы графического лямбда-исчисления
_______________
Простой вариант графического лямбда-исчисления:
- Простой графический лямбда-исчисление
- Пример: оформление комбинаторов S,K,I в простом графическом лямбда-исчислении
_______________
Где я его использую (работа в процессе) и другие полезные ссылки:
В этих двух постах используется древовидный формализм эмерджентных алгебр.
- Параллельный транспорт в пространствах с расширениями, I
- Что это за группа? (Параллельный перенос в пространствах с расширениями, II)
Чтобы понять, как это работает, см. следующие публикации, целью которых является описание конечного дифференциального исчисления как системы перезаписи графов:
следующие публикации, целью которых является описание конечного дифференциального исчисления как системы перезаписи графов:
- Словарь от эмерджентной алгебры до графического лямбда-исчисления (I)
- Словарь от эмерджентной алгебры до графического лямбда-исчисления (II)
- Словарь от эмерджентной алгебры до графического лямбда-исчисления (III)
Машина для химического бетона проект:
- Машина для химического бетона для лямбда-исчисления
- Локальный FAN-IN устраняет глобальный FAN-OUT (I)
- Локальный FAN-IN устраняет GLOBAL FAN-OUT (II)
- Химическая бетонная машина, короткий список ворот и ходов
- Древняя машина Тьюринга помогает машине для химического бетона
- Спиралевидные узоры на полной молнии
- Экстремальное функциональное программирование с помощью биологических компьютеров
- Химическая бетонная машина, детальная (I)
- Химическая бетонная машина, детальная (II)
- Химическая бетонная машина, детальная (III)
- Химическая бетонная машина, детальная (IV)
- Химическая бетонная машина, детальная (V)
- Химическая бетонная машина, детальная (VI)
Проект нейронных сетей:
- Тизер: нейронные сети типа B в графическом лямбда-исчислении (I)
- Тизер: нейронные сети типа B в графическом лямбда-исчислении (II)
- Пара синапсов, один из которых контролирует другой (NN типа B, часть III)
Особенности — APEX Calculus
Интерактивная трехмерная графика: Представленная в версии 3. 0, почти все изображения объектов в пространстве, будь то кривые, поверхности или твердые тела, можно манипулировать, что позволяет учащимся лучше понять иллюстрацию. Видео ниже дает короткую демонстрацию того, на что способен ридер.
0, почти все изображения объектов в пространстве, будь то кривые, поверхности или твердые тела, можно манипулировать, что позволяет учащимся лучше понять иллюстрацию. Видео ниже дает короткую демонстрацию того, на что способен ридер.
Несколько замечаний по поводу этих рисунков:
Эта функция доступна только в настольных версиях Adobe Reader/Acrobat. Насколько мне известно, никакие другие программы просмотра .pdf не поддерживают интерактивность. Другие представления должны нормально открывать .pdf; читатель просто не сможет манипулировать графикой.
Чтобы активировать изображение, нажмите на него. Чтобы повернуть, щелкните/перетащите. Для панорамирования влево/вправо, вверх/вниз используйте CTRL+щелчок. Когда мышь находится над изображением, колесо прокрутки позволяет увеличивать/уменьшать масштаб. Щелкните правой кнопкой мыши изображение, чтобы открыть дополнительные параметры, включая изменение освещения и перспективы.

Эффективный способ рассмотреть изображение поближе — сначала увеличить сам файл .pdf, увеличив изображение на экране. Затем увеличьте графику.
Трехмерная графика значительно увеличивает размеры файлов .pdf. На странице загрузки можно получить цветной .pdf текста без интерактивности. Все изображения выглядят одинаково, ими просто нельзя манипулировать.
Пояснительный текст: Некоторые тексты, похоже, следуют схеме «Определение – Теорема – Пример», где можно научиться делать что-то, по-настоящему не понимая что это они делают и почему они должны быть заинтересованы. APEX Calculus стремится объяснить новые идеи, мотивированные предыдущим материалом или повседневной жизнью.
Здесь показан один из примеров уникальных объяснений, содержащихся в исчислении APEX. Студенты часто испытывают трудности с векторными функциями, даже с «простыми» функциями, график которых представляет собой линию. На иллюстрации показано, что старая концепция «линия определяется точкой и наклоном» по существу совпадает с новой концепцией «линия определяется точкой и направлением».
На иллюстрации показано, что старая концепция «линия определяется точкой и наклоном» по существу совпадает с новой концепцией «линия определяется точкой и направлением».
Примеры: Каждый текст содержит множество примеров, и исчисление APEX не исключение. Версия 4.0 содержит около 500 примеров, призванных продемонстрировать что , как и почему исчисления.
Графика: Учебники, напечатанные традиционными издательствами, содержат великолепную графику, созданную профессиональными графическими дизайнерами. Некоторые открытые тексты имеют не очень хорошую графику. Графика APEX Calculus была создана не только для удовлетворения потребностей — она была создана, чтобы впечатлять. Используя мощь LaTeX и pgfplots, все 2D-изображения основаны на векторах, что означает, что они отлично выглядят независимо от того, насколько сильно вы увеличиваете масштаб, а 3D-изображения, созданные с помощью Asymptote, интерактивны.
Место для заметок: Внизу каждой страницы текста есть пустое пространство шириной 2 дюйма для заметок. Учащиеся могут записывать свои мысли внизу страницы по мере чтения или помещать туда свои заметки, следуя похожим примерам. Учащиеся пишут в своих книгах — это здорово; это подтверждает тот факт, что это их книга, помогает избавиться от мышления «Я просто продам это обратно, когда закончу».
Наборы упражнений: Мы все знаем, что учащимся нужно практиковаться. Обобщая, можно сказать, что верно следующее: в традиционных текстах «слишком много» упражнений, а во многих открытых текстах «слишком мало». Надеюсь, вы обнаружите, что количество упражнений, найденных в APEX Calculus, «в самый раз»
Как в тексте может быть «слишком много» упражнений? Когда набор упражнений содержит более 100 задач, инструктору может быть сложно выбрать, какую из них назначить. Студенты легко пугаются выбора при самостоятельном обучении: должны ли они практиковать их все? Являются ли некоторые более важными, чем другие?
Некоторые разделы требуют большого количества упражнений. При изучении цепного правила учащимся требуется серий практик, поэтому имеет смысл иметь много задач на выбор. А вот другие разделы… не так уж и много.
При изучении цепного правила учащимся требуется серий практик, поэтому имеет смысл иметь много задач на выбор. А вот другие разделы… не так уж и много.
Несколько доказательств: Исчисление APEX содержит лишь несколько доказательств более чем 125 теорем в тексте. Почему это хорошая вещь ?
Большинство студентов, изучающих математику — старшеклассники и первокурсники колледжей — не знают, как читать традиционные учебники по математике, не говоря уже об исследовательской работе по математике. Обычно я читаю статьи по математике, по крайней мере, за два прохода: первый дает мне общее представление о том, о чем статья (при этом я пропускаю доказательства), а во втором проходе я углубляюсь, чтобы понять доказательства. Мои студенты-математики, когда они, наконец, набрались смелости, чтобы действительно прочитать книгу, а не просто искать пример, соответствующий домашнему заданию, быстро увязли в деталях, которые им, откровенно говоря, сейчас знать не нужно.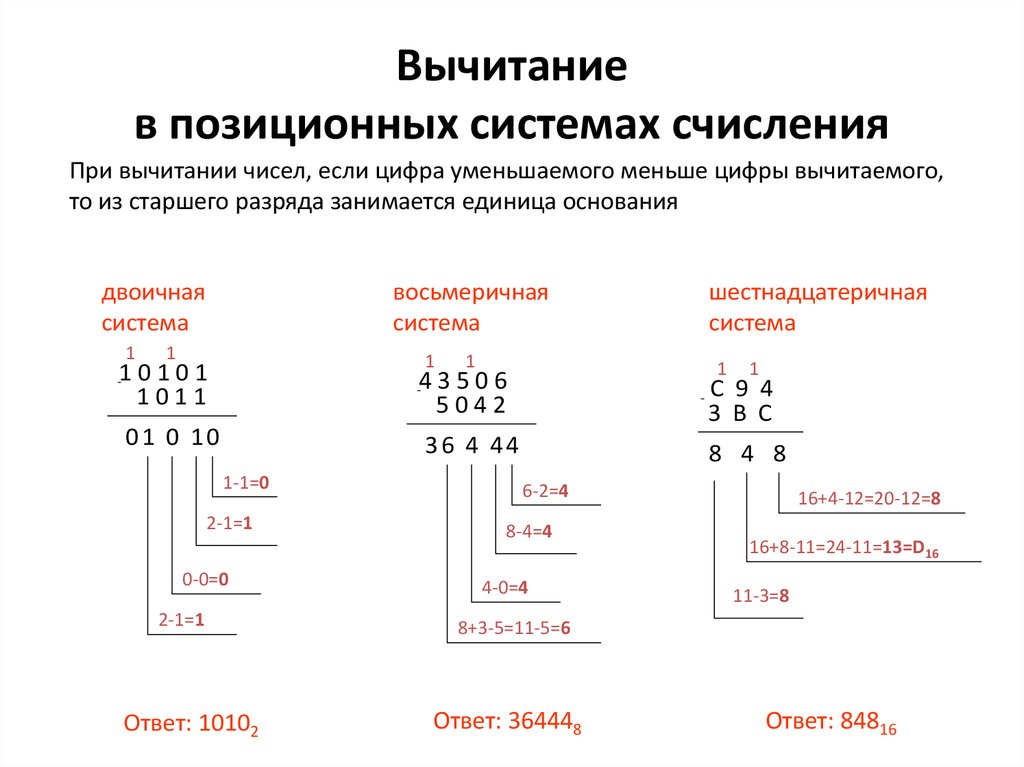

 Затем в быстрой последовательности берут один за другим пеленги всех трех предметов, которые записывают. Сразу же записывают отсчет лага и время взятия пеленгов.
Затем в быстрой последовательности берут один за другим пеленги всех трех предметов, которые записывают. Сразу же записывают отсчет лага и время взятия пеленгов.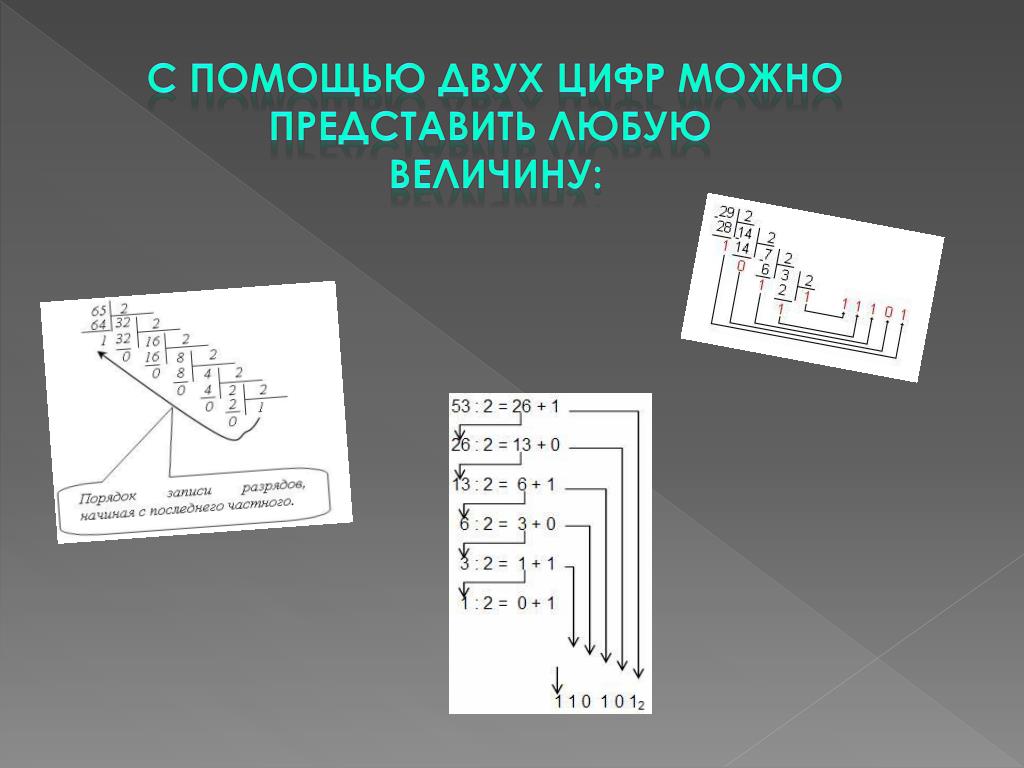
 Точка пересечения дуг будет местом судна. Окружности пересекутся в двух точках, однако счислимое место или хотя бы приближенный пеленг позволят легко определить нужную точку, которая и будет обсервованным местом судна. С помощью РЛС этим способом определения можно пользоваться в условиях плохой видимости.
Точка пересечения дуг будет местом судна. Окружности пересекутся в двух точках, однако счислимое место или хотя бы приближенный пеленг позволят легко определить нужную точку, которая и будет обсервованным местом судна. С помощью РЛС этим способом определения можно пользоваться в условиях плохой видимости.
 Счислимо-обсервованное место обозначается на карте треугольником с точкой посередине.
Счислимо-обсервованное место обозначается на карте треугольником с точкой посередине.