Что такое двоичный код – Vunderkind.Info
Задача сегодняшней публикации – разобраться в том, что такое двоичный код, для каких целей и где используется двоичный код и зачем вообще он нужен.
Двоичный код – это система обозначений из двух элементов, различные комбинации которых служат для представления (кодировки) информации.
В качестве элементов системы наиболее часто выступают цифры «0» и «1». Но в действительности обозначения могут быть произвольными, исходя из характера сведений, которые требуется кодировать.
Главное – чтобы соответствующие элементы обозначали взаимоисключающие либо противоположные по значению данные.
Великолепным примером двоичного кода могут служить любые пары антонимов, к примеру, «да/нет», «белое/черное», «включено/выключено» и т.д.
Для описания двоичного кода используется понятие разряда (более точно – двоичного разряда), объединяющего целочисленную группу элементов двоичного кода.
Например, в системе, использующей базовые элементы 0 и 1, два двоичных разряда могут быть представлены следующими четырьмя комбинациями: 00, 01, 10 и 11.
Три двоичных разряда могут иметь следующий вид: 000, 001, 010, 011, 100, 101, 110 и 111.
Число двоичных разрядов может быть сколь угодно большим в зависимости от характера решаемых задач и объема кодируемой информации.
Форма представления данных с помощью двоичных разрядов характерна для позиционного двоичного кода, лежащего в основе двоичной системы счисления, применяемой сплошь и рядом во всех типах вычислительной техники.
Увеличение разрядности на единицу приведет к удвоению числа комбинаций в позиционном двоичном коде.
При двух символах (смотри примеры выше) мы имеем 4 комбинации, при трех – 8 комбинаций, при четырех – 16 комбинаций, при n символах – 2n комбинаций.
С помощью двух символов можно закодировать практически любую информацию. Доказательством тому служат современные компьютеры, работа которых невозможна без такой кодировки.
Характерная особенность систем счисления, использующих разрядный двоичный код, заключается в возможности обозначения одного и того же числа различной комбинацией символов, отличающихся между собой по разрядности.
Например, в двоичной системе счисления единицу можно представить по-разному: 1, 01, 001, 0001 и т.д.
Нумерация двоичных разрядов осуществляется справа налево.
Если взять двоичный код 01011, то первый разряд будет иметь значение 1, второй разряд – 1, третий разряд – 0, четвертый – 1 и пятый разряд – 0:
Примеры двоичного кода
С помощью трех двоичных разрядов можно обозначить восемь десятичных чисел от 0 до 7:
0 = 000
1 = 001
2 = 010
3 = 011
4 = 100
5 = 101
6 = 110
7 = 111
Эта таблица отражает
Фото 1. Выключатели — прекрасный пример двоичного кода
Поскольку число двоичных разрядов ничем не ограничено, с помощью такой кодировки можно зашифровать любое привычное нам десятичное число.
Чтобы перевести двоичный код обратно в десятичный, нужно 1-ый разряд двоичного кода умножить на 1 (или на 20), 2-ой разряд – на 2 (или на 21), третий разряд – на 4 (или на 22), n-ый разряд — на 2n-1, а затем сложить полученные значения.
Примеры:
111 → 1 * 22 + 1 * 21 + 1 * 20 = 4 + 2 + 1 = 7
101 → 1 * 22 + 0 * 21 + 1 * 20 = 4 + 0 + 1 = 5
Зачем нужен двоичный код
Основное назначение двоичного кода – шифрование и кодирование информации.
Его главные преимущества – минимальное число символов, используемых для кодирования информации, и удобство – с машинной точки зрения – оперирования зашифрованными с их помощью данными.
Допустим, нам необходимо закодировать фразу «ХОЛОДНОЕ ЛЕТО».
Установим произвольные соответствия букв двоичному коду: Х – 000, О – 001, Л – 010, Д – 011, Н – 100, Е – 101, Т – 111.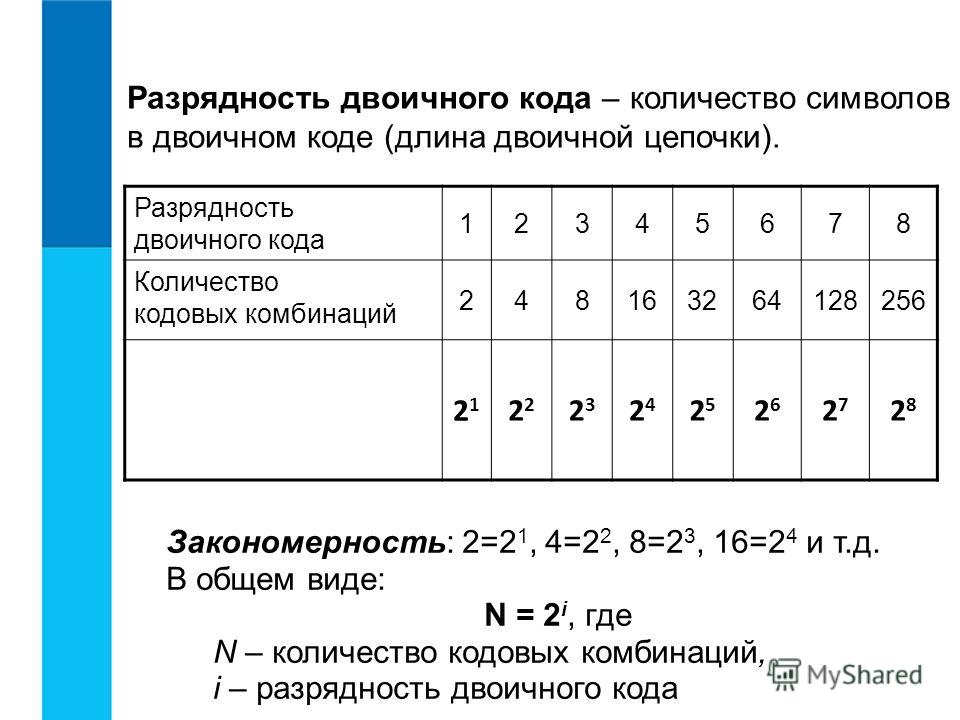
Фото 2. Двоичный код лежит в основе двоичной системы счисления
Тогда закодированная фраза примет следующий вид: 000001010001011100001101010101111001 (36 символов).
Если получатель зашифрованного кода знает, что в основе кодировки каждой буквы лежат три двоичных разряда, то расшифровать фразу ему не составит никакого труда.
В данном случае мы имеем дело с однозначно декодируемым кодом (то есть код может быть расшифрован одним единственным способом).
Для сокращения длины кода может применяться
Тогда кодировщик сознательно отступает от принципа разрядности, присваивая буквам произвольное число разрядов.
Например, если Х будет иметь обозначение 01, О – 00, Л – 100, Д – 101, Н – 110, Е – 111, Т – 1111, то фразе «ХОЛОДНОЕ ЛЕТО» будет соответствовать строка 01001000010111000111100111111100 (32 символа).
В данной фразе будет однозначно декодироваться фрагмент «ХОЛОДНО», после чего дешифровщику придется ломать голову над выбором приемлемой трактовки кода: «Е ЛЕТО», «Е ЛЕЕЛ», «Е ЛТЕО», «ТОЕЕЛ» и т. д.
д.
Данный пример указывает на проблемы с использованием непродуманных комбинаций двоичного кода.
При правильном же подборе кодов неравномерный двоичный код позволяет не только сократить объем передаваемого сообщения, но и начать его дешифровку после поступления уже первых нескольких символов, не дожидаясь пока сообщение будет получено в полном объеме.
Виды двоичных кодов
Представление в памяти компьютера целочисленных значений производится с помощью беззнакового двоичного кода, основанного на представлении двоичных разрядов степенями двойки.
При этом значение минимального числа в n-разрядном двоичном коде будет равно 0, а максимального вычисляться по формуле 2n-1.
К примеру, для шестнадцатиразрядного кода допустимыми будут значения чисел от 0 до 65535.
На практике приходится решать задачи посложнее.
Фото 3. С помощью двоичного кода можно закодировать все что угодно
Машине или компьютеру достаточно трудно объяснить разницу между положительными и отрицательными числами. Отдельного представления требуют и числа с плавающей запятой, дробные или трансцендентные числа.
Отдельного представления требуют и числа с плавающей запятой, дробные или трансцендентные числа.
Инженеры придумали способ, как обходить эти проблемы, не выходя за пределы использования двоичного кода. Для решения озвученных проблем используется
В частности, для определения знака числа используется старший разряд в слове.
Если слово начинается с символа «0», значит число положительное (имеет знак «+»), если с символа «1», значит оно – отрицательное (имеет знак «-»).
При использовании шестнадцатиразрядного кода в таком случае мы сможем зашифровать числа в диапазоне от -32767 до +32767.
Недостаток знакового двоичного кода кроется в необходимости раздельной обработки цифрового и знакового разрядов, что заставляет разработчиков программного обеспечения прибегать к усложненным алгоритмам обработки данных.
Как следствие, программный код увеличивается в объеме, а скорость его работы замедляется.
Видео о двоичном коде:
Двоичный код — Википедия
Материал из Википедии — свободной энциклопедии
Слово «Wikipedia», закодированное двоичным ASCII-кодом.Двои́чный код — это способ представления данных в виде кода, в котором каждый разряд принимает одно из двух возможных значений, обычно обозначаемых цифрами 0 и 1. Разряд в этом случае называется двоичным разрядом.
В случае обозначения цифрами «0» и «1», возможные состояния двоичного разряда наделяются качественным соотношением «1» > «0» и количественными значениями чисел «0» и «1».
Двоичный код может быть непозиционным и позиционным. Позиционный двоичный код лежит в основе двоичной системы счисления, широко распространенной в современной цифровой технике.
Описание
Из комбинаторики известно, что, в случае непозиционного кода, количество комбинаций (кодов) n-разрядного кода является числом сочетаний с повторениями, равно биномиальному коэффициенту:
- (n+k−1k)=(−1)k(−nk)=(n+k−1)!k!(n−1)!{\displaystyle {n+k-1 \choose k}=(-1)^{k}{-n \choose k}={\frac {\left(n+k-1\right)!}{k!\left(n-1\right)!}}}, [возможных состояний (кодов)], где:
n{\displaystyle n} — количество элементов в данном множестве различных элементов (количество возможных состояний, цифр, кодов в разряде),
k{\displaystyle k} — количество элементов в наборе (количество разрядов).
В двоичной системе кодирования (n=2) количество возможных состояний (кодов) равно :
- (n+k−1)!k!(n−1)!=(2+k−1)!k!(2−1)!=(k+1)!k!1!=k+1{\displaystyle {\frac {\left(n+k-1\right)!}{k!\left(n-1\right)!}}={\frac {\left(2+k-1\right)!}{k!\left(2-1\right)!}}={\frac {\left(k+1\right)!}{k!1!}}=k+1}, [возможных состояний (кодов)], то есть
описывается линейной функцией:
- Nkp(k)=k+1{\displaystyle N_{kp}(k)=k+1}, [возможных состояний (кодов)], где
k{\displaystyle k} — количество двоичных разрядов.
Например, в одном 8-ми битном байте (k=8) количество возможных состояний (кодов) равно:
- Nkp(k)=k+1=8+1=9{\displaystyle N_{kp}(k)=k+1=8+1=9}, [возможных состояний (кодов)].
В случае позиционного кода, число комбинаций (кодов) k-разрядного двоичного кода равно числу размещений с повторениями:
- Np(k)=A¯(2,k)=A¯2k=2k{\displaystyle N_{p}(k)={\bar {A}}(2,k)={\bar {A}}_{2}^{k}=2^{k}}, где
k{\displaystyle \ k} — число разрядов двоичного кода.
Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.
При увеличении разрядности позиционного двоичного кода на 1, количество различных комбинаций в позиционном двоичном коде удваивается.
Двоичные коды являются комбинациями двух элементов и не являются двоичной системой счисления, но используются в ней как основа. Двоичный код также может использоваться для кодирования чисел в системах счисления с любым другим основанием. Пример: в двоично-десятичном кодировании (BCD) используется двоичный код для кодирования чисел в десятичной системе счисления.
При кодировании алфавитноцифровых символов (знаков) двоичному коду не приписываются весовые коэффициенты, как это делается в системах счисления, в которых двоичный код используется для представления чисел, а используется только порядковый номер кода из множества размещений с повторениями.
В системах счисления k-разрядный двоичный код, (k-1)-разрядный двоичный код, (k-2)-разрядный двоичный код и т. д. могут отображать одно и то же число. Например, 0001, 001, 01, 1 — одно и то же число — «1» в двоичных кодах с разным числом разрядов — k.
Примеры двоичных чисел
В таблице показаны первые 16 двоичных чисел и их соответствие десятичным и шестнадцатиричным числам.
| Десятичное число | Шестнадцатеричное число | Двоичное число |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
Пример «доисторического» использования кодов
Инки имели свою счётную систему кипу, которая физически представляла собой верёвочные сплетения и узелки. Генри Эртан обнаружил, что в узелках заложен некий код, более всего похожий на двоичную систему счисления[1].
См. также
Примечания
§ 1.2. Представление чисел в компьютере
Ключевые слова:
• разряд
• беззнаковое представление целых чисел
• представление целых чисел со знаком
• представление вещественных чисел
1.2.1. Представление целых чисел
Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).
Рис. 1.2. Ячейка памяти
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.
Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2n-1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.
Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:
Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
Пример 1. Число 5310 = 1101012 в восьмиразрядном представлении имеет вид:
Это же число 53 в шестнадцати разрядах будет записано следующим образом:
При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом.
В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.
На сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/) размещён информационный модуль «Число и его компьютерный код». С помощью этого ресурса вы можете получить дополнительную информацию по изучаемой теме.
Для выполнения операций с отрицательными числами используется дополнительный код, позволяющий заменить операцию вычитания сложением. Узнать алгоритм образования дополнительного кода вы можете с помощью информационного модуля «Дополнительный код», размещённого на сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/).
1.2.2. Представление вещественных чисел
Любое вещественное число А может быть записано в экспоненциальной форме:
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Например, число 472 ООО ООО может быть представлено так: 4,72 • 108, 47,2 • 107, 472,0 • 106 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 ООО ООО будет представлено как 0,472 • 109.
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Пример:
Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112 = 12710, и, следовательно, максимальное значение числа:
0,11111111111111111111111 • 101111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
САМОЕ ГЛАВНОЕ
Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Как в памяти компьютера представляются целые положительные и отрицательные числа?
3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
4. Представьте число 6310 в беззнаковом 8-разрядном формате.
5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100;
б) 00010101.
6. Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
7. Запишите следующие числа в естественной форме:
а) 0,3800456 • 102;
б) 0,245 • 10-3;
в) 1,256900Е+5;
г) 9,569120Е-3.
8. Запишите число 2010,010210 пятью различными способами в экспоненциальной форме.
9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:
а) 217,93410;
б) 7532110;
в) 0,0010110.
10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.
Электронное приложение к уроку
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |
Cкачать материалы урока
ЕГЭ по информатике 2021 — Задание 5 (Алгоритмы, Автоматы)
Привет! Сегодня исследуем интересное 5 задание из
Пятое задание ЕГЭ по информатике в основном связано с алгоритмами и автоматами.
Задача (классическая, Алгоритм):
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу:
а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001;
б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите такое наименьшее число N, для которого результат работы алгоритма больше 97. В ответе это число запишите в десятичной системе счисления.
Решение:
У нас на вход поступает натуральное (обычное, не дробное, положительное) число N.
Рассмотрим первое правило формирование выходного числа. На выходе получается двоичная запись числа N. Нарисуем схематично первое правило формирования выходного числа.
Рассмотрим теперь второе правило формирования числа. Сказано, что дописываются два разряда справа к тому двоичному числу, которое получили в первом пункте.
Про первый дополнительный разряд написано в пункте a второго правила: «складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 10000 преобразуется в запись 100001».
Если сказать более просто, то автомат подсчитывает количество единиц у первоначального двоичного числа N, полученного в первом пункте. Если количество чётное, то автомат в первый дополнительный разряд должен поставить 0. Если количество нечётное, то автомат в первый дополнительный разряд должен поставить 1.
Про второй дополнительный разряд сказано в пункте б второго правила. Автомат сделает тоже самое, что и в предыдущем пункте, только теперь подсчёт единиц будет происходить не только в двоичной записи числа N, но и в первом дополнительном разряде.
В вопросе просят указать входящее наименьшее число N, чтобы автомат выдал число R больше 97.
Т.к. число R должно быть больше 97, то переведём число 98 (97 + 1) в двоичный вид, чтобы можно было оценить входящее число N.
Получилось число 1100010. Будем рассматривать (начиная с 1100010) числа на выполнение правил, которые заданы для автомата. Если все правила будут выполнены, значит, мы получили то число, по которому вычислим изначальное N. Нам нужно получить именно минимальное число, поэтому мы и начали с минимального возможного претендента для числа R (98).
Видим, что подходит число 1100110. В части числа, которая является двоичным представлением N, количество единиц равно 3. Число 3 нечётное, значит, в первом дополнительном разряде должна стоять 1 (единица).
Проверим второй дополнительный разряд. Теперь считаем единицы не только в двоичном представлении числа N, но так же и в первом дополнительном разряде! Количество единиц равно 4. Число 4 чётное. Значит, во втором дополнительном разряде должен стоять 0 (ноль). Все правила работы автомата выполняются в числе 1100110.
Чтобы найти искомое число N, отбросим два дополнительных разряда от найденного 1100110.
Правило: Если от двоичного числа отбросить младший разряд, то оно разделится на 2 целочисленным образом (т.е. делим на 2, если есть остаток, убираем его).
Найдём полученное минимальное число R 1100110 в десятичном представлении. Число 1100010 — 98, 1100011 — 99, 1100100 — 100, 1100101 — 101, 1100110 — 102.
Уберём второй дополнительный разряд у числа 1100110, получается 102 / 2 = 51 (110011). Уберём ещё и первый дополнительный разряд , получается 51 / 2 = 25 (11001).
Значит двоичное представление искомого числа N равно 11001, а десятичное 25.
Ответ: 25.
Изучим ещё одну классическую задачу задания 5 из ЕГЭ по информатике.
Задача (классическая, Автомат)
Автомат получает на вход пятизначное число. По этому числу строится новое число по следующим правилам.
1. Складываются отдельно первая, третья и пятая цифры, а также вторая и четвёртая цифры.
2. Полученные два числа записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 63 179. Суммы: 6 + 1 + 9 = 16; 3 + 7 = 10. Результат: 1016.
Укажите наименьшее число, при обработке которого автомат выдаёт результат 723.
Решение:
В подобных задачах из ЕГЭ по информатике нумерация происходит начиная со старшего разряда.
Составим краткую запись для первого правила:
Второе правило заключается в том, что мы «соединяем» два числа, полученных в первом пункте, причём, сначала идёт меньшее число, а затем большее.
Рассмотрим число 723.
Разбить на числа 72 и 3 нельзя, т.к. вначале пишется меньшее число. Значит, разбиваем на 7 и 23.
Первое число (сумма 1, 3, 5 разрядов) будет 23, т.к. только сумма трёх цифр может дать число 23. Сумма двух цифр максимум может быть 9+9=18. Тогда 7 — это второе число (сумма 2 и 4 разряда.)
Нам нужно указать наименьшее пятизначное входящее число, поэтому стремимся более старшие разряды сделать как можно меньше! Пусть самый старший разряд (1 разряд) равен 1 (минимальное значение для старшего разряда). Тогда нужно с помощью суммы 3-его и 5-ого разряда набрать 22. Но это не возможно, т.к. максимум с двух разрядов получается 9+9=18. Поэтому приходим к выводу, что самое маленькое значение для 1-ого разряда будет 23-18=5, а третий и пятый разряд будут по 9.
Т.к. 7 — это сумма второго и четвёртого разряда, то сделаем второй разряд 0(нулём), а четвёртый 7, чтобы пятизначное число было минимальным.
Получаем окончательный результат 50979.
Ответ: 50979
Следующая задача иногда встречается в тренировочных вариантах ЕГЭ по информатике.
Задача (Кузнечик)
Исполнитель КУЗНЕЧИК живёт на числовой оси. Начальное положение КУЗНЕЧИКА – точка 0. Система команд Кузнечика:
Вперед 7 – Кузнечик прыгает вперёд на 7 единиц,
Назад 5 – Кузнечик прыгает назад на 5 единиц.
Какое наименьшее количество раз должна встретиться в программе команда «Назад 5», чтобы Кузнечик оказался в точке 19?
Решение:
В данной задаче у нас есть числовая ось на которой живёт кузнечик.
Кузнечик может прыгать либо на 7 шагов вперёд, либо на 5 шагов назад. На другое количество шагов Кузнечик прыгать не может!
Обозначим за x — количество прыжков на 7 шагов вперёд, а за y — количество прыжков на 5 шагов назад. x и у — должны быть целые неотрицательные числа.
Составим уравнение:
7x — 5y = 19
Если бы Кузнечик начинал не с нулевой отметки, мы бы прибавили начальную координату к левой части уравнения.
Перегруппируем:
7x — 19 = 5yВыражение в правой части 5y — делиться на 5, значит и 7x — 19 должно делиться на 5. Чтобы выражение в левой части делилось на 5, нужно чтобы 7x оканчивалось либо на 4, либо на 9 (Тогда и выражение 7x — 19 будет оканчиваться либо на 5, либо на 0).
Вспомним таблицу умножения:
Нам не подходит 14, т.к. 14-19
Тогда
5y = 49 — 19 = 30.y = 6
Ответ: 6.
Задача из ЕГЭ по информатике на побитовый сдвиг:
Задача(редкая, сдвиг влево)
У исполнителя, который работает с положительными однобайтовыми двоичными числами, две команды, которым присвоены номера:
1. сдвинь влево
2. вычти 1
Выполняя первую из них, исполнитель сдвигает число на один двоичный разряд влево, причём на место освободившегося бита ставится 0. Выполняя вторую команду исполнитель вычитает из числа 1. Исполнитель начал вычисления с числа 91 и выполнил цепочку команд 112112. Запишите результат в десятичной системе.
Решение:
Здесь есть всего две команды у исполнителя: сдвинуть биты влево и вычесть 1.
Правило: Если к двоичному числу приписать справа ноль, то это число увеличится в два раза.
Сдвиг влево: Возьмём число 150 (1001 0110). После сдвига влево к двоичному числу приписывается справа ноль (т.е. число умножается на 2) 300(1 0010 1100), а левый бит, если общее количество битов больше 8, отбрасывается (т.к. у нас однобайтовое число). Получается 44 (0010 1100) — нули в начале числа тоже отбрасываются. А 44 — остаток от деления 300/256
В нашей задаче число однобайтовое, значит число не превышает 255. Если при умножении на 2, получаем число большее, чем 255, то мы должны взять остаток от деления на 256
осталось проделать цепочку команд 112112.
91 * 2 = 182 (182
182 * 2 = 364 (364 / 256 — остаток 108)
108 — 1 = 107
107 * 2 = 214 (214
214 * 2 = 428 (428 / 256 — остаток 172)
172 — 1 = 171
Если была бы команда сдвиг вправо, то тогда у числа просто убирался бы правый бит (т.е. происходило бы целочисленное деление на 2)
Ответ: 171
В задании 5 ЕГЭ по информатике может встретится задача на исполнителя чертёжника.
Задача (Исполнитель Чертежник)
Исполнитель Чертежник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остается след в виде прямой линии. У исполнителя существуют следующие команды:
Сместиться на вектор (а, Ь) – исполнитель перемещается в точку, в которую можно попасть из данной, пройдя а единиц по горизонтали и b – по вертикали.
Запись: Повторить 5[ Команда 1 Команда 2] означает, что последовательность команд в квадратных скобках повторяется 5 раз.
Чертежник находится в начале координат. Чертежнику дан для исполнения следующий алгоритм:
Сместиться на вектор (5,2)
Сместиться на вектор (-3, 3)
Повторить 3[Сместиться на вектор (1,0)]
Сместиться на вектор (3, 1)
На каком расстоянии от начала координат будет находиться исполнитель Чертежник в результате выполнения данного алгоритма?
Решение:
После первой команды Сместиться на вектор (5,2) Исполнитель чертёжник окажется:
После второй команды Сместиться на вектор (-3, 3)
Следующая команда Повторить 3[Сместиться на вектор (1,0)]
Следующая команда Сместиться на вектор (3, 1)
Расстояние от начала координат находит по теореме Пифагора:
62 + 82 = 100
Значит, расстояние равно 10.
Ответ: 10.
Последняя задача довольно часто печатается в тренировочных заданиях по ЕГЭ по информатике.
Задача (Исполнитель)
У исполнителя УТРОИТЕЛЬ две команды, которым присвоены номера:
1. вычти 1
2. умножь на 3
Первая из них уменьшает число на экране на 1, вторая – увеличивает его в три раза.
Запишите порядок команд в программе получения из числа 3 числа 16, содержащей не более 5 команд, указывая лишь номера команд.
(Например, программа 21211 это программа
умножь на 3
вычти 1
умножь на 3
вычти 1
вычти 1
которая преобразует число 1 в 4.)
Решение:
У нас есть две команды: вычитание 1 и умножить число на 3. Другие действия мы производить не можем!
Нужно получить из 3 -> 16.
В похожих задачах ЕГЭ по информатике лучше всего начать с конца. Шестнадцать умножением на 3 мы никак не получим. Значит, последний командой будет вычитание. Семнадцать (16 + 1) тоже умножением на 3 не получить. Значит, предпоследней командой тоже будет вычитание. Восемнадцать (17 + 1), скорее всего получили умножением на 3! Шесть (18 / 3), получили умножением 2 на 3. Два — это 3 — 1.
Таким образом, получается цепочка команд 1 -> 2 -> 2 -> 1 -> 1
Ответ: 12211
Двоичное счисление на пальцах
Если у вас в школе была информатика, не исключено, что там было упражнение на перевод обычных чисел в двоичную систему и обратно. Маловероятно, что кто-то вам объяснял практический смысл этой процедуры и откуда вообще берётся двоичное счисление. Давайте закроем этот разрыв.
Эта статья не имеет практической ценности — читайте её просто ради интереса к окружающему миру. Если нужны практические статьи, заходите в наш раздел «Где-то баг», там каждая статья — это практически применимый проект.
Отличный план
Чтобы объяснить всё это, нам понадобится несколько тезисов:
- Система записи числа — это шифр.
- Мы привыкли шифровать десятью знаками.
- Но система записи чисел может быть любой. Это условность.
- Двоичная система — это тоже нормальная система.
- Всё тлен и суета.
Система записи — это шифр
Если у нас есть девять коров, мы можем записать их как 🐄🐄🐄🐄🐄🐄🐄🐄🐄 или как 9 × 🐄.
Почему 9 означает «девять»? И почему вообще есть такое слово? Почему такое количество мы называем этим словом? Вопрос философский, и короткий ответ — нам нужно одинаково называть числа, чтобы друг друга понимать. Слово «девять», цифра 9, а также остальные слова — это шифр, который мы выучили в школе, чтобы друг с другом общаться.
Допустим, к нашему стаду прибиваются еще 🐄🐄🐄. Теперь у нас 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄 — двенадцать коров, 12. Почему мы знаем, что 12 — это «двенадцать»? Потому что мы договорились так шифровать числа.
Нам очень легко расшифровывать записи типа 12, 1920, 100 500 и т. д. — мы к ним привыкли, мы учили это в школе. Но это шифр. 12 × 🐄 — это не то же самое, что 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄. Это некая абстракция, которой мы пользуемся, чтобы упростить себе счёт.
Мы привыкли шифровать десятью знаками
У нас есть знаки 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — всего десять знаков. Этим числом знаков мы шифруем количество единиц, десятков, сотен, тысяч и так далее.
Мы договорились, что нам важен порядок записи числа. Мы знаем, что самый правый знак в записи означает число единиц, следующий знак (влево) означает число десятков, потом сотен и далее.
Например, перед нами число 19 547. Мы знаем, что в нём есть:
1 × 10 000
9 × 1000
5 × 100
4 × 10
7 × 1
Если приглядеться, то каждый следующий разряд числа показывает следующую степень десятки:
1 × 104
9 × 103
5 × 102
4 × 101
7 × 100
Нам удобно считать степенями десятки, потому что у нас по десять пальцев и мы с раннего детства научились считать до десяти.
Система записи — это условность
Представим бредовую ситуацию: у нас не 10 пальцев, а 6. И в школе нас учили считать не десятками, а шестёрками. И вместо привычных цифр мы бы использовали знаки ØABCDE. Ø — это по-нашему ноль, A — 1, B — 2, E — 5.
Вот как выглядели бы привычные нам цифры в этой бредовой системе счисления:
| 0 — Ø 1 — A 2 — B 3 — C 4 — D 5 — E | 6 — AØ 7 — AA 8 — AB 9 — AC 10 — AD 11 — AE | 12 — BØ 13 — BA 14 — BB 15 — BC 16 — BD 17 — BE | 18 — CØ 19 — CA 20 — CB 21 — CC 22 — CD 23 — CE | 24 — DØ 25 — DA 26 — DB 27 — DC 28 — DD 29 — DE | 30 — EØ 31 — EA 32 — EB 33 — EC 34 — ED 35 — EE | 36 — AØØ 37 — AØA 38 — AØB 39 — AØC 40 — AØD 41 — AØE |
В этой системе мы считаем степенями шестёрки. Число ABADØ можно было бы перевести в привычную нам десятичную запись вот так:
A × 64 = 1 × 1296 = 1296
B × 63 = 2 × 216 = 432
A × 62 = 1 × 36 = 36
D × 61 = 4 × 6 = 24
Ø × 60 = 0 × 1 = 0
1296 + 432 + 36 + 24 + 0 = 1788. В нашей десятичной системе это 1788, а у людей из параллельной вселенной это ABADØ, и это равноценно.
Выглядит бредово, но попробуйте вообразить, что у нас в сумме всего шесть пальцев. Каждый столбик — как раз шесть чисел. Очень легко считать в уме. Если бы нас с детства учили считать шестёрками, мы бы спокойно выучили этот способ и без проблем всё считали. А счёт десятками вызывал бы у нас искреннее недоумение: «Что за бред, считать числом AD? Гораздо удобнее считать от Ø до E!»
То, как мы шифруем и записываем числа, — это следствие многовековой традиции и физиологии. Вселенной, космосу, природе и стадам коров глубоко безразлично, что мы считаем степенями десятки. Природа не укладывается в эту нашу систему счёта.
Например, свет распространяется в вакууме со скоростью 299 792 458 метров в секунду. Ему плевать, что нам для ровного счёта хотелось бы, чтобы он летел со скоростью 300 тысяч километров в секунду. А ускорение свободного падения тела возле поверхности Земли — 9,81 м/с2. Так и хочется спросить: «Тело, а ты не могло бы иметь ускорение 10 м/с2?» — но телу плевать на наши системы счисления.
Двоичная система (тоже нормальная)
Внутри компьютера работают транзисторы. У них нет знаков 0, 1, 2, 3… 9. Транзисторы могут быть только включёнными и выключенными — обозначим их 💡 и ⚫.
Мы можем научить компьютер шифровать наши числа этими транзисторами так же, как шестипалые люди шифровали наши числа буквами. Только у нас будет не 6 букв, а всего две: 💡 и ⚫. И выходит, что в каждом разряде будет стоять не число десяток в разной степени, не число шестёрок в разной степени, а число… двоек в разной степени. И так как у нас всего два знака, то получается, что мы можем обозначить либо наличие двойки в какой-то степени, либо отсутствие:
| 0 — ⚫ 1 — 💡 2 — 💡⚫ 4 — 💡⚫⚫ | 8 — 💡⚫⚫⚫ 9 — 💡⚫⚫💡 10 — 💡⚫💡⚫ 11 — 💡⚫💡💡 12 — 💡💡⚫⚫ 13 — 💡💡⚫💡 14 — 💡💡💡⚫ 15 — 💡💡💡💡 | 16 — 💡⚫⚫⚫⚫ 17 — 💡⚫⚫⚫💡 18 — 💡⚫⚫💡⚫ 19 — 💡⚫⚫💡💡 20 — 💡⚫💡⚫⚫ 21 — 💡⚫💡⚫💡 21 — 💡⚫💡💡⚫ 23 — 💡⚫💡💡💡 24 — 💡💡⚫⚫⚫ 25 — 💡💡⚫⚫💡 26 — 💡💡⚫💡⚫ 27 — 💡💡⚫💡💡 28 — 💡💡💡⚫⚫ 29 — 💡💡💡⚫💡 30 — 💡💡💡💡⚫ 31 — 💡💡💡💡💡 | 32 — 💡⚫⚫⚫⚫⚫ 33 — 💡⚫⚫⚫⚫💡 34 — 💡⚫⚫⚫💡⚫ 35 — 💡⚫⚫⚫💡💡 36 — 💡⚫⚫💡⚫⚫ 37 — 💡⚫⚫💡⚫💡 38 — 💡⚫⚫💡💡⚫ 39 — 💡⚫⚫💡💡💡 40 — 💡⚫💡⚫⚫⚫ 41 — 💡⚫💡⚫⚫💡 42 — 💡⚫💡⚫💡⚫ 43 — 💡⚫💡⚫💡💡 44 — 💡⚫💡💡⚫⚫ 45 — 💡⚫💡💡⚫💡 46 — 💡⚫💡💡💡⚫ 47 — 💡⚫💡💡💡💡 48 — 💡💡⚫⚫⚫⚫ 49 — 💡💡⚫⚫⚫💡 50 — 💡💡⚫⚫💡⚫ 51 — 💡💡⚫⚫💡💡 52 — 💡💡⚫💡⚫⚫ 53 — 💡💡⚫💡⚫💡 54 — 💡💡⚫💡💡⚫ 55 — 💡💡⚫💡💡💡 56 — 💡💡💡⚫⚫⚫ 57 — 💡💡💡⚫⚫💡 58 — 💡💡💡⚫💡⚫ 59 — 💡💡💡⚫💡💡 60 — 💡💡💡💡⚫⚫ 61 — 💡💡💡💡⚫💡 62 — 💡💡💡💡💡⚫ 63 — 💡💡💡💡💡💡 |
Если перед нами число 💡 ⚫💡⚫⚫ 💡💡⚫⚫, мы можем разложить его на разряды, как в предыдущих примерах:
💡 = 1 × 28 = 256
⚫ = 0 × 27 = 0
💡 = 1 × 26 = 64
⚫ = 0 × 25 = 0
⚫ = 0 × 24 = 0
💡 = 1 × 23 = 8
💡 = 1 × 22 = 4
⚫ = 0 × 21 = 0
⚫ = 0 × 20 = 0
256 + 0 + 64 + 0 + 0 + 8 + 4 + 0 + 0 = 332
Получается, что десятипалые люди могут записать это число с помощью цифр 332, а компьютер с транзисторами — последовательностью транзисторов 💡⚫💡⚫⚫ 💡💡⚫⚫.
Если теперь заменить включённые транзисторы на единицы, а выключенные на нули, получится запись 1 0100 1100. Это и есть наша двоичная запись того же самого числа.
Почему говорят, что компьютер состоит из единиц и нулей (и всё тлен)
Инженеры научились шифровать привычные для нас числа в последовательность включённых и выключенных транзисторов.
Дальше эти транзисторы научились соединять таким образом, чтобы они умели складывать зашифрованные числа. Например, если сложить 💡⚫⚫ и ⚫⚫💡, получится 💡⚫💡. Мы писали об этом подробнее в статье о сложении через транзисторы.
Дальше эти суммы научились получать супербыстро. Потом научились получать разницу. Потом умножать. Потом делить. Потом всё это тоже научились делать супербыстро. Потом научились шифровать не только числа, но и буквы. Научились их хранить и считывать. Научились шифровать цвета и координаты. Научились хранить картинки. Последовательности картинок. Видео. Инструкции для компьютера. Программы. Операционные системы. Игры. Нейросети. Дипфейки.
И всё это основано на том, что компьютер умеет быстро-быстро складывать числа, зашифрованные как последовательности включённых и выключенных транзисторов.
При этом компьютер не понимает, что он делает. Он просто гоняет ток по транзисторам. Транзисторы не понимают, что они делают. По ним просто бежит ток. Лишь люди придают всему этому смысл.
Когда человека не станет, скорость света будет по-прежнему 299 792 458 метров в секунду. Но уже не будет тех, кто примется считать метры и секунды. Такие дела.
Конвертер десятичных чисел в двоичные онлайн
Этот онлайн-калькулятор может переводить числа из одной системы счисления в любую другую, показывая подробный курс решений. А калькулятор рассчитан на:
- Десятичное преобразование в двоичное ,
- Двоичное преобразование в десятичное ,
- Преобразование десятичного в шестнадцатеричное,
- Десятичное преобразование в двоичное метод ,
- Метод преобразования десятичной запятой в двоичную с плавающей запятой ,
- Преобразователь десятичных чисел в двоичные с шагом,
- Десятичная дробь Преобразователь дроби в двоичный.
- Введите числа, которые необходимо перевести.
- Укажите его систему нумерации.
- Укажите, в какую систему счисления переводите.
- Щелкните «Перевести».
- Щелкните «Показать прогресс решений», чтобы просмотреть подробные решения для путешествий.
Валютный перевод чисел имеет одно поле ввода. В это поле необходимо ввести номер, который вы хотите перевести.
После этого обязательно нужно указать, в какой записи вы его ввели.«Его система счисления» Для этого под полем ввода находится график.
Если вы не нашли свою систему, выберите «Другое», и количество будет полем ввода. В этом поле вы должны ввести базовую систему одним числом без пробелов.
Затем вы должны выбрать число, которое вы хотите перевести в какую-то систему. Если вы снова не нашли нужную систему, вставьте ее в «другую».
После нажатия на «ПЕРЕВЕСТИ» результат появится в поле. Если вы хотите получить подробный курс решений, перейдите по соответствующей ссылке.
Перевод чисел в разных системах счисления
Система счисления — это набор символов (цифр) и правила их использования для представления чисел. Есть два типа систем счисления. Непозиционная система — некоторые буквы используются как цифры. Позиционная система — количественное значение числа зависит от его места в вводном номере. Положение фигуры называется разрядом. Номер ранга увеличивается справа налево. Количество различных цифр (символов), используемых в позиционной системе счисления для представления (записи) числа, называется основанием.
Однородная система — для каждой категории набор разрешенных символов (цифр) одинаков. В качестве примера мы используем десятичную систему счисления. Если записать число в однородной 10-й системе, то можно использовать в каждом разряде только одну цифру в диапазоне от 0 до 9, таким образом, допустимое число 450 (класс 1 st — 0, 2 nd — 5, 3 ряд — 4), а 4F5 — нет, так как буква F не входит в набор цифр от 0 до 9.
Почему нужно переносить номера из одной системы в другую?
При выполнении заданий на компьютере ввод исходных данных и вывод результатов вычислений обычно выполняется пользователем в привычной для него десятичной системе счисления.Однако, учитывая, что подавляющее большинство компьютеров используют двоичную систему счисления, возникает необходимость переводить числа из одной системы счисления в другую. Перевод чисел из q-one в десятичное происходит непосредственно из полиномиального выражения определенного числа.
Суть этого перевода — последовательное десятичное число и его частное деление на значение системы счисления q. Деление выполняется до тех пор, пока следующее частное не станет меньше основания q.Вычисленный остаток на последнем шаге — это самая старая (первая) цифра переданного номера. Результатом такого перевода числа в систему счисления q-one является запись последнего частного и всех остатков в обратном порядке.
Десятичная система счисления
Десятичная система счисления — это алфавит цифр, который состоит из десяти общеизвестных чисел и основания 10. Позиция цифры в номере называется разрядом. Ранг номера увеличивается справа налево, от младшего до старшего разряда.В десятичной системе цифра в крайнем правом положении (ранг) представляет количество единиц; сдвинутые на одну позицию влево цифры — число десятков, еще слева — сотни, тысячи и так далее. Соответственно у нас есть категория единиц, разряд десятков и так далее.
Может использоваться набор позиционных систем счисления, где основание равно или больше 2. Для преобразования чисел из десятичной системы счисления в двоичную систему счисления используйте так называемый «алгоритм замены», состоящий из следующих последовательностей:
- Разделите десятичное число A на 2.Частное Q запоминается для следующего шага, а остаток записывается как младший бит двоичного числа.
- Если частное Q не равно 0, возьмите его за новое делимое и повторите процедуру, описанную в шаге 1. Каждый новый остаток (0 или 1) записывается в битах двоичного числа в направлении от младшего разряда (минимум значащий бит) старшему.
- Алгоритм продолжается до тех пор, пока не получится частный Q = 0, а остаток a = 1, полученный в результате шагов 1 и 2.
Двоичная система счисления
Двоичная система счисления теперь используется практически во всех цифровых устройствах. Компьютеры, контроллеры и другие вычислительные устройства выполняют вычисления точно в двоичном формате. Цифровые устройства записи и воспроизведения звука, фото и видео хранят и обрабатывают сигналы в двоичной системе счисления. При передаче информации по цифровым каналам связи используется модель двоичной системы. Система названа так потому, что ее основание системы счисления равно двум (2) или в двоичной системе счисления 102 — это означает, что для изображения числа используются только две цифры «0» и «1».
Двойка, записанная справа внизу от числа, в дальнейшем будет обозначать основание системы счисления. Для десятичной системы основание системы счисления обычно не указывается. Чтобы преобразовать двоичное число в десятичное, это число должно быть записано как произведение суммы степеней основ двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления является наиболее популярным средством записи компактных двоичных цифр.Он широко используется при проектировании и разработке цифровых технологий. Как следует из названия, основанием системы счисления является число 16 или 1016 в шестнадцатеричной системе счисления. Чтобы не было путаницы, при записи чисел в позиционных системах счисления, отличных от десятичной, справа внизу от основных чисел ввода необходимо указывать систему счисления.
Первые десять чисел взяты из десятичной системы (0, 1,…, 8, 9) и к ним добавлены шесть букв (a, b, c, d, e и f). В шестнадцатеричном числе 3f7c2 буквы «f» и «c» являются шестнадцатеричными цифрами.В конце шестнадцатеричного числа может приниматься буква h. Таким образом можно отличить шестнадцатеричные числа от других систем счисления.
Десятичный преобразователь в двоичный
Чтобы использовать этот инструмент преобразования десятичного числа в двоичный , вы должны ввести десятичное значение, например 308, в левое поле ниже, а затем нажмите кнопку «Преобразовать». Таким образом вы можете преобразовать до 19 десятичных символов (макс.значение 9223372036854775807) до двоичного значения .
Результат преобразования десятичного числа в двоичное в базовых числах
Десятичная система
Десятичная система счисления является наиболее часто используемой и стандартной системой в повседневной жизни. В качестве основы (системы счисления) используется число 10. Следовательно, в нем 10 символов: числа от 0 до 9; а именно 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
Как одна из старейших известных систем счисления, десятичная система счисления использовалась многими древними цивилизациями.Сложность представления очень больших чисел в десятичной системе была преодолена с помощью индийско-арабской системы счисления. Индусско-арабская система счисления определяет позиции цифр в числе, и этот метод работает с использованием степеней основания 10; цифры возводятся в степень n th в соответствии с их положением.
Например, возьмем число 2345,67 в десятичной системе счисления:
- Цифра 5 стоит в позиции единиц (10 0 , что равно 1),
- 4 находится на позиции десятков (10 1 )
- 3 находится в позиции сотен (10 2 )
- 2 в тысячах (10 3 )
- Между тем, цифра 6 после десятичной точки находится в десятых долях (1/10, что составляет 10 -1 ), а 7 — в сотых (1/100, что составляет 10 -2 ) позиции
- Таким образом, число 2345.67 также можно представить следующим образом: (2 * 10 3 ) + (3 * 10 2 ) + (4 * 10 1 ) + (5 * 10 0 ) + (6 * 10 -1 ) + (7 * 10 -2 )
Двоичная система
Двоичная система счисления использует число 2 в качестве основания (основание). Как система счисления с основанием 2, она состоит только из двух чисел: 0 и 1.
Хотя она применялась в Древнем Египте, Китае и Индии для различных целей, двоичная система стала языком электроники и компьютеров в мире. современный мир.Это наиболее эффективная система для обнаружения состояния выключения (0) и включения (1) электрического сигнала. Это также основа для двоичного кода, который используется для компоновки данных в компьютерных машинах. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел.
Двоичное число читать проще, чем кажется: это позиционная система; следовательно, каждая цифра в двоичном числе возводится в степень двойки, начиная с самого правого с 2 0 . В двоичной системе каждая двоичная цифра относится к 1 биту.
Примеры преобразования десятичных чисел в двоичные
- (51) 10 = (110011) 2
- (217) 10 = (11011001) 2
- (8023) 10 = (1111101010111) 2
Таблица преобразования десятичных чисел в двоичные
| Десятичное | Двоичное | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 00000001 | |||||||||||
| 2 | 00000010 | |||||||||||
| 3 | 00000011 | |||||||||||
| 4 | 00000100 | 9022 | 7 | 00000111 | ||||||||
| 8 | 00001000 | |||||||||||
| 9 | 00001001 | |||||||||||
| 10 | 00001010 | |||||||||||
| 00001010 | ||||||||||||
| 00001010 | ||||||||||||
| 0000 11 | 00001010 | |||||||||||
| 0000 11 | 902200001101 | |||||||||||
| 14 | 00001110 | |||||||||||
| 15 | 00001111 | |||||||||||
| 16 | 00010000 | |||||||||||
| 17 | 00010011 | |||||||||||
| 2 0 | 00010100 | |||||||||||
| 21 | 00010101 | |||||||||||
| 22 | 00010110 | |||||||||||
| 23 | 00010111 | |||||||||||
| 24 | 24 | 00011010 | ||||||||||
| 27 | 00011011 | |||||||||||
| 28 | 00011100 | |||||||||||
| 29 | 00011101 | |||||||||||
| 30 | ||||||||||||
| 30 | ||||||||||||
| 33 | 00100001 | |||||||||||
| 34 | 00100010 | |||||||||||
| 35 | 00100011 | |||||||||||
| 36 | 00100100 | 00100100 | ||||||||||
| 39 | 902 28 00100111||||||||||||
| 40 | 00101000 | |||||||||||
| 41 | 00101001 | |||||||||||
| 42 | 00101010 | |||||||||||
| 43 | ||||||||||||
| 46 | 00101110 | |||||||||||
| 47 | 00101111 | |||||||||||
| 48 | 00110000 | |||||||||||
| 49 | 00110001 | |||||||||||
| 00110001 | ||||||||||||
| 52 | 00110100 | |||||||||||
| 53 | 00110101 | |||||||||||
| 54 | 00110110 | |||||||||||
| 55 | 00110111 | 00110111 | 58 | 00111010 | ||||||||
| 59 | 00111011 | |||||||||||
| 60 | 00111100 | |||||||||||
| 61 | 00111101 | |||||||||||
| 62 | 001111610 | 62 | 001111610 | 001111610 |
| Десятичное | Двоичное | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 65 | 01000001 | ||||||||||||
| 66 | 01000010 | ||||||||||||
| 67 | 01000011 | ||||||||||||
| 68 | 01000100 | 9022 | 71 | 01000111 | |||||||||
| 72 | 01001000 | ||||||||||||
| 73 | 01001001 | ||||||||||||
| 74 | 01001010 | ||||||||||||
| 01001101 | |||||||||||||
| 78 | 01001110 | ||||||||||||
| 79 | 01001111 | ||||||||||||
| 80 | 01010000 | ||||||||||||
| 81 | |||||||||||||
| 81 | 01010011 | ||||||||||||
| 84 | 01010100 | ||||||||||||
| 85 | 01010101 | ||||||||||||
| 86 | 01010110 | ||||||||||||
| 87 | 01010111 | 881011 | 01011010 | ||||||||||
| 91 | 01011011 | ||||||||||||
| 92 | +01011100 | ||||||||||||
| 93 | +01011101 | ||||||||||||
| 94 | +01011110 | ||||||||||||
| 95 | +01011111 | ||||||||||||
| 96 | 01100000 | ||||||||||||
| 97 | 01100001 | ||||||||||||
| 98 | 01100010 | ||||||||||||
| 99 | 01100011 | ||||||||||||
| 100 | 1011011|||||||||||||
| 1 03 | 01100111 | ||||||||||||
| 104 | 01101000 | ||||||||||||
| 105 | 01101001 | ||||||||||||
| 106 | 01101010 | ||||||||||||
| 107229 | 109229 | 109229 | 01101101 | ||||||||||
| 110 | 01101110 | ||||||||||||
| 111 | 01101111 | ||||||||||||
| 112 | 01110000 | ||||||||||||
| 113 | 113 | 113 | |||||||||||
| 116 | 01110100 | ||||||||||||
| 117 | 01110101 | ||||||||||||
| 118 | 01110110 | ||||||||||||
| 119 | 01110119 | 01110112 | 119 | 01110119 | |||||||||
| 122 | 01111010 | ||||||||||||
| 123 | 01111011 | ||||||||||||
| 124 | 01111100 | ||||||||||||
| 125 | 01111101 | 126 | 01111101 | 126 | 01111101 | 126 | 10000000 |
| Десятичное | Двоичное | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 129 | 10000001 | ||||||||||
| 130 | 10000010 | ||||||||||
| 131 | 10000011 | ||||||||||
| 132 | 10000100 | 10000100 | 9021 10000|||||||||
| 135 | 10000111 | ||||||||||
| 136 | 10001000 | ||||||||||
| 137 | 10001001 | ||||||||||
| 138 | 10001010 | ||||||||||
| 13 | |||||||||||
| 139 | 9022139 | 902210001101 | |||||||||
| 142 | 10001110 | ||||||||||
| 143 | 10001111 | ||||||||||
| 144 | 10010000 | ||||||||||
| 145 | 10010 | ||||||||||
| 145 | 10010011 | ||||||||||
| 148 | 10010100 | ||||||||||
| 149 | 10010101 | ||||||||||
| 150 | 10010110 | ||||||||||
| 151 | 10010116 | 100228 | |||||||||
| 154 | 10011010 | ||||||||||
| 155 | 10011011 | ||||||||||
| 156 | 10011100 | ||||||||||
| 157 | 10011101 | ||||||||||
| 10011101 | 160 | 10100000 | |||||||||
| 161 | 10100001 | ||||||||||
| 162 | 10100010 | ||||||||||
| 163 | 10100011 | ||||||||||
| 164 | 164 | ||||||||||
| 164 | 164 9022 | 10 100110 | |||||||||
| 167 | 10100111 | ||||||||||
| 168 | 10101000 | ||||||||||
| 169 | 10101001 | ||||||||||
| 170 | 10101010 | ||||||||||
| 171 | 10101011 | ||||||||||
| 172 | 10101100 | ||||||||||
| 173 | 10101101 | ||||||||||
| 174 | 10101110 | ||||||||||
| 175 | 10101111 | ||||||||||
| 176 | 10110000 | 10110000 | 10110000 | 179 | 10110011 | ||||||
| 180 | 10110100 | ||||||||||
| 181 | 10110101 | ||||||||||
| 182 | 10110110 | 10110110 | 1839 0228 10111001 | ||||||||
| 186 | 10111010 | ||||||||||
| 187 | 10111011 | ||||||||||
| 188 | 10111100 | ||||||||||
| 189 | 10111101 | ||||||||||
| 190 | 10111110 | ||||||||||
| 191 | 10111111 | ||||||||||
| 192 | 11000000 |
| Десятичное | Двоичное | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 193 | 11000001 | ||||||||
| 194 | 11000010 | ||||||||
| 195 | 11000011 | ||||||||
| 196 | 11000100 | 11000100 | 11000100 | 199 | 11000111 | ||||
| 200 | 11001000 | ||||||||
| 201 | 11001001 | ||||||||
| 202 | 11001010 | ||||||||
| 11001010 | |||||||||
| 11001101 | |||||||||
| 206 | 11001110 | ||||||||
| 207 | 11001111 | ||||||||
| 208 | 11010000 | ||||||||
| 9022 11010011 | |||||||||
| 212 | 11010100 | ||||||||
| 213 | 11010101 | ||||||||
| 214 | 11010110 | ||||||||
| 215 | 110226 | 215 | 110226 | ||||||
| 218 | 11011010 | ||||||||
| 219 | 11011011 | ||||||||
| 220 | 11011100 | ||||||||
| 221 | 11011101 | 221 | 11011101 | 221 | 11011101 | 221 902 224 | 11100000 | ||
| 225 | 11100001 | ||||||||
| 226 | 11100010 | ||||||||
| 227 | 11100011 | ||||||||
| 228 | 228 | ||||||||
| 228 | 11 100110 | ||||||||
| 231 | 11100111 | ||||||||
| 232 | 11101000 | ||||||||
| 233 | 11101001 | ||||||||
| 234 | 11101010 | ||||||||
| 235 | 11101011 | ||||||||
| 236 | 11101100 | ||||||||
| 237 | 11101101 | ||||||||
| 238 | 11101110 | ||||||||
| 239 | 11101111 | ||||||||
| 240 | 11110000 | ||||||||
| 241 | 11110001 | ||||||||
| 242 | 11110010 | ||||||||
| 243 | 11110011 | ||||||||
| 244 | 11110100 | ||||||||
| 245 | 11110101 | ||||||||
| 246 | 11110110 | 11110110 | 11110110 | ||||||
| 9 0228 11111001 | |||||||||
| 250 | 11111010 | ||||||||
| 251 | 11111011 | ||||||||
| 252 | 11111100 | ||||||||
| 253 | 11111101 | ||||||||
| 254 | 11111110 | ||||||||
| 255 | 11111111 |
Выучите двоичные отрицательные числа и дополнение до 2
Двоичные отрицательные числа!
Дополнение к положительным числам.
Введение
До сих пор все было достаточно просто. Теперь становится интересно. Есть несколько способов представить отрицательные числа в двоичном формате. В обычных десятичных числах мы можем просто поставить знак минуса (-) перед числом, чтобы указать, что оно отрицательное. В binray у нас нет такой роскоши, поскольку мы ограничены только 1 и 0.
Сначала мы исследуем две ранние реализации представления отрицательных чисел вместе с их недостатками, а затем подробно рассмотрим метод «Дополнение 2», который является наиболее часто используемым методом.
Величина знака — простой подход
Величина знака (иногда также называемая модулем знака) — самый простой из методов, которые мы можем использовать. Однако он используется не очень часто, так как он также наименее практичен (что вы скоро увидите). Однако понимание величины знака поможет вам лучше понять и оценить другие методы, поэтому я бы рекомендовал вам не пропускать этот раздел.
Знаковой величиной мы обозначаем один из битов (обычно крайний левый, также известный как самый старший бит), чтобы указать, является ли число положительным или отрицательным.Обычно «0» указывает на положительное число, а «1» указывает на отрицательное значение. Таким способом получаем:
Приведенный выше пример иллюстрирует важный момент при работе с отрицательными числами в двоичном формате. Поскольку мы должны назначить конкретный бит индикатором знака , мы должны указать, сколько битов будут представлены числа, и соответственно дополнить. В приведенном выше примере числа представлены с использованием 8 бит.Вы могли так же легко использовать 16, 32, 64 бит и т. Д.
Наблюдения
Представление отрицательных чисел в двоичном формате имеет некоторые интересные побочные эффекты.
Наибольшее число, которое мы можем представить (при заданном количестве битов фактически уменьшается вдвое. Это связано с тем, что остается то же количество комбинаций единиц и нулей, но теперь половина из них предназначена для представления отрицательных чисел. Фактически, со знаком На самом деле величина у нас чуть меньше половины, потому что ноль может быть представлен как 1000000 или 00000000 .С беззнаковыми (или без отрицательных чисел) с 8 битами имеем:
- 00000000 — представляет 0, наименьшее возможное число.
- 11111111 — 255, максимально возможное число.
- Всего представлено 256 возможных чисел.
Тогда как со знаковой величиной имеем:
- 11111111 — представляет -127, наименьшее возможное число.
- 10000000 — соответствует 0.
- 00000000 — тоже 0.
- 01111111 — это 127, максимально возможное число.
- Всего представлено 255 возможных чисел.
Выше мы упоминали, что крайний левый бит обычно обозначается как тот, который указывает знак числа, и что из-за этого нам нужно указать, сколько битов будет использоваться, и что каждое число должно быть дополнено до это количество бит.Можно спросить, почему это должно быть так. Например, почему бы и нет:
Используйте только необходимое количество битов и сделайте последний бит только битом знака. например:
- 4 может быть представлено как: 0100
- -4 как: 1100
- 9 представлено как: 01001
- -9 как: 11001
- и т. Д.
Или поместите знаковый бит как самый правый бит. например:
- 4 можно представить как: 1000
- -4 как: 1001
- 9 представлено как: 10010
- -9 как: 10011
- и т. Д.
На самом деле нет причин, по которым мы не могли бы этого сделать, но это имеет два нежелательных эффекта.Людям, читающим его, становится намного легче ошибаться. Для компьютеров, которым необходимо его интерпретировать, требуется больше обработки. (Это может показаться тривиальным из-за того, насколько мощными являются современные компьютеры, но большая часть этой мощности исходит из того, что они очень эффективны.)
И, наконец, арифметика? К сожалению, при таком способе представления положительных и отрицательных чисел нецелесообразно выполнять с ними арифметические операции. Вот почему в реальном мире величина знака используется очень редко.Однако важно понимать величину знака (и ее недостатки), чтобы полностью понять, почему метод дополнения 2 (поясняется ниже) является предпочтительным методом.
Дополнение до 1
Дополнениедо единицы — это следующий шаг после знаковой величины. Подобно величине знака, самый значимый бит указывает знак числа. Однако для отрицательных чисел мы инвертируем биты по сравнению с обычными. Давайте посмотрим на пример (снова с 8 битами):
Для знака величины:
- 4 будет представлено как: 00000100
- -4 будет представлено как: 100000100
С дополнением на 1 имеем:
- 4 будет представлено как: 00000100
- -4 будет представлено как: 11111011
Дополнение до 1 по-прежнему приводит к 2 значениям, которые представляют 0, 00000000 (0) и 11111111 (-0), но оно имеет преимущество в том, что теперь мы можем выполнять базовую арифметику очень похоже на то, что для беззнаковых (только положительных) двоичных числа.(См. Нашу страницу о двоичной арифметике, если вам нужно напомнить.)
Дополнение 2
Дополнение2 может сначала показаться немного устрашающим, но как только вы поймете механизм, он станет довольно простым.
Что мы делаем, так это утверждаем, что крайний левый бит на самом деле является отрицательным значением, которое он обычно представляет. Мы по-прежнему представляем то же количество значений, но немного смещаем числовую строку вниз. Допустим, мы работаем с 4-битными числами.
Как и в предыдущих методах, нам нужно заранее установить количество бит, которое мы собираемся использовать. Если нашему числу не требуется это количество битов, нам нужно заполнить его нулями.
В обычном двоичном формате без знака мы можем представить 16 значений (от 0 до 15). 4 бита (слева направо) представляют 8, 4, 2 и 1.
Заставляя крайний левый бит представлять -8 вместо 8, мы сдвигаемся на 8 позиций вниз по числовой строке и получаем следующий диапазон значений (7 — -8).4 бита теперь представляют -8, 4, 2 и 1.
Рассмотрим простой пример. В демонстрации ниже вы можете ввести различные 4-битные или 8-битные двоичные числа со знаком и посмотреть, как они преобразуются в десятичные значения.
4 бита 8 бит
Промежуточная сумма в десятичном формате:
Преобразование в и из дополнения 2
Преобразование из двоичного дополнения 2 в десятичное очень похоже на преобразование обычного двоичного (как мы видели в демонстрации выше).Единственное изменение состоит в том, что мы должны помнить о минусе значения самого левого бита.
Преобразование десятичной дроби в двойное дополнение включает в себя еще несколько шагов, но это не так уж сложно.
Если число положительное, то мы можем преобразовать так же, как и для двоичного файла без знака. Однако мы должны заполнить нулями необходимое количество бит. например. если мы работаем с 8 битами и нам нужно представить 6, тогда:
- Десятичная 6 переводится в двоичную систему как 110
- Заполнение становится 00000110
Если число отрицательное, мы сначала преобразуем его, как если бы это было положительное число (не забывая заполнять нулями), а затем инвертируем биты (т.е.переключите все 0 на 1 и наоборот) и, наконец, добавьте 1. Давайте посмотрим на пример (с 8 битами):
–
Давайте разберемся
Если вы просто хотите запомнить шаги, это круто, но многие из вас, вероятно, захотят понять, как работает это преобразование в дополнение 2.
Шаги 1, 2 и 3 довольно просты. Рассмотрим подробнее шаги 4 и 5.
На шаге 4 то, что мы делаем, немного интересно.Если мы проигнорируем крайний левый бит, инвертируя другие цифры, мы создали положительное число, которое можно добавить к нашему исходному числу, чтобы сформировать максимально возможное значение с таким количеством битов. Так, например, если у нас есть:
- 3 бита, то максимальное значение, которое мы можем представить, равно 7, то есть 111.
- Если у нас есть число 2, то это 010 в двоичном формате (с дополнением).
- Обращение цифр дает 101, что равно 5.
- 5 + 2 = 7
Если бы мы тогда сказали 5 минус 7, мы получили бы -2, что является нашим предполагаемым значением.Однако мы всегда будем вычитать число 1, превышающее максимальное число (в двоичной системе следующая цифра слева всегда будет на 1 больше максимального значения всех предыдущих битов).
Помните, что крайний левый бит является отрицательным по отношению к своему нормальному значению, поэтому здесь у нас будет 4-й бит, который обычно равен 8, но теперь равен -8 (отрицательный 1 больше, чем максимальное значение 7 из первых 3 бит). Инвертируя биты, мы устанавливаем это значение в 1, что означает, что он станет 5 минус 8, что равно -3.Затем мы добавляем 1, чтобы отрегулировать это, возвращая его к -2.
Что, если мы получим число больше, чем мы можем представить?
С ванильным (или беззнаковым) двоичным кодом это не проблема, если нам нужно большее число, мы можем просто добавить больше бит соответственно. Однако при использовании двоичного кода со знаком нам нужно утомиться, что количество используемых битов указано заранее, и нам нужно придерживаться этого. Если нам нужно представить большее значение, тогда нам нужно увеличить общее количество используемых бит, например, перейти с 8 бит на 16 бит, помня, что все числа, с которыми мы работаем, нужно будет отрегулировать, или просто принять, что это не может быть сделано.
Арифметика с дополнением до 2
Давайте посмотрим, как мы можем выполнять сложение и вычитание, используя числа с дополнением до 2. По сути, мы делаем то же самое, что и для обычных двоичных чисел без знака. Однако когда мы подходим к последнему шагу, есть небольшое изменение.
Есть несколько сценариев, на которые нам нужно обратить внимание:
- Перенос, происходящий для самого левого бита (т. Е. Создающий результат на 1 бит больше, чем начальные числа), может быть отброшен.(см. ниже, почему это так)
- Если мы складываем два положительных числа и самый левый бит в результате равен 1 , то произошло переполнение.
- Если мы складываем два отрицательных числа и самый левый бит в результате равен 0 , то произошло переполнение. (признак того, что это произошло, также будет заключаться в том, что был сброшенный перенос)
Переполнение возможно только в том случае, если два числа, которые нужно сложить, имеют один и тот же знак (т. Е. Оба положительные или отрицательные).
Под переполнением мы подразумеваем, что результат был числом больше или меньше, чем то, что может быть представлено с использованием данного количества битов.
В симуляторе ниже мы используем 8-битные числа с дополнением до 2. Помните, что наибольшее число, которое мы можем представить, — 127, а наименьшее число — -128, если учитывать, как мы обрабатываем самый левый бит.
Почему такое странное поведение с крайним левым битом?
Во-первых, давайте посмотрим на переполнения.В числах с дополнительным кодом до 2 мы можем определить знак числа, посмотрев на самый левый бит. Если это 0 , то число положительное, а если 1 , то число отрицательное. Если мы сложим два положительных числа, мы ожидаем, что результат будет положительным. Если в нашем результате самый левый бит равен 1, то наш результат — отрицательное число (что может быть не так) и произошло переполнение.
Аналогично, если мы складываем два отрицательных числа, результат также должен быть отрицательным.Если в нашем результате самый левый бит равен 0 , то результат положительный (что может быть не так), и, как следствие, произошло переполнение. Обратите внимание, что для этого должен быть отброшенный перенос в качестве последней операции, и это признак того, что это произошло.
Если мы складываем два отрицательных числа и есть перенос для самого левого бита, это не означает автоматически переполнение. Если самый левый бит после сброса переноса равен 1, то результат действителен.(отбрасываем перенос)
Чтобы понять, как в некоторых случаях мы можем отбросить перенос, но все же получить действительный результат, нам нужно посмотреть, как ведет себя наша числовая линия. С обычными числами каждый раз, когда мы добавляем 1 к нашему числу, мы перемещаемся на 1 пробел вдоль нашей числовой строки. С дополнительными числами 2 происходит то же самое поведение, однако, когда мы достигаем максимальной точки для количества битов, которые у нас есть, мы переносимся на другой конец числовой строки.
С 8 битами, если у нас есть следующее число:
Это представляет 127, что является наибольшим числом в нашей строке дополнительного числа до 2 (для 8 бит).
Если мы прибавим 1 к этому числу (и забудем, что это число с дополнением до 2 на секунду), мы получим:
Что с нормальными двоичными числами без знака будет представлять 128 (1 пробел от 127 в числовой строке), но в дополнении до 2 это представляет -128, что является противоположным концом числовой строки. Представьте, что мы изогнули числовую линию в круг и соединили два конца.
После этого прыжка продолжается нормальное поведение добавления 1 с перемещением на один пробел в числовой строке.например:
Представляет -127, что на один пробел от -128.
Отказ от последнего переноса позволяет нам учесть этот скачок на числовой линии.
Деятельность
Итак, лучший способ научиться этому — практиковать его, и теперь мы заставим вас это сделать.
Предположим 8-битные двоичные числа для следующих действий.