Ответы на тест 1 по Информатике 8 класс (Босова Л.Л. учебник)
Ответы на тест 1 по Информатике 8 класс
«Ответы на тест 1 по Информатике 8 класс» — это пособие для родителей для проверки правильности ответов обучающихся детей (ГДЗ) на «Тестовые вопросы для самоконтроля», указанные в учебнике Информатики в конце 1-й главы. Как утверждают авторы учебника (Л.Л.Босова, А.Ю.Босова) в конце каждой главы приведены тестовые задания, которые помогут оценить, хорошо ли учащиеся освоили теоретический материал и могут ли они применять свои знания для решения возникающих проблем.
Ответы на вопросы помогут родителям оперативно проверить выполнение указанных заданий.
Совокупность знаков, с помощью которых записываются числа, называется:
а) системой счисления
б) цифрами системы счисления
в) алфавитом системы счисления
г) основанием системы счисления
Правильный ответ: в) алфавитом системы счисления
Чему равен результат сложения двух чисел, записанных римскими цифрами: МСМ + LXVIII?
а) 1168
б) 1968
в) 2168
г) 1153
Правильный ответ: б) 1968
Число 301011 может существовать в системах счисления с основаниями:
а) 2 и 10
б) 4 и 3
в) 4 и 8
г) 2 и 4
Правильный ответ: в) 4 и 8
Двоичное число 100110 в десятичной системе счисления записывается как:
а) 36
б) 38
в) 37
г) 46
Правильный ответ: б) 38
В классе 1100102% девочек и 10102 мальчиков.
 Сколько учеников в классе?
Сколько учеников в классе?
а) 10
б) 20
в) 30
г) 40
Правильный ответ: б) 20
Сколько цифр 1 в двоичном представлении десятичного числа 15?
а) 1
б) 2
в) 3
г) 4
Правильный ответ: г) 4
Чему равен результат сложения чисел 1102 и 128?
а) 610
б) 1010
в) 100002
г) 178
Правильный ответ: в) 100002
Ячейка памяти компьютера состоит из однородных элементов, называемых:
а) кодами
б) разрядами
в) цифрами
г) коэффициентами
Правильный ответ: б) разрядами
Количество разрядов, занимаемых двухбайтовым числом, равно:
а) 8
б) 16
в) 32
г) 64
Правильный ответ: б) 16
В знаковый разряд ячейки для отрицательных чисел заносится:
а) +
б) —
в) 0
г) 1
Правильный ответ: г) 1
Вещественные числа представляются в компьютере в:
а) естественной форме
б) развёрнутой форме
в) экспоненциальной форме с нормализованной мантиссой
г) виде обыкновенной дроби
Правильный ответ: в) экспоненциальной форме с нормализованной мантиссой
Какое предложение не является высказыванием?
а) Никакая причина не извиняет невежливость.
б) Обязательно стань отличником.
в) Рукописи не горят.
г) 10112 = 1 • 23 + 0 • 22 + 1 • 21 + 1 • 20
Правильный ответ: б) Обязательно стань отличником
Какое высказывание является ложным?
а) Знаком v обозначается логическая операция ИЛИ.
б) Логическую операцию ИЛИ также называют логическим сложением.
в) Дизъюнкцию также называют логическим сложением.
г) Знаком v обозначается логическая операция конъюнкция.
Правильный ответ: г) Знаком v обозначается логическая операция конъюнкция.
Для какого из указанных значений числа X истинно высказывание ((X < 5) v (X < 3)) ˄ ((X < 2) v (X < 1)) ?
а) 1
б) 2
в) 3
г) 4
Правильный ответ: а) 1
Для какого символьного выражения верно высказывание: «НЕ (Первая буква согласная) И НЕ (Вторая буква гласная)»?
а) abcde
б) bcade
в) babas
г) cabab
Правильный ответ: а) abcde
Некоторый сегмент сети Интернет состоит из 1000 сайтов.
 Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:
Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:
| Ключевое слово | Количество сайтов, для которых данное слово является ключевым |
| Сканер | 200 |
| Принтер | 250 |
| Монитор | 450 |
Сколько сайтов будет найдено по запросу принтер | сканер \ монитор, если по запросу принтер \ сканер было найдено 450 сайтов, по запросу принтер & монитор — 40, а по запросу сканер & монитор — 50?
а) 900
б) 540
в) 460
г) 810
Правильный ответ: г) 810
Какому логическому выражению соответствует следующая таблица истинности?
| A | B | F |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Правильный ответ: в)
Когда сломался компьютер, его хозяин сказал: «Оперативная память не могла выйти из строя».
 Сын хозяина компьютера предположил, что вышел из строя процессор, а жёсткий диск исправен. Пришедший специалист по обслуживанию сказал, что, скорее всего, с процессором всё в порядке, а оперативная память неисправна. В результате оказалось, что двое из них сказали всё верно, а третий — всё неверно. Что же сломалось?
Сын хозяина компьютера предположил, что вышел из строя процессор, а жёсткий диск исправен. Пришедший специалист по обслуживанию сказал, что, скорее всего, с процессором всё в порядке, а оперативная память неисправна. В результате оказалось, что двое из них сказали всё верно, а третий — всё неверно. Что же сломалось?
а) оперативная память
б) процессор
г) процессор и оперативная память
Правильный ответ: б) процессор
На перекрёстке произошло дорожно-транспортное происшествие, в котором участвовали автобус (А), грузовик (Г), легковой автомобиль (Л) и маршрутное такси (М). Свидетели происшествия дали следующие показания. Первый свидетель считал, что первым на перекрёсток выехал автобус, а маршрутное такси было вторым. Другой свидетель полагал, что последним на перекрёсток выехал легковой автомобиль, а вторым был грузовик. Третий свидетель уверял, что автобус выехал на перекрёсток вторым, а следом за ним — легковой автомобиль.
 В результате оказалось, что каждый из свидетелей был прав только в одном из своих утверждений. В каком порядке выехали машины на перекрёсток? В вариантах ответов перечислены подряд без пробелов первые буквы названий транспортных средств в порядке их выезда на перекрёсток:
В результате оказалось, что каждый из свидетелей был прав только в одном из своих утверждений. В каком порядке выехали машины на перекрёсток? В вариантах ответов перечислены подряд без пробелов первые буквы названий транспортных средств в порядке их выезда на перекрёсток:
а) АМЛГ
б) АГЛМ
в) ГЛМА
г) МЛГА
Правильный ответ: б) АГЛМ
Какое логическое выражение соответствует следующей схеме?
Правильный ответ: г)
Вы смотрели «Ответы на тест 1 по Информатике 8 класс (Босова, Ответы на вопросы теста главы 1)»
Перевод систем счисления — онлайн конвертер
Чтобы перевести число из одной системы счисления в другую, воспользуйтесь нашим онлайн конвертером:
Онлайн конвертер
Просто введите целое число и выберете системы счисления.
Для примера переведём число 123 из десятеричной системы в другие:
- в двоичную: 12310 = 11110112
- в восьмеричную: 12310 = 1738
- в шестнадцатеричную: 12310 = 7B16
- в троичную: 12310 = 111203
- в четверичную: 12310 = 13234
- в пятиричную: 12310 = 4435
- в шестиричную: 123
- в семиричную: 12310 = 2347
- в девятиричную: 12310 = 1469
- в одиннадцатиричную: 12310 = 10211
- в двенадцатиричную: 12310 = A312
- в тринадцатиричную: 12310 = 9613
- в четырнадцатиричную: 12310 = 8B14
- в пятнадцатиричную: 12310 = 8315
- в двадцатеричную: 12310 = 6320
Какие бывают системы счисления
Наиболее часто используемыми системами счисления являются:
- двоичная (2) – все числа записываются лишь посредством двух символов: 0 и 1.
 Используется в дискретной математике, информатике и программировании.
Используется в дискретной математике, информатике и программировании. - троичная (3) – числа записываются посредством трёх символов: 0, 1 и 2. Используется в цифровой электронике.
- восьмеричная (8) – числа записываются посредством цифр от 0 до 7. Используется в областях связных с цифровыми устройствами, так как восьмеричные числа легко переводятся в двоичные и обратно.
- десятеричная (10) – числа записываются посредством цифр от 0 до 9. Используется повсеместно.
- двенадцатеричная (12) – числа записываются посредством цифр от 0 до 9 и буквами A и B. Cчёт дюжинами…
- шестнадцатеричная (16) – числа записываются посредством цифр от 0 до 9 и буквами A, B, C, D, E, F. Широко используется в программировании и информатике.
- двадцатеричная (20) – числа записываются посредством цифр от 0 до 9 и буквами A, B, C, D, E, F, G, H, I (или J), J( или K). Исторически используется во многих языках, в частности в языке йоруба, у тлинкитов, в системе записи чисел майя, некоторых азиатских и кавказских языках.
См. также
Двоично-десятичная система счисления 📙 — Информатика
- Обозначение смешанной системы счисления
- Построение в двоично-десятичной системе
- Для чего нужно использование двоично-десятичной системы счисления
- Выгоды применения двоично-десятичной системы
В мире электронно-вычислительных технологий существуют различные системы счислений. Одним из классов систем счисления является класс смешанной системы счисления.
Определение
Смешанная система счисления — это такая система счисления, в которой числа одной системы с основанием Р, записываются цифрами другой системы с основанием Q, причем Q меньше Р. В данной системе Q считается младшим основанием, а Р — старшим, такая система называется Q-Р-ичной.
Таких систем существует несколько, одной из них является двоично-десятичная система счисления.
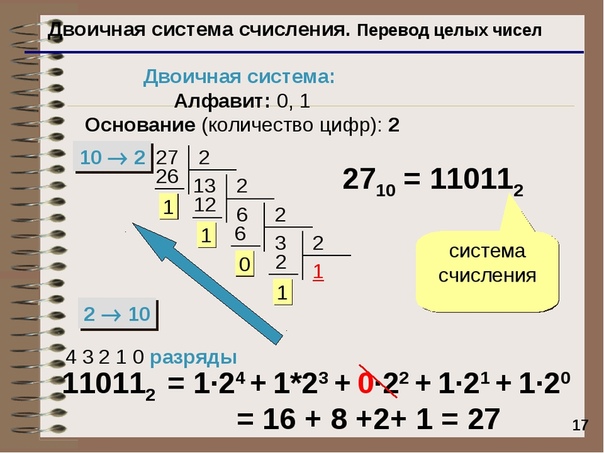
В двоично-десятичной системе счисления каждая десятичная цифра от 0 до 9 производится с помощью четырехразрядного числа, с использованием лишь элементарных цифр 0 и 1. А именно для записи цифры 0 используется код 0000, 1 — 0001, 2 — 0010, 3 — 0011,4 — 0100, 5 — 0101, 6 — 0110, 7 — 0111, 8 — 1000, 9 — 001. Для примера рассмотрим число десятичной системы счисления 925, в двоично-десятичной системе это число запишется как 1001 0010 0101. Формально это выглядит вот как:
А именно для записи цифры 0 используется код 0000, 1 — 0001, 2 — 0010, 3 — 0011,4 — 0100, 5 — 0101, 6 — 0110, 7 — 0111, 8 — 1000, 9 — 001. Для примера рассмотрим число десятичной системы счисления 925, в двоично-десятичной системе это число запишется как 1001 0010 0101. Формально это выглядит вот как:
92510 = 1001001001012-10.
В этой записи используются четверки цифр двоично-десятичной системы, которые последовательно отображают цифры 9, 2 и 5. Эти последовательные четверки цифр называются тетрадами.
В двоичной системе для изображения чисел также используются 0 и 1, но невзирая на это, изображения десятичного числа в двоично-десятичной системе отличается от его записи в двоичной системе счисления. К примеру, та же запись 100100100101 в этих двух системах будет обозначать разное десятичное число. Это выглядит так:
1001001001012-10 = 92510;
1001001001012 = 234110.
Подобное изображение числа зачастую используется в качестве вспомогательного этапа при трансформации числа из двоичной в десятичную систему счисления и наоборот. В двоично-десятичной системе счисления алгоритмы арифметических вычислений многозначных чисел намного сложнее, чем в простых системах счисления, но тем не менее эта система счисления часто используется для этих операций в микросхемах компьютеров и калькуляторов.
В двоично-десятичной системе счисления алгоритмы арифметических вычислений многозначных чисел намного сложнее, чем в простых системах счисления, но тем не менее эта система счисления часто используется для этих операций в микросхемах компьютеров и калькуляторов.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
При корректировке результатов элементарных арифметических операций с числами, записанными с помощью двоично-десятичных кодов, используют специальные команды для преобразования их в двоично-десятичную систему счисления. В данном случае применяется правило: для получения в результате простой арифметической операции сложения или вычитания число в тетраде, большее чем 9, к ней нужно прибавить число 6. Такое уравновешивание по разрядам производится обычно с помощью двоично-десятичной системы счисления. При этом самым целесообразным является комплексное использование двоичной и двоично-десятичной систем счисления, так как при этом количество тактов уравновешивания намного меньшее, чем при использовании иных систем счисления.
Человеческому глазу понятна десятичная система изображения чисел, и мы используем ее практически в любой сфере жизни, где сталкиваемся с числами. Работа электроники построена на использовании двоичной системы вывода чисел. Поэтому вариант применения системы счисления с помощью двоично-десятичных кодов является компромиссным. Двоично-десятичные коды используется в тех микросхемах приборов, где есть потребность частого ввода и вывода десятичных чисел, к примеру, в электронных часах, калькуляторах, таймерах, дисплеях бытовой техники и прочих приборах, в которых нет смысла использовать универсальные микрокоды из-за ограниченного объема памяти.
В арифметических логических устройствах электронно-вычислительных машин есть специальные блоки арифметических вычислений, выполняющих операции на основании двоично-десятичной системы счисления. Во многих случаях это существенно повышает производительность электронно-вычислительных машин. Например, если рассмотреть системы автоматизированной обработки данных, в которых практически не используются арифметические вычисления, то процесс трансформации чисел из одной системы в другую занял бы длительный ресурс времени и памяти. Поэтому в микропроцессорах в таком случае применяются двоичные коды, но при этом они умеют распознавать команды трансформации в двоично-десятичные коды. В итоге результат изображается на дисплее в десятичной форме изображения числа, понятной человеку.
Поэтому в микропроцессорах в таком случае применяются двоичные коды, но при этом они умеют распознавать команды трансформации в двоично-десятичные коды. В итоге результат изображается на дисплее в десятичной форме изображения числа, понятной человеку.
Применение двоично-десятичной системы счисления в комплексе с двоичной системой, которая является одной из основных, позволяет создавать на рынке высокопроизводительные электронно-вычислительные машины. Это становится возможным благодаря применению блока десятичных арифметических операций без необходимости программного трансформирования чисел в двоичную систему.
Не нашли что искали?
Просто напиши и мы поможем
Трансформация чисел в двоично-десятичную систему из десятичной не требует громоздких арифметических вычислений, а является простой операцией с использованием четырехразрядных кодов тетрад, что производится автоматически при помощи элементарных алгоритмических программ.
Так как две двоично-десятичные цифры в сумме занимают всего 1 байт памяти, то с его помощью можно записать любую десятичную цифру от 0 до 99. Таким образом, используя всего лишь 1 байт для изображения двух любых десятичных цифр, возможно записать любое количество двоично-десятичных чисел с необходимым количеством десятичных разрядов.
Системы счисления — Информатика — подготовка к ЕГЭ
Система счисления — это набор символов и правила их применения для представления чисел.
Системы счисления могут быть позиционными и непозиционными. В позиционных системах значение цифры зависит от позиции, на которой стоит цифра в записи числа, а в непозиционных — не зависит.
В качестве примера непозиционной можно привести римскую систему счисления, в которой были приняты семь базовых чисел. В следующей таблице символам римской системы сопоставлены числа в десятичной:
| Символ | I | V | X | L | C | D | M |
| Число | 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Остальные числа получаются в результате сложения и вычитания по следующему правилу: если меньшее базовое число предшествует большему (стоит левее в записи), то оно вычитается, если же за базовым числом стоит меньшее или оно последнее — то складывается с результатом, при этом подряд не должно стоять больше трех одинаковых символов. Например,
Например,
IV: -1 + 5 = 4,
MCDXCVIII: 1000 — 100 + 500 — 10 + 100 + 5 + 1 + 1 + 1 = 1498
Максимальным числом, которое можно представить в классической римской системе является 3999.
В нашей повседневной жизни мы пользуемся десятичной позиционной системой счисления. В ней десять цифр — от 0 до 9, а их значение зависит от позиции. Цифра, которая находится в самом младшем (правом) разряде записи числа, обозначает количество единиц в числе. Цифра в следующем, более старшем разряде (левее самого младшего), обозначает количество десятков, в следующем — количество сотен, и т.д..
Количество цифр, используемых в системе счисления, называется основанием системы. В таблице приведены примеры, распространенных в информатике систем счисления, их основания и наборы цифр (алфавит):
| Система счисления | Основание | Используемые цифры |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Двоичная | 2 | 0, 1 |
| Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| Шестнадцате- ричная |
16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Так как обычных цифр всего десять, то для обозначения остальных цифр в шестнадцатеричной системе используются буквы латинского алфавита.
Основной системой в информатике является двоичная, потому что вычисления реализовать в электронных устройствах оказывается достаточно просто именно в этой системе. Современная компьютерная техника основана на электронных логических элементах, имеющих два уровня сигнала — низкий и высокий, соответствующих нулю и единице.
Ниже приведена таблица первых шестнадцати чисел в двоичной, восьмеричной и шестнадцатеричной системах счисления:
| Основание системы | |||
| 10 | 2 | 8 | 16 |
| 0 | 0000 | 00 | 0 |
| 1 | 0001 | 01 | 1 |
| 2 | 0010 | 02 | 2 |
| 3 | 0011 | 03 | 3 |
| 4 | 0100 | 04 | 4 |
| 5 | 0101 | 05 | 5 |
| 6 | 0110 | 06 | 6 |
| 7 | 0111 | 07 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Можно заметить, что во всех системах при последовательной записи чисел, сначала используется один разряд, в котором меняется цифра (символ алфавита системы), после того, как цифры исчерпаны, для представления следующего числа уже необходимо две цифры и оно обозначается как 10.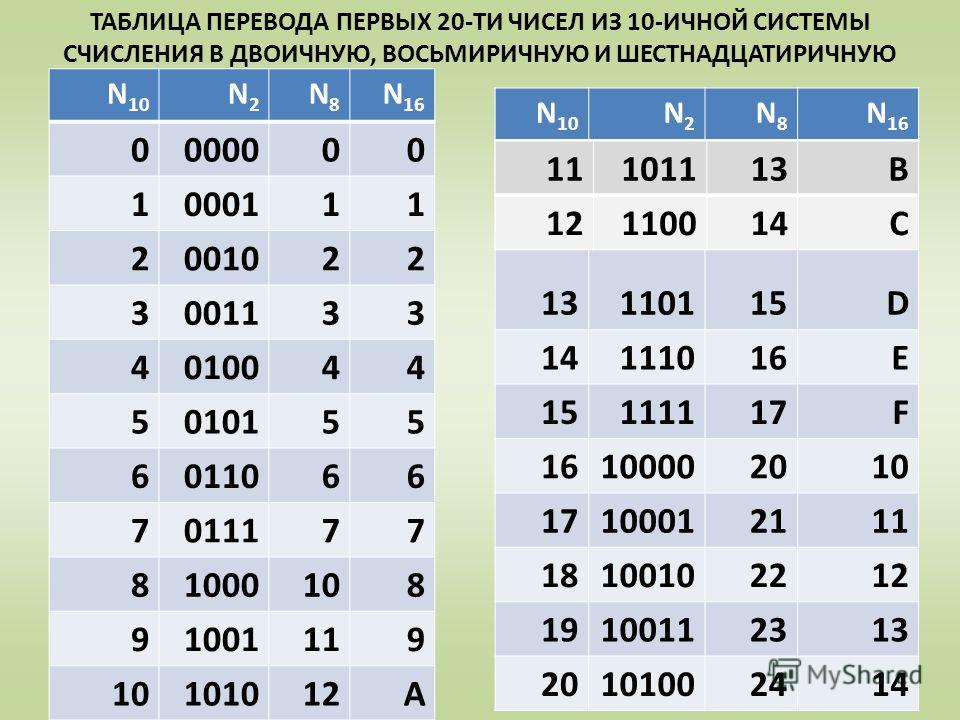 В общем случае имеет место быть равенство:
В общем случае имеет место быть равенство:
q = 10q,
где q — основание системы счисления, а 10q читается как один, ноль. Нижний индекс указывает в какой системе записано число. Для приведенных в таблице систем: 2=102, 8 = 108, 16 = 1016.
Также в таблице можно заметить, что трех-разрядному двоичному числу соответствует одноразрядное восьмеричное, а четырех-разрядному двоичному — одноразрядное шестнадцатеричное. Это значит, что зная эту таблицу, можно производить прямое преобразование между двоичным и восьмеричным, а также между двоичным и шестнадцатеричным числами.
Например, чтобы перевести 11010102 в шестнадцатеричного число, разделим условно число на группы по четыре разряда: 0110 1010, при этом отсчет ведем с младшего (правого) разряда, а группу, в которой разрядов меньше четырех, дополняем справа нулями. По таблице находим соответствие: 0110 — это 6, 1010 — A. Получилось — 6A16.
Переведем число 2738 в двоичный вид. 28 — 0102, 78 — 1112, 38 — 0112, записываем последовательно и получаем — 0101110112.
Перевод в десятичную систему счисления
Для n-разрядного целого числа в десятичной системе справедливо выражение:
Х10 = An-1 ⋅10n-1 + An-2 ⋅10n-2 + … + A1 ⋅101 + A0 ⋅100,
где
Х10 — число, записанное в десятичной системе, в нижнем индексе указано основание системы,
Аn-1 .. А0 — цифры в соответствующих разрядах числа.
Это выражение — разложение десятичного числа по степеням десяти — основания системы. Например, для числа 7583:
758310 = 7⋅103 + 5⋅102 + 8⋅101 + 3⋅100
Аналогичное выражение справедливо для любой позиционной системы счисления:
Xq = An-1⋅qn-1 + An-2⋅qn-2 + .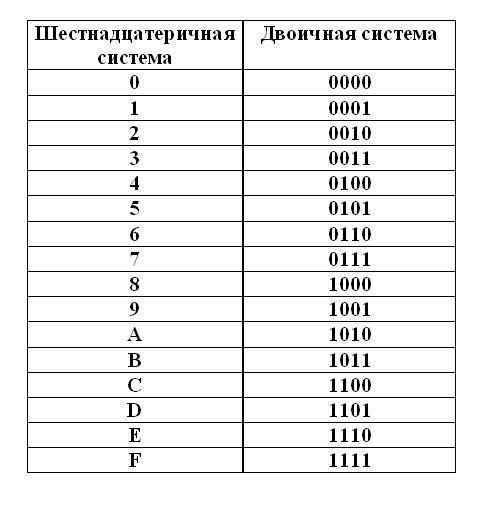
где
q — основание системы счисления,
Xq— число, записанное в системе счисления с основанием q,
Аn-1 .. А0 — цифры в соответствующих разрядах числа.
Например,
2C416 = 2⋅162 + 12⋅161 + 4⋅160 = 2⋅256 + 12⋅16 + 4⋅1 = 512 + 192 + 4 = 70810
Для числа с дробной частью:
Xq = An-1⋅qn-1 + An-2⋅qn-2 + … + A1⋅q1 + A0⋅q0 + A-1⋅q-1 + A-2⋅q-2…
Например,
10011,1012 = 1⋅24 + 0⋅23 + 0⋅22 + 1⋅21 + 1⋅20 + 1⋅2-1 + 0⋅2-2 + 1⋅2-3 =
= 16 + 0 + 0 + 2 + 1 + 0,5 + 0 + 0,125 = 19,62510
Перевод числа из десятичной системы в другие
Для перевода из десятичной системы в другую применяется метод последовательного деления числа на основание системы, в которую переводят, до тех пор, пока частное не окажется меньше основания другой системы. Результат записывается слева направо следующим образом: первым записывается последнее полученное частное, затем записывается каждый остаток последовательного деления в обратном порядке.
Результат записывается слева направо следующим образом: первым записывается последнее полученное частное, затем записывается каждый остаток последовательного деления в обратном порядке.
Например, переведем число 16910 в двоичную систему:
| 169 | 2 | |||||||||||||
| -168 | 84 | 2 | ||||||||||||
| 1 | -84 | 42 | 2 | |||||||||||
| 0 | -42 | 21 | 2 | |||||||||||
| 0 | -20 | 10 | 2 | |||||||||||
| 1 | -10 | 5 | 2 | |||||||||||
| 0 | -4 | 2 | 2 | |||||||||||
| 1 | -2 | 1 | ||||||||||||
| 0 |
Результат записываем, как показано стрелками: 101010012. Заметим, что в результате первого деления, полученный остаток является самым младшим разрядом числа в другой системе счисления.
Заметим, что в результате первого деления, полученный остаток является самым младшим разрядом числа в другой системе счисления.
Чтобы перевести дробную часть числа, представленному в десятичной системе, надо применить другой метод — последовательное умножение дробной части на основание системы, в которую переводим. Допустим, нужно перевести 0,37510 в двоичную систему счисления.
| 0, | 375 | ⋅ 2 |
| 0 | 750 | ⋅ 2 |
| 1 | 500 | ⋅ 2 |
| 1 | 000 |
Вычисления метода удобно записывать в виде столбика, Проводится вертикальная черта, отделяющая дробную часть, Если в результате умножения дробной части получаем число, в котором количество разрядов совпадает с количеством разрядов дробной части, то в следующей строке слева от вертикальной черты пишем 0, если же больше, то старшие разряды полученного произведения, превышающие дробную часть по количеству разрядов. Справа от черты пишем младшие разряды полученного произведения в количестве равным количеству разрядов дробной части.
Справа от черты пишем младшие разряды полученного произведения в количестве равным количеству разрядов дробной части.
В нашем случае, 375 ⋅ 2 = 750, значит, во второй строке пишем слева от черты 0, а справа — 750. Снова умножаем на 2 полученную дробную часть — 750 ⋅ 2 = 1500. Число разрядов 4, поэтому в следующей строке 1 пишем слева от черты, а 500 — справа. Теперь умножаем 500 на 2, заметьте, что умножаем только часть полученного числа, стоящую справа от черты. 500 ⋅ 2 = 1000. В следующей строке пишем 1 слева от черты, 000 — справа. Дальнейшее умножение не имеет смысла, так как будем получать всегда 0. Результатом перевода будет левый столбик — 0,0112.
Не всегда последовательное умножение приводит к получению конечной дроби, тогда умножение проводят столько раз, сколько требуется по условиям задачи, т.е. сколько знаков требуется после запятой.
Переведем 3427,58 из десятичной системы в шестнадцатеричную с точностью дробной части 4 знака после запятой.
Переводим целую часть методом деления:
| 3427 | 16 | ||||
| -32 | 214 | 16 | |||
| 22 | -16 | 13 | |||
| -16 | 54 | ||||
| 67 | 48 | ||||
| 64 | 6 | ||||
| 3 |
Так как 13 в шестнадцатеричной системе — D, то результат — D6316.
Переведем дробную часть:
| 0, | 58 | ∗ 16 |
| 9 | 28 | ⋅ 16 |
| 4 | 48 | ⋅ 16 |
| 7 | 68 | ⋅ 16 |
| 10 | 88 |
Полученное число D63,947A16.
Арифметические операции с числами в двоичной системе счисления
Методы арифметических операций с двоичными числами точно такие, какие используются для операций с десятичными числами. Рассмотрим несколько примеров.
101101112 + 100012
| + | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | ||||
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Записываем числа один под другим, при этом числа должны быть «выровнены» по правому краю. Складываем поразрядно, начиная с младших (правых) разрядов. При этом, если сумма разрядов получается двух-разрядной — старший переносим на следующий разряд общего результата.
Складываем поразрядно, начиная с младших (правых) разрядов. При этом, если сумма разрядов получается двух-разрядной — старший переносим на следующий разряд общего результата.
110110012 — 111012
| . | . | . | . | |||||
| — | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | ||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
10102 ∗ 1012
| ∗ | 1 | 0 | 1 | 0 | ||||
| 1 | 0 | 1 | ||||||
| + | 1 | 0 | 1 | 0 | ||||
| 1 | 0 | 1 | 0 | |||||
| 1 | 1 | 0 | 0 | 1 | 0 | |||
11000102 / 1012
| 110010 | 101 | ||||
| -101 | 1010 | ||||
| 101 | |||||
| -101 | |||||
| 00 | |||||
Свойства двоичных чисел
Число 2N в двоичной системе счисления записывается как единица и N нулей, например
24 = 100002.
Аналогично, для любой другой системы счисления, число qN в q-ой системе счисления записывается как единица и N нулей, например
33 = 10003.
Число 2N — 1 в двоичной системе счисления записывается как N единиц, например
24 — 1 = 1510 = 11112.
Для любой системы счисления, число qN — 1 в q-ой системе счисления записывается как N цифр (q-1), например
34 — 1 = = 22223.
Число 2N — 2K , при K < N в двоичной системе счисления записывается как (N — K) единиц и K нулей, например
25 — 22 = 111002.
Для системы счисления с основанием q, число qN — qK , при K < N записывается как (N — K) цифр (q-1) и K нулей, например
35 — 32 = 222003.
Имеют место быть выражения:
2N + 2N = 2 ∗ 2N = 2N+1,
2N = 2N+1 — 2N,
— 2N = — 2N+1 + 2N.
Задачи для самостоятельного решения
Сколько единиц в двоичной записи числа 113,5?
Сколько единиц в двоичной записи числа 21,25?
Сколько единиц в двоичной записи числа 32,625?
Сколько значащих нулей в двоичной записи числа 29,25?
Сколько значащих нулей в двоичной записи числа 18,125?
Укажите в порядке возрастания через запятую все основания систем, в которых запись десятичного числа 53 оканчивается на 3.
Укажите в порядке возрастания через запятую все основания систем, в которых запись десятичного числа 26 оканчивается на 2.
Укажите в порядке возрастания через запятую все основания систем, в которых запись десятичного числа 33 оканчивается на 1.
Укажите в порядке возрастания через запятую все основания систем, в которых запись десятичного числа 40 оканчивается на 4.
Укажите в порядке возрастания через запятую все основания систем, в которых запись десятичного числа 39 оканчивается на 7.
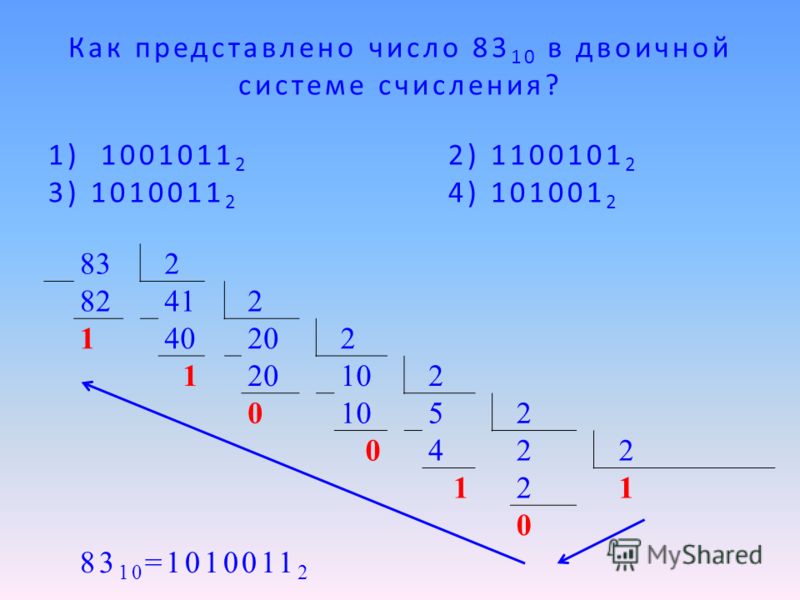
В системе счисления с некоторым основанием десятичное число 43 записывается как 111. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 85 записывается как 151. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 34 записывается как 202. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 148 записывается как 125. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 202 записывается как 244. Укажите это основание.
Укажите через запятую в порядке возрастания все числа, не превосходящие 30, запись которых в двоичной системе счисления оканчивается на 101. Числа указывайте в десятичной системе счисления.
Укажите через запятую в порядке возрастания все числа, не превосходящие 17, запись которых в двоичной системе счисления оканчивается на 11. Числа указывайте в десятичной системе счисления.
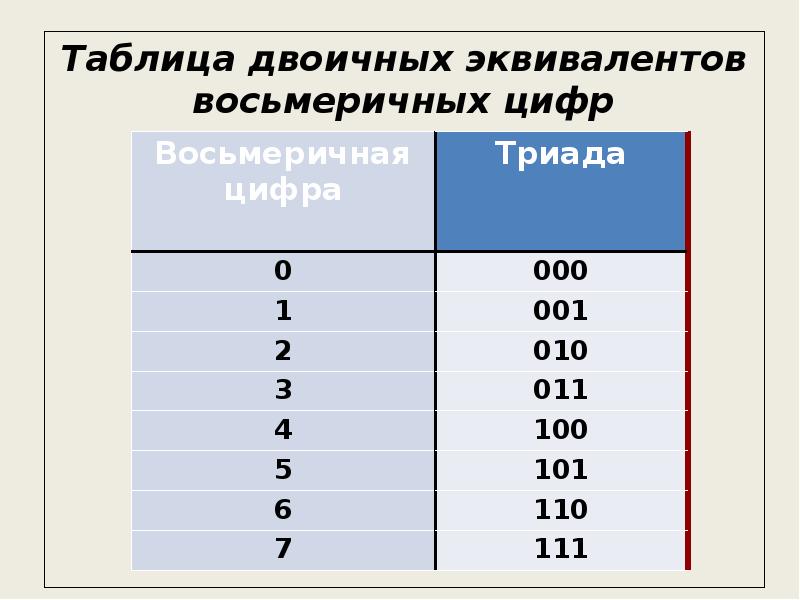
Укажите через запятую в порядке возрастания все числа, не превосходящие 35, запись которых в двоичной системе счисления оканчивается на 110. Числа указывайте в десятичной системе счисления.
Укажите через запятую в порядке возрастания все числа, не превосходящие 33, запись которых в двоичной системе счисления оканчивается на 100. Числа указывайте в десятичной системе счисления.
Укажите через запятую в порядке возрастания все числа, не превосходящие 15, запись которых в двоичной системе счисления оканчивается на 10. Числа указывайте в десятичной системе счисления.
Для кодирования букв А, Б, В, Г решили использовать двух-разрядные двоичные числа (от 002 до 112 соответственно). Какое число получится, если закодировать таким образом последовательность ГБАВ и перевести результат в шестнадцатеричную систему счисления?
Для кодирования букв А, Б, В, Г решили использовать двух-разрядные двоичные числа (от 002 до 112 соответственно).
 Какое число получится, если закодировать таким образом последовательность ВАБГ и перевести результат в восьмеричную систему счисления?
Какое число получится, если закодировать таким образом последовательность ВАБГ и перевести результат в восьмеричную систему счисления?Для кодирования букв А, Б, В, Г решили использовать двух-разрядные двоичные числа (от 002 до 112 соответственно). Какое число получится, если закодировать таким образом последовательность ВГБА и перевести результат в восьмеричную систему счисления?
Для кодирования букв А, Б, В, Г решили использовать двух-разрядные двоичные числа (от 002 до 112 соответственно). Какое число получится, если закодировать таким образом последовательность ГАВБ и перевести результат в шестнадцатеричную систему счисления?
Для кодирования букв А, Б, В, Г решили использовать двух-разрядные двоичные числа (от 002 до 112 соответственно). Какое число получится, если закодировать таким образом последовательность ГВБА и перевести результат в шестнадцатеричную систему счисления?
Переведите десятичное число 13,5 в двоичную систему счисления.
Переведите десятичное число 21,375 в двоичную систему счисления.
Переведите десятичное число 41,25 в двоичную систему счисления.
Переведите десятичное число 38,75 в двоичную систему счисления.
Переведите десятичное число 27,625 в двоичную систему счисления.
Переведите десятичное число 416 в восьмеричную систему счисления.
Переведите десятичное число 510 в восьмеричную систему счисления.
Переведите десятичное число 523 в шестнадцатеричную систему счисления.
Переведите десятичное число 680 в шестнадцатеричную систему счисления.
Переведите десятичное число 495 в шестнадцатеричную систему счисления.
Вычислите значение суммы 1012 + 118 + 1016. Результат запишите в виде десятичного числа.
Вычислите значение суммы 2214 + 558 + 5510. Результат запишите в виде шестнадцатеричного числа.
Вычислите значение разности 1116 — 118. Результат запишите в виде десятичного числа.
Вычислите значение разности 57310 — 5738. Результат запишите в виде шестнадцатеричного числа.
Вычислите значение разности A716 — 110102. Результат запишите в виде шестнадцатеричного числа.
Сколько единиц в двоичной записи восьмеричного числа 73518?
Сколько единиц в двоичной записи восьмеричного числа 12348?
Сколько значащих нулей в двоичной записи восьмеричного числа 75128?
Укажите наибольшее число, двоичная запись которого содержит ровно три значащих нуля и две единицы, причём единицы не стоят рядом. Ответ запишите в десятичной системе счисления.
Укажите наибольшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 9 нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.
Укажите наименьшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 6 нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.
Сколько существует натуральных чисел x, для которых выполняется неравенство 100110112 < x < 100111112? В ответе укажите только количество чисел, сами числа писать не нужно
В системе счисления с основанием N запись числа 87 оканчивается на 2 и содержит не более двух цифр. Чему равно число N? Если у задачи есть несколько решений, выберите наименьшее.
В системе счисления с основанием N запись числа 87 оканчивается на 2 и содержит не менее трёх цифр. Чему равно число N?
Сколько единиц в двоичной записи числа 42014 + 22015 – 8
Сколько значащих нулей в двоичной записи числа 416 + 236 – 16?
Сколько значащих нулей в двоичной записи числа 4512 + 8512 – 2128 – 250?
Сколько единиц в двоичной записи числа 42015 + 8405 – 2150 – 122?
Решите уравнение 121x + 1 = 1017. Ответ запишите в троичной системе счисления. Основание системы счисления указывать не нужно.
Значение арифметического выражения: 98 + 35 – 2 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Значение арифметического выражения: 98 + 35 – 9 – записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
§ 1.1. Системы счисления
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
- система счисления
- цифра
- алфавит
- позиционная система счисления
- основание
- развёрнутая форма записи числа
- свёрнутая форма записи числа
- двоичная система счисления
- восьмеричная система счисления
- шестнадцатеричная система счисления
1.1.1. Общие сведения о системах счисления
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.
В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.
Пример 1. У вавилонян узловыми являлись числа 1, 10, 60; в римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, С, D, М.
Рис. 1.1. Знаки, используемые для записи чисел в различных системах счисления
Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить следующие виды систем счисления:
- 1) унарная система;
- 2) непозиционные системы;
- 3) позиционные системы.
Простейшая и самая древняя система — так называемая унарная система счисления. В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта. Унарную систему ещё называют системой бирок.
Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.
Пример 2. В древнеегипетской системе счисления числа 1, 2, 3, 4, 10, 13, 40 обозначались соответственно следующим образом:
Те же числа в римской системе счисления обозначаются так: I, II, III, IV, X, XIII, XL. Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа.Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Десятичная система
Десятичная система записи чисел, которой мы привыкли пользоваться в повседневной жизни, с которой мы знакомы с детства, в которой производим все наши вычисления, — пример позиционной системы счисления. Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Алгоритмические числа образуются в ней следующим образом: значения цифр умножаются на «веса» соответствующих разрядов, и все полученные значения складываются. Это отчётливо прослеживается в числительных русского языка, например: «три-ста пять-десят семь».
Основанием позиционной системы счисления может служить любое натуральное число q > 1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0, 1, …, q—1, каждое из которых может быть записано с помощью одного уникального символа; младшей цифрой всегда является 0.
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
- Аq = ± (аn-1 • qn-1 + аn-2 • qn-2 + … + а0 • q0 + а-1 • q-1 + … + а-m • q-m). (1)
Здесь:
- А — число;
- q — основание системы счисления;
- аi — цифры, принадлежащие алфавиту данной системы счисления;
- n — количество целых разрядов числа;
- m — количество дробных разрядов числа;
- qi — «вес» i-го разряда.
Запись числа по формуле (1) называется развёрнутой формой записиСвёрнутной формой записи числа называется его представление в виде1 ± an-1an-2…a1a0,a-1…a-m.1 Далее будут рассматриваться только положительные целые числа.
Пример 3. Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
- 1 • 104 + 4 • 103 + 3 • 102 + 5 • 101 + 1 • 100 + 1 • 10-1.
1.1.2. Двоичная система счисления
Двоичной системой счисления называется позиционная система счисления с основанием 2. Для записи чисел в двоичной системе счисления используются только две цифры: 0 и 1.
На основании формулы (1) для целых двоичных чисел можно записать:
- аn-1аn-2…а1а0 = an-1 • 2n-1 + аn-2 • 2n-2 +…+ а0 • 20. (1′)
Например:
- 100112 = 1 • 24 + 0 • 23 + 0 • 22 + 1 • 21 + 1 • 20 = 24 + 21 + 20 = 1910.
Такая форма записи «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
Получим правило перевода целых десятичных чисел в двоичную систему счисления из формулы (1′).
Разделим аn-1 • 2n-1 + аn-2 • 2n-2 + … + а0 • 20 на 2. Частное будет равно аn-1 • 2n-2 + … + а1, а остаток будет равен а0.
Полученное частное опять разделим на 2, остаток от деления будет равен а1.
Если продолжить этот процесс деления, то на n-м шаге получим набор цифр:
- а0, а1, а2, … аn-1,.
которые входят в двоичное представление исходного числа и совпадают с остатками при его последовательном делении на 2.
Таким образом, для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 4. Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выш
двоичных цифр
| Двоичная цифра может быть только 0 или 1 |
В компьютерном мире « b inary dig it » часто сокращается до слова « bit »
Более одной цифры
Итак, есть только два способа получить двоичную цифру ( «0» и «1» или «Вкл.» И «Выкл.» ) … но как насчет 2 или более двоичных цифр?
Запишем их все, начиная с 1 цифры (можете проверить сами с помощью переключателей):
Вот последний список боком:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
И (без ведущих нулей) у нас есть первые 16 двоичных чисел:
| Двоичный: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Это пригодится! Чтобы запомнить последовательность двоичных чисел, просто подумайте:
- «0» и «1» {0,1}
- , затем повторите «0» и «1» еще раз, но с «1» впереди: {0,1,10,11}
- , затем повторите те с «1» впереди: {0,1,10,11,100,101,110,111}
Двоичный калькулятор
Используйте следующие калькуляторы для выполнения сложения, вычитания, умножения или деления двух двоичных значений, а также для преобразования двоичных значений в десятичные значения и наоборот.
Двоичное вычисление — сложение, вычитание, умножение или деление
Преобразовать двоичное значение в десятичное
Преобразовать десятичное значение в двоичное
Калькулятор RelatedHex | Калькулятор IP-подсети
Двоичная система счисления — это система счисления, которая функционирует практически идентично десятичной системе счисления, с которой люди, вероятно, более знакомы. В то время как в десятичной системе счисления используется число 10 в качестве основы, в двоичной системе используется число 2. Кроме того, хотя в десятичной системе используются цифры от 0 до 9, в двоичной системе используются только 0 и 1, и каждая цифра называется битом. .Помимо этих различий, такие операции, как сложение, вычитание, умножение и деление, все вычисляются по тем же правилам, что и десятичная система.
Практически все современные технологии и компьютеры используют двоичную систему из-за простоты ее реализации в цифровых схемах с использованием логических вентилей. Намного проще разработать оборудование, которое должно определять только два состояния: включено и выключено (или истина / ложь, присутствует / отсутствует и т. Д.). Использование десятичной системы требует оборудования, которое может определять 10 состояний для цифр от 0 до 9, и это более сложно.
Ниже приведены некоторые типичные преобразования между двоичными и десятичными значениями:
Двоичное / десятичное преобразование
| Десятичное | Двоичное | |||||||||
| 0 | 0 | |||||||||
| 1 | 1 | |||||||||
| 2 | 10 | |||||||||
| 3 | ||||||||||
| 7 | 111 | |||||||||
| 8 | 1000 | |||||||||
| 10 | 1010 | |||||||||
| 16 | 10000 | |||||||||
| 20 | 1010045 | |||||||||
| 2 n | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 9000 9000 | 90009000 | 00 | 1 | 0 |
| Цель: 18 | 18-16 = 2 | → | 2 — 2 = 0 | ||||||
Преобразование из двоичной в десятичную систему проще .Определите все значения разряда, в которых встречается 1, и найдите сумму значений.
Пример: 10111 = (1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (1 × 2 1 ) + (1 × 2 0 ) = 23
Отсюда: 16 + 4 + 2 + 1 = 23.
Сложение двоичных файлов
Двоичное сложение следует тем же правилам, что и сложение в десятичной системе, за исключением того, что вместо переноса 1, когда добавленные значения равны 10, перенос происходит, когда результат сложения равен 2.Обратитесь к примеру ниже для пояснения.
Обратите внимание, что в двоичной системе счисления:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, переносим 1, т.е. 10
EX:
| 1 0 | 1 1 | 1 1 | 1 0 | 1 | ||
| + | 000 | 000 | 1 | |||
| = | 1 | 0 | 0 | 1 | 0 | 0 |
Единственная реальная разница между двоичным и десятичным сложением состоит в том, что значение 2 двоичная система эквивалентна 10 в десятичной системе.Обратите внимание, что единицы с надстрочным индексом представляют собой перенесенные цифры. Распространенная ошибка, на которую следует обратить внимание при выполнении двоичного сложения, — это случай, когда 1 + 1 = 0 также имеет 1, перенесенную из предыдущего столбца вправо. Значение внизу должно быть равно 1 из перенесенного на 1, а не 0. Это можно увидеть в третьем столбце справа в приведенном выше примере.
Двоичное вычитание
Подобно двоичному сложению, есть небольшая разница между двоичным и десятичным вычитанием, за исключением тех, которые возникают из-за использования только цифр 0 и 1.Заимствование происходит в любом случае, когда вычитаемое число больше, чем число, из которого оно вычитается. При бинарном вычитании заимствование необходимо только тогда, когда 1 вычитается из 0. Когда это происходит, 0 в столбце заимствования по существу становится «2» (изменение 0-1 на 2-1 = 1), в то время как уменьшение 1 в заимствованном столбце на 1. Если следующий столбец также равен 0, заимствование должно происходить из каждого последующего столбца, пока столбец со значением 1 не может быть уменьшен до 0.Обратитесь к примеру ниже для пояснения.
Обратите внимание, что в двоичной системе счисления:
- 0 — 0 = 0
0 — 1 = 1, заимствовать 1, в результате -1 переносится на
1 — 0 = 1
1-1 = 0
EX1:
| -1 1 | 2 0 | 1 | 1 | 1 | ||
| — | 0 | 0004 10000004 1000|||||
| = | 0 | 1 | 0 | 1 | 0 | |
EX2:
| -1 1 | 2-1 0 | 0 | ||
| — | 0 | 1 | 1 | 24|
| 0 | 1 | |||
Обратите внимание, что отображаемые верхние индексы — это изменения, которые происходят с каждым битом при заимствовании.Столбец заимствования по существу получает 2 от заимствования, а столбец, из которого заимствовано, уменьшается на 1.
Двоичное умножение
Двоичное умножение, возможно, проще, чем его десятичный аналог. Поскольку используются только значения 0 и 1, результаты, которые должны быть добавлены, либо те же, что и для первого члена, либо 0. Обратите внимание, что в каждой последующей строке необходимо добавить заполнитель 0, а значение сдвинуть влево, как в десятичном умножении. Сложность двоичного умножения возникает из-за утомительного двоичного сложения, зависящего от количества битов в каждом члене.Обратитесь к примеру ниже для пояснения.
Обратите внимание, что в двоичной системе счисления:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | ||||||
| × | 09 9001 9001 | 00040 | 1 | 1 | 1 | |||||
| + | 1 | 0 | 1 | 1 | 1 | 0 | ||||
| 0 | 0 | 1 | 0 | 1 | ||||||
Как видно из приведенного выше примера, процесс двоичного умножения такой же, как и при десятичном умножении.Обратите внимание, что заполнитель 0 написан во второй строке. Обычно заполнитель 0 визуально не присутствует при десятичном умножении. Хотя то же самое можно сделать в этом примере (с предполагаемым заполнителем 0, а не явным), он включен в этот пример, потому что 0 актуален для любого двоичного калькулятора сложения / вычитания, подобного тому, который представлен на этой странице. Без отображения 0 можно было бы ошибиться, исключив 0 при добавлении двоичных значений, показанных выше.Еще раз обратите внимание, что в двоичной системе любой 0 справа от 1 имеет значение, а любой 0 слева от последней единицы в значении — нет.
EX:
- 1 0 1 0 1 1 0 0
= 0 0 1 0 1 0 1 1 0 0
≠ 1 0 1 0 1 1 0 0 0 0
Бинарный отдел
Процесс двоичного деления аналогичен длинному делению в десятичной системе счисления. Дивиденд по-прежнему делится на делитель таким же образом, с единственной существенной разницей, заключающейся в использовании двоичного, а не десятичного вычитания.Обратите внимание, что хорошее понимание двоичного вычитания важно для проведения двоичного деления. Обратитесь к примеру ниже, а также к разделу двоичного вычитания для пояснения.
(. 4) | — Pandia.ru
ПРЕДСТАВЛЕНИЕ ДАННЫХ И ЦИФРОВАЯ ЭЛЕКТРОНИКА
Представление данных
Люди используют компьютеры для работы со многими видами данных, включая чисел, текст, музыку, фотографии и видео.Представление данных — это процесс преобразования этих различных данных в форму (сегодня цифровую), которую компьютеры могут использовать для обработки.
Большинство компьютеров — это цифровых устройств , которые работают с отдельными отдельными и отдельными данными, такими как цифры 1 и 0. Напротив, аналоговое устройство работает с непрерывными данными. По аналогии, традиционный выключатель света имеет два дискретных состояния: включено и выключено, поэтому это цифровое устройство.С другой стороны, переключатель диммера имеет вращающийся диск , который контролирует непрерывный диапазон яркости. Следовательно, это аналоговое устройство. Большинство компьютеров используют простейшие цифровые технологии, их схемы имеют только два возможных состояния. Для удобства предположим, что одно из этих состояний включено, а другое выключено. Обсуждая эти состояния, мы обычно обозначаем включенное состояние цифрой 1 и выключенное состояние нулем. Эти единицы и нули обозначаются как двоичных цифр .Именно из этого члена мы получаем слово бит двоичная цифра . Компьютеры используют последовательности битов для цифрового представления чисел, букв, знаков препинания, музыки, изображений и видео.
Числовые данные состоят из чисел, которые могут использоваться в арифметических компьютерах, представляют числовые данные с использованием двоичной системы счисления, также называемой основанием 2. Двоичная система счисления состоит только из двух цифр: 0 и 1. В этой системе нет таких цифр, как 2. , поэтому число два в двоичном формате представляется как 10 (произносится как один ноль).В двоичном формате вы считаете 0 (ноль), 1 (один), 10 (один ноль) вместо того, чтобы считать 0, 1, 2 в десятичном формате. Важно понимать, что двоичная система счисления позволяет компьютерам представлять практически любое число, просто используя нули и единицы, которые удобно преобразовывать в электрические сигналы включения и выключения.
Символьные данные состоят из букв, символов и цифр, которые не используются в арифметических операциях. Цифровой компьютер использует ряд битов для представления букв, символов, а компьютеры , используют несколько типов кодов для представления символьных данных, включая ASCII, EBCDIC и Unicode. ASCII (произносится как ASK ee, Американский стандартный код для обмена информацией) требует только семь бит для каждого символа. ASCII требует кодов на 128 символов.
Расширенный набор ASCII, называемый Extended ASCII, использует восемь битов для представления каждого символа. Использование восьми битов вместо семи позволяет Extended ASCII до предоставлять коды для 256 символов. Unicode (произносится как YOU ni code) использует шестнадцать битов и предоставляет коды для 65 000 символов.
Для работы с музыкой и изображениями они должны быть оцифрованы. Термин от до оцифровка означает для преобразования необработанных аналоговых данных в цифровой формат, представленный нулями и единицами. Фотография или рисунок можно оцифровать, рассматривая их как серию цветных точек. Каждой точке присвоено двоичное число в соответствии с ее цветом. Цифровое изображение — это просто список номеров цветов для всех содержащихся в нем точек. Точно так же музыка может быть оцифрована с помощью , присвоив нотам двоичные коды .
Все данные, с которыми работает ваш компьютер, хранятся в файлах в виде длинных серий единиц и нулей. Ваш компьютер должен знать, следует ли интерпретировать эти единицы и нули как код ASCII, двоичные числа или код изображения или звука. Чтобы избежать путаницы с , большинство компьютерных файлов содержат заголовок файла с информацией о коде, используемом для представления данных файла. Заголовок файла может быть прочитан компьютером, но никогда не появляется при чтении информации заголовка, компьютер может определить, как было закодировано содержимое файла.
Количество битов и байтов
Несмотря на то, что слово бит является сокращением для двоичной цифры, оно может быть дополнительно сокращено, обычно в нижнем регистре b. байт состоит из восьми битов и обычно обозначается как прописная буква B. Скорость передачи обычно выражается в битах, тогда как объем памяти обычно выражается в байтах.
При работе с компьютерами вы часто встретите ссылок , например, 50 килобит в секунду.В обычном использовании килограмм, обозначаемый сокращенно K, означает тысячу. В десятичной системе счисления, которую мы используем ежедневно, число 1000 равно 10 в третьей степени или 10³. В мире компьютеров, где основание 2 является нормой, килограмм точно равен 1024, или 2¹º. Килобит (Кбайт или Кбит) составляет 1024 бита, мегабит — это 1 048 576 или 2 ² бит, гигабит — 1 073 741 824 бит или 2 º бит.
Цифровая электроника
Поскольку большинство компьютеров являются электронными устройствами, биты принимают форму электрических импульсов, которые могут проходить по цепям, почти так же, как электричество течет по проводу, когда вы включаете выключатель света.Все схемы, микросхемы и механические компоненты, составляющие компьютер, предназначены для работы с битами . Большинство из этих основных компонентов размещены в системном блоке компьютера. Системный блок компьютера обычно содержит печатные платы, запоминающие устройства и источник питания, который преобразует ток из настенной розетки переменного тока в постоянный ток, используемый компьютерными схемами.
Термины «компьютерный чип», «микрочип» и «чип» возникли как технический жаргон для интегральных схем.Интегральная схема ( IC ) представляет собой сверхтонкий слой полупроводникового материала, заполненный микроскопическими элементами схемы, такими как провода, транзисторы, конденсаторы , , , , логические вентили и резисторы. Полупроводниковые материалы — это вещества, обладающие свойствами между проводником и изолятором. Ассортимент микросхем внутри компьютера включает микропроцессор, модули памяти и вспомогательные схемы. Основная плата компьютера, называемая системной платой , , материнской платой или основной платой, содержит все необходимые микросхемы и обеспечивает связь между ними.
Понимание черт. Отметьте следующие утверждения как истинные или ложные.
1. И аналоговые, и цифровые устройства работают с непрерывными данными.
2. Двоичная система позволяет компьютерам представлять любое число или символ.
3. Чем больше битов используется для представления символьных данных, тем больше количество символов обеспечивается определенным кодом.
4.Чтобы узнать код, используемый для представления данных, компьютер должен прочитать заголовок файла.
5. Процесс оцифровки используется для преобразования цифровых данных в аналоговые.
6. Постоянный ток преобразуется в переменный ток, чтобы компьютер мог работать.
7. Интегральную схему часто называют Unicode.
Словарный запас
1. Сопоставьте близкие по значению слова.
1.повернуть 2. разрешить 3. задействовать 4. требовать 5. предоставлять 6. интерпретировать | а) разрешить б) понять в) раскрутить d) обеспечить e) необходимо f) применить |
2. Заполните поля, выбрав из представленных вариантов.
1. Основная память — только небольшой объем памяти для данных и инструкций, требуемых ЦП.
a) позволяет b) преобразовывает c) обеспечивает d) вращать
2. Чтобы изготовить микросхему, можно улучшить проводящие свойства отдельных частей микросхемы.
а) электрические импульсы б) полупроводниковый материал в) цифровые устройства г) двоичные числа
3. Некоторые микросхемы на материнской плате вставляются в специальные гнезда и разъемы, которые необходимо удалить для ремонта.
a) разрешить b) назначить c) избежать d) включить
4. Обслуживание даже встраиваемых компьютеров людьми.
a) преобразование b) диапазон c) использование d) требование
5. Самые мощные компьютерные системы с суперкомпьютерами с самой высокой скоростью обработки.
a) вращать b) упоминаются как c) избегать d) включать
6. Каждое нажатие клавиши на клавиатуре представляет собой буквенный символ в цифровом коде, понятном машине.
a) преобразует b) требует c) позволяет d) обеспечивает
7. В большинстве компьютеров с простейшими цифровыми технологиями их схемы имеют только два возможных состояния.
a) назначить b) использовать c) требовать d) диапазон
3. Составьте двухсловные выражения, объединяющие слова из двух списков.Затем заполните пробелы в следующих предложениях. Некоторые слова можно использовать более одного раза.
A: данные B: данные
разная цифра
встроенный заголовок
двоичная цепь
представление файла
символ
числовой
1. Двоичная система счисления представляет собой последовательность единиц и нулей.
2. Ан содержит микроскопические элементы, такие как провода, транзисторы и конденсаторы, которые размещены на очень маленьком квадрате полупроводникового материала.
3. Процесс преобразования данных в форму, которую компьютеры могут использовать для обработки, называется.
4. Сегодня компьютеры обычно представляют в цифровом виде.
5. Компьютер обрабатывает буквы и символы в слове, которые могут быть представлены строкой из нулей и единиц.
6. Все материалы, с которыми работает ваш компьютер, хранятся в файлах в виде длинных строк.
7. A хранится вместе с файлом и содержит информацию о коде, используемом для представления данных файла.
4. Заполните пробелы в тексте.
Большинство современных компьютеров — это электронные, цифровые устройства, которые работают с данными, закодированными в виде двоичных цифр, также известных как ___. Для представления числовых данных компьютер может использовать систему счисления ___. Для представления символьных данных компьютер использует расширенный ___, EBCDIC или Unicode. Эти коды также обеспечивают цифровое представление цифр от 0 до 9, которые отличаются от чисел тем, что они обычно не используются в математических компьютерах, а также ___ звуки, изображения и видео в единицах и нулях.
A ___ — это одиночная 1 или 0, тогда как ___ — это последовательность из восьми единиц и нулей. Скорость передачи обычно измеряется в ___, но объем памяти обычно измеряется в ___ или гигабайтах.
Встроенные типы— документация Python 3.9.1
В следующих разделах описаны стандартные типы, встроенные в переводчик.
Основными встроенными типами являются числа, последовательности, сопоставления, классы, экземпляры и исключения.
Некоторые классы коллекций изменяемы. Методы сложения, вычитания или
переставить своих участников на место и не возвращать конкретный предмет, никогда не возвращать
сам экземпляр коллекции, но Нет .
Некоторые операции поддерживаются несколькими типами объектов; в частности,
практически все объекты можно сравнить на равенство, проверить на истинность
значение и преобразован в строку (с помощью функции repr () или
немного другая функция str () ).Последняя функция неявно
используется, когда объект записывается функцией print () .
Проверка истинности
Любой объект может быть протестирован на истинность для использования в , если или в то время как условие или как операнд логических операций ниже.
По умолчанию объект считается истинным, если его класс не определяет __bool __ () , который возвращает False или метод __len __ () , который
возвращает ноль при вызове с объектом.Вот большинство встроенных
объектов, считающихся ложными:
константы, определенные как ложные:
НетиЛожь.ноль любого числового типа:
0,0,0,0j,Decimal (0),Дробь (0, 1)пустых последовательностей и коллекций:
'',(),[],{},set (),диапазон (0)
Операции и встроенные функции, которые имеют логический результат, всегда возвращают 0 или False для false и 1 или True для true, если не указано иное.(Важное исключение: логические операции или , и всегда возвращают
один из их операндов.)
Логические операции — и , или , не
Это логические операции, упорядоченные по возрастанию приоритета:
Эксплуатация | Результат | Банкноты |
|---|---|---|
| если x ложно, то y , иначе х | (1) |
| , если x ложно, то x , иначе л | (2) |
| если x ложно, то | (3) |
Примечания:
Это оператор короткого замыкания, поэтому он оценивает только второй аргумент, если первый неверен.
Это оператор короткого замыкания, поэтому он оценивает только второй аргумент, если первое верно.
notимеет более низкий приоритет, чем небулевы операторы, поэтомуnot a == bявляется интерпретируется какnot (a == b), аa == not bявляется синтаксической ошибкой.
Сравнения
В Python восемь операций сравнения. У всех они одинаковые
приоритет (который выше, чем у логических операций).Сравнения могут
быть скованным произвольно; например, x x x
В этой таблице приведены операции сравнения:
Эксплуатация | Значение |
|---|---|
| строго меньше |
| меньше или равно |
| строго больше |
| больше или равно |
| равно |
| не равно |
Binary Tutorial - Понятие и управление двоичными числами
Системы счисления!
Теория чисел и принцип работы двоичных чисел.
Введение
Числа повсюду вокруг нас, и по большей части мы принимаем их как должное. Если бы я предложил вам 1337 долларов, вы были бы счастливы, потому что знаете, что это довольно разумная сумма. Система счисления - это средство представления количества вещей. Десятичная дробь - это лишь одна из нескольких систем счисления, а другие, в типичной двоичной системе, важны для понимания в различных областях, особенно в вычислительной технике.
В нашем введении в двоичные, шестнадцатеричные и восьмеричные числа для начинающих вы изучите двоичные преобразования и арифметику с интерактивными демонстрациями и подробными объяснениями.
Наброски
Это двоичное руководство разделено на 3 раздела. В общем, я рекомендую вам проработать их по порядку, но если вы пришли сюда только для того, чтобы узнать о конкретной теме, тогда кто я такой, чтобы вас тормозить, просто идите прямо вперед.
- Системы счисления - Прочтите ниже, чтобы узнать о теории чисел.
- Преобразования - Как преобразовать двоичное в десятичное, шестнадцатеричное и восьмеричное числа.
- Арифметика - Узнайте, как выполнять различные арифметические операции с двоичными числами.
- Отрицательные числа - Узнайте, как работать с отрицательными числами в двоичном формате.
- Плавающая точка и дроби - Узнайте, как преобразовывать десятичные числа в двоичные дроби и числа с плавающей запятой и обратно.
Шаблоны и ярлыки
Когда вы работаете с системами счисления, вы можете сделать много сокращений по адресу:
- упростят работу с ними.
- поможет проверить вашу работу / выявить глупые ошибки, которые вы могли совершить.
Я укажу на некоторые из них, когда мы проработаем материал, но вы всегда должны искать их самостоятельно (не только при работе с числами, но и в других областях).
В общем, вы хотите следить за шаблонами, а затем думать о том, как вы можете использовать эти шаблоны для своей выгоды. Со временем вы научитесь их замечать.
Десятичная система
Десятичная система счисления - это та, с которой мы наиболее знакомы, мы используем ее каждый день.Десятичная дробь - это то, что мы называем позиционной системой счисления. То есть положение цифр придает смысл значению, которое они представляют. Другие системы счисления (двоичная, шестнадцатеричная и восьмеричная) также являются позиционными, поэтому, как только мы поймем основную теорию десятичной системы, мы сможем легко применить ее для понимания других систем.
Давайте посмотрим на пример:
Если у меня есть число 31415, на самом деле это означает:
30 000 + 1 000 + 400 + 10 + 5
А точнее:
| 3 * 10 4 | 30 000 |
| 1 * 10 3 | 1 000 |
| 4 * 10 2 | 400 |
| 1 * 10 1 | 10 |
| 5 * 10 0 | 5 |
В десятичном виде по основанию 10 .Это означает, что у нас есть 10 символов для представления значений (0–9). При перемещении по каждой позиции мы умножаем это число на 10 в степень этой позиции (начиная с 0 в крайнем правом углу).
Помните: любое значение в степени 0 всегда равно 1
Decimal удобна в качестве системы счисления, поскольку каждый раз, когда мы увеличиваем степень, все, что нам нужно сделать, это добавить еще один 0. Для каждой цифры в числе добавьте количество нулей, необходимых для позиции, и вы получите его позиционное значение.Затем каждая цифра естественным образом совпадает с общим числом.
двоичный
Binary следует тому же шаблону, что и Decimal, за исключением того, что вместо основания 10 это base 2 . Вместо 10 символов для представления значений у нас есть два (0 и 1).
Итак, Decimal - это система счисления с основанием 10, у нас есть 10 символов и умножается на степень 10. Отсюда следует, что Binary - это система счисления с основанием 2, у нас есть два символа и мы умножаем на степень 2.
Давайте посмотрим на пример:
Если у меня есть двоичное число 101010, это переводится в десятичное как:
32 + 0 + 8 + 0 + 2 + 0 = 42
или:
| 1 * 2 5 | 32 |
| 0 * 2 4 | 0 |
| 1 * 2 3 | 8 |
| 0 * 2 2 | 0 |
| 1 * 2 1 | 2 |
| 0 * 2 0 | 0 |
Как вы можете видеть из этого примера, двоичный код не так удобен для чтения и работы, как десятичный.Вы можете спросить, зачем тогда вообще использовать двоичный код? Ответ заключается в том, что это более простой формат для работы с компьютерами. Его также можно использовать в других областях как ярлык для представления настроек.
Поскольку все степени двойки, кроме 0, приводят к четному числу, единственный способ получить нечетное число - это иметь самую правую цифру, равную 1. Это можно использовать в качестве быстрой проверки при выполнении преобразований, которые вы еще не сделали. глупая ошибка.
Шестнадцатеричный и восьмеричный
Две другие системы счисления, которые обычно используются в вычислениях, - это шестнадцатеричная и восьмеричная.Это обе системы счисления.
- Шестнадцатеричная система счисления по основанию 16
- Восьмеричное число - основание 8
Оба они тесно связаны с двоичным кодом. Вы заметите, что:
Это не относится к десятичной системе счисления (нет степени 2, равной 10). Это дает шестнадцатеричные и восьмеричные характеристики по отношению к двоичным, которых нет у десятичных. Мы исследуем их в следующем разделе, преобразования.
Для шестнадцатеричного числа мы увеличиваем до 15 (помните, что мы начинаем с 0).Когда мы дойдем до 9, мы добавим буквы алфавита A - F, чтобы представить 10-15 (см. Справочную таблицу ниже).
Возьмем десятичное число 27.
В шестнадцатеричном формате это будет 1B, что в десятичном формате означает:
1 * 16 1 + 11 * 16 0 = 16 + 11
В восьмеричном формате это будет 33, что в десятичном представлении означает:
3 * 8 1 + 3 * 8 0 = 24 + 3
Префиксы
Как вы можете видеть из приведенных выше примеров, числа потенциально могут выглядеть одинаково, независимо от того, являются ли они двоичными, десятичными, восьмеричными или шестнадцатеричными.Если бы я дал вам число 2F7, вы бы сразу поняли, что оно шестнадцатеричное, но если бы я дал вам число 101, оно будет:
- 101 в двоичном формате и 5 в десятичном формате
- 101 в десятичной форме
- 101 в шестнадцатеричном формате и 257 в десятичном формате
- 101 в восьмеричной системе и 65 в десятичной системе
??
Как видите, количество, которое представляет 101, сильно различается в зависимости от используемой базы. Чтобы избежать этой двусмысленности, мы добавляем префиксы к номерам, чтобы идентифицировать их основу.
- Десятичное число не имеет префикса.
- Шестнадцатеричный имеет префикс Ox, например: Ox1B
- Octal имеет префикс O, например: O421
- Binary имеет префикс Ob, например: Ob1101
Некоторые люди вместо этого используют суффикс, но они не так популярны:
- Десятичное число не имеет суффикса.
- Шестнадцатеричный имеет суффикс H, например: 1BH
- Octal имеет суффикс O, например: 421O
- Binary имеет суффикс B, например: 1101B
Примечание: для префиксов и суффиксов выше это заглавная буква o, а не ноль.
На протяжении большей части этого урока я не буду использовать префиксы, а буду определять базу напрямую, чтобы было понятнее.
Справочная таблица
Вот справочная таблица для различных систем счисления.
| Десятичный | двоичный | восьмеричное | Шестнадцатеричный |
|---|---|---|---|
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | А |
| 11 | 1011 | 13 | В |
| 12 | 1100 | 14 | С |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | Ф |
Вы заметите, что в двоичном файле есть шаблон.