Разное

Численное интегрирование метод трапеций: Численное интегрирование методом трапеций

Содержание

Метод трапеций

Сегодня мы познакомимся с еще одним методом численного интегрирования, методом трапеций. С его помощью мы будем вычислять определенные интегралы с заданной степенью точности. В статье мы опишем суть метода трапеций, разберем, как выводится формула, сравним метод трапеции с методом прямоугольника, запишем оценку абсолютной погрешности метода. Каждый из разделов мы проиллюстрируем примерами для более глубокого понимания материала.

Метод трапеций

Предположим, что нам нужно приближенно вычислить определенный интеграл ∫abf(x)dx, подынтегральная функция которого y=f(x) непрерывна на отрезке [a;b]. Для этого разделим отрезок [a;b] на несколько равных интервалов длины h точками  a=x0<x1<x2<…<xn-1<xn=b. Обозначим количество полученных интервалов как n.

Найдем шаг разбиения: h=b-an. Определим узлы из равенства xi=a+i·h, i=0, 1,…, n.

На элементарных отрезках рассмотрим подынтегральную функцию xi-1; xi, i=1, 2,.., n.

При бесконечном увеличении n сведем все случаи к четырем простейшим вариантам:

Выделим отрезки xi-1; xi, i=1, 2,. .., n. Заменим на каждом из графиков функцию y=f(x) отрезком прямой, который проходит через точки с координатами xi-1; fxi-1 и xi; fxi. Отметим их на рисунках синим цветом.

Возьмем выражение f(xi-1)+f(xi)2·h в качестве приближенного значения интеграла ∫xi-1xif(x)dx. Т.е. примем ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.

Давайте посмотрим, почему метод численного интегрирования, который мы изучаем, носит название метода трапеций. Для этого нам нужно выяснить, что с точки зрения геометрии означает записанное приближенное равенство.

Для того, чтобы вычислить площадь трапеции, необходимо умножить полусуммы ее оснований на высоту. В первом случае площадь криволинейной трапеции примерно равна трапеции с основаниями  f(xi-1), f(xi) высотой h. В четвертом из рассматриваемых нами случаев заданный интеграл ∫xi-1xf(x)dx приближенно равен площади трапеции с основаниями -f(xi-1), -f(xi)  и высотой h, которую необходимо взять со знаком «-». Для того, чтобы вычислить приближенное значение определенного интеграла ∫xi-1xif(x)dx во втором и третьем из рассмотренных случаев, нам необходимо найти разность площадей красной и синей областей, которые мы отметили штриховкой на расположенном ниже рисунке.

Подведем итоги. Суть метода трапеций заключается в следующем: мы можем представить определенный интеграл ∫abf(x)dx  в виде суммы интегралов вида ∫xi-1xif(x)dx на каждом элементарном отрезке и в последующей приближенной замене ∫xi-1xif(x)dx≈f(xi-1)+f(xi)2·h.

Формула метода трапеций

Вспомним пятое свойство определенного интеграла: ∫abf(x)dx=∑i=1n∫xi-1xif(x)dx. Для того, чтобы получить формулу метода трапеций, необходимо вместо интегралов ∫xi-1xif(x)dx подставить их приближенные значения: ∫xi-1xif(x)dx=∑i=1n∫xi-1xif(x)dx≈∑i=1nf(xi-1)+f(xi)2·h==h3·(f(x0)+f(x1)+f(x1)+f(x2)+f(x2)+f(x3)+…+f(xn))==h3·f(x0)+2∑i=1n-1f(xi)+f(xn)⇒∫xi-1xif(x)dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)

Определение 1

Формула метода трапеций: ∫xi-1xif(x)dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)

Оценка абсолютной погрешности метода трапеций

Оценим абсолютную погрешность метода трапеций следующим образом:

Определение 2

δn≤maxx∈[a;b]f»(x)·n·h412=maxx∈[a;b]f»(x)·b-a312n2

Графическая иллюстрация метода трапеций

Графическая иллюстрация метода трапеций приведена на рисунке:

Примеры вычислений

Разберем примеры использования метода трапеций для приближенного вычисления определенных интегралов. Особое внимание уделим двум разновидностям заданий:

  • вычисление определенного интеграла методом трапеций для данного числа разбиения отрезка n;
  • нахождение приближенного значения определенного интеграла с оговоренной точностью.

При заданном n все промежуточные вычисления необходимо проводить с достаточно высокой степенью точности. Точность вычислений должна быть те выше, чем больше n.

Если мы имеем заданную точность вычисления определенного интеграла, то все промежуточные вычисления необходимо проводить на два и более порядков точнее. Например, если задана точность до 0,01, то промежуточные вычисления мы проводим с точностью до 0,0001 или 0,00001. При больших n промежуточные вычисления необходимо проводить с еще более высокой точностью.

Рассмотрим приведенное выше правило на примере. Для этого сравним значения определенного интеграла, вычисленного по формуле Ньютона-Лейбница и полученного по методу трапеций.

Итак, ∫057dxx2+1=7arctg(x)05=7arctg 5≈9,613805.

Пример 1

Вычислим по методу трапеций определенный интеграл ∫057×2+1dx для n равным 10.

Решение

Формула метода трапеций имеет вид ∫xi-1xif(x)dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)

Для того, чтобы применить формулу, нам необходимо вычислить шаг h по формуле h=b-an , определить узлы xi=a+i·h, i=0, 1,…, n, вычислить значения подынтегральной функции f(x)=7×2+1.

Шаг разбиения вычисляется следующим образом: h=b-an=5-010=0.5. Для вычисления подынтегральной функции в узлах xi=a+i·h, i=0, 1,…, n будем брать четыре знака после запятой:

i=0: x0=0+0·0.5=0⇒f(x0)=f(0)=702+1=7i=1: x1=0+1·0.5=0.5⇒f(x1)=f(0.5)=70,52+1=5,6…i=10: x10=0+10·0.5=5⇒f(x10)=f(5)=752+1≈0,2692

Внесем результаты вычислений в таблицу:

i012345678910
xi00.51
1,5		22,533,544,55
f(xi)75,63,52,15381,40,96550,70,52830,41170,32940,2692

Подставим полученные значения в формулу метода трапеций: ∫057dxx2+1≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)==0,52·7+2·5,6+3,5+2,1538+1,4+0,9655+0,7+0,5283+0,4117+0,3294+0,2692=9,6117

Сравним наши результаты с результатами, вычисленными по формуле Ньютона-Лейбница. Полученные значения совпадают до сотых.

Ответ: ∫057dxx2+1=9,6117

Пример 2

Вычислим по методу трапеций значение определенного интеграла ∫12112×4+13x-160dx с точностью до 0,01.

Решение

Согласно условию задачи a = 1; b = 2, f(x)=112×4+13x-160; δn≤0,01.

Найдем n, которое равно количеству точек разбиения отрезка интегрирования, с помощью неравенства для оценки абсолютной погрешности δn≤maxx∈[a;b]f»(x)·(b-a)312n2. Сделаем мы это следующим образом: мы найдем значения n, для которых будет выполняться неравенство maxx∈[a;b]f»(x)·(b-a)312n2≤0,01. При данных n формула трапеций даст нам приближенное значение определенного интеграла с заданной точностью.

Для начала найдем наибольшее значение модуля второй производной функции на отрезке [1; 2].

f'(x)=112×4+13x-160’=13×3+13⇒f»(x)=13×3+13’=x2

Вторая производная функция является квадратичной параболой f»(x)=x2. Из ее свойств мы знаем, что она положительная и возрастает на отрезке [1; 2]. В связи с этим maxx∈[a;b]f»(x)=f»(2)=22=4.

В приведенном примере процесс нахождения maxx∈[a;b]f»(x) оказался достаточно простым. В сложных случаях для проведения вычислений можно обратиться к наибольшим и наименьшим значениям функции. После рассмотрения данного примера мы приведем альтернативный метод нахождения maxx∈[a;b]f»(x).

Подставим полученное значение в неравенство maxx∈[a;b]f»(x)·(b-a)312n2≤0,01

4·(2-1)312n2≤0,01⇒n2≥1003⇒n≥5,7735

Количество элементарных интервалов, на которые разбивается отрезок интегрирования n является натуральным числом. Для поведения вычислений возьмем n равное шести. Такое значение n позволит нам достичь заданной точности метода трапеций при минимуме расчетов.

Вычислим шаг: h=b-an=2-16=16.

Найдем узлы xi=a+i·h, i=1, 0,…, n, определим значения подынтегральной функции в этих узлах:

i=0: x0=1+0·16=1⇒f(x0)=f(1)=112·14+13·1-160=0,4i=1: x1=1+1·16=76⇒f(x1)=f76=112·764+13·76-160≈0,5266…i=6: x10=1+6·16=2⇒f(x6)=f(2)=112·24+13·2-160≈1,9833

Результаты вычислений запишем в виде таблицы:

i012
3		456
xi1764332531162
fxi0,40,52660,69110,90521,18191,53591,9833

Подставим полученные результаты в формулу трапеций:

∫12112×4+13x-160dx≈h3·f(x0)+2∑i=1n-1f(xi)+f(xn)==112·0,4+2·0,5266+0,6911+0,9052+1,1819+1,5359+1,9833≈1,0054

Для проведения сравнения вычислим исходный интеграл по формуле Ньютона-Лейбница:

∫12112×4+13x-160dx=x560+x26-x6012=1

Как видим, полученной точности вычислений мы достигли.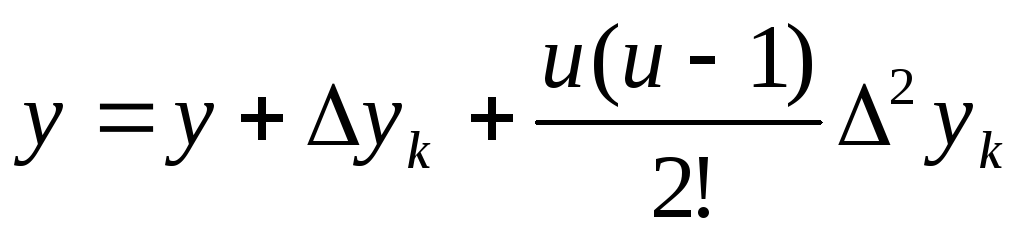

Ответ: ∫12112×4+13x-160dx≈1,0054

Для подынтегральных функций сложного вида нахождение числа n из неравенства для оценки абсолютной погрешности не всегда просто. В этом случае будет уместен следующий метод.

Обозначим приближенное значение определенного интеграла, которое было получено по методу трапеций для n узлов, как In. Выберем произвольное число n. По формуле метода трапеций вычислим исходный интеграл при одинарном (n=10) и удвоенном (n=20) числе узлов и найдем абсолютную величину разности двух полученных приближенных значений I20-I10.

Если абсолютная величина разности двух полученных приближенных значений меньше требуемой точности I20-I10<δn, то мы прекращаем вычисления и выбираем значение  I20 , которое можно округлить до требуемого порядка точности.

Если абсолютная величина разности двух полученных приближенных значений больше требуемой точности, то необходимо повторить действия с удвоенным количеством узлов (n=40).

Такой метод требует проведения большого объема вычислений, поэтому разумно использовать вычислительную технику для экономии времени.

Решим с помощью приведенного выше алгоритма задачу. С целью экономии времени опустим промежуточные вычисления по методу трапеций.

Пример 3

Необходимо вычислить определенный интеграл ∫02xexdx по методу трапеций с точностью до 0,001.

Решение

Возьмем n равное 10 и 20. По формуле трапеций получим  I10=8,4595380, I20=8,4066906.

I20-I10=8,4066906-8,4595380=0,0528474>0,001, что требует продолжения вычислений.

Возьмем n равное 40: I40=8,3934656.

I40-I20=8,3934656-8,4066906=0,013225>0,001, что также требует продолжения вычислений.

Возьмем n равное 80: I80=8,3901585.

I80-I40=8,3901585-8,3934656=0,0033071>0,001, что требует проведения еще одного удвоения числа узлов.

Возьмем n равное 160: I160=8,3893317.

I160-I80=8,3893317-8,3901585=0,0008268<0,001

Получить приближенное значение исходного интеграла можно округлив I160=8,3893317 до тысячных: ∫02xexdx≈8,389.

Для сравнения вычислим исходный определенный интеграл по формуле Ньютона-Лейбница: ∫02xexdx=ex·(x-1)02=e2+1≈8,3890561.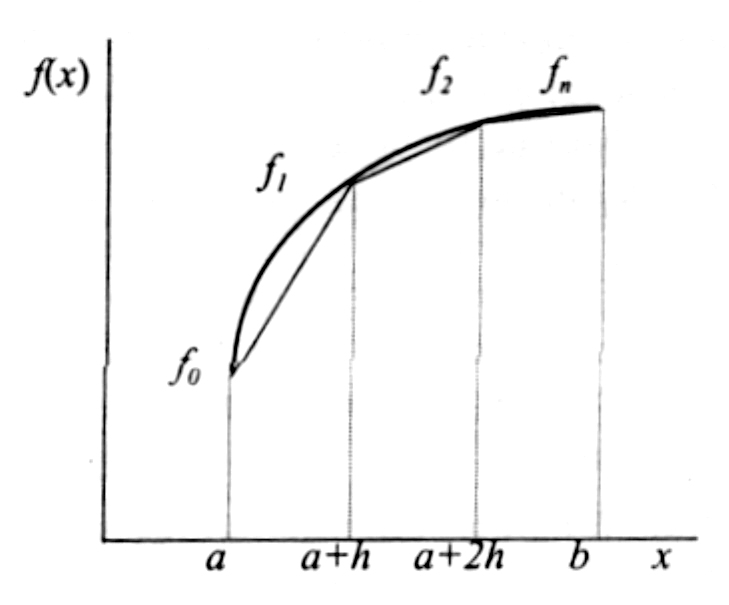

Требуемая точность достигнута.

Ответ: ∫02xexdx≈8,389

Погрешности

Промежуточные вычисления для определения значения определенного интеграла проводят в большинстве своем приближенно. Это значит, что при увеличении n начинает накапливаться вычислительная погрешность.

Сравним оценки абсолютных погрешностей метода трапеций и метода средних прямоугольников:

δn≤maxx∈[a;b]f»(x)n·h412=maxx∈[a;b]f»(x)·b-a312n2δn≤maxx∈[a;b]f»(x)n·h424=maxx∈[a;b]f»(x)·b-a324n2.

Метод прямоугольников для заданного n при одинаковом объеме вычислительной работы дает вдвое меньшую погрешность. Это делает метод более предпочтительным в тех случаях, когда известны значения функции в средних отрезках элементарных отрезков.

В тех случаях, когда интегрируемые функции задаются не аналитически, а в виде множества значений в узлах, мы можем использовать метод трапеций.

Если сравнивать точность метода трапеций и метода правых и левых прямоугольников, то первый метод превосходит второй в точности результата.

Интегрирование в MS EXCEL. Метод трапеций

history 20 ноября 2022 г.
    Группы статей

file_download Файл примера

Вычислим в MS EXCEL определенный интеграл методом трапеций (англ. Trapezoidal Rule). Оценим ошибку интегрирования, построим график функции.

В интернете есть много сайтов по автоматическому вычислению интегралов аналитическими и численными методами. Но, как правило, про использованный метод численного интегрирования ничего не говорится, а корректность вычислений проверить невозможно. В данном примере все вычисления прозрачны и можно задать необходимое количество интервалов разбиения. Правда, данный метод имеет относительно невысокую точность по сравнению с другими методами (если сравнивать его с методом Симпсона и методом интерполяционного полинома Лагранжа).

Так как функция, стоящая под знаком интеграла в общем случае может быть любая, то значение интеграла не всегда можно вычислить аналитически. Однако, можно воспользоваться тем фактом, что согласно теории, значение интеграла численно равно площади фигуры образованной графиком функции и осью Х (фигура выделена цветом).

Таким образом, задача нахождения интеграла сводится к нахождению площади этой фигуры. Площадь фигуры в общем случае можно найти численными методами, разбивая ее на простые однотипные фигуры, например трапеции. Т.к. площадь каждой трапеции найти легко, то простым суммированием площадей можно найти и интеграл. Платой за универсальность является ошибка интегрирования, которую впрочем можно оценить (будет показано далее).

Фактически метод трапеций основан на линейной интерполяции, т.е. график функции y = f(x) представляется в виде ломаной, соединяющей точки (xi, yi) прямыми линиями.

Площадь каждой трапеции можно найти следующим образом (см. рисунок ниже).

Фактически задача по нахождению интеграла сводится в основном к построению таблицы значений функции y=f(x) для заданных Х и нахождению их суммы. Интеграл можно найти с помощью вот такой простой формулы:

Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥3−5𝑥2+6𝑥+1. 2+6*B19+1.

Вычисленное приближенное значение интеграла для данной функции в интервале [0;4] равно 9,340, а точное 9,333, т.е. ошибка составляет менее 0,1%. Ниже показано как ее оценить.

В файле примера на листе «настраиваемый интервал» сделана форма для работы с разными количествами интервалов разбиения. При изменении количества интервалов график перестраивается автоматически, формулы для вычисления интеграла не нужно переписывать (как, впрочем, и расширять/ убавлять таблицу значений).

На рисунке ниже показано откуда появляется ошибка интегрирования. Для первых 2-х трапеций (образованы красными линиями) площадь меньше чем у истинной функции (синяя линия). Для следующих 2-х — площадь больше. Из этого следует, что метод трапеций хорошо работает для осциллирующих функций, когда ошибки компенсируют друг друга.

Простой многочлен был выбран в качестве демонстрационной функции, чтобы можно было вычислить интеграл точно и потом найти истинную ошибку, чтобы иметь возможность сравнить ее с оценкой.

К сожалению, для нахождения оценки ошибки потребуется вычислить первую производную. Сделать это чаще всего не сложно, но автоматизировать это в EXCEL не получится. Поэтому при изменении подинтегральной функции приходится вносить изменения в несколько формул на листе, а точнее — в 2 ячейки С19 и G31 (в файле примера они выделены красным). После ввода формул их нужно скопировать вниз.

В наем случае полученная оценка ошибки совпала с истинной ошибкой, что говорит о том что мы не ошиблись при вычислении производной и вводе формул на лист.

Совет: всегда оценивайте ошибку интегрирования.

 


Правило трапеций — Формула | Формула трапеций

В математике правило трапеций, также известное как правило трапеций или правило трапеций, представляет собой метод аппроксимации определенного интеграла в численном анализе. Правило трапеций — это правило интегрирования, используемое для вычисления площади под кривой путем деления кривой на маленькие трапеции. Сумма всех площадей маленьких трапеций даст площадь под кривой. Давайте разберемся с формулой правила трапеций и ее доказательством, используя примеры в следующих разделах.

1. Что такое правило трапеций?
2. Формула трапециевидной линейки
3. Вывод формулы правила трапеций
4. Как применить правило трапеций?
5. Часто задаваемые вопросы о правиле трапеций

Что такое правило трапеций?

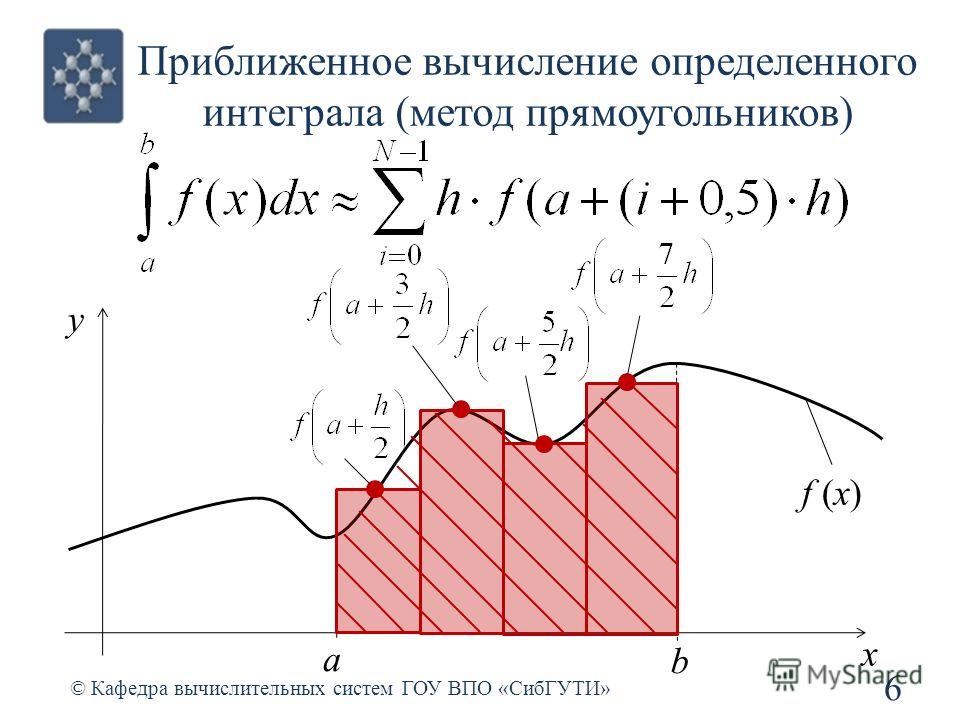
Правило трапеций применяется для решения определенного интеграла формы b ∫ a f(x) dx путем аппроксимации области под графиком функции f(x) трапецией и вычисления ее область. По правилу трапеций мы оцениваем площадь под кривой, разделив общую площадь на маленькие трапеции, а не на прямоугольники.

Формула трапециевидной линейки

Мы применяем формулу правила трапеций для решения определенного интеграла путем вычисления площади под кривой путем деления общей площади на маленькие трапеции, а не на прямоугольники. Это правило используется для аппроксимации определенных интегралов, где оно использует линейные аппроксимации функций. Правило трапеций берет среднее значение левой и правой суммы.

Пусть y = f(x) непрерывна на [a, b]. Разделим интервал [a, b] на n равных подынтервалов, каждый шириной h = (b — a)/n,

, так что a = x 0 < x 1 < x 2 < ⋯ < x n = b

Площадь = (h/2) [y 0  + 2 (y 1  + y 2  + y 3  + ….. + y 1 ) + у n ]

где,

  • у 0 , у 1 ,у 2 …. – значения функции при x = 1, 2, 3….. соответственно.

Вывод формулы правила трапеций

Мы можем вычислить значение определенного интеграла, используя трапеции, чтобы разделить площадь под кривой для данной функции.

Правило трапеций Утверждение: Пусть f(x) — непрерывная функция на интервале (a, b). Теперь разделите интервалы (a, b) на n равных подинтервалов шириной

Δx = (b — a)/n , такой, что a = x 0 < x 1  < x 2  < x 3  <…..< x 3

7 n 0 Тогда формула правила трапеций для площади, аппроксимирующей определенный интеграл b ∫ a f(x)dx, определяется как: 2 [f(x 0 ) + 2f(x 1 ) + 2f(x 2 ) +….2f(x n-1 ) + f(x n )]

где, x i = a + i△x

Если n → ∞, правая часть выражения приближается к определенному интегралу

Чтобы доказать правило трапеций, рассмотрим кривую, показанную на рисунке выше, и разделим площадь под этой кривой на трапеции. Мы видим, что первая трапеция имеет высоту Δx и параллельные основания длины y 0 или f(x 0 ) и y 1 или f 1 . Таким образом, площадь первой трапеции на приведенном выше рисунке может быть определена как

(1/2) Δx [f(x 0 ) + f(x 1 )]

Площади остальных трапеций равны (1/2)Δx [f(x 1 ) + f(x 2 )], (1/2)Δx [f(x 2 ) + f(x 3 )] и скоро.

Следовательно,

∫ b a f(x) dx ≈ (1/2)Δx (f(x 0 )+f(x 1 ) ) + (1/2)Δx f(x 1 )+f(x 2 ) ) + (1/2)∆x (f(x 2 )+f(x 3 ) ) + … + (1/2)∆x (f( n-1 ) + f(x n ))

После вынесения общего множителя ( 1/2)Δx и объединяя подобные члены, имеем

∫ b a f(x) dx≈ (Δx/2) (f(x 0 )+2 f(x 1 ) +2 f(x 2 )+2 f(x 3 )+ … +2f( n-1 ) + f(x n ) )

Как применить правило трапеций?

Правило трапеций можно применять для решения определенного интеграла любой заданной функции. Он вычисляет площадь под кривой, образованной функцией, путем деления ее на трапеции и является менее точным методом по сравнению с правилом Симпсона. И правило Симпсона, и правило трапеций дают приближенное значение, но правило Симпсона приводит к еще более точному приближенному значению интегралов, потому что правило Симпсона использует квадратичное приближение вместо линейного приближения.

Выполните следующие шаги, чтобы применить правило трапеций, чтобы найти площадь под заданной кривой, y = f(x).

  • Шаг 1: Запишите количество подинтервалов «n» и интервалов «a» и «b».
  • Шаг 2: Примените формулу для расчета ширины подинтервала, h (или) △x = (b — a)/n
  • Шаг 3: Подставьте полученные значения в формулу правила трапеций, чтобы найти приблизительную площадь заданной кривой,
    b ∫ a f(x)dx ≈ T n = (△x/2) [f(x 0 ) + 2 f(x 1 ) + 2 f(x 2 ) +….+ 2 f( n-1 ) + f( n )], где x i = a + i△x

Давайте рассмотрим несколько примеров, чтобы лучше понять правило трапеций.

Часто задаваемые вопросы о правиле трапеций

Почему используется правило трапеций?

Правило трапеций — это правило интегрирования, используемое для вычисления площади под кривой путем деления кривой на маленькие трапеции. Сумма всех площадей маленьких трапеций даст площадь под кривой. Согласно этому правилу, площадь под кривой оценивается путем деления общей площади на маленькие трапеции, а не на прямоугольники.

Что такое формула правила трапеций?

Формула правила трапеций: Площадь = (h/2)[y 0 +y n +2(y 1 +y 2 +y 3 +…..+y н-1 )]

где,

  • у 0 , у 1 ,у 2 …. – значения функции при x = 1, 2, 3….. соответственно.
  • ч = небольшой интервал (x 1 — x 0 )

Почему эта формула называется правилом трапеций?

Правило называется трапециевидным, потому что при оценке площади под кривой (определенного интеграла) общая площадь делится на маленькие трапеции, а не на прямоугольники. Затем находим площади этих маленьких трапеций на определенном интервале.

Используя формулу правила трапеций, найдите площадь, когда h = 2, y

0 = 4, y 1 = 8, y 2 = 12, y 3 = 15.

Используя формулу трапеции Площадь = (h/2)[y 0 +y n +2(y 1 +y 2 +y 3 +…..+y n-1 )]

= (2/2) [4+15+2( 8+12)]
= 1[19+40]
= 1[59]
= 59
Следовательно, площадь под кривой равна 59 кв. ед.

2.5: Численное интегрирование — средняя точка, трапеция, правило Симпсона

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    10269

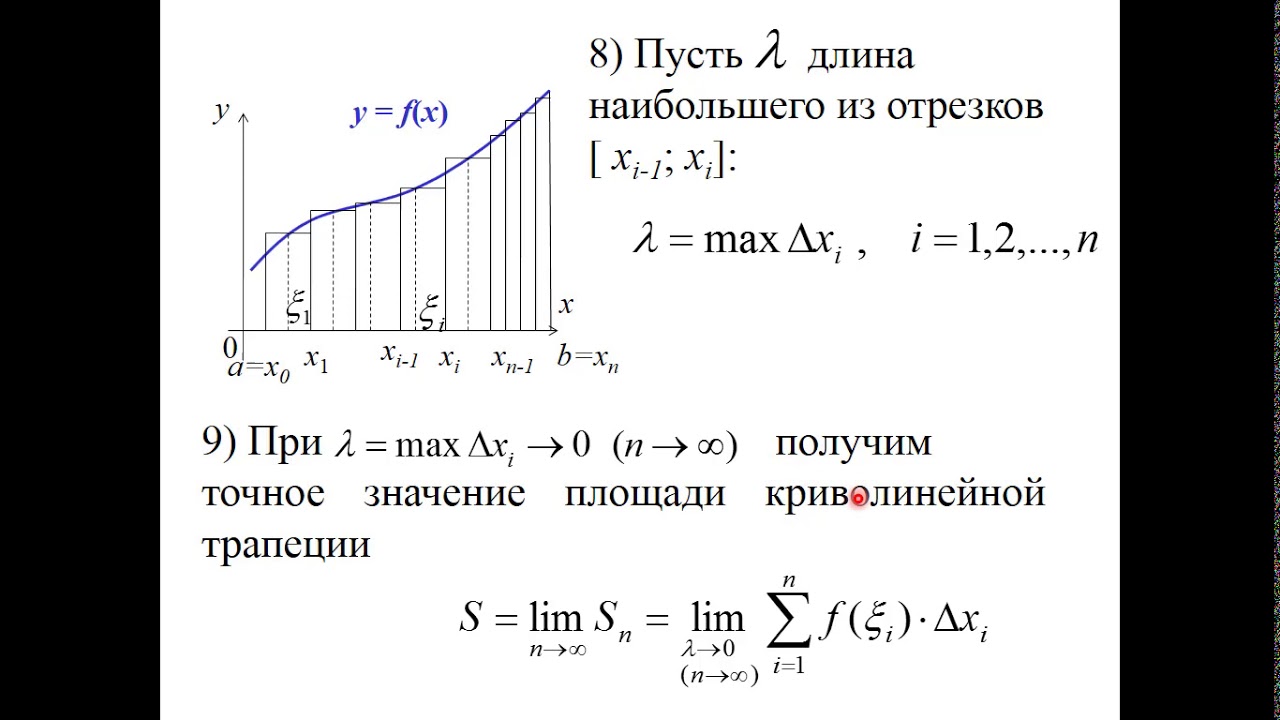    • Эта страница является черновиком и находится в активной разработке. b_af(x)\,dx\ ). Напомним, что сумма Римана функции \(f(x)\) по интервалу \([a,b]\) получается выбором разбиения 9n_{i=1}f(m_i)Δx\) соответствует сумме площадей прямоугольников, аппроксимирующих площадь между графиком \(f(x)\) и осью \(x\) над \([ а, б]\). На графике показаны прямоугольники, соответствующие \(M_4\) для неотрицательной функции на замкнутом интервале \([a,b].\)

    Рисунок \(\PageIndex{1}\): Правило средней точки аппроксимирует площадь между график \(f(x)\) и оси \(x\) путем суммирования площадей прямоугольников со средними точками, являющимися точками на \(f(x)\).

    Пример \(\PageIndex{1}\): использование правила средней точки с \(M_4\) 92\,dx\) с использованием четырех подынтервалов. Сравните результат с действительным значением этого интеграла.

    Решение: Каждый подинтервал имеет длину \( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Следовательно, подынтервалы состоят из

    \[\left[0,\ tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2} ,\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right]. \nonumber\]

    Середины этих подинтервалов являются \(\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right \}.\) Таким образом, 92_1\frac{1}{x}\,dx.\)

    Подсказка

    \( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)

    Ответить

    \(\dfrac{24}{35}\)

    Правило трапеций

    Мы также можем аппроксимировать значение определенного интеграла, используя трапеции, а не прямоугольники. На рисунке \(\PageIndex{2}\) область под кривой аппроксимирована трапециями, а не прямоугольниками.

    Рисунок \(\PageIndex{2}\): Трапеции можно использовать для аппроксимации площади под кривой, таким образом, аппроксимируя определенный интеграл.

    Правило трапеций для оценки определенных интегралов использует трапеции, а не прямоугольники для аппроксимации площади под кривой. Чтобы получить представление об окончательной форме правила, рассмотрите трапеции, показанные на рисунке \(\PageIndex{2}\). Мы предполагаем, что длина каждого подынтервала равна \(Δx\). Во-первых, напомним, что площадь трапеции с высотой \(h\) и длинами оснований \(b_1\) и \(b_2\) определяется выражением \(\text{Area}=\frac{1}{ 2}h(b_1+b_2)\). Мы видим, что первая трапеция имеет высоту \(Δx\) и параллельные основания длины \(f(x_0)\) и \(f(x_1)\). Таким образом, площадь первой трапеции на рисунке \(\PageIndex{2}\) равна 9b_af(x)\,dx≈\frac{Δx}{2}\big(f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f( x_4)\big).\nonumber\]

    Обобщая, сформулируем формально следующее правило.

    Правило трапеций

    Предположим, что \(f(x)\) непрерывно над \([a,b]\). Пусть \(n\) — натуральное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \( P=\{x_0,x_1,x_2…,x_n\}.\ )

    Набор

    \[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_ {n−1})+f(x_n)\big).\] 9nf(x_i)Δx.\)

    То есть \(L_n\) и \(R_n\) аппроксимируют интеграл, используя левую и правую конечные точки каждого подинтервала соответственно. Кроме того, внимательное изучение рисунка \(\PageIndex{3}\) позволяет нам сделать следующие замечания об использовании правил трапеций и правил середины для оценки определенного интеграла неотрицательной функции. Правило трапеций имеет тенденцию систематически завышать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически занижать значение определенного интеграла на интервалах, где функция вогнута вниз. С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично занижая значение определенного интеграла на тех же самых типах интервалов. Это приводит нас к гипотезе о том, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеций. 92_1\frac{1}{x}\,dx.\)

    Подсказка

    Множество \(Δx=\dfrac{1}{2}.\) Концы подынтервалов являются элементами множества \(P=\left\{1,\frac{3}{2},2\right \}.\)

    Ответить

    \(\dfrac{17}{24}\)

    Абсолютная и относительная погрешность

    Важным аспектом использования этих правил численной аппроксимации является вычисление погрешности их использования для оценки значения определенного интеграла. 2\,dx\), используя правило средней точки, найденное в Пример \(\PageIndex{1}\). 92_1\frac{1}{x}\,dx\) в \(\frac{24}{35}\) с использованием \(T_2\). Фактическое значение этого интеграла равно \(\ln 2\). Используя \(\frac{24}{35}≈0,6857\) и \(\ln 2≈0,6931,\), вычислите абсолютную ошибку и относительную ошибку.

    Подсказка

    Используйте предыдущие примеры в качестве руководства.

    Ответить

    абсолютная ошибка \(\приблизительно 0,0074,\) и относительная ошибка \(\приблизительно 1,1\%\)

    Границы погрешности для средней точки и правил трапеций

    В двух предыдущих примерах мы смогли сравнить нашу оценку интеграла с фактическим значением интеграла; однако у нас обычно нет такой роскоши. В общем, если мы аппроксимируем интеграл, мы делаем это потому, что не можем легко вычислить точное значение самого интеграла. Поэтому часто полезно иметь возможность определить верхнюю границу ошибки приближения интеграла. 2\,dx.\)

    Подсказка

    \(f»(x)=2,\) поэтому \(M=2.\)

    Ответить

    \(\dfrac{1}{192}\)

    Правило Симпсона

    С помощью правила средней точки мы оценили площади областей под кривыми с помощью прямоугольников. В некотором смысле мы аппроксимировали кривую кусочно-постоянными функциями. С помощью правила трапеций мы аппроксимировали кривую, используя кусочно-линейные функции. Что, если бы мы вместо этого аппроксимировали кривую с помощью кусочно-квадратичных функций? С 9{x_4}_{x_2}f(x)\,dx\) с интегралом от другой квадратичной функции, проходящей через \( (x_2,f(x_2)), \,(x_3,f(x_3)),\) и \((x_4,f(x_4)).\) Этот процесс продолжается с каждой последующей парой подынтервалов.

    Рисунок \(\PageIndex{4}\): С помощью правила Симпсона мы приближаем определенный интеграл, интегрируя кусочно-квадратичную функцию.

    Чтобы понять формулу, которую мы получаем для правила Симпсона, мы начнем с вывода формулы для этого приближения для первых двух подынтервалов. Проходя через вывод, мы должны помнить о следующих соотношениях: 9{x_4}_{x_0}f(x)\,dx=\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f( x_3)+f(x_4)).\nonumber\]

    Шаблон продолжается, когда мы добавляем пары подынтервалов к нашему приближению. Общее правило можно сформулировать следующим образом.

    Правило Симпсона

    Предположим, что \(f(x)\) непрерывно над \([a,b]\). Пусть \(n\) — четное положительное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \(P=\{x_0,x_1,x_2,…,x_n\}. \) Набор 9b_af(x)\,dx.\nonumber\]

    Точно так же, как правило трапеций является средним значением правил левой и правой руки для оценки определенных интегралов, правило Симпсона может быть получено из правил средней точки и правил трапеций с помощью взвешенное среднее. Можно показать, что \(S_{2n}=(\dfrac{2}{3})M_n+(\dfrac{1}{3})T_n\).

    Также можно ограничить ошибку при использовании правила Симпсона для аппроксимации определенного интеграла. Граница ошибки задается следующим правилом: 92_1\frac{1}{x}\,dx.\)

    Подсказка

    \[S_2=(\frac{1}{3}Δx(f(x_0)+4f(x_1)+f(x_2))\]

    Ответить

    \(\frac{25}{36}\)

    Ключевые понятия