Bigdecimal java округление: Как использовать BigDecimal в Java

Class BigDecimal Класс BigDecimal предоставляет операции для арифметики, управления масштабом, округления, сравнения, хеширования и преобразования формата.

java.lang.Object

java.lang.Number

java.math.BigDecimal

Все реализованные интерфейсы:

Serializable, Comparable<BigDecimal>

public class BigDecimal extends Number implements Comparable<BigDecimal>

Неизменяемые десятичные числа со знаком произвольной точности. BigDecimal состоит из произвольной точности целогоunscaled valueи 32-битное целое числоscale. Если шкала нулевая или положительная, шкала представляет собой количество цифр справа от десятичной точки. Если шкала отрицательна, немасштабированное значение числа умножается на десять в степени отрицания шкалы. Таким образом, значение числа, представленного BigDecimal , равно (unscaledValue × 10-scale) .

Класс BigDecimal предоставляет операции для арифметики, управления масштабом, округления, сравнения, хеширования и преобразования формата. Метод toString

toString() обеспечивает каноническое представление BigDecimal .

Класс BigDecimal дает пользователю полный контроль над поведением округления. Если режим округления не указан и точный результат не может быть представлен, выдается исключение ArithmeticException ;в противном случае вычисления могут выполняться с выбранной точностью и режимом округления путем предоставления операции соответствующего объекта MathContext .В любом случае для управления округлением предусмотрено восемь режимов округления . Использование целочисленных полей в этом классе (например, ROUND_HALF_UP ) для представления режима округления не рекомендуется; вместо этого следует использовать значения перечисления перечисления enum RoundingMode например, RoundingMode.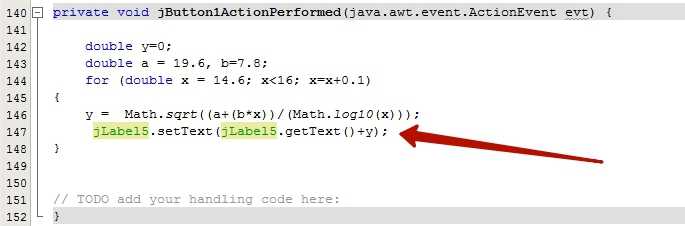

HALF_UP ).

Когда объект MathContext предоставляется с параметром точности 0 (например, MathContext.UNLIMITED ), арифметические операции являются точными, как и арифметические методы, которые не MathContext объект MathContext . Как следствие вычисления точного результата, параметр режима округления объекта MathContext с параметром точности 0 не используется и, следовательно, не имеет значения. В случае деления точное частное может иметь бесконечно длинное десятичное разложение; например, 1, деленная на 3. Если частное имеет неопределенное десятичное раскрытие и операция указана для возврата точного результата, генерируется ArithmeticException . В противном случае возвращается точный результат деления, как и для других операций.

Когда параметр точности не равен 0, правила арифметики

BigDecimal в целом совместимы с выбранными режимами работы арифметики, определенными в ANSI X3.274-1996 и ANSI X3. 274-1996 / AM 1-2000 (раздел 7.4). В отличие от этих стандартов BigDecimal включает множество режимов округления. Любые конфликты между этими стандартами ANSI и спецификацией BigDecimal разрешаются в пользу BigDecimal .

Поскольку одно и то же числовое значение может иметь различные представления (с различными масштабами),правила арифметики и округления должны определять как числовой результат,так и масштаб,используемый в представлении результата.Различные представления одного и того же числового значения называются членами одного и того же числа.cohort. Естественный порядок BigDecimal считает BigDecimal одной когорты равными друг другу. Напротив, метод equals

требует, чтобы и числовое значение, и представление были одинаковыми, чтобы выполнялось равенство. Результаты таких методов, как scale и unscaledValue() , будут различаться для численно равных значений с разными представлениями.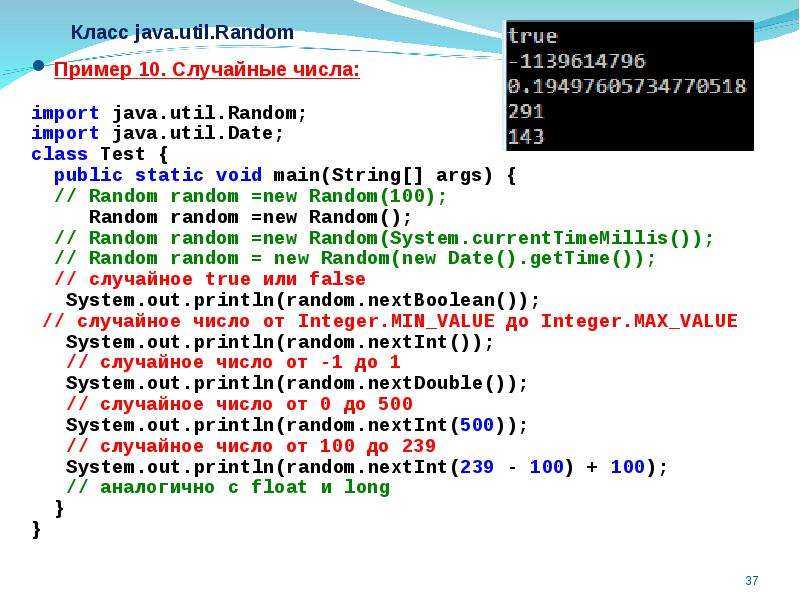

Обычно режимы округления и настройки точности определяют, как операции возвращают результаты с ограниченным числом цифр, когда точный результат имеет больше цифр (возможно, бесконечно много в случае деления и квадратного корня), чем количество возвращаемых цифр. Во- первых, общее количество цифр возврата задается MathContext «s precision настройки; это определяет результатprecision. Подсчет цифр начинается с самой левой ненулевой цифры точного результата. Режим округления определяет, как любые отброшенные конечные цифры влияют на возвращаемый результат.

Для всех арифметических операторов операция выполняется так, как если бы сначала вычислялся точный промежуточный результат, а затем округлялся до количества цифр, заданного настройкой точности (при необходимости), с использованием выбранного режима округления. Если точный результат не возвращается, некоторые разряды точного результата отбрасываются. Когда округление увеличивает величину возвращаемого результата, новая позиция цифры может быть создана путем переноса, распространяющегося на начальную цифру «9».

Например, округление значения 999,9 до трех цифр с округлением в большую сторону будет численно равно одной тысяче, представленной как 100×10 ¹ . В таких случаях новая «1» является первой цифрой возвращаемого результата.

Для методов и конструкторов с параметром MathContext

, если результат неточный, но режим округления UNNECESSARY , будет выброшено исключение ArithmeticException .

Помимо логически точного результата,каждая арифметическая операция имеет предпочтительный масштаб для представления результата.Предпочтительная шкала для каждой операции приведена в таблице ниже.

Предпочтительные шкалы для результатов арифметических операций

Operation	Предпочтительная шкала результата
Add	max(addend.scale(), augend.scale())
Subtract	max(minuend.scale(), subtrahend.scale())
Multiply	multiplier. scale() + multiplicand.scale()
Divide	dividend.scale() — divisor.scale()
Square root	radicand.scale()/2

Эти шкалы используются в методах, возвращающих точные арифметические результаты; за исключением того, что для точного деления может потребоваться больший масштаб, поскольку точный результат может содержать больше цифр. Например, 1/32 — 0.03125 .

Перед округлением шкала логического точного промежуточного результата является предпочтительной шкалой для этой операции. Если точный числовой результат не может быть представлен в цифрах precision , округление выбирает набор цифр для возврата, а масштаб результата уменьшается от масштаба промежуточного результата до наименьшего масштаба, который может представлять фактически возвращенные цифры precision . Если точный результат может быть представлен с precision цифр, возвращается представление результата со шкалой, наиболее близкой к предпочтительной шкале.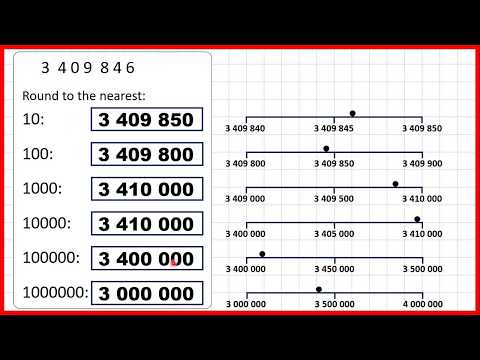 В частности, точно представимое частное может быть представлено с

precision меньшей, чем точностьцифр, удалив конечные нули и уменьшив масштаб. Например, округление до трех цифр с использованием режима округления пола ,
19/100 = 0.19 // integer=19, scale=2
but
21/110 = 0.190 // integer=190, scale=3

Обратите внимание,что для сложения,вычитания и умножения,уменьшение масштаба будет равно количеству позиций цифр точного результата,которые отбрасываются.Если округление приводит к распространению переноса для создания новой позиции с более высокими разрядами,дополнительная цифра результата отбрасывается,чем при отсутствии новой позиции с новыми разрядами.

Другие методы могут иметь несколько иную семантику округления. Например, результат метода pow с использованием указанного алгоритма может иногда отличаться от округленного математического результата более чем на одну единицу в последнем разряде, одинulp.

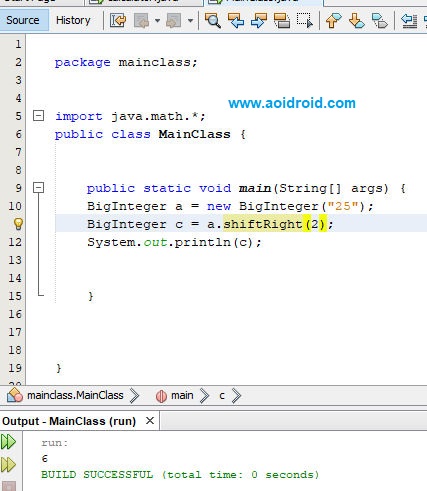
Для управления масштабом BigDecimal предусмотрено два типа операций BigDecimal операции масштабирования/округления и операции перемещения десятичной точки. Операции масштабирования/округления ( setScale и round ) возвращают BigDecimal , значение которого примерно (или точно) равно значению операнда, но масштаб или точность которого соответствуют указанному значению; то есть они увеличивают или уменьшают точность сохраненного числа с минимальным влиянием на его значение. Операции перемещения десятичной точки ( movePointLeft и movePointRight ) возвращают BigDecimal , созданный из операнда путем перемещения десятичной точки на указанное расстояние в указанном направлении.

Как 32-битное целое число, набор значений для шкалы большой, но ограниченный. Если масштаб результата превысит диапазон 32-разрядного целого числа из-за переполнения или потери значимости, операция может вызвать исключение ArithmeticException .

Для краткости и ясности во всем описании методов BigDecimal используется псевдокод . Выражение псевдокода (i + j) является сокращением для « BigDecimal , значение которого совпадает со значением BigDecimal i , добавленным к значению BigDecimal j ». Выражение псевдокода (i == j) является сокращением для « true тогда и только тогда, когда BigDecimal i представляет то же значение, что и BigDecimal j ». Аналогично интерпретируются и другие выражения псевдокода. Квадратные скобки используются для представления конкретной пары

BigInteger и масштабирования, определяющей BigDecimal значение; например [19, 2] — это BigDecimal , численно равное 0,19 и имеющее масштаб 2.

Все методы и конструкторы для этого класса NullPointerException при передаче ссылки на null объект для любого входного параметра.

API Note:

Следует проявлять осторожность , если BigDecimal объекты используются в качестве ключей в SortedMap или элементов в SortedSet начиная с BigDecimal «сnatural orderingэто не согласуется с равными . См Comparable , SortedMap или SortedSet для получения дополнительной информации.Начиная с пересмотренного в 2008 годуСтандарт IEEE 754 для арифметики с плавающей точкойрассмотрел десятичные форматы и операции. Хотя в десятичной арифметике, определенной IEEE 754 и этим классом, есть большое сходство, есть и заметные различия. Фундаментальное сходство, разделяемое BigDecimal и десятичной арифметикой IEEE 754, заключается в концептуальной операции вычисления математического бесконечно точного вещественного значения операции с последующим отображением этого действительного числа в представимое десятичное значение с плавающей запятой в соответствии с политикой округления .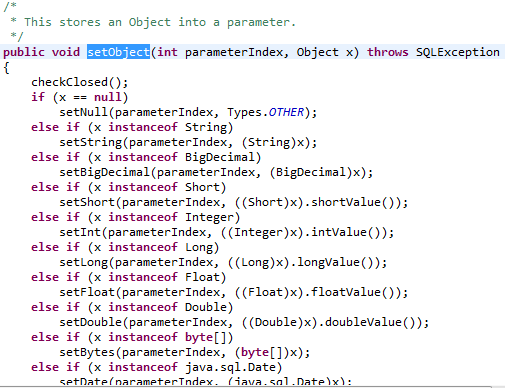 Политика округления называется режимом округления для BigDecimal .и называется атрибутом направления округления в IEEE 754-2019. Когда точное значение невозможно представить, политика округления определяет, какое из двух представимых десятичных значений, заключенных в скобки для точного значения, будет выбрано в качестве вычисленного результата. Обе системы разделяют также понятие предпочтительной шкалы / предпочтительного показателя степени .

Для различий IEEE 754 включает несколько типов значений, не моделируемых BigDecimal , включая отрицательный нуль, знаковые бесконечности и NaN (не число). IEEE 754 определяет форматы, которые параметризуются основанием (двоичным или десятичным), числом разрядов точности и диапазоном показателей. Формат определяет набор представляемых значений. Большинство операций принимают в качестве входных данных одно или несколько значений заданного формата и выдают результат в том же формате. Масштаб BigDecimal эквивалентен отрицанию экспоненты значения IEEE 754 .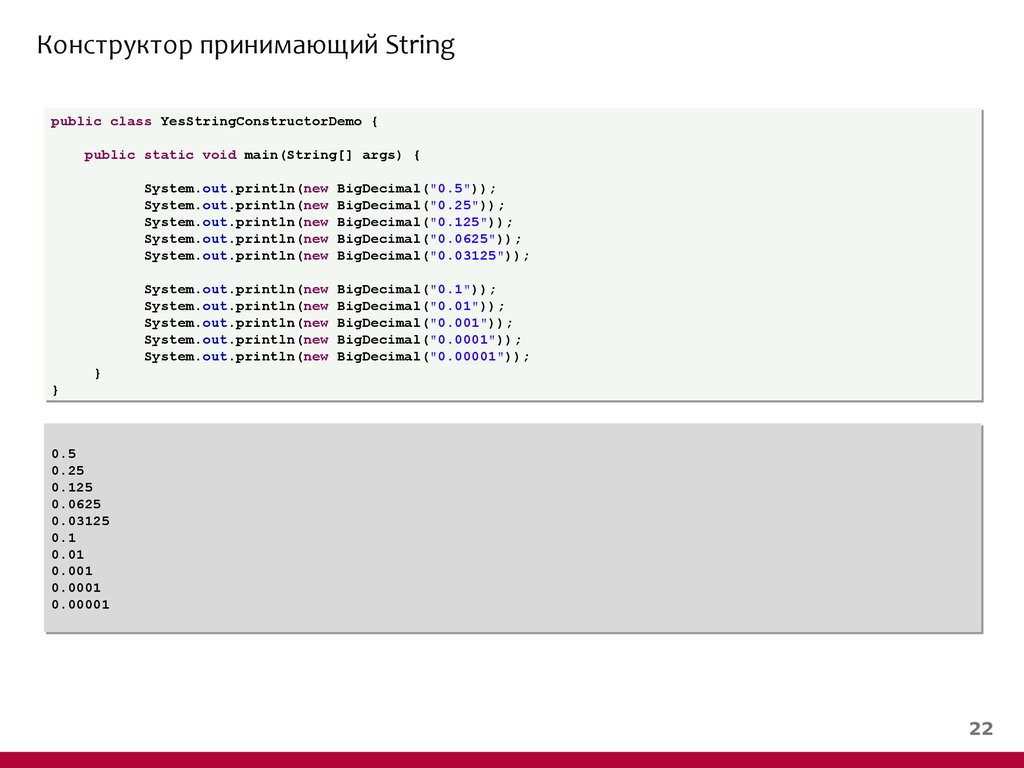 BigDecimal не имеют формата в том же смысле; все значения имеют одинаковый возможный диапазон масштаба/показателя, а немасштабированное значение имеет произвольную точность. Вместо этого для BigDecimal , принимающие параметр MathContext , если MathContext имеет ненулевую точность, набор возможных представляемых значений для результата определяется точностью аргумента MathContext . Например, в BigDecimal , если ненулевое трехзначное число и ненулевое четырехзначное число умножаются вместе в контексте объекта MathContext , имеющего точность три, результат будет состоять из трех цифр (при условии отсутствия переполнения или потери значимости и т. д. ).

Политики округления, реализованные операциями BigDecimal , указанными режимами округления, являются надлежащим надмножеством атрибутов направления округления IEEE 754.

BigDecimal Арифметика BigDecimal больше всего будет напоминать десятичную арифметику IEEE 754, если для округления всех начальных значений и промежуточных операций используется MathContext , соответствующий десятичному формату IEEE 754, например decimal64 или decimal128 .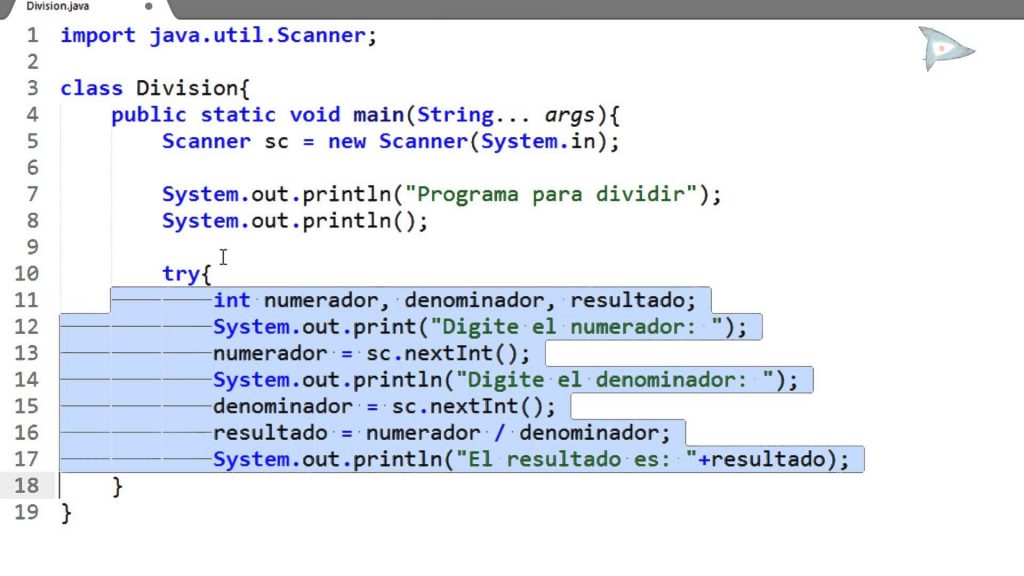 Вычисленные числовые значения могут отличаться, если диапазон степени аппроксимируемого формата IEEE 754 превышен, поскольку MathContext не ограничивает масштаб результатов BigDecimal . Операции, которые генерируют NaN или точную бесконечность, такие как деление на ноль, ArithmeticException BigDecimal ArithmeticException в арифметике BigDecimal .

Since:

1.1

See Also:

• BigInteger
• MathContext
• RoundingMode
• SortedMap
• SortedSet
• Стандарт IEEE для арифметики с плавающей запятой
• Serialized Form

---

© 1993, 2022, Oracle and/or its affiliates. All rights reserved.
Documentation extracted from Debian’s OpenJDK Development Kit package.
Licensed under the GNU General Public License, version 2, with the Classpath Exception.
Various third party code in OpenJDK is licensed under different licenses (see Debian package).
Java and OpenJDK are trademarks or registered trademarks of Oracle and/or its affiliates.
https://docs.oracle.com/en/java/javase/19/docs/api/java.base/java/math/BigDecimal.html

---

OpenJDK 19

• Class Void

• Class WrongThreadException

• Field Summary

• Methods declared in class java. lang.

• 1
• …
• 545
• 546
• 547
• 548
• 549
• …
• 6528
• Next

6.

6 Не используйте числа с плавающей точкой для точных значений

Некоторые нецелые значения, например десятичные дроби в стоимостном выражении (долларо-центы), требуют точности. Числа с плавающей точкой не являются точными, и манипулирование ими приведет к ошибкам округления. В общем, не очень хорошо использовать плавающую точку для представления таких точных величин, как денежные суммы. Использование плавающей точки для вычислений стоимости является решением данной проблемы. Числа с плавающей точкой лучше всего приберечь для таких значений, например измерения, где величины являются изначально неточными.

6.7 Большие десятичные дроби для маленьких чисел

С появлением JDK 1.3 разработчики Java получили альтернативу для нецелых чисел: BigDecimal. BigDecimal является стандартным классом, без специальной поддержки в компиляторе, для представления двоичных чисел произвольной разрядности и выполнения арифметических действий над ними. По сути дела BigDecimal представлен как недифференцированное значение произвольной разрядности и коэффициент масштабирования, который указывает насколько сдвинуть влево десятичную точку для получения значения, разбитого на дробную и целую части.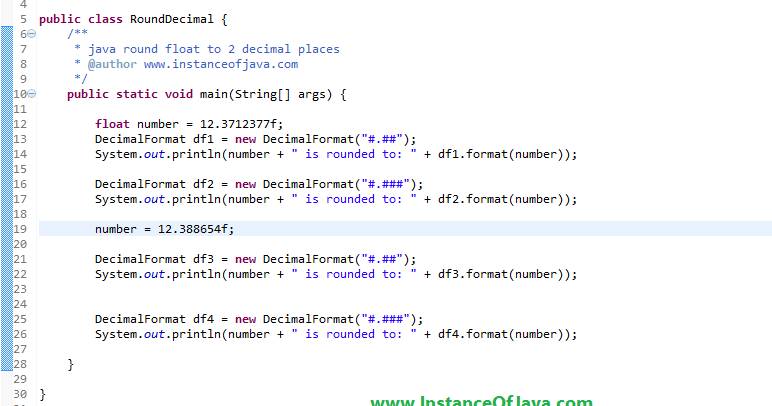 Итак, число, представленное BigDecimal является unscaledValue*10-scale .

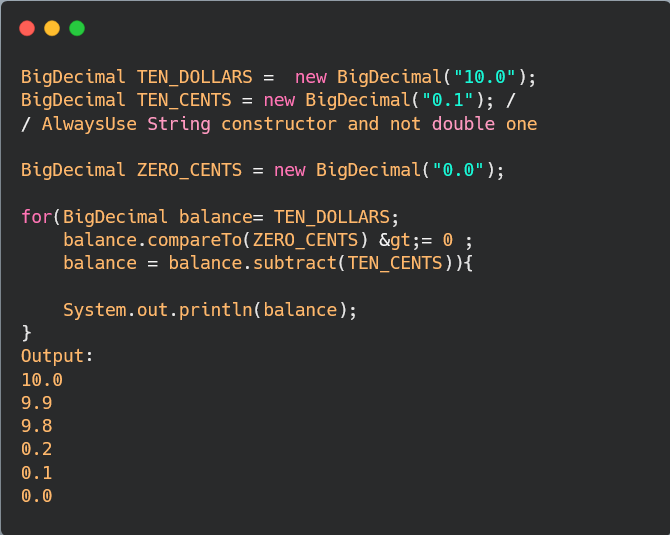
Арифметические действия над значениями BigDecimal реализуются с помощью методов для сложения, вычитания, умножения и деления. Поскольку объекты BigDecimal являются неизменяемыми, то каждый из этих методов производит новый объект BigDecimal. В итоге BigDecimal не слишком хорошо подходит для интенсивных вычислений из-за затрат на создание объекта, но он спроектирован для представления точных десятичных чисел. Если Вам необходимо представить такие точные величины как денежные суммы, то BigDecimal прекрасно подойдет для этой задачи.

6.8 Все методы сравнения не созданы равными

Как и у всех типов с плавающей точкой, у BigDecimal тоже есть несколько особенностей. А именно, будьте осторожны с использованием метода equals() для проверки тождественности чисел. Два значения BigDecimal, представляющих одно и то же число, но имеющих различные коэффициенты масштабирования (например, 100.00 и 100.000) не будут равными при использовании метода equals(). Тем не менее, метод compareTo() будет считать их равными, а, следовательно, Вы должны использовать compareTo() вместо equals() при количественном сравнении двух значений BigDecimal.

Существуют некоторые случаи, когда для получения точных результатов недостаточно двоичной арифметики с произвольной разрядностью. Например, деление 1 на 9 выдает бесконечную периодическую двоичную дробь .111111… По этой причине BigDecimal позволяет Вам явно контролировать округление при выполнении операций деления. Точное деление на показатель степени 10 поддерживается методом movePointLeft().

6.9 Используйте BigDecimal в качестве типа обмена

В SQL-92 есть тип данных DECIMAL, который является точным числовым типом для представления десятичных чисел с фиксированной точкой и выполняет основную арифметическую операцию над двоичными числами. В некоторых диалектах SQL предпочитают называть этот тип NUMERIC, а другие также содержат тип данных MONEY, который определяется как десятичное число с двумя знаками справа от десятичной дроби.

Если Вы хотите сохранить число в поле DECIMAL в базе данных или извлечь значение из поля DECIMAL, то как можно убедиться в том, что число будет передано точно? Вы не хотите использовать методы setFloat() и getFloat(), обеспечиваемые JDBC классами PreparedStatement и ResultSet, поскольку конвертация из числа с плавающей точкой в десятичное число может привести к потере точности. Вместо этого, используйте setBigDecimal() и getBigDecimal() методы PreparedStatement и ResultSet.

Аналогично, XML-инструменты привязки данных, например, Castor, сгенерируют механизмы получения и установки для десятичных атрибутов и элементов (которые поддерживаются в качестве основного типа данных в XSD-схеме), используя BigDecimal.

режимов округления | ICU Documentation

Contents

1. Comparison of Rounding Modes
   1. Half Even
   2. Half Odd
   3. Half Down
   4. Half Up
   5. Down
   6. Up
   7. Half Ceiling
   8. Half Floor
   9. Ceiling
   10. Floor
   11. Ненужные
2. Прочие ссылки/сравнения

---

Следующие режимы округления используются с десятичным форматированием ICU. Обратите внимание, что использование ICU терминов «вниз» и «вверх» здесь несколько расходится с другими определениями, но эквивалентно тем же режимам, которые используются в Java JDK.

Сравнение режимов округления

На этой диаграмме показаны значения от -2,0 до 2,0 с шагом 0,1, а также показан результирующий формат ICU при форматировании без десятичных цифр.

Примечание. Некоторые из приведенных ниже параметров недоступны в ICU4J, поскольку мы используем JDK RoundingMode.

00528080 9008. 0080

#	Потолок	Пол		UP	Halfen	Halfodd			Halfodd			HALFFLOOR	HALFDOWN	HALFUP	#
-2.0	-2	-2	-2	-2	-2	-2	-2	-2	-2	-2	-2. 0
-1.9	-1	-2	-1	-2	-2	-2	-2	-2	-2	-2	-1.9
-1.8	-1	-2	-1	-2	-2	-2	-2	-2	-2	-2	-1.8
-1.7	-1	-2	-1	-2	-2	-2	-2	-2	-2	-2	-1,7
-1.6	-1	-2	-1	-2	-2	-2	-2	-2	-2	-2	-1.6
-1.5	-1	-2	-1	-2	-2	-1	-1	-2	-1	-2	-1. 5
-1,4	-1	-2	-1	-2	-1	-1	-1	-1	-1	-1	-1.4
-1.3	-1	-2	-1	-2	-1	-1	-1	-1	-1	-1	-1.3
-1.2	-1	-2	-1	-2	-1	-1	-1	-1	-1	-1	-1.2
-1.1	-1	-2	-1	-2	-1	-1	-1	-1	-1	-1	-1.1
-1.0	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1. 0
-0.9	-0	-1	-0	-1	-1	-1	-1	-1	-1	-1	-0.9
-0.8	-0	-1	-0	-1	-1	-1	-1	-1	-1	-1	-0,8
-0,7	-0	-1	-0	-1	-1	-1	-1	-1	-1	-1	-0.7
-0.6	-0	-1	-0	-1	-1	-1	-1	-1	-1	-1	-0.6
-0.5	-0	-1	-0	-1	-0	-1	-0	-1	-0	-1	-0. 5
-0.4	-0	-1	-0	-1	-0	-0	-0	-0	-0	-0	-0.4
-0.3	-0	-1	-0	-1	-0	-0	-0	-0	-0	-0	-0.3
-0.2	-0	-1	-0	-1	-0	-0	-0	-0	-0	-0	-0.2
-0.1	-0	-1	-0	-1	-0	-0	-0	-0	-0	-0	-0,1
0.0	0	0	0	0	0	0	0	0	0	0	0. 0
0.1	1	0	0	1	0	0	0	0	0	0	0.1
0.2	1	0	0	1	0	0	0	0	0	0	0.2
0.3	1	0	0	1	0	0	0	0	0	0	0.3
0.4	1	0	0	1	0	0	0	0	0	0	0.4
0.5	1	0	0	1	0	1	1	0	0	1	0.5
0. 6	1	0	0	1	1	1	1	1	1	1	0.6
0.7	1	0	0	1	1	1	1	1	1	1	0.7
0.8	1	0	0	1	1	1	1	1	1	1	0.8
0.9	1	0	0	1	1	1	1	1	1	1	0.9
1.0	1	1	1	1	1	1	1	1	1	1	1.0
1.1	2	1	1	2	1	1	1	1	1	1	1. 1
1.2	2	1	1	2	1	1	1	1	1	1	1.2
1.3	2	1	1	2	1	1	1	1	1	1	1.3
1.4	2	1	1	2	1	1	1	1	1	1	1.4
1.5	2	1	1	2	2	1	2	1	1	2	1.5
1.6	2	1	1	2	2	2	2	2	2	2	1.6
1. 7	2	1	1	2	2	2	2	2	2	2	1.7
1.8	2	1	1	2	2	2	2	2	2	2	1.8
1.9	2	1	1	2	2	2	2	2	2	2	1.9
2.0	2	2	2	2	2	2	2	2	2	2	2,0
#	Поток	Пол			Пол			Пол						Halfodd	Halfceliling	Halffloor	Halfdown	Halfup	#

Половина

Это ICU. Значения точно на отметке 0,5 (половина) (показаны пунктиром на графике) округляются до ближайшей четной цифры. Это часто называют округлением банкира, потому что в среднем оно не содержит смещения. Это режим по умолчанию, указанный для операций с плавающей запятой IEEE 754.

Также известен как привязка к четному, округление к ближайшему, RN или RNE.

Половина нечетного

Аналогичен получетному, но округляется до ближайшего нечетного числа, а не до четного.

Half Down

Значения точно на отметке 0,5 (половина) округляются в меньшую сторону (следующее меньшее абсолютное значение, ближе к нулю).

Half Up

Значения точно на отметке 0,5 (половина) округляются в большую сторону (следующее большее абсолютное значение, отличное от нуля).

Вниз

Все значения округляются до следующего меньшего абсолютного значения (округляются до нуля или RZ).

Также известен как: усечение, потому что незначащие десятичные разряды просто удаляются.

Вверх

Все значения округляются до следующего большего абсолютного значения (от нуля).

Half Ceiling

Значения точно на отметке 0,5 (половина) округляются до положительной бесконечности (+∞).

Это режим округления по умолчанию в ECMAScript. В CSS он известен как «ближайший».

Half Floor

Значения точно на отметке 0,5 (половина) округляются до отрицательной бесконечности (-∞).

Потолок

Все значения округлены до положительной бесконечности (+∞). Также известен как RI для раундов до бесконечности.

Этаж

Все значения округлены до минус бесконечности (-∞). Также известен как RMI для раундов до минус бесконечности.

Ненужный

Режим «Ненужный» не выполняет никакого округления, а вместо этого возвращает ошибку, если значение не может быть точно представлено без округления.

Другие ссылки/Сравнение

• Документация по десятичному контексту (используется ICU4C для реализации округления): http://speleotrove. com/decimal/decifaq1.html#rounding
• Документация по Java 7: http://docs.oracle.com/javase/7 /docs/api/java/math/RoundingMode.html
• Правила округления IEEE 754: http://en.wikipedia.org/wiki/IEEE_754-2008#Rounding_rules
• Статья в Википедии об округлении: http://en.wikipedia .org/wiki/Rounding#Tie-breaking
• Диаграмма режима округления в реальном времени: Диаграмма режима округления и исходный код

---

Как округлить число до N знаков после запятой — Support

RavenEXP 2 августа 2018 г., 13:08

1

Итак, я увидел этот пост о моей проблеме (печать с плавающей запятой с определенным количеством десятичных чисел)

И мне было интересно, можно ли использовать метод или что-то еще, а не «%. 2f». формат (значение), чтобы добиться того же

2 лайков

фваско 2 августа 2018 г. , 15:12

2

Вы должны лучше объяснить свою проблему.

Технически нельзя округлить число с плавающей запятой IEEE 754 0,1 до первого десятичного знака.

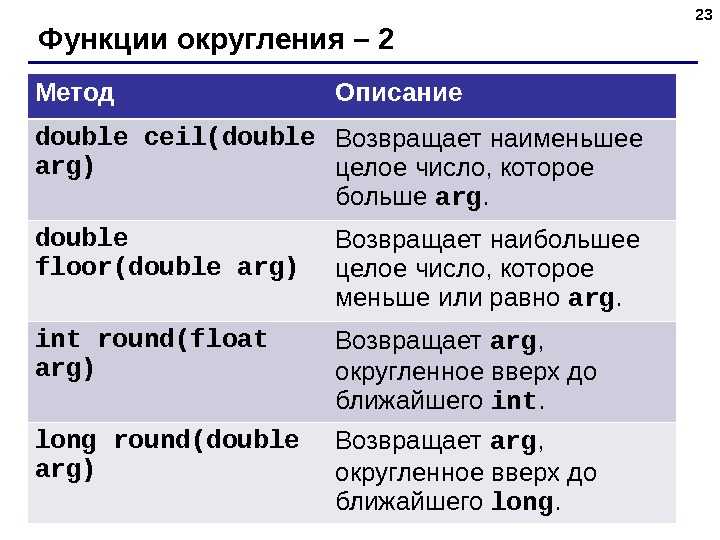
Однако вы можете использовать

 fun Double.round(decimals: Int): Double {
    множитель переменной = 1,0
    повтор (десятичные числа) { множитель * = 10 }
    возврат раунда (этот * множитель) / множитель
}
 

7 лайков

RavenEXP 2 августа 2018 г., 16:25

3

Я просто пытаюсь сократить число, скажем, до 2 знаков после запятой.

например я хочу превратить:
pi=3.14159265359
в просто
pi=3.14

Надеюсь вы меня понимаете знаете или хотя бы яснее понимаете.

1 Нравится

16 января 2019 г., 2:28

4

Если вы хотите округлить двойное значение до определенных знаков после запятой и напечатать его, вы можете использовать java.math.BigDecimal.

 импорт java.math.BigDecimal
импортировать java.math.RoundingMode
десятичное значение = BigDecimal(3.14159265359).setScale(2, RoundingMode.HALF_EVEN)
println(десятичный) // 3.14
 

Или, если вы просто хотите сравнить его с округленным значением, вы можете использовать метод округления.

 импорт kotlin.math.round
println(раунд(3.14159265359 * 100)/100 == 3,14)//правда
 

Вы можете сделать то же самое с методом расширения @fvasco.

 3.14159265359.раунд(2) // 3.14
 

2 лайка

Драки 15 сентября 2019 г. , 19:03

5

На этот * множитель показывает:

Требуется: Int, Найдено: Double

фваско 16 сентября 2019 г., 8:01 утра

6

Пожалуйста, рассмотрите возможность импорта round(Double) from kotlin.math.round

2 лайка

Драки 16 сентября 2019 г., 8:14

7

забава Double.round(десятичные числа: Int = 2): Double = "%.${десятичные числа}f".format(this).toDouble()

4 нравится

дальюкинг 19 сентября 2019 г. , 3:47

8

Вы должны понимать, что существует разница между округлением для вывода, которое вы можете сделать с помощью String.format и других методов, и значением, точно равным 3,14. Если вы используете тип double, у вас НИКОГДА, НИКОГДА не будет значения, точно равного 3,14. Даже если у вас есть утверждение типа:

 val a = 3.14
 

Переменная a на самом деле не точно равна значению 3.14. На самом деле это равно 3,1400000000000001243449.78758017532527446746826171875 [Редактировать: я изначально сказал 3.14000010448046875, что является точным значением значения с плавающей запятой 3.14f] .

Если вам нужно значение, точно равное 3,14, ЕДИНСТВЕННЫЙ способ получить его (для JVM) — использовать BigDecimal.

3 лайков

Джонатан.Хаас 19 сентября 2019 г. , 8:55

9

далюкинг:

На самом деле это 3,14000010448046875.

Возможно, так и было бы в случае с числами с плавающей запятой (я не проверял), но числа с удвоением гораздо точнее. Но и точно 3.14 тоже конечно не будет.

дальюкинг 19 сентября 2019 г., 11:34

10

И для float, и для double одно и то же, что ни один из них не может точно представлять 3.14. Но я случайно показал представление с плавающей запятой, а не двойное. 3.14 как двойное точно равно 3.1400000000000001243449n, где m и n являются целыми числами и практически не ограничены. m=314 и n=-2 дают точное значение 3,14.

Вот почему лучший совет при представлении денег — никогда не использовать float или double и всегда использовать BigDecimal. Вы можете использовать int или long для представления количества пенни, если знаете, что диапазон ограничен. См. Практика Java->Представление денег

Недостатком BigDecimal является то, что он медленнее и громоздче в использовании (в меньшей степени в Kotlin), поскольку для него нет встроенной аппаратной поддержки.

феллахи.али 9 октября 2019 г., 16:58

11

Привет;
Как получить точное значение 3,14, я пытался получить его следующим образом:

 val pi = 3,14
println(pi) // Я получил: 3.14
 

Почему?

нбилык 9 октября 2019 г., 17:10

12

Для преобразования чисел в текст я бы рекомендовал использовать java. text.NumberFormat для JVM и Intl.NumberFormat для JS

Они дополнительно будут обрабатывать локализацию десятичных разделителей и разделителей тысяч.

толстяк79 9 октября 2019 г., 18:36

13

феллахи.али:

Я пытался получить это следующим образом:

 знач. пи = 3,14
println(pi) // Я получил: 3.14
 

Почему?

Строковое представление значений с плавающей запятой во многих языках усекается таким образом. Даже если значение не точно равно 3,14, вывод может выглядеть так. Это не означает, что он по существу равен 3,14. При использовании значения в вычислениях используется точное значение.

1 Нравится

9 октября 2019 г. , 20:59

15

Обычно при преобразовании для вывода Java (которое затем переносится в Kotlin) будет выводить кратчайшее строковое представление, которое ближе к точному значению, чем к следующему представимому значению с плавающей запятой. Таким образом, если вы попытаетесь проанализировать это строковое представление, вы получите точно такое же значение.

Литерал 3.14 преобразуется в двойное число, имеющее точное значение 3,140000000000000124344978758017532527446746826171875.

The representable double values ​​on either side of this value are:
3.139999999999999680255768491635799407958984375
and
3.1400000000000005684341886080801486968994140625

When converting the value to string it outputs 3.14 because that is the shortest representation that is closest to that exact value than it is to either of эти 2 окружающих значения.

Тот факт, что он печатает 3,14, не означает, что 3,14 является его точным значением. Обратите внимание, что этот код также выводит 3.14:

 val pi = 3.140000000000000124344978758017532527446746826171875
println(пи)
 

На самом деле существует бесконечное количество представлений текстовых чисел, которые вы можете поместить в этот код и все равно получить 3.14 (например, любые цифры, которые вы добавляете к этому коду, ничего не изменят).

К вашему сведению, если вы хотите узнать точное значение, преобразуйте его в BigDecimal:

 println (BigDecimal (pi))
 

2 лайка

тагаев 17 декабря 2020 г., 7:01

16

Взгляните на этот метод, в моем случае он работает:

 fun Double.roundTo(numFractionDigits: Int): Double {
  val factor = 10.0.pow(numFractionDigits.toDouble())
  return (это * фактор).roundToInt() / фактор
}
 

я позаимствовал это у: java — Round Double до 1 десятичного знака kotlin: от 0,0449с 99 до 0,1 17 декабря 2020 г.