Коэффициент корреляция Пирсона в дипломе по психологии
Коэффициент корреляции Пирсона в курсовых, дипломных и магистерских работах по психологии используется для выявления взаимосвязи двух переменных, измеренных на одной и той же выборке. Это могут быть как психологические показатели (тревожность, самооценка, самоактуализация, осмысленность жизни), так и не психологические (успешность учебной деятельности, возраст, стаж).
Для вычисления коэффициента корреляции Пирсона необходимо иметь:
- Выборку испытуемых (желательно не менее 10 человек).
- Результаты диагностики какого-либо показателя в этой группе испытуемых, например, эффективности профессиональной деятельности сотрудников.
- Результаты тестирования другого показателя, например, уровня рефлективности сотрудников.
- Таблицу исходных данных, в которой в двух столбцах приведены значения измеренных показателей (в нашем случае профессиональная эффективность и рефлективность).

Далее, используя данные из этой сводной таблицы результатов психодиагностики можно проверить гипотезу о том, есть ли между эффективностью сотрудников и рефлективностью взаимосвязь. Для решения этой задачи и проверки гипотезы можно использовать коэффициент корреляции Пирсона.
Коэффициент корреляции Пирсона относится к числу параметрических статистических критериев. Это означает, что для его использования в курсовой, дипломной или магистерской работе по психологии необходимо, чтобы психологические показатели удовлетворяли ряду условий, в частности, были распределены по нормальному закону. Если это условие не выполняется, то для анализа взаимосвязей между параметрами использовать коэффициент ранговой корреляции Спирмена.
В выпускных квалификационных работах по психологии чаще всего не проводится проверка нормальности распределения показателей, поэтому следует использовать коэффициент корреляции рангов Спимрмена.
Расчёт коэффициента корреляции Пирсона
Вычислить коэффициент корреляции Пирсона можно вручную, а можно рассчитать при помощи статистических программ.
Логика расчета коэффициент корреляции Пирсона в самом общем и приближенном виде состоит в том, что анализируются знаки отклонений показателей двух величин от средних значений.
Например, для каждого испытуемого рассчитываются разности между его показателем по эффективности и рефлексивности и средним значением. Далее эти разности перемножаются для каждого испытуемого и суммируются для всей выборки.
Если знак полученного произведения отрицательный — корреляция обратная. Если знак произведения положительный – прямая. Величина произведения по модулю отражает величину корреляции, то есть силу взаимосвязи между показателями.
Анализ результатов расчета коэффициента корреляции Пирсона
Значение коэффициента корреляции Пирсона может располагаться в диапазоне значений от 1- до 1.
Отрицательные значения свидетельствуют об обратной взаимосвязи между показателями. Например, чем выше рефлексивность, тем ниже эффективность деятельности. Это справедливо для профессий, где погруженность в собственные проживания вредит делу. Работникам МЧС надо спасать людей, а не рефлексировать. Поэтому взаимосвязь между этим и показателями в данной выборке, скорее всего, оказалась бы отрицательной.
Положительные значения свидетельствуют о прямой взаимосвязи между показателями. Например, чем выше рефлексивность, тем выше эффективность деятельности. Это справедливо для профессий, где внимание к внутренней жизни помогает делу. Например, для психотерапевтов для проведения успешной работы с клиентами важно постоянно анализировать собственные переживания. Поэтому в группе практических психологов взаимосвязь между эффективностью и рефлексивностью, с большой долей вероятности, оказалась бы положительной.
Важно определить не только знак (направление) взаимосвязи, но и уровень ее значимости – силу связи между показателями. Чем выше численное значение коэффициента корреляции Пирсона по абсолютному значению (без учета знака), тем выше степень взаимосвязи между показателями.
Чем выше численное значение коэффициента корреляции Пирсона по абсолютному значению (без учета знака), тем выше степень взаимосвязи между показателями.
Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать
| Чтобы получить статистические критерии для таблиц сопряженности, щелкните на кнопке Statistics… (Статистика) в диалоговом окне Crosstabs. Откроется диалоговое окно Crosstabs: Statistics (Таблицы сопряженности: Статистика) (см. рис. 11.9). Рис. 11.9: Диалоговое окно Crosstabs: Statistics Флажки в этом диалоговом окне позволяют выбрать один или несколько критериев.
Эти критерии рассматриваются в двух последующих разделах, причем из-за того, что критерий хи-квадрат имеет большое значение в статистических вычислениях, ему посвящен отдельный раздел. Тест хи-квадрат (X2) При проведении теста хи-квадрат проверяется взаимная независимость двух переменных таблицы сопряженности и благодаря этому косвенно выясняется зависимость обоих переменных. Две переменные считаются взаимно независимыми, если наблюдаемые частоты (fо) в ячейках совпадают с ожидаемыми частотами (fe). Для того, чтобы провести тест хи-квадрат с помощью SPSS, выполните следующие действия:
Вы получите следующую таблицу сопряженности. Пол * Психическое состояние Таблица сопряженности
Кроме того, в окне просмотра будут показаны результаты теста хи-квадрат: Chi-Square Tests (Тесты хи-квадрат)
а. Для вычисления критерия хи-квадрат применяются три различных подхода:
Критерий хи-квадрат по Пирсону Обычно для вычисления критерия хи-квадрат используется формула Пирсона: Здесь вычисляется сумма квадратов стандартизованных остатков по всем полям таблицы сопряженности. Поэтому поля с более высоким стандартизованным остатком вносят более весомый вклад в
численное значение критерия хи-квадрат и, следовательно, — в значимый результат. Согласно правилу, приведенному в разделе 8.9,
стандартизованный остаток 2 (1,96) или более указывает на значимое расхождение между наблюдаемой и ожидаемой частотами в той или ячейке таблицы. В рассматриваемом примере формула Пирсона дает максимально значимую величину критерия хи-квадрат (р<0,0001). Если рассмотреть стандартизованные остатки в отдельных полях таблицы сопряженности, то на основе вышеприведенного правила можно сделать вывод, что эта значимость в основном определяется полями, в которых переменная psyche имеет значение «крайне неустойчивое». У женщин это значение сильно повышено, а у мужчин — понижено. Корректность проведения теста хи-квадрат определяется двумя условиями:
Однако в рассматриваемом примере это условие выполняется не полностью. Как указывает примечание после таблицы теста хи-квадрат, 25% полей имеют ожидаемую частоту менее 5.
Однако, так как допустимый предел в 20% превышен лишь ненамного и эти поля, вследствие своего очень малого стандартизованного остатка, вносят весьма незначительную долю в величину критерия хи-квадрат,
это нарушение можно считать несущественным. Критерий хи-квадрат с поправкой на правдоподобие Альтернативой формуле Пирсона для вычисления критерия хи-квадрат является поправка на правдоподобие: При большом объеме выборки формула Пирсона и подправленная формула дают очень близкие результаты. В нашем примере критерий хи-квадрат с поправкой на правдоподобие составляет 23,688. Тест Мантеля-Хэнзеля Дополнительно в таблице сопряженности под обозначением linear-by-linear («линейный-по-линейному») выводится значение теста Мантеля-Хэнзеля (20,391). Эта форма критерия хи-квадрат с поправкой Мантеля-Хэнзеля — еще одна мера линейной зависимости между строками и столбцами таблицы сопряженности. Она определяется как произведение коэффициента корреляции Пирсона на количество наблюдений, уменьшенное на единицу: Полученный таким образом критерий имеет одну степень свободы. Метод Мантеля-Хэнзеля используется всегда, когда в диалоговом окне Crosstabs: Statistics установлен флажок Chi-square. | |||||||
Условия и ограничения применения критерия хи-квадрат Пирсона
⇐ ПредыдущаяСтр 9 из 28Следующая ⇒1. Сопоставляемые показатели должны быть измерены в номинальной шкале (например, пол пациента — мужской или женский) или в порядковой (например, степень артериальной гипертензии, принимающая значения от 0 до 3).
2. Данный метод позволяет проводить анализ не только четырехпольных таблиц, когда и фактор, и исход являются бинарными переменными, то есть имеют только два возможных значения (например, мужской или женский пол, наличие или отсутствие определенного заболевания в анамнезе…). Критерий хи-квадрат Пирсона может применяться и в случае анализа многопольных таблиц, когда фактор и (или) исход принимают три и более значений.
3. Сопоставляемые группы должны быть независимыми, то есть критерий хи-квадрат не должен применяться при сравнении наблюдений «до-«после». В этих случаях проводится тест Мак-Немара(при сравнении двух связанных совокупностей) или рассчитывается Q-критерий Кохрена(в случае сравнения трех и более групп).
В этих случаях проводится тест Мак-Немара(при сравнении двух связанных совокупностей) или рассчитывается Q-критерий Кохрена(в случае сравнения трех и более групп).
4. При анализе четырехпольных таблиц ожидаемые значения в каждой из ячеек должны быть не менее 10. В том случае, если хотя бы в одной ячейке ожидаемое явление принимает значение от 5 до 9, критерий хи-квадрат должен рассчитываться с поправкой Йейтса. Если хотя бы в одной ячейке ожидаемое явление меньше 5, то для анализа должен использоваться точный критерий Фишера.
5. В случае анализа многопольных таблиц ожидаемое число наблюдений не должно принимать значения менее 5 более чем в 20% ячеек.
Как рассчитать критерий хи-квадрат Пирсона?
Для расчета критерия хи-квадрат необходимо:
1. Рассчитываем ожидаемое количество наблюденийдля каждой из ячеек таблицы сопряженности (при условии справедливости нулевой гипотезы об отсутствии взаимосвязи) путем перемножения сумм рядов и столбцов с последующим делением полученного произведения на общее число наблюдений. Общий вид таблицы ожидаемых значений представлен ниже:
Общий вид таблицы ожидаемых значений представлен ниже:
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | (A+B)*(A+C) / (A+B+C+D) | (A+B)*(B+D)/ (A+B+C+D) | A + B |
| Фактор риска отсутствует (0) | (C+D)*(A+C)/ (A+B+C+D) | (C+D)*(B+D)/ (A+B+C+D) | C + D |
| Всего | A + C | B + D | A+B+C+D |
2. Находим значение критерия χ2по следующей формуле:
где i – номер строки (от 1 до r), j – номер столбца (от 1 до с), Oij– фактическое количество наблюдений в ячейке ij, Eij – ожидаемое число наблюдений в ячейке ij.
В том случае, если число ожидаемого явления меньше 10 хотя бы в одной ячейке, при анализе четырехпольных таблиц должен рассчитываться критерий хи-квадрат с поправкой Йейтса. Данная поправка позволяет уменьшить вероятность ошибки первого типа, т.е обнаружения различий там, где их нет. Поправка Йейтса заключается в вычитании 0,5 из абсолютного значения разности между фактическим и ожидаемым количеством наблюдений в каждой ячейке, что ведет к уменьшению величины критерия хи-квадрат.
Данная поправка позволяет уменьшить вероятность ошибки первого типа, т.е обнаружения различий там, где их нет. Поправка Йейтса заключается в вычитании 0,5 из абсолютного значения разности между фактическим и ожидаемым количеством наблюдений в каждой ячейке, что ведет к уменьшению величины критерия хи-квадрат.
Формула для расчета критерия χ2 с поправкой Йейтса следующая:
3. Определяем число степеней свободыпо формуле: f = (r – 1) × (c – 1). Ссответственно, для четырехпольной таблицы, в которой 2 ряда (r = 2) и 2 столбца (c = 2), число степеней свободы составляет f2×2 = (2 — 1)*(2 — 1) = 1.
4. Сравниваем значение критерия χ2 с критическим значениемпри числе степеней свободы f (по таблице).
Данный алгоритм применим как для четырехпольных, так и для многопольных таблиц.
Как интерпретировать значение критерия хи-квадрат Пирсона?
В том случае, если полученное значение критерия χ2 больше критического, делаем вывод о наличии статистической взаимосвязи между изучаемым фактором риска и исходом при соответствующем уровне значимости.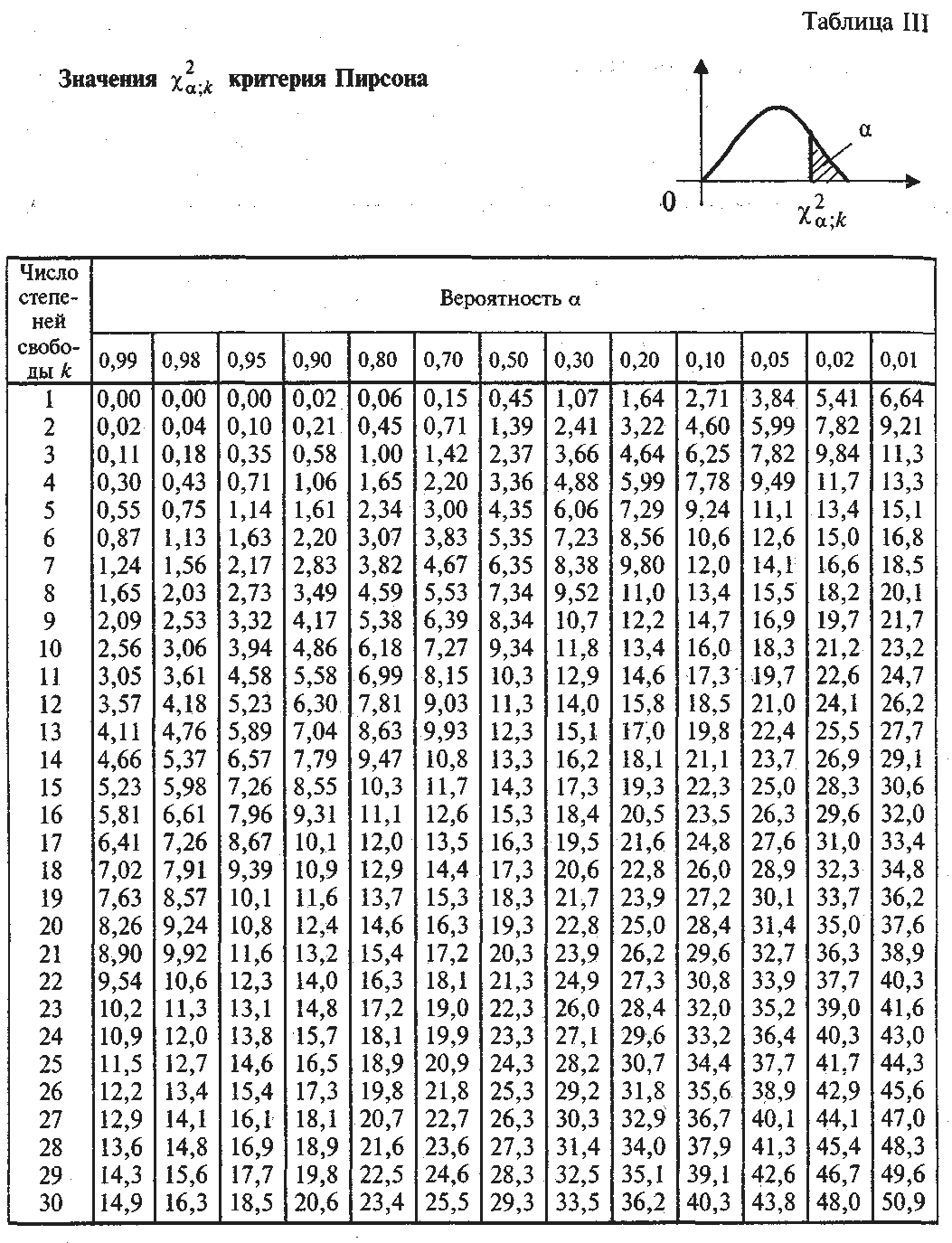
Пример расчета критерия хи-квадрат Пирсона
Определим статистическую значимость влияния фактора курения на частоту случаев артериальной гипертонии по рассмотренной выше таблице:
| Артериальная гипертония есть (1) | Артериальной гипертонии нет (0) | Всего | |
| Курящие (1) | |||
| Некурящие (0) | |||
| Всего |
1. Рассчитываем ожидаемые значения для каждой ячейки:
| Артериальная гипертония есть (1) | Артериальной гипертонии нет (0) | Всего | |
| Курящие (1) | (70*72)/150 = 33.6 | (70*78)/150 = 36. 4 4
| |
| Некурящие (0) | (80*72)/150 = 38.4 | (80*78)/150 = 41.6 | |
| Всего |
2. Находим значение критерия хи-квадрат Пирсона:
χ2 = (40-33.6)2/33.6 + (30-36.4)2/36.4 + (32-38.4)2/38.4 + (48-41.6)2/41.6 = 4.396.
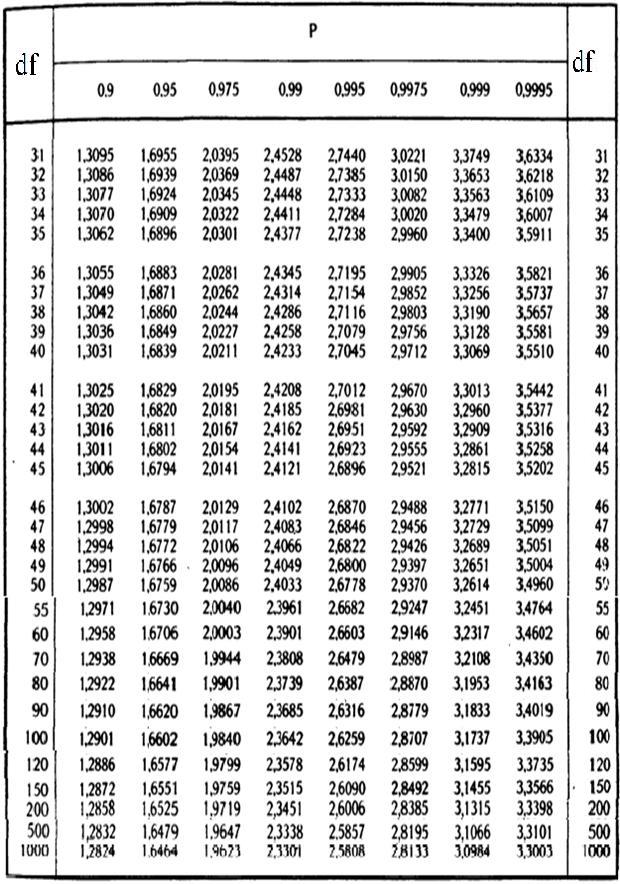
3. Число степеней свободы f = (2-1)*(2-1) = 1. Находим по таблице критическое значение критерия хи-квадрат Пирсона, которое при уровне значимости p=0.05 и числе степеней свободы 1 составляет 3.841.
4. Сравниваем полученное значение критерия хи-квадрат с критическим: 4.396 > 3.841, следовательно зависимость частоты случаев артериальной гипертонии от наличия курения — статистически значима. Уровень значимости данной взаимосвязи соответствует p<0.05.
| Число степеней свободы, f | χ2 при p=0. 05 05
| χ2 при p=0.01 |
| 3.841 | 6.635 | |
| 5.991 | 9.21 | |
| 7.815 | 11.345 | |
| 9.488 | 13.277 | |
| 11.07 | 15.086 | |
| 12.592 | 16.812 | |
| 14.067 | 18.475 | |
| 15.507 | 20.09 | |
| 16.919 | 21.666 | |
| 18.307 | 23.209 | |
| 19.675 | 24.725 | |
| 21.026 | 26.217 | |
| 22.362 | 27.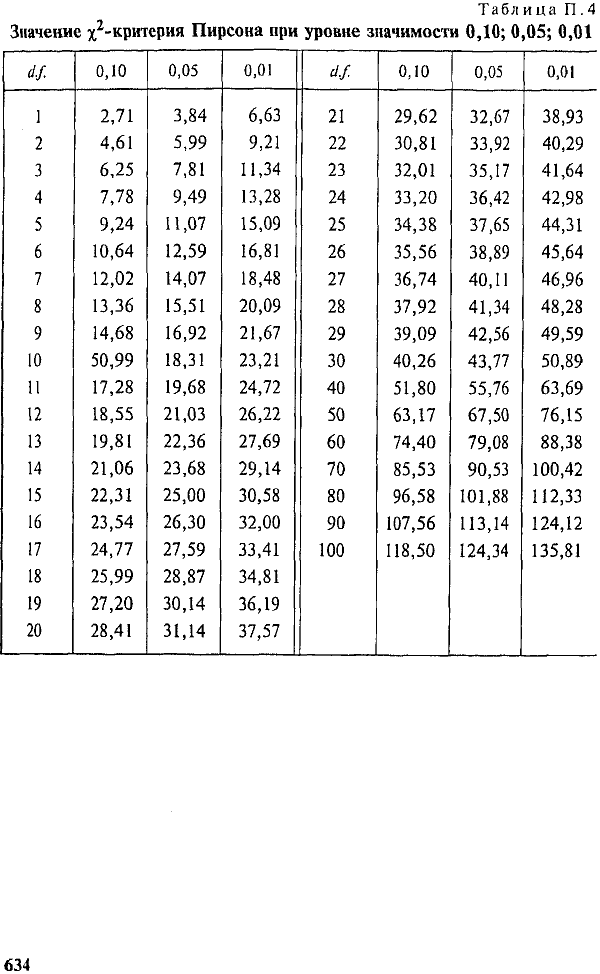 688 688
| |
| 23.685 | 29.141 | |
| 24.996 | 30.578 | |
| 26.296 | ||
| 27.587 | 33.409 | |
| 28.869 | 34.805 | |
| 30.144 | 36.191 | |
| 31.41 | 37.566 |
билет №_6_
Центральные процессоры современных персональных компьютеров. Машинное представление чисел. Команды, адресация операндов, индексные регистры. Команды условного и безусловного перехода. Массивы.
Читайте также:
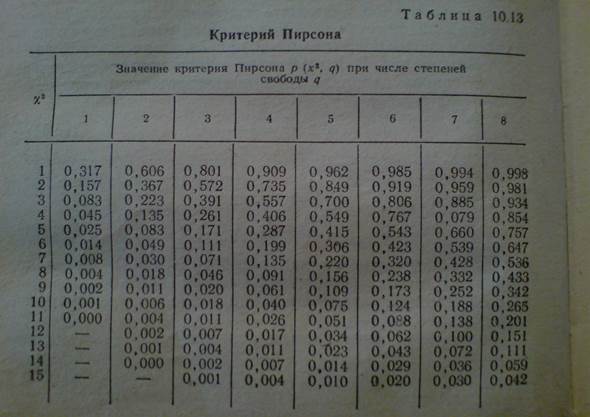
Расчет критерия согласия Пирсона
Расчет критерия согласия Пирсона Организация опросов | ИНСТРУКЦИЯ ДЛЯ БРИГАДИРОВ | ИНСТРУКЦИЯ ДЛЯ ИНТЕРВЬЮЕРОВ | Этап полевых работ | ПРОТОКОЛ КОНТРОЛЯ | Анализ документов | Контент-анализа в ОСИ | Социологическое наблюдение | Кто проводил______________________________________ | Сочетание и комбинирование методов сбора информации || fi | f’i | fi – f’i | (fi – f’i)2 | (fi – f’i)2/ fi | ||||
| 4,1 | –1,1 | 1,21 | 0,30 | |||||
| 3,9 | 1,1 | 1,21 | 0,31 | |||||
| 9,7 | 6,3 | 39,69 | 4,09 | |||||
| 9,3 | –6,3 | 39,69 | 4,27 | |||||
| 5,6 | 0,4 | 0,16 | 0,03 | |||||
| 5,4 | –0,4 | 0,16 | 0,03 | |||||
| 10,2 | –1,2 | 1,44 | 0,14 | |||||
| 9,8 | 1,2 | 1,44 | 0,15 | |||||
| 21,4 | –4,4 | 19,36 | 0,90 | |||||
| 20,6 | 4,4 | 19,36 | 0,94 | |||||
| å=11,16 |
l2=11,16.
При числе степеней свободы 4 и уровне значимости 0,05 находим табличное значение l2табл =9,5. Так как l2расч>l2табл, гипотеза о независимости признаков в строке и столбце таблицы отвергается.
Критерий “хи-квадрат” вычисляется для подтверждения гипотезы о независимости признаков, но он не характеризует тесноту связи. Для определения тесноты связи можно использовать коэффициенты сопряженности Пирсона и Крамера. Они рассчитываются для таблиц размером схk, если признаки измерены в шкале наименований.
1. Коэффициент сопряженности Пирсона
. (5.10)
Коэффициент может принимать значения только от 0 до 1 (0 – отсутствие сопряженности, 1 – полная сопряженность). Однако этот коэффициент не может принимать значения, равные 1, максимальное возможное значение зависит от числа строк и столбцов. Например, для таблиц 4х4 максимальное значение коэффициента 0,87.
Для нашего примера
.
2. Коэффициент сопряженности Крамера
, (5.11)
где k – минимальное число из числа строк и столбцов.
Для нашего примера
.
Оценка значимости полученных коэффициентов производится по критерию l2.
Для случая дихотомических (таблицы 2х2) признаков (например, пола, партийного положения, семейного положения, шкалы “да – нет”) мера связи между двумя признаками оценивается с помощью коэффициента ассоциации Пирсона.
, (5.12)
где а, b, c, d – эмпирические частоты в ячейках таблицы.
Рассчитаем этот коэффициент на примере корреляционной табл. 5.4.
Таблица 5.4
| Достаточно ли представлены, на Ваш взгляд, женщины Вашего населенного пункта в органах власти и управления? | Пол | В целом по массиву | |
| Мужской | Женский | ||
| Да | a | b | 13 (a+b) |
| Нет | c | d | 48 (c+d) |
| В целом по массиву | (a+c) | (b+d) |
Значимость полученного коэффициента также производится по критерию l2.
Среди непараметрических методов оценки тесноты связи наибольшее значение имеют коэффициенты ранговой корреляции Спирмена и Кендала. Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками при условии, что их значения можно упорядочить или проранжировать по степени убывания или возрастания признака. Ранг – это порядковый номер значений признака, расположенных в порядке убывания или возрастания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Данные ранги называют связными. Коэффициент ранговой корреляции Спирмена в случае несвязных рангов вычисляется по формуле:
, (5,13)
где di – разности рангов, l – число пар рангов. Коэффициент изменяется от –1 до +1. При l > 30 значимость коэффициента проверяется на основе t-критерия Стьюдента. Расчетное значение критерия:
Расчетное значение критерия:
. (5.14)
Значение коэффициента считается значимым, если tрасч>tкр.
При l £ 30 значимость коэффициента при заданном уровне значимости и определенном объеме выборочных данных проверяется по таблице.
Вычисления коэффициента Спирмена для связных рангов более громоздки. Поэтому на практике для связных и несвязных рангов удобнее использовать формулу для несвязных рангов. Вычисление коэффициента приведено в табл. 5.5:
Таблица 5.5
Сравнение основных жизненных ценностей студентов
в 1987 и 1991 гг.
| Жизненные ценности | Ранг | Ранг | ||||||
| 1. Иметь верных друзей | 91,1 | 81,5 | ||||||
2. Любовь Любовь
| 68,7 | 55,6 | ||||||
| 3. Интересная профессия | 71,0 | 41,1 | ||||||
| 4. Учеба | 38,9 | 9,6 | ||||||
| 5. Уважение к старшим | 39,0 | 5,7 | ||||||
| 6. Сила | 20,7 | 30,9 | ||||||
| 7. Деньги | 27,0 | 43,6 | ||||||
8. Интеллект Интеллект
| 35,8 | 17,5 | 6,5 | |||||
| 9. Творчество | 20,2 | 4,8 | ||||||
| 10. Стремление создать семью | 41,2 | 14,3 | ||||||
| 11. Мода | 30,2 | 13,6 | ||||||
| 12. Музыка | 16,0 | 16,0 | ||||||
| 13. “Фирменные” вещи | 14,2 | 17,5 | 6,5 | |||||
14. Карьера Карьера
| 11,0 | 16,5 | ||||||
| 15. Секс | 5,4 | 14,0 |
В нашем примере 8-я и 13-я позиции делят между собой шестое и седьмое места. Поэтому им соответственно приписываем ранг (6+7)/2, т. е. 6,5.
Используя данные, построим рабочую таблицу.
Таблица 5.6
Расчет коэффициента ранговой корреляции Спирмена.
| Номер признака | Ранг | Разность пар рангов | Квадрат разности рангов | |||||
| переменной | I | II | di | di2 | ||||
| –2 | ||||||||
| –8 | ||||||||
| –10 | ||||||||
| 6,5 | 0,5 | 0,25 | ||||||
| –5 | ||||||||
| –7 | ||||||||
| –5 | ||||||||
| 6,5 | 0,5 | 0,25 | ||||||
| å=383,5 |
Подставляем данные в формулу:
.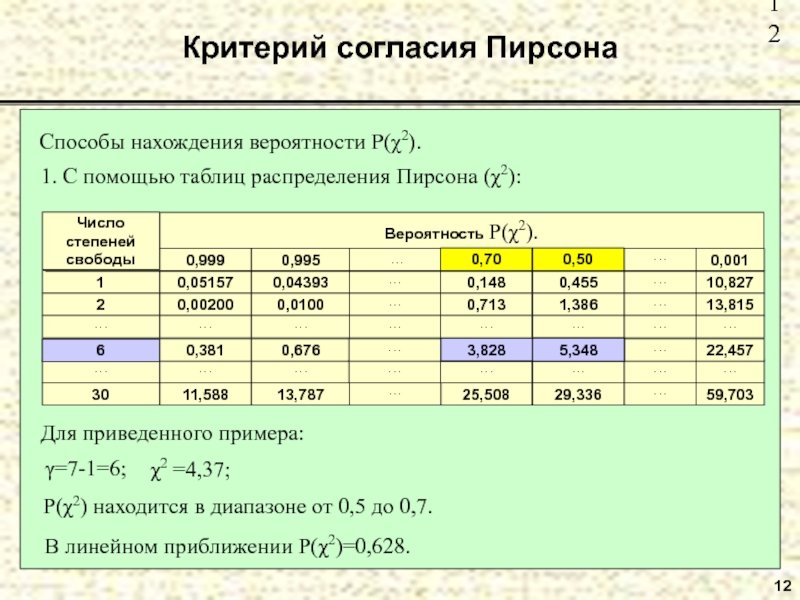
Из таблицы критических значений Спирмена находим, что при l=15 и уровне значимости 0,05 rs должен быть не ниже 0,517. В нашем случае он равен 0,315, следовательно, между жизненными ценностями молодежи в 1987 и 1991 гг. нет значимой связи.
Для установления связи между количественными признаками (например, возрастом, зарплатой, количеством членов семьи) используется линейный коэффициент корреляции Пирсона (определение формы связи признаков можно осуществить путем построения графика взаимного изменения в декартовой системе координат).
, (5.15)
где x – факторный признак, y – результативный признак.
. (5.16)
Для оценки существенности коэффициента корреляции используется критерий t (при n<50).
Полученное значение критерия сравнивается при заданном числе степеней свободы (df=n–2) и уровне значимости с табличным значением (табл. распределения Стьюдента). Если вычисленное значение критерия больше табличного, гипотеза о независимости признаков отвергается.
Проверку гипотезы об отсутствии связи можно сделать и без вычислений, пользуясь таблицей, составленной Р. Фишером. В этой таблице показывается величина коэффициента корреляции, которая может считаться существенной при данном количестве наблюдений. При пользовании таблицей величину коэффициента корреляции следует искать для числа степеней свободы, равного n–2. Чтобы считаться существенным при заданном уровне значимости, он должен быть не ниже табличного значения.
Линейный коэффициент корреляции может принимать любые значения в пределах от –1 до +1. Чем ближе коэффициент к 1 по абсолютной величине, тем теснее связь между признаками. Знак при коэффициенте линейной корреляции указывает на направление связи: при прямой зависимости коэффициент положительный, при противоположной – отрицательный, 0 – отсутствие линейной зависимости между признаками.
Предположим, что задача исследования состоит в определении степени зависимости уровня успеваемости студентов от уровня их удовлетворенности избранной специальностью. В качестве исходных данных взяты (в баллах) уровень успеваемости по студенческим группам и уровень удовлетворенности выбранной специальностью.
В качестве исходных данных взяты (в баллах) уровень успеваемости по студенческим группам и уровень удовлетворенности выбранной специальностью.
Таблица 5.7
Дата добавления: 2015-10-02; просмотров: 93 | Нарушение авторских прав
mybiblioteka.su — 2015-2021 год. (0.03 сек.)
Расчет критерия согласия Пирсона
Расчет критерия согласия Пирсона| fi | f’i | fi – f’i | (fi – f’i)2 | (fi – f’i)2/ fi | ||||
| 4,1 | –1,1 | 1,21 | 0,30 | |||||
| 3,9 | 1,1 | 1,21 | 0,31 | |||||
| 9,7 | 6,3 | 39,69 | 4,09 | |||||
| 9,3 | –6,3 | 39,69 | 4,27 | |||||
| 5,6 | 0,4 | 0,16 | 0,03 | |||||
| 5,4 | –0,4 | 0,16 | 0,03 | |||||
| 10,2 | –1,2 | 1,44 | 0,14 | |||||
| 9,8 | 1,2 | 1,44 | 0,15 | |||||
| 21,4 | –4,4 | 19,36 | 0,90 | |||||
| 20,6 | 4,4 | 19,36 | 0,94 | |||||
| å=11,16 |
l2=11,16.
При числе степеней свободы 4 и уровне значимости 0,05 находим табличное значение l2табл =9,5. Так как l2расч>l2табл, гипотеза о независимости признаков в строке и столбце таблицы отвергается.
Критерий “хи-квадрат” вычисляется для подтверждения гипотезы о независимости признаков, но он не характеризует тесноту связи. Для определения тесноты связи можно использовать коэффициенты сопряженности Пирсона и Крамера. Они рассчитываются для таблиц размером схk, если признаки измерены в шкале наименований.
1. Коэффициент сопряженности Пирсона
. (5.10)
Коэффициент может принимать значения только от 0 до 1 (0 – отсутствие сопряженности, 1 – полная сопряженность). Однако этот коэффициент не может принимать значения, равные 1, максимальное возможное значение зависит от числа строк и столбцов. Например, для таблиц 4х4 максимальное значение коэффициента 0,87.
Для нашего примера
.
2. Коэффициент сопряженности Крамера
, (5.11)
где k – минимальное число из числа строк и столбцов.
Для нашего примера
.
Оценка значимости полученных коэффициентов производится по критерию l2.
Для случая дихотомических (таблицы 2х2) признаков (например, пола, партийного положения, семейного положения, шкалы “да – нет”) мера связи между двумя признаками оценивается с помощью коэффициента ассоциации Пирсона.
, (5.12)
где а, b, c, d – эмпирические частоты в ячейках таблицы.
Рассчитаем этот коэффициент на примере корреляционной табл. 5.4.
Таблица 5.4
| Достаточно ли представлены, на Ваш взгляд, женщины Вашего населенного пункта в органах власти и управления? | Пол | В целом по массиву | |
| Мужской | Женский | ||
| Да | a | b | 13 (a+b) |
| Нет | c | d | 48 (c+d) |
| В целом по массиву | (a+c) | (b+d) |
Значимость полученного коэффициента также производится по критерию l2.
Среди непараметрических методов оценки тесноты связи наибольшее значение имеют коэффициенты ранговой корреляции Спирмена и Кендала. Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками при условии, что их значения можно упорядочить или проранжировать по степени убывания или возрастания признака. Ранг – это порядковый номер значений признака, расположенных в порядке убывания или возрастания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Данные ранги называют связными. Коэффициент ранговой корреляции Спирмена в случае несвязных рангов вычисляется по формуле:
, (5,13)
где di – разности рангов, l – число пар рангов. Коэффициент изменяется от –1 до +1. При l > 30 значимость коэффициента проверяется на основе t-критерия Стьюдента. Расчетное значение критерия:
Расчетное значение критерия:
. (5.14)
Значение коэффициента считается значимым, если tрасч>tкр.
При l £ 30 значимость коэффициента при заданном уровне значимости и определенном объеме выборочных данных проверяется по таблице.
Вычисления коэффициента Спирмена для связных рангов более громоздки. Поэтому на практике для связных и несвязных рангов удобнее использовать формулу для несвязных рангов. Вычисление коэффициента приведено в табл. 5.5:
Таблица 5.5
Сравнение основных жизненных ценностей студентов
в 1987 и 1991 гг.
| Жизненные ценности | Ранг | Ранг | ||||||
| 1. Иметь верных друзей | 91,1 | 81,5 | ||||||
2. Любовь Любовь
| 68,7 | 55,6 | ||||||
| 3. Интересная профессия | 71,0 | 41,1 | ||||||
| 4. Учеба | 38,9 | 9,6 | ||||||
| 5. Уважение к старшим | 39,0 | 5,7 | ||||||
| 6. Сила | 20,7 | 30,9 | ||||||
| 7. Деньги | 27,0 | 43,6 | ||||||
8. Интеллект Интеллект
| 35,8 | 17,5 | 6,5 | |||||
| 9. Творчество | 20,2 | 4,8 | ||||||
| 10. Стремление создать семью | 41,2 | 14,3 | ||||||
| 11. Мода | 30,2 | 13,6 | ||||||
| 12. Музыка | 16,0 | 16,0 | ||||||
| 13. “Фирменные” вещи | 14,2 | 17,5 | 6,5 | |||||
14. Карьера Карьера
| 11,0 | 16,5 | ||||||
| 15. Секс | 5,4 | 14,0 |
В нашем примере 8-я и 13-я позиции делят между собой шестое и седьмое места. Поэтому им соответственно приписываем ранг (6+7)/2, т. е. 6,5.
Используя данные, построим рабочую таблицу.
Таблица 5.6
Расчет коэффициента ранговой корреляции Спирмена.
| Номер признака | Ранг | Разность пар рангов | Квадрат разности рангов | |||||
| переменной | I | II | di | di2 | ||||
| –2 | ||||||||
| –8 | ||||||||
| –10 | ||||||||
| 6,5 | 0,5 | 0,25 | ||||||
| –5 | ||||||||
| –7 | ||||||||
| –5 | ||||||||
| 6,5 | 0,5 | 0,25 | ||||||
| å=383,5 |
Подставляем данные в формулу:
.
Из таблицы критических значений Спирмена находим, что при l=15 и уровне значимости 0,05 rs должен быть не ниже 0,517. В нашем случае он равен 0,315, следовательно, между жизненными ценностями молодежи в 1987 и 1991 гг. нет значимой связи.
Для установления связи между количественными признаками (например, возрастом, зарплатой, количеством членов семьи) используется линейный коэффициент корреляции Пирсона (определение формы связи признаков можно осуществить путем построения графика взаимного изменения в декартовой системе координат).
, (5.15)
где x – факторный признак, y – результативный признак.
. (5.16)
Для оценки существенности коэффициента корреляции используется критерий t (при n<50).
Полученное значение критерия сравнивается при заданном числе степеней свободы (df=n–2) и уровне значимости с табличным значением (табл. распределения Стьюдента). Если вычисленное значение критерия больше табличного, гипотеза о независимости признаков отвергается.
Проверку гипотезы об отсутствии связи можно сделать и без вычислений, пользуясь таблицей, составленной Р. Фишером. В этой таблице показывается величина коэффициента корреляции, которая может считаться существенной при данном количестве наблюдений. При пользовании таблицей величину коэффициента корреляции следует искать для числа степеней свободы, равного n–2. Чтобы считаться существенным при заданном уровне значимости, он должен быть не ниже табличного значения.
Линейный коэффициент корреляции может принимать любые значения в пределах от –1 до +1. Чем ближе коэффициент к 1 по абсолютной величине, тем теснее связь между признаками. Знак при коэффициенте линейной корреляции указывает на направление связи: при прямой зависимости коэффициент положительный, при противоположной – отрицательный, 0 – отсутствие линейной зависимости между признаками.
Предположим, что задача исследования состоит в определении степени зависимости уровня успеваемости студентов от уровня их удовлетворенности избранной специальностью. В качестве исходных данных взяты (в баллах) уровень успеваемости по студенческим группам и уровень удовлетворенности выбранной специальностью.
В качестве исходных данных взяты (в баллах) уровень успеваемости по студенческим группам и уровень удовлетворенности выбранной специальностью.
Таблица 5.7
Дата добавления: 2015-07-11; просмотров: 171 | Нарушение авторских прав
Читайте в этой же книге: Этап оформления результатов исследования | Организация опросов | ИНСТРУКЦИЯ ДЛЯ БРИГАДИРОВ | ИНСТРУКЦИЯ ДЛЯ ИНТЕРВЬЮЕРОВ | Этап полевых работ | Анализ документов | Контент-анализа в ОСИ | Социологическое наблюдение | Кто проводил______________________________________ | Сочетание и комбинирование методов сбора информации |
mybiblioteka.su — 2015-2021 год. (0.029 сек.)
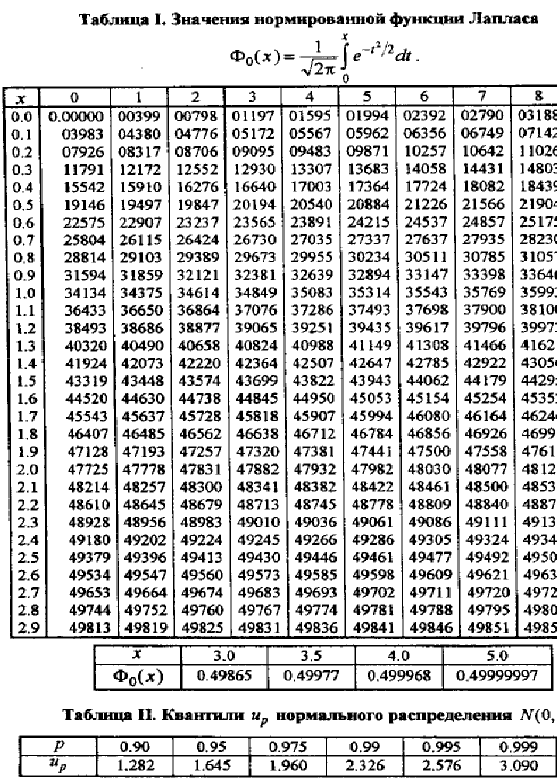
| Значения (критические) коэффициента корреляции Пирсона r для различных уровней значимости и различного числа степеней свободы (размеров выборки). Источник: Fisher R.
Инструкция для поиска вероятности ошибки (p) для вычисленного коэффициента.
| |||||||||||
Функция ПИРСОН для расчета коэффициента корреляции Пирсона в Excel
Функция ПИРСОН используется для вычисления коэффициента корреляции Пирсона r. Эта функция используется в работе, когда необходимо отразить степень линейной зависимости между двумя массивами данных. В Excel есть несколько функций, с помощью которых можно получить тот же результат, но универсальность и простота функции Пирсона делают выбор в ее пользу.
Как работает ПИРСОН в Excel?
Рассмотрим пример вычисления корреляции Пирсона между двумя массивами данных с помощью функции ПИРСОН в MS EXCEL.Первый массив представляет значения температуры, второй — давление в определенный летний период. Пример заполненной таблицы представлен на рисунке:
Задача следующая: необходимо определить соотношение температуры и давления для июня месяца.
Пример решения с функцией ПИРСОН при анализе в Excel
- Выберите ячейку C17, в которой должен быть вычислен критерий Пирсона в качестве результата, и нажмите мастер-кнопку функции «fx» или комбинацию горячих клавиш (SHIFT + F3).Откроется мастер функций, в поле Категория выберите «Статистический».
 В списке статистических функций выберите и нажмите Ok:
В списке статистических функций выберите и нажмите Ok: - В меню аргументов выберите Массив 1; в примере это утренняя температура воздуха, а затем массив 2 — атмосферное давление.
- В результате в ячейке C17 мы получаем коэффициент корреляции Пирсона. В нашем случае он отрицательный и примерно равен -0,14.
Этот показатель -0,14 от Пирсона, вернувшего функцию, указывает на неблагоприятную зависимость температуры и давления в раннее время суток.
Взаимодействие с другими людьмиПошаговая инструкция функции ПИРСОН
Коэффициент корреляции — наиболее удобный индикатор сопряженности количественных признаков.
Задача: Определить линейный коэффициент корреляции Пирсона.
Пример решения:
- В таблице приведены данные для группы курильщиков. Первый массив x представляет возраст курильщика, второй массив y представляет количество сигарет, выкуриваемых за день.
- Выберите ячейку B4, в которой будет вычисляться результат, и нажмите мастер-кнопку функции fx (SHIFT + F3).

- В группе «Статистика» выберите функцию ПИРСОН.
- Выберите массив 1 — возраст курения, затем массив 2 — количество выкуриваемых сигарет в день.
- Нажмите кнопку OK и посмотрите критерий нормального распределения Пирсона в ячейке B4.
Таким образом, согласно результату расчета, статистический вывод эксперимента выявил отрицательную связь между возрастом и количеством выкуриваемых сигарет в день.
Корреляционный анализ Пирсона в Excel
Задание: студентам были предложены тесты на визуальное и вербальное мышление.Было измерено среднее время решения тестовых задач в секундах. Психолога интересует вопрос: есть ли связь между временем решения этих проблем?
Пример решения: исходные данные представляем в виде таблицы:
- Переместите курсор в ячейку F2. Откройте мастер функций fx (SHIFT + F3) или введите его вручную.
- Выберите функцию.
- Выберите с помощью мыши массив1 B3: B21, затем массив2 C3: C21.

- Нажимаем ОК и в ячейке F2 получаем критерий совместимости Пирсона.
Интерпретация результата расчета по Пирсону
Значение коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше -1. Эти два числа +1 и -1 являются границами для коэффициента корреляции. Если результат вычислений дает значение больше +1 или меньше -1, значит, в вычислениях произошла ошибка.
Если модуль корреляции близок к 1, то это соответствует высокому уровню связи между переменными.
Скачать примеры функции ПИРСОН для корреляции в Excel
Если получен знак минус, то большее значение одного знака соответствует меньшему значению другого. Другими словами, при наличии знака минус увеличение одной переменной (знака, значения) соответствует уменьшению другой переменной. Эта зависимость называется обратно пропорциональной. Эти положения очень важно четко понимать для правильной интерпретации полученной корреляционной зависимости.
Корреляция Пирсона
Пояснения > Социальные исследования> Анализ > Корреляция Пирсона
Описание | Пример | Обсуждение | Видеть также
Описание
Пирсон разработал очень распространенный способ измерения корреляции, часто называемый Корреляция произведение-момент Пирсона. Используется, когда оба переменные не менее уровень интервала и данные параметрический.
Рассчитано путем деления ковариации двух переменных на произведение их стандартных отклонения.
r = СУММ ((x i — xbar) (y — ybar)) / ((n — 1) * s x * s y )
Где x и y — переменные, x i — одно значение x, xbar — среднее значение всех x, n — количество переменных, а s x — это стандартное отклонение всех x.
r также может рассматриваться как
r 2 = объясненная вариация / общая вариация
где вариация рассчитывается как сумма Площадей, SS
Другими словами, именно пропорция вариации может быть
объяснил. Высокая объясненная пропорция — это хорошо, а значение единицы — идеально
корреляция. Например, значение r 0,8 объясняет 64% дисперсии.
Высокая объясненная пропорция — это хорошо, а значение единицы — идеально
корреляция. Например, значение r 0,8 объясняет 64% дисперсии.
Коэффициент Пирсона, рассчитанный по населению, обозначается греческой буквой «ро». (ρ). При вычислении по образцу он обозначается буквой «r».
Коэффициент детерминации рассчитывается как r 2 .
Пример
| х | y | x-xbar | y-ybar | (x-xbar) * (y-ybar) | |
| 1 | 2 | -3.7 | -2,3 | 8,51 | |
| 3 | 5 | -1,7 | 0,7 | -1,19 | |
| 5 | 6 | 0. 3 3 | 1,7 | 0,51 | |
| 6 | 6 | 1,3 | 1,7 | 2,21 | |
| 8 | 7 | 3.3 | 2,7 | 8,91 | |
| 9 | 7 | 4,3 | 2,7 | 11,61 | |
| 6 | 5 | 1. 3 3 | 0,7 | 0,91 | |
| 4 | 3 | -0,7 | -1,3 | 0,91 | |
| 3 | 1 | -1.7 | -3,3 | 5,61 | |
| 2 | 1 | -2,7 | -3,3 | 8,91 | |
| n: | 10 | ||||
| Всего: | 57 | 43 | 46. | ||
| xbar | ybar | ||||
| Значит: | 4.70 | 4,30 | (xbar — это среднее значение x) | ||
| s x | с г | ||||
| Стандартное отклонение: | 5841396591085739″ x:fmla=»=STDEV(B2:B11)»> 2.58 | 2,36 | |||
Отсюда:
Пирсона r = сумма ((x i — xbar) (y — ybar)) / ((n — 1) * s x * s y )
= 0.854
Это довольно высокий показатель, показывающий умеренно хорошую корреляцию между наборами числа.
Обсуждение
Пирсон является параметрической статистикой и предполагает:
- Нормальный распространение.
- Интервал или данные о соотношении.
- Линейная зависимость между X и Y
Коэффициент детерминации r 2 представляет собой процент
разница в иждивении
переменная объясняется зависимой переменной.
Корреляция объясняет некоторую разницу, но не все. Это работает на квадратичный закон, поэтому корреляция 0,5 указывает на то, что независимая переменная объясняет 25% дисперсии зависимой переменной и корреляцию 0,9 составляет 81% дисперсии.
Это означает, что необъяснимое отклонение обозначено (1-r 2 ). Обычно это происходит из-за случайных факторов.
КорреляцияПирсона также известна как продукт-момент Пирсона Корреляция или Коэффициент корреляции выборки .’r’ также известен как ‘Пирсона r’.
См. Также
корреляция Спирмена, Корреляция Кендалла, Типы надежность
Компьютерный тест на знание английского языка
PTE Academic помог мне осуществить мою мечту — зарегистрироваться в качестве медсестры. Формат теста хоть и сложен, но вполне достижим, если много практиковаться. Я буду поощрять любого сдавать PTE Academic.Я также считаю, что задачи простые и понятные.
Faith
Я собираюсь поступить в аспирантуру в Австралии и очень счастлив, потому что PTE Academic признан всеми австралийскими университетами. Практический тест с оценками на веб-сайте Pearson был чрезвычайно полезен во время моего обзора. В день экзамена экзаменаторы были очень профессиональны и строго соблюдали правила. Я получил результаты своих тестов через 24 часа. Академический экзамен PTE — это действительно «быстрый и справедливый тест по английскому языку».»
Практический тест с оценками на веб-сайте Pearson был чрезвычайно полезен во время моего обзора. В день экзамена экзаменаторы были очень профессиональны и строго соблюдали правила. Я получил результаты своих тестов через 24 часа. Академический экзамен PTE — это действительно «быстрый и справедливый тест по английскому языку».»
Raymond Angelo
Так как экзамен проводится на компьютере, экзаменующийся может эффективно использовать свои навыки.
Damith
Good? Номер один
Rajesh Kumar
Я бы порекомендовал PTE Academic, поскольку он удобнее выбирать дату экзамена и легко получать результаты.
Govinda
Что мне больше всего понравилось в этом тесте, так это доброта людей в месте проведения. Очень дружелюбный персонал, который помог мне почувствовать себя лучше расслаблен.Я не чувствовал стресса от экзамена, и это было для меня решающим.
Lina
Быстрое бронирование и очень быстрая публикация результатов! Настоятельно рекомендуется, чем любой другой тест по английскому языку 🙂
Eillen
Подготовка и преданность делу для достижения желаемого результата — ключевой фактор в получении желаемого результата.
Nila
PTE Academic — хороший тест по английскому языку. Подготовка улучшила мой английский язык.
Джордж
Что мне нравится в тесте, так это скорость выставления оценок и объективный подход к выставлению оценок.
Ngoc
PTE более практичен и менее напряжен, чем многие другие тесты по английскому языку. Это помогло мне подтвердить мою стипендию и поступить в университет моей мечты. Без PTE я бы лишился этих жизненных возможностей. Это действительно обновленный тест.
Iya
PTE Academic точно отражает способность человека общаться на стандартном английском языке. Я бы предпочел этот экзамен другим доступным тестам, поскольку он устраняет элементы человеческой предвзятости при выставлении оценок.В отличие от других экзаменов на знание английского языка, PTE Academic требует меньше времени, когда дело доходит до подготовки к экзамену и заполнения отчета о результатах.
Selva Mariappan
Мне нравится тот факт, что за выставлением оценок не стоит ни один человек. Это исключает возможность получения необъективной оценки.
Это исключает возможность получения необъективной оценки.
Pietro
Pearson Test of English Academic — отличный экзамен на знание английского языка! Тест состоит исключительно из всех необходимых базовых компонентов английского языка, и вы пройдете всестороннее тестирование.Более того, вы получите результаты в течение нескольких дней после сдачи экзамена!
Maxximillian Ray
Самое лучшее в PTE Academic — это проводить тесты на компьютерах. Его формат довольно прост для понимания, и в Интернете доступно множество материалов, которые могут вам помочь.
Jagrut Gajraj
PTE Academic — это действительно честный тест на знание английского языка, и люди могут на него положиться.
Prudencia
Pearson — это наиболее объективный и эффективный способ проверить мои знания английского языка.Экзамен честный и точный, плюс я получил свои результаты за 24 часа! 100% рекомендую.
Ян Мишель
Я знаю Пирсона уже пару лет и скажу, что у меня был отличный опыт прохождения PTE Academic. Offline Test дал мне достаточно информации, чтобы понять, что мне нужно, и тест довольно справедливый. Спасибо за профессионализм, Пирсон!
Offline Test дал мне достаточно информации, чтобы понять, что мне нужно, и тест довольно справедливый. Спасибо за профессионализм, Пирсон!
Веллингтон
PTE Академический формат теста позволяет улучшить результаты по всем разделам с практикой.Существует положительная корреляция между часами, потраченными на практический материал, и оценкой. Я считаю очень ценной возможность пройти тренировочные тесты с оценкой.
Тина Сегал
Оценка прошла без сбоев. Каждый шаг — от записи на онлайн-тест до регистрации на месте в тестовом центре — выполняется легко и быстро. Логистика и организация тестового центра также довольно удобны, и самое лучшее — это быстрое получение результатов теста. Подготовительные материалы, доступные на официальном сайте, тоже очень эффективны.
Rajeswari
PTE Academic переориентировал меня на правильное письмо по-английски каждый день. Мне понравился тест и даже больше, когда я получил желаемый результат.
Шаллу
Учебные материалы были удобны для использования. Тестирование в день прошло гладко. Очень профессионально сделано !! Очень счастлив!!!
Тестирование в день прошло гладко. Очень профессионально сделано !! Очень счастлив!!!
Аманда Смит
Никакого человеческого общения, никакого ожидания разговора. Вы просто получите оценки по своему качеству.
Shafayet Ullah
Я считаю PTE Academic наиболее объективным, эффективным, удобным и действенным тестом по английскому языку, доступным для профессионалов.Я определенно порекомендую PTE Academic своим друзьям, которые хотят учиться за границей.
Рут Камилла Авена
Это хорошо разработанный тест, который фактически измеряет уровень владения английским языком кандидатов. Я подумал, что тест был блестяще разработан, интерактивен и действительно отражает языковые способности человека.
Усман Ашраф
PTE Academic дает точные и быстрые результаты. Я уже сдавал 2 экзамена по английскому до этого и не могу получить желаемые баллы в письменной форме.Спасибо PTE Academic!
Katrina Sarmiento
Лучшее в PTE Academic — это то, что он основан на компьютере и дает быстрые результаты, что не только снижает беспокойство по поводу результатов, но и экономит много времени.
Rohit Makhija
Отличный способ сдать экзамен по академическому английскому. Приветливый персонал и непринужденная обстановка. Во время экзамена не ощущал никакого давления. У меня было уединение, и я чувствовал себя так, как будто учился дома.
Emina Music
У PTE Academic много преимуществ.1. Тест проходит за один раз. Не нужно возвращаться к другим разделам, как к другим тестам. 2. Результаты доступны через 5 дней. 3. Формат теста легко подобрать с 2-3 пробными тестами. 4. Учебные материалы для теста легко доступны в Интернете. 5. Сам сайт очень интерактивен, и вся информация доступна.
Сухайб Ахмед Кавиш
Тест хорошо разработан, и без вмешательства человека, это справедливая оценка языковых навыков. Экзамен охватывает множество вопросов, которые точно проверяют языковые навыки.
Наузер Ахмед Пир
Как интерпретировать коэффициент корреляции r
- Образование
- Математика
- Статистика
- Как интерпретировать коэффициент корреляции r
По статистике Деборы Дж. Рамси
Рамси
,
коэффициент корреляции r измеряет силу и направление линейной зависимости между двумя переменными на диаграмме рассеяния. Значение r всегда находится между +1 и –1.Чтобы интерпретировать его значение, посмотрите, к какому из следующих значений ближе всего ваша корреляция r :
Точно — 1. Идеальная прямая зависимость (отрицательная) под уклон
— 0,70. Сильный спуск (отрицательная) линейная зависимость
— 0,50. Отношение умеренного спуска (отрицательное)
— 0,30. Слабый спуск (отрицательная) линейная зависимость
0. Нет линейной зависимости
+0.30. Слабая линейная зависимость подъема (положительная)
+0,50. Умеренно восходящие (позитивные) отношения
+0,70. Прочная (положительная) линейная зависимость
Ровно +1.
 Идеальное линейное соотношение подъема (положительное)
Идеальное линейное соотношение подъема (положительное)
Если диаграмма рассеяния не указывает на наличие хотя бы некоторой линейной зависимости, корреляция не имеет большого значения.Зачем измерять степень линейной зависимости, если не о чем говорить? Однако вы можете принять идею отсутствия линейной связи двумя способами: 1) если никакой связи не существует, вычисление корреляции не имеет смысла, потому что корреляция применяется только к линейным отношениям; и 2) Если существует сильная связь, но она не является линейной, корреляция может вводить в заблуждение, потому что в некоторых случаях существует сильная кривая связь. Вот почему так важно сначала изучить диаграмму рассеяния.
Диаграммы рассеяния с корреляциями а) +1.00; б) –0,50; в) +0,85; г) +0,15.
На приведенном выше рисунке показаны примеры того, как выглядят различные корреляции с точки зрения силы и направления отношений. На рисунке (a) показана корреляция почти +1, на рисунке (b) показана корреляция –0,50, на рисунке (c) показана корреляция +0,85, а на рисунке (d) показана корреляция +0,15. Сравнивая рисунки (а) и (с), вы видите, что рисунок (а) представляет собой почти идеальную прямую линию подъема, а рисунок (с) показывает очень сильный линейный узор подъема (но не такой сильный, как рисунок (а)).Рисунок (b) спускается вниз, но точки несколько разбросаны в более широкой полосе, показывая, что линейная зависимость присутствует, но не такая сильная, как на рисунках (a) и (c). На рисунке (d) ничего не видно (и не должно быть, поскольку его корреляция очень близка к 0).
Сравнивая рисунки (а) и (с), вы видите, что рисунок (а) представляет собой почти идеальную прямую линию подъема, а рисунок (с) показывает очень сильный линейный узор подъема (но не такой сильный, как рисунок (а)).Рисунок (b) спускается вниз, но точки несколько разбросаны в более широкой полосе, показывая, что линейная зависимость присутствует, но не такая сильная, как на рисунках (a) и (c). На рисунке (d) ничего не видно (и не должно быть, поскольку его корреляция очень близка к 0).
Многие люди ошибаются, полагая, что корреляция –1 — это плохо, потому что это указывает на отсутствие связи. Верно как раз наоборот! Корреляция –1 означает, что данные выстроены по идеальной прямой линии, что является самой сильной отрицательной линейной зависимостью, которую вы можете получить.Знак «-» (минус) просто указывает на отрицательную взаимосвязь, нисходящую линию.
Насколько близко это значение достаточно близко к –1 или +1, чтобы указать на достаточно сильную линейную зависимость? Большинству статистиков нравится видеть корреляции, превышающие по крайней мере +0,5 или –0,5, прежде чем они будут слишком взволнованы. Однако не ожидайте, что корреляция всегда будет 0,99; помните, это реальные данные, а реальные данные не идеальны.
Однако не ожидайте, что корреляция всегда будет 0,99; помните, это реальные данные, а реальные данные не идеальны.
Об авторе книги
Дебора Дж.Рамси, доктор философии, , профессор статистики и специалист по статистике в области образования в Университете штата Огайо. Она является автором статистической рабочей книги для чайников, статистики II для чайников, и вероятности для чайников .
Корреляция
Когда два набора данных прочно связаны друг с другом, мы говорим, что они имеют Высокая корреляция .
Слово «Корреляция» состоит из Co- (что означает «вместе») и Relation
- Корреляция Положительная , когда значения увеличиваются вместе на и
- Корреляция Отрицательная , когда одно значение уменьшается, , когда другое увеличивается
Предполагается, что корреляция — линейная (после линии).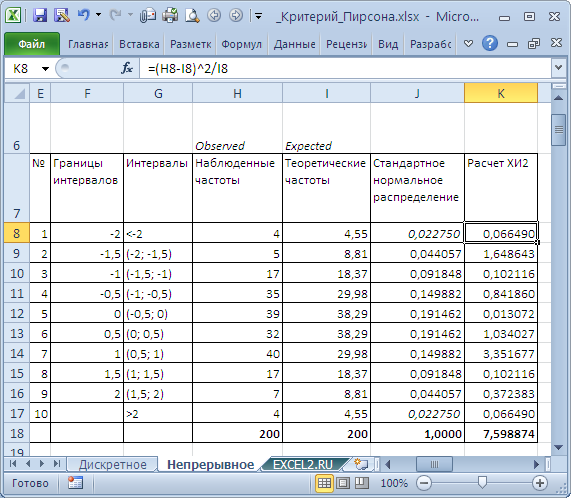
Корреляция может иметь значение:
- 1 — идеальная положительная корреляция
- 0 — корреляция отсутствует (значения вообще не связаны)
- -1 — идеальная отрицательная корреляция
Значение показывает, насколько хороша корреляция (не насколько крутой является линия), и положительна она или отрицательна.
Пример: продажа мороженого
Местный магазин мороженого отслеживает, сколько мороженого они продают, в зависимости от температуры в тот день. Вот их цифры за последние 12 дней:
| Продажи мороженого в зависимости от температуры | |
| Температура ° C | Продажа мороженого |
|---|---|
| 14.2 ° | $ 215 |
| 16,4 ° | $ 325 |
| 11,9 ° | $ 185 |
| 15,2 ° | $ 332 |
| 18,5 ° | $ 406 |
| 22,1 ° | $ 522 |
| 19,4 ° | $ 412 |
| 25,1 ° | $ 614 |
| 23,4 ° | $ 544 |
18. 1 ° 1 ° | $ 421 |
| 22,6 ° | 445 долларов США |
| 17,2 ° | 408 долл. США |
А вот те же данные, что и точечная диаграмма:
Мы легко видим, что теплая погода и более высокие продажи идут рука об руку. Отношения хорошие, но не идеальные.
На самом деле корреляция 0,9575 … посмотрим в конце, как я ее рассчитал.
Также попробуйте Калькулятор корреляции.Плохая корреляция на кривых
Расчет корреляции работает правильно только для прямолинейных отношений.
Наше мороженое Пример: Была жара!
Становится так жарко, что люди не подходят к магазину, и продажи начинают падать на .
Вот последний график:
Теперь значение корреляции составляет 0 : «Нет корреляции» …!
Вычисленное значение корреляции равно 0 (я вычислил), что означает «отсутствие корреляции».
Но мы можем видеть, что данные следуют красивой кривой , которая достигает пика около 25 ° C.
Но вычисление корреляции недостаточно «умно», чтобы увидеть это.
Мораль истории: создайте точечный график и посмотрите на него!
Вы можете увидеть взаимосвязь, которой нет при вычислении.
«Корреляция не является причинно-следственной связью»
Распространенная поговорка — «Корреляция не является причинно-следственной связью».
То, что на самом деле означает, так это то, что корреляция не доказывает, что одно вызывает другое:
- Одно может вызвать другое
- Другой может вызвать первый
- Они могут быть связаны разными вещами
- Или это может быть случайность!
Может быть много причин, по которым данные имеют хорошую корреляцию.
Пример: солнцезащитные очки и мороженое
Наш магазин мороженого определяет, сколько солнцезащитных очков было продано в большом магазине за день, и сравнивает их с продажами мороженого:
Корреляция между продажами солнцезащитных очков и мороженого высока
Означает ли это, что солнцезащитные очки заставляют людей хотеть мороженого?
Пример: бедные пригороды с большей вероятностью будут иметь высокое загрязнение.
Почему?
- Бедные люди загрязняют окружающую среду?
- Загрязненные пригороды — единственное место, которое могут себе позволить бедные люди?
- Это обычное звено, такое как фабрики с низкооплачиваемой работой и большим загрязнением окружающей среды?
Пример: реальный случай!
Несколько лет назад опрос сотрудников выявил сильную положительную корреляцию между «Изучение внешнего курса» и дней болезни .
Означает ли это:
- Учеба вызывает у них тошноту?
- Больные много учатся?
- Или они солгали о болезни, чтобы больше учиться?
Без дополнительных исследований мы не можем понять, почему.
Как рассчитать
Как я вычислил значение 0,9575 вверху?
Я использовал «Корреляцию Пирсона». Существует программное обеспечение, которое может его вычислить, например функция CORREL () в Excel или LibreOffice Calc…
. .. а вот как рассчитать самому:
.. а вот как рассчитать самому:
Назовем два набора данных «x» и «y» (в нашем случае температура x , а продажи мороженого y ):
- Шаг 1. Найдите среднее значение x и среднее значение y
- Шаг 2. Вычтите среднее значение x из каждого значения x (назовите их « a ») и вычтите среднее значение y из каждого значения y (назовите их « b »).
- Шаг 3: Вычислить: ab , a 2 и b 2 для каждого значения
- Шаг 4: Суммируем ab , суммируем a 2 и суммируем b 2
- Шаг 5. Разделите сумму ab на квадратный корень из [(сумма 2 ) × (сумма b 2 )]
Вот как я рассчитал первый пример мороженого (значения округлены до 1 или 0 знаков после запятой):
В виде формулы это:
Где:
- Σ — это сигма, символ «суммирования»
- — каждое значение x за вычетом среднего значения x (обозначено как «a» выше)
- — каждое значение y за вычетом среднего значения y (выше обозначено буквой b)
Вам, вероятно, не придется так рассчитывать, но, по крайней мере, вы знаете, что это не «волшебство», а просто набор рутинных вычислений.

 Подтвердите выбор кнопкой Continue.
Подтвердите выбор кнопкой Continue.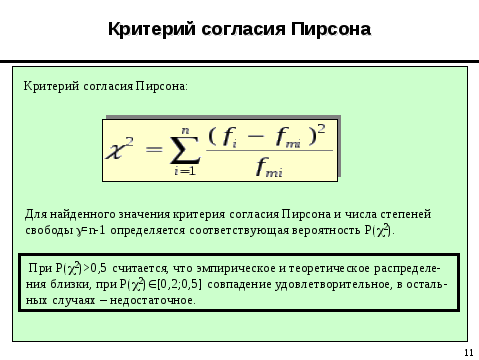 Residual
Residual Sig. (2-sided)
Sig. (2-sided)  2 cells (25,0%) have expected count less than 5. The minimum expected count is 2,49 (2 ячейки (25%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 2,49.)
2 cells (25,0%) have expected count less than 5. The minimum expected count is 2,49 (2 ячейки (25%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 2,49.)

 Однако для данных, относящихся к номинальной шкале, этот критерий неприменим.
Однако для данных, относящихся к номинальной шкале, этот критерий неприменим. A., Frank Y. Statistical Tables for Biological, Agricultural and Medical Research, 6th ed., published by Longman Group, Ltd., London (previously published by Oliver and Boyd, Edinburgh), Table VII.
A., Frank Y. Statistical Tables for Biological, Agricultural and Medical Research, 6th ed., published by Longman Group, Ltd., London (previously published by Oliver and Boyd, Edinburgh), Table VII.
 90
90