Асимметрия – Финансовая энциклопедия
Что такое Асимметрия?
Асимметрия относится к искажению или асимметрии симметричной колоколообразной кривой или нормального распределения в наборе данных. Если кривая смещена влево или вправо, говорят, что она перекошена. Асимметрия может быть определена количественно как представление степени, в которой данное распределение отличается от нормального распределения. Нормальное распределение имеет перекос, равный нулю, в то время как логнормальное распределение , например, будет демонстрировать некоторую степень перекоса вправо.
Три распределения вероятностей, изображенные ниже, имеют положительный наклон (или наклон вправо) в возрастающей степени. Распределения с отрицательным наклоном также известны как распределения с перекосом влево. Асимметрия используется вместе с эксцессом, чтобы лучше судить о вероятности попадания событий в хвосты распределения вероятностей.
Ключевые моменты
- Асимметрия в статистике – это степень искажения симметричной колоколообразной кривой в распределении вероятностей.

- Распределения могут демонстрировать правую (положительную) асимметрию или левую (отрицательную) асимметрию в различной степени.
- Инвесторы отмечают асимметрию при оценке распределения доходности, поскольку оно, как и эксцесс, учитывает крайние значения набора данных, а не сосредотачивается исключительно на среднем.
Объяснение асимметрии
Помимо положительного и отрицательного перекоса, можно также сказать, что у распределений есть нулевой или неопределенный перекос. На кривой распределения данные на правой стороне кривой могут сужаться иначе, чем данные на левой стороне. Эти сужения известны как «хвосты». Отрицательный перекос относится к более длинному или толстому хвосту в левой части распределения, а положительный перекос относится к более длинному или толстому хвосту справа.
Среднее положительно перекос данных будет больше , чем медиана . В распределении с отрицательным перекосом все обстоит как раз наоборот: среднее значение отрицательно искаженных данных будет меньше медианы. Если графики данных симметричны, распределение имеет нулевую асимметрию, независимо от того, насколько длинные или толстые хвосты.
Если графики данных симметричны, распределение имеет нулевую асимметрию, независимо от того, насколько длинные или толстые хвосты.
Есть несколько способов измерить перекос. Первый и второй коэффициенты асимметрии Пирсона – два общих. Первый коэффициент асимметрии Пирсона, или асимметрия режима Пирсона, вычитает моду из среднего и делит разницу на стандартное отклонение . Второй коэффициент асимметрии Пирсона, или медиана асимметрии Пирсона, вычитает медианное значение из среднего, умножает разницу на три и делит произведение на стандартное отклонение.
Измерение перекоса
Существует несколько способов измерения перекоса. Первый и второй коэффициенты перекоса Пирсона – два распространенных. Первый коэффициент перекоса Пирсона, или модальный перекос Пирсона, вычитает моду из среднего значения и делит разницу на стандартное отклонение. Второй коэффициент перекоса Пирсона, или медианный перекос Пирсона, вычитает медиану из среднего значения, умножает разницу на три и делит произведение на стандартное отклонение.
Формулы для коэффициента перекоса Пирсона следующие:
где:
Sk1=первый коэффициент перекоса Пирсона и Sk2 – второй
s=стандартное отклонение для выборки
Xˉ=среднее значение
Mo=модальное (модальное) значение
Md= медианное значение
Первый коэффициент асимметрии Пирсона полезен, если данные демонстрируют сильную моду. Если данные имеют слабую моду или несколько мод, второй коэффициент Пирсона может быть предпочтительным, поскольку он не полагается на моду как на меру центральной тенденции.
Что вам говорит асимметрия?
Инвесторы отмечают асимметрию при оценке распределения доходности, поскольку оно, как и эксцесс , учитывает крайние значения набора данных, а не сосредотачивается исключительно на среднем. Краткосрочные и среднесрочные инвесторы, в частности, должны обращать внимание на крайности, потому что они с меньшей вероятностью будут удерживать позицию достаточно долго, чтобы быть уверенными в том, что среднее сработает само.
Инвесторы обычно используют стандартное отклонение для прогнозирования будущей доходности, но стандартное отклонение предполагает нормальное распределение. Поскольку несколько распределений доходности приближаются к нормальному, асимметрия – лучший показатель, на котором основываются прогнозы производительности. Это связано с риском перекоса.
Поскольку несколько распределений доходности приближаются к нормальному, асимметрия – лучший показатель, на котором основываются прогнозы производительности. Это связано с риском перекоса.
Риск асимметрии – это повышенный риск появления точки данных с высокой асимметрией в искаженном распределении. Многие финансовые модели, которые пытаются предсказать будущую доходность актива, предполагают нормальное распределение, в котором меры центральной тенденции равны. Если данные искажены, такая модель всегда будет недооценивать риск перекоса в своих прогнозах. Чем больше искажены данные, тем менее точной будет эта финансовая модель.
Асимметрия и эксцесс. Коэффициент асимметрии и эксцесс распределения. Теория вероятностей и математическая статистика
Краткая теория
При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.
Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
Коэффициент асимметрии характеризует скошенность распределения по отношению к математическому ожиданию. Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания.
На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию
,
а кривая II – отрицательную (левостороннюю)
.
Кроме вышеописанного коэффициента, для характеристики асимметрии рассчитывают также показатель асимметрии Пирсона:
Коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента третьего порядка.
Для оценки «крутости», т. е. большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой — эксцессом.
Эксцессом (или коэффициентом эксцесса) случайной величины называется число:
Число 3 вычитается из отношения потому, что для наиболее часто встречающегося нормального распределения отношение .
Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные — отрицательным
эксцессом.
Примеры решения задач
Задача 1
Для заданного вариационного ряда вычислить коэффициенты асимметрии и эксцесса.
| 0-0.4 | 0.4-0.8 | 0.8-1.2 | 1.2-1.6 | 1.6-2.0 | 2.0-2.4 | Итого | |
| 3 | 17 | 21 | 25 | 24 | 10 | 100 |
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Составим расчетную таблицу
| Интервалы | Середина интервала, | |||||
| 0 – 0.4 | 0.2 | 3 | 0.6 | 3.763 | -4.215 | 4.721 |
| 0.4 – 0.8 | 0.6 | 17 |
10.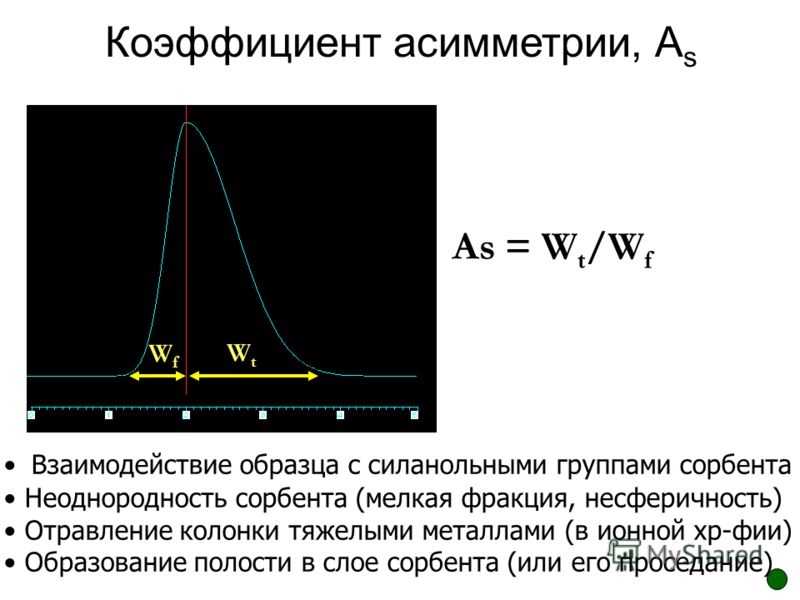 2 2
|
8.813 | -6.345 | 4.569 |
| 0.8 – 1.2 | 1.0 | 21 | 21.0 | 2.150 | -0.688 | 0.220 |
| 1.2 – 1.6 | 1.4 | 25 | 35.0 | 0.160 | 0.013 | 0.001 |
| 1.6 – 2 | 1.8 | 24 |
43. 2 2
|
5.530 | 1.274 | |
| 2 – 2.4 | 2.2 | 10 | 22.0 | 7.744 | 6.815 | 5.997 |
| Итого | — | 100 | 132.0 | 28.160 | -1.766 | 16.782 |
Средняя:
Найдем моду — варианту, которой соответствует наибольшая частота.
Дисперсия:
Среднее квадратическое отклонение:
Коэффициент асимметрии Пирсона:
Коэффициент асимметрии можно найти по формуле:
Центральный момент 3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Центральный момент 4-го порядка:
Получаем:
Задача 2
Для заданного вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и эксцесса методом произведений, используя условные моменты.
| 0-0.4 | 0.4-0.8 | 0.8-1.2 | 1.2-1.6 |
1. 6-2.0 6-2.0
|
2.0-2.4 | Итого | |
| 3 | 17 | 21 | 25 | 24 | 10 | 100 |
Решение
Составим расчетную таблицу
Перейдем к условным вариантам
В качестве ложного нуля возьмем 3-ю варианту 0
Условные варианты вычислим по формуле:
где 4 (разность между соседними вариантами)
| Интервалы | Середина интервала, | ||||||
0 – 0. 4 4
|
0.2 | -2 | 3 | -6 | 12 | -24 | 48 |
| 0.4 – 0.8 | -1 | 17 | -17 | 17 | -17 | 17 | |
| 0.8 – 1.2 | 1.0 | 0 | 21 | 0 | 0 | 0 | 0 |
1. 2 – 1.6 2 – 1.6
|
1.4 | 1 | 25 | 25 | 25 | 25 | 25 |
| 1.6 – 2 | 1.8 | 2 | 24 | 48 | 96 | 192 | 384 |
| 2 – 2.4 | 2.2 | 3 | 10 | 30 | 90 | 270 | 810 |
| Итого | — | — | 100 | 80 | 240 | 446 | 1284 |
Условный момент 1-го порядка:
Средняя:
Условный момент 2-го порядка:
Дисперсия:
Среднее квадратическое отклонение:
Коэффициент асимметрии можно найти по формуле:
Условный момент 3-го порядка:
Центральный момент 3-го порядка:
Получаем:
Эксцесс можно найти по формуле:
Условный момент 4-го порядка:
Центральный момент 4-го порядка:
Получаем:
Определения и примеры в статистике
К
Уилл Кентон
Полная биография
Уилл Кентон — эксперт в области экономики и инвестиционного законодательства. Ранее он занимал руководящие должности редактора в Investopedia и Kapitall Wire, имеет степень магистра экономики Новой школы социальных исследований и степень доктора философии по английской литературе Нью-Йоркского университета.
Ранее он занимал руководящие должности редактора в Investopedia и Kapitall Wire, имеет степень магистра экономики Новой школы социальных исследований и степень доктора философии по английской литературе Нью-Йоркского университета.
Узнайте о нашем редакционная политика
Обновлено 18 декабря 2022 г.
Рассмотрено
Шарлин Райнхарт
Рассмотрено Шарлин Райнхарт
Полная биография
Шарлин Райнхарт является дипломированным бухгалтером, CFE, председателем комитета общества CPA штата Иллинойс и имеет степень в области бухгалтерского учета и финансов Университета ДеПола.
Узнайте о нашем Совет финансового контроля
Факт проверен
Кэтрин Бир
Факт проверен Кэтрин Бир
Полная биография
Кэтрин Бир — писатель, редактор и архивариус из Нью-Йорка. У нее большой опыт исследовательской и писательской деятельности, она освещала такие разнообразные темы, как история общественных садов Нью-Йорка и выступление Бейонсе на фестивале Coachella в 2018 году.
У нее большой опыт исследовательской и писательской деятельности, она освещала такие разнообразные темы, как история общественных садов Нью-Йорка и выступление Бейонсе на фестивале Coachella в 2018 году.
Узнайте о нашем редакционная политика
Что такое асимметричное распределение?
Асимметричное распределение — это ситуация, при которой значения переменных встречаются с нерегулярной частотой, а среднее значение, медиана и мода возникают в разных точках. Асимметричное распределение демонстрирует асимметрию. Напротив, гауссово или нормальное распределение, когда оно изображено на графике, имеет форму колоколообразной кривой, а две стороны графика симметричны.
Основные выводы
- Асимметричное распределение имеет место, когда распределение дохода от инвестиций в актив имеет искаженный или асимметричный характер.
- Асимметричное распределение противоположно симметричному распределению, при котором доход от инвестиций следует регулярной схеме, часто изображаемой в виде кривой нормального распределения.
- Колоколообразная кривая — это распространенный тип графика в инвестициях, который показывает распределение данных и может помочь инвесторам проанализировать историческую доходность актива.
- Во время волатильных рыночных действий результаты инвестиций могут быть искажены, что приводит к асимметричным схемам распределения.
Понимание асимметричного распределения
Колоколообразная кривая — это распространенный тип графика, показывающий распределение данных. Доходность фондового рынка иногда напоминает колоколообразные кривые, что позволяет инвесторам анализировать их на предмет закономерностей распределения вероятностей доходности актива.
Асимметричное распределение возникает, когда распределение доходов от инвестиций не является симметричным с нулевой асимметрией. Распределение с отрицательной асимметрией называется асимметрией влево, потому что у него более длинный левый хвост на графике. Напротив, распределение с положительной асимметрией называется асимметричным вправо и имеет более длинный правый хвост.
Инвесторы должны заботиться о том, как распределяются данные о доходности инвестиций. Классы активов (акции, облигации, товары, валюта, недвижимость и т. д.) подлежат различному распределению доходности. Это также относится к секторам в пределах этих классов активов (например, технологии, здравоохранение, основные продукты и т. д.), а также к портфелям, состоящим из комбинаций этих классов активов или секторов.
Эмпирически они следуют асимметричным моделям распределения. Это связано с тем, что эффективность инвестиций часто искажается периодами высокой волатильности рынка или необычной фискальной и денежно-кредитной политикой, во время которых доходность может быть аномально высокой или низкой.
Асимметричное и симметричное распределение
В отличие от асимметричного распределения, симметричное распределение имеет место, когда значения переменных появляются с предсказуемой частотой, а среднее значение, медиана и мода встречаются в одних и тех же точках. Колоколообразная кривая является классическим примером симметричного распределения. Если бы вы провели линию посередине кривой, левая и правая стороны были бы зеркальными отражениями друг друга. Ключевая концепция технической торговли, симметричное распределение, предполагает, что с течением времени поведение цены актива будет соответствовать этой кривой распределения.
Колоколообразная кривая является классическим примером симметричного распределения. Если бы вы провели линию посередине кривой, левая и правая стороны были бы зеркальными отражениями друг друга. Ключевая концепция технической торговли, симметричное распределение, предполагает, что с течением времени поведение цены актива будет соответствовать этой кривой распределения.
Акции «голубых фишек», как правило, демонстрируют предсказуемую кривую колокола и часто имеют более низкую волатильность.
Примеры асимметричного распределения
Отклонение от «нормальной» доходности чаще происходило в последние два десятилетия, начиная с Интернет-пузыря в конце 1990-х годов. Эта волатильность сохранялась во время других заметных событий, таких как террористические атаки 11 сентября, крах пузыря на рынке жилья и последующий финансовый кризис, а также в годы количественного смягчения, которое подошло к концу в 2017 году. мягкая денежно-кредитная политика может стать следующей главой волатильности рынка и более асимметричного распределения доходов от инвестиций.
Особые указания
Учитывая, что разрушительные события и чрезвычайные явления происходят чаще, чем ожидалось, инвесторы могут улучшить свои модели распределения активов, включив допущения об асимметричном распределении. Традиционные модели среднего отклонения, разработанные Гарри Марковицем, были основаны на предположениях о том, что доходность класса активов распределяется нормально. Традиционные модели распределения активов хорошо работают в устойчивых «нормальных» рыночных условиях.
Однако традиционные модели распределения активов могут не защитить портфели от серьезных рисков снижения, когда рынки становятся ненормальными. Моделирование с предположениями об асимметричном распределении может помочь снизить волатильность портфелей и снизить риски потери капитала.
Asymmetry® « ASYMMETRY® Наблюдения
ASYMMETRY® Observations — это наблюдения Майка Шелла за поведением инвесторов, вызывающим направленные ценовые тренды, глобальную макроэкономику, тактическую торговлю ETF, импульсную торговлю акциями, хеджирование, торговлю волатильностью и управление рисками, которые создают асимметричную доходность инвестиций.
 Асимметричный профиль доходности — это профиль риска/вознаграждения с положительной асимметрией между прибылью и убытком. Майк Шелл — основатель Shell Capital Management, LLC и управляющий портфелем ASYMMETRY® Global Tactical 9.0039
Асимметричный профиль доходности — это профиль риска/вознаграждения с положительной асимметрией между прибылью и убытком. Майк Шелл — основатель Shell Capital Management, LLC и управляющий портфелем ASYMMETRY® Global Tactical 9.0039Асимметрия ® в отсутствии баланса или симметрии. Асимметрия – это дисбаланс – перекос или наклон в одну сторону больше, чем в другую. В теории вероятностей и статистике асимметрия является мерой асимметрии распределения вероятностей. Асимметрия — это мера степени асимметрии распределения. Если левый хвост больше правого, говорят, что функция имеет отрицательную асимметрию. Если правый хвост больше, он имеет положительный перекос. Если они равны, то асимметрия равна нулю.
Асимметричное распределение (асимметрия). Если разделить распределение пополам по его среднему (или медианному) значению, распределение значений по обе стороны от этой центральной точки не будет одинаковым (т.
е. несимметричным), и распределение будет считаться «асимметричным». ”
Симметричное распределение (Симметрия). Если разделить распределение пополам по его среднему значению (или медиане), то распределение значений будет «зеркальным отражением» относительно этой центральной точки.
Форма распределения, нормальность. Важным аспектом «описания» переменной является форма ее распределения, которая сообщает вам частоту значений из разных диапазонов переменной. Как правило, исследователя интересует, насколько хорошо распределение может быть аппроксимировано нормальным распределением (см. анимацию ниже для примера этого распределения). Простая описательная статистика может предоставить некоторую информацию, относящуюся к этому вопросу. Например, если асимметрия (которая измеряет отклонение распределения от симметрии) явно отличается от 0, тогда это распределение асимметрично, а нормальное распределение совершенно симметрично.
Если эксцесс (который измеряет остроконечность распределения) явно отличается от 0, то распределение либо более плоское, либо более остроконечное, чем обычно; эксцесс нормального распределения равен 0,
Источник: StatSoft
ASYMMETRY® и ASYMMETRY Investment Program® являются зарегистрированными товарными знаками Shell Capital Management, LLC. com
Copyright 2013. АСИММЕТРИЯ ® Наблюдения Все права защищены.
ASYMMETRY® Observations — это наблюдения Майка Шелла за поведением инвесторов, вызывающим направленные ценовые тренды, глобальную макроэкономику, тактическую торговлю ETF, импульсную торговлю акциями, хеджирование, торговлю волатильностью и управление рисками, которые создают асимметричную доходность инвестиций. Асимметричный профиль доходности — это профиль риска/вознаграждения с положительной асимметрией между прибылью и убытком. Майк Шелл является основателем Shell Capital Management, LLC и портфельным менеджером ASYMMETRY® Global Tactical. Для получения дополнительной информации посетите сайт www.Shell-Capital.com
Для получения дополнительной информации посетите сайт www.Shell-Capital.com
Введите свой адрес электронной почты, чтобы следить за ASYMMETRY® Observations и получать уведомления о новых сообщениях по электронной почте.
Адрес электронной почты:
- Тенденция фондового рынка США после обновления
- Мы могли бы задушить VIX!
- Тенденции вслед за природным газом и мазутом
- Ничто так не меняет энтузиазм инвесторов, как ценовой тренд
- ой хлыст
- Фондовый рынок возобновляет нисходящий тренд
- Фондовый рынок выходит на краткосрочный более высокий уровень риска
- Тенденция, динамика и широта сектора США до октября 2022 г.
- Волатильность фондового рынка остается повышенной
- Инвестирование в акции сопряжено с рисками, которые вы должны быть готовы нести или активно управлять и хеджировать.
- Разворот
- Тенденция фондового рынка проверяется
- Фондовый рынок находится в переломной точке
- Каждый новый ценовой тренд начинается с контртренда
- После того, как давление продаж приведет к снижению цен на акции до достаточно низкого уровня, мы увидим изменение настроений
- Инфляция снижается в соответствии с этим анализом тенденций сырьевых товаров
- Медвежьи рынки с экономической рецессией длятся дольше и более серьезны
- Технологии растущих секторов, потребительские циклические товары и услуги связи более недооценены, чем стоимость?
- Стратегии систематического хеджирования с защитой от пут терпели неудачу или терпели неудачу на этом медвежьем рынке
- Фундаментальная оценка: фондовый рынок дешевый или дорогой?
- Наблюдения за тенденциями фондового рынка, рынка облигаций и настроений инвесторов
- Работает ли следование за трендом на акциях?
- Фондовый рынок опережает ФРС и что может произойти дальше
- Подразумеваемая волатильность указывает на другое возможное расширение волатильности.

- Спред доходности 10-2-летних казначейских облигаций продолжает указывать на предупреждение о возможной рецессии
- Крайне медвежьи настроения инвесторов в конечном итоге становятся бычьими для фондового рынка
- Следуя тренду инфляции и риска облигаций
- Как мы узнаем, неизбежна ли рецессия
- Nasdaq возобновляет нисходящий тренд
- Широта фондового рынка указывает на внутреннюю слабость и скрытый медвежий рынок
- Пузырь фондового рынка США
- Market Action Скидки на все
- Цель — более мощный мотиватор, чем деньги.
- Уильям Дж. О’Нил об Эго
- Интересная конвергенция акций малых и крупных компаний
- Технический анализ — это анализ психологии масс людей, поэтому его также называют поведенческими финансами.
- Ожидаемая волатильность для S&P 500 исчезает
- Эд Сейкота об определении размера позиции
- Равный вес S&P 500 растет
- Метод умных денег: как выбирать акции, как профессионал хедж-фонда — об асимметричных выплатах
- Учимся читать кардиограммы здоровья рынка
- Общий рыночный цикл влияет почти на каждую акцию
- Это хорошее время, чтобы уменьшить риски или хеджировать риски.

