Арифметика остатков: Национальный исследовательский университет «Высшая школа экономики»

Исследовательская работа по теме «Арифметика остатков»

МБОУ Средняя общеобразовательная школа №7

Исследовательская работа по теме:

«Арифметика остатков»

Выполнил:

 Луцев Андрей Романович,

ученик 7А класса

МБОУ СОШ №7

г. Сальск

Руководитель:

Устимова Нина Владимировна,

учитель математики МБОУ СОШ №7 г. Сальска

 

                                                                Сальск, 2012

---

Содержание

1. Введение.

2. Основная часть.

3. Практическая часть.

4. Заключение.

5. Литература.

Введение

Решая олимпиадные задачи  на делимость чисел, я столкнулся с проблемой:

как  не выполняя громоздких вычислений, найти остаток от деления на натуральное число суммы, произведения больших чисел и степеней с натуральным показателем или установить делимость нацело.

В связи с этой проблемой  мной была поставлена цель: найти простой способ нахождения остатка при делении на натуральное число.

Для этого мне нужно было решить следующие задачи:

1. Установить факт существования простого способа решения сложных олимпиадных задач на делимость чисел.
2. Если этот способ существует, найти его.

Математика для всех нас начинается с целых чисел. Всюду – дома, в школе, в магазине, в троллейбусе или автобусе – мы складываем, умножаем, делим целые числа. Иногда разделить нацело нельзя – получается остаток, и многое зависит от того, каков этот остаток. Такие случаи я и рассматриваю в своей работе «Арифметика остатков» или арифметика сравнений. «Арифметика остатков» — одна из глав высшей арифметики, имеет отношение и к элементарной арифметике. Многие вопросы элементарной арифметики связаны с этой темой: и деление с остатком, и признаки делимости, и отыскание наибольшего общего делителя, и многое другое. Но эта тема имеет и самостоятельную ценность – арифметика сравнений представляет собой простой пример «необычной», «экзотической» арифметики, в которой действуют сложение и умножение, возведение в степень, вычитание и деление, подчиняющиеся тем же законам, что и в обычной арифметике. Необычность ее в том, что в ней имеется лишь конечное число не равных друг другу или несравнимых друг с другом чисел.

 На основе сказанного выдвинута гипотеза: существует наиболее рациональный способ нахождения остатков при делении больших чисел на натуральное число.

Основная часть

Со скоростью ЭВМ.

Каков будет остаток от деления числа 7778*7779*7780*7781*7782*7783 на 7?

 Для решения этой задачи нам не потребуется ЭВМ. Каждый научится решать такие задачи в уме. Надо только знать немного арифметику, но не обычную, которую в школе учат, а так называемую «арифметику остатков» или «арифметику сравнений». Так называется глава серьёзной математической науки – «теории чисел».

Сравнение целых чисел по модулю.

С арифметикой остатков мы сталкиваемся буквально на каждом шагу. Вот несколько примеров.

Пример 1. В коридоре висит счетчик. Взглянем на него. Он показывает, предположим, 0729 киловатт-часов. А на самом деле сколько электроэнергии израсходовано с момента установки счетчика? 729 кВт . ч? Или 10729? Или, может быть 30729? По показанию счетчика этого не скажешь. Ведь после 9999 на счетчике будет 0000, и счет начнется сначала. Счетчик так задуман, что указывает не полный расход энергии, а только остаток от деления израсходованного числа киловатт-часов на 10000.

Пример 2. Когда мы пошли в школу, на часах было ровно 8, а когда ложились спать, часы показывали 10, а 10 – 8 = 2. Но разве прошло 2 часа с того момента, как мы ушли в школу? Нет, не 2, а целых 14. Дело в том, что стрелки, дойдя до 12.00, каждый раз начинают отсчет времени заново, с нуля. Часы нам показывают не полное время, прошедшее с момента, когда они показывали 0.00, а лишь остаток от деления его на 12.

Можно еще много привести примеров и задач, в которых основную роль играет не частное от деления одного целого числа на другое, а остаток. Для решения такого вида задач была создана «арифметика остатков». Познакомимся с ней поближе.

Рассмотрим остатки от деления на 7. Делитель в теории чисел называется «модулем», а числа, дающие при делении на модуль 7 одинаковые остатки, называются «равноостаточными» или «сравнимыми по модулю 7». Два числа а и b при делении на некоторый модуль m дают одинаковые остатки, т.е. сравнимы по модулю m, записывается так:

                        .

Рассмотрим следующую таблицу:

0	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31	32	33	34
35	36	37	38	39	40	41
42	43	44	45	46	47	48
49	50	51	52	53	…	…
…	…	…	…	…	…	…

  Эта таблица построена следующим образом: все целые числа выписаны подряд построчно, по семь чисел в каждой строке. Поэтому соседние числа одного столбца отличаются на 7, а значит при делении на 7 будут давать одинаковые остатки. В первом столбце оказались числа, делящиеся на 7 без остатка, во втором – дают при делении на 7 остаток 1 и т.д.  Известно, что при делении на m, образуется m различных видов остатков: 0, 1, 2, …, m – 1. Остатки в таблице выделены жирным шрифтом – это верхние числа каждого столбца. Можно сказать, что в один столбец попали те и только те числа, которые при делении на 7 равноостаточны, т.е. сравнимы по модулю 7. Итак, все числа разбились на 7 классов: в класс с индексом 0 попали числа, которые при делении на 7 дают в остатке 0 (делятся на 7 без остатка), в класс с индексом 1 – числа, дающие при делении на 7 в остатке 1, и т.д.

Правило определения класса. Чтобы узнать, в каком классе находится некоторое число, надо найти остаток от деления этого числа на m. Этот остаток равен индексу класса. 

    Если разность двух чисел делится на 7 без остатка, то оба числа попадают в один столбец, в один класс. Делаем выводы.

Вывод 1. В один класс попадают все числа, дающие при делении на модуль один и тот же остаток.

Вывод 2. Два числа принадлежат к одному и тому же классу тогда и только тогда, когда их разность делится без остатка на модуль.

Вывод 3. Остаток от деления суммы на модуль не изменится, если одно из слагаемых или каждое слагаемое заменить другим числом того же класса (в частности, индексом того же класса). В буквенном виде это свойство можно записать так:

если  и , то , т.е. сравнения можно складывать.

Вывод 4.  Остаток от деления произведения нескольких чисел на модуль М не изменится, если один из сомножителей ( или даже каждый из сомножителей)  заменить числом того же класса.

   Основные свойства сравнений напоминают свойства обычных равенств: сравнения можно также вычитать, перемножать, возводить в степень, умножать на любое целое число, не равное нулю:

,

,

,

.

Практическая часть

Пример 1. Не проводя обычных вычислений, найти остаток от деления на 7 следующей суммы:      8+79+780+7781+77782+777783.

Решение: остатки от деления слагаемых на 7 равны 1,2,3,4,5,6; например, 77782=77777+5, а 777783=777777+6, значит индексы классов, в которых находятся слагаемые, равны 1,2,3,4,5,6.

Воспользуемся выводом третьим и заменим в данной сумме каждое слагаемое индексом его класса – индекс суммы от этого не изменится. Остаётся найти остаток от деления суммы   на 7

1+2+3+4+5+6=21

Эта сумма делится на 7 без остатка, значит, и данная в условии сумма делится на 7 без остатка.

Используя обозначения, можно решение этой задачи записать так:

8 ≡ 1(mod 7), 79 ≡ 2(mod 7), 780 ≡3(mod 7), 7781 ≡4(mod 7), 77782 ≡5(mod 7), 777783 ≡6(mod 7) ,

8+79+780+7781+77782+777783 ≡ 1+2+3+4+5+6 = 21 ≡ 0    (mod 7)

Ответ: сумма делится на 7 без остатка.

Теперь мы уже можем попытаться решить задачу, с которой начали:

 «Со скоростью ЭВМ».

Каков будет остаток от деления числа 7778*7779*7780*7781*7782*7783 на 7?

 Вместо суммы здесь стоит произведение.  Посмотрим, не обладает ли произведение таким же свойством, что и сумма.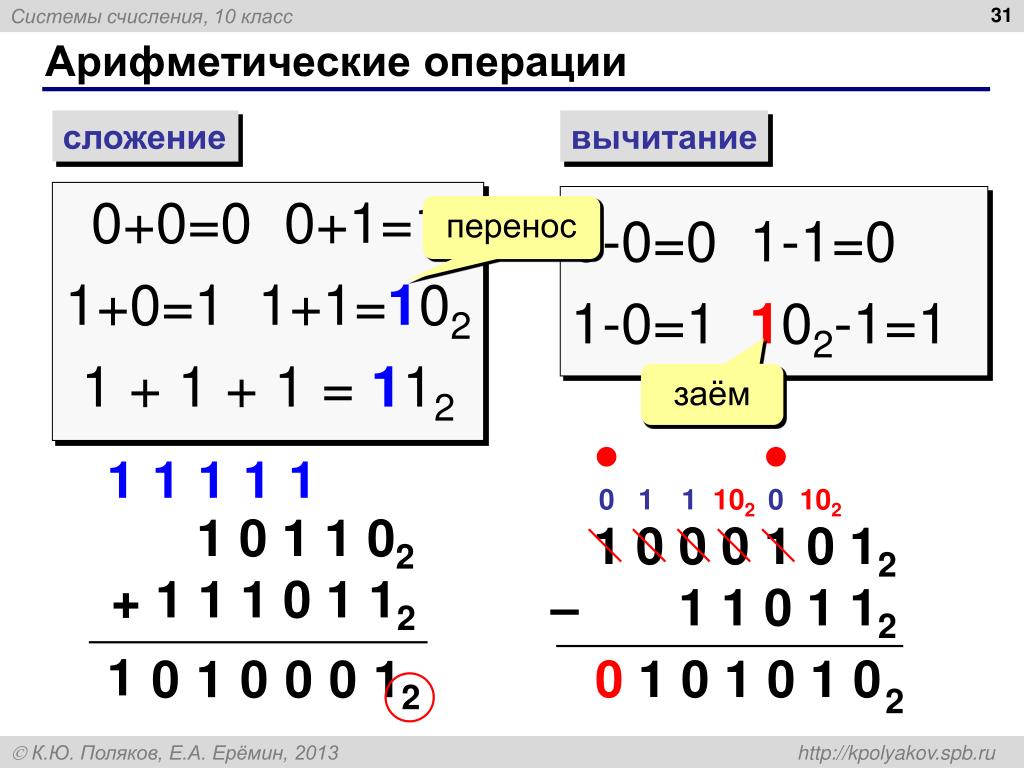

Рассмотрим произведение нескольких, скажем, трех чисел: А, В и С.

Что произойдёт если в произведении АВС число А заменить другим числом того же класса А1? Так как А1 отличается от А на число, кратное 7, то А1=А+7К, где К – некоторое  целое число.

Значит, А1ВС = (А+7К) ВС = АВС+7КВС.

Отсюда видно, что АВС и А1ВС принадлежат к одному классу (отличаются на число кратное 7) .

   Мы можем заменить каждое число индексом его класса. Пользуясь обозначениями теории чисел, можно записать:

если  А ≡ В (mod M), C ≡ D (mod M),то AC ≡ BD (mod M),

т.е. сравнения по одному и тому же модулю можно перемножить.

Теперь нам не трудно решить первую задачу (со скоростью ЭВМ).

 Остаток не изменится, если мы все сомножители заменим индексами их классов, равными 1,2,3,4,5 и 6 соответственно.

Так как 1*2*3*4*5*6 =720 = 20 ≡ 6 (mod 7),

Ответ:  искомый остаток равен 6.

Все наши рассуждения применимы и в том случае, когда вместо модуля 7 используется любое другое натуральное число М, отличное от единицы. В этом случае, вместо таблицы из семи столбцов придётся рассматривать таблицу, содержащую М столбцов.

Пример 2. Доказать, что 776776 + 777777 + 778778 не делится на 3.

Решение: воспользуемся арифметикой вычетов по модулю 3. Так как 776 ≡ 2 (mod 3), то 7762 ≡ 4 ≡ 1 (mod 3), а 776776=  (7762)388 ≡1388 ≡ 1 (mod 3).

 778 ≡ 1 (mod 3) и 778778 ≡ 1778 ≡ 1 (mod 3).

 777 ≡ 0 (mod 3) и 777777 ≡ 0 (mod 3).

Складывая эти сравнения, получим: 776776 + 777777 + 778778 ≡ 1 + 0 + 1 ≡ 2 (mod 3), т.е. данная сумма даёт при делении на 3 остаток, равный 2.

Пример 3. Задача из учебника «Алгебра и начала анализа»10класс под редакцией Ю.М.Колягина. Найти остаток от деления 3946 на 5.

Решение: 39 = 4 (mod 5), 3946 = 446 (mod 5)

Выпишем степени 4: 41 = 4  42 = 16  43 = 64, т.е. 4 в нечётной степени, 6 в чётной степени. Число 46- чётное, значит последняя цифра  446 равна 6. 6 ≡ 1 (mod 5).

Ответ: остаток 1.

Пример 4.

В некотором месяце 3 четверга пришлись на четные числа.

Какой день недели был 26 числа этого месяца?

Решение:

В месяце 3 четных четверга, значит всего 5 четвергов т.к. в неделе 7 дней, то четверги чередуются: четный и нечетный.

Первый четверг – может быть 1,2 или 3 числом, если в месяце 31 день, и 1или 2 числом если в месяце 30 дней.

Значит: Первый четверг – 2 число, а Пятый четверг: 30, следовательно 26 число – это воскресенье.

Ответ: 26 число – это воскресенье.

Заключение.

Изучив «Арифметику остатков», я теперь легко решаю многие олимпиадные задачи на делимость чисел.

Литература.

В своей работе я использовал информацию из книг:

Гусев В.А., Орлов А.И., Розенталь А.Л. Внеклассная работа по математике. Москва, «Просвещение»,1984.

Фарков А.В., математические олимпиады в школе. М.,«Просвещение»,2011.

Колягин Ю.М., учебник «Алгебра и начало анализа», 10 класс.

Тезисы.

Тема: «Арифметика остатков».

Автор работы: ученик 7 «А» класса МОУ СОШ №7 Луцев Андрей Романович.

Руководитель: Устимова Нина Владимировна.

Цель: Выяснение существования лёгкого способа решения олимпиадных задач на делимость чисел, не выполняя громоздких вычислений.

Задача:

1. Установить факт существования рационального способа решения сложных олимпиадных задач на делимость чисел.
2. В случае положительного ответа – поиск этого способа, предоставляющего лёгкое и быстрое нахождение решения олимпиадных задач, не выполняя громоздких вычислений.

В ходе работы выявлено:

1. С помощью «арифметики остатков» можно легко решать разные сложные задачи.

Вывод 1. В один класс попадают все числа, дающие при делении на модуль один и тот же остаток.

Вывод 2. Два числа принадлежат к одному и тому же классу тогда и только тогда, когда их разность делится без остатка на модуль.

Вывод 3. Остаток от деления суммы на модуль не изменится, если одно из слагаемых или каждое слагаемое заменить другим числом того же класса.

Вывод 4.  Остаток от деления произведения нескольких чисел на модуль М не изменится, если один из сомножителей  заменить числом того же класса.

Пример 2.

В месяце 5 четвергов, так как четверги чередуются по четности и не четности.

30 дней – 1,2 четверг.  31 день -1,2,3 четверг

7*4+2=30 – 5 четверг.  29 – среда   26 – воскресенье.

Заключение.

Изучив «Арифметику остатков», я теперь легко решаю многие олимпиадные задачи на делимость чисел.

11. Введение в арифметику остатков

Предыдущий урок:
10. Конечные подгруппы движений прямой и окружности

Следующий урок:
12. Таблицы умножения остатков

Рассматриваем примеры арифметики остатков из жизни. Решаем задачи о днях недели в арифметике остатков по модулю 7. Изучаем обозначения. Строим таблицы сложения по модулю 2 и 7.

Пройти занятие

1

Введение в арифметику остатков

Видео

2

Летоисчисление и время

Конспект

3

Построение аккордов. Дни недели

Конспект

4

Дни недели. Задачи

Конспект

5

Арифметика остатков

Конспект

6

Задача на арифметику остатков

Задание

7

Введение в арифметику остатков

Тест

Материалы для скачивания

dwnld_solid

pdf

103. 53 КБ

Введение в арифметику остатков (конспект)

Выпуск этого урока поддержали:

8.7: Остаточная арифметика — инженерные LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

48337

• Эрик Леман, Ф. Томсон Лейтон и Альберти Р. Мейер
• Google и Массачусетский технологический институт через MIT OpenCourseWare

Лемма о сравнении 8.6.1 утверждает, что два числа конгруэнтны тогда и только тогда, когда их остатки равны, поэтому мы можем понять конгруэнтность, выполняя арифметические действия с остатками.

И если все, что нам нужно, это остаток по модулю \(n\) ряда сложений, умножений, вычитаний, применяемых к некоторым числам, мы можем брать остатки на каждом шаге, так что все вычисление будет включать только числа в диапазоне \([0 ..п)\).

Общий принцип вычисления остатков

Чтобы найти остаток от деления на \(n\) результата серии сложений и умножений, примененных к некоторым целым числам

• заменить каждый целочисленный операнд его остатком при делении на \(n\),
• сохранить каждый результат сложения или умножения в диапазоне \([0..n)\), немедленно заменив любой результат вне этого диапазона его остатком при делении на \(n\).

9{1111111} \\ &= 27 \end{выровнено}\]

Обратите внимание, что было бы катастрофической ошибкой заменить показатель степени его остатком . Общий принцип применяется к числам, состоящим из 90 068 операндов, 90 069 плюсов и раз, тогда как показатель степени — это число, определяющее, сколько умножений нужно выполнить. Следите за этим.

Пришло время уточнить общий принцип и то, почему он работает. Для начала давайте введем обозначение \(+n\) для выполнения сложения и последующего получения остатка от деления на \(n\), как указано в общем принципе; аналогично для умножения:

\[\begin{align} i + _n j &::= \text{rem}(i + j, n), \\ i \cdot _n j &::= \text{rem}(ij, n ). \end{aligned}\]

Общий принцип — это просто повторное применение следующей леммы.

Лемма 8.7.1.

\[\begin{align} \label{8.7.3} \text{rem}(i + j, n) &= \text{rem}(i, n) + _n \text{rem}(j , n), \\ \label{8.7.4} \text{rem}(ij, n) &= \text{rem}(i, n) + _n \text{rem}(j, n), \end {align}\]

Доказательство . По следствию 8.6.3, \(i \equiv \text{rem}(i, n)\) и \(j \equiv \text{rem}(j, n)\), поэтому по лемме о сравнении 8.6.4

\[\nonumber i + j \equiv \text{rem}(i, n) + \text{rem}(j, n) \pmod n.\]

По следствию 8.6.3 снова остатки на все стороны этого сравнения равны, что сразу дает (\ref{8. 7.3}). Идентичное доказательство применимо к (\ref{8.7.4}). \(\quad \blacksquare\)

Набор целых чисел в диапазоне \([0 . . . n)\) вместе с операциями \(+_n\) и \(\cdot n\) обозначается как \ (\mathbb{Z}_{n}\), кольцо целых чисел по модулю \(n\). Как следствие леммы 8.7.1, в \(\mathbb{Z}_{n}\ выполняются известные правила арифметики), например:

\[\nonumber (i \cdot _n j) \cdot _n k =i \cdot _n(j \cdot _n k).\]

Эти индексы-\(n\) в арифметических операциях действительно забивают все дело, поэтому вместо этого мы просто напишем «\((\mathbb{Z }_{n})\)» сбоку, чтобы получить более простое уравнение:

\[\nonumber (i \cdot j) \cdot k=i \cdot(j \cdot k)\left(\mathbb{ Z}_{n}\справа)\]

В частности, все следующие равенства ⁸ верны в \(\mathbb{Z}_{n}\):

\[\begin{aligned} (i \cdot j) \cdot k &= i \cdot(j \cdot k) & \text { (ассоциативность } \cdot), \\ (i+j)+k &=i+(j+k) &\text { (ассоциативность }+), \ \ 1 \cdot k &= k & \text{идентификатор для }\cdot), \\ 0+k &= k & \text{(идентификатор для }+), \\
k+(-k) &= 0 & \text{(инверсия для }+), \\
i+j &= j+i & \text{(перестановочность } +) \\
i \cdot(j+k) &= (i \cdot j)+(i \cdot k) & \text{(дистрибутивность)}, \\
i \cdot j &= j \cdot i & \text{ (коммутативность }\cdot) \end{aligned}\]

Ассоциативность подразумевает знакомый факт, что можно безопасно опускать скобки в произведениях:

\[\nonumber k_1 \cdot k_2 \cdots k_m\]

выходит то же самое в \(\mathbb{Z}_n\) независимо от того, как оно заключено в скобки.

Общая идея заключается в том, что арифметика остатков очень похожа на обычную арифметику. Но есть пара исключений, которые мы собираемся изучить.

 

⁸ Множество с операциями сложения и умножения, удовлетворяющими этим равенствам, называется коммутативным кольцом. Помимо \(\mathbb{Z}_n\), примерами коммутативных колец являются целые числа, рациональные числа, действительные числа и многочлены с целыми коэффициентами. С другой стороны, набор \(\{\mathbf{T, F}\}\) значений истинности с \(\text{ИЛИ}\) для сложения и \(\text{И}\) для умножения равен не коммутативное кольцо, потому что оно не удовлетворяет ни одному из этих равенств. Целые матрицы \(n \times n\) не являются коммутативным кольцом, поскольку они не удовлетворяют ни одному из этих равенств.

---

Эта страница под названием 8.7: Remainder Arithmetic распространяется по лицензии CC BY-NC-SA, ее авторами, ремиксами и/или кураторами являются Эрик Леман, Ф. Томсон Лейтон и Альберти Р. Мейер (MIT OpenCourseWare).

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Эрик Леман, Ф. Томсон Лейтон и Альберти Р. Мейер

   Лицензия

   CC BY-NC-SA

2. Теги

   1. остаток
   2. остаточная арифметика

Развлечение с модульной арифметикой – BetterExplained

Недавно один читатель предложил мне написать о модульной арифметике (она же «вычитание остатка»). Я не особо задумывался об этом, но понял, что модуль чрезвычайно мощный: он должен быть в нашем умственном наборе инструментов рядом со сложением и умножением.

Вместо того, чтобы бить вас формулами по лицу, давайте рассмотрим идею, которой мы тонко владели годами. Есть хорошая статья о модульной арифметике, которая вдохновила меня на этот пост.

Нечетное, четное и тричетное

Вскоре после открытия целых чисел (1, 2, 3, 4, 5…) мы поняли, что они делятся на две группы:

• Четные: делятся на 2 (0, 2, 4, 6). ..)
• Нечетный: не делится на 2 (1, 3, 5, 7…)

Почему это различие важно? Это начало абстракции — мы замечаем свойств числа (например, четность или нечетность), а не только само число («37»).

Это огромно — это позволяет нам исследовать математику на более глубоком уровне и находить отношения между набирает цифр, а не конкретных. Например, мы можем создать такие правила:

• Четный x Четный = Четный
• Нечетное x Нечетное = Нечетное
• Чет x Нечет = Чет

Эти правила являются общими — они работают на уровне свойств. (Интуитивно у меня есть химическая аналогия, что «четность» — это молекула, которой обладают некоторые числа, и ее нельзя удалить путем умножения.)

Но четность/нечетность — это очень специфическое свойство: деление на 2. А как насчет числа 3? Как насчет этого:

• «Три» означает, что число делится на 3 (0, 3, 6, 9…)
• «Тродд» означает, что вы , а не  делитесь на 3 (1, 2, 4, 5, 7, 8…)

Странно, но работает. Вы заметите несколько вещей: есть два типа throdd. Такое число, как «4», на 1 меньше, чем тричетырнадцать (остаток 1), а число 5 — на два (остаток 2).

Быть «три-семь» — это еще одно свойство числа. Возможно, это не так полезно сразу, как чет/нечет, но оно есть: мы можем создавать правила, такие как «три семь х тривен = тривен» и так далее.

Но это сходит с ума. Мы не можем все время составлять новые слова.

Ввод по модулю

Операция по модулю (сокращенно «mod» или «%» во многих языках программирования) — это остаток при делении. Например, «5 mod 3 = 2», что означает, что 2 – это остаток при делении 5 на 3.

Преобразуя повседневные термины в математические выражения, «четное число» – это число, в котором «0 mod 2», т. е. имеет остаток 0 при делении на 2. Нечетное число равно «1 mod 2» (имеет остаток 1).

Почему это круто? Итак, наши «четные/нечетные» правила становятся такими:

• Четный x Четный = 0 x 0 = 0 [четный]
• Нечетное x Нечетное = 1 x 1 = 1 [нечетное]
• Четный x Нечетный = 0 x 1 = 0 [четный]

Круто, да? Довольно легко разобраться — мы преобразовали «свойства» в настоящие уравнения и нашли несколько новых фактов.

Сколько будет четное x четное x нечетное x нечетное? Ну, это 0 x 0 x 1 x 1 = 0. На самом деле, вы можете видеть, что если где-нибудь умножить на четное , то весь результат будет нулевым… Я имею в виду даже :).

Математика с часами

Коварная особенность модульной математики заключается в том, что мы уже использовали ее для измерения времени — иногда называемую «арифметикой часов».

Например: сейчас 7:00 (утра/вечера не имеет значения). Где будет часовая стрелка через 7 часов?

Хрм. 7 + 7 = 14, но мы не можем показать «14:00» на часах. Значит, должно быть 2. Мы рассуждаем интуитивно и в математических терминах:

• (7 + 7) по модулю 12 = (14) по модулю 12 = 2 по модулю 12 [2 — это остаток от деления 14 на 12]

Уравнение «14 mod 12 = 2 mod 12» означает, что «14 часов» и «2 часа» выглядят одинаково на 12-часовых часах. Они конгруэнтны , обозначены тройным знаком равенства: 14 ≡ 2 по модулю 12.

Другой пример: сейчас 8:00. Где будет большая рука через 25 часов?

Вместо того, чтобы прибавлять 25 к 8, вы можете понять, что 25 часов — это просто «1 день + 1 час». Таким образом, часы переведутся на 1 час вперед, в 9:00.

• (8 + 25) по модулю 12 ≡ (8) по модулю 12 + (25) по модулю 12 ≡ (8) по модулю 12 + (1) по модулю 12 ≡ 9мод 12

Вы интуитивно преобразовали 25 в 1 и прибавили это к 8.

Забавное свойство: математика просто работает

Используя часы в качестве аналогии, мы можем выяснить, «просто работают» ли правила модульной арифметики (они работают).

Сложение/Вычитание

Допустим, два раза выглядят одинаково на наших часах («2:00» и «14:00»). Если мы добавим к ним одинаковые «x» часов, что произойдет?

Ну меняют на столько же на часах! 2:00 + 5 часов ≡ 14:00 + 5 часов — оба будут показывать 7:00.

Почему? Ну, нас никогда не волновали лишние «12:00», которые таскал с собой 14-й. Мы можем просто добавить 5 к остатку 2, который есть у обоих, и они продвинутся одинаково. Для всех конгруэнтных чисел (2 и 14) сложение и вычитание дают одинаковый результат.

Умножение

Труднее понять, остается ли умножение неизменным. Если 14 ≡ 2 (mod 12), можем ли мы умножить обе части и получить тот же результат?

Посмотрим — что получится, если умножить на 3?

Ну, 2 часа * 3 ≡ 6 часов. Но что такое «14:00» * 3?

Помните, 14 = 12 + 2. Таким образом, мы можем сказать

• 14 * 3 = (12 + 2) * 3 = (12 * 3) + (2 * 3) mod 12

Первую часть (12 * 3) можно игнорировать! «12-часовое переполнение», которое носит с собой 14, просто повторяется несколько раз. Но кого это волнует? Мы все равно игнорируем переполнение.

При умножении важен только остаток, который равен 2 часам для 14:00 и 2:00. Интуитивно я вижу, что умножение не меняет отношения с модульной математикой (вы можете умножить обе части модульного отношения и получить тот же результат). Смотрите ссылку выше для более строгих доказательств — это мои интуитивные карандашные линии.

Использование модульной арифметики

Теперь самое интересное — чем полезна модульная арифметика?

Простые расчеты времени

Мы делаем это интуитивно, но неплохо дать этому название. Ваш рейс прибывает в 15:00. Задержка на 14 часов. В какое время он приземлится?

Ну, 14 ≡ 2 по модулю 12. Поэтому я думаю об этом как о «2 часах и переключении утра/вечера», поэтому я знаю, что это будет «3 + 2 = 5 утра».

Это немного сложнее, чем простой оператор по модулю, но принцип тот же.

Размещение предметов в случайных группах

Предположим, у вас есть люди, которые купили билеты в кино с номером подтверждения. Вы хотите разделить их на 2 группы.

Чем ты занимаешься? «Шансы здесь, четы там». Вам не нужно знать, сколько билетов было выдано (первая половина, вторая половина), каждый может определить свою группу мгновенно (без обращения в центральный орган), и схема работает по мере того, как все больше людей покупают билеты.

Нужно 3 группы? Разделите на 3 и возьмите остаток (он же мод 3). У вас будут группы «0», «1» и «2».

В программировании по модулю вы можете разместить элементы в хеш-таблице: если в вашей таблице N записей, преобразуйте ключ элемента в число, выполните mod N и поместите элемент в это ведро (возможно, сохраняя связанный список там). По мере увеличения размера вашей хэш-таблицы вы можете пересчитать модуль для ключей.

Выбор случайного предмета

В реальной жизни я использую модуль. Действительно. У нас есть 4 человека, играющих в игру, и нужно выбрать кого-то, кто пойдет первым. Сыграй в мини-игру мод N! Назовите людям номера 0, 1, 2 и 3.

Теперь все говорят «раз, два, три, стрелять!» и высовывает случайное количество пальцев. Сложите их и разделите на 4 — тот, кто точно наберет остаток, ходит первым. (Например: если сумма пальцев равна 11, тот, у кого было «3», ходит первым, так как 11 по модулю 4 = 3).

Это быстро и работает.

Запуск задач в цикле

Предположим, задачи должны выполняться по определенному расписанию:

• Задача A выполняется 3 раза в час
• Задача B выполняется 6 раз в час
• Задача C выполняется 1 раз в час

Как вы храните эту информацию и составляете расписание? В одну сторону:

• Таймер должен запускаться каждую минуту (отслеживайте минуты как «n»)
• 3x/час означает один раз каждые 60/3 = 20 минут. Таким образом, задача A запускается всякий раз, когда «n % 20 == 0»
• Задача B запускается всякий раз, когда «n % 10 == 0»
• Задача C запускается всякий раз, когда «n % 60 == 0»

О, вам нужна задача C1, которая выполняется 1 раз в час, но не в то же время, что и задача C? Конечно, запустите его, когда «n mod 60 == 1» (по-прежнему один раз в час, но не так, как C1).

Мысленно я вижу цикл, который хочу «побить» с различными интервалами, поэтому вставляю мод. Удобно то, что хиты могут перекрываться независимо друг от друга. В этом отношении это немного похоже на XOR (каждое XOR может быть многоуровневым — но это уже другая статья!).

Точно так же при программировании вы можете распечатать каждый сотый элемент журнала, выполнив: if (n % 100 == 0){ print… }.

Это очень гибкий и простой способ запуска элементов по расписанию. На самом деле, это способ ответить на проверку вменяемости FizzBuzz. Если в вашем batbelt нет операции по модулю, вопрос становится намного сложнее.

Нахождение свойств чисел

Предположим, я сказал вам следующее:

• a = (47 * 2 * 3)

Что вы можете сделать быстро? Что ж, «а» должно быть четным, так как оно равно чему-то, что включает умножение на 2.

Если бы я также сказал вам:

• а = (39 * 7)

Ты бы отказался. Не потому, что вы «знаете», что два продукта разные, а потому, что один явно четный, а другой нечетный. Есть проблема: а не может быть одним и тем же числом в обоих, начиная с 9.Свойства 0068 не соответствуют .

Такие вещи, как «четный», «три» и «mod n», являются более общими свойствами, чем отдельные числа, и мы можем проверить их согласованность. Таким образом, мы можем использовать модуль, чтобы выяснить, согласуются ли числа, не зная, что они собой представляют!

Если я скажу вам это:

• 3a + 5b = 8
• 3а + б = 2

Можно ли решить эти уравнения с целыми числами? Давайте посмотрим:

• 3a + 5b = 8… давайте «mod 3 it»: 0 + 2b ≡ 2 mod 3 или b ≡ 1 mod 3
• 3a + b = 2… давайте «mod 3 it»: 0 + b ≡ 2 mod 3), или b ≡ 2 mod 3

Противоречие, молодцы! Б не может быть одновременно «1 по модулю 3» и «2 по модулю 3» — это так же абсурдно, как быть четным и нечетным одновременно!

Но есть одна загвоздка: числа вроде «1,5» не четные и не нечетные — они не целые! Модульные свойства применяются к целым числам, поэтому мы можем сказать, что b не может быть целым числом .

Потому что на самом деле мы можем решить это уравнение:

• (3а + 5б) – (3а +б) = 8 – 2
• 4b = 6
• б = 1,5
• 3а + 1,5 = 2, поэтому 3а = 0,5 и а = 1/6

Не соблазняйтесь силой модуля! Знайте его пределы: это относится к целым числам.

Криптография

Игра с числами имеет очень важное применение в криптографии. Это слишком много, чтобы охватить здесь, но модуль используется в обмене ключами Диффи-Хеллмана — используется при настройке SSL-соединений для шифрования веб-трафика.

Простой английский

Компьютерщики любят использовать технические слова в обычном контексте. Вы можете услышать «X такое же, как Y по модулю Z», что примерно означает «Игнорируя Z, X и Y одинаковы».

Например:

• b и B идентичны, капитализация по модулю
• iTouch и iPad идентичны по модулю размера 😉

Вперед и вверх

Странно думать о «полезности» оператора по модулю — это все равно, что кто-то спрашивает, почему экспоненты полезны.