Arg z комплексные числа: Комплексные числа онлайн

Онлайн калькулятор: Комплексные числа

УчебаМатематикаАлгебра

Калькулятор отображает комплексное число на комплексной плоскости, отображает число в различных формах, вычисляет модуль, главный аргумент и сопряженное число для заданного комплексного числа.

Начиная с 16 века математики столкнулись с необходимостью введения комплексных чисел, то есть чисел вида a+bi, где a,b — вещественные числа, i — мнимая единица — число, для которого выполняется равенство: i²=-1.

Интересно проследить, как менялось представление о комплексных числах с течением времени. Вот некоторые цитаты из древних трудов:

• XVI век : Эти сложнейшие величины бесполезны, хотя и весьма хитроумны. ¹
• XVII век : Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием. ²
• XVIII век : Квадратные корни из отрицательных чисел не равны нулю, не меньше нуля и не больше нуля. Из сего видно, что квадратные корни из отрицательных чисел не могут находиться среди возможных чисел. Поэтому, нам не остается ничего другого, как признать их невозможными числами. Это ведет нас к понятию таких чисел, которые по своей природе невозможны и обычно называются мнимыми или воображаемыми, потому что их только в уме представить можно. ³
• XIX век Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы и иероглифы нелепых количеств. ⁴

Известно три способа записи комплексного числа z:

Алгебраическая запись комплексного числа

,
где a и b — вещественные числа, i — мнимая единица. a — действительная часть, bi — мнимая часть.

Тригонометрическая запись комплексного числа

,
где r — модуль комплексного числа:

, который соответствует расстоянию от точки на комплексной плоскости до начала координат, а φ — угол наклона вектора 0-z к оси действительных значений или аргумент комплексного числа.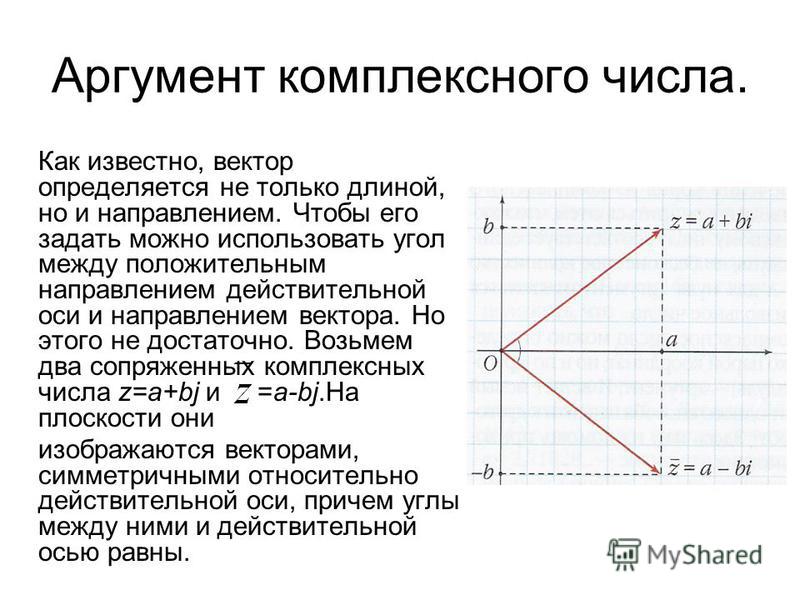

Показательная запись комплексного числа

была введена Леонардом Эйлером для сокращения тригонометрической записи.

Комплексное число

Комплексное число

Точность вычисления

Знаков после запятой: 2

В тригонометрической форме

 

В показательной форме

 

Комплексное число

 

Модуль

 

Главный аргумент (радианы)

 

Главный аргумент (градусы)

 

Сопряженное число

 

Комплексная плоскость

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Значение аргумент комплексного числа определяется с точностью до , для всех целых k. Главный аргумент — это значение аргумента, лежащее в диапазоне (-π..π].
Главный аргумент вычисляется как арктангенс двух аргументов мнимой и действительной части комплексного числа:
, см Арктангенс с двумя аргументами

Над комплексным числом возможны все алгебраические операции:

Действия над комплексными числами

Число 1 (z1)

ОперацияСложитьВычестьУмножитьПоделитьВозвести в степеньИзвлечь корень

Число 2 (z2)

Показатель степени

Точность вычисления

Знаков после запятой: 2

Результат (z)

 

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Сложение комплексных чисел

Комплексные числа складываются ровно так же, как и многочлены:

Умножение комплексных чисел

Помня о том, что i*i=-1, легко выразить формулу для умножения комплексных чисел:

Деление комплексных чисел

Формулу деления комплексных чисел проще всего вывести, путем умножения числителя и знаменателя на сопряженное комплексное число, для того, чтобы избавиться от мнимой единицы в знаменателе:

Сопряженное комплексное число, это число вида:

Раскрывая скобки получаем:

Возведение в целую степень

Проще всего комплексное число возводить в степень используя показательную форму:

формула вытекает из формулы Муавра:

Вычисление корня степени n

Из формулы Муавра вытекает решение для корней степени n из комплексного числа:
,
всего получается n корней, где k = 0..n-1 — целое число, определяющее индекс корня. Корни располагаются на комплексной плоскости, как вершины правильного многоугольника.

---

1. Дж. Кардано, Великое искусство, (1539) ↩

2. Г. Лейбниц, приписываемый ему афоризм ↩

3. Л. Эйлер, Универсальная арифметика (1768) § 142-143 ↩

4. Л. Карно, Размышления о метафизике исчисления бесконечно малых (1797) § 150 ↩

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Вычисление значения полинома с комплексными числами.
• • Стандартный вид числа
• • Взаимно простые числа и попарно взаимно простые числа
• • Дата плюс/минус число недель
• • Определитель матрицы методом Гаусса
• • Раздел: Алгебра ( 46 калькуляторов )

 Алгебра главный аргумент комплексная плоскость комплексное число Комплексные числа Математика модуль сопряженное комплексное число число

 PLANETCALC, Комплексные числа

Anton2020-11-03 14:19:36

Калькулятор комлексных чисел | Вычисление выражений, содержащих комплексные числа

Калькулятор комплексных чисел позволяет вычислять арифметические выражения, содержащие комплексные числа, знаки арифметических действий (+, -, *, /, ^), а также некоторые математические функции.

4

5

6

i

(

)

π

e

1

2

3

sin

cos

tg

ctg

ln

.

√

sh

ch

th

cth

abs

Скрыть клавиатуру

С решением

Тригонометрическая форма

Показательная форма

Десятичных знаков:

Вычислить

Вычислено выражений:

Как пользоваться калькулятором

1. Введите в поле ввода выражение с комплексными числами
2. Укажите, требуется ли вывод решения переключателем «С решением»
3. Нажмите на кнопку «Построить»

Ввод комплексных чисел

комплексные числа можно вводить в следующих трёх форматах:

• Только действительная часть: 2, 2.5, -6.7, 12.25
• Только мнимая часть: i, -i, 2i, -5i, 2.16i, -12.5i
• Действительная и мнимая части: 2+i, -5+15i, -7+2.5i, -6+i
• Математические константы: π, e

Поддерживаемые операции и математические функции

• Арифметические операции: +, -, *, /, ^
• Получение абсолютного значения числа: abs
• Базовые математические функции: exp, ln, sqrt
• Получение действительной и мнимой частей: re, im
• Тригонометрические функции: sin, cos, tg, ctg
• Гиперболические функции: sh, ch, th, cth
• Обратные тригонометрические функции: arcsin, arccos, arctg, arcctg
• Обратные гиперболические функции: arsh, arch, arth, arcth

Примеры корректных выражений

• (2+3i)*(5-7i)
• sh(i)
• (4+i) / (3 — 4i)
• sqrt(2i)
• (-3+4i)*2i / exp(2i + (15 — 8i)/4 — 3. 75)

Комплексные числа

Комплексные числа — это числа вида x+iy, где x, y — вещественные числа, а i — мнимая единица (специальное число, квадрат которого равен -1, то есть i2 = -1).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.

Примеры комплексных чисел

• 4+3i — действительная часть = 4, мнимая = 3
• -2+i — действительная часть = -2, мнимая = 1
• i — действительная часть = 0, мнимая = 1
• -i — действительная часть = 0, мнимая = -1
• 10 — действительная часть = 10, мнимая = 0

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi² = (ac — bd) + (bc + ad)i
• деление:

  a + bi

  c + di

  =

  (a + bi)(c — di)

  c² + d²

  =

  (ac + bd)

  c² + d²

  +

  (bc — ad)

  c² + d²

  i

Примеры

Найти сумму чисел 5+7i и 5. 5-2i:
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом:5+7i + 5.5-2i = 10.5 + 5i

Найти разность чисел 12-i и -2i:
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом:12-i — (-2i) = 12 + i

Найти произведение чисел 2+3i и 5-7i:
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом:2+3i * (5-7i) = 31 + i

Найти отношение чисел 75-50i и 3+4i:
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом:75-50i / (3+4i) = 1 - 18i

Другие действия над комплексными числами

Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:

• Получение действительной части числа: Re(z) = a
• Получение мнимой части числа: Im(z) = b
• Модуль числа: |z| = √(a2 + b2)
• Аргумент числа: arg z = arctg(b / a)
• Экспонента: e^z = e^a·cos(b) + i·e^a
  ·sin(b)
• Логарифм: Ln(z) = ln |z| + i·arg(z)
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arch z, arth z, arcth z

Примеры

Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(4² + (-3)²) = √25 = 5

Формы представления комплексных чисел

Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.

• Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей: x+iy, где x — действительная часть, а y — мнимая часть
• Тригонометричкая форма — запись вида r·(cos φ + isin φ), где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z))
• Показательная форма — запись вида r·eiφ, где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))

Пример:

Переведите число 1+i в тригонометрическую и показательную формы:

Решение:

• Найдём радиус (модуль) комплексного числа r: r = √(1² + 1²) = √2
• Найдём аргумент числа: φ = arctan() = = 45°
• Запишем результат в тригонометрической форме: √2·(cos(45°) + isin(45°))
• Запишем результат в показательной форме: √2·eπi/4

Значение, формула и способ определения

Комплексное число является важным разделом математики, поскольку оно представляет собой комбинацию действительных и мнимых элементов. В графическом представлении горизонтальная линия используется для действительных чисел, а вертикальные линии используются для построения мнимых чисел. Две концепции, которые появляются на картинке с графическим представлением комплекса №. находятся; модуль и аргумент.

Модуль в математике — это квадратный корень из суммы квадратов действительной части и мнимой части комплексного числа. С другой стороны, аргумент — это угол, созданный с положительным направлением реальной оси. В этой статье мы узнаем об аргументе формул комплексных чисел с определением, решенными примерами и свойствами.

Аргумент для комплексных чисел

Комплексное число обычно записывается как z=a + ib или z=x+iy, где «a или x» — действительные числа, а «ib или iy» — мнимая часть. Комплексная плоскость похожа на декартову плоскость и иллюстрирует геометрическую интерпретацию комплексных чисел. Здесь действительная часть находится на действительной оси (т. е. оси x), а мнимая часть — на мнимой оси (т. е. оси y).

Аргументом комплексного числа является угол наклона между действительной осью и комплексным числом в направлении комплексного числа. Он обозначается символом arg(z) или «θ» или «φ». Посмотрите на изображение ниже, чтобы понять то же самое.

Узнайте больше о полярной форме комплексных чисел .

Формула для аргумента комплексных чисел

Рассмотрим приведенный ниже рисунок для комплексного номера. (Z) здесь «OZ» — это отрезок, проведенный из начала координат. Для отрезка OZ — это модуль комплексного числа. Аргумент Z — это угол, проведенный от положительной оси к отрезку прямой.

Для z = x + iy = r(cos θ + isin θ)

, где x — действительная часть, обозначаемая \(Re_z\), а y — мнимая часть, обозначаемая \(Im_z\), оба действительны числа. Аргумент z обозначается θ, который измеряется в радианах и задается формулой: 9{-1}\left(\frac{y}{x}\right)\)

Главный аргумент комплексного числа

Аргумент, рассчитанный на предыдущем шаге, имеет некоторую неоднозначность. Причина в том, что sin(θ + 2π) = sin θ, а также cos(θ + 2π) = cos θ по той причине, что sin и cos являются периодическими функциями θ с периодом 2π.

Следовательно, можно установить соглашение, согласно которому θ должно лежать в интервале длины 2π. Одним из наиболее распространенных соглашений является принятие −π < θ ≤ π. А вот и новое определение θ, которое читается как главное значение аргумента комплексных чисел, обозначаемое обозначением Arg z.

Следовательно, если z=r(cosΘ+isinΘ), где r>0 и −π<Θ≤π, то;

Главный аргумент формулы комплексного числа; arg(z)=Arg(z)+2nπ,n∈Z

Отсюда следует, что главный аргумент комплексных чисел лежит в интервале −π<Θ≤π (-π, π].

Аргумент комплексного числа в разных квадрантах

В предыдущем заголовке мы узнали об определении, формуле для аргумента и главном аргументе Теперь давайте разберемся с формулой и условием для аргумента комплексных чисел в разных квадрантах.

Случай 1. Когда комплексное число z = x + i y присутствует в первом квадранте, т. е. когда x > 0 и y > 0, тогда Arg z= Arctan(y/x).

Случай 2. Когда координаты комплексного числа z = (x + i y) лежат во втором квадранте, т.е. значения x < 0 и y > 0, то Arg z= π + Arctan(y /Икс).

Случай 3. Если комплексное число z = (x + i y) находится в 3-м квадранте, т. е. значение x < 0 и y < 0, то Arg z= −π + Arctan(y/x) .

Случай 4. Если комплексное число z = (x + i y) лежит в четвертом квадранте, т.е. значение x > 0 и y < 0, то Arg z= Arctan(y/x).

Узнайте здесь о различных операциях с комплексными числами.

Как определить аргумент комплексных чисел?

Давайте теперь перейдем к пониманию того, как определить аргумент комплексных чисел с примером и подробными шагами.

Шаг 1: Для заданного номера комплекса получить действительную и мнимую составляющие. Например, если z=x+iy, то здесь x=действительная часть, а y=мнимая часть. 9{-1}\влево(\фракция{у}{х}\вправо)\).

Шаг 3: Значение, полученное с помощью единицы «радиан», является значением комплексного аргумента для данного числа.

Свойства аргумента комплексного числа

Некоторые из важных свойств аргумента комплексных чисел: из \(z_1\) и \(z_2\) равно сложению слагаемых, взятых по отдельности. 9n\right)=nArgz+2\pi N_n\)

Аргумент комплексного числа Решенные примеры

Прочитав о формуле, связанных свойствах и о том, как найти аргумент данного комплексного числа; давайте попрактикуемся в некоторых решенных примерах, чтобы понять то же самое.

Решено Пример 1: Определить аргумент заданного комплексного числа\(3 + i\sqrt{3}\).

Решение: Рассмотрим\(3 + i\sqrt{3} =z\)

Для приведенного выше уравнения действительная часть, т.е. x =3, и мнимая часть, т.е. y=\(\sqrt{3}\ ) 9{-1}\left(\sqrt{3}\right)\)

\(\arg(z)=\frac{\pi}{3}\)

Главный аргумент= \(\frac{\pi {3}+2n\pi\)

Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Часто задаваемые вопросы о аргументе комплексного числа

В.1 Каков аргумент комплексного числа z?

Отв.1 Аргумент комплекса нет. скажем, z = x + iy — это угол, обратный функции тангенса, где мнимая часть комплексного числа делится на действительную часть.

Q.2 Как рассчитывается arg z?

Ответ 2 Чтобы определить значение arg z, выберите действительную и мнимую составляющие и подставьте значения в формулу. Значение, полученное в единице «радиан», является значением arg z. 9{-1}\влево(\фракция{у}{х}\вправо)\).

Q.4 Что является главным аргументом для комплексных чисел?

Ответ 4 Основным аргументом является соглашение, согласно которому θ лежит в интервале длины 2π. 2}\).

Скачать публикацию в формате PDF

Численность, математика и статистика — Набор академических навыков

Модуль и аргумент

Главное меню ContentsToggle 1 Диаграмма Аргана 1.1 Определение 1.2 Рабочий пример 2 Модуль и аргумент 2.1 Определение 3 Рабочие примеры 4 Видео пример 5 Рабочая тетрадь 6 Проверь себя 7 Внешние ресурсы

Диаграмма Аргана

Определение

Диаграмма Аргана имеет горизонтальную ось, называемую реальной осью , и вертикальную ось, называемую .0263 мнимая ось .

В координатах $(a,b)$ нанесено комплексное число $z = a + bi$, где $a$ — действительная часть комплексного числа, а $b$ — мнимая часть.

|center

Рабочий пример

Пример 1

Нанесите следующие комплексные числа на диаграмму Аргана.

\begin{align} z_1 &= 3+i \\ z_2 &= -2-4i \\ z_3 &=-1+3i \\ z_4 &= -2i \end{align}

Решение

Модуль и аргумент

Определение

Любое комплексное число $z$ может быть представлено точкой на диаграмме Аргана. Мы можем соединить эту точку с началом координат с помощью отрезка. Длина отрезка называется модулем комплексного числа и обозначается $\lvert z \rvert$. Угол, измеренный от положительной вещественной оси до отрезка, называется аргументом комплексного числа, обозначается как $arg(z)$ и часто обозначается как $\theta$. Модуль и аргумент можно вычислить с помощью тригонометрии. 92}\]

При вычислении аргумента комплексного числа необходимо сделать выбор между взятием значений в диапазоне $[-\pi,\pi]$ или в диапазоне $[0,\pi]$. Оба эквивалентны и одинаково действительны. На этой странице мы будем использовать соглашение $-\pi \lt \theta \lt \pi$.

«Наивный» способ вычисления угла к точке $(a,b)$ заключается в использовании $\arctan(\frac{b}{a})$, но поскольку $\arctan$ принимает значения только в диапазон $[-\frac{\pi}{2},\frac{\pi}{2}]$, это даст неверный результат для координат с отрицательной $x$-компонентой. Это можно исправить, добавив или вычтя $\pi$, в зависимости от того, в каком квадранте диаграммы Аргана находится точка.

• Первый квадрант: $\theta = \arctan\left(\dfrac{b}{a}\right)$.
• Второй квадрант: $\theta = \arctan\left(\dfrac{b}{a}\right) + \pi$.
• Третий квадрант: $\theta = \arctan\left(\dfrac{b}{a}\right) -\pi$.
• Четвертый квадрант: $\theta = \arctan\left(\dfrac{b}{a}\right)$.

При принятии решения о том, какую формулу использовать, рекомендуется нарисовать диаграмму Аргана комплексного числа.

Примечание: обратите внимание на случай, когда $a=0$, т.е. комплексное число не имеет вещественной части. В этом случае метод $\arctan$ не работает, но аргументом является либо $\frac{\pi}{2}$, либо $-\frac{\pi}{2}$ для чисел с положительными и отрицательными мнимых частей соответственно.

Пример

$z_1=1+i$ имеет аргумент \[\arg z_1 = \arctan \left(\dfrac{1}{1}\right) = \arctan (1) = \dfrac{\pi} {4}.\]

Однако тот же расчет для $z_2=-1-i$ дает $\arctan \left(\frac{-1}{-1}\right) = \arctan (1) = \ dfrac{\pi}{4}$, тот же номер! 92}\\ &=\sqrt{9+4}\\ &=\sqrt{13} \end{align}

Поскольку комплексное число находится в первом квадранте диаграммы Аргана, мы можем использовать $\arctan \ frac{2}{3}$ без изменений, чтобы найти аргумент. 2}\\ &=\sqrt{16}\\ &=4 \end{align } 92}\\ &=\sqrt{4+25}\\ &=\sqrt{29} \end{align}

Поскольку $z$ находится во втором квадранте диаграммы Аргана, нам нужно добавить $\pi $ к результату, полученному из $\arctan \left(\frac{5}{-2}\right)$.

\begin{align} \arg z &= \arctan \left(\frac{5}{-2}\right) + \pi \\ &=-1,19 + \pi \\ &= 1,95 \text{ радианы (до 2 д.п.)} \end{align}

Пример 4

Найдите модуль и аргумент комплексного числа $z = -4-3i$.

Решение

|центр 92}\\ &=\sqrt{16+9}\\ &=\sqrt{25}\\ &=5 \end{align}

Поскольку $z$ лежит в третьем квадранте диаграммы Аргана, нам нужно чтобы вычесть $\pi$ из результата $\arctan \left(\frac{-3}{-4}\right)$.

\begin{align} \arg z &= \arctan \left(\frac{-3}{-4}\right) — \pi\\ &= \arctan \left(\frac{3}{4} \right) — \pi\\ &= 0,64 — \pi \\ &= -2,50 \text{ радианы (до 2 d.p.)} \end{align}

Примечание: В качестве альтернативы ответ мог быть дан в диапазон $0 \lt \theta \lt 2\pi$, где мы бы добавили $\pi$ вместо вычитания и получили ответ $\arg z = 3,67$ радиан (к 2 д. п.) 92}\\ &=\sqrt{1+16}\\ &=\sqrt{17} \end{align}

Поскольку $z$ лежит в четвертом квадранте диаграммы Аргана, нам не нужно изменять результат $\arctan \left(\frac{-4}{1}\right)$, чтобы найти аргумент.

\begin{align} \arg z &= \arctan \left(\frac{-4}{1}\right)\\ &= \arctan \left(-4\right) \\ &= -1.33 \ text{ радианы (до 2 d.p.)} \end{align}

Пример видео

Профессор Робин Джонсон рисует комплексные числа $z=-1-i$ и $z=-4+3i$ на диаграмме Аргана, и находит их модуль и аргумент.

Рабочая тетрадь

Эта рабочая тетрадь, созданная HELM, является хорошим пособием по повторению, содержащим ключевые моменты для исправления и множество рабочих примеров.

• Диаграммы Аргана и полярная форма

Проверь себя

Проверь себя: тест Numbas по нахождению модуля и аргумента

Внешние ресурсы

• Листовка с диаграммой Аргана в math center.