Cyclic Redundancy Checking (CRC32) | Уроки и примеры программирования
by Clifford M. RocheПредисловие
В этой статье я намерен передать основные аспекты CRC32 алгоритма. Это относительно простая статья, прежде всего источник информации — демо для Borland C++ и MSVC++ NET. (которые должны быть легко переносимы на MSVC++6) также доступен с настоящей статьей.
Небольшое понимание математики (многочлен деления) было бы полезно, но я пишу эту статью так, чтобы оно не потребовалось. Вы, однако, должны понимать C++ — это само собой подразумевается.
Зачем использовать CRC32?
Мне оно понадобилось для одного из своих небольших проектов — я решил написать приложение для онлайн обновления, которое просто генерирует уникальную подпись для набора файлов, сравнивает эти значения с подписью мастер-списка на сервере, и обновляет файлы, которые не соответствуют этой подписи.
Есть несколько способов, которыми я могу проверить целостность файлов и решить, требуется ли обновить их с главного сервера. Приходят на ум время создания/таймстамп, размер файла и CRC32. Есть и некоторые, очевидно, более сложные способы, такие как учет файлов в базе данных, однако нет необходимости слишком всё усложнять. То же самое касается большинства видов применения CRC32 в играх. Кроме того, большинство из более сложных алгоритмов примеряют гораздо больше вычислений, чем CRC32.
CRC32, изо всех представленных вариантов, в настоящее время является наиболее приемлемым, поскольку вам не придется беспокоиться о файлах, которые имеют одинаковый размер или дату изменения (очень часто такое бывает с растровыми изображениями, а также несколькими другими распространенными типами игровых файлов) и у нас нет повода беспокоиться о неточном времени создания файла/таймстампа из-за их изменения. Хотя CRC32 не совершенный алгоритм, и всегда есть шанс, что 2 файла будет иметь одинаковое значение CRC32, случаи эти настолько редки, что CRC32 становится идеальным кандидатом для генерации подписи файла.
CRC32 значение содержит 32-битное (4-байтовое) число (также известное как подпись), что однозначно определяет указанный кусок данных. Преимуществом CRC32 для контрольных подписей является и то, что его алгоритм устроен так, что небольшие изменения в файле (будь то изменение, удаление или вставка) должны вызывать большие изменения в подписи CRC32. CRC32 имеет 2 ^ 32 возможных значений; в общей сложности 4.294967E +09.
По этим причинам подписи CRC32 очень полезны в играх, так как оставляет нам простор для творчества. Они могут быть использованы для проверки файлов, чтобы увидеть, были ли изменены, чтобы помочь предотвратить попытки взлома игры с целью читерства, или они могут быть использованы для проверки файлов или данных, которые передаются по интернету во время игры, такие как файл карты, например.
Как CRC32 работает?
CRC32 это несколько сложный процесс, и состоит он из многих математических операций. Но вот как он, как правило, работает:
Сначала мы собираемся взять значение многочлена, и с этим значением мы генерируем CRC32 поиска. В конце этой статьи я покажу, как правильно создать обзорную таблицу с данным многочленом. Далее мы возьмём данные, для которых хотим сгенерировать подпись CRC32, и специальная функция сгенерирует обновлённое значение CRC32 для каждого байта в файле, строке или структуре, которую мы проверяем. Это делается для каждого байта в строке, структуре или файле. После завершения самое обновлённое значение становится подписью.
Сердце алгоритма CRC32 — простая система, которая принимает переданный байт для вычисления из набора данных, и текущее значение CRC32, которое есть у нас, и выполняет поиск в нашей обзорной таблице. Если нет текущего значения CRC32, мы должны использовать 0xFFFFFFFF. Немного математики, а именно — многочлен деления, и функция вернет обновленное значение CRC32.
Реализация очень проста.
Класс
Так наш класс будет выглядеть.
class ECRC32 {
public:
static DWORD CRC32ByString( LPCTSTR, DWORD& );
static DWORD CRC32ByFile( LPCTSTR, DWORD& );
static DWORD CRC32ByStruct( BYTE*, DWORD, DWORD& );
private:
static bool GetFileSize( HANDLE, DWORD& );
static inline void GetCRC32( BYTE, DWORD& );
static DWORD CRC32Table[256];
};
Всё просто — у нас есть функция для каждого типа данных, который мы планируем использовать, которая будет генерировать для них CRC32 подписи. У нас также есть две приватные функций, одна будет вычислять размер файла — необходимо для правильной работы внутренних алгоритмов, вторая для выполнения другой математики и обновления значения CRC32 для конкретного байта.
Существует также один статический массив, он просто хранит для нас таблицу CRC32. На самом деле вам не нужно хранить эту таблицу постоянно, если не хотите. Используя конструктор и деструктор, вы можете создавать и очищать таблицу только тогда, когда планируете использовать её. Для наших целей более целесообразно использовать таблицу, так как это может значительно уменьшить время обработки.
Создание таблицы подстановки
Для создания таблицы поиска необходимо указать многочленное значение для использования, которое даст нам значения, которые мы используем в нашей таблице. Многочленное значение, которое вы используете, теоретически должно уменьшить вероятность дубликатов подписей в ваших данных, однако математика, скрывающаяся за одним из этих значений, является слишком сложной и не входит в рамки данной статьи. Это нормально, так как для нас уже выбрали оптимальное значение. Значение, которое мы будем использовать для создания нашей таблицы, будет 0x04c11db7.
Следовательно, этот многочлен также используется многими другими приложениями и системами, такими как WinZip, PKZip, и Ethernet.
Примечание: Вам нужно будет генерировать таблицу по крайней мере один раз, даже если вы используете фиксированную таблицу. Если, конечно, вы используете таблицу, представленную в моём демо.
Прежде чем продолжить — стандартные CRC состояния, которые мы должны отражать значениями в нашей таблице поиска, что может быть сделано, отражая многочлен. В этом случае 0x04c11db7 становится 0xedb88320. Хотя некоторые уравнения будут отражать значения в таблице, поскольку они их и создают, я собираюсь отражать многочлен. В конечном счёте это заканчивается лишь тем, что мы используем меньше строк кода.
Примечание: Отражение — это простой процесс реверса бинарной структуры данного бинарного сегмента. Например, 10100111 станет при отражении 11100101.
DWORD dwPolynomial = 0xEDB88320;
DWORD* CRC32Table = NULL;
CRC32Table = new DWORD[256];
DWORD dwCRC;
for(int i = 0; i < 256; i++)
{
dwCRC = i;
for(int j = 8; j > 0; j—)
{
if(dwCRC & 1)
dwCRC = (dwCRC >> 1) ^ dwPolynomial;
else
dwCRC >>= 1;
}
CRC32Table[i] = dwCRC;
}
Простой цикл через все 256 записей и создав значения поиска, основанного на позиции в таблице многочлена.
В зависимости от вашей ситуации вы можете хотеть или не хотеть тратить циклы процессора, чтобы сохранить регенерирующую таблицу каждый раз, когда Вы хотите создать подпись. Если это ваш случай, просто выделите этот код в отдельное приложение, сохраняйте дамп таблиц в файл, на экран, или где вам наиболее удобно, и копируйте и вставляйте значения прямо в таблицу. Хотя и ценой 256 * 4 байт памяти (что на самом деле не много), вы резко улучшите врёмя расчета без необходимости постоянно пересчитывать таблицы.
Для тех из вас, кто пытается создать таблицу использованием полиномиальных перечисленных выше первых 14 значений должен выглядеть следующим образом:
0x00000000, 0x77073096, 0xEE0E612C, 0x990951BA,
0x076DC419, 0x706AF48F, 0xE963A535, 0x9E6495A3,
0x0EDB8832, 0x79DCB8A4, 0xE0D5E91E, 0x97D2D988,
0x09B64C2B, 0x7EB17CBD, 0xE7B82D07, 0x90BF1D91
Рассчет CRC32
Имея таблицу поиска, мы можем взглянуть на функцию GetCRC32. Эта функция принимает один байт и предыдущее вычисленное значение CRC32 (если таковое существует).
inline void ECRC32::GetCRC32(const BYTE byte, DWORD &dwCRC32){
dwCRC32 = (( dwCRC32 ) >> 8 )^ CRC32Table[( byte )^(( dwCrc32 ) & 0x000000FF )];
}
Первое, что нужно отметить — это то, что функция является встроенной. Для тех из вас, кто не понимает этой особенности, где бы ваш код ни делал вызов этой функции, вместо апрыгания на место функции в памяти каждый раз (что потреблять несколько циклов), процессор будет на самом деле вставить копию кода функции в то место, откуда функция была вызвана. Может быть, функция и занимает только цикл или два, но это происходит каждый раз, когда функция вызывается, и если вы попытаетесь вычислить CRC32 значение 4gig файла, вы увидите, почему один или два цикла для каждого обрабатываемого байта могут реально сэкономить много время.
Обратите внимание: использование встроенных функций не следует воспринимать легкомысленно. Это может привести к весьма значительному увеличению объема итогового кода и может в конечном итоге счёте привести к снижению общей производительности приложения, потребляя слишком много памяти (что что приводит к недостатку ресурсов и ошибкам во время выполнения приложения). В нашей ситуации GetCRC32 вызывается весьма ограниченно и, таким образом, общий размер приложения не имеет значения.
Вы также можете посмотреть на спецификацию __fastcall. __fastcall работает путем передачи аргументов в функцию через регистры процессора, в отличие от стандартного способа прохождения их через стек. Это может привести к заметному увеличению скорости так же, как это делает inline.
С переданным байтом и предыдущим его CRC32 значением функциия выполняет деление многочлена, со ссылкой ссылкой на таблицу, и обновление CRC32 подписи.
Расчет для структур
Две предыдущих основные функции — ядро нашего CRC32 алгоритма. Все, что осталось сделать — прочитать данные и, используя эти две функции, создать CRC32 подпись для них.
DWORD ECRC32::CRC32ByStruct( BYTE* byStruct, DWORD dwSize, DWORD &dwCRC32 ){
// MAKE SURE WE HAVE A VALID BYTE STREAM
if( byStruct == NULL ){
return -1;
}
dwCRC32 = 0xFFFFFFFF;
// LOOP TO READ THE STRUCTURE
for( DWORD i = 0; i < dwSize; i++ ){
GetCRC32( *byStruct, dwCRC32 );
byStruct++;
}
// FINISH UP
dwCRC32 = ~dwCRC32;
return 0;
}
Функция принимает в BYTE указатель на базовый адрес структуры, и проходит в цикле через каждый байт этой структуры, передавая значение каждого байта в GetCRC32 вместе с предыдущим значением CRC32. В ситуации, когда предыдущие CRC32 значение неизвестно, мы просто присваиваем значение 0xFFFFFFFF.
Перед заполнением структуры с данными, которые будут обработаны, очень важно, инициализировать всю структуру в NULL, потому что структуры, как правило, дополняются до 8 байт. Другими словами, если у вас есть структура, которая имеет 7 символов (7 байт), sizeof(структура) вернёт 8 байт. Последний бит будет инициализирован как «мусорное» значение и не может быть такими же, если вы воссоздать структуру позже с теми же данными. Это будет изменять итоговое значение CRC32. Существует еще один вариант — при передаче размера структуры, если вы знаете точный размер структуры без разделителя, вы можете использовать это значение, что заставит наш алгоритм игнорировать любые дополнительные байты-разделители. Однако не следует смешивать два метода, поскольку это будет приводить к различным несовпадениям CRC32 значения двух идентичных структур.
Расчет для файла
Расчет подписи CRC для файла очень похож, и хотя функция, делающая это, кажется несколько более сложной — в действительности это не так. Однако мы должны добавить дополнительную функцию, которая будет вычислять размер файла перед обработкой.
bool ECRC32::GetFileSize( const HANDLE hFile, DWORD &dwSize ){
// WE HAVE TO HAVE A VALID HANDLE
if( hFile == INVALID_HANDLE_VALUE ){
return false;
}
// NOW WE CAN GET THE FILE SIZE
bool bException = false;
dwSize = 0;
try {
// SETS THE UPPER AND LOWER SIZE VALUES
dwSize = GetFileSize( hFile, NULL );
if( dwSize == INVALID_FILE_SIZE ){
bException = true;
dwSize = 0;
}
}
// SOMETHING SCREWED UP
catch( … ) {
bException = true;
}
return !bException;
}
Эта функция вызывается внутри CRC32ByFile, поэтому мы не должны о ней сильно беспокоиться. Что происходит в идеале — после того, как CRC32ByFile открыла указанный файл (успешно, мог бы я добавить), будет сделана попытка передать указатель файла и указатель на DWORD, который вернет рассчитанный размер. Функция возвращает true, если это удалось.
Следующий код на самом деле читает файл и передает данные в наш CRC32 алгоритм.
// OPEN THE SPECIFIED FILE
if(( hFile = CreateFile( strFileName, GENERIC_READ,
FILE_SHARE_READ, NULL, OPEN_EXISTING, FILE_ATTRIBUTE_NORMAL
| FILE_FLAG_SEQUENTIAL_SCAN, NULL )) == INVALID_HANDLE_VALUE ){
// THIS MEANS THAT WE HAVE AN ERROR
dwErrorCode = -1;
}
// CALCULATE THE CRC32 SIGNATURE
else {
BYTE cBuffer[ 512 ];
DWORD dwBytesInOut, dwLoop;
bool bSuccess = false;
bSuccess = ReadFile( hFile, cBuffer, sizeof( cBuffer ),
&dwBytesInOut, NULL );
while( bSuccess && dwBytesInOut ){
for( dwLoop = 0; dwLoop < dwBytesInOut; dwLoop++ );
GetCRC32( cBuffer[ dwLoop ], dwCRC32 );
bSuccess = ReadFile( hFile, cBuffer, sizeof( cBuffer ), &dwBytesInOut, NULL );
}
}
Это небольшой фрагмент кода из функции, представленой в демо, который принимает файл, открывает его, заполняет буфер данными, вычисляет CRC32-значение для этих данных и повторяется, пока не дойдёт до конца файла.
Другие применения CRC
CRC32, как и в играх, также используется вне игр по тем же причинам — для проверки целостности файлов и данных, когда они каким-то способом копируются.
Великолепное расширение подобного метода использования, которое также широко используются в играх, будет добавить значение CRC32 в пакеты, которые вы посылаете по Интернету; это гарантирует, что данные, которые поступают в место назначения — те же, какими были перед отправкой. Хотя TCP и UDP протоколы хранят значения CRC в заголовках, они будут только проверять, как передаётся каждый пакет. Структуры и данные, которые отправляются в нескольких пакетах, могут в итоге прийти повреждёными и использованными в таком виде без проверки CRC.
CRC может даже быть использована в целях безопасности, чтобы убедиться, что текстовые сообщения и другие типы сообщений не изменены намеренно. Это система, которая обычно используется в PGP при подписании сообщения таким образом, что получающая сторона может проверить, что оно было отправлено действительно вами, тем, кто его подписал. PGP не использует CRC32 для создания подписей, алгоритм CRC32 несколько слаб для таких ситуаций. Другие общие алгоритмы, используемые для этих целей — это MD5, SHA8, SHA256 и т.д. Они называются HASH-алгоритмы и используются обычно в целях безопасности.
Если вам нужно использовать генератор подписей, который производит большее количество значений, чем CRC32 и должен иметь большую, чем CRC32, точность, обратите внимание на эти три алгоритма.
И наконец, если у вас есть какие-либо замечания, вопросы, и так далее, вы легко можете найти меня в irc на канале #gamedev под ником kurifu или seta.
Войдите, чтобы оставить комментарий:
masandilov.ru
C++ — Быстрый алгоритм CRC?
Я хочу создать 32-битное число из ASCII-строки. Алгоритм CRC32 — это именно то, что я ищу, но я не могу его использовать, потому что таблица, которую он требует, слишком велика (для встроенных систем, где ресурсы ОЧЕНЬ редки).
Итак: какие-либо предложения для быстрого и тонкого алгоритма CRC? Не имеет значения, когда столкновения немного более вероятны, чем с оригинальным CRC32.
Спасибо!
8
Решение
Реализации CRC используют таблицы для скорости. Они не обязательны.
Вот краткий CRC32, использующий полином Кастаньоли (тот же, который используется в инструкции Intel crc32), или полином Ethernet (тот же, что используется в zip, gzip и т. Д.).
#include <stddef.h>
#include <stdint.h>
/* CRC-32C (iSCSI) polynomial in reversed bit order. */
#define POLY 0x82f63b78
/* CRC-32 (Ethernet, ZIP, etc.) polynomial in reversed bit order. */
/* #define POLY 0xedb88320 */
uint32_t crc32c(uint32_t crc, const unsigned char *buf, size_t len)
{
int k;
crc = ~crc;
while (len--) {
crc ^= *buf++;
for (k = 0; k < 8; k++)
crc = crc & 1 ? (crc >> 1) ^ POLY : crc >> 1;
}
return ~crc;
}
Начальный crc значение должно быть ноль. Процедура может быть вызвана последовательно с порциями данных для обновления CRC. Вы можете развернуть внутренний цикл для скорости, хотя ваш компилятор может сделать это для вас в любом случае.
23
Другие решения
Очевидно, что самая большая таблица поиска принесет наилучшую производительность, но вы можете использовать любую (меньшую) таблицу для поиска в 16,8 или 4 бита.
Итак, размеры таблицы для crc32:
16bit-lookup: 4*2^16=256k
8bit-lookup: 4*2^8=1k
4bit-lookup: 4*2^4=64byte
4-битная таблица в четыре раза медленнее 16-битной.
Что вы должны использовать, зависит от ваших требований к скорости.
Как упоминает Лука Ране, неплохо было бы поместить таблицу во флэш-память, но на многих платформах недостаточно использовать const ключевое слово.
Чаще всего вам нужно поместить таблицу в раздел, помещенный во flash, изменив командный файл компоновщика.
0
web-answers.ru
14. Прямой табличный алгоритм вычисления сrc32.
Как и любой табличный алгоритм, табличный алгоритм вычисления CRC32 требует задания CRC-таблицы. Ее можно задать в програм’ме статически, явно прописав значения элементов таблицы в сегменте кода, или динамически, вычислив значения элементов таблицы перед началом расчета CRC. Ниже приведена программа вычисления CRC-таблицы для полинома 04clldb7.
Прямой табличный алгоритм CRC32 удобно рассматривать со стороны участников процесса, как это мы делали выше. Источник выполняет следующие действия.
:prgO9_O5.asm — программа вычисления CRC-таблицы для полинома 04clldb7.
.data
;С1<С32-таблица для прямого табличного алгоритма вычисления CRC32
tabl_32_direct dd 256 dup (0)
len_tabl_32_direct =$-tabl_32_direct
adr_tabl_32_direct dd tabl_32_direct
polinom dd 04clldb7h
.code
les di.adr_tabl_32_direct
add di,len_tabl_32_direct-4
std :идем назад по таблице
mov ex,255
mov ebx.polinom /
ml: xor eax.eax
shrd eax.ecx,8
push ex сложенные циклы
mov ex.8 m2: shl eax.l
jnc m3 :старшие разряды неравны — выполняем сдвиг (частное нас не интересует)
;старшйе разряды равны — выполняем XOR:
xor eax.ebx :ax XOR polinom
шЗ:loop m2
pop ex
1. Делает начальную установку регистра, в котором будет производиться формирование CRC, значением OFFFFFFFFh.
2. Вычисляет значение CRC для каждого байта исходной последовательности, принцип которой показан на схеме (см. рис. 9.9). Читатель понимает, что хотя эта схема иллюстрирует принцип вычисления CRC16, но для 32-разрядного алгоритма нужно только увеличить размер элементов таблицы до 32 бит и задействовать весь регистр ЕАХ.
3. Объединяет по XOR итоговое значение в ЕАХ со значением OFFFFFFFFh.
4. Добавляет вычисленное значение в конец двоичной исходной последовательности. После этого его можно передать по назначению.
Ниже приведена программа вычисления CRC32 по прямому табличному алгоритму.
;prg09_06.asm — программа вычисления CRC32 по прямому табличному алгоритму.
исходная битовая последовательность в символах
bit_string db «123456789»
len_bit_string=$-bit_string
сгс_32 dd 0 ;сюда мы поместим рассчитанное значение CRC32
adr_bit_string dd bit_string
;СЯС32-таблица для прямого табличного алгоритма вычисления CRC32
tabl_32_direct dd 256 dup (0)
len_tabl_32_direct =$-tabl_32_direct
adr_tabl_32_direct dd tabl_32_direct
polinom dd 04clldb7h
.code
:—-………расчитываем CRC32 таблицу
les di.adr_tabl_32_direct
add di.len_tabl_32_direct-4 * std ;идем назад по таблице
mov ex.255
mov ebx, polinom
ml: xor eax.eax
shrd eax.ecx.8
push ex сложенные циклы
mov ex.8
m2: shl eax.l
jnc m3 :старшие разряды неравны — выполняем сдвиг (частное нас не интересует)
:старшие разряды равны — выполняем XOR:
xor eax.ebx :ax XOR polinom
m3: loop m2
pop ex
stosd
loop ml
:…..—……закончили расчет CRC32 таблицы
mov eax, OFFFFFFFFh
Ids si.adr_bit_string
mov cx.len_bit_string
m4: xor ebx.ebx
shld ebx.eax.8
shl eax.8
xor bl.[si]
xor eax. tabl_32_direct[bx]
inc si
1 oop m4 :запишем crc-32 в конец (или начало, см. обсуждение ниже) последовательности:
xor eax. OFFFFFFFFh
mov crc_32.eax ;добавляем в конец исходной последовательности
Значение CRC32 для строки «123456789» равно 9c970409h.
Если для источника стандарт определяет практически однозначную последовательность действий, то для приемника возможны несколько вариантов поведения. Отметим два из них.
В первом варианте критерием для вывода о целостности полученного приемником сообщения является результат сравнения или нулевой результат.
1. Выполнить начальную установку регистра, в котором будет производиться формирование значения CRC.
2. Вычислить значение CRC для каждого байта полученной последовательности, принцип которой показан на схеме (см. рис. 9.9 и замечания выше о различиях CRC16 и CRC32).
3. Объединить по XOR итоговое значение в ЕАХ со значением OFFFFFFFFh.
4. Далее можно сделать одно из двух действий:
сравнить значение в ЕАХ со значением CRC, полученным вместе с сообщением, — если они равны, то полученное сообщение идентично исходному;
пропустить байты со значением CRC через процесс получения CRC наравне с другими байтами — об успехе будет свидетельствовать нулевое значение (этот вариант предпочтительнее, так как не предполагает получение предварительных сведений о длине начальной последовательности без учета исходного значения CRC).
Во втором варианте критерием для вывода о целостности полученного приемником сообщения является фиксированная двоичная константа 6b202ca2h.
1. Выполнить начальную установку регистра, в котором будет производиться формирование CRC, в значение OFFFFFFFFh;
2. Вычислить значение CRC32 для каждого байта полученной последовательности (вместе со значением CRC32 в конце), принцип которой показан на схеме (см. рис. 9.9 и замечания выше о различиях CRC16 и CRC32). Должно получиться фиксированное двоичное значение — 6b202ca2h. Необ ходимо заметить, что в литературе можно встретить другое значение — 0debb20e3h, но у автора получалось первое.
Основное отличие этих двух вариантов в том, что нужно каким-то образом отделять контролируемую строку и ее значение CRC32. Избежать прямого отслеживания длины принимаемой строки на стороне приемника можно путем формирования источником значения CRC32 в начале исходной строки либо вообще вне строки. Последний случай, например, характерен для программы, которая отслеживает целостность файлов в некотором каталоге. Тогда результаты подсчета CRC для каждого файла хранятся в некотором служебном файле. Если такой вариант вас не устраивает, тогда следует написать код приемника для прямого табличного алгоритма так, как это сделано для приемника в зеркальном табличном алгоритме. Попробуйте самостоятельно определить константу, соответствующую успешному принятию приемником исходной строки.
Учитывая практическую важность обоих вариантов и для демонстрации разнообразия подходов к проблеме вычисления CRC32, работу приемника для прямого табличного алгоритма продемонстрируем на примере первого варианта, приемник «зеркального» табличного алгоритма CRC32 разработаем исходя из положений второго варианта. Но вы должны понимать, что правильное понимание принципов расчета CRC позволяет вам при соответствующей доработке кода поменять варианты работы приемников. В поле сгс_32 должно быть значение CRC32, рассчитанное предыдущей программой. Автор специально не стал объединять эти программы. Пусть это сделает читатель в нужном для его текущей работы контексте.
;prg09_06.asm — программа вычисления CRC32 по прямому табличному алгоритму.
исходная битовая последовательность в символах
bit_string db «123456789»
len_bit_string=$-bit_string
сгс_32 dd 0 ;сюда мы поместим рассчитанное значение CRC32
adr_bit_string dd bit_string
;СЯС32-таблица для прямого табличного алгоритма вычисления CRC32
tabl_32_direct dd 256 dup (0)
len_tabl_32_direct =$-tabl_32_direct
adr_tabl_32_direct dd tabl_32_direct
polinom dd 04clldb7h
.code
:—-………расчитываем CRC32 таблицу
les di.adr_tabl_32_direct
add di.len_tabl_32_direct-4 * std ;идем назад по таблице
mov ex.255
mov ebx, polinom
ml: xor eax.eax
shrd eax.ecx.8
push ex сложенные циклы
mov ex.8
m2: shl eax.l
jnc m3 :старшие разряды неравны — выполняем сдвиг (частное нас не интересует)
:старшие разряды равны — выполняем XOR:
xor eax.ebx :ax XOR polinom
m3: loop m2
popex
pushexсложенные циклы
mov ex,8 m2: shl eax.l
jnc m3 ;старшие разряды не равны — выполняем сдвиг (частное нас не интересует) :старшие разряды равны — выполняем XOR:
хог eax.ebx:ax XOR polinom m3: loop m2
pop сх
stosd
loop ml : закончили расчет СРО2-таблицы
mov eax. OFFFFFFFFh
Ids si,adr_bit_string
mov cx,len_bit_string m4: xor ebx.ebx
shld ebx.eax,8
shl eax.8
xor bl.[si]
xor eax. tabl_32_direct[bx]
inc si
1 oop m4
xor eax. OFFFFFFFFh
;если исходная последовательность цела, то должно получиться значение crc32=9c970409h ;его можно сравнить с исходным и на этом закончить работу или продолжить до победного. :то есть до 0:
mov ex.4 : 4 (длина сгс_32) :в si адрес сгс_32
mov ebx.crc_32
bswap ebx
mov crc_32.ebx m5: xor ebx.ebx
shld ebx.eax.8
shl eax.8
xor bl.[si]
xor eax. tabl_32_direct[bx]
inc si
loop m5 :должен быть О
Заметьте, что для получения нулевого результата нам пришлось использовать команду BSWAP, чтобы «перевернуть» «значение в поле сгс_32.
studfiles.net
algorithm — Быстрый алгоритм CRC32 для обратного порядка бит
Я работаю с микроконтроллером, который вычисляет контрольную сумму CRC32 данных, которые я загружаю в нее флеш-память «на лету». Это, в свою очередь, может быть использовано для проверки правильности загрузки, путем проверки полученной контрольной суммы после того, как все данные будут загружены.
Единственная проблема заключается в том, что микроконтроллер меняет порядок битов входных байтов, когда он запускает стандартный расчет crc32. Это, в свою очередь, означает, что мне нужно отменить каждый байт в данных на хосте программирования, чтобы вычислить сумму CRC32 для проверки. Поскольку хост программирования несколько ограничен, это происходит довольно медленно.
Я полагаю, что, если возможно изменить CRC32-обратную таблицу, чтобы я мог выполнять поиск без необходимости изменять порядок бит, алгоритм проверки будет работать во много раз быстрее. Но я, похоже, не могу понять, как это сделать.
Чтобы пояснить изменение байта, мне нужно изменить входные байты следующим образом:
01 02 03 04 → 80 40 C0 20
Конечно, гораздо проще увидеть разворот в двоичном представлении:
00000001 00000010 00000011 00000100 → 10000000 01000000 11000000 00100000
Изменить Вот код PoC Python, который я использую, чтобы проверить правильность вычисления CRC32, однако это отменяет каждый байт (ae медленный путь).
EDIT2 Я также включил мою неудачную попытку создания перестановочной таблицы поиска и использования стандартного алгоритма LUT CRC32.
Код выплевывает правильное эталонное значение CRC, а затем неправильно LUT рассчитывается CRC впоследствии.
import binascii
CRC32_POLY = 0xEDB88320
def reverse_byte_bits(x):
'''
Reverses the bit order of the giveb byte 'x' and returns the result
'''
x = ((x<<4) & 0xF0)|((x>>4) & 0x0F)
x = ((x<<2) & 0xCC)|((x>>2) & 0x33)
x = ((x<<1) & 0xAA)|((x>>1) & 0x55)
return x
def reverse_bits(ba, blen):
'''
Reverses all bytes in the given array of bytes
'''
bar = bytearray()
for i in range(0, blen):
bar.append(reverse_byte_bits(ba[i]))
return bar
def crc32_reverse(ba):
# Reverse all bits in the
bar = reverse_bits(ba, len(ba))
# Calculate the CRC value
return binascii.crc32(bar)
def gen_crc_table_msb():
crctable = [0] * 256
for i in range(0, 256):
remainder = i
for bit in range(0, 8):
if remainder & 0x1:
remainder = (remainder >> 1) ^ CRC32_POLY
else:
remainder = (remainder >> 1)
# The correct index for the calculated value is the reverse of the index
ix = reverse_byte_bits(i)
crctable[ix] = remainder
return crctable
def crc32_revlut(ba, lut):
crc = 0xFFFFFFFF
for x in ba:
crc = lut[x ^ (crc & 0xFF)] ^ (crc >> 8)
return ~crc
# Reference test which gives the correct CRC
test = bytearray([1, 2, 3, 4, 5, 6, 7, 8])
crcrev = crc32_reverse(test)
print("0x%08X" % (crcrev & 0xFFFFFFFF))
# Test using permutated lookup table, but standard CRC32 LUT algorithm
lut = gen_crc_table_msb()
crctst = crc32_revlut(test, lut)
print("0x%08X" % (crctst & 0xFFFFFFFF))
Есть ли у кого-нибудь намеки на то, как это можно сделать?
qaru.site
c — Как рассчитывается контрольная сумма CRC32?
Полином для CRC32:
х 32 + х 26 + х 23 + х 22 + х 16 + х 12 + х 11 + х 10 + х 8 + х 7 + х 5 + х 4 + х 2 + х + 1
Или в шестнадцатеричном и двоичном виде:
0x 01 04 C1 1D B7
1 0000 0100 1100 0001 0001 1101 1011 0111
Наибольший член (x 32) обычно не записывается явно, поэтому он может быть представлен в шестнадцатеричном виде так же, как
0x 04 C1 1D B7
Не стесняйтесь считать 1 и 0, но вы обнаружите, что они совпадают с полиномом, где 1 — это бит 0 (или первый бит), а x — это бит 1 (или второй бит).
Почему этот полином? Потому что должен быть стандарт, заданный полином, и стандарт был установлен IEEE 802.3. Также чрезвычайно трудно найти многочлен, который эффективно обнаруживает различные битовые ошибки.
Вы можете думать о CRC-32 как о серии «Бинарная арифметика без переносов» или в основном «XOR и операции сдвига». Это технически называется полиномиальной арифметикой.
Чтобы лучше понять это, подумайте об этом умножении:
(x^3 + x^2 + x^0)(x^3 + x^1 + x^0)
= (x^6 + x^4 + x^3
+ x^5 + x^3 + x^2
+ x^3 + x^1 + x^0)
= x^6 + x^5 + x^4 + 3*x^3 + x^2 + x^1 + x^0
Если мы предположим, что x является основанием 2, то получим:
x^7 + x^3 + x^2 + x^1 + x^0
Зачем? Поскольку 3x ^ 3 — это 11x ^ 11 (но нам нужно только 1 или 0 предварительных цифр), поэтому мы переносим:
=1x^110 + 1x^101 + 1x^100 + 11x^11 + 1x^10 + 1x^1 + x^0
=1x^110 + 1x^101 + 1x^100 + 1x^100 + 1x^11 + 1x^10 + 1x^1 + x^0
=1x^110 + 1x^101 + 1x^101 + 1x^11 + 1x^10 + 1x^1 + x^0
=1x^110 + 1x^110 + 1x^11 + 1x^10 + 1x^1 + x^0
=1x^111 + 1x^11 + 1x^10 + 1x^1 + x^0
Но математики изменили правила так, что это мод 2. Таким образом, любой двоичный полиномиальный мод 2 — это просто сложение без переноса или XOR. Итак, наше оригинальное уравнение выглядит так:
=( 1x^110 + 1x^101 + 1x^100 + 11x^11 + 1x^10 + 1x^1 + x^0 ) MOD 2
=( 1x^110 + 1x^101 + 1x^100 + 1x^11 + 1x^10 + 1x^1 + x^0 )
= x^6 + x^5 + x^4 + 3*x^3 + x^2 + x^1 + x^0 (or that original number we had)
Я знаю, что это прыжок веры, но это за пределами моей способности линейного программиста. Если вы опытный студент CS или инженер, я бросаю вызов, чтобы сломать это. Каждый выиграет от этого анализа.
Итак, чтобы проработать полный пример:
Original message : 1101011011
Polynomial of (W)idth 4 : 10011
Message after appending W zeros : 11010110110000
Теперь мы разделим расширенное сообщение на Poly, используя арифметику CRC. Это то же разделение, что и раньше:
1100001010 = Quotient (nobody cares about the quotient)
_______________
10011 ) 11010110110000 = Augmented message (1101011011 + 0000)
=Poly 10011,,.,,....
-----,,.,,....
10011,.,,....
10011,.,,....
-----,.,,....
00001.,,....
00000.,,....
-----.,,....
00010,,....
00000,,....
-----,,....
00101,....
00000,....
-----,....
01011....
00000....
-----....
10110...
10011...
-----...
01010..
00000..
-----..
10100.
10011.
-----.
01110
00000
-----
1110 = Remainder = THE CHECKSUM!!!!
Деление дает частное, которое мы отбрасываем, и остаток, который является вычисленной контрольной суммой. На этом заканчивается расчет. Обычно контрольная сумма затем добавляется к сообщению и результат передается. В этом случае передача будет: 11010110111110.
В качестве делителя используйте только 32-разрядное число, а в качестве дивиденда — весь поток. Выбросьте частное и оставьте остаток. Прикрепите остаток в конце вашего сообщения, и у вас будет CRC32.
Средний обзор парня:
QUOTIENT
----------
DIVISOR ) DIVIDEND
= REMAINDER
- Возьмите первые 32 бита.
- Биты сдвига
- Если 32 бита меньше, чем DIVISOR, перейдите к шагу 2.
- XOR 32 бита от DIVISOR. Переходите к шагу 2.
(Обратите внимание, что поток должен делиться на 32 бита, или он должен быть дополнен. Например, 8-битный поток ANSI должен быть дополнен. Также в конце потока разделение останавливается.)
user295190 27 янв. ’11 в 0:212011-01-27 00:21
qaru.site
Иллюстрированный самоучитель по задачам и примерам Assembler › Вычисление CRC › «Зеркальный» табличный алгоритм CRC32 [страница — 192] | Самоучители по программированию
«Зеркальный» табличный алгоритм CRC32
В заключение данного раздела обсудим «зеркальный» вариант табличного алгоритма – алгоритм CRC32 (V.42 МККТТ). Этот вариант вычисления CRC обязан своим возникновением существованию последовательного интерфейса, который посылает биты, начиная с наименее значимого (бит 0) и заканчивая самым старшим (бит 7), то есть в обратном порядке. В «зеркальном» регистре все биты отражены относительно центра. Например, 10111011001 есть отражение значения 10011011101.
Вместо того чтобы менять местами биты перед их обработкой, можно зеркально отразить все значения и действия, участвующие в прямом алгоритме. При этом направление расчетов поменяется – байты теперь будут сдвигаться вправо, полином 04clldb7h зеркально отразится относительно его центра, в результате получится значение 0edb88320h. СRС32-таблица будет зеркальным отражением аналогичной таблицы для прямого алгоритма (рис. 9.10).
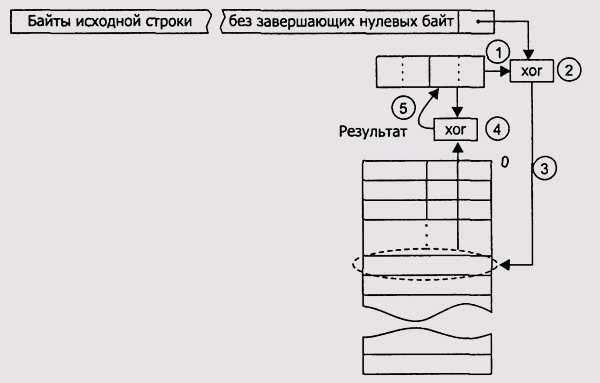
Рис. 9.10. Схема «Зеркального» табличного алгоритма
Для зеркального алгоритма вычисления CRC32 процесс вычисления такой же, за исключением порядка – сдвиги и заполнение регистра осуществляются вправо. Ниже приведена программа вычисления таблицы для зеркального алгоритма CRC32 и полинома 0EDB88320h.
;prg09_08.asm – программа вычисления таблицы для зеркального алгоритма CRC32 :и полинома 0EDB88320h .data :СRС32-таблица для зеркального табличного алгоритма вычисления CRC32 tabl_32_mirror dd 256 dup (0) len_tabl_32jrrirror=$-tabl_32_mirror adr_tabl_32jTrirror dd tabl_32_mirror polinom dd 0EDB88320h .code les di.adr_tabl_32_mirror add di,len_tabl_32_mirror-4 std;идем назад по таблице mov ex.255 mov ebx.polinom ml: xor eax.eax mov al.cl;индекс в таблице для вычисления CRC push ex сложенные циклы mov ex.8 m2: shr eax.l jnc m3;старшие разряды не равны – выполняем сдвиг (частное нас не интересует) ;старшие разряды равны – выполняем XOR: xor eax.ebx:ax XOR polinom m3: loop m2 pop ex stosd loop ml
samoychiteli.ru
knigechka: Прямой табличный алгоритм CRC32
Как и любой табличный алгоритм, табличный алгоритм вычисления CRC32 требует задания CRC-таблицы. Ее можно задать в програм’ме статически, явно прописав значения элементов таблицы в сегменте кода, или динамически, вычислив значения элементов таблицы перед началом расчета CRC. Ниже приведена программа вычисления CRC-таблицы для полинома 04clldb7.
Прямой табличный алгоритм CRC32 удобно рассматривать со стороны участников процесса, как это мы делали выше. Источник выполняет следующие действия.
:prgO9_O5.asm — программа вычисления CRC-таблицы для полинома 04clldb7.
.data
;С1<С32-таблица для прямого табличного алгоритма вычисления CRC32
tabl_32_direct dd 256 dup (0)
len_tabl_32_direct =$-tabl_32_direct
adr_tabl_32_direct dd tabl_32_direct
polinom dd 04clldb7h
.code
les di.adr_tabl_32_direct
add di,len_tabl_32_direct-4
std :идем назад по таблице
mov ex,255
mov ebx.polinom /
ml: xor eax.eax
shrd eax.ecx,8
push ex сложенные циклы
mov ex.8 m2: shl eax.l
jnc m3 :старшие разряды неравны — выполняем сдвиг (частное нас не интересует)
;старшйе разряды равны — выполняем XOR:
xor eax.ebx :ax XOR polinom
шЗ:loop m2
pop ex
- 1. Делает начальную установку регистра, в котором будет производиться формирование CRC, значением OFFFFFFFFh.
2. Вычисляет значение CRC для каждого байта исходной последовательности, принцип которой показан на схеме (см. рис. 9.9). Читатель понимает, что хотя эта схема иллюстрирует принцип вычисления CRC16, но для 32-разрядного алгоритма нужно только увеличить размер элементов таблицы до 32 бит и задействовать весь регистр ЕАХ.
3. Объединяет по XOR итоговое значение в ЕАХ со значением OFFFFFFFFh.
4. Добавляет вычисленное значение в конец двоичной исходной последовательности. После этого его можно передать по назначению.
Ниже приведена программа вычисления CRC32 по прямому табличному алгоритму.
;prg09_06.asm — программа вычисления CRC32 по прямому табличному алгоритму.
исходная битовая последовательность в символах
bit_string db «123456789»
len_bit_string=$-bit_string
сгс_32 dd 0 ;сюда мы поместим рассчитанное значение CRC32
adr_bit_string dd bit_string
;СЯС32-таблица для прямого табличного алгоритма вычисления CRC32
tabl_32_direct dd 256 dup (0)
len_tabl_32_direct =$-tabl_32_direct
adr_tabl_32_direct dd tabl_32_direct
polinom dd 04clldb7h
.code
:—-………расчитываем CRC32 таблицу
les di.adr_tabl_32_direct
add di.len_tabl_32_direct-4 * std ;идем назад по таблице
mov ex.255
mov ebx, polinom
ml: xor eax.eax
shrd eax.ecx.8
push ex сложенные циклы
mov ex.8
m2: shl eax.l
jnc m3 :старшие разряды неравны — выполняем сдвиг (частное нас не интересует)
:старшие разряды равны — выполняем XOR:
xor eax.ebx :ax XOR polinom
m3: loop m2
pop ex
stosd
loop ml
:…..—……закончили расчет CRC32 таблицы
mov eax, OFFFFFFFFh
Ids si.adr_bit_string
mov cx.len_bit_string
m4: xor ebx.ebx
shld ebx.eax.8
shl eax.8
xor bl.[si]
xor eax. tabl_32_direct[bx]
inc si
1 oop m4 :запишем crc-32 в конец (или начало, см. обсуждение ниже) последовательности:
xor eax. OFFFFFFFFh
mov crc_32.eax ;добавляем в конец исходной последовательности
Значение CRC32 для строки «123456789» равно 9c970409h.
Если для источника стандарт определяет практически однозначную последовательность действий, то для приемника возможны несколько вариантов поведения. Отметим два из них.
В первом варианте критерием для вывода о целостности полученного приемником сообщения является результат сравнения или нулевой результат.
- 1. Выполнить начальную установку регистра, в котором будет производиться формирование значения CRC.
2. Вычислить значение CRC для каждого байта полученной последовательности, принцип которой показан на схеме (см. рис. 9.9 и замечания выше о различиях CRC16 и CRC32).
3. Объединить по XOR итоговое значение в ЕАХ со значением OFFFFFFFFh.
4. Далее можно сделать одно из двух действий:- сравнить значение в ЕАХ со значением CRC, полученным вместе с сообщением, — если они равны, то полученное сообщение идентично исходному;
- пропустить байты со значением CRC через процесс получения CRC наравне с другими байтами — об успехе будет свидетельствовать нулевое значение (этот вариант предпочтительнее, так как не предполагает получение предварительных сведений о длине начальной последовательности без учета исходного значения CRC).
Во втором варианте критерием для вывода о целостности полученного приемником сообщения является фиксированная двоичная константа 6b202ca2h.
- 1. Выполнить начальную установку регистра, в котором будет производиться формирование CRC, в значение OFFFFFFFFh;
2. Вычислить значение CRC32 для каждого байта полученной последовательности (вместе со значением CRC32 в конце), принцип которой показан на схеме (см. рис. 9.9 и замечания выше о различиях CRC16 и CRC32). Должно получиться фиксированное двоичное значение — 6b202ca2h. Необ ходимо заметить, что в литературе можно встретить другое значение — 0debb20e3h, но у автора получалось первое.
Основное отличие этих двух вариантов в том, что нужно каким-то образом отделять контролируемую строку и ее значение CRC32. Избежать прямого отслеживания длины принимаемой строки на стороне приемника можно путем формирования источником значения CRC32 в начале исходной строки либо вообще вне строки. Последний случай, например, характерен для программы, которая отслеживает целостность файлов в некотором каталоге. Тогда результаты подсчета CRC для каждого файла хранятся в некотором служебном файле. Если такой вариант вас не устраивает, тогда следует написать код приемника для прямого табличного алгоритма так, как это сделано для приемника в зеркальном табличном алгоритме. Попробуйте самостоятельно определить константу, соответствующую успешному принятию приемником исходной строки.
Учитывая практическую важность обоих вариантов и для демонстрации разнообразия подходов к проблеме вычисления CRC32, работу приемника для прямого табличного алгоритма продемонстрируем на примере первого варианта, приемник «зеркального» табличного алгоритма CRC32 разработаем исходя из положений второго варианта. Но вы должны понимать, что правильное понимание принципов расчета CRC позволяет вам при соответствующей доработке кода поменять варианты работы приемников. В поле сгс_32 должно быть значение CRC32, рассчитанное предыдущей программой. Автор специально не стал объединять эти программы. Пусть это сделает читатель в нужном для его текущей работы контексте.
;prg09_06.asm — программа вычисления CRC32 по прямому табличному алгоритму.
исходная битовая последовательность в символах
bit_string db «123456789»
len_bit_string=$-bit_string
сгс_32 dd 0 ;сюда мы поместим рассчитанное значение CRC32
adr_bit_string dd bit_string
;СЯС32-таблица для прямого табличного алгоритма вычисления CRC32
tabl_32_direct dd 256 dup (0)
len_tabl_32_direct =$-tabl_32_direct
adr_tabl_32_direct dd tabl_32_direct
polinom dd 04clldb7h
.code
:—-………расчитываем CRC32 таблицу
les di.adr_tabl_32_direct
add di.len_tabl_32_direct-4 * std ;идем назад по таблице
mov ex.255
mov ebx, polinom
ml: xor eax.eax
shrd eax.ecx.8
push ex сложенные циклы
mov ex.8
m2: shl eax.l
jnc m3 :старшие разряды неравны — выполняем сдвиг (частное нас не интересует)
:старшие разряды равны — выполняем XOR:
xor eax.ebx :ax XOR polinom
m3: loop m2
pop ex
push ex сложенные циклы
mov ex,8 m2: shl eax.l
jnc m3 ;старшие разряды не равны — выполняем сдвиг (частное нас не интересует) :старшие разряды равны — выполняем XOR:
хог eax.ebx:ax XOR polinom m3: loop m2
pop сх
stosd
loop ml : закончили расчет СРО2-таблицы
mov eax. OFFFFFFFFh
Ids si,adr_bit_string
mov cx,len_bit_string m4: xor ebx.ebx
shld ebx.eax,8
shl eax.8
xor bl.[si]
xor eax. tabl_32_direct[bx]
inc si
1 oop m4
xor eax. OFFFFFFFFh
;если исходная последовательность цела, то должно получиться значение crc32=9c970409h ;его можно сравнить с исходным и на этом закончить работу или продолжить до победного. :то есть до 0:
mov ex.4 : 4 (длина сгс_32) :в si адрес сгс_32
mov ebx.crc_32
bswap ebx
mov crc_32.ebx m5: xor ebx.ebx
shld ebx.eax.8
shl eax.8
xor bl.[si]
xor eax. tabl_32_direct[bx]
inc si
loop m5 :должен быть О
Заметьте, что для получения нулевого результата нам пришлось использовать команду BSWAP, чтобы «перевернуть» «значение в поле сгс_32.
Предлагаю ознакомиться с аналогичными статьями:
knigechka.blogspot.com