Системы счисления
Кодирование информации — представление информации в той или иной стандартной форме.
Например, письменность и арифметика — кодирование речи и числовой информации, музыку кодируют с помощью нот.
Чтобы использовать числа их нужно как-то записывать и называть.
Самые первые системы нумерации возникли в древнем Египте и Месопотамии — применяли иероглифы.
Системы счисления — способы кодирования числовой информации, то есть способ записи чисел с помощью некоторого алфавита, символы которого называют цифрами.
В древнем Вавилоне делили час на 60 минут, угол на 360 градусов, англосаксы начали делить год на 12 месяцев, сутки на два периода по 12 часов, продолжительность года 360 суток.
В Риме семь чисел обозначают буквами. 1-I, 5-V, 10-X, 50- L,100-C, 500-D, 1000-M.
IV (4=5-1)
VI (6=5+1)
Значение числа определяется как сумма или разность цифр числа. Это непозиционная система счисления.
Славяне числа кодировали буквами А=1, В=2, Г=3; чтобы избежать путаницы ставился специальный знак ~ титло. Алфавитная система счисления. Славянская нумерация сохранялась до конца XVII века.
При Петре I возобладала так называемая арабская нумерация. Славянская нумерация сохранилась в богослужебных книгах.
Самой популярной системой кодирования чисел оказалась позиционная, десятичная. Используются десять цифр. Значение каждой определяется той позицией, которую цифра занимает в записи числа.
Эта система пришла из Индии, где она появилась не позднее VI века, европейцы заимствовали ее у арабов, назвав ее арабской. Из арабского языка заимствовано слово «цифра». Причина ее возникновения анатомическая — 10 пальцев. Анатомическая система счисления (существовали пятеричные, двадцатеричные системы счисления).
Например, 23 — три единицы, два десятка 32 — две единицы, три десятка 400 — 4 сотни, два 0 вклад в число не дают, нужны для того, чтобы указывать позицию 4.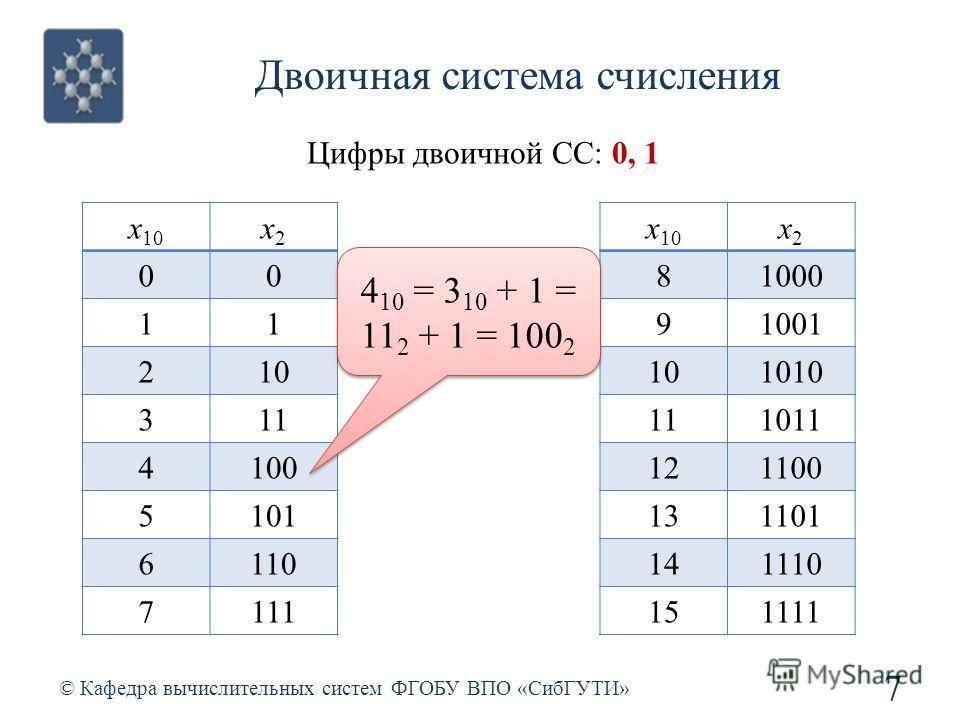
В десятичной позиционной системе особую роль играет число 10 и его степени, например, 1996 — 6 единиц, 9 десятков, 9 сотен 1 тысяча или 1996=6+9*10+9*100+1*1000, т.к.1000=103, 100=102, 10=101, таким образом, 1996=1*103 + 9*102 + 9*101 +6*100.
Любое число в нулевой степени равно единице 0,10 = 1
То есть любое 4-х значное число можно записать в следующем виде:
N=a3*103+a2*102+a1*101+a0*100
a3, a2, a1, a0-десятичные цифры, от 1 до 9 или коэффициенты 3 2 1 0 — разряды, степени числа 10 со степенями называют основанием системы счисления.
Но основанием системы может быть не обязательно число 10, мы можем записать число в р-ичной системе, где основанием будут степени числа р. Любое число N в р-ичной системе мы можем представить в виде формулы:
N=an*Pn+an-1*Pn-1+.
..+a1*P1+a0*P0
Если взять за основание 60, то придется использовать 60 разных цифр. Такая система была в Древнем Вавилоне. Если основанием возьмем 2, получим систему всего с двумя цифрами 0 и 1. К сожалению, в этой системе даже небольшие числа записываются слишком длинно, так 1995 в двоичной системе записывается 199510=111110010112
Система счисления, где 2 является основанием системы называется двоичной системой счисления, относится к машинной системе счисления, к машинным системам счисления относятся и восьмеричная и шестнадцатеричная. Таким образом существуют следующие системы счисления: вавилонская, римская, алфавитные, анатомические, машинные.
Системы счисления делятся также на позиционные и непозиционные.
Перевод из двоичной системы счисления в десятичную.
Как узнать чему равно девятизначное двоичное число N=1111101002
Подпишем сверху каждый разряд
87654321010 — 1 разряды (степени двойки)
1111101002
В двоичной системе особую роль играет двойка и ее степени.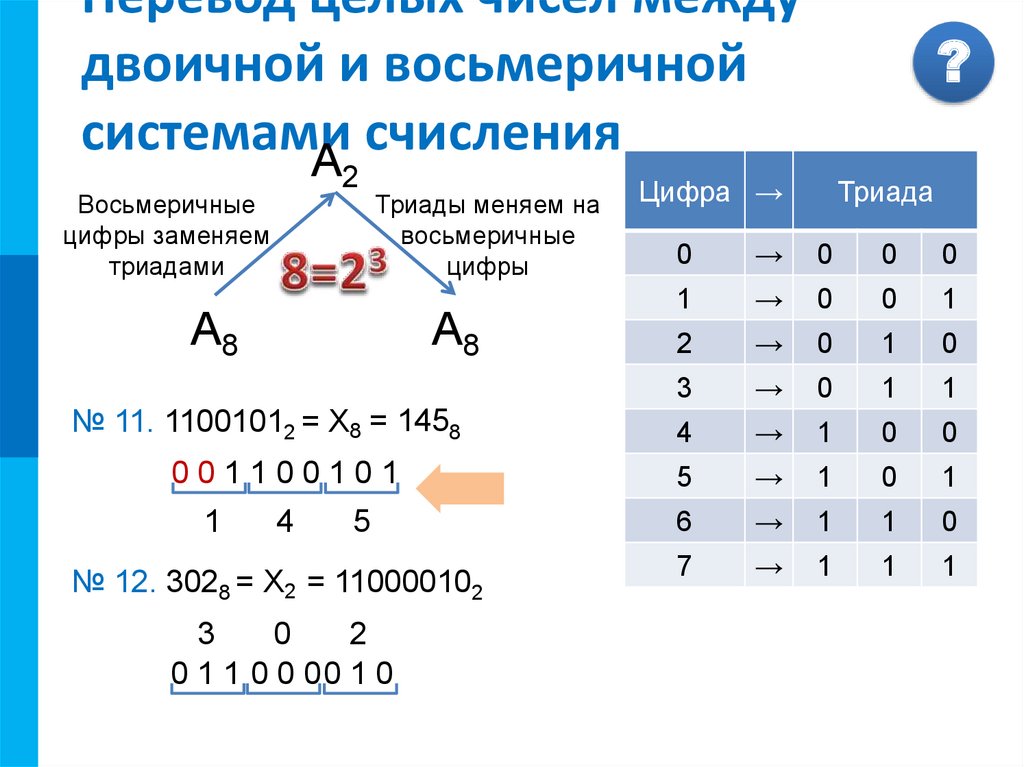
Таким образом:
111110100=1*28 +1*27 +1*26 +1*25 +1*24 +0*23 +1*22 +0*21 +0*20 =1*256+1*128+1*64 +1*32 +1*16 +0*8 +1*4 +0*2 +0*1=256 + 128 + 64 + 32 + 16 + 0 + 4 + 0 +0 =500
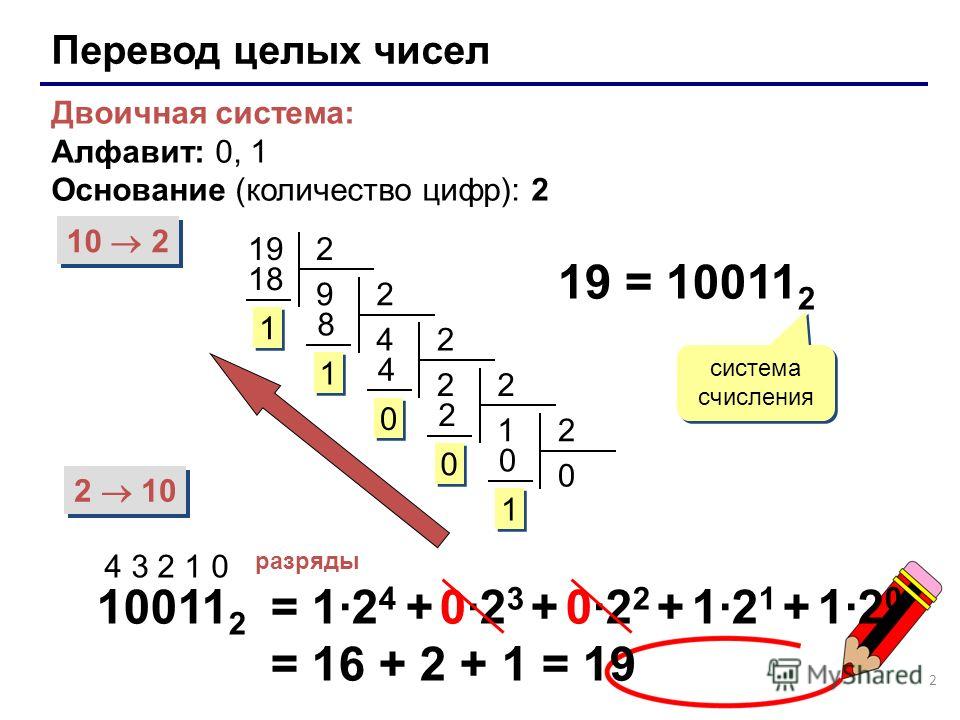
Перевод из десятичной системы счисления в двоичную.
Пусть нужно перевести в двоичную систему число 234. Будем делить 234 последовательно на 2 и запоминать остатки, не забывая про нулевые.
Выписав все остатки, начиная с последнего 3 в обратном порядке, получим двоичное разложение числа.
23410 = 111010102
Восьмеричная и шестнадцатеричная системы счисления.
Запись числа в двоичной системе удобна для компьютера, но громоздка для человека. На помощь приходят системы, родственные двоичной восьмеричная система счисления использует 8 цифр: 0,1,2,3,4,5,6,7.
Единица, записанная в самом младшем разряде означает просто единицу (1*8 в нулевой степени), та же единица в следующем разряде обозначает 8 (1*8 в первой степени), в следующем 64 (1*8 во второй степени) и так далее.
2 1 0 1 — разряды (степени восьмерки)
1008 = 1*82 + 0*81 + 0*80 = 1*64 + 0 + 0 = 64 10
8 — это 2 в третьей степени. При переводе в восьмеричную систему двоичное число из трех цифр записывается одной цифрой.
Восьмеричная запись | Двоичное представление |
впереди стоящий 0 ничего не значит |
0 | 000 | |
1 | 001 | |
2 | 010 | |
3 | 011 | |
4 | 100 | |
5 | 101 | |
6 | 110 | |
111 |
Для перевода из двоичной в восьмеричную число, записанное в двоичной системе делим на триады справа налево
Например, 11011100011=11 011 100 011 и заменить каждую группу одной восьмеричной цифрой 2 2 4 2 и получим 22428
Для перевода числа из восьмеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную систему, представив каждую цифру в виде триады (1 в двоичной системе 1 добавляем до триады впереди 00)
6 | 1 | 1 |
110 | 001 | 001 |
Еще компактней выглядит запись двоичного числа в шестнадцатеричной системе счисления.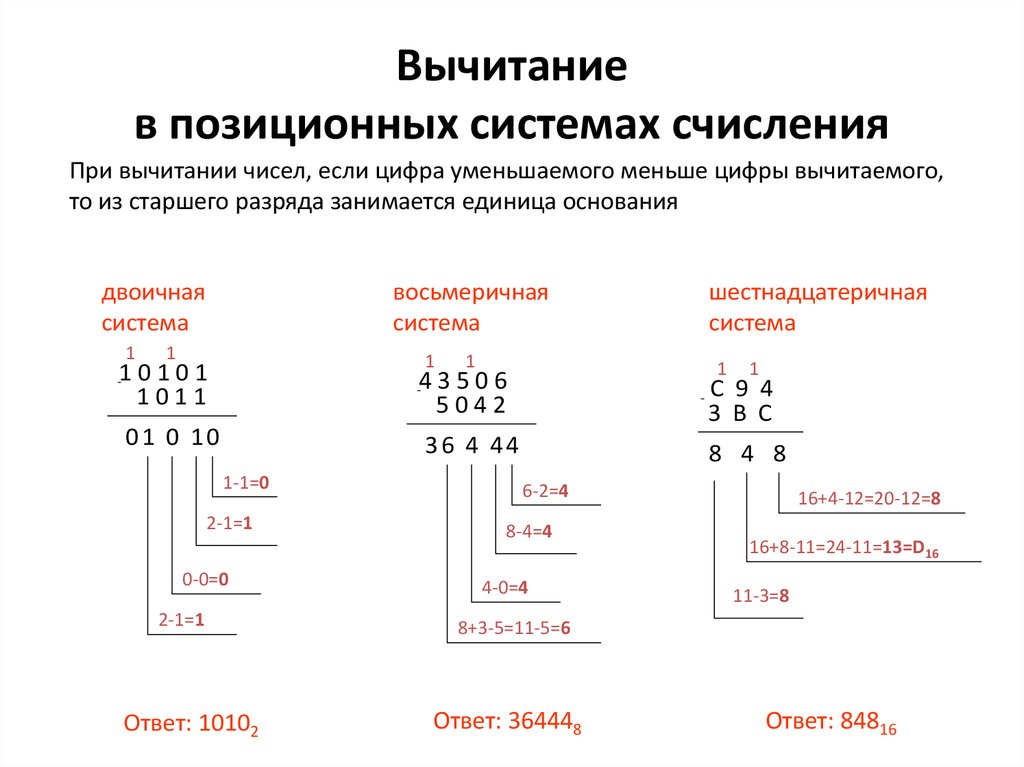
Для первых 10 из 16 шестнадцатеричных цифр используются привычные цифры 0 1 2 3 4 5 6 7 8 9, а для остальных используют первые буквы латинского алфавита
A-10 D-13
B-11 E-14
C-12 F-15
Цифра 1 в самом младшем разряде означает 1, в следующем разряде означает 16 (в первой степени), в следующем разряде 16*16 (162)=256, в следующем разряде 1*163 и так далее.
10016 =25610
Цифра F, записанная в самом младшем разряде означает 15 в десятичной системе, F в следующем разряде означает 15*16 в первой степени в десятичной системе и т.д.
2 1 0 — 1 разряды (степени числа 16)
Число 21016=10*162+15*161+0*160
21016=10*256+240+0*1=2560+240+0=280010
2 1 0
BAD16=11*162+1 0*161+13*1 60 = 11 * 256+10 *16+13*1=2816+160+13=298910
16 — это 2 в четвертой степени.
Для перевода числа из шестнадцатеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную, представив каждую цифру в виде сочетания четырех 1 и 0
A | O | F | AOF16 |
1010 | 0000 | 1111 |
Как осуществить перевод чисел из двоичной системы в шестнадцатеричную? Необходимо разбить число, записанное в двоичной системе на группы по 4 разряда справа налево, заменив каждую группу одной шестнадцатеричной цифрой.
1101 | 1010 | 1101 | в двоичной |
11 | 10 | 13 | в десятичной |
B | A | D | в шестнадцатеричной |
10 | 2 | 8 | 16 |
| 0 | 000 | 0 | 0 |
| 1 | 001 | 1 | 1 |
| 2 | 010 | 2 | 2 |
| 3 | 011 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Курс Harvard CS50 — Лекция: Двоичная система счисления
Harvard CS50
0 уровень , 3 лекция
Открыта
У нас 10 пальцев, и система — десятичная.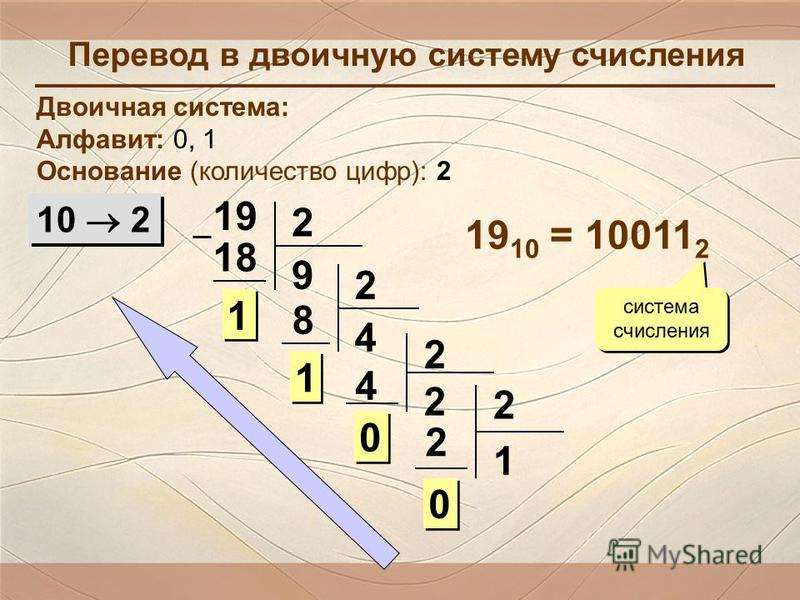
То есть, любое, сколь угодно большое число мы можем представить с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. В зависимости от того, где в числе стоит цифра, она может означать разное: если эта цифра последняя, то она расположена в разряде единиц, предпоследняя — разряд десятков, еще левее — разряд сотен и так далее. По сути, любое число можно расписать в виде суммы цифр, каждая из которых умножена на десять в определенной степени. В случае единиц, эта степень — нулевая.
Например,
1573 = 3*100 + 7*101 + 5*102 + 1*103.
Число, на степень которого умножаются цифры называется базой системы счисления. Для десятичной системы базой, логично, является десятка.
У компьютера пальцев нет, но есть два состояния: условно «ток идет» и «ток не идет», нулик и единичка. Соответственно все числа (да и вообще информация) в памяти компьютера состоят только из двух цифр — 0 и 1. Их расположение, как и в случае десятичной системы счисления, указывает на разряд.
Только теперь число можно разложить на сумму цифр, помноженных не на степени десятки, а степени двойки.
0 в двоичной системе = 0 1 в двоичной системе = 1 2 в двоичной системе = 10 710=1112
Научитесь переводить из двоичной системы в десятичую. Вы, наверное, уже поняли, как это делается — просто берем цифру числа начиная с самой правой и умножаем её на базу системы счисления в степени, соответствующей её разряду, так с каждым разрядом. Затем складываем все получившиеся таким образом числа.
Пример:
Давайте найдем десятичный аналог двоичного числа 1011012
- Самая правая единичка = 1*20
- Следующий нулик = 0*21
- Третья справа единичка = 1*22
- Четвертая = 1*23
- … и так далее
1011012 = 1*20 + 0*21 + 1*22 + 1*23 + 0*24 + 1*25 = 1 + 0 + 4 + 8 + 0 + 32 = 4510
Представьте восемь лампочек, выставленных в ряд.
У каждой из них — свой собственный выключатель.
Каждая из лампочек — это разряд. Да что представлять, вспомните самую первую лекцию (там есть такой агрегат) или вот вам виджет: cdn.cs50.net/2016/x/psets/0/pset0/bulbs.html
Поиграйтесь с ним, «прочувствуйте» двоичную систему.
Тут тоже всё просто, если понимать суть.
Пример:
У нас есть десятичное число 5710. Чтобы перевести его в двоичную систему, нужно определить, какая максимальная степень двойки не превосходит это число.
26 = 64. Это явно многовато. А вот 25 = 32.
Мы определили старший разряд. 3210 = 1000002. Теперь ищем следующий разряд. 57-32 = 25. Теперь для 25 ищем степень двойки, которая не превосходит 25. 24 = 16. Значит, следующий разряд у нас тоже равен 1. 32+16 = 4810 = 1100002. 57 – 48 = 9. 23 = 8, это меньше, чем 9. Значит следующий разряд тоже будет единичкой.
32 + 16 + 8 = 5610 = 1110002. 57 - 56 = 1, то есть осталась только одна степень 20. Таким образом, 5710 = 1110012.
На этом все =) Переходите к следующей лекции!
9 в двоичном формате — Как преобразовать 9 из десятичного в двоичный?
9 в двоичном формате равно 1001. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, которые равны 0 и 1 (биты). Мы использовали 4 бита для представления 9 в двоичном виде. В этой статье давайте узнаем, как преобразовать десятичное число 9 в двоичное.
Как преобразовать 9 в двоичном виде?
Шаг 1: Разделите 9 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0,9.0005
| Дивиденд | Остаток |
|---|---|
| 9/2 = 4 | 1 |
| 4/2 = 2 | 0 |
| 2/2 = 1 | 0 |
| 1/2 = 0 | 1 |
Шаг 2: Запишите остаток снизу вверх, т.
е. в обратном хронологическом порядке. Это даст двоичный эквивалент 9.
Следовательно, двоичный эквивалент десятичного числа 9 равен 1001.
Давайте посмотрим на значение десятичного числа 9 в различных системах счисления.
- 9 в двоичном виде: 9₁₀ = 1001₂
- 9 в восьмеричной системе: 9₁₀ = 11₈
- 9 в шестнадцатеричном формате: 9₁₀ = 9₁₆
- 1001₂ в десятичном формате: 9₁₀
Постановка задачи:
☛Связанные темы
- Двоичный код в десятичный
- Калькулятор преобразования десятичной системы в двоичную
- Двоично-десятичный калькулятор
- 111 в двоичном формате — 1101111
- 216 в двоичном формате — 11011000
- 18 в двоичном формате — 10010
- 145 в двоичном формате — 10010001
- 95 в двоичном формате — 1011111
- 2 в двоичном формате — 10
- 100 в двоичном формате — 1100100
Часто задаваемые вопросы по 9 в двоичном формате
Что такое 9 в двоичном формате?
9 в двоичном формате равно 1001.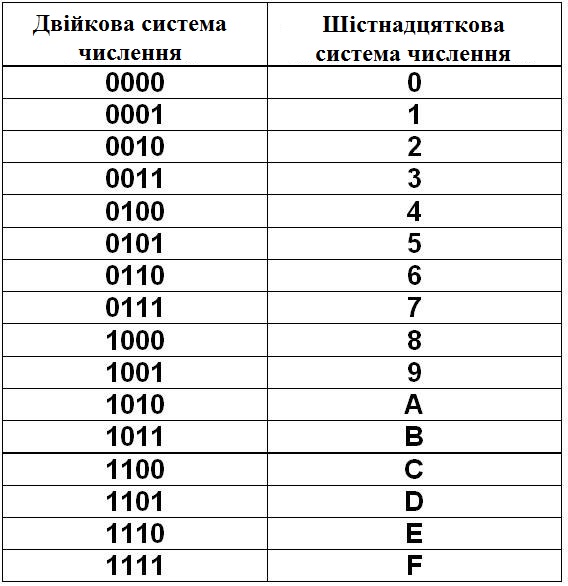
Чтобы найти десятичный эквивалент в двоичном, разделите 9 последовательно на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.
Сколько бит имеет число 9 в двоичном формате?
Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 9 в двоичном формате, т.е. 1001. Таким образом, мы использовали 4 бита для представления 9 в двоичном формате.
Что такое двоичный эквивалент 9 + 57?
9 в двоичной системе счисления равно 1001, а 57 равно 111001. Мы можем сложить двоичный эквивалент 9 и 57, используя правила двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 равно перенос на следующий бит]. Следовательно, (1001)₂ + (111001)₂ = (1000010)₂, что есть не что иное, как 66.
Найдите значение 10 × 9 в двоичной форме.
Мы знаем, что 9 в двоичном формате равно 1001, а 10 равно 1010. Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0; 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 1001 × 1010 = 1011010, что равно 90 в десятичной системе счисления.
[9 × 10 = 90]
Как преобразовать 9 в двоичный эквивалент?
Мы можем разделить 9 на 2 и продолжать деление, пока не получим 0. Записывайте остаток на каждом шаге.
- 9 mod 2 = 1 — LSB (младший значащий бит)
- 4 мод 2 = 0
- 2 мод 2 = 0
- 1 mod 2 = 1 — MSB (старший бит)
Записать остатки от MSB до LSB. Следовательно, десятичное число 9 в двоичном виде можно представить как 1001.
Рабочие листы по математике и
наглядный учебный план
[Решено] Какое двоичное число соответствует десятичному числу 9?
Этот вопрос был ранее задан в
Официальная газета 3: состоялась 25 сентября 2020 Shift 1
Просмотр всех NET Papers>
- 1100
- 1001
- 0111
- 1011
- 0111
- 1011
- .
Бесплатно
КТ 1: История Индии
35,2 тыс. пользователей
10 вопросов
10 баллов
6 минут
Система счисления — это способ представления или выражения чисел.
Вы слышали о различных типах систем счисления, таких как целые числа и действительные числа. Но в контексте компьютеров мы определяем другие типы систем счисления. Это:- Десятичная система счисления
- Двоичная система счисления
- Восьмеричная система счисления и
- Шестнадцатеричная система счисления
Двоичная система счисления:
- Двоичная система счисления — это один из четырех типов системы счисления.
- В компьютерных приложениях, где двоичные числа представлены только двумя символами или цифрами, то есть 0 (ноль) и 1 (единица).
- Двоичные числа здесь представлены в системе счисления с основанием 2.
- Например, (101)2 – это двоичное число. Каждая цифра в этой системе называется битом.
Здесь мы покажем вам шаг за шагом, как преобразовать десятичное число 9к бинарному.
Шаг 1) Разделите 9 на 2, чтобы получить частное. Оставьте Целую часть для следующего шага и отложите остаток в сторону.
Шаг 2) Разделите целую часть частного из шага 1 на 2. Снова сохраните целую часть и отложите остаток в сторону.
Шаг 3) Повторяйте шаг 2 выше, пока целая часть не станет равной 0.
Шаг 4) Запишите остатки в обратном порядке, чтобы получить ответ на 9 в виде двоичного числа.Важные моменты
Здесь мы покажем нашу работу, чтобы вы могли следить за ней:
Десятичное число
Операция
Коэффициент
Остаток
Двоичный номер
9
÷ 2
4
1
1
4
÷ 2
2
0
01
2
÷ 2
1
0
001
1
÷ 2
0
1
1001
Следовательно, двоичный эквивалент десятичного числа 91001.
Вы слышали о различных типах систем счисления, таких как целые числа и действительные числа. Но в контексте компьютеров мы определяем другие типы систем счисления. Это:
