2019 в восьмеричной системе: Перевод 2019 из десятичной в восьмеричную систему счисления

Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная

«Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная».

 

Автор: Гребенников Александр Николаевич
Должность: учитель информатики

Учебное заведение: ГБОУ школа – интернат № 67
Населённый пункт: Пушкинский район Санкт–Петербурга
Наименование материала: статья
Тема: «Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная».

 

Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная.

Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.

Каждая позиционная система использует определенный алфавит цифр и основание. В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения цифр соседних разрядов числа.

 В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (10 цифр) — это позиционная система счисления. А во второй – I, V, X, L, C, D, M (1, 5, 10, 50, 100, 500, 1000) — это непозиционная система счисления.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет.

Например:

11 – здесь первая единица обозначает 10, а вторая – 1.
I I – здесь обе единицы обозначают единицу.

Основание системы счисления – это количество знаков, которое используется для записи цифр.

Разряд — это позиция цифры в числе. Разрядность числа — количество цифр, из которых состоит число (например, 362 — трехразрядное число, 1001101 — восьмиразрядное число).

Разряды нумеруются справа на лево (например, в числе 793 семёрка занимает первый разряд, а тройка — третий).

Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления.

456, 567, 678 – здесь цифра 6 в первом случае обозначает 6, во втором – 60, а в третьем – 600.

XXV, XVI, XII – здесь, где бы ни стояла цифра X, она везде обозначает десять единиц. Другими словами, величина, обозначаемая знаком X, не зависит от его позиции.

В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется 10 цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная (используются 8 цифр от 0 до 7),  шестнадцатеричная (используются 16 цифр 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F).

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т. к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел). 

Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

 

 

 

Системы счисления
Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

 

 

Двоичная система счисления.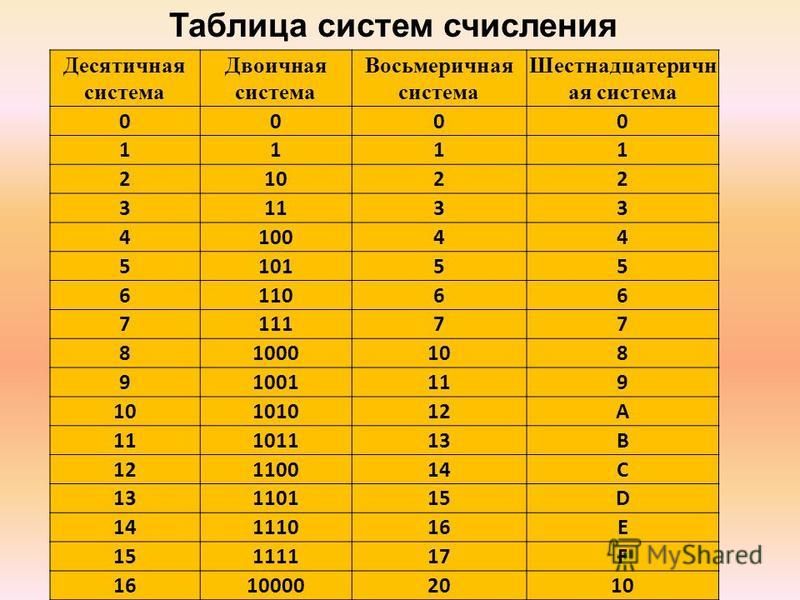

 

Почему двоичная система счисления так распространена?

Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую  информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания. Поэтому для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.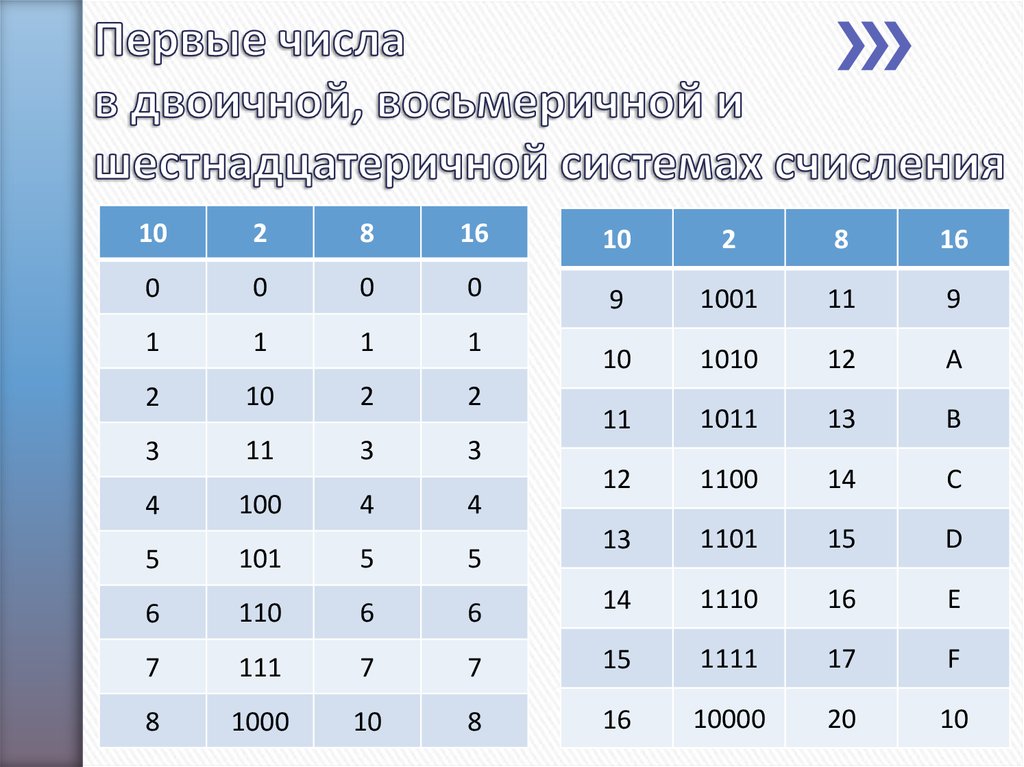

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни. 

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 11011 ₂   —  число в двоичной системе счисления.

Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием ₂, например:

  2   1   0

101 ₂ =1⋅2 ² +0⋅2 ¹ +1⋅2 ⁰ .

 В десятичной системе счисления это число будет выглядеть так:

  2   1   0 

110 ₂ =4+0+1=5 .

 Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2  до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём десятичное число 15 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

 

 

15	2
-14	7	2
1	-6	3	2
	1	-2	1
		1

 

 

Получили 15 ₁₀ =1111 ₂.

 

Попробуем считать в двоичной системе:
 0 – это ноль
 1 – это один (и это предел разряда)
 10 – это два
 11 – это три (и это снова предел)
 100 – это четыре
 101 – пять
 110 – шесть
 111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную.

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные. 

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1567 = 1000 + 500 + 60 + 7

Можно пойти еще дальше и разложить так:

  3   2   1   0

1567 ₁₀= 1 * 10³ + 5 * 10² + 6 * 10¹ + 7 * 10⁰

Посмотрите на эту запись внимательно. Здесь цифры 1, 5, 6 и 7 — это набор цифр из которых состоит число 1567. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

 6   5   4   3   2   1   0

1000101₂ = 1*2⁶ + 0*2⁵ + 0*2⁴ + 0*2³ + 1*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2⁶ + 0*2⁵ + 0*2⁴ + 0*2³ + 1*2² + 0*2¹ + 1*2⁰ = 64 + 0 + 0 + 0 + 4 + 0 + 1 = 69₁₀

Т.е. число 10001001 по основанию 2 равно числу 69 по основанию 10. Записать это можно так:

1000101₂ = 69₁₀

Восьмеричная система счисления

Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

 000 – 0
 001 – 1
 010 – 2
 011 – 3
 100 – 4
 101 – 5
 110 – 6
 111 – 7

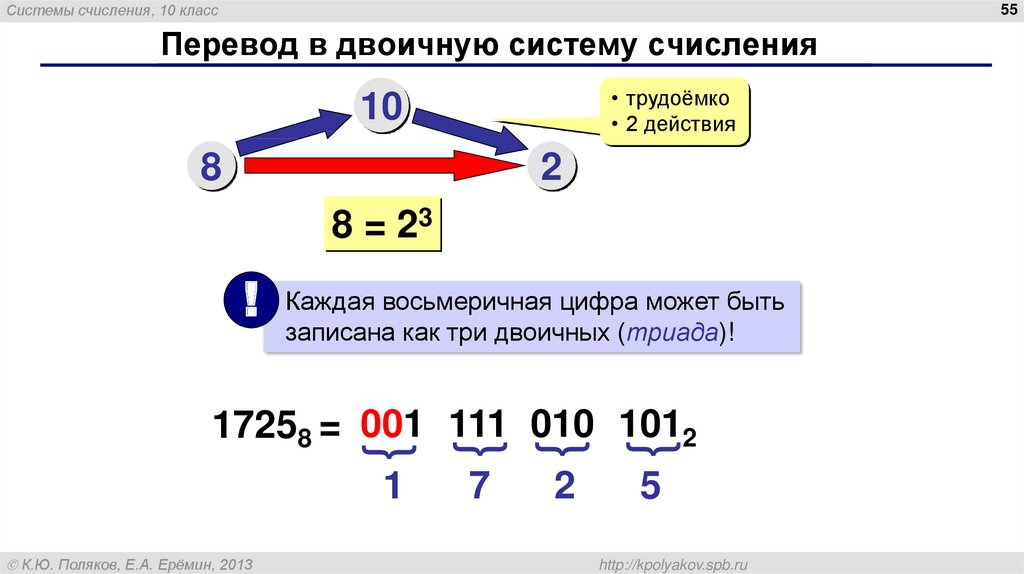
Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки (триады) и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:

2²2¹2⁰

 4   2  1                                                4 2 1  4 2 1   4 2 1     (Складываем цифры над единицами)

1110101₂ = 1 011 101 = 001 110 101 = 1 6 5 = 165₈

Т. е число 1011101 в двоичной системе счисления равно числу 165 в восьмеричной системе счисления. Или 1110101₂ = 165₈.

Обратный перевод. Допустим, требуется перевести число 103₈ (не заблуждайтесь! 100 в восьмеричной системе – это не 103 в десятичной) в двоичную систему счисления.

2²2¹2⁰

 4   2  1                        4 2 1   4 2 1   4 2 1      (1=421, 0=421, 3=42+1  зелёные – 0, красные – 1)

103₈ = 1 0 3 = 001 000 011 = 001000011 = 1000011₂ 

Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:

  2    1    0

672₈ = 6 * 8² + 7 * 8¹ + 2 * 8⁰ = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 442₁₀
      2    1    0

100₈ = 1 * 8² + 0 * 8¹ + 0 * 8⁰ = 64₁₀

Шестнадцатеричная система счисления

 

Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел.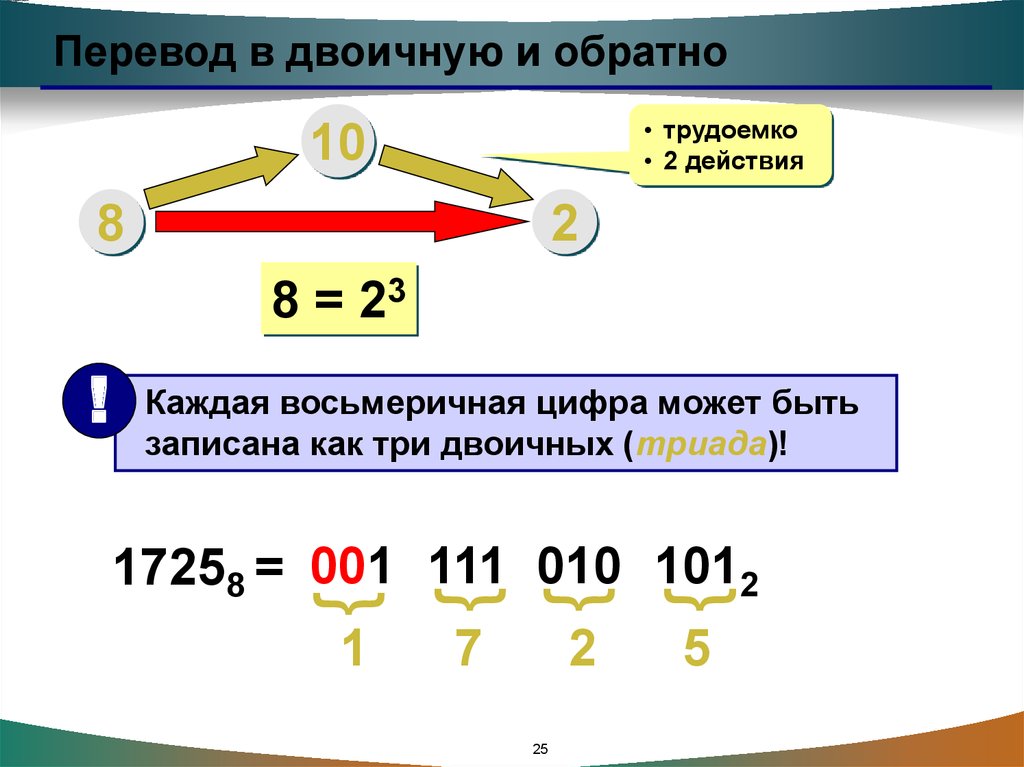 При шестнадцатеричной записи числа получаются более компактными.

В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15). 

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда (тетрады), начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:

Например:

2³2²2¹2⁰                  

 8  4   2   1                           8 4 2 1  8 4 2 1    8 4 2 1      (Складываем цифры над единицами)

 _11011010101 = 0110 1101  0101 = 6 13 5 = 6D5

Если потребуется, то число 6D5 можно перевести в десятичную систему счисления следующим образом (D следует заменить на соответствующее данному символу число в десятичной системе счисления – это 13):

   2    1    0

6D5₁₆ = 6 * 16² + 13 * 16¹ + 5 * 16⁰ = 6 * 256 + 208 + 5 = 1749₁₀

Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.

1    0

FF₁₆ = 15 * 16¹ + 15 * 16⁰ = 240 + 15 = 255 

255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние

 

 

 

Конвертер систем счисления, перевод двоичной, десятичной и других

С давних времен люди использовали разные способы и методы счета. Они постоянно менялись и совершенствовались, адаптировались к текущим потребностям. Сегодня общепринята во всем мире десятичная система счисления, наряду с ней используются и другие. Самыми востребованными, в основном в программировании, являются двоичная, восьмеричная и шестнадцатеричная. Быстрый перевод разных чисел из одной системы в другую сделает Онлайн конвертер систем счисления.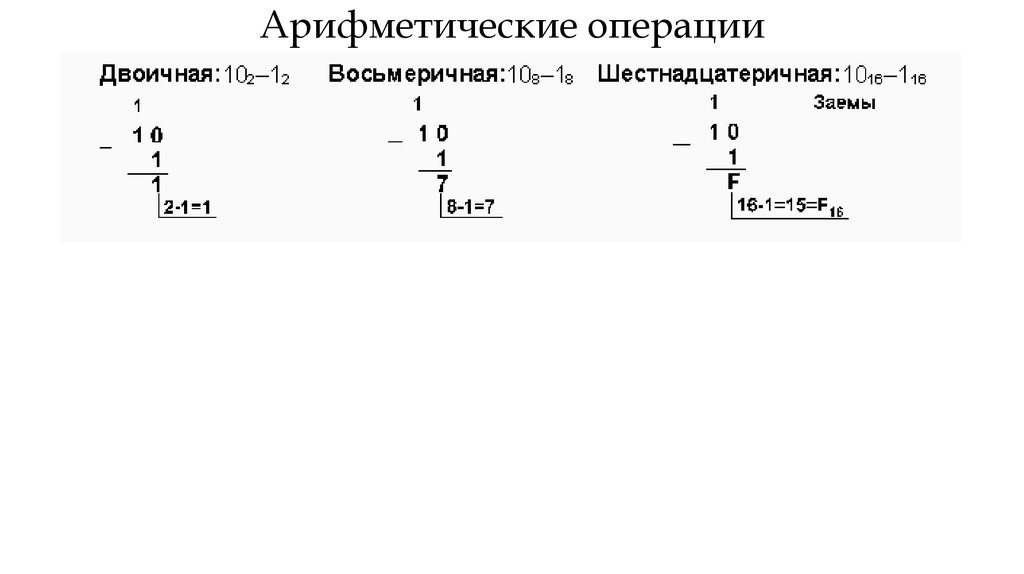

Содержание

1. Первые системы счисления
2. Счет в Древнем Вавилоне
3. Современные система счисления
4. Десятичная система
5. Двоичная (бинарная) система
6. Алгоритм перевода из десятичной системы в двоичную и наоборот
7. Из десятичной в двоичную
8. Из двоичной в десятичную
9. Восьмеричная система
10. Шестнадцатеричная система

Первые системы счисления

С тех пор, как между людьми появились торговые отношения, возникла необходимость счета. Первоначально это была единичная система в виде зарубок на палке или камне. Дальше она совершенствовалась и становилась сложнее. Причем устно посчитать было намного проще, чем как-то записать эту информацию. Однако со временем появились знаки, с помощью которых их можно было записать.

Самая примитивная система счисления — единичная. В ней всего один символ. Все последовательные числа образуются его простым повторением.

Главным образом, это была непозиционная система счисления, где каждому числу соответствовал свой символ.

Непозиционная система построена по такому принципу — в ней есть отдельные символы для нескольких чисел, а затем последовательные символы для их кратных. Числа создаются путем добавления дополнительных символов.

 

Еще в третьем тысячелетии до нашей эры в Египте для обозначения чисел стали использовались иероглифы. Примерно в то же время в Древней Греции для записи чисел использовали буквы своего алфавита. Причем это была первая буква от названия цифры:

 

знак	значение	название
Ι	1	ἴος «иос»
Π	5	πέντε «пенте»
Δ	10	δέκα «дека»
Η	100	ἑκατόν «хекатон»
Χ	1 000	χίλιοι «хилиой»
Μ	10 000	μύριοι «мюриой»

Свои записи чисел были разработаны и в Древнем Риме. Уже тогда Были сформулированы правила для создания новых чисел и проведения с ними разных операций — прибавления, сложения, убавления, деления и т.д. Так появились первые системы счисления.

Система счисления — это способ написания чисел и набор правил, которые позволяют нам выполнять с ними разные математические операции.

Для каждой системы существует набор символов, что используются для записи чисел. Эти знаки — цифры. Их можно складывать различными способами, создавая бесконечное количество комбинаций.

Счет в Древнем Вавилоне

Особого внимания заслуживает достижение ученых Вавилона. Еще четыре тысячи лет назад, они создали первую в мире позиционную систему счисления. Она базировалась на использовании двух значков, где вертикальный клин — 1, а горизонтальный — 10:

 

Как была построена запись чисел хорошо видно на рисунке.

В шестидесятеричной системе в первый разряд входили числа от одного до шестидесяти  — это была основа.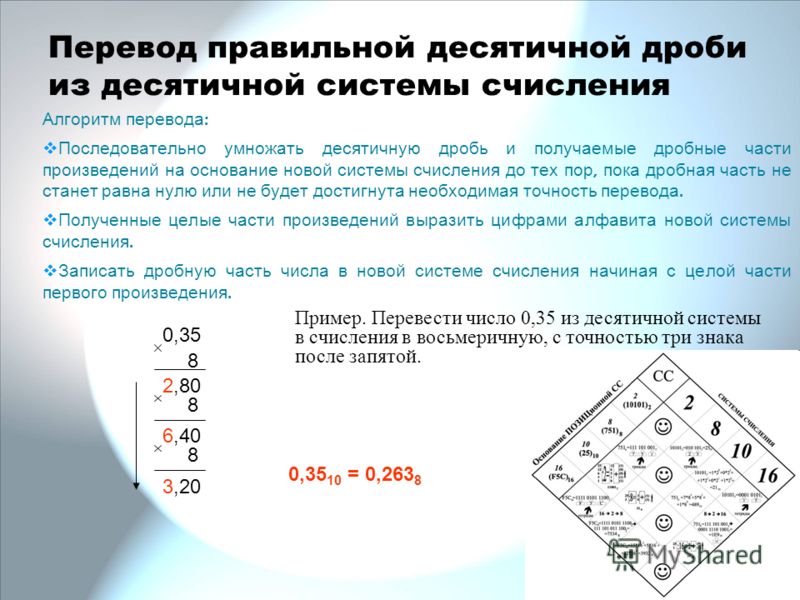 60 единиц из первого разряда образовывали единицу второго разряда, 60 единиц из второго разряда — единицу третьего и т. д. Этот метод счета был разработан на основе шумерской двенадцатеричной системы.

Шестидесятеричная система настолько универсальная и точная, что мы успешно используем ее и сегодня. Ведь именно по ней вавилонские ученые систематизировали время- и летоисчесление. Их год составлял 360 дней, а час 60 минут.

Современные система счисления

Сегодня все мы пользуемся позиционными системы счисления. Их характерными особенностями являются:

1. Использование ограниченного количества цифр, которые имеют последовательные значения 0, 1, 2,… Это никоим образом не ограничивает размер записываемых чисел.
2. Каждой позиционной системе присваивается определенное значение, которое мы называем базой. Количество цифр равно базовому значению. Для десятичной системы у нас есть набор из 10 цифр, потому что база равна 10. В шестеричной системе цифр будет 6 {0, 1, 2, 3, 4, 5}. В системах с основанием больше 10 нужно больше цифр, чем определено для десятичной системы. Эта проблема решается просто — для записи чисел комбинируют цифры и буквы латинского алфавита. Например, для двенадцатеричной системы берут двенадцать символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Цифра A равна 10, а цифра B =11.
3. Значение цифры в записи зависит от ее положения, отсюда и название « позиционная система». Каждой из них присваивается вес. Он равен последовательным базовым мощностям, отсчитываемым справа.
4. Значение числа в обозначении позиции рассчитывается как сумма произведений цифр на веса их позиций.

Десятичная система

Для большинства из нас естественным способом представления чисел является десятичная система. В ней мы учимся считать с детства. Она является основой преподавания математики в школах, ее мы используем в повседневной жизни. Для записи чисел в десятичной системе используют 10 символов: ноль, один, два, три, четыре, пять, шесть, семь, восемь и девять. Они обозначены как: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Отсюда и название.

Десятичное представление счета было создано много веков назад, возможно, потому, что у нас десять пальцев. Эта система позволяет не только просто и рационально представить любое число, независимо от его размера, но и легко выполнять все арифметические операции. Десятичная система является самой распространенной из всех, которые использовались в истории.

Двоичная (бинарная) система

С развитием компьютерных технологий оказалось, что для технических устройств слишком сложно использовать такое большое количество знаков. Это привело к практическому применению систем счета, отличных от десятичной. В информатике первое место занимает двоичная система счисления. Также известная как бинарная, реже ее называют «ноль-один»,

В двоичном счете используют только два цифровых значения «0» и «1». Такой набор является оптимальным для записи любого числа.

Первое число — 0 (ноль), оно не отличается от других систем,

Следующее — 1 (один).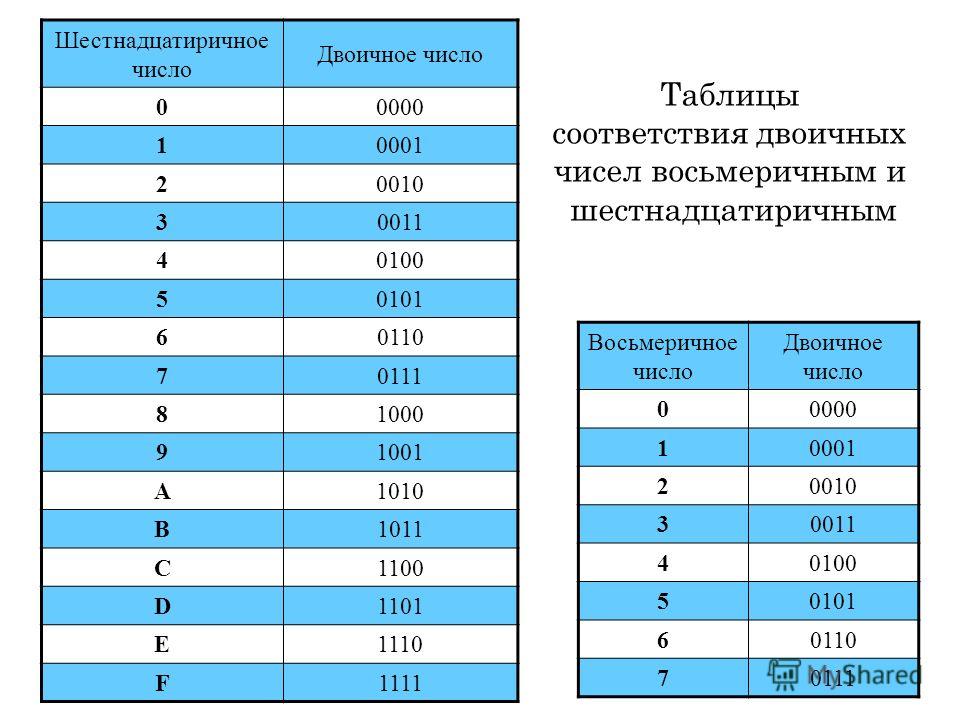 В двоичной системе это число тоже существует, оно так и записывается — 1. Дальше по счету идет — 2 (два). Такой цифры при двоичном счете нет, поэтому добавляем еще одну позицию, которая перемещается вправо, она равна нулю. Таким образом, число 2 в десятичной форме имеет записывается, как «10».

Последующие числа из десятичной системы в двоичной выглядят так:

• 3 — записываем, как «11»,
• 4 — «100»,
• 5 — «101»,
• 6 — «110»,
• 7 — «111»,
• 8 — «1000»,
• 9 — «1001» и т.д.

Принцип все время один и тот же. Двоичный знак (0 или 1) называется битом. Название bit происходит от английского термина Binary Digit. Отсюда и второе название — бинарная система. Хотя в ней присутствуют только 0 и 1, любое число можно записать в двоичном формате. Когда нужен быстрый перевод, чтобы избежать ошибок, используйте конвертер систем счисления.

Алгоритм перевода из десятичной системы в двоичную и наоборот

Перевести числа из двоичной системы в десятичную или из десятичной в двоичную совсем не сложно.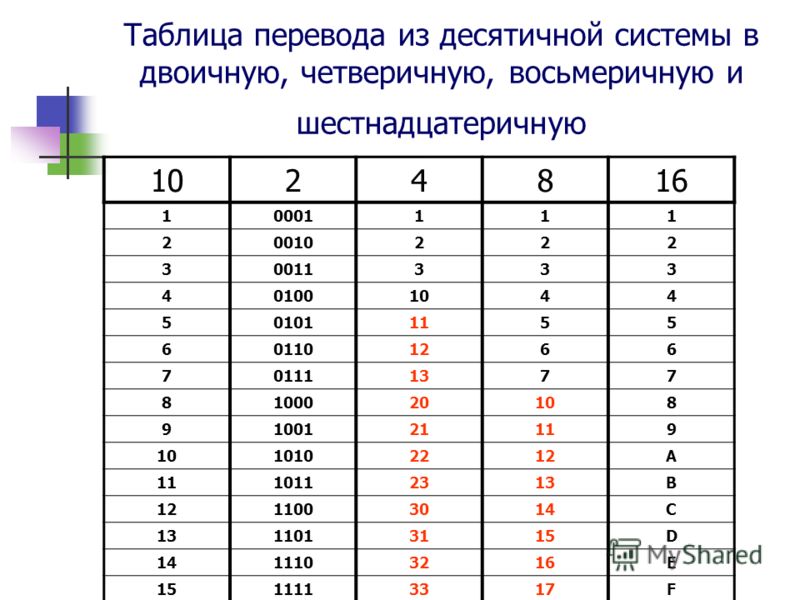 Здесь главное понять по какому алгоритму проводить действия. Объясним на примере числа «29», которое мы уже использовали.

Из десятичной в двоичную

Для такого перевода можно использовать один из двух способов: метод деления на основание (в данном случае 2) или метод подбора степеней (тоже для двойки).

Метод деления визуально более понятный и поэтому используется чаще. Для перевода десятичное число делим обычным способом, «в столбик». на основание.

Для двоичной системы основание число 2, поскольку используем только два символа «0» и «1».

Если в результате деления есть остаток, то ставим «1», если делится без остатка, то ставим «0». Полученное таким образом двоичное число записываем от последнего результата к первому — справа-налево. Как это сделать хорошо видно на рисунке.

Для того чтобы перевести десятичное число в двоичное по методу подбора степеней, необходимо расписать ряд степени двойки и суммировать их.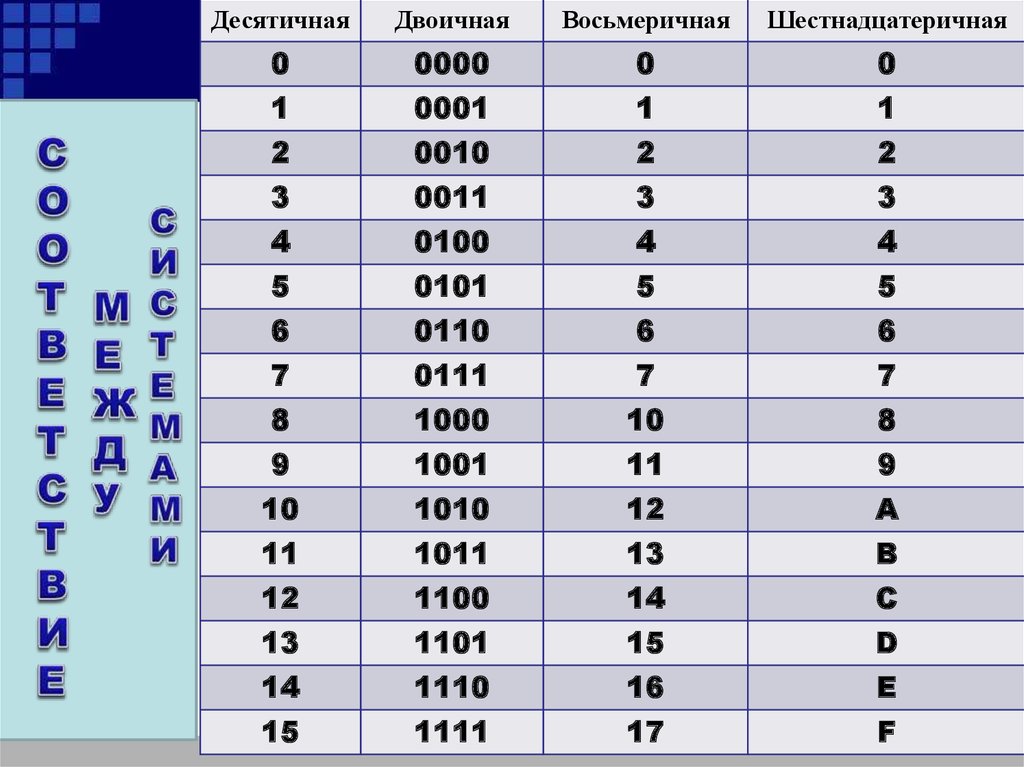 В результате должно получиться исходное число. При этом если степень используем, то ставим «1», если не используем, то «0». Рассмотрим на конкретном примере «29». Распишем степени: 2⁰= 1, 2¹= 2, 2²= 4, 2³= 8, 2⁴= 16.

Суммируем от наибольшего значения к наименьшему — 16 + 8 + 4 + 2 + 1

В результате у нас получится 31. Как видим, двойка здесь лишняя, ее мы не используем. Теперь вместо числа, которое мы берем запишем «1», а которое нам не подошло «0».

• 16 это 1;
• 8 это 1;
• 4 это 1;
• 2 это 0;
• 1 это 1

29 в двоичной системе — 11101. Если надо переводить много чисел, используйте конвертер систем счисления.

Чтобы упростить возведение двойки в степень, мы сделали для вас таблицу.

Из двоичной в десятичную

Берем двоичное число 11101. Расписываем сумму степеней. Так как у нас 5 символов, то самая большая степень это 2⁴, поскольку есть нулевая. Умножаем каждую цифру двоичного числа на соответствующую степень (см. рисунок).

1×2⁴ + 1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 16 + 8 + 4 + 0 + 1 = 29

Для удобства приведем таблицу, но проще использовать конвертер систем счисления.

Восьмеричная система

В восьмеричной системе используют восемь цифр: 0, 1, 2, 3, 4, 5, 6 и 7 — отсюда и название. Она также позиционная и работает по тому же принципу, что и десятичная. Это означает, что когда цифра достигает своего максимального значения, то дальнейший счет идет путем увеличения позиции.

Объясним на примере. Давайте преобразуем последовательные числа и посмотрим, в чем разница.

• Число ноль (0) одинаково в обеих системах.
• То же самое и для единицы (1), двойки (2), тройки (3) и т.д. вплоть до семи (7).

Дальше ситуация усложняется, на очереди еще один номер — восемь. Восьмеричная система не знает такой цифры. Здесь срабатывает такой же принцип, как для двойки в двоичной. Таким образом,

число восемь «8» по десятичной системе в восьмеричной будет записано «10»,

• «9» — как «11»,
• «10» — как 12,
• «11» — как «13»,
• «12» — как «14» и т.д.

Это легко проверить, используя метод позиционирования. Составляем уравнение для «14» по восьмеричной —

1 × 8 + 4 × 1 = 8+4 = 12 по десятичной.

Как переводить из десятичной системы в восьмеричную и шестнадцатеричную хорошо видно на рисунке.

Быстро и без ошибок с таким переводом справится наш конвертер систем счисления.

 

Шестнадцатеричная система

Позиционная система, в которой для записи чисел используются цифры и буквы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. От других систем она отличается самой короткой записью чисел. Таким значением легче манипулировать, и он потребляет меньше памяти. Например, число

• «12» в десятеричной,
• «1100» в двоичной,
• «14» в восьмеричной,
• «С» в шестнадцатеричной.

В информатике шестнадцатеричная система используется, например, для адресации ячеек памяти устройствами или для кодирования цветов, используемых на веб-сайтах.

Как следует из названия, в основе этой системы лежит число 16. Поскольку она позиционная, то в обозначении числа каждая позиция имеет значение в шестнадцать раз больше, чем предыдущая. По логике чисел должно быть шестнадцать. Первые десять, как обычно — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Дальше для односимвольной маркировки используют буквы алфавита:

• 10 — А,
• 11 — В,
• 12 — С,
• 13 — D,
• 14 — E,
• 15 — F.

«16», по той же логике, что и в предидущих системах у нас будет «10».

Принято, что если в начале числа есть буква, перед ней следует ставить ноль, здесь он не имеет никакого значения — это является чисто формальным.

Чтобы избежать путаницы при записи числового ряда, принято писать «h» после каждого шестнадцатеричного числа. Последовательность будет выглядеть так:

0h, 1h, 2h, 3h, 4h, 5h, 6h, 7h, 8h, 9h, 0Ah, 0Bh, 0Ch, 0Dh, 0Eh, 0Fh, 10h, 11h, 12h, 13h, 14h, 15h, 16h, 17h, 18h, 19h, 1Ah, 1Bh, 1Ch, 1Dh, 1Eh, 1Fh, 20h, 21h, 22h, и т.д., что почти похоже на десятичную систему, за исключением того, что есть еще шесть цифр. Также важен способ произношения шестнадцатеричных чисел. Например, число 212h читается не «двести двенадцать», а «два-один-два» и соответствует 530 в десятичном счете.

Кроме этих основных используются и многие другие системы счисления — троичная, четверичная, пятеричная, семеричная и т.д. Какие символы для записи чисел используются для них указано в таблице.

Быстро конвертировать из одной в другую вы можете используя конвертер систем счисления.

Как переводить двоичные числа в другие системы счисления вы узнаете из видео

Читайте далее:

Онлайн конвертер длины, перевод всех систем измерения, метрическая, британо-американская, старорусская, морская, астрономическая, типографская

Онлайн конвертер объема, единицы и системы измерения, конвертация величин объема

Онлайн конвертер площади, единицы измерения площади в разных системах, их быстрый перевод

Онлайн конвертер массы, современные системы и единицы измерения массы

Конвертер температур, перевод градусов Цельсия, Фаренгейта, Кельвина, Реомюра

Онлайн конвертер плотности, формулы расчета и единицы измерения

Как преобразовать 2019 из шестнадцатеричной в восьмеричную

Что такое 2019 шестнадцатеричный в восьмеричном? 2019 из шестнадцатеричного в восьмеричное — это 20031. Здесь мы покажем вам, как записать 0x2019 в восьмеричном формате и как преобразовать 2019 из шестнадцатеричного в 8-ричный.

Число:

От: двоичный [с основанием 2] троичный [с основанием 3] четверичный [с основанием 4] пятеричный [с основанием 5] десятеричный [с основанием 6] семеричный [с основанием 7] восьмеричный [с основанием 8] ненарочный [с основанием 9] десятичный [ с основанием 10] одиннадцатеричный [с основанием 11] двенадцатеричный [с основанием 12] трехдесятеричный [с основанием 13] четырехдесятичный [с основанием 14] пятидесятичный [с основанием 15] шестнадцатеричный [с основанием 16] семидесятеричный [с основанием 17] октодесятеричный [с основанием- 18] шестнадцатеричный [основание-19] десятичный [по основанию-20] недесятеричный [по основанию-21] двенадцатеричный [по основанию-22] трехдесятеричный [по основанию-23] тетрадесятичный [по основанию-24] пятидесятеричный [по основанию-25] тройничный [по основанию-30] двенадцатеричный [по основанию-32]

К: двоичный [с основанием 2] троичный [с основанием 3] четверичный [с основанием 4] пятеричный [с основанием 5] десятеричный [с основанием 6] семеричный [с основанием 7] восьмеричный [с основанием 8] ненарочный [с основанием 9] десятичный [ с основанием 10] одиннадцатеричный [с основанием 11] двенадцатеричный [с основанием 12] трехдесятеричный [с основанием 13] четырехдесятичный [с основанием 14] пятидесятичный [с основанием 15] шестнадцатеричный [с основанием 16] семидесятеричный [с основанием 17] октодесятеричный [с основанием- 18] шестнадцатеричный [основание-19] десятичный [по основанию-20] недесятеричный [по основанию-21] двенадцатеричный [по основанию-22] трехдесятеричный [по основанию-23] тетрадесятичный [по основанию-24] пятидесятеричный [по основанию-25] тройничный [по основанию-30] двенадцатеричный [по основанию-32]

20031 ₈

В системе счисления мы знаем, что шестнадцатеричная система счисления — это шестнадцатеричная, а восьмеричная — восьмеричная. Чтобы преобразовать шестнадцатеричное число 2019 в восьмеричное, выполните следующие действия:

Для этого сначала преобразуйте шестнадцатеричное число в десятичное, а затем полученное десятичное число в восьмеричное

92 и так далее справа налево
1. Сложите все произведения, полученные на шаге 1, чтобы получить десятичный эквивалент заданного шестнадцатеричного значения.
2. Затем разделите десятичное значение, полученное на шаге 2, на 8, учитывая частное и остаток.
3. Продолжайте делить частное на 8, пока не получите нулевое частное.
4. Затем просто запишите остатки в обратном порядке, чтобы получить восьмеричный эквивалент десятичного числа.

Сначала преобразовать 2019 ₁₆ into decimal, by using above steps:

= 2019 ₁₆
= 2 × 16 ³ 0 × 16 ² 1 × 16 ¹ 9 × 16 ⁰
= 8217 ₁₀

Теперь нам нужно преобразовать 8217 ₁₀ в восьмеричное число

8217/8 = 1027 с остатком 1
1027/8 = 128 с остатком 3
128/8 = 16 с остатком 0
16/8 = 2 с остатком 03 0 2 / 8 = 0 с остатком 2

Тогда просто запишите остатки в обратном порядке, чтобы получить ответ, Шестнадцатеричное число 2019converted to octal is therefore equal to :

20031

Here are some more examples of hexadecimal to octal conversion

• 201A hexadecimal to octal
• 201B hexadecimal to octal
• 201C hexadecimal to octal
• 201D hexadecimal to octal

Десятичный 2019 в восьмеричном | работа, решение

Как написать восьмеричное число 2019?

2019 записывается как 3743 в восьмеричном формате

Преобразование из/в десятичное число в двоичное.