Шестнадцатиричная система счисления — Практическая электроника
В прошлой статье мы с Вами разбирали двоичную и двоично-десятичную систему счисления. С помощью калькулятора Windows мы переводили числа из двоичной системы в десятичную. Представьте себе, что нам надо перевести число из десятичной в двоичную систему счисления. Такое безобидное число, как 9999 в двоичной системе будет выглядеть уже как 10 0111 0000 1111. Не очень то и удобно, так ведь? С такими числами работает только компьютер и другие цифровые девайсы.
Системы счисления
Если подробнее вдаваться в компьютерные системы, то комп даже на знает, что такое единичка, а что такое ноль. Это для нас понятно, что единичка — это «ДА» , «ИСТИНА», а ноль это — «НЕТ», «ЛОЖЬ». В компьютерах, микропроцессорах, микроконтроллерах да и во всех цифровых микросхемах используются другие понятия единицы и нуля. Напряжение есть и оно соответствует норме — это ЕДИНИЧКА, напряжение маленькое или его нет — это НОЛЬ. Именно так и оперируют цифровые микросхемы и вся сложнейшая цифровая электроника ;-). ЕДИНИЦА И НОЛЬ! 🙂
Именно так и оперируют цифровые микросхемы и вся сложнейшая цифровая электроника ;-). ЕДИНИЦА И НОЛЬ! 🙂
А вам слабо написать программу на единичках и нулях? Я думаю, это не под силу даже самому наяренному программеру в мире. Люди недолго думали и для удобства написания чисел придумали сначала восьмеричную систему счисления, а потом и шестнадцатеричную. Если помните, в двоичной системе счисления только два знака: 1 и 0. В десятичной — 10 знаков: 0 1 2 3 4 5 6 7 8 9, восьмеричной системе счисления используются только 8 знаков: 0 1 2 3 4 5 6 7. В шестнадцатеричной системе счисления знаков целых 16 штук! Чтобы не мудрить, взяли первые 9 знаков от десятичной системы счисления, а остальные от английского алфавита. Итого — 0 1 2 3 4 5 6 7 8 9 A B C D E F — ровненько 16 знаков.
Почему раньше не использовали десятичную систему вместо восьмеричной? Ведь в десятичной было на два знака больше? Все упиралось в байты. Как вы помните, 8 бит — это один Байт. Именно поэтому было удобно использовать восьмеричную и шестнадцатеричную системы счисления, кратную восьмерке, чем десятеричную. В последнее время самая крутая считается шестнадцатеричная система счисления. Именно она в большинстве используется в микроконтроллерах и в других цифровых микросхемах.
Как вы помните, 8 бит — это один Байт. Именно поэтому было удобно использовать восьмеричную и шестнадцатеричную системы счисления, кратную восьмерке, чем десятеричную. В последнее время самая крутая считается шестнадцатеричная система счисления. Именно она в большинстве используется в микроконтроллерах и в других цифровых микросхемах.
Перевод из одной системы счисления в другую
Как же нам переводить числа из одной системы счисления в другую? Здесь все просто, следуем примеру из второй главы, где написано, как использовать калькулятор Windows для перевода чисел из десятичной системы в двоичную. С помощью этого калькулятора мы также можем переводить числа из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и обратно. Запускаем наш калькулятор, пишем от балды число «123» в десятичной системе счисления. Для этого ставим маркер на «Dec» и для красоты «1 байт».
Для того, чтобы перевести это число в двоичную систему счисления, ставим маркер на «Bin» и получаем число «123» в двоичной системе счисления.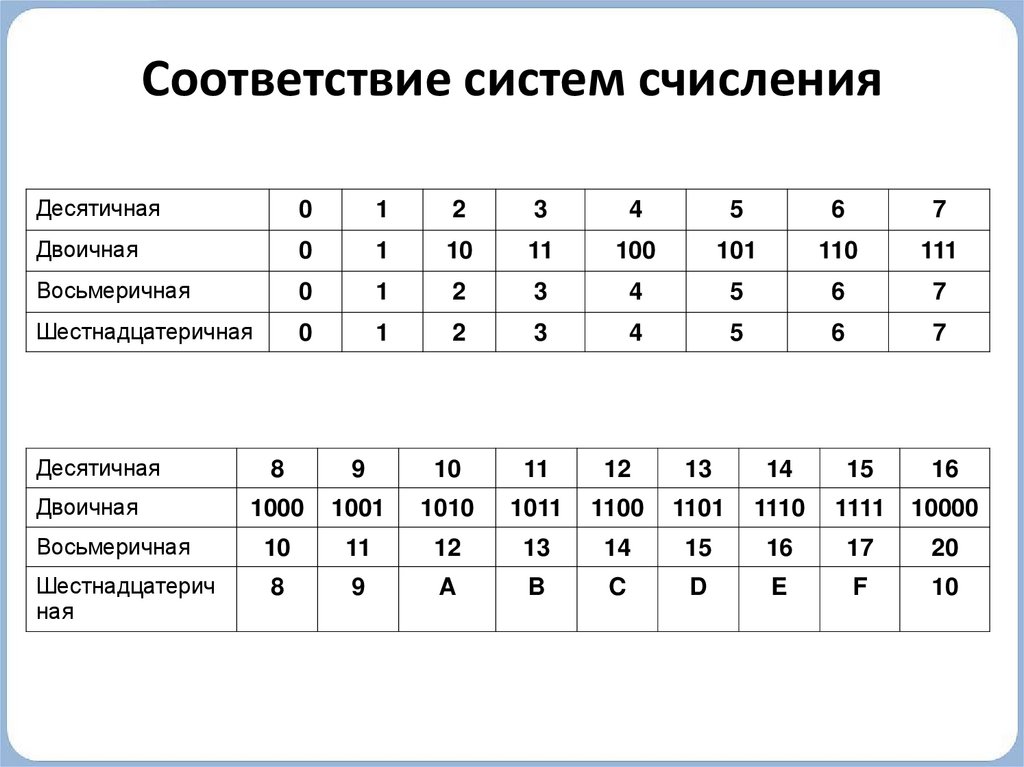
Для перевода в восьмеричную систему ставим маркер на «Oct».
Ну и для перевода в шестнадцатеричную систему ставим маркер на «Hex».
Все операции взаимозаменяемы. Это значит, что мы можем перевести число из двоичной в шестнадцатеричную, из восьмеричной в двоичную и так далее. Чтобы не спутать системы счисления и знать, какое число записано, после каждого записанного числа снизу ставится его индекс системы счисления. Например:
7ВС16 — значит число записано в шестнадцатеричной системе счисления
10112 — в двоичной системе
4578 — в восьмеричной системе
998510 — в десятеричной системе.
Перевод чисел из одной системы счисления в другую
В современной вычислительной технике
информация чаще всего кодируется с помощью последовательности сигналов всего
двух видов: включено или невключено, намагничено или ненамагничено, высокое или
низкое напряжение и т. Система счисления — совокупность приемов наименования и обозначения чисел. Системы счисления разделяются на две группы: позиционные и непозиционные. Позиционной называется система счисления, в которой значение цифры зависит от ее места (позиции) в ряду цифр, обозначающих число. Системы, не обладающие этим свойством, называются непозиционными (римская система счисления). Основанием позиционной системы счисления называется число цифр, которое используют при записи. В ЭВМ часто используется восьмеричная и шестнадцатеричная системы счисления. В восьмеричной системе счисления числа записываются с помощью восьми цифр (0 1 2 3 4 5 6 7). Сама восьмерка записывается двумя цифрами: 10. Для записи чисел в шестнадцатеричной системе необходимо уже располагать шестнадцатью различными символами, используемыми как цифры: 10-я: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16-я: 0 1 2 3 4 5 6 7 8 9 А В С D E F Пример 1. Правило: Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание и т.д. до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего. 46 = 1011002. Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления. 672 = 12408. Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления. 934 = 3А616. Пример 4. Переведем в двоичную систему счисления положительную десятичную дробь 0.3. Правило: Чтобы перевести положительную
десятичную дробь в двоичную, нужно дробь умножить на 2. Целую часть
произведения взять в качестве первой цифры после запятой в двоичной дроби, а
дробную часть вновь умножить на 2.
Дробная часть 0,6 уже была на втором шаге вычислений. Поэтому вычисления будут повторяться. Следовательно в двоичной системе счисления число 0,3 представляется периодической дробью: 0,3 = 0,0(1001)2. Пример 5. Переведем в двоичную систему счисления положительную десятичную дробь 0,625. 0,625 = 0,1012. Замечание: Перевод десятичного числа в двоичную систему счисления проводится отдельно для его целой и дробной части. Пример 6. Переведем в десятичную систему счисления двоичное число 1011,011. Правило: Чтобы перевести число из двоичной
системы в десятичную систему счисления, нужно двоичное число представить в виде
суммы степеней двойки с коэффициентами-цифрами и найти эту сумму. 1011,0112 = 1•23+0•22+1•21 +1•20+0•2–1+1•2–2+1•2–3 =1•8+1•2+1+1•(1/2)2+1•(1/2)3 = 8+2+1+1/4+1/8 = 11,3751011,0112 = 11,37510. Пример 7. Переведем в десятичную систему счисления восьмеричное число 511. 5118 = 5•82+1•81+1•80 =5•64+1•8+1 = 329 5118 = 32910. Пример 8. Переведем в десятичную систему счисления шестнадцатеричное число 1151. 1•163+1•162+5•161+1•160 = 1•4096+1•256+5•16+1 = 4096+256+80+1 = 4433. 115116 = 443310. Пример 9. Переведем двоичное 1100001111010110 число в восьмеричную форму. Правило: Для преобразования двоичного
числа в восьмеричное необходимо двоичную последовательность разбить на группы
по три цифры справа налево и каждую группу заменить соответствующей
восьмеричной цифрой. Переведем наше число в восьмеричную и шестнадцатеричную системы: 1100001111010110 1 100 001 111 010 110 1100 0011 1101 0110 1 4 1 7 2 6 С 3 D 6 Аналогично осуществляется и обратное преобразование: для этого каждую цифру восьмеричного или шестнадцатеричного числа заменяют группой из трех или четырех цифр. Например: A B 5 1 1 7 7 2 0 4 1010 1011 0101 0001 1 111 111 010 000 100 |
Почему шестнадцать так сладко?
Почему шестнадцать так сладко?
Давным-давно люди разработали систему счета, основанную на десятках, по очень веской причине.
Но эта система не так хорошо работает для компьютеров. Так была изобретена другая система: шестнадцатеричная, или «шестнадцатеричная».
«Hexadeci-» означает 16. Вместо 10 цифр (от 0 до 9) шестнадцатеричный код содержит 16 цифр (от 0 до 15). Hex использует буквы для цифр старше 9:
А = 10
В = 11
С = 12
Д = 13
Е = 14
F = 15
Вместо преобразования данных космического корабля из двоичных в десятичные числа инженеры преобразуют двоичные числа в шестнадцатеричные.
С какой стати им это делать?
Ну, не всякая информация, которая поступает в компьютер или выходит из него, на самом деле является числом. Иногда это действительно ИСТИННО или ложно, включено или выключено или является одним из «множественных вариантов». Иногда информация представляет собой слово. Получается, что hex и бинарник созданы друг для друга.
Чтобы нам было легче говорить, вот несколько терминов.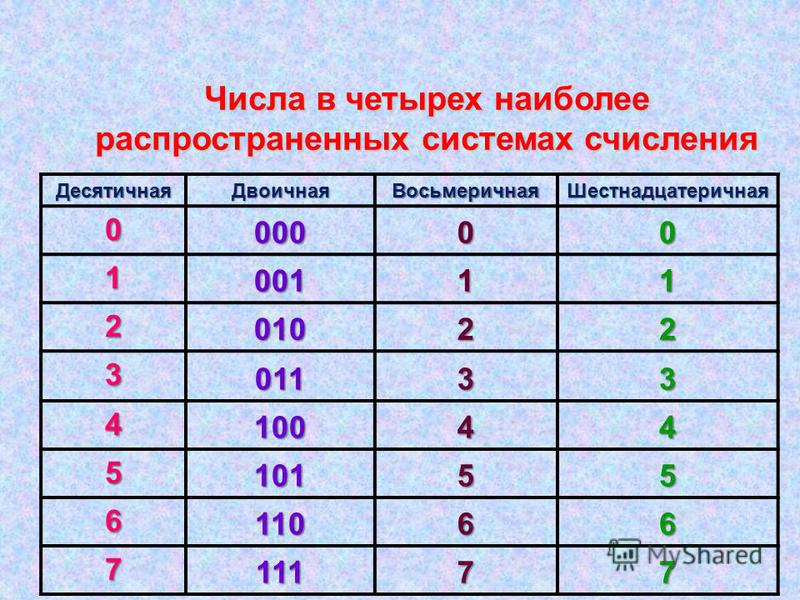 Одна двоичная цифра называется бит . Четыре бита, сгруппированные вместе, называются полубайтом . И два байта составляют (что еще?) байт!
Одна двоичная цифра называется бит . Четыре бита, сгруппированные вместе, называются полубайтом . И два байта составляют (что еще?) байт!
Если вы расположите биты пополам всеми возможными способами, вы получите только 16 вариантов.
Видишь? Мы знаем, что шестнадцатеричное число 9 может только быть 1001 в двоичном виде. И шестнадцатеричный номер A может быть , только может быть 1010.
Одна двоичная цифра называется бит . Четыре бита, сгруппированные вместе, называются полубайтом . И два байта составляют (что еще?) байт!
Шестнадцатеричный формат оказался отличным способом сжатия данных. Вы можете поместить четыре отдельных фрагмента информации в одну шестнадцатеричную цифру.
Таким образом, космический инженер может сказать, что в конкретном полубайте первый бит означает, что переключатель нагревателя установлен в положение ВКЛ (если 1) или ВЫКЛ (если 0).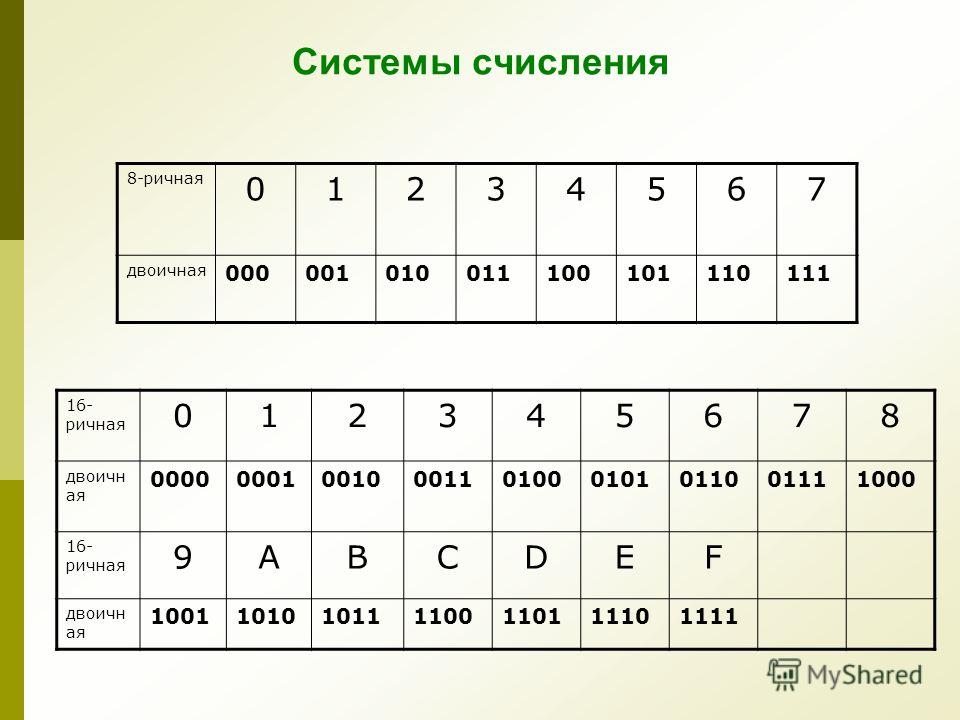 Второй бит может означать, что частица пыли попала (1) или не попала (0) в крошечный датчик. И так далее.
Второй бит может означать, что частица пыли попала (1) или не попала (0) в крошечный датчик. И так далее.
Десятичные числа не так удобны. Например, посмотрите на эти:
| 9999 | 1001 1001 1001 1001 | 39 321 |
| АОАО | 1010 0000 1010 0000 | |
| АААА | 1010 1010 1010 1010 | 43 690 |
Что число 39 321 говорит вам о двоичном числе, равном ему? Без специального калькулятора мало что перевести! Но шестнадцатеричное число 9999 точно говорит вам, какие биты являются единицами, а какие — нулями!
Итак, вы видите, математические системы очень похожи на языки.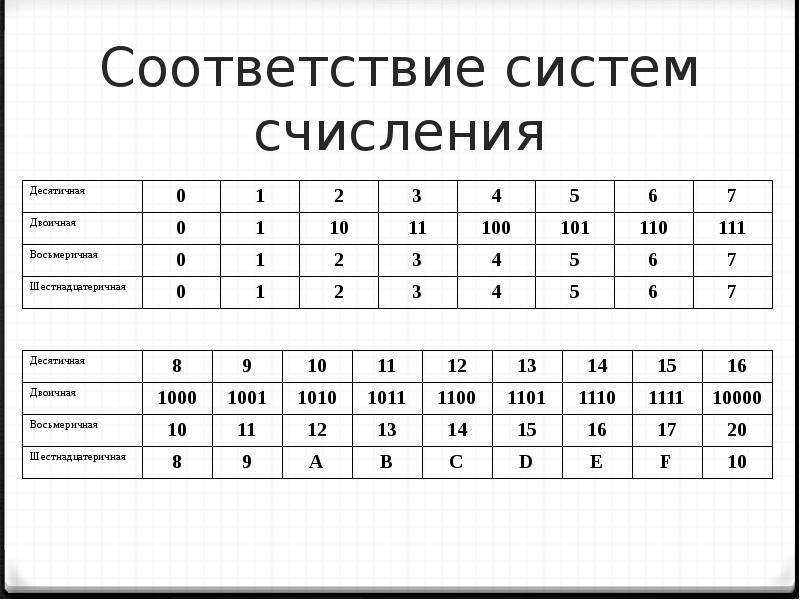 Мы изобретаем их для наших целей. И именно на языке шестнадцатеричных чисел сейчас основаны почти все компьютеры и космические корабли!
Мы изобретаем их для наших целей. И именно на языке шестнадцатеричных чисел сейчас основаны почти все компьютеры и космические корабли!
Если вам это понравилось, вам может понравиться:
Исследование электромагнитного спектра
Галерея изображений технологий НАСА
Добро пожаловать в Space Place Live!
Шестнадцатеричные (по основанию 16) числа — катализатор2
Последнее обновление:
В своей статье о числах по основанию 2 (двоичным) я говорил о разнице между десятичными (по основанию 10) числами мы используем в нашей повседневной жизни и числа с основанием 2. В этой статье рассматриваются шестнадцатеричные числа (с основанием 16). Понимание системы base-16 имеет решающее значение для понимания адресов IPv6.
Резюме по основанию 10 и 2
В качестве краткого обзора, десятичная система использует десять цифр: от 0 до 9. Конечно, вы можете считать больше 9. Для этого вы просто используете более одной цифры. Итак, чтобы пройти дальше 9, вы меняете значение на 0 и добавляете 1 слева. Это дает вам число 10.
Конечно, вы можете считать больше 9. Для этого вы просто используете более одной цифры. Итак, чтобы пройти дальше 9, вы меняете значение на 0 и добавляете 1 слева. Это дает вам число 10.
Система с основанием 2 имеет только два значения: 0 и 1. Чтобы представить число больше 1, вы снова используете более одной цифры. Чтобы получить число 2, вы меняете число на 0 и ставите перед ним 1. Итак, в системе счисления 2 число 2 записывается как 10.
База-16
База-16 использует 16 значений: числа от 0 до 9 и буквы от A до F. До числа 9 десятичная и шестнадцатеричная системы идентичны: число 10 с основанием 9 также является 9 в база-16. У нас нет единого числа для десяти, поэтому в базе 16 используются буквы от A до F. Буква A равна 10, B равна 11 и т. д. увеличены. Можете ли вы догадаться, что такое десятичное число 16 по основанию 2 и 16?
База-10 | База-2 | База-16 ---------+--------+-------- 0 | 0 | 0 1 | 1 | 1 2 | 10 | 2 3 | 11 | 3 4 | 100 | 4 5 | 101 | 5 6 | 110 | 6 7 | 111 | 7 8 | 1000 | 8 9| 1001 | 9 10 | 1010 | А 11 | 1011 | Б 12 | 1100 | С 13 | 1101 | Д 14 | 1110 | Е 15 | 1111 | Ф
Для обоих вам нужно изменить число на 0 и добавить 1 слева. Представление десятичного числа 15 по основанию 2 равно 1111, поэтому 16 становится 10000. Точно так же буква F является наибольшим значением в основании 16. Таким образом, следующим значением становится 10.
Представление десятичного числа 15 по основанию 2 равно 1111, поэтому 16 становится 10000. Точно так же буква F является наибольшим значением в основании 16. Таким образом, следующим значением становится 10.
Преобразование шестнадцатеричной системы счисления в десятичную
Приведенная выше таблица удобна, но она не поможет вам преобразовать большие числа с основанием 16 в десяточную. Конечно, есть формула для преобразования основания 16 в основание 10. Для каждого шестнадцатеричного символа вам необходимо вычислить десятичное значение, а затем сложить итог. Чтобы вычислить отдельные десятичные значения, вы работаете справа налево. Самое правое шестнадцатеричное значение умножается на 16
Это немного абстрактно, поэтому давайте рассмотрим несколько примеров. Начнем с внесения изменений в приведенную выше таблицу. Все значения base-16 имеют только один символ. Итак, формула представляет собой просто число с основанием 16, умноженное на 16 0 . Поскольку 16 * 0 равно 0, значения не меняются:
Поскольку 16 * 0 равно 0, значения не меняются:
Base-10 | База-16 в базу-10 ---------+------------------------ 0 | 0 х 16 0 = 0 1 | 1 х 16 0 = 1 2 | 2 х 16 0 = 2 3 | 3 х 16 0 = 3 4 | 4 х 16 0 = 4
Стоит отметить, что «нулевая степень» всегда возвращает 1, а не 0, как можно было ожидать (почему я рассказываю в своей статье о числах с основанием 2). Таким образом, мы просто умножаем самое правое значение на 1.
Далее, давайте посмотрим на число 10 с основанием 16. Теперь у нас есть два значения: 1 и 0. Чтобы преобразовать шестнадцатеричное число, мы начнем с правого- наибольшее значение и умножьте его на 16 0 . Это дает нам ноль, так как 0 * 1 ничему не равно. Далее мы берем 1 и умножаем на 16 1 . Это возвращает 16, поэтому шестнадцатеричное число 10 преобразуется в десятичное число 16 (16 + 0 = 16).
Расчет можно записать следующим образом:
(1x16 1 ) + (0x16 0 ) = 16
Или вам может показаться более читаемым:
1 x 16 1 16
0 х 16 0 0
----
База-10 16
Если это имеет смысл, то мы можем попробовать что-то более сложное: преобразование ACDC в десятичное число.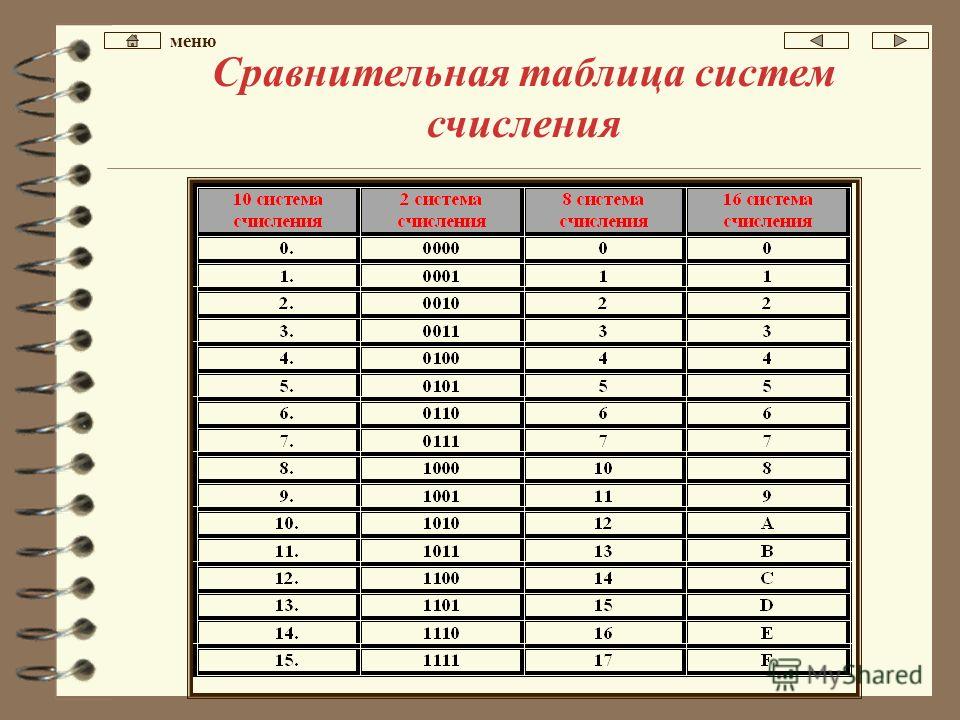 Для этого вы выполняете ту же магию. Вы начинаете с самого правого значения ( D , что является десятичным числом 12) и продвигаетесь влево:
Для этого вы выполняете ту же магию. Вы начинаете с самого правого значения ( D , что является десятичным числом 12) и продвигаетесь влево:
10 x 16 3 = 10 x 4096 = 40960
12 х 16 2 = 12 х 256 = 3072
13 х 16 1 = 13 х 16 = 208
12 х 16 0 = 12 х 1 = 12
-----
База-10 44252
Преобразование числа с основанием 10 в число с основанием 16
Преобразование числа с основанием 10 в шестнадцатеричное работает так же, как преобразование числа с основанием 10 в двоичное число. Вы делите число на показатель степени (16) и продолжаете делить результат до тех пор, пока частное не станет равным 0. На каждом шаге вы умножаете остаток на 16, чтобы получить шестнадцатеричное значение.
Как всегда, проще всего объяснить это на нескольких примерах. Давайте переработаем десятичное число 44252 и проверим, переводится ли оно в ACDC :
Коэффициент | 16 * Остаток | Шестнадцатеричный
------------------------------+----+ -----
44252/16 = 2765,75 (2765) | 16 * 0,75 = 12 | С
2765/16 = 172,8125 (172) | 16 * 0,8125 = 13 | Д
172 / 16 = 10,75 (10) | 16 * 0,75 = 12 | С
10/16 = 0,625 (0) | 16 * 0,625 = 10 | А
Последним шагом является объединение шестнадцатеричных значений, начиная с последнего значения. Итак, это дает нам ACDC .
Итак, это дает нам ACDC .
Еще один пример: тот же рецепт работает для десятичного числа 16 :
Частное | 16 * Остаток | Шестнадцатеричный
------------------------------+----+ -----
16/16 = 1,0 (1) | 16 * 0 = 0 | 0
1/16 = 0,0625 (0) | 16 * 0,0625 = 1 | 1
Преобразование базы 2 в базу 16
Конечно, вы также можете конвертировать из двоичного в шестнадцатеричный и наоборот. Чтобы преобразовать основание 2 в основание 10, вы разбиваете двоичное значение на блоки из четырех цифр (известные как 9).0264 nibbles ), а затем найдите шестнадцатеричное значение для каждого блока. Чтобы найти шестнадцатеричные значения, вы можете обратиться к слегка измененной таблице base-2, 10 и 16:
Base-10 | База-2 | База-16 ---------+--------+-------- 0 | 0000 | 0 1 | 0001 | 1 2 | 0010 | 2 3 | 0011 | 3 4 | 0100 | 4 5 | 0101 | 5 6 | 0110 | 6 7 | 0111 | 7 8 | 1000 | 8 9 | 1001 | 9 10 | 1010 | А 11 | 1011 | Б 12 | 1100 | С 13 | 1101 | Д 14 | 1110 | Е 15 | 1111 | Ф
Единственная разница с таблицей, которую я показал ранее, заключается в том, что все числа с основанием 2 теперь состоят из четырех цифр (т.
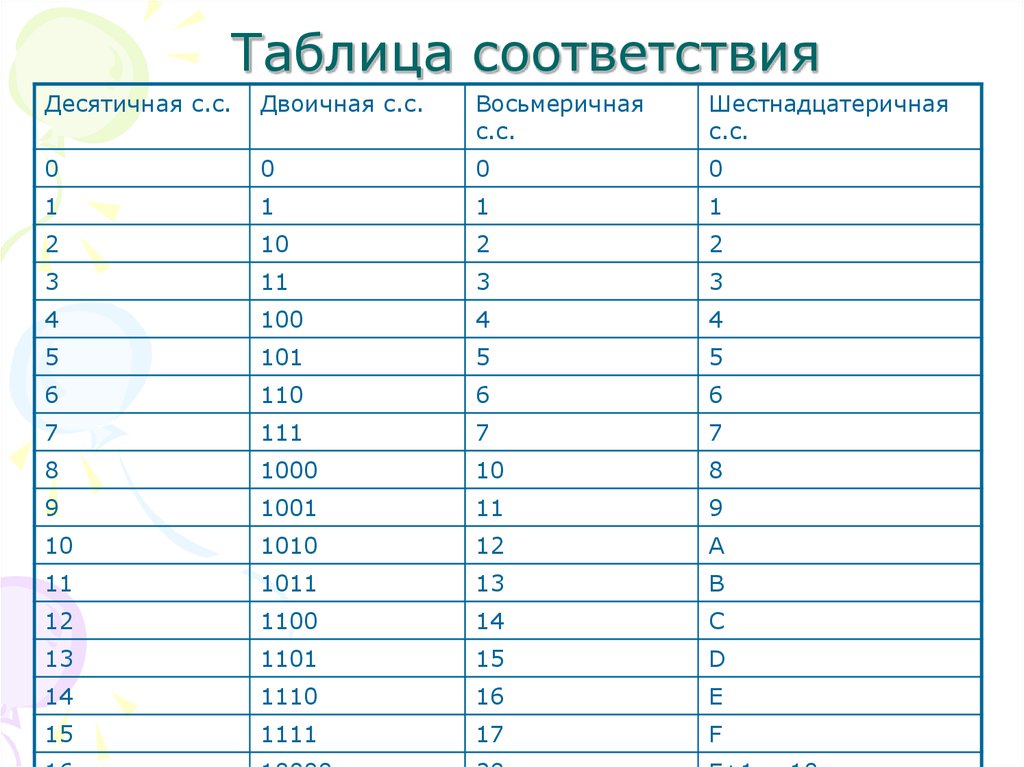 д. Принято обозначать одно состояние цифрой 0, а другое —
1. Такое представление информации в цифровом виде называют двоичным. Набор
(последовательность) из нулей и единиц называют двоичным кодом.
д. Принято обозначать одно состояние цифрой 0, а другое —
1. Такое представление информации в цифровом виде называют двоичным. Набор
(последовательность) из нулей и единиц называют двоичным кодом.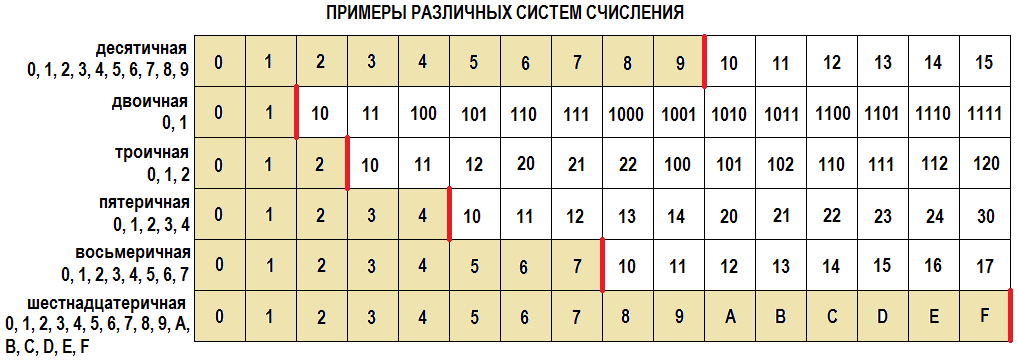 Переведем
десятичное число 45 в двоичную систему счисления.
Переведем
десятичное число 45 в двоичную систему счисления. В качестве следующей цифры двоичной дроби
взять целую часть этого произведения, а дробную часть произведения снова
умножить на 2 и т.д. до получения после запятой заданного количества цифр.
В качестве следующей цифры двоичной дроби
взять целую часть этого произведения, а дробную часть произведения снова
умножить на 2 и т.д. до получения после запятой заданного количества цифр.