Повторение
Умножение и деление на разрядную единицу    
Как и в десятичной системе счисления, так и в любой другой, умножение и деление чисел на разрядные единицы (элементы базиса) сводится к передвижению запятой на соответствующее количество знаков влево или вправо.
k |
3.
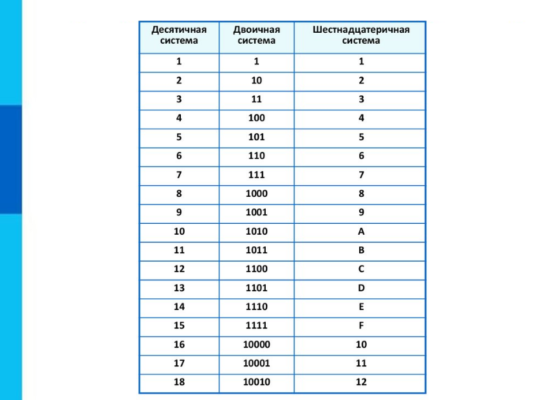 1.4 Другие системы счисления, используемые в компьютерных технологиях
1.4 Другие системы счисления, используемые в компьютерных технологияхВверх
Восьмеричная система счисления. Числа, записанные в системе с основанием 8, называются восьмеричными. Основание системы счисления — q = 8. Изображение чисел производится восьмью цифрами: 0, 1, 2, 3, 4, 5, 6, 7. Восьмеричная система счисления используется в ЭВМ для кодирования команд в целях сокращения записи.
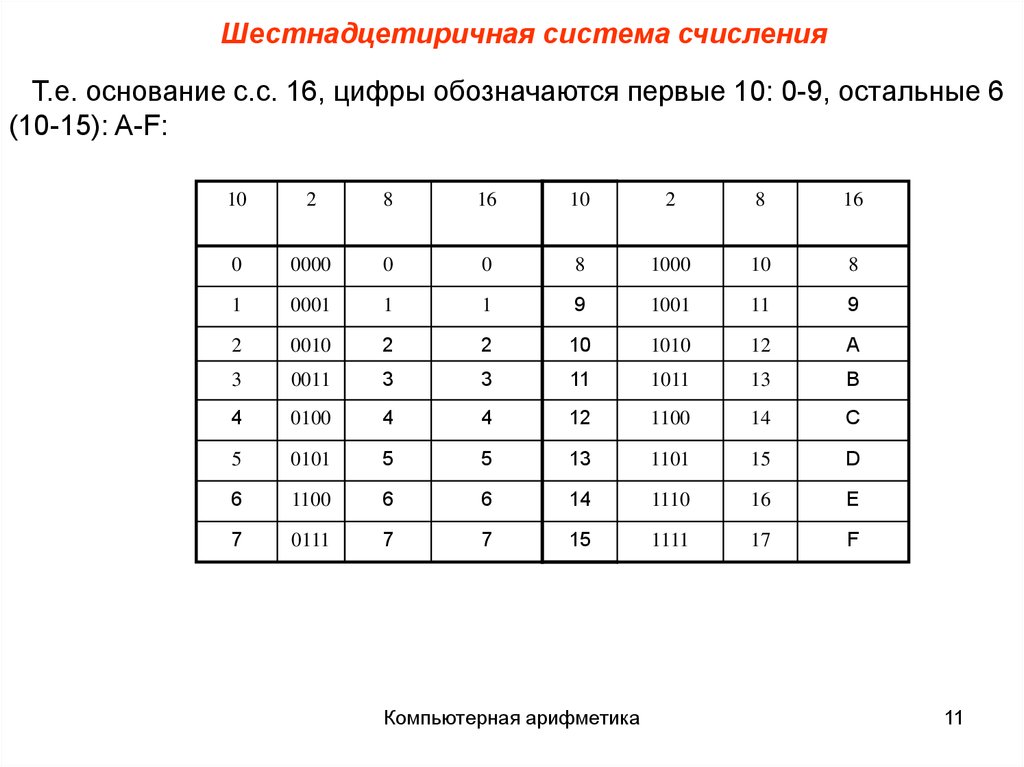
Шестнадцатеричная система счисления. Основание системы счисления — q = 16. В шестнадцатеричной системе счисления алфавит включает в себя 16 символов (цифры и буквы): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F. Широко применяется для написания кодов операций констант и других специальных слов, не требующих перевода в десятичную систему счисления. В таблице 3.1 приведен алфавит для четырех систем счисления.
Таблица 3.1 — Алфавит систем счисления.
Основание | Название | Алфавит |
2 | двоичная | 0 1 |
8 | восьмеричная | 0 1 2 3 4 5 6 7 |
10 | десятичная | 0 1 2 3 4 5 6 7 8 9 |
16 | шестнадцатеричная | 0 1 2 3 4 5 6 7 8 9 A B C D E F |
Любое число по
специальным правилам можно перевести
из одной системы счисления в другую.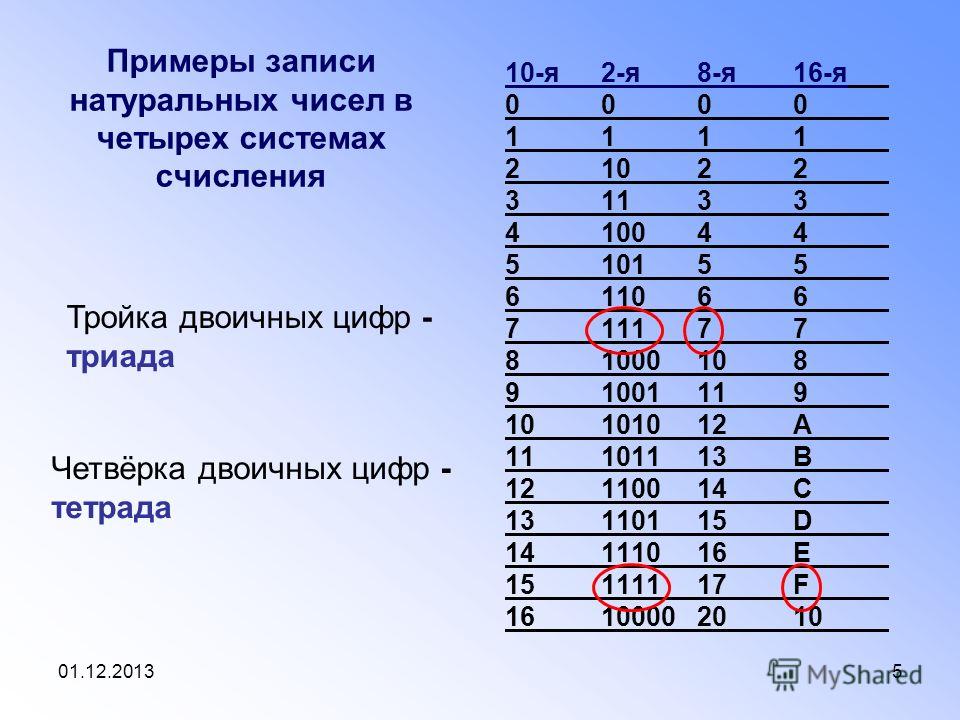 Рассмотрим эти правила.
Рассмотрим эти правила.
Допустим, число Х из системы счисления с основанием q требуется перевести в систему счисления с основанием p. Числа, имеющие целую и дробные части, переводятся в два этапа: вначале целая часть числа, а затем дробная.
Перевод целых чисел из одной системы счисления в другую осуществляется по следующему правилу:
— целую часть числа делим на новое основание p;
— полученный от деления первый остаток является младшей цифрой целой части числа с основанием р;
— деление будем производить до тех пор, пока не получим частное меньше делителя;
— последнее частное дает старшую цифру числа с основанием р.
Пример. Число 19110 перевести в восьмеричную систему счисления.
Перевод
осуществим методом последовательного
деления десятичного числа 191 на 8. Остатки
от деления образуют восьмеричное число:
Остатки
от деления образуют восьмеричное число:
в результате .
Перевод дробных чисел из одной системы счисления в другую. Предположим, что правильную дробь Х, представленную в системе с основанием q, требуется перевести в систему счисления с основанием р. Перевод осуществляется по следующему правилу:
— исходное число умножаем на новое основание р;
— полученная при этом целая часть произведения является первой искомой цифрой;
— дробную часть снова умножаем на основание р и т.д.
Пример. Перевести число 0,187510 в восьмеричную и шестнадцатеричную системы.
Здесь вертикальная черта отделяет целые
части чисел от дробных частей. Результат: .
Результат: .
Перевод из двоичной в восьмеричную и шестнадцатеричную систему счисления и обратно. Восьмеричная и шестнадцатеричная системы счисления являются вспомогательными системами при подготовке задачи к решению. Удобство ее использования состоит в том, что числа соответственно в 3 и 4 раза короче двоичной системы, а перевод в двоичную систему и обратно несложен и выполняется простым механическим способом.
Для того чтобы произвольное двоичное число записать в системе счисления с основанием , нужно:
данное двоичное число разбить слева и справа (целую и дробную части) на группы по n цифр в каждой;
если в последних правой и левой группах окажется меньше n разрядов, то их надо дополнить справа и слева нулями до нужного числа разрядов;
рассмотреть каждую группу как n
— разрядное двоичное число и записать
ее соответствующей цифрой в системе
счисления с основанием
.
Значит для того чтобы произвольное число записать в системе счисления с основанием , т. е. перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления. Применительно к компьютерной информации часто используются системы счисления с основанием 8 (восьмеричная) и 16 (шестнадцатеричная).
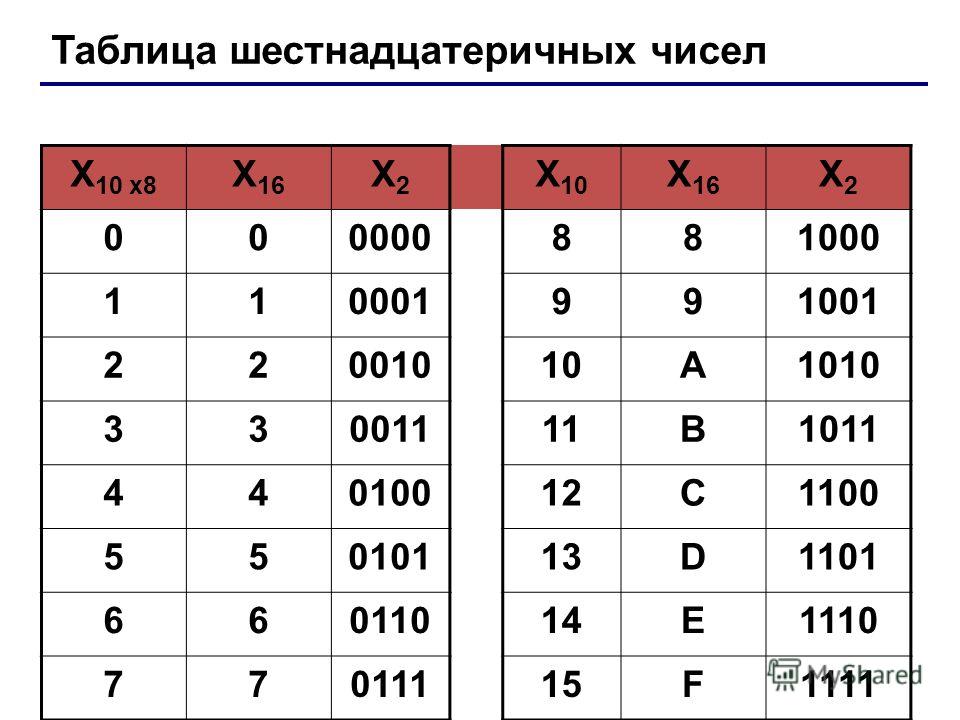
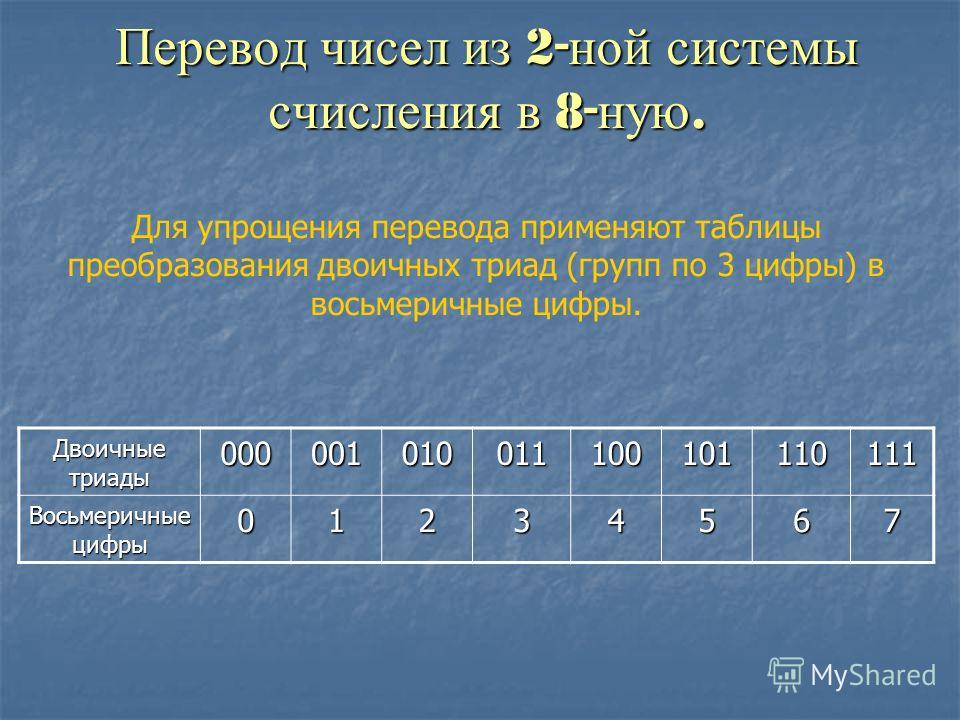
Перевод двоичных чисел в восьмеричную систему счисления. Для того чтобы двоичное число записать в восьмеричной системе счисления, необходимо разбить его на триады (т.е. группы по 3 цифры, так как ), начиная от запятой, отделяющей целую часть от дробной части. После этого каждая триада заменяется одной соответствующей ей восьмеричной цифрой. Недостающие справа и слева цифры восполняются нулями. Связь между двоичной и восьмеричной системами счисления приведена в таблице 3.2. Каждой восьмеричной цифре соответствует тройка двоичных чисел.
Таблица 3.2 — Двоично-восьмеричная таблица
8 – ричная система счисления | 2 –ичная система счисления |
0 | 000 |
1 | 001 |
2 | 010 |
3 | 011 |
4 | 100 |
5 | 101 |
6 | 110 |
7 | 111 |
Пример.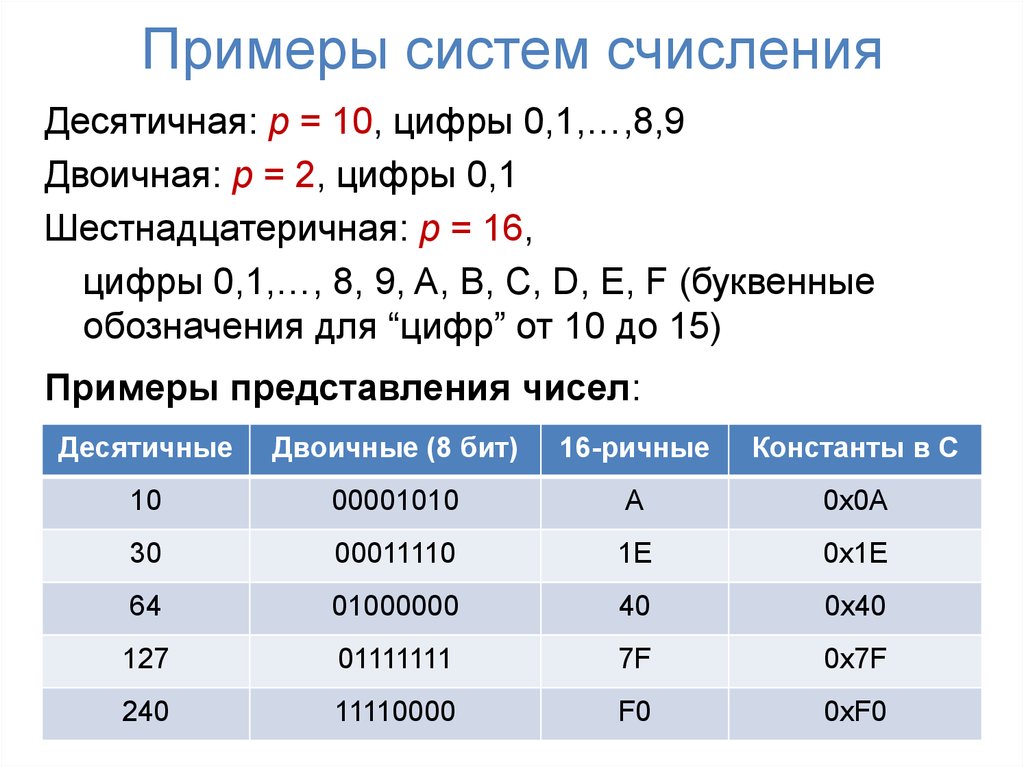 Перевести число в
восьмеричную систему счисления.
Перевести число в
восьмеричную систему счисления.
Перевод двоичных чисел в шестнадцатеричную систему счисления. Для того чтобы двоичное число записать в 16-ричной системе счисления, необходимо разбить его на тетрады (группы из 4 цифр, т.к. ), начиная от запятой, в обе стороны. После этого каждая тетрада заменяется соответствующей ей 16-ричной цифрой. В этом случае используется двоично-шестнадцатеричная таблица.
Таблица 3.3 — Двоично-шестнадцатеричная таблица.
16 – ричная система счисления | 2 – ичная система счисления | 16 – ричная система счисления | 2 – ичная система счисления |
0 | 0000 | 8 | 1000 |
1 | 0001 | 9 | 1001 |
2 | 0010 | A | 1010 |
3 | 0011 | B | 1011 |
4 | 0100 | C | 1100 |
5 | 0101 | D | 1101 |
6 | 0110 | E | 1110 |
7 | 0111 | F | 1111 |
Пример Перевести число 1011101,101112 в шестнадцатеричную систему счисления.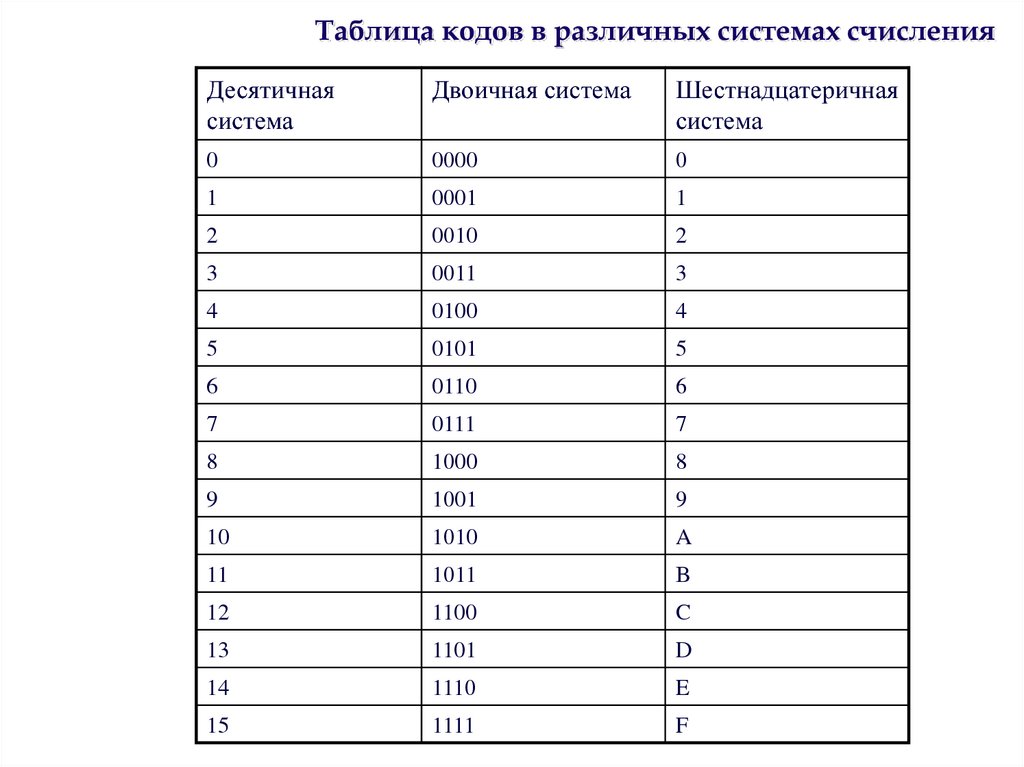
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления. Для перевода 8-ричного числа в двоичную систему счисления достаточно каждую восьмеричную цифру заменить соответствующей ей двоичной триадой. Для перевода 16-го числа в двоичную систему счисления достаточно каждую шестнадцатеричную цифру заменить соответствующей ей двоичной тетрадой.
Пример. Число перевести в шестнадцатеричную систему счисления и восьмеричную.
Перевод осуществляется следующим образом:
0010 | 1010 | 0011, | 0101 | 1001 |
2 | А | 3 | 5 | 9 |
т. е.
е.
001 | 010 | 100 | 011, | 010 | 110 | 010 |
1 | 2 | 4 | 3 | 2 | 6 | 2 |
т.е.
При переходе из 8-ричного счисления в 16-ричное счисление и обратно используется вспомогательный, двоичный код числа.
Пример. Перевести число перевести в 16-ичное счисление, 1CD, в 8–е счисление
7 6 0 2 F 8 2
С E 4 5 6 7 6 3 4
1 C D 4 7 1 5 2
Шестнадцатеричное число в двоичное — значение, таблица преобразования, примеры, часто задаваемые вопросы
Преобразование шестнадцатеричного числа в двоичное выполняется для получения двоичного эквивалента шестнадцатеричного числа. Система счисления бывает четырех типов, а именно: двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Каждая из этих систем счисления имеет свое собственное основное число, которое помогает в процессе преобразования. Шестнадцатеричное преобразование в двоичное выполняется по их соответствующим базовым числам. Давайте узнаем больше о том, как преобразовать шестнадцатеричные числа в двоичные числа.
Система счисления бывает четырех типов, а именно: двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Каждая из этих систем счисления имеет свое собственное основное число, которое помогает в процессе преобразования. Шестнадцатеричное преобразование в двоичное выполняется по их соответствующим базовым числам. Давайте узнаем больше о том, как преобразовать шестнадцатеричные числа в двоичные числа.
| 1. | Что такое преобразование шестнадцатеричных чисел в двоичные? |
| 2. | шагов для преобразования шестнадцатеричной системы счисления в двоичную |
| 3. | Преобразование шестнадцатеричных чисел в двоичные с десятичной точкой |
| 4. | Часто задаваемые вопросы о преобразовании шестнадцатеричных чисел в двоичные |
Что такое преобразование шестнадцатеричной системы в двоичную?
Преобразование шестнадцатеричных чисел в двоичные — это процесс преобразования шестнадцатеричного числа с основанием 16 в двоичное число с основанием 2. Преобразование шестнадцатеричных чисел в двоичные важно, поскольку компьютеры понимают только двоичный язык. Следовательно, все другие типы систем счисления также преобразуются в двоичные числа. Преобразование шестнадцатеричного в двоичное не может быть выполнено напрямую. Шестнадцатеричное число должно быть преобразовано в десятичное число, а затем преобразовано в двоичное число. Прежде чем мы перейдем к этапам преобразования, давайте посмотрим, что такое шестнадцатеричные и двоичные числа.
Преобразование шестнадцатеричных чисел в двоичные важно, поскольку компьютеры понимают только двоичный язык. Следовательно, все другие типы систем счисления также преобразуются в двоичные числа. Преобразование шестнадцатеричного в двоичное не может быть выполнено напрямую. Шестнадцатеричное число должно быть преобразовано в десятичное число, а затем преобразовано в двоичное число. Прежде чем мы перейдем к этапам преобразования, давайте посмотрим, что такое шестнадцатеричные и двоичные числа.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления имеет базовое число 16 и использует шестнадцать цифр/алфавитов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и A, B, C, D, E, F. Здесь A-F шестнадцатеричной системы счисления означают соответственно числа 10-15 десятичной системы счисления. Эта система используется в компьютерах для сокращения больших строк двоичной системы. Самая большая одиночная цифра — F (на 1 меньше основания 16). Каждая цифра в шестнадцатеричной системе счисления представляет степень основания (16). Например: \(7B4_{16}, 9F_{16}, 3B1A_{16}\) — некоторые примеры чисел в шестнадцатеричной системе счисления.
Например: \(7B4_{16}, 9F_{16}, 3B1A_{16}\) — некоторые примеры чисел в шестнадцатеричной системе счисления.
Двоичная система счисления
Двоичная система счисления использует только две цифры: 0 и 1 с базовым числом 2. Цифры 0 и 1 называются битами, а 8 битов вместе составляют байт. Данные в компьютерах хранятся в виде битов и байтов. Двоичная система счисления не работает с другими числами, такими как 2,3,4,5 и так далее. Например: \(10001_2, 111101_2, 1010101_2 \) — некоторые примеры чисел в двоичной системе счисления.
шагов для преобразования шестнадцатеричной системы в двоичную
Чтобы преобразовать шестнадцатеричное число в двоичное, нам нужно сначала преобразовать шестнадцатеричное число в десятичное число, чтобы, наконец, преобразовать его в двоичное число. Один из наиболее важных аспектов, который следует помнить, заключается в том, что каждое шестнадцатеричное число дает 4 двоичных цифры. Преобразование шестнадцатеричного в двоичное может происходить двумя способами. Во-первых, после преобразования шестнадцатеричного числа в десятичное число мы преобразуем десятичное число, используя процесс деления для получения двоичного числа. Во-вторых, мы можем напрямую использовать таблицу преобразования шестнадцатеричной в десятичную в двоичную. Давайте посмотрим на шаги обоих методов.
Во-первых, после преобразования шестнадцатеричного числа в десятичное число мы преобразуем десятичное число, используя процесс деления для получения двоичного числа. Во-вторых, мы можем напрямую использовать таблицу преобразования шестнадцатеричной в десятичную в двоичную. Давайте посмотрим на шаги обоих методов.
Метод 1: преобразование шестнадцатеричных чисел в десятичные и двоичные (без таблицы преобразования)
Этот метод требует как умножения, так и деления чисел с использованием соответствующих базовых чисел. Шестнадцатеричное основание числа равно 16, основание десятичного числа равно 10, а основание двоичного числа равно 2. Давайте рассмотрим шаги:
- Шаг 1: Запишите шестнадцатеричное число и найдите его эквивалентное десятичное число. .
- Шаг 2: Чтобы найти десятичный эквивалент, мы умножаем каждую цифру на 16 n-1 , где цифра находится на n-й позиции.
- Шаг 3: После умножения чисел сложите произведение этих чисел, чтобы получить десятичное число.

- Шаг 4: Чтобы преобразовать десятичное число в двоичное, мы делим десятичное число на 2, отбрасывая остаток и деля частное на 2, пока не получим ноль.
- Шаг 5: Когда частное равно нулю, мы упорядочиваем остаток снизу вверх, т. е. в обратном порядке, чтобы получить двоичное число.
Давайте рассмотрим пример для лучшего понимания. Преобразование шестнадцатеричного \((100)_{16}\) в двоичное.
Шаг 1 + 2: преобразовать \((100)_{16}\) в десятичное число, умножив каждую цифру на 16 n-1 . Умножьте
\((100)_{16}\) = 1 × 16 (3-1) + 0 × 16 (2-1) + 0 × 16 (1-1)
\((100)_{16}\) = 1 × 16 2 + 0 × 16 1 + 0 × 16 0
Шаг 3: Умножьте числа и добавьте произведение, чтобы получить десятичное число.
\((100)_{16}\) = 1 × 256 + 0 × 16 + 0 × 1
\((100)_{16}\) = 256 + 0 + 0
\((100 )_{16}\) = 256
Следовательно, \((100)_{16}\) = \((256)_{10}\)
Шаг 4: Преобразование десятичного числа \((256) _{10}\) в двоичное число путем деления числа на 2 до тех пор, пока частное не станет равным нулю.
Следовательно, \((256)_{10}\) = \((100000000)_{2}\)
Шаг 5: После получения двоичного файла выполняется преобразование.
Следовательно, \((100)_{16}\) = \((100000000)_{2}\).
Метод 2: Преобразование шестнадцатеричного в десятичное в двоичное (с таблицей преобразования)
Этот метод является прямой процедурой, просто взглянув на таблицу диалога, мы можем преобразовать шестнадцатеричное в двоичное. Шаги довольно просты, давайте посмотрим на них:
- Шаг 1: Запишите шестнадцатеричное число .
- Шаг 2: Найдите эквивалентное десятичное число каждой из цифр, взглянув на таблицу преобразования.
- Шаг 2: Получив десятичное число, просмотрев ту же таблицу, мы можем преобразовать его в двоичное.
- Шаг 3: Объедините все двоичные числа, чтобы получить окончательное двоичное число.
Давайте рассмотрим пример для лучшего понимания. Преобразование шестнадцатеричного \((E5B)_{16}\) в двоичное.
Шаг 1: У нас есть шестнадцатеричное число как \((E5B)_{16}\).
Шаг 2: Глядя на таблицу преобразования, найдите эквивалент каждой цифры.
E = \((14)_{10}\) , 5 = \((5)_{10}\) , B = \((11)_{10}\)
Шаг 3: После получается десятичное число каждой цифры, глядя на таблицу преобразования, преобразуйте каждое десятичное число в двоичное.
\((14)_{10}\) = \((1110)_{2}\)
\((5)_{10}\) = \((0101)_{2}\)
\((11)_{10}\) = \((1011)_{2}\)
Шаг 4: Объедините все двоичные числа, чтобы получить окончательное число.
Следовательно, \((E5B)_{16}\) = \((111001011011)_{2}\).
Преобразование шестнадцатеричных чисел в двоичные с десятичной точкой
Чтобы преобразовать шестнадцатеричное число в двоичное, мы используем метод, аналогичный тому, что использовался в предыдущем разделе. Мы используем таблицу преобразования для преобразования шестнадцатеричных чисел в двоичные. При преобразовании с десятичной запятой мы используем те же шаги, но не учитываем нули, расположенные в самой правой части, поскольку они называются конечными нулями. Давайте посмотрим на пример, преобразуем \((0.C48)_{16}\) в двоичный файл.
Давайте посмотрим на пример, преобразуем \((0.C48)_{16}\) в двоичный файл.
Шаг 1: У нас есть шестнадцатеричный вид \((0.C48)_{16}\).
Шаг 2: Глядя на таблицу преобразования, найдите эквивалент каждой цифры. Ноль в расчет не берем.
C = \((12)_{10}\) , 4 = \((4)_{10}\) , 8 = \((8)_{10}\)
Шаг 3: После получается десятичное число каждой цифры, глядя на таблицу преобразования, преобразуйте каждое десятичное число в двоичное.
\((12)_{10}\) = \((1100)_{2}\)
\((4)_{10}\) = \((0100)_{2}\)
\((8)_{10}\) = \((1000)_{2}\)
Шаг 4: Объедините все двоичные числа, чтобы получить окончательное число. Ноль перед десятичным числом будет записан вместе с последним двоичным числом.
Следовательно, \((0.C48)_{16}\) = \((110001001000)_{2}\).
Связанные темы
Вот несколько интересных тем, связанных с преобразованием шестнадцатеричных чисел в двоичные, взгляните.
- Двоично-десятичный калькулятор
- Калькулятор преобразования десятичной системы в двоичную
- Преобразование десятичной дроби в двоичную формулу
Часто задаваемые вопросы о преобразовании шестнадцатеричных чисел в двоичные
Что такое преобразование шестнадцатеричной системы в двоичную?
Преобразование шестнадцатеричных чисел в двоичные помогает получить двоичный эквивалент шестнадцатеричной цифры. Двоичная и шестнадцатеричная системы счисления имеют свои собственные базовые числа, которые помогают в процессе преобразования. Базовое число шестнадцатеричного числа равно 16, а базовое число двоичного числа равно 2. Чтобы преобразовать шестнадцатеричное число в двоичное, нам нужно преобразовать шестнадцатеричные цифры в десятичные, чтобы, наконец, преобразовать их в двоичные.
Двоичная и шестнадцатеричная системы счисления имеют свои собственные базовые числа, которые помогают в процессе преобразования. Базовое число шестнадцатеричного числа равно 16, а базовое число двоичного числа равно 2. Чтобы преобразовать шестнадцатеричное число в двоичное, нам нужно преобразовать шестнадцатеричные цифры в десятичные, чтобы, наконец, преобразовать их в двоичные.
Как преобразовать шестнадцатеричное число в двоичное?
Преобразование шестнадцатеричных чисел в двоичные осуществляется двумя разными способами. Первый метод заключается в преобразовании шестнадцатеричной цифры в десятичную путем умножения каждой цифры на 16 n-1 и сложения их вместе. Далее преобразуйте десятичное число в двоичное, разделив десятичное число на 2, пока частное не станет равным нулю. Как только цель достигнута, двоичное число получается путем записи остатка снизу вверх. Второй метод выполняется напрямую с помощью таблицы преобразования.
Как преобразовать шестнадцатеричное число в двоичное с десятичной точкой?
Преобразование шестнадцатеричного в двоичное с десятичной точкой выполняется простым способом с помощью таблицы преобразования. Вот шаги:
Вот шаги:
- Напишите шестнадцатеричные цифры.
- Преобразуйте каждую цифру в эквивалентное десятичное число с помощью таблицы преобразования.
- После получения десятичного числа найдите двоичный эквивалент каждого десятичного числа.
- После получения каждого двоичного числа запишите их все вместе, чтобы получить окончательное двоичное число.
Что такое 9C в двоичном формате?
Чтобы найти двоичное число в шестнадцатеричном формате, нам нужно сначала преобразовать шестнадцатеричное число в десятичное, а затем в двоичное. Итак, шестнадцатеричная 9С при преобразовании в десятичную записывается как:
9 = 9 и С = 12, глядя на таблицу преобразования.
9 × 16 1 + 12 × 16 0 = 144 + 12 = 156.
\(9C_16\) = \(156_10\).
Следовательно, двоичное значение равно \(9C_16\) = \(10011100_2\).
Что такое шестнадцатеричный FF в двоичном формате?
Чтобы преобразовать шестнадцатеричный FF в двоичный, мы сначала преобразуем его в десятичный, а затем в двоичный. Вот шаги:
Вот шаги:
FF в десятичном виде записывается как F = \(15_10\) и F = \(15_10\).
Преобразование десятичного числа в двоичное, \(15_10\) = \((1111)_{2}\) и \(15_10\) = \((1111)_{2}\)
Следовательно, \(FF_16\) ) = \((11111111)_{2}\).
Какое основание используется для преобразования шестнадцатеричных чисел в двоичные?
Чтобы преобразовать шестнадцатеричное число в двоичное, мы сначала преобразуем шестнадцатеричное число в десятичное число, используя базовое число 16, которое является базовым числом шестнадцатеричного числа. Как только десятичное число получено, мы используем основание двоичной системы счисления, то есть 2, для преобразования десятичного числа в двоичное. Следовательно, шестнадцатеричный код преобразуется в двоичный.
Шестнадцатеричная система счисления (определение, преобразование и примеры)
Двоичная система счисления является естественным выбором для систем с двумя состояниями. Но в этой системе числа имеют тенденцию становиться короткими, а довольно длинными.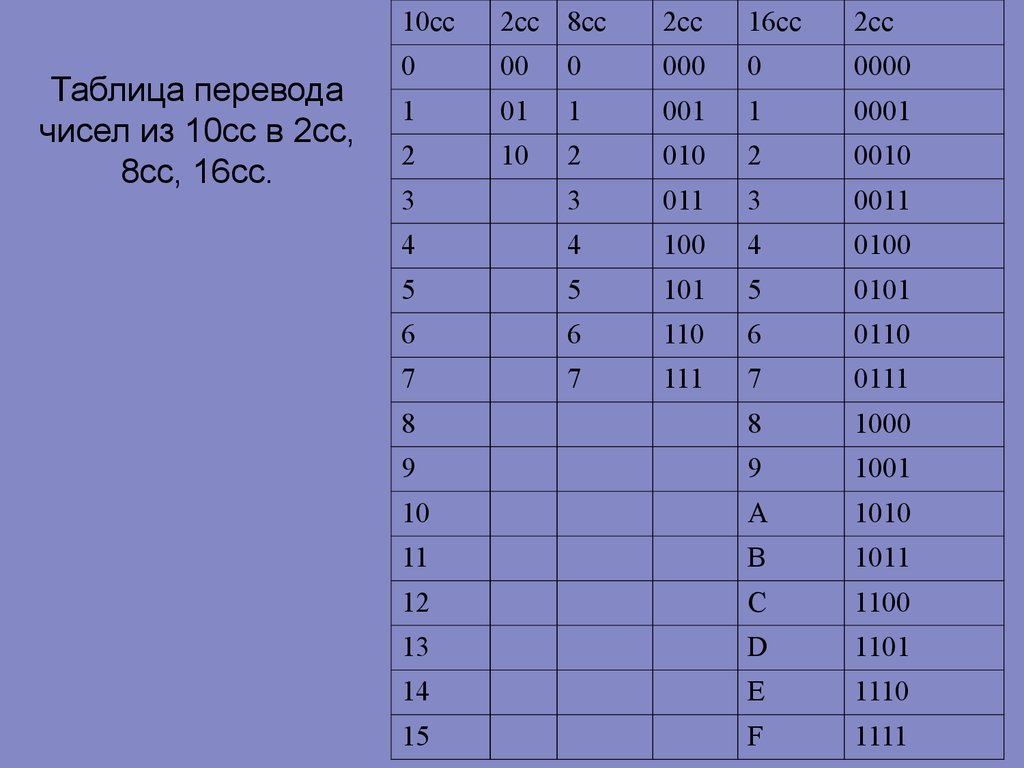 Следовательно, чтобы уменьшить длину данного числа, довольно часто используется шестнадцатеричная система счисления. Шестнадцатеричная система счисления имеет основание 16, то есть состоит из 16 цифр и символов. В нем используются цифры от 0 до 9, а также буквы A, B, C, D, E и F. Поскольку для представления цифр в шестнадцатеричной системе счисления используются как числовые цифры, так и алфавиты, это число 9.0249 буквенно-цифровая система счисления . В таблице 44.3 показано соотношение между шестнадцатеричным, десятичным и двоичным форматами. Важно отметить, что шестнадцатеричные (сокращение от шестнадцатеричных) цифры от A до F эквивалентны десятичным значениям от 10 до 15.
Следовательно, чтобы уменьшить длину данного числа, довольно часто используется шестнадцатеричная система счисления. Шестнадцатеричная система счисления имеет основание 16, то есть состоит из 16 цифр и символов. В нем используются цифры от 0 до 9, а также буквы A, B, C, D, E и F. Поскольку для представления цифр в шестнадцатеричной системе счисления используются как числовые цифры, так и алфавиты, это число 9.0249 буквенно-цифровая система счисления . В таблице 44.3 показано соотношение между шестнадцатеричным, десятичным и двоичным форматами. Важно отметить, что шестнадцатеричные (сокращение от шестнадцатеричных) цифры от A до F эквивалентны десятичным значениям от 10 до 15.
Из таблицы 44.3 видно, что существует 16 комбинаций 4-битных двоичных чисел и наборов 4-битные двоичные числа можно вводить в компьютер в виде шестнадцатеричных (шестнадцатеричных) цифр. Эти числа должны быть преобразованы в двоичные представления с использованием схем преобразования шестнадцатеричных чисел в двоичные, прежде чем они смогут быть обработаны цифровыми схемами.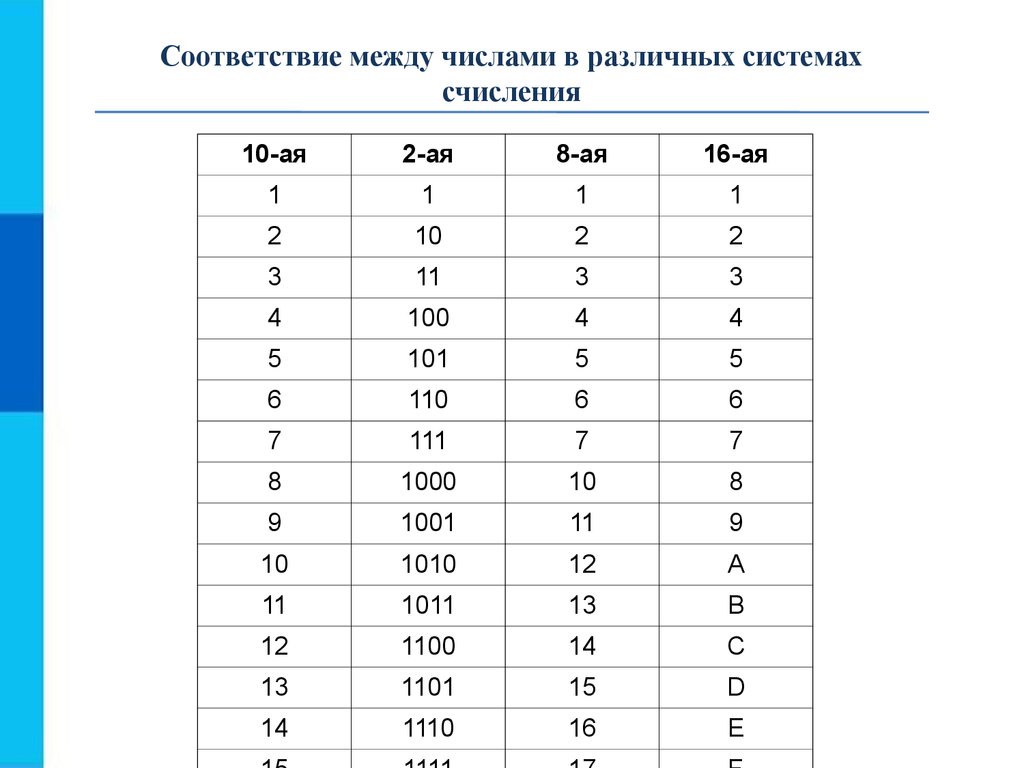 Эта система широко используется в микропроцессорной работе.
Эта система широко используется в микропроцессорной работе.
Как мы будем считать в шестнадцатеричной системе счисления, когда дойдем до F ? Просто начните с другого столбца и продолжайте следующим образом:
С двумя шестнадцатеричными цифрами мы можем сосчитать до FF 16 , что равно 255 10 . Для подсчета сверх этого требуются три шестнадцатеричных цифры. Например, 100 16 равно 256 10 , 101 16 равно 257 10 и так далее. Максимальное трехзначное шестнадцатеричное число — FFF 16 , что равно 4095 10 .
Преобразование шестнадцатеричных чисел в десятичные: Шестнадцатеричное число можно преобразовать в его десятичный эквивалент, умножив каждую шестнадцатеричную цифру на ее вес, а затем взяв сумму этих произведений. Веса шестнадцатеричных чисел являются возрастающими степенями 16 (справа налево). Для четырехзначного шестнадцатеричного числа веса следующие:
Для четырехзначного шестнадцатеричного числа веса следующие:
Для иллюстрации рассмотрим несколько примеров.
Пример 44.41: Найдите десятичный эквивалент шестнадцатеричного числа 1A53.
Решение:
Пример 44.42: Преобразовать (FF3B) 16 в эквивалентное десятичное число.
Решение:
Преобразование десятичного числа в шестнадцатеричное:
Повторное деление десятичного числа на 16 даст эквивалентное шестнадцатеричное число, образованное остатком от каждого деления. Это похоже на повторное деление на 2 для десятичного преобразования в двоичное и повторное деление на 8 для десятичного преобразования в восьмеричное. Следующие примеры иллюстрируют процедуру.
Example 44.44: Convert the following number: (374.37) 10 = ( ) 16
Solution:
Hexadecimal-To-Binary Conversion:
Hex числа могут быть преобразованы в эквивалентные двоичные числа путем замены каждой шестнадцатеричной цифры ее эквивалентным 4-битным двоичным числом. Эта процедура проиллюстрирована ниже.
Эта процедура проиллюстрирована ниже.
Пример 44.46: Выполните следующее преобразование: (1684) 16– () 2
Решение:
Пример 44,47: Преобразование следующего числа (A6B.F5) 16 → (?) 2 66.
Решение: Преобразовывая каждую шестнадцатеричную цифру в двоичное число битов, мы имеем
Преобразование двоичного кода в шестнадцатеричный:
Преобразование из двоичного в шестнадцатеричный процесс является обратным вышеописанному. Двоичное число группируется в группы по 4 бита, начиная с LSB и продвигаясь к MSB для целой части, а затем каждая группа из четырех бит заменяется ее шестнадцатеричным представлением. Нули добавляются по мере необходимости для завершения 4-битной группы.
Для дробной части описанная выше процедура повторяется с бита, следующего за двоичной точкой, и движется вправо.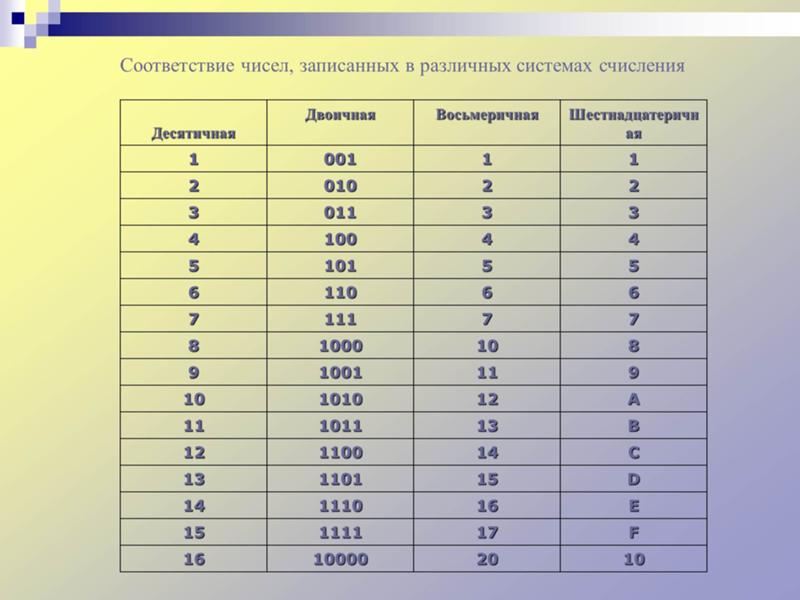
Пример 44.49: Преобразование длинного двоичного числа 1001001101010001 в восьмеричное и шестнадцатеричное.
Решение: (1001001101010001) 2
Преобразование из шестнадцатеричного в восьмеричное и наоборот.
Шестнадцатеричные числа могут быть преобразованы в эквивалентные восьмеричные числа, а восьмеричные числа могут быть преобразованы в эквивалентные шестнадцатеричные числа путем преобразования шестнадцатеричного/восьмеричного числа в эквивалентное двоичное, а затем в восьмеричное/шестнадцатеричное соответственно. Процедура иллюстрируется следующим примером.
Пример 44.50: Преобразовать (F2A4) 16 в ( ) 8 .
Решение: (F2A4) 16
Пример 44.51: Преобразовать шестнадцатеричное число A5F1 в эквивалентное восьмеричное число.
Решение:
Шестнадцатеричная арифметика:
Правила арифметических операций с шестнадцатеричными числами аналогичны правилам для десятичных, восьмеричных и двоичных чисел.

 Переведем десятичное число 3 258 в двоичную и 16-ричную системы счисления. Получим 1100101110102 и СВА16. Значит, 1100101110102 = СВА16.
Переведем десятичное число 3 258 в двоичную и 16-ричную системы счисления. Получим 1100101110102 и СВА16. Значит, 1100101110102 = СВА16. 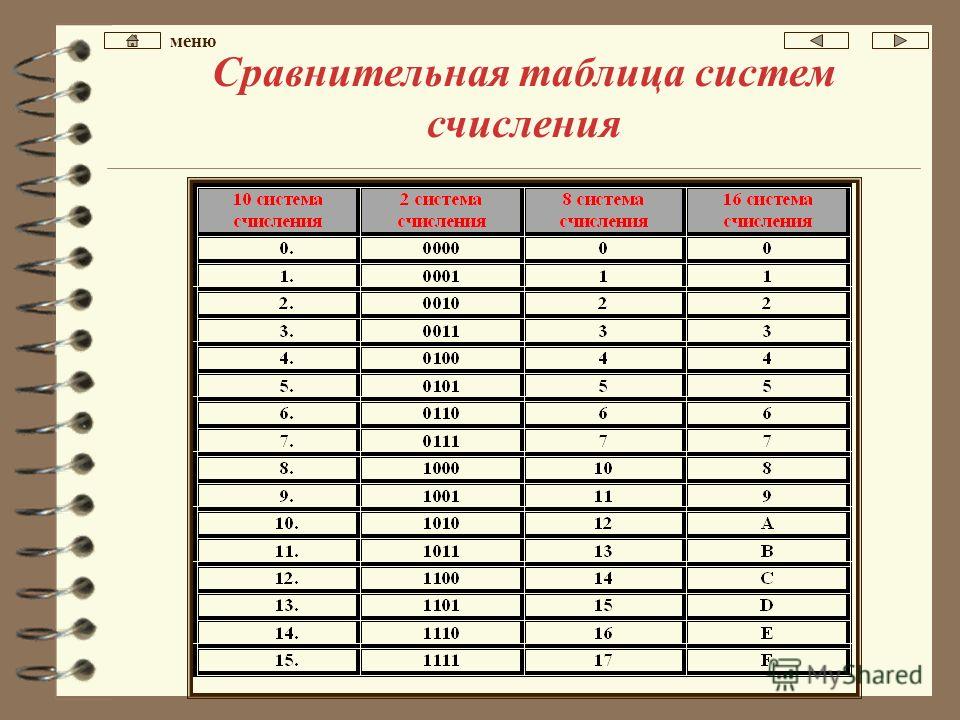
 А также в общем случае — для всех пар систем счисления, в которых основание одной системы счисления есть некая степень основания другой системы счисления.
А также в общем случае — для всех пар систем счисления, в которых основание одной системы счисления есть некая степень основания другой системы счисления.