14 в шестнадцатеричной системе: Перевод чисел из десятичной системы в двоичную

Число 14, 0x00000E, четырнадцать — BiKubik.com

Энциклопедия чисел

Свойства натурального числа 14, 0x00000E, 0xE:

Системы счисления Основные свойства Степени, корни

Тригонометрия Хэши, криптография Языки программирования

Дата и время Цвет по числу Интернет

Другие свойства

Рейтинг 7 из 10, оценок: 17.

Системы счисления, перевод в систему счисления

Десятичное число 14

• 14 в шестнадцатеричной системе счисления

  E

• 14 в двоичной системе счисления

  1110

• 14 в восьмеричной системе счисления

  16

Шестнадцатеричное число E

• E в десятичной системе

  14

• E в двоичной системе

  1110

• E в восьмеричной системе

  16

Двоичное число 1110

• 1110 в десятичной системе

  14

• 1110 в шестнадцатеричной системе

  E

• 1110 в восьмеричной системе

  16

Восьмеричное число 16

• 16 в десятичной системе

  14

• 16 в шестнадцатеричной системе

  E

• 16 в двоичной системе

  1110

Основные арифметические и алгебраические свойства

• Число 14 на русском языке, number in Russian, число 14 прописью:

  четырнадцать

• Четность

  Четное число 14

• Разложение на множители, делители числа 14

  2, 7, 1

• Простое или составное число

  Составное число 14

• Числа делящиеся на целое число 14

  28, 42, 56, 70, 84, 98, 112, 126

• Число 14 умноженное на число два

  28

• 14 деленное на число 2

  7

• Список 8-ми простых чисел перед числом

  13, 11, 7, 5, 3, 2

• Сумма десятичных цифр

  5

• Количество цифр

  2

• Десятичный логарифм 14

  1. 1461280356782

• Натуральный логарифм 14

  2.6390573296153

• Это число Фибоначчи?

  Нет

• Число на 1 больше числа 14,
  следующее число

  число 15

• Число на 1 меньше числа 14,
  предыдущее число

  13

Степени числа, корни

• 14 во второй степени (в квадрате)
  (функция x в степени 2 — x²)

  196

• В третьей степени (в кубе, 14 в степени 3, x³) равно

  2744

• Корень квадратный из 14

  3.7416573867739

• Корень кубический из числа 14 =

  2.4101422641752

Тригонометрические функции, тригонометрия

• Синус, sin 14 градусов, sin 14°

  0.2419218956

• Косинус, cos 14 градусов, cos 14°

  0.9702957263

• Тангенс, tg 14 градусов, tg 14°

  0. 2493280028

• Синус, sin 14 радиан

  0.99060735569487

• Косинус, cos 14 радиан

  0.13673721820783

• Тангенс, tg 14 радиан равно

  7.2446066160948

• 14 градусов, 14° =

  0.24434609527921 радиан

• 14 радиан =

  802.14091318315 градуса, 802.14091318315°

Контрольные суммы, хэши, криптография

• MD-5 хэш(14)

  aab3238922bcc25a6f606eb525ffdc56

• CRC-32, CRC32(14)

  2788221432

• SHA-256 hash, SHA256(14)

  8527a891e224136950ff32ca212b45bc93f69fbb801c3b1ebedac52775f99e61

• SHA1, SHA-1(14)

  fa35e192121eabf3dabf9f5ea6abdbcbc107ac3b

• ГОСТ Р 34.11, GOST R 34.11-94, GOST(14)

  50b528dddf51669edbf0ae3cb6555af9818bbdfd3e20a39ad3e70ad301e4781e

• Base64

  MTQ=

Языки программирования

• C++, CPP, C значение 14

  0x00000E, 0xE

• Delphi, Pascal значение числа 14

  $00000E

Дата и время

• 14-й день простого и високосного года

  14 января

• Конвертация UNIX timestamp 14 в дату и время

  UTC

  четверг, 1 января 1970 г. , 0:00:14 GMT

  в Москве, Россия

  четверг, 1 января 1970 г., 3:00:14 Московское стандартное время

  в Лондоне, Великобритания

  четверг, 1 января 1970 г., 1:00:14 GMT+01:00

  в Нью-Йорке, США

  среда, 31 декабря 1969 г., 19:00:14 Восточно-американское стандартное время

Интернет

• Конвертация в IPv4 адрес Интернет

  0.0.0.14

• 14 в Википедии:

  14

Другие свойства числа

• Короткая ссылка на эту страницу, DEC

  https://bikubik.com/ru/14

• Короткая ссылка на эту страницу, HEX

  https://bikubik.com/ru/xE

• Номер телефона

  14

• Телефонный код страны

  +14

Цвет по числу 14, цветовая гамма

• html RGB цвет 14, 16-ричное значение

  #00000E — (0, 0, 14)

• HTML CSS код цвета #00000E

  . color-mn { color: #00000E; }
  .color-bg { background-color: #00000E; }

Цвет для данного числа 14

 

Здесь вы можете изменить составляющую цвета для данного числа 14 или цвета 00000E:

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления имеет алфавит, состоящий из 16 цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, c, d, e, f.

При записи числа в шестнадцатеричной системе для записи цифр обозначающих числа 10, 11, 12. 13, 14. 15 используются соответственно буквы А, В, С, D, E, F.

Перевод чисел из шестнадцатеричной системы в десятичную

Перевести любое шестнадцатеричное число в десятичное можно по уже известной формуле

Примеры.

1. АЕ07₁₆=10∙16³+14∙16²+0∙16¹+7∙16⁰=44551₁₀.

2. 100₁₆=1∙16²+0∙16¹+0∙16⁰=256₁₀.

3. 58₁₆=5∙16¹+8∙16⁰=.88₁₀.

4. 2А₁₆=2∙16¹+10∙16⁰=42₁₀.

5. D₁₆ = 13₁₀.

Перевод числа из десятичной системы в шестнадцатеричную осуществляется также, как в двоичную.

Перевод чисел из шестнадцатеричной системы в двоичную и обратно

Перевести любое шестнадцатеричное число в двоичное можно следующим образом. Каждая цифра шестнадцатеричной записи числа записывается четырехзначным двоичным числом — тетрадой. После этого нули, стоящие слева, можно отбросить.

016 = 00002	416 = 01002	816 = 10002	C16 = 1100 2
116 = 00012	516 = 01012	916 = 10012	D16 = 11012
216 = 00102	616 = 01102	A16 = 10102	E16 = 11102
316 = 00112	716 = 01112	B16 = 10112	F16 = 11112

1) D= 11012.

2) 2A= 0010 10102= 1010102.

3) 5816= 0101 10002= 10110002.

И наоборот, перевести любое двоичное число в шестнадцатеричное можно аналогичным образом. Каждые четыре двоичные цифры, считая справа налево, записываются одной шестнадцатеричной цифрой. Эти цифры располагаются также справа налево.

Примеры.

1. 1101₂=D.

2. 101010₂= 10 1010₂= 2A.

3. 1011000₂= 101 1000₂= 58₁₆.

Восьмеричная система счисления

Восьмеричная система счисления имеет алфавит, состоящий из 8 цифр:

0, 1, 2, 3, 4, 5, 6, 7.

Перевод числа из десятичной системы в восьмеричную и обратно осуществляется по аналогии с переводом в двоичную / из двоичной.

Перевод чисел из восьмеричной системы в двоичную и обратно

Каждая цифра восьмеричной записи числа записывается трехзначным двоичным числом — триадой.

08 = 0002	48 = 1002
18 = 0012	58 = 1012
28 = 0102	68 = 1102
38 = 0112	78 = 1112

Примеры.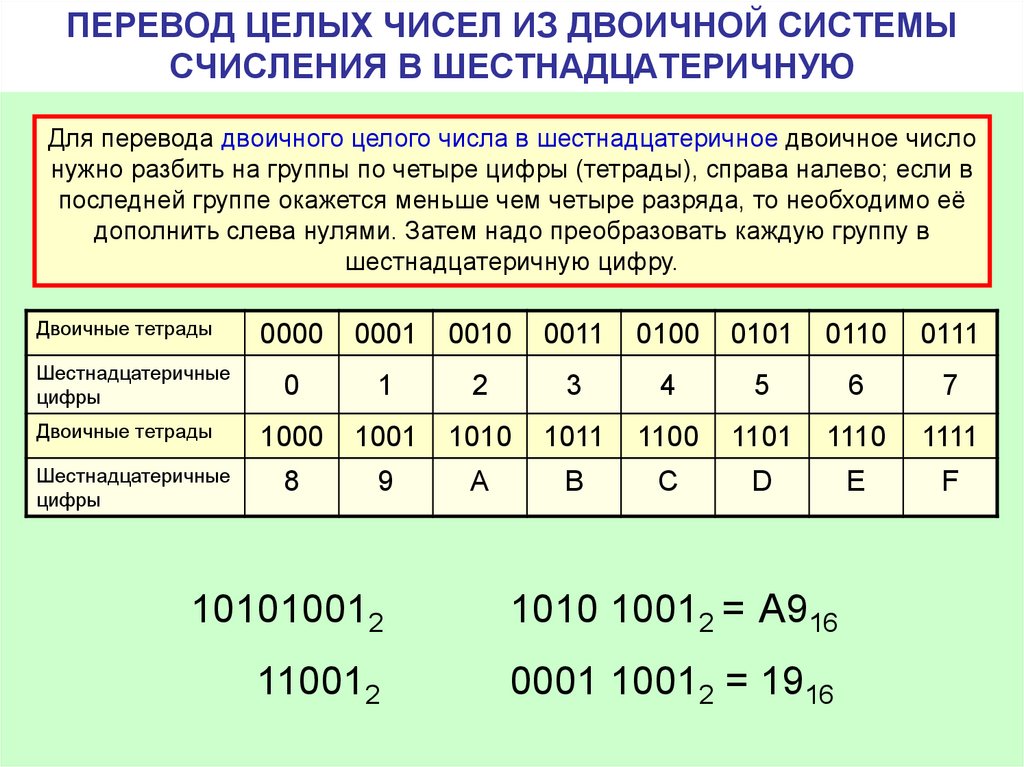

2563₈= 010 101 110 011₂=10101110011₂.

1001101₂= 001 001 101₂= 115₈.

Методические материалы для лабораторного занятия №1

Тема лабораторного занятия: Системы счисления. Измерение информации.

Количество часов: 2.

Примеры с решениями

1. Перевод из p-ичной системы в 10-ичную. Пусть надо перевести число в некоторой системе счисления в десятичную. Для этого надо представить его в виде

.

11100110₂ = 1∙2⁷ + 1∙2⁶ + 1∙2⁵ + 0∙2⁴ + 0∙2³ + 1∙2² + 1∙2¹ + 0∙2⁰ = 128 + 64 + 32 + 4 + 2 = 230₁₀.

2401₅ = 2∙5³ + 4∙5² + 0∙5¹ + 1∙5⁰ = 250 + 100 + 0 + 1 = 351.

2. Перевод из 10-ичной системы в p-ичную.

2.1 98₁₀ → Х₂.

Делим число на 2. Затем делим неполное частное на 2. Продолжаем до тех пор, пока неполное частное не станет меньше 2, т.е. равным 1.

1. 98 : 2 = 49. Остаток — 0.

2. 49 : 2 = 24. Остаток — 1.

3. 24 : 2 = 12. Остаток — 0.

4. 12 : 2 = 6. Остаток — 0.

5. 6 : 2 = 3. Остаток — 0.

6. 3 : 2 = 1. Остаток — 1.

Так как последнее неполное частное равно 1, процесс окончен. Записываем все остатки снизу вверх, начиная с последнего неполного частного, и получаем число 1100010. Итак 98₁₀ = 1100010₂.

2. 2 2391₁₀ → Х₁₆.

Делим число на 16. Затем делим неполное частное на 16. Продолжаем до тех пор, пока неполное частное не станет меньше 16.

1. 2391 : 16 = 149. Остаток — 7.

2. 149 : 16 = 9. Остаток — 5.

Так как последнее неполное частное (9) меньше 16, процесс окончен. Записываем, начиная с последнего неполного частного, все остатки снизу вверх и получаем число 957. Итак 2391

10 = 957₁₆.

2.3 12165₁₀ → Х₂.

Если переводить делением в двоичную систему, то получится довольный громоздкий процесс. Можно сначала перевести число в восьмеричную систему, а затем заменять восьмеричные цифры справа налево триадами.

12165₁₀ = 27605₈ = 010 111 110 000 101 = 10111110000101.

3. Определение основания системы счисления p.

Один мальчик так написал о себе: «Пальцев у меня 24, на каждой руке по 5, а на ногах 12». Как такое может быть?

Решение. Надо определить основание системы счисления p. Так как мы знаем, что пальцев на ногах всего 10₁₀, то 12_p=1∙p+2 = 10₁₀. Отсюда получаем уравнение p + 2 = 10  p = 8. Значит, мальчик имел в виду числа в восьмеричной системе. Действительно, всего пальцев 24₈ = 2∙8+4 = 20₁₀, а на ногах — 12₈ = 1∙8+2 = 10₁₀.

Шестнадцатеричный калькулятор онлайн

Если вам необходимо произвести математические операции в шестнадцатеричной системе счисления воспользуйтесь нашим онлайн калькулятором:

+−×÷ANDORXOR =

Просто введите шестнадцатеричные числа, выберите операцию и получите результат.

Калькулятор может производить следующие действия:

• сложение +
• вычитание −
• умножение ×
• деление ÷
• логическое И (AND)
• логическое ИЛИ ( OR)
• исключающее ИЛИ (XOR)

Сложение в шестнадцатеричной системе счисления

Сложение двух шестнадцатеричных чисел производится столбиком, как и в десятичной системе, но по следующим правилам:

+	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
2	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11
3	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12
4	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13
5	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14
6	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14	15
7	7	8	9	A	B	C	D	E	F	10	11	12	13	14	15	16
8	8	9	A	B	C	D	E	F	10	11	12	13	14	15	16	17
9	9	A	B	C	D	E	F	10	11	12	13	14	15	16	17	18
A	A	B	C	D	E	F	10	11	12	13	14	15	16	17	18	19
B	B	C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A
C	C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B
D	D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C
E	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D
F	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D	1E

Пример

Для примера сложим F4240 и 7A120:

+		F	4	2	4	0
		7	A	1	2	0
	1	6	E	3	6	0

F4240₁₆ + 7A120₁₆ = 16E360₁₆

(1 000 000₁₀ + 500 000₁₀ = 1 500 000₁₀)

Вычитание в шестнадцатеричной системе счисления

Правила вычитания шестнадцатеричных чисел обратны правилам сложения (см. таблицу выше).

Пример

Для примера вычтем из числа 16E360 число F4240:

–	1	6	E	3	6	0
		F	4	2	4	0
		7	A	1	2	0

16E360₁₆ − F4240₁₆ = 7A120₁₆

(1 500 000₁₀ − 1 000 000₁₀ = 500 000₁₀)

Умножение чисел в шестнадцатеричной системе счисления

Умножение шестнадцатеричных чисел производится по следующим правилам:

×	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	0	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E
3	0	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D
4	0	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C
5	0	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B
6	0	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A
7	0	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69
8	0	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	0	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87
A	0	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96
B	0	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5
C	0	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4
D	0	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3
E	0	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2
F	0	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1

Пример

Для примера перемножим числа 1F4 и 2D:

×		1	F	4
			2	D
+	1	9	6	4
	3	E	8
	5	7	E	4

1F4₁₆ × 2D₁₆ = 57E4₁₆

(500₁₀ × 45₁₀ = 22500₁₀)

Деление шестнадцатеричных чисел

Деление шестнадцатеричных чисел выполняется по тому же принципу, что и деление десятичных, например:

Пример

Для примера разделим число 7D0 на 2:

7D0₁₆ ÷ 2₁₆ = 3E8₁₆

(2000₁₀ ÷ 2₁₀ = 1000₁₀)

См.

также

5 в шестнадцатеричной системе. Шестнадцатеричная и двоичная системы счисления

Шестнадцатеричная система счисления имеет алфавит, состоящий из 16 цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, c, d, e, f.

При записи числа в шестнадцатеричной системе для записи цифр обозначающих числа 10, 11, 12. 13, 14. 15 используются соответственно буквы А, В, С, D, E, F.

Перевод чисел из шестнадцатеричной системы в десятичную

Перевести любое шестнадцатеричное число в десятичное можно по уже известной формуле

Примеры.

АЕ07 16 =10∙16 3 +14∙16 2 +0∙16 1 +7∙16 0 =44551 10 .

100 16 =1∙16 2 +0∙16 1 +0∙16 0 =256 10 .

58 16 =5∙16 1 +8∙16 0 =.88 10 .

2А 16 =2∙16 1 +10∙16 0 =42 10 .

Перевод числа из десятичной системы в шестнадцатеричную осуществляется также, как в двоичную.

Перевод чисел из шестнадцатеричной системы в двоичную и обратно

Перевести любое шестнадцатеричное число в двоичное можно следующим образом. Каждая цифра шестнадцатеричной записи числа записывается четырехзначным двоичным числом — тетрадой . После этого нули, стоящие слева, можно отбросить.

2) 2A= 0010 1010 2 = 101010 2 .

3) 58 16 = 0101 1000 2 = 1011000 2 .

И наоборот, перевести любое двоичное число в шестнадцатеричное можно аналогичным образом. Каждые четыре двоичные цифры, считая справа налево, записываются одной шестнадцатеричной цифрой. Эти цифры располагаются также справа налево.

Примеры.

2. 101010 2 = 10 1010 2 = 2A.

3. 1011000 2 = 101 1000 2 = 58 16 .

Восьмеричная система счисления

Восьмеричная система счисления имеет алфавит, состоящий из 8 цифр:

0, 1, 2, 3, 4, 5, 6, 7.

Перевод числа из десятичной системы в восьмеричную и обратно осуществляется по аналогии с переводом в двоичную / из двоичной.

Перевод чисел из восьмеричной системы в двоичную и обратно

Каждая цифра восьмеричной записи числа записывается трехзначным двоичным числом — триадой .

Примеры.

2563 8 = 010 101 110 011 2 =10101110011 2 .

1001101 2 = 001 001 101 2 = 115 8 .

Методические материалы для лабораторного занятия №1

Тема лабораторного занятия: Системы счисления. Измерение информации.

Количество часов: 2.

Примеры с решениями

Перевод из p -ичной системы в 10-ичную. Пусть надо перевести число в некоторой системе счисления в десятичную. Для этого надо представить его в виде

11100110 2 = 1∙2 7 + 1∙2 6 + 1∙2 5 + 0∙2 4 + 0∙2 3 + 1∙2 2 + 1∙2 1 + 0∙2 0 = 128 + 64 + 32 + 4 + 2 = 230 10 .

2401 5 = 2∙5 3 + 4∙5 2 + 0∙5 1 + 1∙5 0 = 250 + 100 + 0 + 1 = 351.

Перевод из 10-ичной системы в p -ичную.

2.1 98 10 → Х 2 .

Делим число на 2. Затем делим неполное частное на 2. Продолжаем до тех пор, пока неполное частное не станет меньше 2, т.е. равным 1.

98: 2 = 49. Остаток — 0 .

49: 2 = 24. Остаток — 1 .

24: 2 = 12. Остаток — 0 .

12: 2 = 6. Остаток — 0 .

6: 2 = 3. Остаток — 0 .

3: 2 = 1 . Остаток — 1 .

Так как последнее неполное частное равно 1, процесс окончен. Записываем все остатки снизу вверх, начиная с последнего неполного частного, и получаем число 1100010. Итак 98 10 = 1100010 2 .

2.2 2391 10 → Х 16 .

Делим число на 16. Затем делим неполное частное на 16. Продолжаем до тех пор, пока неполное частное не станет меньше 16.

2391: 16 = 149. Остаток — 7 .

149: 16 = 9 . Остаток — 5 .

Так как последнее неполное частное (9) меньше 16, процесс окончен. Записываем, начиная с последнего неполного частного, все остатки снизу вверх и получаем число 957. Итак 2391 10 = 957 16 .

2.3 12165 10 → Х 2 .

Если переводить делением в двоичную систему, то получится довольный громоздкий процесс. Можно сначала перевести число в восьмеричную систему, а затем заменять восьмеричные цифры справа налево триадами.

12165 10 = 27605 8 = 010 111 110 000 101 = 10111110000101.

Определение основания системы счисления p .

Один мальчик так написал о себе: «Пальцев у меня 24, на каждой руке по 5, а на ногах 12». Как такое может быть?

Решение. Надо определить основание системы счисления p . Так как мы знаем, что пальцев на ногах всего 10 10 , то 12 p =1∙p +2 = 10 10 . Отсюда получаем уравнение p + 2 = 10  p = 8. Значит, мальчик имел в виду числа в восьмеричной системе. Действительно, всего пальцев 24 8 = 2∙8+4 = 20 10 , а на ногах — 12 8 = 1∙8+2 = 10 10 .

0123456789ABCDEF. Приняв за основание число 16, получаем шестнадцатеричную систему счисления. Здесь мы можем воспользоваться 10 знаками десятичной системы, добавив еще 6 знаков – буквы латинского алфавита (A, B, C, D, E, F): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 10 11 12 13 14 15 Всего 16 разных знаков составляют алфавит шестнадцатеричной системы счисления. Можно записать любое число включая все эти знаки: А37, 1В45, F302, 1A3C5… — обратите внимание: используем знаки от 0 до F. Для шестнадцатеричной системы счисления q=16. Содержание.

Слайд 32 из презентации «История счёта и систем счисления» . Размер архива с презентацией 2292 КБ.

Информатика 9 класс

краткое содержание других презентаций

««Моделирование» 9 класс» — Моделирование как метод познания. Файловая система ПК. Тест завершён. Птолемей построил модель мира. Модель человека в виде детской куклы. Удобнее всего при описании траектории движения объекта использовать информационную модель. Существующие признаки объекта. Описание дерева. Удобнее всего использовать информационную модель. Список депутатов государственной Думы. Список учащихся школы; план классных комнат.

«История счёта и систем счисления» — Основание системы счисления. Десятки. Десятичное число. Славянская кириллическая нумерация. Нумерация. Цветок лотоса. Позиция цифры в числе называется разрядом. Положение цифры. В древние времена люди ходили босиком. Позиционная система счисления характеризуется своим основанием. Деление на основание. Запись чисел нового типа. Умножение двоичных чисел. Перевод десятичного числа. Арифметические действия.

«Сортировка в электронных таблицах» — Сортировка и поиск данных в электронных таблицах. Поиск данных в ЭТ. Порядок проведения вложенной сортировки. Отдел. Условия поиска записей. Запишите фамилии. Практическая работа. Сортировка по возрастанию. Порядок следования строк. Сортировка и поиск данных. Оклад и возраст. Рефлексивный экран. Сортировка данных. Выберите примеры баз данных. Сортировка записей. Разница между записью и полем. Порядок использования автофильтра.

«Циклические программы» — Составить программу. Найти сумму. Введите целое число. Найти количество трехзначных натуральных чисел. Найти сумму натуральных чисел. Вычислить. Цикл с постусловием. Напечатать на экране таблицу. Первоначальный взнос. Цикл с предусловием. Делители. Циклические программы. Информатика. Табулирование функции. Понятие цикла. Цикл с параметром. Ввод исходных данных. Таблица перевода долларов. Найти количество чисел.

«Моделирование как метод научного познания» — Таблица типа «объекты-объекты-один». Описания объекта. Метод познания окружающего мира. Решение задач. Образовательные ресурсы. Пятеро ребят. Формализация. Этапы моделирования. Мальчик. Иерархическая модель. Описание объекта моделирования. Юра. Сирень. Обозначения серверов. Технические модели. Ярусные диаграммы. Диаграмма. Тип. Моделирование как метод познания. Модели на графах. Задачи, решаемые с помощью графов.

«Что такое электронная почта» — Адрес электронной почты. Маршутизация почты. Письмо. Как работает электронная почта. X-mailer. Вопрос появления электронной почты. Дата. Копия. Электронное письмо. Структура письма. История электронной почты. Отправитель. Электронная почта.

Шестнадцатеричная система счисления. аша первая программа.

Для написания программ на Ассемблере, необходимо разобраться с шестнадцатеричной системой счисления. Ничего сложного в ней нет. Мы используем в жизни десятичную систему. Уверен, что вы все ее знаете, поэтому я постараюсь объяснить шестнадцатеричную систему, проводя аналогию с десятичной.

Итак, в десятичной системе если мы к какому-нибудь числу справа добавим нуль, то это число увеличится в 10 раз. Например: 1 х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В этой системе мы используем цифры от 0 до 9, т.е. десять разных цифр (собственно, поэтому она и называется десятичная).

В шестнадцатеричной системе мы используем, соответственно, шестнадцать «цифр». Я специально написал слово «цифр» в кавычках, т.к. в ней используются не только цифры. Да и в самом деле как так? Объясняю: от 0 до 9 мы считаем так же, как и в десятичной, а вот дальше будет так: A, B, C, D, E, F. Число F, как не трудно посчитать, будет равно 15 в десятичной системе (см. табл. 1).

Десятичное число	Шестнадцатеричное число

Таблица 1. Десятичная и шестнадцатеричная системы.

Т.о., если мы к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз.

Пример 1: 1 х 16 = 10; 10 х 16 = 100; 100 х 16 = 1000 и т.д.

Вы смогли отличить в Примере 1 шестнадцатеричные числа от десятичных? А из этого ряда: 10, 12, 45, 64, 12, 8, 19? Это могут быть как шестнадцатеричные, так и десятичные. Для того, чтобы не было путаницы, и компьютер смог бы однозначно отличить одни числа от других, в Ассемблере принято после шестнадцатеричного числа ставить символ h или H (H это сокращение от англ. hexadecimal (шестнадцатеричное). Для краткости его иногда называют просто Hex ) . А после десятичного ничего не ставить. Т.к. числа от 0 до 9 в обоих системах имеют одинаковые значения, то числа, записанные как 5 и 5h одно и тоже.

Т.о. Пример 1 (см. выше) правильнее будет записать так: 1 х 16 = 10h; 10h x 16 = 100h; 100h x 16 = 1000h. Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h = 1000h.

Для чего нужна шестнадцатеричная система, мы рассмотрим в последующих выпусках. А в данный момент для нашего примера программы, который будет рассмотрен ниже, нам необходимо знать о существовании шестнадцатеричных чисел.

Итак, подведем итог. Шестнадцатеричная система счисления состоит из 10 цифр (от 0 до 9) и 6 букв латинского алфавита (A, B, C, D, E, F). Если к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз. Очень важно уяснить данную тему , так как мы будем постоянно использовать ее при написании программ.

Теперь немного о том, как я буду строить примеры на Ассемблере. Не совсем удобно приводить их в HTML-формате, поэтому сперва будет сам код программы с пронумерованными строчками, а сразу же после него объяснения и примечания.

Примерно так:

строк	Код программы
(1)	mov ah,9

Объяснения:

В строке (1) мы делаем то-то, а в строке (15) то-то.

Огромная просьба: НЕ копируйте программы со страницы в буфер, а затем не вставляйте их в Блокнот (или еще куда-нибудь)! Перепечатывайте их вручную в текстовом редакторе. Если есть принтер, то выделите программу, распечатайте выделенный фрагмент, а затем перебейте в редактор с бумаги. Все примеры нужно набирать самостоятельно! Это ускорит запоминание операторов.

И еще. Строчные и ПРОПИСНЫЕ буквы в Ассемблере не различаются. Записи вида:

Ассемблером воспринимаются одинаково. Можно, конечно, заставить Ассемблер различать строчные и ПРОПИСНЫЕ символы, но мы пока этого делать не будем. Для удобства чтения программы лучше всего операторы печатать строчными буквами, а названия подпрограмм и меток начинать с прописной. Но это как кому будет удобно.

Итак, переходим к нашей первой программе:

(1) CSEG segment

(2) org 100h

(4) Begin:

(6) mov ah,9

(7) mov dx,offset Message

(8) int 21h

(10) int 20h

(11)

(12) Message db «Hello, world!$»

(13) CSEG ends

(14) end Begin

Для того, чтобы объяснить все операторы данного примера, нам потребуется несколько выпусков. Поэтому описание некоторых команд мы просто опустим на данном этапе. Просто считайте, что так должно быть. В самое ближайшее время мы рассмотрим эти операторы подробно. Итак, строки с номерами (1), (2) и (13) вы просто игнорируете.

Строки (3), (5), (9) и (11) остаются пустыми. Это делается для наглядности. Ассемблер их будет просто опускать.

Теперь перейдем к рассмотрению остальных операторов. Со строки (4) начинается код программы. Это метка, указывающая Ассемблеру на начало кода. В строке (14) стоят операторы end Begin ( Begin англ. начало; end конец). Это конец программы. Вообще вместо слова Begin можно было бы использовать что-нибудь другое. Например, Start:. В таком случае, нам пришлось бы и завершать программу End Start (14).

Строки (6) (8) выводят на экран сообщение Hello, world!. Здесь придется вкратце рассказать о регистрах процессора (более подробно эту тему мы рассмотрим в следующем выпуске).

Регистр процессора это специально отведенная память для хранения какого-нибудь числа.

Например:

Если мы хотим сложить два числа, то в математике запишем так:

A, B и C это своего рода регистры (если говорить о компьютере), в которых могут хранится некоторые данные. А=5 можно прочитать как: Присваиваем А число 5 .

Для присвоения регистру какого-нибудь значения, в Ассемблере существует оператор mov (от англ. move загрузить). Строку (6) следует читать так: Загружаем в регистр AH число 9 (проще говоря, присваиваем AH число 9). Ниже рассмотрим зачем это надо.

В строке (7) загружаем в регистр DX адрес сообщения для вывода (в данном примере это будет строка Hello, world!$ ).

Прерывания будут подробно рассматриваться в последующих выпусках. Здесь я скажу несколько слов.

Прерывание MS-DOS это своего рода подпрограмма (часть MS-DOS) , которая находится постоянно в памяти и может вызываться в любое время из любой программы.

Рассмотрим вышесказанное на примере (мелким шрифтом выделим примечания ):

Программа сложения двух чисел

НачалоПрограммы

A=5 в переменную A заносим значение 5

B=8 в переменную B значение 8

ВызовПодпрограммы Сложение

теперь С равно 13

A=10 тоже самое, только другие числа

B=25

ВызовПодпрограммы Сложение

теперь С равно 35

КонецПрограммы

Подпрограмма Сложение

C=A+B

ВозвратИзПодпрограммы возвращаемся в то место, откуда вызывали

КонецПодпрограммы

В данном примере мы дважды вызвали подпрограмму Сложение , которая сложила два числа, переданные ей в переменных A и B. Результат помещается в переменную С. Когда вызывается подпрограмма, компьютер запоминает с какого места она была вызвана, а затем, когда закончила работу подпрограмма, компьютер возвращается в то место, откуда она вызывалась. Т.о. можно вызывать подпрограммы неопределенное количество раз с любого места.

При выполнении строки (8) программы на Ассемблере мы вызываем подпрограмму (в данном случае это называется прерывание), которая выводит на экран строку. Для этого мы, собственно, и помещаем необходимые значения в регистры. Всю необходимую работу (вывод строки, перемещение курсора) берет на себя подпрограмма. Эту строку можно прочитать так: вызываем двадцать первое прерывание ( int от англ. interrupt прерывание). Обратите внимание, что после числа 21 стоит буква h. Это, как мы уже знаем, шестнадцатеричное число (33 в десятичной системе). Конечно, нам ничего не мешает заменить строку int 21h на int 33. Программа будет работать корректно. Просто в Ассемблере принято указывать номер прерывания в шестнадцатеричной системе.

В строке (10) мы, как вы уже догадались, вызываем прерывание 20 h. Для вызова данного прерывания не нужно указывать какие-либо значения в регистрах. Оно выполняет только одну задачу: выход из программы (выход в DOS). В результате выполнения прерывания 20h, программа вернется туда, откуда ее запускали (загружали, вызывали). Например, в Norton Commander или DOS Navigator.

Строка (12) содержит сообщение для вывода. Первое слово ( message сообщение) название сообщения. Оно может быть любым (например, mess или string и пр.). Обратите внимание на строку (7), в которой мы загружаем в регистр DX адрес нашего сообщения.

Можно создать еще одну строку, которую назовем Mess2. Затем, начиная со строки (9) вставим следующие команды:

(10) mov dx,offset Mess2

(13) Message db «Hello, world!$»

(14) Mess2 db «Это Я! $»

и ассемблировать нашу программу заново. Надеюсь, что вы догадались, что произойдет

Обратите внимание на последний символ в строках Message и Mess2 — $. Он указывает на конец строки. Если мы его уберем, то 21 h прерывание продолжит вывод до тех пор, пока не встретится где-нибудь в памяти символ $. На экране мы увидим мусор .

Если у вас есть отладчик, то можно посмотреть как будет работать наша программа.

Целю настоящего выпуска не было разобраться подробно с каждым оператором . Это невозможно, т.к. у вас еще недостаточно знаний. Я полагаю, что уже через 3-4 выпуска вы поймете принцип и структуру программы на Ассемблере. Может быть, вам показался язык Ассемблера чрезвычайно сложным, но это, поверьте, с первого взгляда.

Всем, кто общается с компьютером или другой цифровой техникой, приходилось встречать загадочные записи типа 10FEF, которые кажутся непосвященным каким-то шифром. Что скрывается за этими символами? Оказывается, это просто цифры. Те, которые использует шестнадцатиричная

Системы счисления

Каждый школьник знает или хотя бы где-то слышал, что все цифры, которые мы обычно используем, образуют Это название она носит просто потому, что различных символов в ней всего десять (от 0 до 9). Любое число в нашей привычной системе может быть записано с их помощью. Однако, оказывается, использовать ее удобно бывает далеко не всегда. Например, при обмене информацией между цифровыми устройствами проще всего применять систему счисления, в которой есть только две цифры: «0» — нет сигнала — или «1» — есть сигнал (напряжение или что-то еще). Она называется двоичной. Однако, чтобы описать процессы внутри таких устройств с ее помощью, придется выполнять слишком длинные и трудные для понимания записи. Поэтому была придумана шестнадцатиричная система счисления.

Понятие шестнадцатеричной системы

Почему же для цифровых устройств используется именно система, которая содержит шестнадцать разных символов? Как известно, информация в компьютерах передается в виде байтов, которые обычно содержат 8 бит. А единица данных — машинное слово — включает в себя 2 байта, то есть 16 бит. Таким образом, с помощью шестнадцати разных символов можно описать ту информацию, которая является мельчайшей частицей при обмене. Шестнадцатиричная система счисления включает наши привычные цифры (естественно, от 0 до 9), а также первые буковки (A, B, C, D, E, F). Именно с помощью этих символов принято записывать любую единицу информации. С ними можно производить любые арифметические действия. То есть сложение, вычитание, умножение, деление. Результатом также будет шестнадцатеричное число.

Где применяется

Шестнадцатиричная система используется для записи кодов ошибок. Они могут возникать при работе различных программных продуктов. Например, так кодируются ошибки операционной системы. Каждое число при этом стандартное. Можно выяснить, какая именно ошибка произошла в процессе работы, расшифровав его с помощью инструкции. Также применяются такие символы при написании программ на языках низкого уровня, например ассемблере. Шестнадцатиричная система счисления любима программистами еще и потому, что ее составляющие очень легко могут быть переведены в двоичные, которые являются «родными» для всей цифровой техники. С помощью таких символов описывают также цветовые схемы. Кроме того, абсолютно все файлы в компьютере (и текстовые, и графические, и даже музыкальные или видео) представляются после трансляции в виде последовательности Просматривать исходный удобнее всего как раз в виде шестнадцатеричных символов.

Конечно, любое число можно записать в различных системах счисления. Это и десятичная, и двоичная, и шестнадцатеричная. Чтобы перевести слово из одной из них в другую, следует воспользоваться таким сервисом, как переводчик систем счисления, или сделать это самостоятельно с помощью определенного алгоритма.

Для представления чисел в микропроцессоре используется двоичная система счисления .
При этом любой цифровой сигнал может иметь два устойчивых состояния: «высокий уровень» и «низкий уровень». В двоичной системе счисления для изображения любого числа используются две цифры, соответственно: 0 и 1. Произвольное число x=a n a n-1 ..a 1 a 0 ,a -1 a -2 …a -m запишется в двоичной системе счисления как

x = a n ·2 n +a n-1 ·2 n-1 +…+a 1 ·2 1 +a 0 ·2 0 +a -1 ·2 -1 +a -2 ·2 -2 +…+a -m ·2 -m

где a i — двоичные цифры (0 или 1).

Восьмеричная система счисления

В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего.

Шестнадцатеричная система счисления

В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:

10 10 = A 16 12 10 = C 16 14 10 = E 16
11 10 = B 16 13 10 = D 16 15 10 = F 16 .

Например, число 175 10 в шестнадцатеричной системе счисления запишется как AF 16 . Действительно,

10·16 1 +15·16 0 =160+15=175

В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10

Двоично-восьмеричные и двоично-шестнадцатеричные преобразования

Двоичная система счисления удобна для выполнения арифметических действий аппаратными средствами микропроцессора, но неудобна для восприятия человеком, поскольку требует большого количества разрядов. Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.

Три разряда восьмеричной системы счисления реализуют все возможные комбинации восьмеричных цифр в двоичной системе счисления: от 0 (000) до 7(111). Чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда (триады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от него тоже можно добавить незначащие нули до заполнения всех триад. Затем каждая триада заменяется восьмеричной цифрой.

Пример: Преобразовать число 1101110,01 2 в восьмеричную систему счисления.

Объединяем двоичные цифры в триады справа налево. Получаем

001 101 110,010 2 = 156,2 8 .

Чтобы перевести число из восьмеричной системы в двоичную, нужно каждую восьмеричную цифру записать ее двоичным кодом:

156,2 8 = 001 101 110,010 2 .

Четыре разряда шестнадцатеричной системы счисления реализуют все возможные комбинации шестнадцатеричных цифр в двоичной системе счисления: от 0 (0000) до F(1111). Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.

Пример: Преобразовать число 1101110,11 2 в шестнадцатеричную систему счисления.

Объединяем двоичные цифры в тетрады справа налево. Получаем

0110 1110,1100 2 = 6E,C 16 .

Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно каждую шестнадцатеричную цифру записать ее двоичным кодом.

Шестнадцатеричная система счисления простыми словами. Примеры

Автор Савельев Николай На чтение 4 мин Просмотров 1. 2к. Опубликовано 18.05.2022 Обновлено 19.05.2022

Шестнадцатеричная система (англ. — Hexadecimal system ) —  это базовая система счисления с снованием 16. Она, наряду с десятичной и двоичной, является одной из наиболее часто встречающихся систем счисления в мире электроники и программирования. Важно понимать, как она работает, потому что во многих случаях имеет смысл представлять число в ней, а не в двоичной или десятичной.

Шестнадцатеричная система счисления — позиционная система счисления по основанию 16.

Википедия

Существует 16 возможных цифр, которые используют для представления чисел. 10 числовых значений, которые вы привыкли видеть в десятичных числах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9; эти значения по-прежнему представляют то же значение, что и в десятичной системе. Остальные шесть цифр представлены как A, B, C, D, E и F, которые соответствуют числам 10, 11, 12, 13, 14 и 15.

Возможно, Вы столкнетесь с представлением чисел от 10 до 15 в верхнем и нижнем регистрах. Оба варианта считаются верными. Например, A3F — это то же число, что и a3f.

Эта таблица показывает какой шестнадцатеричной цифре эквивалентно значение в десятичном и двоичном формате.

Десятичный (основание 10)	Двоичный (основание 2)	Шестнадцатеричный (основание 16)
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	А
11	1011	B
12	1100	С
13	1101	D
14	1110	Е
15	1111	F

таблица 16 ричной системы счисления

Содержание

1. Перевод из шестнадцатеричной системы и в нее
2. Преобразование из десятичной в шестнадцатеричную систему и обратно
3. Преобразование из двоичной в шестнадцатеричную систему и обратно
4. Использование шестнадцатеричной системы
5. Цвета

Перевод из шестнадцатеричной системы и в нее

Преобразование из десятичной в шестнадцатеричную систему и обратно

Чтобы перевести десятичное число в шестнадцатеричное, нужно следовать простому алгоритму преобразования:

1. Делим десятичное число на 16.
2. Записываем остаток и переводим его в шестнадцатеричный формат.
3. Делим результат прошлого действия снова на 16.
4. Повторяем, пока в результате мы не получим 0.
5. Переписываем записанные остатки в обратном порядке.
6. Пример:

   Переведем десятеричное число 1515 в шестнадцатеричную систему

Деление	Частное	Остаток	Порядок записи (от последнего к первому)
1515/16	94	11 = B	3
94/16	5	14 = E	2
5/16	0	5 = 5	1

Ответ: 5EB

Читайте также: Проверяю стратегию Мартингейла на Python и показываю, почему она не работает

Чтобы перевести шестнадцатеричное число в десятичное, нужно каждую цифру с конца этого числа умножить на 16 в степени, соответствующей разряду этой цифры.

Преобразование из двоичной в шестнадцатеричную систему и обратно

Чтобы перевести двоичное число в шестнадцатеричное, нужно разделить его на группы по 4 цифры и заменить каждую группу на эквивалент из таблицы

• Пример:

  Переведем двоичное число 1010000011111 в шестнадцатеричную систему

  Для этого разбиваем число на группу по 4 цифры: 0001 0100 0001 1111

  0001 = 1; 0100 = 4; 0001 = 1; 1111 = F

  Ответ: 141F

Чтобы сделать обратное преобразование, нужно просто каждую цифру шестнадцатеричного числа заменить на эквивалент по таблице

• Пример:

  Переведем шестнадцатеричное число 141F в двоичную систему

  1= 0001; 4 = 0100; 1 = 0001; F = 1111

  Ответ: 1010000011111

Использование шестнадцатеричной системы

По большей части, шестнадцатеричные коды используются во многих областях вычислительной техники для сокращения двоичного кода до более понятной формы. Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:

• Ссылки на цвета в HTML и CSS
• Язык ассемблера
• Сообщения об ошибках

Цвета

Hex система счисления может использоваться для представления цветов на сайтах и в программах редактирования изображений в формате #RRGGBB (# = показатель того, что число было записано в шестнадцатеричном формате, RR = красный, GG = зеленый, BB = синий). Этот система использует две шестнадцатеричных цифры для каждого цвета, например, #AA3300.

Как одна шестнадцатеричная цифра представляет 4 бита, так две шестнадцатеричные цифры вместе составляют 8 бит (1 байт). Значения для каждого цвета находятся в диапазоне от 00 до FF.  В двоичной системе, 00 — это 00000000, а FF — это 11111111. Это дает 256 возможных значений для каждого из трех цветов (256 красных х 256 зеленых х 256 синих), а в сумме это больше 16 миллион цветов.

• #FF0000 будет самым чистым красным цветом — Максимум красного, 0 зеленого и 0 синего.
• Черный это #000000 — ни красного, ни зеленого, ни синего.
• Белый — это #FFFFFF — при смешении всех цветов.

Visual Basic с нуля. Перевод из шестнадцатеричной системы счисления в десятичную.

Visual Basic с нуля. Перевод из шестнадцатеричной системы счисления в десятичную.

	Статьи к пособию-самоучителю on-line «Visual Basic с нуля»
	Шестнадцатеричное представление числа. Перевод из шестнадцатеричной системы счисления в десятичную.
	Скачать исходник примера Hex	Дата создания 03.06.2005 {Автор 4us}

Если ты, мой уважаемый друг еще не столкнулся с необходимостью перевода в шестнадцатеричную систему и обратно, то рано или поздно, это произойдет. Я не хочу говорить о том, что именно шестнадцатеричная система главная в программировании, это и так ясно. С ней постоянно сталкивается даже обычный пользователь, например, при определении RGB цвета во всех приличных программах. А уж человеку, поставившему на свой компьютер Visual Basic и сам бог велел.
При описании флагов или объявлении констант мы постоянно пользуемся именно шестнадцатеричным представлением числа, не говоря о том, что сканирование и поиск данных в двоичных файлах вообще без этой системы в некоторых случаях невозможен. Поэтому я считаю своим долгом очень кратко сказать следующее:
в шестнадцатеричной системе 16 цифр (это не открытие), последние шесть из которых представляются латинскими буквами A, B, C, D, E и F. Представление чисел в шестнадцатиричной форме (и на всякий случай в двоичной) показано в таблице:

Десятичная	Шестнадцатеричная	Двоичная
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Чтобы явно задать число в шестнадцатеричном виде, надо перед числом поставить символы &H. Например, оператор
b=&h25
присваивает переменной b значение 21 в десятичном представлении.
Для перевода в шестнадцатеричное представление в VB имеется функция Hex:
переменная= Hex (число)
где число — любое строковое или числовое выражение. Если число не целое, то оно округляется до ближайшего целого,
Эта функция возвращает (обратите внимание) строковое шестнадцатеричное представление числа до 8 знаков. Если число имеет недопустимое значение (Null ), то функция возвращает пустое значение. Если число является пустым значением (Empty), то функция возвращает ноль.
Ну тут и так все ясно и не для этого я пишу эту статейку. А пишу я ее вот для чего.
Иногда возникает необходимость преобразовать шестнадцатеричное число в десятичное. Для этого существует определенный алгоритм. Допустим нам надо преобразовать число A20D14 в десятичное.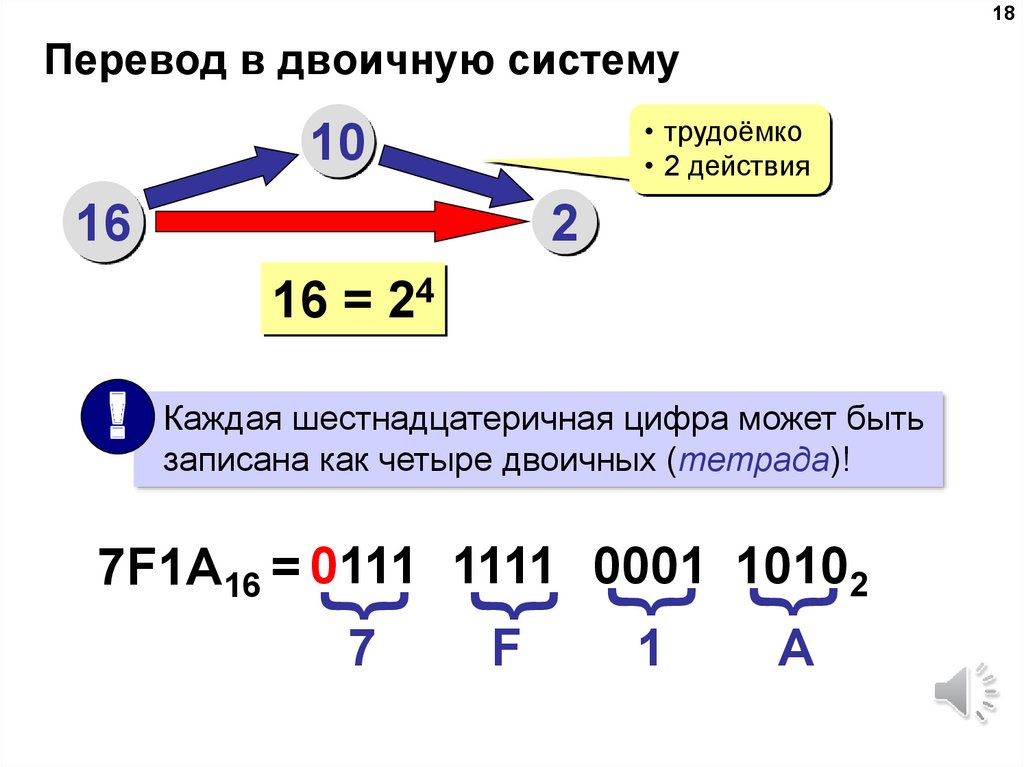 0)=10620180

Т. е. мы получаем сумму произведений из шестнадцатеричной цифры, представленой в десятичном виде, умноженную на 16 (основание системы счисления) в степени «позиция шестнадцатиричной цифры справа» минус 1. Этот алгоритм легко реализовать программно. Удобнее это оформить функцией в стандартном модуле, с тем, чтобы в проекте пользоваться ей так же как и функцией Hex. Содержимое модуля может выглядеть приблизительно так:

Option Explicit
‘Объявим функцию, где в heximal мы будем передавать наше шестнадцатеричное число
Function ConvertDec(heximal) As Long
‘объявим две переменные
‘одну для шестнадцатеричной цифры числа
Dim Simvol As String
‘вторую для соответствующей ему десятичной цифры
Dim DesChislo As Long
‘а так же переменную для цикла
Dim x As Long
‘обнулим
ConvertDec = 0
‘переберем все цифры шестнадцатеричного числа
‘и каждой поставим в соотвествие десятичную
For x = 1 To Len(heximal)
Simvol = Mid(heximal, x, 1)
If UCase(Simvol) = «A» Then
DesChislo = 10
ElseIf UCase(Simvol) = «B» Then
DesChislo = 11
ElseIf UCase(Simvol) = «C» Then
DesChislo = 12
ElseIf UCase(Simvol) = «D» Then
DesChislo = 13
ElseIf UCase(Simvol) = «E» Then
DesChislo = 14
ElseIf UCase(Simvol) = «F» Then
DesChislo = 15
Else
DesChislo = Val(Simvol)
End If
‘накапливаем в нашей функции результат
ConvertDec = ConvertDec + DesChislo * 16 ^ (Len(heximal) — x)
Next x
‘вот и все
End Function

Теперь мы можем на форме проекта разместить четыре TextBox’а и сделать в Text1 и Text2 перевод чисел в шестнадцатеричное представление и наоборот соответственно.

Private Sub Text1_Change()
If Text1 <> «» Then Text3 = Hex(Text1) Else Text3 = «»
End Sub

Private Sub Text2_Change()
If Text2 <> «» Then Text4 = ConvertDec(Text2) Else Text4 = «»
End Sub

Скачать это все можно вверху страницы.

 

Copyright © 2005 4us

Сайт создан в системе uCoz

Таблица преобразования десятичной-шестнадцатеричной-двоичной системы

Таблица преобразования десятичной-шестнадцатеричной-двоичной системы

The first, fourth, seventh, and tenth columns list a decimal value. The second, fifth, eighth, and eleventh columns list a matching hexadecimal value for the decimal values. The third, sixth, ninth, and twelfth columns list a matching binary value for the decimal values.»>

Декабрь	Шестигранник	Корзина		декабрь	Шестигранник	Корзина		декабрь	Шестигранник	Корзина		декабрь	Шестнадцатеричный	Корзина
0	0	00000000		64	40	01000000		128	80	10000000		192	с0	11000000
1	1	00000001		65	41	01000001		129	81	10000001		193	с1	11000001
2	2	00000010		66	42	01000010		130	82	10000010		194	с2	11000010
3	3	00000011		67	43	01000011		131	83	10000011		195	с3	11000011
4	4	00000100		68	44	01000100		132	84	10000100		196	с4	11000100
5	5	00000101		69	45	01000101		133	85	10000101		197	с5	11000101
6	6	00000110		70	46	01000110		134	86	10000110		198	с6	11000110
7	7	00000111		71	47	01000111		135	87	10000111		199	с7	11000111
8	8	00001000		72	48	01001000		136	88	10001000		200	с8	11001000
9	9	00001001		73	49	01001001		137	89	10001001		201	с9	11001001
10	и	00001010		74	4а	01001010		138	8а	10001010		202	примерно	11001010
11	б	00001011		75	4б	01001011		139	8б	10001011		203	кб	11001011
12	в	00001100		76	4с	01001100		140	8с	10001100		204	куб. см	11001100
13	д	00001101		77	4д	01001101		141	8д	10001101		205	компакт-диск	11001101
14	и	00001110		78	4е	01001110		142	8e	10001110		206	CE	11001110
15	ф	00001111		79	4ф	01001111		143	8f	10001111		207	в сравнении с	11001111
16	10	00010000		80	50	01010000		144	90	10010000		208	д0	11010000
17	11	00010001		81	51	01010001		145	91	10010001		209	д1	11010001
18	12	00010010		82	52	01010010		146	92	10010010		210	д2	11010010
19	13	00010011		83	53	01010011		147	93	10010011		211	д3	11010011
20	14	00010100		84	54	01010100		148	94	10010100		212	д4	11010100
21	15	00010101		85	55	01010101		149	95	10010101		213	д5	11010101
22	16	00010110		86	56	01010110		150	96	10010110		214	д6	11010110
23	17	00010111		87	57	01010111		151	97	10010111		215	д7	11010111
24	18	00011000		88	58	01011000		152	98	10011000		216	д8	11011000
25	19	00011001		89	59	01011001		153	99	10011001		217	д9	11011001
26	1а	00011010		90	5а	01011010		154	9а	10011010		218	да	11011010
27	1б	00011011		91	5б	01011011		155	9б	10011011		219	дб	11011011
28	1с	00011100		92	5с	01011100		156	9с	10011100		220	постоянный ток	11011100
29	1д	00011101		93	5д	01011101		157	9д	10011101		221	дд	11011101
30	1е	00011110		94	5e	01011110		158	9е	10011110		222	из	11011110
31	1ф	00011111		95	5f	01011111		159	9ф	10011111		223	дф	11011111
32	20	00100000		96	60	01100000		160	а0	10100000		224	е0	11100000
33	21	00100001		97	61	01100001		161	а1	10100001		225	е1	11100001
34	22	00100010		98	62	01100010		162	а2	10100010		226	е2	11100010
35	23	00100011		99	63	01100011		163	а3	10100011		227	е3	11100011
36	24	00100100		100	64	01100100		164	а4	10100100		228	е4	11100100
37	25	00100101		101	65	01100101		165	а5	10100101		229	e5	11100101
38	26	00100110		102	66	01100110		166	а6	10100110		230	е6	11100110
39	27	00100111		103	67	01100111		167	а7	10100111		231	е7	11100111
40	28	00101000		104	68	01101000		168	а8	10101000		232	е8	11101000
41	29	00101001		105	69	01101001		169	а9	10101001		233	е9	11101001
42	2а	00101010		106	6а	01101010		170	аа	10101010		234	Шт.	11101010
43	2б	00101011		107	6б	01101011		171	аб	10101011		235	иб	11101011
44	2с	00101100		108	6с	01101100		172	ак	10101100		236	эк	11101100
45	2д	00101101		109	6д	01101101		173	объявление	10101101		237	изд	11101101
46	2е	00101110		110	6e	01101110		174		10101110		238	ее	11101110
47	2ф	00101111		111	6f	01101111		175	и	10101111		239	и	11101111
48	30	00110000		112	70	01110000		176	б0	10110000		240	ф0	11110000
49	31	00110001		113	71	01110001		177	б1	10110001		241	ф1	11110001
50	32	00110010		114	72	01110010		178	б2	10110010		242	ф2	11110010
51	33	00110011		115	73	01110011		179	б3	10110011		243	ф3	11110011
52	34	00110100		116	74	01110100		180	б4	10110100		244	ф4	11110100
53	35	00110101		117	75	01110101		181	б5	10110101		245	ф5	11110101
54	36	00110110		118	76	01110110		182	б6	10110110		246	ф6	11110110
55	37	00110111		119	77	01110111		183	б7	10110111		247	ф7	11110111
56	38	00111000		120	78	01111000		184	б8	10111000		248	ф8	11111000
57	39	00111001		121	79	01111001		185	б9	10111001		249	ф9	11111001
58	3а	00111010		122	7а	01111010		186	ба	10111010		250	фа	11111010
59	3б	00111011		123	7б	01111011		187	бб	10111011		251	фб	11111011
60	3с	00111100		124	7с	01111100		188	до н. э.	10111100		252	фк	11111100
61	3д	00111101		125	7д	01111101		189	бд	10111101		253	фд	11111101
62	3е	00111110		126	7e	01111110		190	будет	10111110		254	и	11111110
63	3f	00111111		127	7ф	01111111		191	бф	10111111		255	и далее	11111111

: Это документ afdl в базе знаний.
Последнее изменение: 2017-11-29 15:56:21 .

преобразовать десятичное число 14 в шестнадцатеричное

Как записать 14 в шестнадцатеричное (с основанием 16)?

14 e в шестнадцатеричной форме

Котировки Преобразование в другие базы Бинарный: Четвертичный: Восьмеричный: Десятичный: Шестнадцатеричный: База 32:

Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования десятичной базы. Здесь вы можете найти ответ на такие вопросы, как: преобразовать десятичное число 14 в шестнадцатеричное или преобразование десятичного числа в шестнадцатеричное.

Dec	Hex	Oct	Bin
0	0	0	0
1	1	1	1
2	2	2	10
3	3	3	11
4	4	4	100
5	5	5	101
6	6	6	110
7	7	7	111
8	8	10	1000
9	9	11	1001
10	A	12	1010
11	B	13	1011
12	C	14	1100
13	D	15	1101
14	E	16	1110
15	F	17	1111

Dec	Hex	Oct	Bin
16	10	20	10000
17	11	21	10001
18	12	22	10010
19	13	23	10011
20	14	24	10100
21	15	25	10101
22	16	26	10110
23	17	27	10111
24	18	30	11000
25	19	31	11001
26	1A	32	11010
27	1B	33	11011
28	1C	34	11100
29	1D	35	11101
30	1E	36	11110
31	1F	37	11111

Dec	Hex	Oct	Bin
32	20	40	100000
33	21	41	100001
34	22	42	100010
35	23	43	100011
36	24	44	100100
37	25	45	100101
38	26	46	100110
39	27	47	100111
40	28	50	101000
41	29	51	101001
42	2A	52	101010
43	2B	53	101011
44	2C	54	101100
45	2D	55	101101
46	2E	56	101110
47	2F	57	101111

Dec	Hex	Oct	Bin
48	30	60	110000
49	31	61	110001
50	32	62	110010
51	33	63	110011
52	34	64	110100
53	35	65	110101
54	36	66	110110
55	37	. 0022	111001
58	3A	72	111010
59	3B	73	111011
60	3C	74	111100
61	3D	75	111101
62	3E	76	111110
63	3F	77	111111

Dec	Hex	Oct	Bin
64	40	100	1000000
65	41	101	1000001
66	42	102	1000010
.0022	1000100
69	45	105	1000101
70	46	106	1000110
71	47	107	1000111
72	48	110	1001000
73	49	111	1001001
74	4A	112	1001010
75	4B	113	1001011
76	4C	114	1001100
77	4D	115	1001101
78	4E	116	1001110
79	4F	117	1001111

120202020202020 2

3444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444318318318183н

2020202020202021. 2183 Hex Oct Bin 80 50 120 1010000 81 51 121 1010001 82 52 122 1010010 83 53.0021 55 125 1010101 86 56 126 1010110 87 57 127 1010111 88 58 130 1011000 89 59 131 1011001 90 5A 132 1011010 91 5B 133 1011011 92 5C 134 1011100 93 5D 135 1011101 94 5E 136 1011110 95 5F 137 1011111

Dec	Hex	Oct	Bin
96	60	140	1100000
97	61	141	1100001
98	62	142	1100010
99	63	143	1100011
100	64	144	1100100
101	65	145	1100101
102	66	146	1100110
103	67	147	1100111
104	68	150	1101000
105	69	151	1101001
106	6A	152	1101010
107	6B	153	1101011
108	6C	154	1101100
109	6D	155	1101101
110	6E	156	1101110
111	6F	157	1101111

Dec	Hex	Oct	Bin
112	70	160	1110000
113	71	161	1110001
114	72	162	1110010
115	73	163	1110011
116	74	164	1110100
117	75	165	1110101
118	76	166	1110110
119	77	167	1110111
120	78	170	1111000
121	79	171	1111001
122	7A	172	1111010
123	7B	173	1111011
124	7C	174	1111100
125	7D	175	1111101
126	7E	176	1111110
127	7F	177	1111111

Dec	Hex	Oct	Bin
128	80	200	10000000
129	81	201	10000001
130	82	202	10000010
131	83	203	10000011
132	84	204	10000100
133	85	205	10000101
134	86	206	10000110 2922	. 0020	135	87	207	10000111
136	88	210	10001000
137	89	211	10001001
138	8A	212	10001010
139	8B	213	10001011
140	8C	214	10001100
141	8D	215	10001101
142	8E	216	10001110
143	8F	217	10001111

Dec	Hex	Oct	Bin
144	90	220	10010000
145	91	221	10010001
146	92	222	10010010
147	93	223	10010011
148	94	224	10010100
149	95	225	10010101
150	96	226	10010110
151	97	227	10010111
152	98	230	10011000
153	99	231	10011001
154	9A	232	10011010
155	9B	233	10011011
156	9C	234	10011100
157	9D	235	10011101
158	9E	236	10011110
159	9F	237	10011111

Dec	Hex	Oct	Bin
160	A0	240	10100000
161	A1	241	10100001
162	A2	242	10100010
163	A3	243	10100011
164	A4	244	10100100
165	A5	245	10100101
166	A6	246	10100110
167	A7	247	10100111
168	A8	250	10101000
169	A9	251	10101001
170	AA	252	10101010
171	AB	253	10101011
172	AC	254	10101100
173	AD	255	10101101
174	AE	256	10101110
175	AF	257	10101111

2020201

Dec	Hex	Oct	Bin
176	B0	260	10110000
177	B1	261	10110001	2
	10110001	2
		10110001	1		10110001	19121		. 0022	B2	262	10110010
179	B3	263	10110011
180	B4	264	10110100
181	B5	265	10110101
182	B6	266	10110110
183	B7	267	10110111
184	B8	270	10111000
185	B9	271	10111001
186	BA	272	10111010
187	BB	273	10111011
188	BC	274	10111100
189	BD	275	10111101
190	BE	276	10111110
191	BF	277	10111111

Dec	Hex	Oct	Bin
192	C0	300	11000000
193	C1	301	11000001
194	C2	302	11000010
195	C3	303	11000011
196	C4	304	11000100
197	C5	305	11000101
198	C6	306	11000110
199	C7	307	11000111
200	C8	310	11001000
201	C9	311	11001001
202	CA	312	11001010
203	CB	313	11001011
204	CC	314	11001100
205	CD	315	11001101
206	CE	316	11001110
207	CF	317	11001111

Dec	Hex	Oct	Bin
208	D0	320	11010000
209	D1	321	11010001
210	D2	322	11010010
211	D3	323	11010011
212	D4	324	11010100
213	D5	325	11010101
214	D6	326	11010110
215	D7	327	11010111
216	D8	330	11011000
217	D9	331	11011001
218	DA	332	11011010
219	DB	333	11011011
220	DC	334	11011100
221	DD	335	11011101
222	DE	336	11011110
223	DF	337	11011111

Dec	Hex	Oct	Bin
224	E0	340	11100000
225	E1	341	11100001
226	E2	342	11100010
227	E3	343	11100011
228	E4	344	11100100
229	E5	345	11100101
230	E6	346	11100110
231	E7	347	11100111
232	E8	350	11101000
233	E9	351	11101001
234	EA	352	11101010
235	EB	353	11101011
236	EC	354	11101100
237	ED	355	11101101
238	EE	356	11101110
239	EF	357	11101111

121120120121121121121

Dec	Hex	Oct	Bin
240	F0	360	11110000
241	F1	361	11110001
242	F2	362	11110010
243
243
243
243
2400 2
240021
0021 363	11110011
244	F4	364	11110100
245	F5	365	11110101
246	F6	366	11110110
247	F7	367	11110111
248	F8	370	11111000
249	F9	371	11111001
250	FA	372	11111010
251	FB	373	11111011
252	FC	374	11111100
253	FD	375	11111101
254	FE	376	11111110
	11111110
	11111110
	11111110
	11111110
	11111110
		11111110
	0022	FF	377	11111111

Преобразователь базы чисел

Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.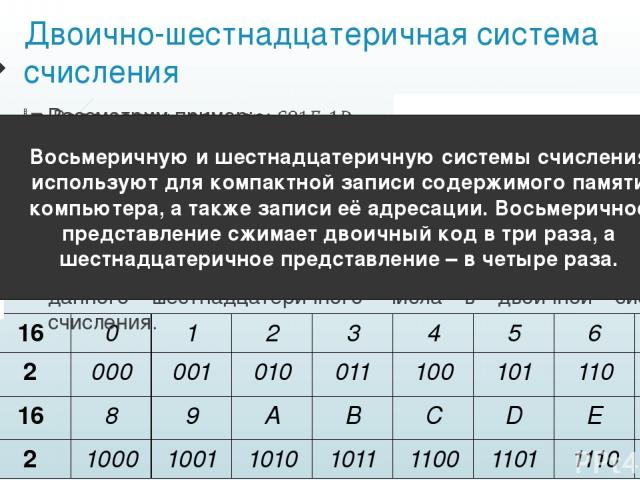

• Десятичный до шестнадцатеричной
• 10101 Двоичный до десятичного десятичного.4977
  • восьмеричное число в шестнадцатеричное
  • C0 шестнадцатеричное число в двоичное
  • E800 шестнадцатеричное число в восьмеричное

  Преобразователь десятичного числа в шестнадцатеричное

  Преобразователь десятичного числа в шестнадцатеричное

  Главная›Преобразование›Преобразование чисел›Десятичное число в шестнадцатеричное

  От BinaryDecimalOctalHexadecimalText

  Кому BinaryDecimalOctalHexadecimalText

  Введите десятичное число

  Шестнадцатеричный номер

  Дополнение до 2 с шестнадцатеричным знаком

  Двоичный номер

  Группировка цифр

  Little endian

  Адрес

  Данные

  Big endian

  Адрес

  Данные

  Шаги десятичного преобразования в шестнадцатеричный

  Разделите на 16, чтобы получить цифры из остатков:

  Деление на 16	Частное	Остаток (Цифра)	Цифра #

  Преобразователь шестнадцатеричных чисел в десятичные ►

  Как преобразовать десятичные числа в шестнадцатеричные

  Шаги преобразования:

  1. Разделите число на 16.
  2. Получить целое частное для следующей итерации.
  3. Получить остаток от шестнадцатеричной цифры.
  4. Повторяйте шаги, пока частное не станет равным 0.

  Пример #1

  Преобразование 7562 ₁₀ в шестнадцатеричный:

  Деление на 16	Частное (целое число)	Остаток (десятичный)	Остаток (шестнадцатеричный)	Цифра #
  7562/16	472	10	А	0
  472/16	29	8	8	1
  29/16	1	13	Д	2
  1/16	0	1	1	3

  SO 7562 ₁₀ = 1D8A ₁₆

  Пример № 2

  Преобразование 35631 ₁₀ в HEX:

  Дивизион на 16	Частное	Остаток (десятичный)	Остаток (шестнадцатеричный)	Цифра #
  35631/16	2226	15	Ф	0
  2226/16	139	2	2	1
  139/16	8	11	Б	2
  8/16	0	8	8	3

  So 35631 ₁₀ = 8B2F ₁₆

  Таблица преобразования десятичных чисел в шестнадцатеричные

  Десятичное число Основание 10		Шестнадцатеричный база 16
  0	0
  1	1
  2	2
  3	3
  4	4
  5	5
  6	6
  7	7
  8	8
  9	9
  10	А
  11	Б
  12	С
  13	Д
  14	Е
  15	Ф
  16	10
  17	11
  18	12
  19	13
  20	14
  21	15
  22	16
  23	17
  24	18
  25	19
  26	1А
  27	1Б
  28	1С
  29	1Д
  30	1Э
  40	28
  50	32
  60	3С
  70	46
  80	50
  90	5А
  100	64
  200	С8
  1000	3E8
  2000	7D0

  Преобразователь шестнадцатеричной системы в десятичную ►

   

  ---

  См.

  также
  • Преобразователь шестнадцатеричного кода в десятичный
  • Преобразователь десятичной системы в двоичную
  • Преобразователь десятичного числа в восьмеричное
  • Преобразователь десятичных чисел в дроби
  • Преобразователь десятичных чисел в проценты
  • Как преобразовать десятичное число в шестнадцатеричное
  • Преобразователь текста ASCII в шестнадцатеричный
  • Преобразователь цветов RGB в Hex
  • Системы счисления
  • Преобразование номера
  • 16 десятичных до шестнадцатеричных
  • 64 десятичный в шестнадцатеричный
  • 255 десятичный в шестнадцатеричный

  Напишите, как улучшить эту страницу

  ПРЕОБРАЗОВАНИЕ ЧИСЕЛ

  • ASCII, шестнадцатеричный, двоичный, десятичный преобразователь
  • Преобразователь текста ASCII в двоичный код
  • Преобразователь текста ASCII в шестнадцатеричный
  • Базовый преобразователь
  • Двоичный преобразователь
  • Преобразователь двоичного кода в текст ASCII
  • Преобразователь двоичного кода в десятичный
  • Преобразователь двоичного кода в шестнадцатеричный
  • Преобразователь даты в римские цифры
  • Преобразователь десятичных чисел в дроби
  • Преобразователь десятичных чисел в проценты
  • Преобразователь десятичной системы в двоичную
  • Преобразователь десятичного числа в восьмеричное
  • Преобразователь десятичного числа в шестнадцатеричный
  • Преобразователь градусов в градусы, минуты, секунды
  • Перевод градусов,мин,сек в градусы
  • Перевод градусов в радианы
  • Преобразователь дроби в десятичную дробь
  • Преобразователь дробей в проценты
  • Шестнадцатеричный/десятичный/восьмеричный/двоичный преобразователь
  • Преобразователь текста Hex в ASCII
  • Преобразователь шестнадцатеричного кода в двоичный
  • Преобразователь шестнадцатеричного кода в десятичный
  • Преобразователь восьмеричных чисел в десятичные
  • Преобразователь процентов в десятичные числа
  • Преобразователь процентов в дроби
  • Конвертер процентов в ppm
  Конвертер
  • частей на миллион в проценты
  Конвертер
  • ppm в ppb
  Конвертер
  • ppm в ppt
  Конвертер
  • ppb в ppm
  Конвертер
  • ppt в ppm
  • преобразователь частей на миллион
  • Перевод радиан в градусы
  • Преобразователь римских цифр
  • Преобразователь экспоненциальной записи

  RAPID TABLES

  • Рекомендовать сайт
  • Отправить отзыв
  • О

  Конвертер шестнадцатеричных чисел в десятичные

  От BinaryDecimalOctalHexadecimalText

  Кому BinaryDecimalOctalHexadecimalText

  Введите шестнадцатеричный номер

  Десятичное число

  Десятичное число из дополнения до 2 со знаком

  Двоичный номер

  Десятичные шаги вычисления

  Преобразователь десятичного числа в шестнадцатеричное ►

  Как преобразовать шестнадцатеричное число в десятичное

  Обычное десятичное число представляет собой сумму цифр, умноженных на степень 10.

  137 по основанию 10 равно каждой цифре, умноженной на соответствующую степень 10:

  137 ₁₀ = 1×10 ² +3×10 ¹ +7×10 ⁰ = 100+30+7

  Шестнадцатеричные числа читаются одинаково, но каждая цифра считается в степени 16 вместо степени 10.

  Для шестнадцатеричного числа с n цифрами:

  D _N-1 … D ₃ D ₂ D ₁ D ₀

  Умножение каждая цифра HEX с его соответствующей мощностью 16 и суммированием:

  . = D _N-1 × 16 ^N-1 + … + D ₃ × 16 ³ + D ₂ × 16 ² + D ₁ × 16 ¹ + D ₁ × 16 ¹ + D ₁ × 16 ¹ + D d ₀ ×16 ⁰

  Пример #1

  3B по основанию 16 равно каждой цифре, умноженной на соответствующую ей 16 ^N :

  3B ₁₆ = 3 × 16 ¹ +11 × 16 ⁰ = 48 +11 = 59 ₁₀

  Пример № 2

  E7A9 в базе 16 равный. С соответствующим 16 ^{9 N} :

  E7A9 ₁₆ = 14 × 16 ³ +7 × 16 ² +10 × 16 ¹ +9 × 16999 0 = 57344 +1792 +160 +160 +160 +160 +160 +160 +160 +160 +160 +950 + ⁰ = 57344 +1792 +160 + ⁰ = 57344 +1792 +160 +^{. = 59305 ₁₀}

  Пример #3

  0,8 по основанию 16:

  0,8 ₁₆ = 0×16 ⁰ +8×16 ^-1 = 0+0,5 = 0,5 ₁₀

  Таблица преобразования шестнадцатеричных чисел в десятичные

  Шестнадцатеричный основание 16	Десятичный с основанием 10	Расчет
  0	0	—
  1	1	—
  2	2	—
  3	3	—
  4	4	—
  5	5	—
  6	6	—
  7	7	—
  8	8	—
  9	9	—
  А	10	—
  Б	11	—
  С	12	—
  Д	13	—
  Е	14	—
  Ф	15	—
  10	16	1×16 1 +0×16 0 = 16
  11	17	1×16 1 +1×16 0 = 17
  12	18	1×16 1 +2×16 0 = 18
  13	19	1×16 1 +3×16 0 = 19
  14	20	1×16 1 +4×16 0 = 20
  15	21	1×16 1 +5×16 0 = 21
  16	22	1×16 1 +6×16 0 = 22
  17	23	1×16 1 +7×16 0 = 23
  18	24	1×16 1 +8×16 0 = 24
  19	25	1×16 1 +9×16 0 = 25
  1А	26	1×16 1 +10×16 0 = 26
  1Б	27	1×16 1 +11×16 0 = 27
  1С	28	1×16 1 +12×16 0 = 28
  1Д	29	1×16 1 +13×16 0 = 29
  1Э	30	1×16 1 +14×16 0 = 30
  1F	31	1×16 1 +15×16 0 = 31
  20	32	2×16 1 +0×16 0 = 32
  30	48	3×16 1 +0×16 0 = 48
  40	64	4×16 1 +0×16 0 = 64
  50	80	5×16 1 +0×16 0 = 80
  60	96	6×16 1 +0×16 0 = 96
  70	112	7×16 1 +0×16 0 = 112
  80	128	8×16 1 +0×16 0 = 128
  90	144	9×16 1 +0×16 0 = 144
  А0	160	10×16 1 +0×16 0 = 160
  В0	176	11×16 1 +0×16 0 = 176
  С0	192	12×16 1 +0×16 0 = 192
  Д0	208	13×16 1 +0×16 0 = 208
  E0	224	14×16 1 +0×16 0 = 224
  Ф0	240	15×16 1 +0×16 0 = 240
  100	256	1×16 2 +0×16 1 +0×16 0 = 256
  200	512	2×16 2 +0×16 1 +0×16 0 = 512
  300	768	3×16 2 +0×16 1 +0×16 0 = 768
  400	1024	4×16 2 +0×16 1 +0×16 0 = 1024

  Преобразователь десятичного числа в шестнадцатеричный ►

   

  ---

  См.

  также
  • Преобразователь десятичного числа в шестнадцатеричный
  • Преобразователь шестнадцатеричного кода в двоичный
  • Преобразователь двоичного кода в десятичный
  • Преобразователь восьмеричных чисел в десятичные
  • Как преобразовать шестнадцатеричный формат в десятичный
  • Преобразователь текста Hex в ASCII
  • Преобразователь цвета Hex в RGB
  • Системы счисления
  • Преобразование номера
  • 10 шестнадцатеричный в десятичный
  • 7F шестнадцатеричный в десятичный
  • FF шестнадцатеричный в десятичный

  Таблица преобразования — десятичная, шестнадцатеричная, восьмеричная, двоичная

  Декабрь Шестигранник окт Корзина 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 А В С D Е F 000 001 002 003 004 005 006 007 010 011 012 013 014 015 016 017 00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111	Декабрь Шестигранник окт Корзина 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 020 021 022 023 024 025 026 027 030 031 032 033 034 035 036 037 00010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111	Декабрь Шестигранник окт Корзина 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F 040 041 042 043 044 045 046 047 050 051 052 053 ​​ 054 055 056 057 00100000 00100001 00100010 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111	Декабрь Шестигранник окт Корзина 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F 060 061 062 063 064 065 066 067 070 071 072 073 074 075 076 077 00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111
  Декабрь Шестигранник окт Корзина 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F 100 101 102 103 104 105 106 107 110 111 112 113 114 115 116 117 01000000 01000001 01000010 01000011 01000100 01000101 01000110 01000111 01001000 01001001 01001010 01001011 01001100 01001101 01001110 01001111	Декабрь Шестигранник окт Корзина 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F 120 121 122 123 124 125 126 127 130 131 132 133 134 135 136 137 01010000 01010001 01010010 01010011 01010100 01010101 01010110 01010111 01011000 01011001 01011010 01011011 01011100 01011101 01011110 01011111	Декабрь Шестигранник окт Корзина 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 60 61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F 140 141 142 143 144 145 146 147 150 151 152 153 154 155 156 157 01100000 01100001 01100010 01100011 01100100 01100101 01100110 01100111 01101000 01101001 01101010 01101011 01101100 01101101 01101110 01101111	Декабрь Шестигранник окт Корзина 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 70 71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F 160 161 162 163 164 165 166 167 170 171 172 173 174 175 176 177 01110000 01110001 01110010 01110011 01110100 01110101 01110110 01110111 01111000 01111001 01111010 01111011 01111100 01111101 01111110 01111111
  Декабрь Шестигранник окт Корзина 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 80 81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F 200 201 202 203 204 205 206 207 210 211 212 213 214 215 216 217 10000000 10000001 10000010 10000011 10000100 10000101 10000110 10000111 10001000 10001001 10001010 10001011 10001100 10001101 10001110 10001111	Декабрь Шестигранник окт Корзина 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F 220 221 222 223 224 225 226 227 230 231 232 233 234 235 236 237 10010000 10010001 10010010 10010011 10010100 10010101 10010110 10010111 10011000 10011001 10011010 10011011 10011100 10011101 10011110 10011111	Декабрь Шестигранник окт Корзина 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 А0 А1 А2 А3 А4 А5 А6 А7 A8 A9 AA AB AC AD AE AF 240 241 242 243 244 245 246 247 250 251 252 253 254 255 256 257 10100000 10100001 10100010 10100011 10100100 10100101 10100110 10100111 10101000 10101001 10101010 10101011 10101100 10101101 10101110 10101111	Декабрь Шестигранник окт Корзина 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF 260 261 262 263 264 265 266 267 270 271 272 273 274 275 276 277 10110000 10110001 10110010 10110011 10110100 10110101 10110110 10110111 10111000 10111001 10111010 10111011 10111100 10111101 10111110 10111111
  Декабрь Шестигранник 9 окт. 0022 Корзина 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF 300 301 302 303 304 305 306 307 310 311 312 313 314 315 316 317 11000000 11000001 11000010 11000011 11000100 11000101 11000110 11000111 11001000 11001001 11001010 11001011 11001100 11001101 11001110 11001111	Декабрь Шестигранник окт Корзина 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF 320 321 322 323 324 325 326 327 330 331 332 333 334 335 336 337 11010000 11010001 11010010 11010011 11010100 11010101 11010110 11010111 11011000 11011001 11011010 11011011 11011100 11011101 11011110 11011111	9 декабря0022 Шестигранник окт Корзина 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF 340 341 342 343 344 345 346 347 350 351 352 353 354 355 356 357 11100000 11100001 11100010 11100011 11100100 11100101 11100110 11100111 11101000 11101001 11101010 11101011 11101100 11101101 11101110 11101111	декабрь Шестигранник окт Корзина 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC ФД ФЭ ФФ 360 361 362 363 364 365 366 367 370 371 372 373 374 375 376 377 11110000 11110001 11110010 11110011 11110100 11110101 11110110 11110111 11111000 11111001 11111010 11111011 11111100 11111101 11111110 11111111

  Преобразователь десятичных и шестнадцатеричных чисел

  Чтобы использовать этот инструмент для преобразования десятичных чисел в шестнадцатеричные , вы должны ввести десятичное значение, например 79, в левое поле ниже, а затем нажмите кнопку «Конвертировать». Таким образом, вы можете преобразовать до 19 десятичных символов (макс. значение72036854775807) в шестнадцатеричный формат.

  Десятичное значение (макс.:72036854775807)

  Шестнадцатеричное значение преобразование подкачки: Hex в Decimal

  Преобразование десятичного числа в шестнадцатеричное приводит к базовым числам

  Десятичная система счисления

  Десятичная система счисления является наиболее часто используемой и стандартной системой в повседневной жизни. В качестве основы (основания) используется число 10. Следовательно, он имеет 10 символов: цифры от 0 до 9; а именно 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

  Как одна из старейших известных систем счисления, десятичная система счисления использовалась многими древними цивилизациями. Трудность представления очень больших чисел в десятичной системе была преодолена индо-арабской системой счисления. Индо-арабская система счисления дает позиции цифрам в числе, и этот метод работает с использованием степени основания 10; цифры возводятся до n ^-й мощности, в соответствии со своим положением.

  Например, возьмем число 2345,67 в десятичной системе:

  • Цифра 5 стоит на позиции единиц (10 ⁰ , что равно 1),
  • 4 стоит на позиции десятков (10 ¹ )
  • 3 стоит на позиции сотен (10 ² )
  • 2 находится в позиции тысяч (10 ³ )
  • При этом цифра 6 после запятой находится в десятых долях (1/10, что равно 10 ^-1 ) и 7 находится в сотых (1/100, то есть 10 ^-2 ) позиции
  • Таким образом, число 2345,67 можно также представить следующим образом: (2 * 10 ³ ) + (3 * 10 ² ) + (4 * 10 ¹ ) + (5 * 10 ⁰ ) + (6 * 10 ^-1 ) + (7 * 10 ^-2 )

  Шестнадцатеричная система (шестнадцатеричная система)

  Шестнадцатеричная система (коротко шестнадцатеричная) использует число 16 в качестве основания (основания). 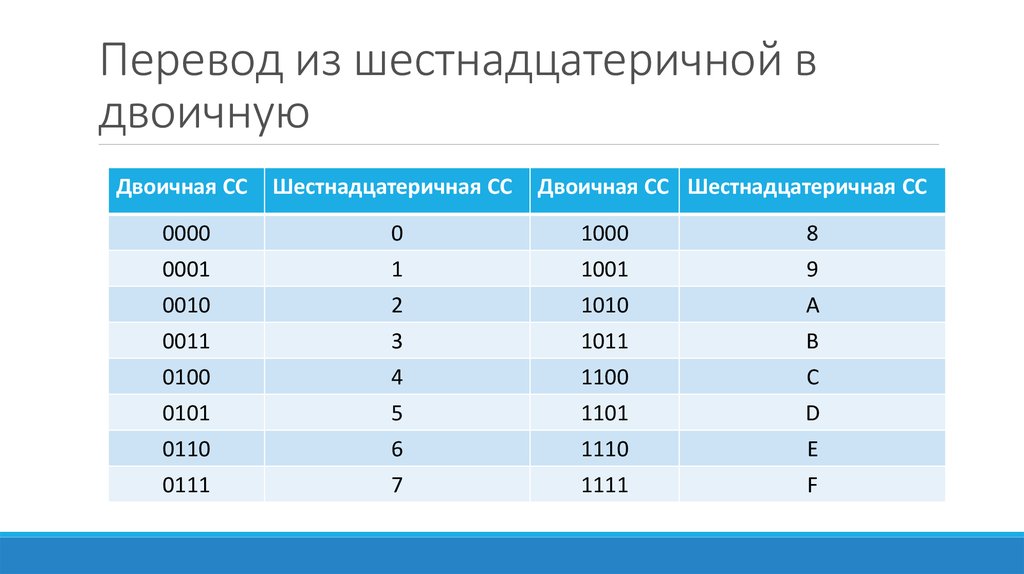В системе счисления с основанием 16 используется 16 символов. Это 10 десятичных цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).) и первые шесть букв английского алфавита (A, B, C, D, E, F). Буквы используются из-за необходимости представлять значения 10, 11, 12, 13, 14 и 15 каждое в одном единственном символе.

  Hex используется в математике и информационных технологиях как более удобный способ представления двоичных чисел. Каждая шестнадцатеричная цифра представляет четыре двоичных цифры; следовательно, hex — это язык для записи двоичного кода в сокращенной форме.

  Четыре двоичных разряда (также называемых полубайтами) составляют половину байта. Это означает, что один байт может содержать двоичные значения от 0000 0000 до 1111 1111. В шестнадцатеричном формате они могут быть представлены более удобным образом, в диапазоне от 00 до FF.

  В программировании HTML цвета могут быть представлены 6-значным шестнадцатеричным числом: FFFFFF представляет белый цвет, тогда как 000000 представляет черный цвет.

  Преобразование десятичного числа в шестнадцатеричное

  Преобразование десятичного числа в шестнадцатеричное может быть достигнуто путем применения повторяющегося алгоритма деления и остатка. Проще говоря, десятичное число многократно делится по основанию 16. Между этими делениями остатки дают шестнадцатеричный эквивалент в обратном порядке.

  Вот как шаг за шагом преобразовать десятичное число в шестнадцатеричное:

  • Шаг 1 : Если заданное десятичное число меньше 16, шестнадцатеричный эквивалент тот же. Помня, что буквы A, B, C, D, E и F используются для значений 10, 11, 12, 13, 14 и 15, преобразуйте их соответствующим образом. Например, десятичное число 15 будет F в шестнадцатеричном формате.
  • Шаг 2 : Если данное десятичное число равно 16 или больше, разделите число на 16.
  • Шаг 3 : Запишите остаток.
  • Шаг 4 : Разделите часть до запятой вашего частного еще раз на 16. 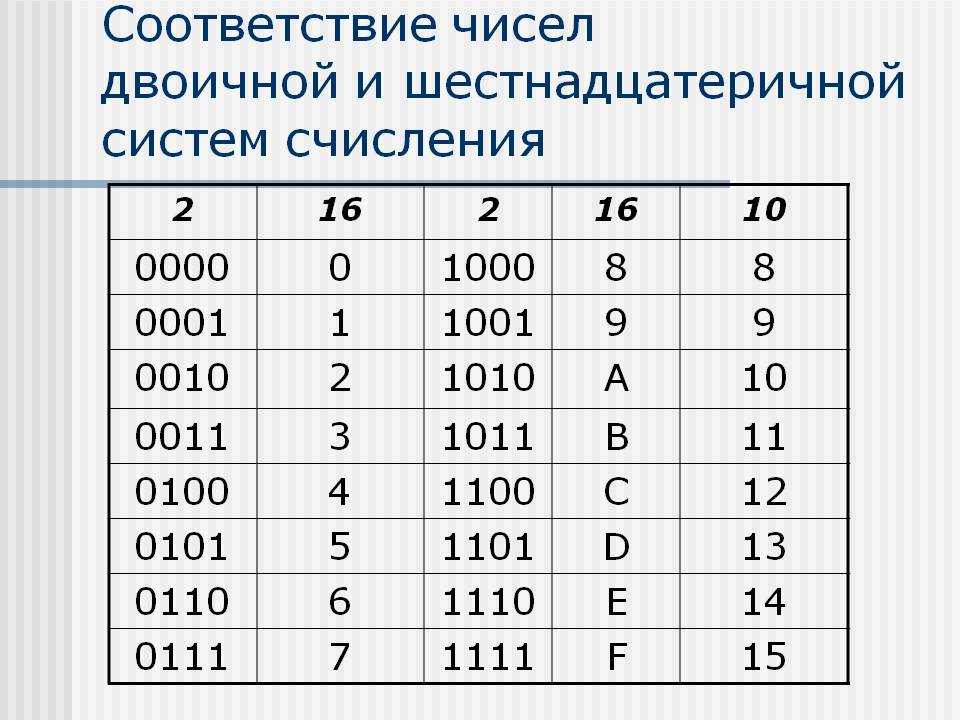Запишите остаток.
  • Шаг 5 : Продолжайте этот процесс деления на 16 и записывая остатки до тех пор, пока последняя десятичная цифра, которая у вас останется, не будет меньше 16.
  • Шаг 6 : Когда последняя десятичная цифра меньше 16, частное будет меньше 0, а остаток будет самой цифрой.
  • Шаг 7 : Последний остаток, который вы получите, будет старшей цифрой вашего шестнадцатеричного значения, а первый остаток шага 3 будет младшей значащей цифрой. Поэтому, когда вы записываете остатки в обратном порядке — начиная снизу со старшей цифры и идя вверх — вы достигнете шестнадцатеричного значения данного десятичного числа.

  Теперь давайте применим эти шаги, например, к десятичному числу (501) ₁₀

  Шаг 1: Поскольку 501 больше 16, разделите на 16.
  501 ÷ 16 = 31,3125
  Шаг 2: Чтобы вычислить остаток, нужно часть после запятой умножить на 16.
  0,3125 * 16 = 5
  Таким образом, первый остаток (и наименее значащая цифра в шестнадцатеричном формате) равен 5. 
  Шаг 3: Разделите 31 (часть частного до запятой) на 16.
  31 ÷ 16 = 1,9375
  Шаг 4: Рассчитайте остаток.
  0,9375 * 16 = 15
  Шаг 5: Разделите целую часть последнего частного на 16.
  1 ÷ 16 = 0,0625
  Шаг 6: Рассчитайте остаток.
  0,0625 * 16 = 1
  Шаг 7: Остатки, написанные снизу вверх, дают вам шестнадцатеричные значения 1, 15 и 5.
  Поскольку 15 равняется F в шестнадцатеричных цифрах, (501)  10  = (1F5)  16  

  Десятичные в HEX -преобразование. 4253 ÷ 16 = 265,8125 0,8125 * 16 = 13 (Остаток 13, эквивалент D в шестнадцатеричном формате) 265 ÷ 16 = 16,5625 0,5625 * 16 = 9(Остаток 9) 16 ÷ 16 = 1 (Остаток 0) 1 ÷ 16 = 0,0625 0,00625*16:1 (Остаток 1) Прочтите остатки от наиболее значимого к наименее — снизу вверх: 109D. 109D шестнадцатеричный эквивалент (4253)

  ₁₀

  Пример 2: (16) ₁₀ = (10) ₁₆

  16 ÷ 16 = 1 (Остаток 0)
  1 ÷ 16 = 0,0625
  0,00625*16:1 (Остаток 1)
   

  Пример 3: (45) ₁₀ = (2D) ₁₆

  45 ÷ 16 = 2,8125
  0,8125 * 16 = 13 (Остаток 13, эквивалент D в шестнадцатеричном формате)
  2 ÷ 16 = 0,125
  0,125 * 16 = 2 (Остаток 2)
   

  Таблица преобразования десятичных и шестнадцатеричных чисел

  Десятичное число	Шестнадцатеричное число
  1	1
  2	2
  3	3
  4	4
  5	5
  6	6
  7	7
  8	8
  9	9
  10	A
  11	B
  12	C
  13	D
  14	E
  15	F
  16	10
  17	11
  18	12
  19	13
  20	14
  21	15
  22	16
  23	17
  24	18
  25	19
  26	1A
  27	1B
  28	1C
  29	1D
  30	1E
  31	1F
  32	20
  33	21
  34	22
  35	23
  36	24
  37	25
  38	26
  39	27
  40	28
  41	29
  42	2A
  43	2B
  44	2C
  45	2D
  46	2E
  47	2F
  48	30
  49	31
  50	32
  51	33
  52	34
  53	35
  54	36
  55	37
  56	38
  57	39
  58	3A
  59	3B
  60	3C
  61	3D
  62	3E
  63	3F
  64	40
  65	41
  66	42
  67	43
  68	44
  69	45
  70	46
  71	47
  72	48
  73	49
  74	4A
  75	4B
  76	4C
  77	4D
  78	4E
  79	4F
  80	50

  Десятичный	Шестнадцатеричный
  81	51
  82	52
  83	53
  84	0021 54
  85	55
  86	56
  87	57
  88	58
  89	59
  90	5A
  91	5B
  92	5C
  93	5D
  94	5E
  95	5F
  96	60
  97	61
  98	62
  99	63
  100	64
  101	65
  102	66
  103	67
  104	. 0022	6A
  107	6B
  108	6C
  109	6D
  110	6E
  111	6F
  112	70
  113	71
  114	72
  115	73
  116	74
  117	75
  118	76
  119	77
  120	78
  121	79
  122	7A
  123	7B
  124	7C
  125	7D
  126	7E
  127	7F
  128	80
  129	81
  130	82
  131	83
  132	84
  133	85
  134	86
  135	87
  136	88
  137	89
  138	8A
  139	8B
  140	8C
  141	8D
  142	8E
  143	8F
  144	90
  145	91
  146	92
  147	93
  148	94
  149	95
  150	96
  151	97
  152	98
  153	99
  154	9A
  155	9B
  156	9C
  157	9D
  158	9E
  159	9F
  160	A0

  Десятичный	Шестнадцатеричный
  161	A1
  162	A2
  163	A3
  164	A4
  165	A5
  166	A6
  167	А7
  168	А8
  169	A9
  170	AA
  171	AB
  172	AC
  173	AD
  174	AE
  175	AF
  176	B0
  177	B1
  178	B2
  179	B3
  180	B4
  181	B5
  182	B6
  183	B7
  184	B8
  185	B9
  186	BA
  187	BB
  188	до н. э.0	BE
  191	BF
  192	C0
  193	C1
  194	C2
  195	C3
  196	C4
  197	C5
  198	C6
  199	C7
  200	C8
  201	C9
  202	CA
  203	CB
  204	CC
  205	CD
  206	CE
  207	CF
  208	D0
  209	D1
  210	D2
  211	D3
  212	D4
  213	D5
  214	D6
  215	D7
  216	D8
  217	D9
  218	DA
  219	DB
  220	DC
  221	DD
  222	DE
  223	DF
  224	E0
  225	E1
  226	E2
  227	E3
  228	E4
  229	E5
  230	E6
  231	E7
  232	E8
  233	E9
  234	EA
  235	EB
  236	EC
  237	ED
  238	EE
  239	EF
  240	F0

  Десятичный	Шестнадцатеричный
  241	F1
  242	F2
  243	F3
  244	F4
  245	F5
  246	F6
  247	F7
  248	F8
  249	F9
  250	FA
  251	FB
  252	FC
  253	FD
  254	FE
  255	FF
  256	100
  257	101
  258	102
  259	103
  260	104
  261	105
  262	106
  263	107
  264	108
  265	109
  266	10A
  267	10B
  268	10C
  269	10D
  270	10E
  271	10F
  272	110
  273	111
  274	112
  275	113
  276	114
  277	115
  278	116
  279	117
  280	118
  281	119
  282	11A
  283	11B
  284	11C
  285	11D
  286	11E
  287	11F
  288	120
  289	121
  290	122
  291	. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт