Число 12 в шестнадцатеричной системе. Шестнадцатеричный код
Возникла в древнем Вавилоне. В Индии система работает в виде позиционной десятичной нумерации с использованием нуля, у индусов данную систему чисел позаимствовала арабская нация, у них, в свою очередь, взяли европейцы. В Европе эту систему стали называть арабской.
Позиционная система счисления — значение всех цифр зависит от позиции (разряда) данной цифры в числе.
Примеры , стандартная десятичная система счисления — это позиционная система. Допустим, дано число 453 . Цифра 4 обозначает сотни и соответствует числу 400, 5 — кол-во десятков и соответствует значению 50 , а 3 — единицы и значению 3 . Легко заметить, что с увеличением разряда увеличивается значение. Таким образом, заданное число запишем в виде суммы 400+50+3=453.
Шестнадцатеричная система счисления.
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления.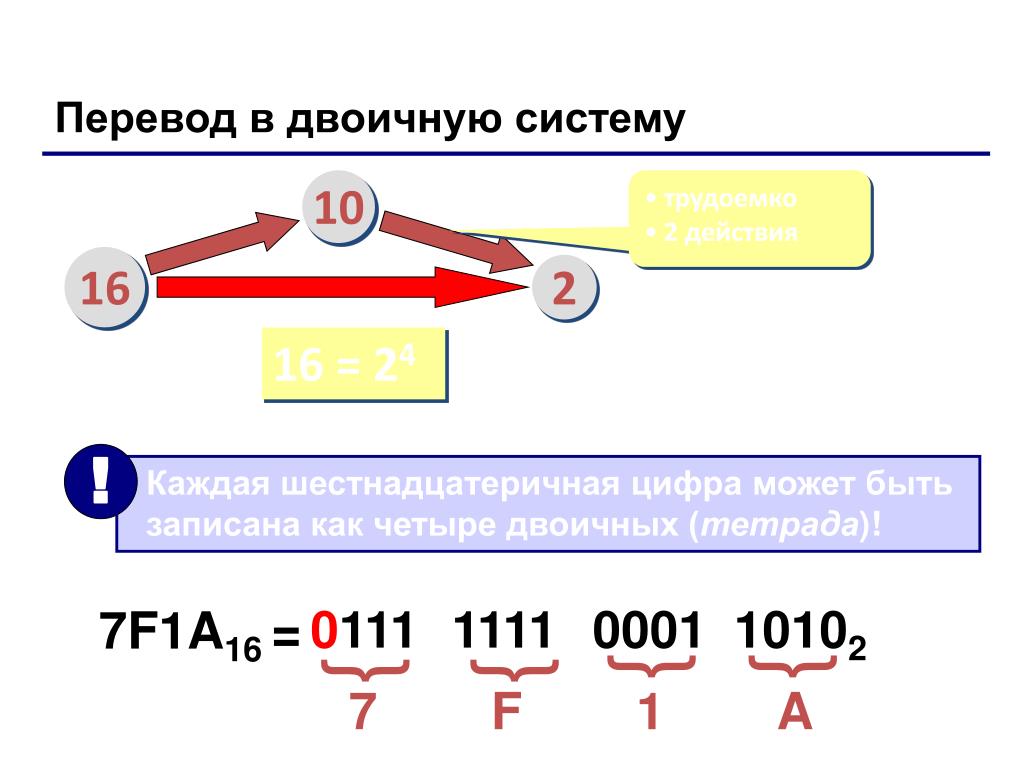
Записывая числа в восьмеричной системе счисления мы получаем довольно компактные выражения, однако в шестнадцатеричной системе мы получаем выражения более компактными.
Первыми десятью цифрами из шестнадцати шестнадцатеричных цифрах является стандартный интервал 0 — 9 , последующие шесть цифр выражают при помощи первых букв латинского алфавита: A , B , C , D , E , F . Перевод из шестнадцатеричной системы в двоичную систему и в обратную сторону делают аналогично процессу для восьмеричной системы.
Применение шестнадцатеричной системы счисления.
Шестнадцатеричную систему счисления довольно хорошо используют в современных компьютерах, например с ее помощью указывают цвет: #FFFFFF — белый цвет.
Перевод чисел из одной системы счисления в другую.
Перевод чисел из шестнадцатеричной системы в десятичную.
Что бы перевести шестнадцатеричное число в десятичное , нужно заданное число привести к виду суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например , переведем шестнадцатеричное число 5A3 в десятичное. Здесь 3 цифры. Исходя их выше сказанного правила, приведем его к виду суммы степеней с основанием 16:
5A3 16 = 3·16 0 +10·16 1 +5·16 2 = 3·1+10·16+5·256 = 3+160+1280 = 1443 10
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот.
Для перевода многозначного двоичного числа в шестнадцатеричную систему необходимо разделить его на тетрады справа налево и поменять все тетрады соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную необходимо поменять каждую все цифры на соответствующие тетрады из таблицы перевода, которую вы найдете ниже.
Например :
010110100011 2 = 0101 1010 0011 = 5A3 16
Таблица перевода чисел.
Алгоритм перевода чисел из одной системы счисления в другую.
1. Из десятичной системы счисления:
- делим число на основание переводимой системы счисления;
- находим остаток от деления целой части числа;
- записываем все остатки от деления в обратном порядке;
2. Из двоичной системы счисления:
- для перевода в десятичную систему счисления находим сумму произведений основания 2 на соответствующую степень разряда;
- для перевода числа в восьмеричную разбиваем число на триады.
Например, 1000110 = 1 000 110 = 1068
- для перевода числа из двоичной системы счисления в шестнадцатеричную разбиваем число на группы по 4 разряда.
Например, 1000110 = 100 0110 = 4616.
Таблицы для перевода:
Двоичная СС | Шестнадцатеричная СС |
0000 | |
0001 | |
0010 | |
0011 | |
0100 | |
0101 | |
0110 | |
0111 | |
1000 | |
1001 | |
1010 | |
1011 | |
1100 | |
1101 | |
1110 | |
1111 |
Для представления чисел в микропроцессоре используется двоичная система счисления
.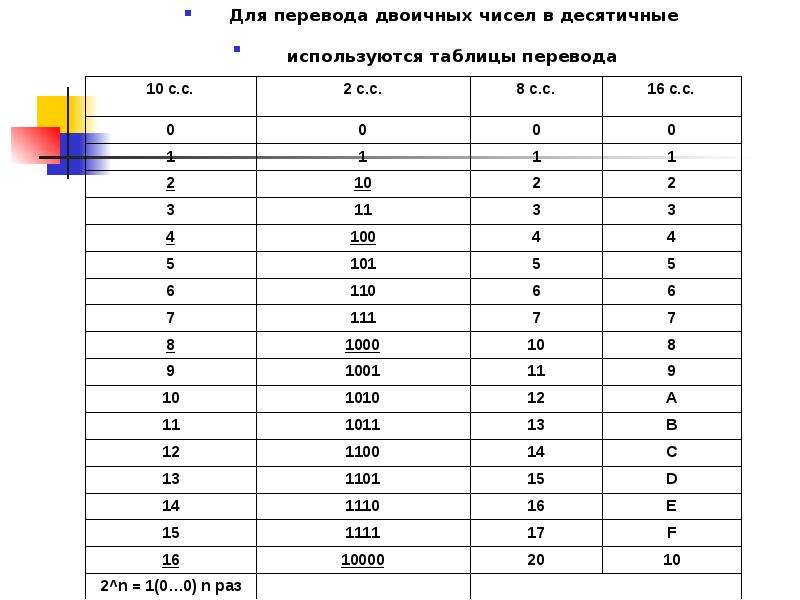
При этом любой цифровой сигнал может иметь два устойчивых состояния: «высокий уровень» и «низкий уровень». В двоичной системе счисления для изображения любого числа используются две цифры, соответственно: 0 и 1. Произвольное число
x = a n ·2 n +a n-1 ·2 n-1 +…+a 1 ·2 1 +a 0 ·2 0 +a -1 ·2 -1 +a -2 ·2 -2 +…+a -m ·2 -m
где a i — двоичные цифры (0 или 1).
Восьмеричная система счисления
В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:
10 10 = A 16 12 10 = C 16 14 10 = E 16
11 10 = B 16 13 10 = D 16 15 10 = F 16 .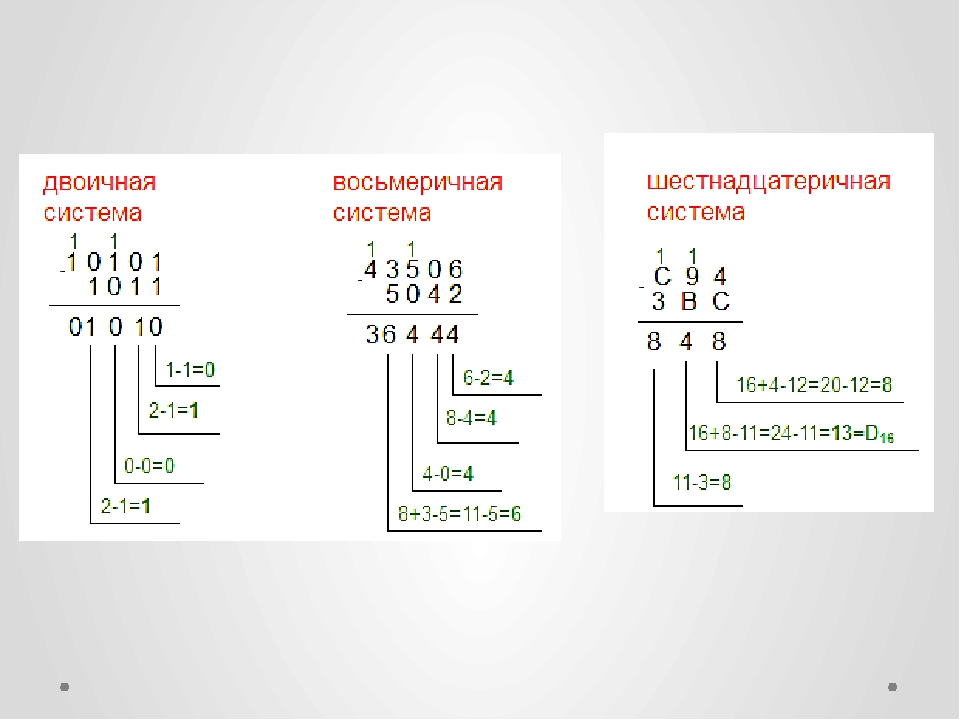
Например, число 175 10 в шестнадцатеричной системе счисления запишется как AF 16 . Действительно,
10·16 1 +15·16 0 =160+15=175
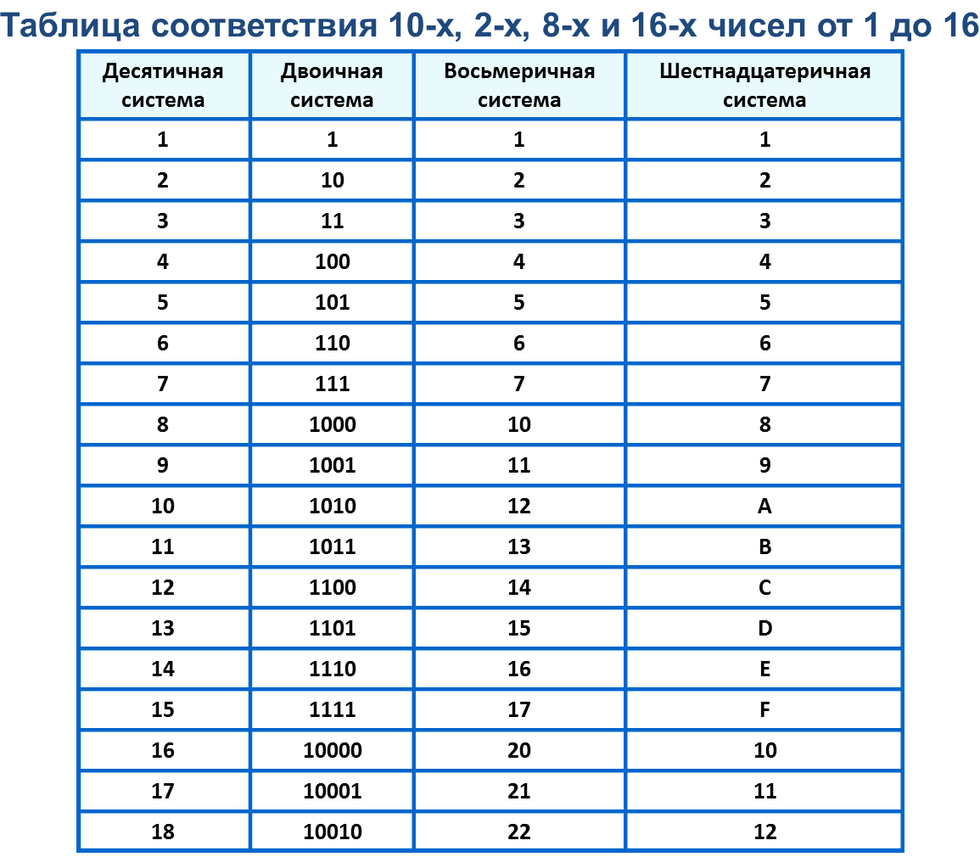
В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
Двоично-восьмеричные и двоично-шестнадцатеричные преобразования
Двоичная система счисления удобна для выполнения арифметических действий аппаратными средствами микропроцессора, но неудобна для восприятия человеком, поскольку требует большого количества разрядов. Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.
Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.
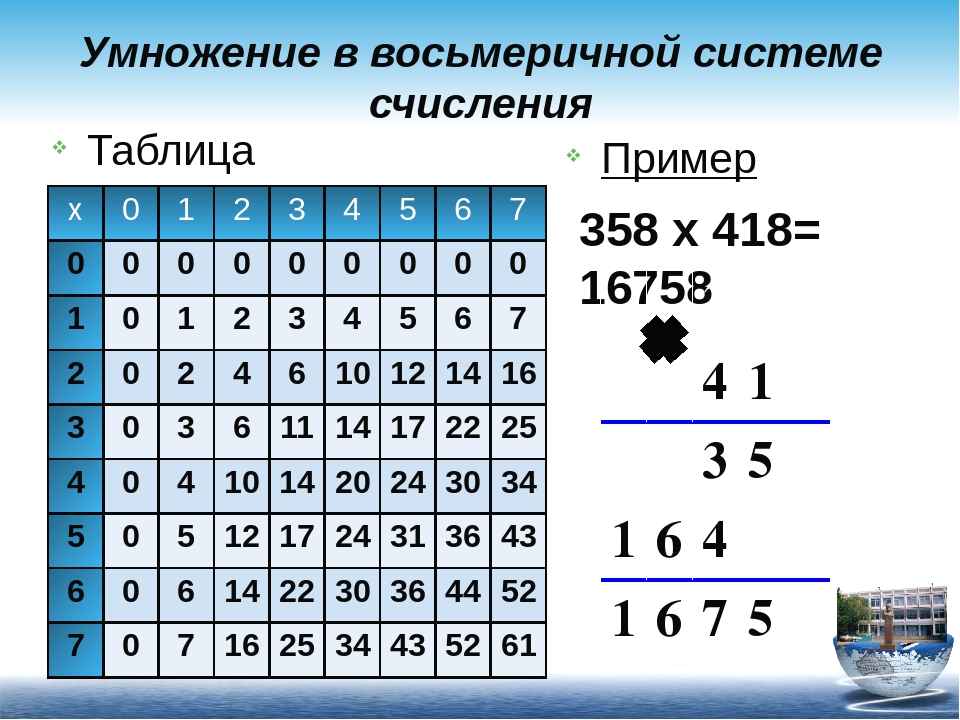
Три разряда восьмеричной системы счисления реализуют все возможные комбинации восьмеричных цифр в двоичной системе счисления: от 0 (000) до 7(111). Чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда (триады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от него тоже можно добавить незначащие нули до заполнения всех триад. Затем каждая триада заменяется восьмеричной цифрой.
Пример: Преобразовать число 1101110,01 2 в восьмеричную систему счисления.
Объединяем двоичные цифры в триады справа налево. Получаем
001 101 110,010 2 = 156,2 8 .
Чтобы перевести число из восьмеричной системы в двоичную, нужно каждую восьмеричную цифру записать ее двоичным кодом:
156,2 8 = 001 101 110,010 2 .
Четыре разряда шестнадцатеричной системы счисления реализуют все возможные комбинации шестнадцатеричных цифр в двоичной системе счисления: от 0 (0000) до F(1111). Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.
Пример: Преобразовать число 1101110,11 2 в шестнадцатеричную систему счисления.
Объединяем двоичные цифры в тетрады справа налево. Получаем
0110 1110,1100 2 = 6E,C 16 .
Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно каждую шестнадцатеричную цифру записать ее двоичным кодом.
Шестнадцатеричная система счисления. аша первая программа.
Для написания
программ на Ассемблере, необходимо
разобраться с шестнадцатеричной
системой счисления.
Итак, в десятичной системе если мы к какому-нибудь числу справа добавим нуль, то это число увеличится в 10 раз. Например: 1 х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В этой системе мы используем цифры от 0 до 9, т.е. десять разных цифр (собственно, поэтому она и называется десятичная).
В шестнадцатеричной системе мы используем, соответственно, шестнадцать «цифр». Я специально написал слово «цифр» в кавычках, т.к. в ней используются не только цифры. Да и в самом деле как так? Объясняю: от 0 до 9 мы считаем так же, как и в десятичной, а вот дальше будет так: A, B, C, D, E, F. Число F, как не трудно посчитать, будет равно 15 в десятичной системе (см. табл. 1).
Десятичное число | Шестнадцатеричное число |
 Десятичная и шестнадцатеричная системы.
Десятичная и шестнадцатеричная системы.Т.о., если мы к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз.
Пример 1: 1 х 16 = 10; 10 х 16 = 100; 100 х 16 = 1000 и т.д.
Вы смогли отличить в Примере 1 шестнадцатеричные числа от десятичных? А из этого ряда: 10, 12, 45, 64, 12, 8, 19? Это могут быть как шестнадцатеричные, так и десятичные. Для того, чтобы не было путаницы, и компьютер смог бы однозначно отличить одни числа от других, в Ассемблере принято после шестнадцатеричного числа ставить символ h или H (H это сокращение от англ. hexadecimal (шестнадцатеричное). Для краткости его иногда называют просто Hex ) . А после десятичного ничего не ставить. Т.к. числа от 0 до 9 в обоих системах имеют одинаковые значения, то числа, записанные как 5 и 5h одно и тоже.
Т.о. Пример 1 (см.
выше) правильнее будет записать
так: 1 х 16 = 10h; 10h x 16 = 100h; 100h x 16 = 1000h.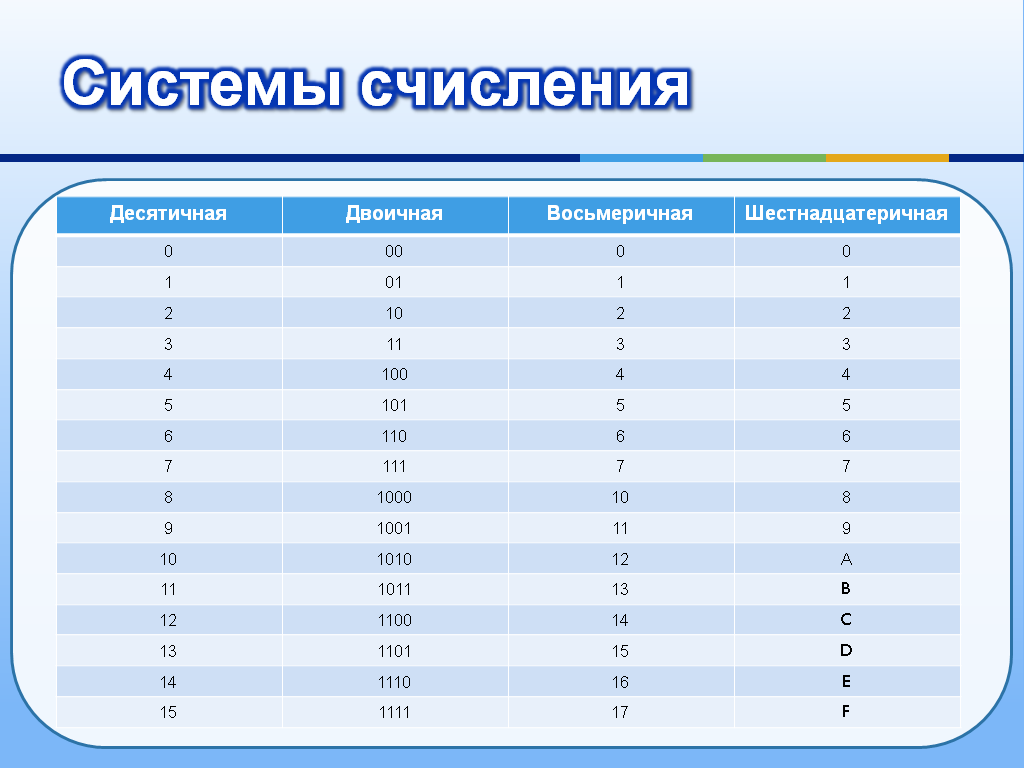 Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h =
1000h.
Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h =
1000h.
Для чего нужна шестнадцатеричная система, мы рассмотрим в последующих выпусках. А в данный момент для нашего примера программы, который будет рассмотрен ниже, нам необходимо знать о существовании шестнадцатеричных чисел.
Итак, подведем итог. Шестнадцатеричная система счисления состоит из 10 цифр (от 0 до 9) и 6 букв латинского алфавита (A, B, C, D, E, F). Если к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз. Очень важно уяснить данную тему , так как мы будем постоянно использовать ее при написании программ.
Теперь немного о том, как я буду строить примеры на Ассемблере. Не совсем удобно приводить их в HTML-формате, поэтому сперва будет сам код программы с пронумерованными строчками, а сразу же после него объяснения и примечания.
Примерно так:
| строк | Код программы |
| (1) | mov ah,9 |
Объяснения:
В строке (1) мы
делаем то-то, а в строке (15) то-то.
Огромная просьба: НЕ копируйте программы со страницы в буфер, а затем не вставляйте их в Блокнот (или еще куда-нибудь)! Перепечатывайте их вручную в текстовом редакторе. Если есть принтер, то выделите программу, распечатайте выделенный фрагмент, а затем перебейте в редактор с бумаги. Все примеры нужно набирать самостоятельно! Это ускорит запоминание операторов.
И еще. Строчные и ПРОПИСНЫЕ буквы в Ассемблере не различаются. Записи вида:
Ассемблером воспринимаются одинаково. Можно, конечно, заставить Ассемблер различать строчные и ПРОПИСНЫЕ символы, но мы пока этого делать не будем. Для удобства чтения программы лучше всего операторы печатать строчными буквами, а названия подпрограмм и меток начинать с прописной. Но это как кому будет удобно.
Итак, переходим к нашей первой программе:
(1) CSEG segment
(2) org 100h
(4) Begin:
(6) mov ah,9
(7) mov dx,offset Message
(8) int 21h
(10) int 20h
(11)
(12) Message db «Hello, world!$»
(13) CSEG ends
(14) end Begin
Для того, чтобы
объяснить все операторы данного
примера, нам потребуется несколько
выпусков. Поэтому описание
некоторых команд мы просто опустим
на данном этапе. Просто считайте,
что так должно быть. В самое
ближайшее время мы рассмотрим эти
операторы подробно. Итак, строки с
номерами (1), (2) и (13) вы просто
игнорируете.
Поэтому описание
некоторых команд мы просто опустим
на данном этапе. Просто считайте,
что так должно быть. В самое
ближайшее время мы рассмотрим эти
операторы подробно. Итак, строки с
номерами (1), (2) и (13) вы просто
игнорируете.
Строки (3), (5), (9) и (11) остаются пустыми. Это делается для наглядности. Ассемблер их будет просто опускать.
Теперь перейдем к рассмотрению остальных операторов. Со строки (4) начинается код программы. Это метка, указывающая Ассемблеру на начало кода. В строке (14) стоят операторы end Begin (Begin англ. начало; end конец). Это конец программы. Вообще вместо слова Begin можно было бы использовать что-нибудь другое. Например, Start:. В таком случае, нам пришлось бы и завершать программу End Start (14).
Строки (6) (8) выводят на экран сообщение Hello, world!. Здесь придется вкратце рассказать о регистрах процессора (более подробно эту тему мы рассмотрим в следующем выпуске).
Регистр
процессора это специально
отведенная память для хранения
какого-нибудь числа.
Например:
Если мы хотим сложить два числа, то в математике запишем так:
A, B и C это своего рода регистры (если говорить о компьютере), в которых могут хранится некоторые данные. А=5 можно прочитать как: Присваиваем А число 5 .
Для присвоения регистру какого-нибудь значения, в Ассемблере существует оператор mov (от англ. move загрузить). Строку (6) следует читать так: Загружаем в регистр AH число 9 (проще говоря, присваиваем AH число 9). Ниже рассмотрим зачем это надо.
В строке (7) загружаем в регистр DX адрес сообщения для вывода (в данном примере это будет строка Hello, world!$ ).
Прерывания будут подробно рассматриваться в последующих выпусках. Здесь я скажу несколько слов.
Прерывание MS-DOS это своего рода
подпрограмма (часть MS-DOS) , которая находится
постоянно в памяти и может
вызываться в любое время из любой
программы.
Рассмотрим вышесказанное на примере (мелким шрифтом выделим примечания ):
Программа сложения двух чисел
НачалоПрограммы
A=5 в переменную A заносим значение 5
B=8 в переменную B значение 8
ВызовПодпрограммы Сложение
теперь С равно 13
A=10 тоже самое, только другие числа
B=25
ВызовПодпрограммы Сложение
теперь С равно 35
КонецПрограммы
Подпрограмма Сложение
C=A+B
ВозвратИзПодпрограммы возвращаемся в то место, откуда вызывали
КонецПодпрограммы
В данном примере
мы дважды вызвали подпрограмму Сложение ,
которая сложила два числа,
переданные ей в переменных
A и
B.
Результат помещается в переменную
С. Когда вызывается подпрограмма,
компьютер запоминает с какого
места она была вызвана, а затем,
когда закончила работу
подпрограмма, компьютер
возвращается в то место, откуда она
вызывалась. Т.о. можно вызывать
подпрограммы неопределенное
количество раз с любого места.
Т.о. можно вызывать
подпрограммы неопределенное
количество раз с любого места.
При выполнении строки (8) программы на Ассемблере мы вызываем подпрограмму (в данном случае это называется прерывание), которая выводит на экран строку. Для этого мы, собственно, и помещаем необходимые значения в регистры. Всю необходимую работу (вывод строки, перемещение курсора) берет на себя подпрограмма. Эту строку можно прочитать так: вызываем двадцать первое прерывание (int от англ. interrupt прерывание). Обратите внимание, что после числа 21 стоит буква h. Это, как мы уже знаем, шестнадцатеричное число (33 в десятичной системе). Конечно, нам ничего не мешает заменить строку int 21h на int 33. Программа будет работать корректно. Просто в Ассемблере принято указывать номер прерывания в шестнадцатеричной системе.
В строке (10) мы, как
вы уже догадались, вызываем
прерывание 20
h.
Для вызова данного прерывания не
нужно указывать какие-либо
значения в регистрах. Оно выполняет
только одну задачу: выход из
программы (выход в DOS). В результате
выполнения прерывания 20h, программа
вернется туда, откуда ее запускали
(загружали, вызывали). Например, в
Norton
Commander или
DOS
Navigator.
В результате
выполнения прерывания 20h, программа
вернется туда, откуда ее запускали
(загружали, вызывали). Например, в
Norton
Commander или
DOS
Navigator.
Строка (12) содержит сообщение для вывода. Первое слово (message сообщение) название сообщения. Оно может быть любым (например, mess или string и пр.). Обратите внимание на строку (7), в которой мы загружаем в регистр DX адрес нашего сообщения.
Можно создать еще одну строку, которую назовем Mess2. Затем, начиная со строки (9) вставим следующие команды:
(10) mov dx,offset Mess2
(13) Message db «Hello, world!$»
(14) Mess2 db «Это Я! $»
и ассемблировать нашу программу заново. Надеюсь, что вы догадались, что произойдет
Обратите внимание на последний символ в строках Message и Mess2 — $. Он указывает на конец строки. Если мы его уберем, то 21 h прерывание продолжит вывод до тех пор, пока не встретится где-нибудь в памяти символ $. На экране мы увидим мусор .
Если у вас есть отладчик, то можно
посмотреть как будет работать наша
программа.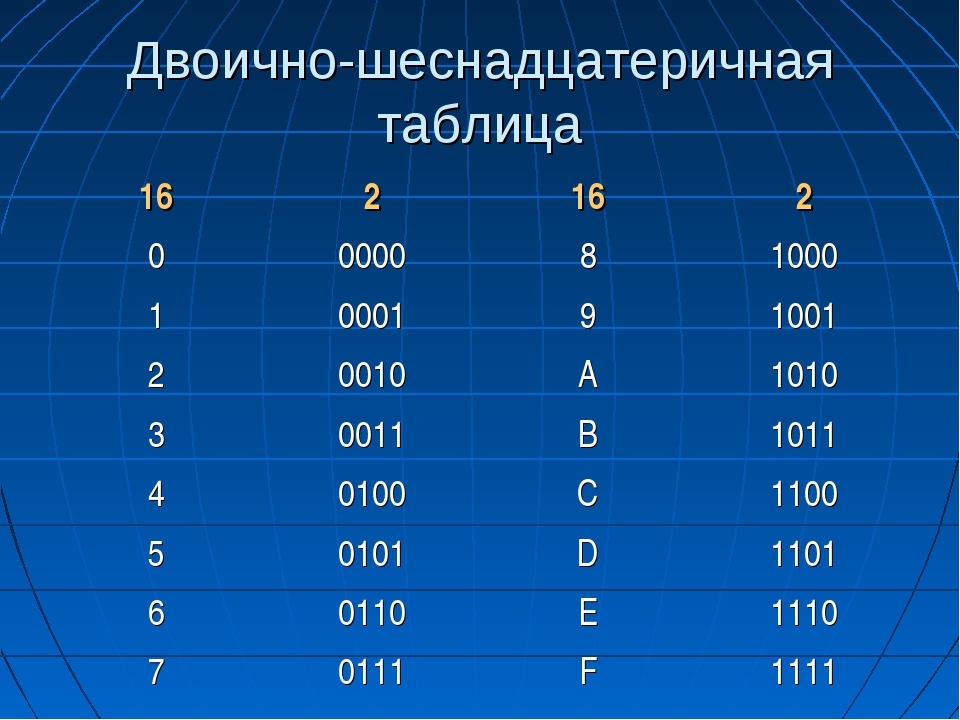
Целю настоящего выпуска не было разобраться подробно с каждым оператором . Это невозможно, т.к. у вас еще недостаточно знаний. Я полагаю, что уже через 3-4 выпуска вы поймете принцип и структуру программы на Ассемблере. Может быть, вам показался язык Ассемблера чрезвычайно сложным, но это, поверьте, с первого взгляда.
Привычная для человека система счисления – десятичная. В ее основу входят десять цифр от 0 до 9. Шестнадцатеричную систему отличает наличие в ней первых шести букв латинского алфавита для записи чисел помимо основных цифр. То есть после цифры 9 следует символ «A», который соответствует числу 10 для десятичной системы. Соответственно, F в шестнадцатеричной системе – это 16 в десятичной. Использование шестнадцати символов в системе – неслучайный выбор.
Единица информации – бит. Восемь бит образуют байт. Существует понятие, как машинное слово – это единица данных, представляющая собой два , то есть шестнадцать бит. Таким образом, используя шестнадцать различных символов, можно описывать любую информацию, которая при обмене данных будет наименьшей частицей. С ними можно производить любые арифметические действия, результат, соответственно, получится тоже в шестнадцатеричной системе.
С ними можно производить любые арифметические действия, результат, соответственно, получится тоже в шестнадцатеричной системе.
Для того чтобы отличать, что число записано в шестнадцатеричной системе, после него записывают букву «h» или нижний индекс «16».
Применение
Наиболее широкое применение шестнадцатеричной системы счисления – это коды ошибок программных продуктов, например, операционной системы. Числа, заложенные в этих кодах, стандартизированы. Имея специальную таблицу, всегда можно определить, что именно означает та или иная ошибка.
В языках низкого уровня, максимально приближенным к машинным кодам шестнадцатеричная система применяется для написания программ. Многие программисты используют ее и при работе с языками высокого уровня, потому что числа в этой системе при помощи специальной таблицы соответствия легко переводятся в двоичную систему, на которой основана работа всей цифровой техники. Любая информация в компьютере, будь то музыкальный файл или текстовый документ, после трансляции представлена последовательностью исходного двоичного кода, а его удобнее просматривать представленным символами шестнадцатеричной системы.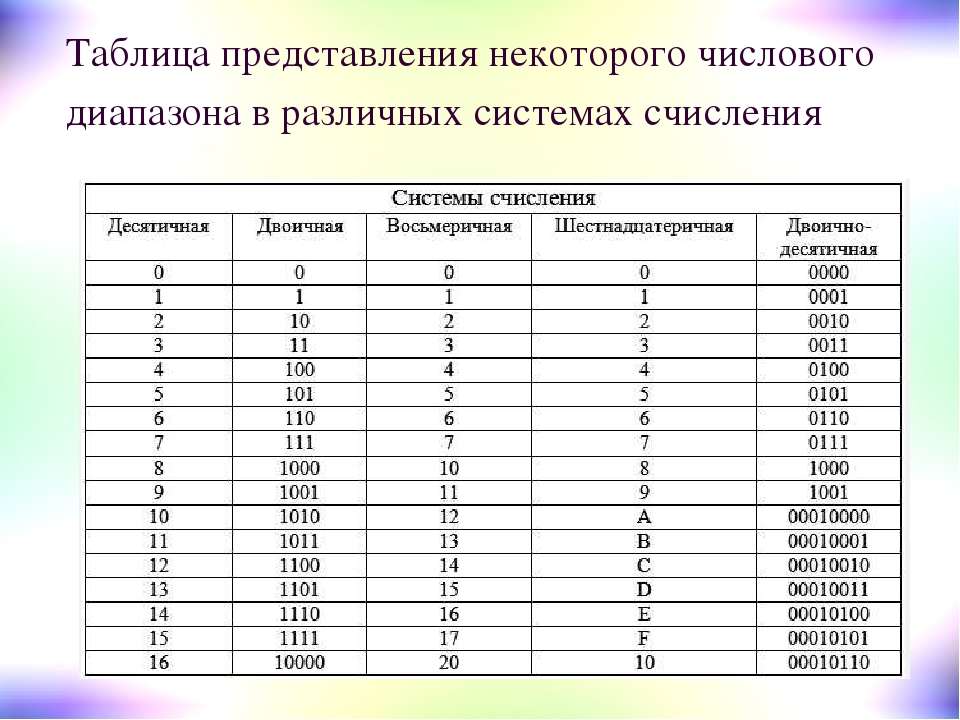
Также одно из применений шестнадцатеричных символов – описание цветовых схем, то есть три компонента R, G, B описываются соответствующим данной системе способом. Данный подход к записи получил название шестнадцатеричный цвет
Возможность просмотреть программу в шестнадцатеричном коде позволяет отладить ее, внести изменения, а злоумышленниками данный подход используется для взлома программ.
Для написания программ на Ассемблере, необходимо разобраться с шестнадцатеричной системой счисления. Ничего сложного в ней нет. Мы используем в жизни десятичную систему. Уверен, что вы все ее знаете, поэтому я постараюсь объяснить шестнадцатеричную систему, проводя аналогию с десятичной.
Итак, в десятичной
системе если мы к какому-нибудь
числу справа добавим нуль, то это
число увеличится в 10 раз. Например: 1
х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В
этой системе мы используем цифры от
0 до 9, т.е. десять разных цифр
(собственно, поэтому она и
называется десятичная).
В шестнадцатеричной системе мы используем, соответственно, шестнадцать «цифр». Я специально написал слово «цифр» в кавычках, т.к. в ней используются не только цифры. Да и в самом деле как так? Объясняю: от 0 до 9 мы считаем так же, как и в десятичной, а вот дальше будет так: A, B, C, D, E, F. Число F, как не трудно посчитать, будет равно 15 в десятичной системе (см. табл. 1).
Десятичное число | Шестнадцатеричное число |
Т.о., если мы к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз.
Пример 1: 1 х
16 = 10; 10 х 16 = 100; 100 х 16 = 1000 и т. д.
д.
Вы смогли отличить в Примере 1 шестнадцатеричные числа от десятичных? А из этого ряда: 10, 12, 45, 64, 12, 8, 19? Это могут быть как шестнадцатеричные, так и десятичные. Для того, чтобы не было путаницы, и компьютер смог бы однозначно отличить одни числа от других, в Ассемблере принято после шестнадцатеричного числа ставить символ h или H (H это сокращение от англ. hexadecimal (шестнадцатеричное). Для краткости его иногда называют просто Hex ) . А после десятичного ничего не ставить. Т.к. числа от 0 до 9 в обоих системах имеют одинаковые значения, то числа, записанные как 5 и 5h одно и тоже.
Т.о. Пример 1 (см. выше) правильнее будет записать так: 1 х 16 = 10h; 10h x 16 = 100h; 100h x 16 = 1000h. Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h = 1000h.
Для чего нужна шестнадцатеричная система, мы рассмотрим в последующих выпусках. А в данный момент для нашего примера программы, который будет рассмотрен ниже, нам необходимо знать о существовании шестнадцатеричных чисел.
Итак, подведем итог. Шестнадцатеричная система счисления состоит из 10 цифр (от 0 до 9) и 6 букв латинского алфавита (A, B, C, D, E, F). Если к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз. Очень важно уяснить данную тему , так как мы будем постоянно использовать ее при написании программ.
Теперь немного о том, как я буду строить примеры на Ассемблере. Не совсем удобно приводить их в HTML-формате, поэтому сперва будет сам код программы с пронумерованными строчками, а сразу же после него объяснения и примечания.
Примерно так:
| строк | Код программы |
| (1) | mov ah,9 |
Объяснения:
В строке (1) мы делаем то-то, а в строке (15) то-то.
Огромная просьба: НЕ копируйте программы со страницы в буфер, а затем не вставляйте их в Блокнот (или еще куда-нибудь)! Перепечатывайте их вручную в текстовом редакторе. Если есть принтер, то выделите программу, распечатайте выделенный фрагмент, а затем перебейте в редактор с бумаги. Все примеры нужно набирать самостоятельно! Это ускорит запоминание операторов.
И еще. Строчные и ПРОПИСНЫЕ буквы в Ассемблере не различаются. Записи вида:
Ассемблером воспринимаются одинаково. Можно, конечно, заставить Ассемблер различать строчные и ПРОПИСНЫЕ символы, но мы пока этого делать не будем. Для удобства чтения программы лучше всего операторы печатать строчными буквами, а названия подпрограмм и меток начинать с прописной. Но это как кому будет удобно.
Итак, переходим к нашей первой программе:
(1) CSEG segment
(2) org 100h
(4) Begin:
(6) mov ah,9
(7) mov dx,offset Message
(8) int 21h
(10) int 20h
(11)
(12) Message db «Hello, world!$»
(13) CSEG ends
(14) end Begin
Для того, чтобы объяснить все операторы данного примера, нам потребуется несколько выпусков. Поэтому описание некоторых команд мы просто опустим на данном этапе. Просто считайте, что так должно быть. В самое ближайшее время мы рассмотрим эти операторы подробно. Итак, строки с номерами (1), (2) и (13) вы просто игнорируете.
Строки (3), (5), (9) и (11) остаются пустыми. Это делается для наглядности. Ассемблер их будет просто опускать.
Теперь перейдем к рассмотрению остальных операторов. Со строки (4) начинается код программы. Это метка, указывающая Ассемблеру на начало кода. В строке (14) стоят операторы end Begin (Begin англ. начало; end конец). Это конец программы. Вообще вместо слова Begin можно было бы использовать что-нибудь другое. Например, Start:. В таком случае, нам пришлось бы и завершать программу End Start (14).
Строки (6) (8) выводят на экран сообщение Hello, world!. Здесь придется вкратце рассказать о регистрах процессора (более подробно эту тему мы рассмотрим в следующем выпуске).
Регистр процессора это специально отведенная память для хранения какого-нибудь числа.
Например:
Если мы хотим сложить два числа, то в математике запишем так:
A, B и C это своего рода регистры (если говорить о компьютере), в которых могут хранится некоторые данные. А=5 можно прочитать как: Присваиваем А число 5 .
Для присвоения регистру какого-нибудь значения, в Ассемблере существует оператор mov (от англ. move загрузить). Строку (6) следует читать так: Загружаем в регистр AH число 9 (проще говоря, присваиваем AH число 9). Ниже рассмотрим зачем это надо.
В строке (7) загружаем в регистр DX адрес сообщения для вывода (в данном примере это будет строка Hello, world!$ ).
Прерывания будут подробно рассматриваться в последующих выпусках. Здесь я скажу несколько слов.
Прерывание MS-DOS это своего рода подпрограмма (часть MS-DOS) , которая находится постоянно в памяти и может вызываться в любое время из любой программы.
Рассмотрим вышесказанное на примере (мелким шрифтом выделим примечания ):
Программа сложения двух чисел
НачалоПрограммы
A=5 в переменную A заносим значение 5
B=8 в переменную B значение 8
ВызовПодпрограммы Сложение
теперь С равно 13
A=10 тоже самое, только другие числа
B=25
ВызовПодпрограммы Сложение
теперь С равно 35
КонецПрограммы
Подпрограмма Сложение
C=A+B
ВозвратИзПодпрограммы возвращаемся в то место, откуда вызывали
КонецПодпрограммы
В данном примере мы дважды вызвали подпрограмму Сложение , которая сложила два числа, переданные ей в переменных A и B. Результат помещается в переменную С. Когда вызывается подпрограмма, компьютер запоминает с какого места она была вызвана, а затем, когда закончила работу подпрограмма, компьютер возвращается в то место, откуда она вызывалась. Т.о. можно вызывать подпрограммы неопределенное количество раз с любого места.
При выполнении строки (8) программы на Ассемблере мы вызываем подпрограмму (в данном случае это называется прерывание), которая выводит на экран строку. Для этого мы, собственно, и помещаем необходимые значения в регистры. Всю необходимую работу (вывод строки, перемещение курсора) берет на себя подпрограмма. Эту строку можно прочитать так: вызываем двадцать первое прерывание (int от англ. interrupt прерывание). Обратите внимание, что после числа 21 стоит буква h. Это, как мы уже знаем, шестнадцатеричное число (33 в десятичной системе). Конечно, нам ничего не мешает заменить строку int 21h на int 33. Программа будет работать корректно. Просто в Ассемблере принято указывать номер прерывания в шестнадцатеричной системе.
В строке (10) мы, как вы уже догадались, вызываем прерывание 20 h. Для вызова данного прерывания не нужно указывать какие-либо значения в регистрах. Оно выполняет только одну задачу: выход из программы (выход в DOS). В результате выполнения прерывания 20h, программа вернется туда, откуда ее запускали (загружали, вызывали). Например, в Norton Commander или DOS Navigator.
Строка (12) содержит сообщение для вывода. Первое слово (message сообщение) название сообщения. Оно может быть любым (например, mess или string и пр.). Обратите внимание на строку (7), в которой мы загружаем в регистр DX адрес нашего сообщения.
Можно создать еще одну строку, которую назовем Mess2. Затем, начиная со строки (9) вставим следующие команды:
(10) mov dx,offset Mess2
(13) Message db «Hello, world!$»
(14) Mess2 db «Это Я! $»
и ассемблировать нашу программу заново. Надеюсь, что вы догадались, что произойдет
Обратите внимание на последний символ в строках Message и Mess2 — $. Он указывает на конец строки. Если мы его уберем, то 21 h прерывание продолжит вывод до тех пор, пока не встретится где-нибудь в памяти символ $. На экране мы увидим мусор .
Если у вас есть отладчик, то можно посмотреть как будет работать наша программа.
Целю настоящего выпуска не было разобраться подробно с каждым оператором . Это невозможно, т.к. у вас еще недостаточно знаний. Я полагаю, что уже через 3-4 выпуска вы поймете принцип и структуру программы на Ассемблере. Может быть, вам показался язык Ассемблера чрезвычайно сложным, но это, поверьте, с первого взгляда.
Калькулятор систем счисления
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Система счисления — это способ представления числа. Одно и то же число может быть представлено в различных видах. Например, число 200 в привычной нам десятичной системе может иметь вид 11001000 в двоичной системе, 310 в восьмеричной и C8 в шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Шестнадцатеричная система счисления. Наиболее распространена в современных компьютерах. При помощи неё, например, указывают цвет. #FF0000 — красный цвет. Для записи числа используются цифры от 0 до 9 и буквы A,B,C,D,E,F, которые соответственно обозначают числа 10,11,12,13,14,15.
Перевод в десятичную систему счисления
Преобразовать число из любой системы счисления в десятичную можно следующим образом: каждый разряд числа необходимо умножить на Xn, где X — основание исходного числа, n — номер разряда. Затем суммировать полученные значения.
abcx = (a*x2 + b*x1 + c*x0)10
Примеры:5678 = (5*82 + 6*81 + 7*80)10 = 37510
1102 = (1*22 + 1*21 + 0*20)10 = 610
A516 = (10*161 + 5*160)10 = 16510
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
375 / 8 = 46 (остаток 7)
46 / 8 = 5 (остаток 6)
5 / 8 = 0 (остаток 5)
Записываем остатки и получаем 5678Перевод из двоичной системы в восьмеричную
Способ 1:
Для перевода в восьмеричную систему нужно разбить двоичное число на группы по 3 цифры справа налево. В последней (самой левой) группе вместо недостающих цифр поставить слева нули. Для каждой полученной группы произвести умножение каждого разряда на 2n, где n — номер разряда.
11012 = (001) (101) = (0*22 + 0*21 + 1*20) (1*22 + 0*21 + 1*20) = (0+0+1) (4+0+1) = (1) (5) = 158
Способ 2:
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
| Триада | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
101110102 = (010) (111) (010) = 2728
Перевод из двоичной системы в шестнадцатеричную
Способ 1:
Разбиваем число на группы по 4 цифры справа налево. Последнюю (левую) группу дополним при необходимости ведущими нулями. Внутри каждой полученной группы произведем умножение каждой цифры на 2n, где n — номер разряда, и сложим результаты.
110102 = (0001) (1010) = (0*23 + 0*22 + 0*21 + 1*20) (1*23 + 0*22 + 1*21 + 0*20) = (0+0+0+1) (8+0+2+0) = (1) (10) = 1A16
Способ 2:
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
1011111002 = (0001) (0111) (1100) = 17C16
Перевод из восьмеричной системы в двоичную
Способ 1:
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Возьмем число 438.
Делим последовательно 4 на 2 и получаем остатки 0,0,1. Записываем их в обратном порядке. Получаем 100.
Делим последовательно 3 на 2 и получаем остатки 1,1. Записываем их в обратном порядке и дополняем ведущими нулями до трех разрядов. Получаем 011.
Записываем вместе и получаем 1000112
Способ 2:
Используем таблицу триад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Триада | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
3518 = (011) (101) (001) = 0111010012 = 111010012
Перевод из шестнадцатеричной системы в двоичную
Способ 1:
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Способ 2:
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
D816 = (1101) (1000) = 110110002
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Шестнадцатеричная система счисления — Интеллектуальная Кобринщина
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.
В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:
Например:
10001100101 = 0100 0110 0101= 465
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние.
Быстро учимся считать в двоичной и шестнадцатеричной системе
Введение
Иногда возникает потребность быстро прочитать или записать числа в двоичной или шестнадцатеричной системе счисления, например, работая с различными байтовыми редакторами,при расчете формул с побитовыми операциями или работе с цветом. Часто в таких ситуациях нет возможности долго переводить числа с помощью формул или калькулятора. О быстрых способах перехода между системами счисления пойдет речь в данной статье.
Переход от десятичной системы к двоичной
Первый случай – считаем от десятичной системы к двоичной. Основное, что нужно помнить в данном случае – это ряд степеней двойки (1, 2, 4, 8, 16, 32, 64, 128 и т.д.). Даже если его вы не знаете, то ничего не стоит каждое следующее число умножать на двойку. Так как младшие разряды идут справа, а старшие – слева, то будем их записывать в обратном порядке справа налево.
Для примера будем переводить число 115. Дальше смотрим, если значение разряда помещается в число, то вычитаем из него это значение и ставим в этом разряде 1, иначе ставим 0.
Обратный перевод еще проще – нужно просуммировать все значения разрядов, которые отмечены единичками: 64+32+16+2+1 = 115.
Переход к шестнадцатеричной системе
Теперь давайте разберемся с шестнадцатеричной системой. Имея ввиду то, что количество чисел, которые кодируются тетрадой (4 бита) и одним шестнадцатеричным символом совпадают, то соответственно каждый символ кодирует одну двоичную тетраду.
В результате получили число 0х73. Главное помнить, что А = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Если есть потребность перевести десятичное число в шестнадцатеричное или наоборот, то здесь проще всего будет сначала перевести число в двоичное представление, а затем только в шестнадцатеричное или десятеричное соответственно.
В итоге мы научились быстро переводить числа из одной системы счисления в другую. Главное, что нужно помнить — степени двойки и уметь хорошо складывать и вычитать. Детальнее о машинной математике вы можете узнать во втором уроке курса C# Стартовый.
Попрактикуйтесь самостоятельно и переведите несколько чисел из одной системы в другую, сверяясь с калькулятором. Немного практики — и вы всему научитесь.
Цвет | htmlbook.ru
В HTML цвет задается одним из двух путей: с помощью шестнадцатеричного кода и по названию некоторых цветов. Преимущественно используется способ, основанный на шестнадцатеричной системе исчисления, как наиболее универсальный.
Шестнадцатеричные цвета
Для задания цветов в HTML используются числа в шестнадцатеричном коде. Шестнадцатеричная система, в отличие от десятичной системы, базируется, как следует из ее названия, на числе 16. Цифры будут следующие: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Числа от 10 до 15 заменены латинскими буквами. В табл. 6.1 приведено соответствие десятичных и шестнадцатеричных чисел.
| Десятичные | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестнадцатеричные | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Числа больше 15 в шестнадцатеричной системе образуются объединением двух чисел в одно (табл. 6.2). Например, числу 255 в десятичной системе соответствует число FF в шестнадцатеричной.
| Десятичные | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестнадцатеричные | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C |
Чтобы не возникало путаницы в определении системы счисления, перед шестнадцатеричным числом ставится символ решетки #, например #aa69cc. При этом регистр значения не имеет, поэтому допустимо писать #F0F0F0 или #f0f0f0.
Типичный цвет, используемый в HTML, выглядит следующим образом.
<body bgcolor="#fa8e47">Здесь цвет фона веб-страницы задан как #FA8E47. Символ решетки # перед числом означает, что оно шестнадцатеричное. Первые две цифры (FA) определяют красную составляющую цвета, цифры с третьей по четвертую (8E) — зеленую, а последние две цифры (47) — синюю. В итоге получится такой цвет.
Каждый из трех цветов — красный, зеленый и синий — может принимать значения от 00 до FF, что в итоге образует 256 оттенков. Таким образом, общее количество цветов может быть 256х256х256 = 16.777.216 комбинаций. Цветовая модель, основанная на красной, зеленой и синей составляющей получила название RGB (red, green, blue; красный, зеленый, синий). Эта модель аддитивная (от add — складывать), при которой сложение всех трех компонент образует белый цвет.
Чтобы легче ориентироваться в шестнадцатеричных цветах, примите во внимание некоторые правила.
- Если значения компонент цвета одинаковы (например: #D6D6D6), то получится серый оттенок. Чем больше число, тем светлее цвет, значения при этом меняются от #000000 (черный) до #FFFFFF (белый).
- Ярко-красный цвет образуется, если красный компонент сделать максимальным (FF), а остальные компоненты обнулить. Цвет со значением #FF0000 самый красный из возможных красных оттенков. Аналогично обстоит с зеленым цветом (#00FF00) и синим (#0000FF).
- Желтый цвет (#FFFF00) получается смешением красного с зеленым. Это хорошо видно на цветовом круге (рис. 6.1), где представлены основные цвета (красный, зеленый, синий) и комплементарные или дополнительные. К ним относятся желтый, голубой и фиолетовый (еще называемым пурпурным). Вообще, любой цвет можно получить смешением близлежащих к нему цветов. Так, голубой (#00FFFF) получается за счет объединения синего и зеленого цвета.
Рис. 6.1. Цветовой круг
Цвета по шестнадцатеричным значениям не обязательно подбирать эмпирическим путем. Для этой цели подойдет графический редактор, умеющий работать с разными цветовыми моделями, например, Adobe Photoshop. На рис. 6.2 показано окно для выбора цвета в этой программе, линией обведено полученное шестнадцатеричное значение текущего цвета. Его можно скопировать и вставить к себе в код.
Рис. 6.2. Окно для выбора цвета в программе Photoshop
Веб-цвета
Если установить качество цветопередачи монитора в 8 бит (256 цветов), то один и тот же цвет может показываться в разных браузерах по-своему. Это связано со способом отображения графики, когда браузер работает со своей собственной палитрой и не может показать цвет, который у него в палитре отсутствует. В этом случае цвет заменяется сочетанием пикселов других, близких к нему, цветов, имитирующих заданный. Чтобы цвет оставался неизменным в разных браузерах, ввели палитру так называемых веб-цветов. Веб-цветами называются такие цвета, для каждой составляющей которых — красной, зеленой и синей — устанавливается одно из шести значений — 0 (00), 51 (33), 102 (66), 153 (99), 204 (CC), 255 (FF). В скобках указано шестнадцатеричное значение данной компоненты. Общее количество цветов из всех возможных сочетаний дает 6х6х6 — 216 цветов. Пример веб-цвета — #33FF66.
Основная особенность веб-цвета заключается в том, что он показывается одинаково во всех браузерах. В данный момент актуальность веб-цветов весьма мала из-за повышения качества мониторов и расширения их возможностей.
Цвета по названию
Чтобы не запоминать совокупность цифр, вместо них можно использовать имена широко используемых цветов. В табл. 6.3 приведены имена популярных названий цветов.
| Имя цвета | Цвет | Описание | Шестнадцатеричное значение |
|---|---|---|---|
| black | Черный | #000000 | |
| blue | Синий | #0000FF | |
| fuchsia | Светло-фиолетовый | #FF00FF | |
| gray | Темно-серый | #808080 | |
| green | Зеленый | #008000 | |
| lime | Светло-зеленый | #00FF00 | |
| maroon | Темно-красный | #800000 | |
| navy | Темно-синий | #000080 | |
| olive | Оливковый | #808000 | |
| purple | Темно-фиолетовый | #800080 | |
| red | Красный | #FF0000 | |
| silver | Светло-серый | #C0C0C0 | |
| teal | Сине-зеленый | #008080 | |
| white | Белый | #FFFFFF | |
| yellow | Желтый | #FFFF00 |
Не имеет значения, каким способом вы задаете цвет — по его имени или с помощью шестнадцатеричных чисел. По своему действию эти способы равны. В примере 6.1 показано, как установить цвет фона и текста веб-страницы.
Пример 6.1. Цвет фона и текста
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd">
<html>
<head>
<title>Цвета</title>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8">
</head>
<body bgcolor="teal" text="#ffffff">
<p>Пример текста</p>
</body>
</html>В данном примере цвет фона задается с помощью атрибута bgcolor тега <body>, а цвет текста через атрибут text. Для разнообразия значение у атрибута text установлено в виде шестнадцатеричного числа, а у bgcolor с помощью зарезервированного ключевого слова teal.
Иллюстрированный самоучитель по цифровой графике › Системы счисления › Шестнадцатеричная система счисления [страница — 42] | Самоучители по графическим программам
Шестнадцатеричная система счисления
Теперь предстоит совсем легкая прогулка, связанная с шестнадцатеричной системой счисления. В этом случае, надеемся, вы подозреваете и, видимо, справедливо, что у нас должно теперь быть 16 различных цифр.
Но, как мы знаем, традиционных («арабских») цифр всего десять. А требуется шестнадцать. Получается, что не хватает шести знаков.
Замечание
Таким образом, возникает чисто дизайнерская задача по теме «Знаки» – придумать недостающие символы для цифр.
Значит, в свое время специалистам необходимо было придумать какие-нибудь новые знаки. Но когда-то, в начале компьютерной эры, особого выбора в знаках не было. Программисты располагали только знаками цифр и букв. Поэтому они пошли по элементарному пути: взяли первые буквы латинского алфавита в качестве цифр, тем более что исторически это не первый случай (мы уже упоминали, что первоначально вместо цифр многие народы использовали буквы).
Замечание
Надеемся, что всем понятно, почему в этом случае нельзя использовать, например, числа «10», «11», «12» и т. д.? Потому что, если мы говорим о шестнадцатеричной системе счисления, то должно быть шестнадцать цифр, а не чисел.
И десятичное число «10» стали обозначать латинской буквой «А» (точнее, «цифрой А»). Соответственно, дальше идут цифры «В», «С», «D», «Е» и «Р.
Поскольку мы намеревались построить шестнадцатеричную систему, то, начиная с нуля, здесь как раз и получится 16 цифр. Например, цифра «D» – это десятичное число «13», а цифра «F» – это десятичное число «15».
Когда к шестнадцатеричному числу «F» прибавляем единицу, то, поскольку эти цифры у нас кончились, в этом разряде ставим «О», а в следующий разряд переносим единицу, поэтому получается, что десятичное число «16» будет представлено в шестнадцатеричной системе счисления числом «10», т. е. получается «шестнадцатеричная десятка». Соединим десятичные и шестнадцатеричные числа в единую таблицу (табл. 4.5).
Таблица 4.5. Соответствие десятичных и шестнадцатеричных чисел.
| Десятичное число | Шестнадцатеричное число | Десятичное число | Шестнадцатеричное число |
|---|---|---|---|
| 0-9 | 0-9 | 29 | 1D |
| 10 | А | 30 | 1Е |
| 11 | В | 31 | 1F |
| 12 | С | 32-41 | 20-29 |
| 13 | D | 42-47 | 2A-2F |
| 14 | Е | 48-255 | 30-FF |
| 15 | F | 256 | 100 |
| 16 | 10 | 512 | 200 |
| 17-25 | 11-19 | 1024 | 400 |
| 26 | 1А | 1280 | 500 |
| 27 | 1В | 4096 | 1000 |
| 28 | 1C |
Шестнадцатеричная система используется, чтобы более компактно записывать двоичную информацию. В самом деле, «шестнадцатеричная тысяча», состоящая из четырех разрядов, в двоичном виде занимает тринадцать разрядов (100016 = 10000000000002).
При обсуждении систем счисления неоднократно фигурировали «десятки», «сотни» и «тысячи», поэтому необходимо обратить внимание на так называемые «круглые» числа.
Новости за 7 дней.
Сколько предметов домашнего обихода должно быть под рукой в ванной комнате? Их десятки. И что с ними делать? Как правило, они не отличаются выдающимся дизайном. Основой набора мебели для ванной комнаты Step стали популярные накладные раковины, устанавливаемые на столешницу, для которых предусмот….
Ассортимент гофрированных труб из нержавеющей стали торговой марки Stahlmann пополнился новыми диаметрами: 40А и 50А. Компания «Электросистемы и технологии» (входит в ГК «ССТ), официальный дистрибьютор бренда Stahlmann, по многочисленным просьбам клиентов расширила ассортимент гибких гофрированны….
Компания группы PORCELANOSA Grupo представляет свои новые коллекции напольного покрытия для наружного применения и самые инновационные технические решения для ванных комнат и систем гидроизоляции в официальных магазинах Испании и Португалии. Butech расширяет свой каталог продукции и технических реш….
В ассортименте EKF появилась эргономичная розетка для кухни со встраиваемой техникой. Новинка c разъёмами типа РШ-ВШ позволяет удобно и эстетично подключить сразу два прибора – варочную панель и духовку. Преимущества нового изделия: привлекательная цена – можно сэкономить до 20 % бюджета; ла….
Серия MPT включает четыре модели носимых видеорегистраторов Dahua со встроенными видеокамерами для ведения аудио- и видеозаписи непосредственно на месте события и формирования в случае происшествия доказательной базы. Эти мобильные устройства предназначены для использования в сфере обеспечения обще….
Одноабонентская вызывная панель IP-видеодомофона VTO2211G-WP обладает элегантным дизайном и тонкой легкой конструкцией. При этом она оснащена всем необходимым для быстрой установки и удобства эксплуатации. Помимо проводного интерфейса Ethernet, который также поддерживает подачу питания PoE, вызывн….
Стремительное развитие технологий и рост современных городов значительно влияют на наш образ жизни, дизайн и архитектуру. В интерьерах стиль лофт лучше всего отражает урбанистический дух, предоставляя простор для творчества и самовыражения. Новая коллекция мебели AQUATON ЛОФТ Урбан объединяет ос….
Решить проблему размещения на плоских кровлях дополнительного оборудования призваны два инновационных технических решения, разработанных Группой компаний fischer, мировым лидером в разработке и производстве современных крепежных изделий. Новые кровельные опоры — FFRB и FFRBH — призваны сделать эксп….
За изысканным интерьером всегда стоит качественный крепёж, который позволяет надёжно фиксировать полки, картины, люстры и другие аксессуары. Именно эту задачу решает серия пластиковых дюбелей с крюком EasyHook — новинка компании fischer, мирового лидера в сфере инновационных крепёжных решений. В с….
Качественная краска для деревянного пола – эффективное решение при реставрации старого или обустройстве нового напольного покрытия. Правильно подобранный ЛКМ защитит дерево от истирания, исцарапывания, влаги, ультрафиолета, сохранит красивую фактуру дерева, придаст нужный оттенок, а также продлит с….
Представляем НОВИНКУ – клей SUPERFLEX K77 Белый для керамической плитки и керамогранита. SUPERFLEX K77 Белый – высокоэластичный плиточный клей на основе белого цемента для укладки любого типа плитки из керамогранита, клинкера, керамики и натурального камня, в том числе крупного формата. Свойства….
Динамики подавляющего большинства телевизоров хорошо справляются лишь с воспроизведением голосов дикторов новостей, а вот для музыки и спецэффектов в кино требуется более серьезное решение. Вот только большие колонки полноформатного домашнего кинотеатра — далеко не самый удобный и комфортный выход ….
Устройства ввода — это та часть компьютера, с которой мы напрямую контактируем каждый день. И именно от них часто зависит, насколько удобно нам будет работать, учиться или играть. Поэтому компания SVEN постоянно расширяет ассортимент компьютерных мышей и клавиатур, предлагая все новые решения. Ко….
Выбирайте паровую станцию, чтобы почувствовать себя обладателем профессиональной техники для домашнего использования. По сравнению с классическими паровыми утюгами, паровая станция VT-2430 позволит Вам гладить белье в несколько раз быстрее и качественнее. Отгладить костюм, брюки, платье, плащ или ….
Новый цвет — море сочетаний. За поисками этого оттенка мы отправились в Северную Европу. Нам нужен был серый, который вызывает ассоциацию с природой, а не бетонными джунглями. Глядя на пейзажи Исландии, мы поняли: «Вот он. Тот самый цвет». Спокойный, насыщенный, с теплым коричневым подтоном. ….
Компания dormakaba рада предложить Вам бесшумные решения для межкомнатных дверей — защёлки DORMA со смещённым магнитным ригелем серии 940-М WC и 940-М PZ. Товар на складе. Цвет исполнения торцевой планки замка: АВ – античная бронза и SN – матовый никель. Магнитные замки рекомендуются для установ….
Стилизованный рисунок натюрморта с кофе в обрамлении кофейных зернышек и сегменты с надписями на кофейную тематику чередуются с плитками, воспроизводящими фактуру шероховатого камня. Баланс между акцентными и фоновыми элементами решен в пользу фона, что создает воздушность композиции, но при этом с….
Нежный узор из стилизованных полевых цветов. Плавными каллиграфическими росчерками он заполняет пространство, создавая легкий, вальсирующий ритм композиции. Отдельные элементы узора не объединены в сетку или колонны, традиционные для ритмики обойных принтов, а соединены в V-образные пересечения со….
Ветки, усыпанные некрупными цветами, застилают все полотно. Цельность композиции и наполненность пространства дизайна создают умиротворяющую обстановку и успокаивающий ритм. Тонкие веточки почти полностью укрыты цветами, присутствуют в узоре минимально. Переходы между элементами сглажены, отсутст….
Компактная вилка PPG16-42-201 с заземлением имеют разборную конструкцию и выполнена из ABS пластика и латунных токоведущих контактов. Заземляющие стальные контакты, предусмотренные в конструкции, позволяют безопасно эксплуатировать электроприборы. Применение: Вилки разборные STEKKER серии PPG п….
Коробка «Express» 53800R теперь выпускаются в обновленном конструктиве. 8 герметичных вводов расположены по периметру коробки с максимальным размером вводов до 25 мм, а 2 дополнительных отверстия – на торцевой части коробки (их размер до 20 мм). Теперь есть возможность использовать c ответвительны….
Ассортимент шкафов из фибергласа пополнился новинками – в линейке появились цельнолитые навесные шкафы. Корпуса, изготовленные по этой технологии, имеют более высокую степень пыле- и влагозащиты и меньшую стоимость. При этом в новых моделях реализуются и все преимущества фибергласа: абсолютная кор….
Беспроводная технология LoRa – отличное решение для управления уличным освещением как для целых районов или дорог, так и для ограниченных участков – парковок ТЦ, дворов ЖК, парков и скверов. Достаточно «защелкнуть» в светильник «умный» LoRa контроллер через стандартный NEMA разъем и освещение управ….
Ассортимент Werkel™ пополнился розетками с подсветкой в новых цветах: серебряный и слоновая кость. Кроме своей основной функции — питания электроприборов, розетка с помощью подсветки помогает обозначить себя в темное время суток. Подсветка создает равномерное рассеянное свечение, подходящее для ….
“Освещение придает пространству индивидуальный шарм. Важно, чтобы оно было отражением владельцев, подчеркивало многогранность дизайнерской идеи, даже в сдержанном и минималистичном интерьере.” — Добрый день! Меня зовут Заблодская Камилия, дизайнер студии «Time» с пятилетним опытом, и сегодня я под….
Идеально вписываются в любой интерьер и экономят средства на электроэнергии! ЭРА обновила ассортимент светодиодных ламп со штырьковым цоколем G4-G9, созданных для прямой замены предшественника – галогенной лампы. Капсульный светодиод мощностью 3-6 Вт излучает столько же света, сколько галогенная л….
К летнему сезону сформирован хороший товарных запас по силовым удлинителям ЭРА для дачных и строительных работ. Второй квартал это самое горячее время для данной товарной группы, предлагаем обратить внимание на ассортимент. Серия ЭРА RPx — удлинители на пластиковой катушке; Серия ЭРА RMx — уд….
Компания ФОКУС представляет новый светильник ЖКХ 10, разработанный для освещения подъездов, лестничных площадок, коридоров и вспомогательных помещений. Благодаря степени защиты IP 65, обеспечивающей достаточную защиту от влаги и пыли, светильник так же можно размещать в помещениях с повышенной вл….
Компания представляет новую мебель для ванных комнат и спален, а также инновационную линейку кухонных гарнитуров, изготовленных из дерева и XTONE, для организации функциональных пространств. Компания Gamadecor делает выбор в пользу бесконечных и функциональных пространств за счет использования див….
Коллекция Chic пополнилась новой моделью: дверная ручка-кноб. Ручка-кноб Chic, повторяя сдержанный и элегантный стиль, который обеспечил успех этой коллекции, дополняет предложение каталога. Классический и – как ни парадоксально – современный стиль этой коллекции позволяет легко сочетать ручки с….
В новой светодиодной ленте мы улучшили конструктив, заменили токоведущие провода на медные проводники в плате и сделали более толстую подложку. Это позволило снизить нагрев ленты на 10% и, как следствие, обеспечить долгий срок службы, а также увеличить ее прочность. Назначение у светодиодной лен….
Elektrostandard™ представляет новую светодиодную лампу BLE2745 с функцией изменения цветовой температуры. Для смены цвета свечения не требуется никакого дополнительного оборудования, управление происходит при помощи обычного выключателя. Чтобы получить необходимый оттенок достаточно поочередно н….
Ассортимент Elektrostandard™ расширен новыми диммируемыми Wi-Fi реле 76002/00 и 76003/00. Как и обычные Wi-Fi реле они предназначенные для дистанционного управления освещением. Особенность реле заключается в том, что с помощью них можно настраивать яркость освещения у светильников, поддерживающих ….
Умная розетка Wi-Fi предназначена для дистанционного управления электроприборами. Контроль состояния и управление розетки осуществляется с помощью любого смартфона или планшета, подключенного к сети интернет. Приложение Minimir Home позволяет программировать сценарии работы подключенных электроп….
Ассортимент Elektrostandard™ расширен новыми сериями дизайнерской светодиодной ленты 12 и 24 В: — с гибкой основой; — в черном цвете; — MIX белых диодов; — RGBWW, RGBNW, RGBCW и RGBWWCW; — со светодиодной матрицей COB. Гибкая лента 12 В имеет фигурную плату, позволяющей изгибать ее на пл….
Новая функциональная интерьерная подсветка Kofro L и R LED создаст комфортное освещение для чтения книг в вечернее время и пополнит заряд вашего смартфона. Подсветка с беспроводным зарядным устройством позволяет заряжать гаджеты без подключения проводов. У подсветки есть два источника света: све….
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
Преобразователь десятичной системы в шестнадцатеричную
Чтобы использовать этот инструмент преобразователя из десятичного в шестнадцатеричный формат , вы должны ввести десятичное значение, например 79, в левое поле ниже, а затем нажмите кнопку «Преобразовать».Таким образом, вы можете преобразовать до 19 десятичных символов (максимальное значение72036854775807) в шестнадцатеричное.
Результат преобразования десятичного в шестнадцатеричный в базовых числах
Десятичная система
Десятичная система счисления является наиболее часто используемой и стандартной системой в повседневной жизни. Он использует число 10 в качестве основы (системы счисления). Следовательно, в нем 10 символов: числа от 0 до 9; а именно 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
Как одна из старейших известных систем счисления, десятичная система счисления использовалась многими древними цивилизациями.Сложность представления очень больших чисел в десятичной системе была преодолена с помощью индийско-арабской системы счисления. Индусско-арабская система счисления дает позиции цифрам в числе, и этот метод работает с использованием степеней основания 10; цифры возводятся в степень n th в соответствии с их положением.
Например, возьмите число 2345,67 в десятичной системе счисления:
.- Цифра 5 находится в позиции единиц (10 0 , что равно 1),
- 4 находится на позиции десятков (10 1 )
- 3 находится в разряде сотен (10 2 )
- 2 находится на позиции тысяч (10 3 )
- Между тем, цифра 6 после десятичной точки находится в десятых долях (1/10, что составляет 10 -1 ), а 7 — в сотых (1/100, что составляет 10 -2 ) позиции
- Таким образом, число 2345.67 также можно представить в следующем виде: (2 * 10 3 ) + (3 * 10 2 ) + (4 * 10 1 ) + (5 * 10 0 ) + (6 * 10 -1 ) + (7 * 10 -2 )
Шестнадцатеричная система (шестнадцатеричная система)
Шестнадцатеричная система (сокращенно шестнадцатеричная) использует число 16 в качестве основания (системы счисления). В системе счисления с основанием 16 используется 16 символов. Это 10 десятичных цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и первые шесть букв английского алфавита (A, B, C, D, E, F).Буквы используются из-за необходимости представлять значения 10, 11, 12, 13, 14 и 15 каждое в одном символе.
Шестнадцатеричный формат используется в математике и информационных технологиях как более удобный способ представления двоичных чисел. Каждая шестнадцатеричная цифра представляет четыре двоичных цифры; следовательно, шестнадцатеричный — это язык для записи двоичного кода в сокращенной форме.
Четыре двоичных разряда (также называемые полубайтами) составляют полбайта. Это означает, что один байт может нести двоичные значения от 0000 0000 до 1111 1111.В шестнадцатеричном формате они могут быть представлены более дружелюбно, от 00 до FF.
В программировании html цвета могут быть представлены шестизначным шестнадцатеричным числом: FFFFFF представляет белый цвет, тогда как 000000 представляет черный.
Как преобразовать десятичную дробь в шестнадцатеричную
Преобразование десятичного числа в шестнадцатеричное может быть достигнуто путем применения алгоритма повторного деления и остатка. Проще говоря, десятичное число многократно делится на основание 16. В промежутках между этими делениями остатки дают шестнадцатеричный эквивалент в обратном порядке.
Вот как шаг за шагом преобразовать десятичное в шестнадцатеричное:
- Шаг 1 : Если заданное десятичное число меньше 16, шестнадцатеричный эквивалент будет таким же. Помня, что буквы A, B, C, D, E и F используются для значений 10, 11, 12, 13, 14 и 15, конвертируйте соответственно. Например, десятичное число 15 будет в шестнадцатеричном формате F.
- Шаг 2 : Если заданное десятичное число 16 или больше, разделите его на 16.
- Шаг 3 : Запишите остаток.
- Шаг 4 : Разделите часть перед десятичной точкой вашего частного еще раз на 16. Запишите остаток.
- Шаг 5 : Продолжайте этот процесс деления на 16 и запоминания остатков до тех пор, пока последняя десятичная цифра не станет меньше 16.
- Шаг 6 : Когда последняя десятичная цифра меньше 16, частное будет меньше 0, а остаток будет самой цифрой.
- Шаг 7 : Последний полученный остаток будет самой старшей цифрой шестнадцатеричного значения, а первый остаток от шага 3 — младшей значащей цифрой.Следовательно, когда вы записываете остатки в обратном порядке — начиная снизу со старшей цифры и идя вверх, вы получите шестнадцатеричное значение данного десятичного числа.
Теперь применим эти шаги, например, к десятичному числу (501) 10
Шаг 1. Поскольку 501 больше 16, разделите на 16. 501 ÷ 16 = 31,3125 Шаг 2: Чтобы вычислить остаток, вам нужно умножить часть после десятичной точки на 16. 0,3125 * 16 = 5 Таким образом, первый остаток (и младшая цифра в шестнадцатеричном формате) равен 5.Шаг 3: Разделите 31 (часть частного до десятичной точки) на 16. 31 ÷ 16 = 1,9375 Шаг 4: Рассчитайте остаток. 0,9375 * 16 = 15 Шаг 5: Разделите целую часть последнего частного на 16. 1 ÷ 16 = 0,0625 Шаг 6: Рассчитайте остаток. 0,0625 * 16 = 1 Шаг 7: Остатки, записанные снизу вверх, дают вам шестнадцатеричные значения 1, 15 и 5. Поскольку 15 равно F в шестнадцатеричной системе счисления, (501) 10 = (1F5) 16
Примеры преобразования десятичных чисел в шестнадцатеричные
Пример 1: (4253) 10 = (109D) 16
4253 ÷ 16 = 265.8125 0,8125 * 16 = 13 (остаток 13, эквивалент D в шестнадцатеричном формате) 265 ÷ 16 = 16,5625 0,5625 * 16 = 9 (остаток 9) 16 ÷ 16 = 1 (остаток 0) 1 ÷ 16 = 0,0625 0,00625 * 16: 1 (остаток 1) Прочтите остатки от наиболее значимых к наименее важным - снизу вверх: 109D. 109D шестнадцатеричный эквивалент (4253) 10
Пример 2: (16) 10 = (10) 16
16 ÷ 16 = 1 (остаток 0) 1 ÷ 16 = 0,0625 0,00625 * 16: 1 (остаток 1)
Пример 3: (45) 10 = (2D) 16
45 ÷ 16 = 2.8125 0,8125 * 16 = 13 (остаток 13, эквивалент D в шестнадцатеричном формате) 2 ÷ 16 = 0,125 0,125 * 16 = 2 (остаток 2)
Таблица преобразования десятичных чисел в шестнадцатеричные
| Десятичное | Шестнадцатеричное | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | E | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | 11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 18 | 13 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | 14 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | 15 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | 16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | 18 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | 19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | 1A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | 1B | 1D | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | 1E | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | 1F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | 20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | 21 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | 24 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | 25 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | 26 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | 27 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | 2A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | 2B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | 2C | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | 2D | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | 2E | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | 2F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | 30 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51 | 33 | |
| 52 | 34 | |
| 53 | 35 | |
| 54 | 36 | |
| 55 | 37 | |
| 39 | ||
| 58 | 3A | |
| 59 | 3B | |
| 60 | 3C | |
| 61 | 3D | |
| 64 | 40 | |
| 65 | 41 | |
| 66 | 9000 4 42||
| 67 | 43 | |
| 68 | 44 | |
| 69 | 45 | |
| 70 | 46 | |
| 71 | 72 | |
| 73 | 49 | |
| 74 | 4A | |
| 75 | 4B | |
| 76 | 4C | |
| 77 | ||
| 79 | 4 этаж | |
| 80 | 50 |
| Десятичное | Шестнадцатеричное | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 81 | 51 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | 52 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 | 53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 | 54 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | 57 | |
| 88 | 58 | |
| 89 | 59 | |
| 90 | 5A | |
| 91 | 5B | 5D |
| 94 | 5E | |
| 95 | 5F | |
| 96 | 60 | |
| 97 | 61 | |
| 100 | 64 | |
| 101 | 65 | |
| 102 | 9 0004 66||
| 103 | 67 | |
| 104 | 68 | |
| 105 | 69 | |
| 106 | 6A | |
| 107 | 6A||
| 107 | ||
| 109 | 6D | |
| 110 | 6E | |
| 111 | 6F | |
| 112 | 70 | |
| 113 | 9009||
| 115 | 73 | |
| 116 | 74 | |
| 117 | 75 | |
| 118 | 76 | |
| 119 | 77 | 119 | 77 | 121 | 79 |
| 122 | 7A | |
| 123 | 7B | |
| 124 | 7C | |
| 125 | 7D | |
| 126 | 7E | |
| 127 | 7F | |
| 128 | 130 | 82 |
| 131 | 83 | |
| 132 | 84 | |
| 133 | 85 | |
| 134 | 86 | |
| 88 | ||
| 137 | 89 | |
| 138 | 8A | |
| 139 | 8B | |
| 140 | 8C | |
| 143 | 8F | |
| 144 | 90 | 145 | 91 |
| 146 | 92 | |
| 147 | 93 | |
| 148 | 94 | |
| 149 | ||
| 97 | ||
| 152 | 98 | |
| 153 | 99 | |
| 154 | 9A | |
| 155 | 9B | 9D |
| 158 | 9E | |
| 159 | 9F | |
| 160 | A0 |
| Десятичное | Шестнадцатеричное | ||
|---|---|---|---|
| 161 | A1 | ||
| 162 | A2 | ||
| 163 | A3 | ||
| 164 | A4 | ||
| 165 | |||
| A | 167 | A7 | |
| 168 | A8 | ||
| 169 | A9 | ||
| 170 | AA | ||
| 171 | 9004 170009|||
| AB | |||
| AD | |||
| 174 | AE | ||
| 175 | AF | ||
| 176 | B0 | ||
| 177 | B1 | 9004 177B1 | 9004 170009 B3|
| 180 | B4 | ||
| 181 | B5 | ||
| 182 | B6 | ||
| 183 | B7 | ||
| 184 | B8 | ||
| 185 | B9 | ||
| 186 | |||
| 186 | |||
| 186 | BA | до н.э. | |
| 189 | BD | ||
| 190 | BE | ||
| 191 | BF | ||
| 192 | C0 | 1 | |
| 195 | C3 | ||
| 196 | C4 | ||
| 197 | C5 | ||
| 198 | C6 | ||
| 201 | C9 | ||
| 202 | CA | ||
| 203 90 009 | CB | ||
| 204 | CC | ||
| 205 | CD | ||
| 206 | CE | ||
| 207 | CF | CF | |
| 210 | D2 | ||
| 211 | D3 | ||
| 212 | D4 | ||
| 213 | D5 | ||
| 216 | D8 | ||
| 217 | D9 | ||
| 218 | DA | ||
| 219 | DB | ||
| 220 | |||
| 220 | 222 | DE | |
| 223 | DF | ||
| 224 | E0 | ||
| 225 | E1 | ||
| 226 | E2 | ||
| 227 | E3 | ||
| 228 | E4 | ||
| 229 9009 | |||
| 229 | |||
| 231 | E7 | ||
| 232 | E8 | ||
| 233 | E9 | ||
| 234 | EA | ||
| 235 | |||
| 235 | EB 237 | ED | |
| 238 | EE | ||
| 239 | EF | ||
| 240 | F0 |
| Десятичное | Шестнадцатеричное | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 241 | F1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 242 | F2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 243 | F3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 244 | F4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 247 | F7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 248 | F8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 249 | F9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 250 | FA | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 251 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 251 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| FD | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 254 | FE | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 255 | FF | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 256 | 100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 257 | 101 | 257 | 101 | 4 90000009 103||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 260 | 104 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 261 | 105 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 262 | 106 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 263 | 107 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 264 | 108 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 265 | 109 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 266 | 268 | 10C | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 269 | 10D | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 270 | 10E | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 271 | 10F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 272 | 1103 | 0009112 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 275 | 113 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 276 | 114 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 277 | 115 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 278 | 116 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 281 | 119 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 282 | 11A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 283 | 11B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 284 | 11C | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 285 | 11D | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 286 | 11E | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 287 | 289 | 121 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 290 | 122 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 291 | 123 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 292 | 124 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 293 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 293 | 1253 | 0009127 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 296 | 128 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 297 | 129 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 298 | 12A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 299 | 12B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 302 | 12E | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 303 | 12 Ф | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 304 | 130 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 305 | 131 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 306 | 132 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 307 | 133 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 308 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 310 | 136 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 311 | 137 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 312 | 138 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 313 | 139 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 314 | 316 | 13C | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 317 | 13D | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 318 | 13E | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 319 | 13F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 320 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Двоичное в шестнадцатеричное [изменить | изменить источник]
Для изменения числа с двоичного на шестнадцатеричное используется метод группировки.Двоичное число разделено на группы по четыре цифры, начиная справа. Затем эти группы преобразуются в шестнадцатеричные числа, как показано на приведенной выше диаграмме для шестнадцатеричных чисел от 0 до F. Для перехода с шестнадцатеричного числа выполняется обратное. Каждая шестнадцатеричная цифра заменяется двоичной, и группировка обычно удаляется.
| Двоичный | Группы | шестигранник | |||
|---|---|---|---|---|---|
| 01100101 | 0110 | 0101 | 65 | ||
| 010010110110 | 0100 | 1011 | 0110 | 4B6 | |
| 1101011101011010 | 1101 | 0111 | 0101 | 1010 | D75A |
Когда количество битов в двоичном числе не кратно 4, оно дополняется нулями, чтобы сделать это так.Примеры:
- двоичное 110 = 0110, что составляет 6 шестнадцатеричных чисел.
- в двоичном формате 010010 = 00010010, что составляет 12 шестнадцатеричных чисел.
Шестнадцатеричное в десятичное [изменить | изменить источник]
Существует два распространенных способа преобразования числа из шестнадцатеричного в десятичное.
Первый метод чаще всего выполняется при ручном преобразовании:
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0–9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
- Сохраняйте сумму преобразованных чисел на каждом шаге ниже.
- Начать с младшей шестнадцатеричной цифры. Это цифра на правом конце. Это будет первый предмет в сумме.
- Возьмем вторую наименьшую значащую цифру. Это рядом с цифрой на правом конце. Умножьте десятичное значение цифры на 16. Добавьте это к сумме.
- Сделайте то же самое для третьей младшей значащей цифры, но умножьте ее на 16 2 (то есть на 16 в квадрате или 256).Добавьте это к сумме.
- Продолжайте для каждой цифры, умножая каждое место на другую степень 16. (4096, 65536 и т. Д.)
| Расположение | ||||||
|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | 2 | 1 | |
| Значение | 1048576 (16 5 ) | 65536 (16 4 ) | 4096 (16 3 ) | 256 (16 2 ) | 16 (16 1 ) | 1 (16 0 ) |
Следующий метод чаще используется при программном преобразовании числа.Ему не нужно знать, сколько цифр имеет число до его начала, и оно никогда не умножается более чем на 16, но на бумаге оно выглядит длиннее.
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0–9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
- Сохраняйте сумму преобразованных чисел на каждом шаге ниже.
- Начните со старшей цифры (цифра в крайнем левом углу). Это первая позиция в сумме.
- Если существует другая цифра, умножьте сумму на 16 и добавьте десятичное значение следующей цифры.
- Повторяйте вышеуказанный шаг до тех пор, пока цифры не исчезнут.
Пример: 5Fh и 3425h в десятичном формате, метод 1
|
|
Пример: 5Fh и 3425h в десятичном формате, метод 2
|
|
Преобразование десятичного числа 12 в шестнадцатеричное
12 из десятичного в шестнадцатеричный — из десятичного в шестнадцатеричный Пошаговый преобразователь / калькулятор базы чисел.
Преобразование из / в десятичное, шестнадцатеричное, восьмеричное и двоичное. Калькулятор преобразования десятичного основания. Здесь вы можете найти ответы на такие вопросы, как: Преобразовать десятичное число 12 в шестнадцатеричное или десятичное в шестнадцатеричное преобразование.
Таблица десятичных, двоичных, шестнадцатеричных и восьмеричных диаграмм
| Dec | Hex | Oct | Bin | ||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | ||
| 1 | 1 | 1 | 00092 | 10 | |
| 3 | 3 | 3 | 11 | ||
| 4 | 4 | 4 | 100 | ||
| 5 | 900 | 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 | ||
| 8 | 8 | 10 | 1000 | 000 90091001 | |
| 10 | A | 12 | 1010 | ||
| 11 | B | 13 | 1011 | 90 019||
| 12 | C | 14 | 1100 | ||
| 13 | D | 15 | 1101 | ||
| 14 | E | 11 | 000000917 | 1111 |
| Dec | Hex | Oct | Bin | |||
|---|---|---|---|---|---|---|
| 16 | 10 | 20 | 10000 | |||
| 17 | 11 | 21 | 000000922 | 10010 | ||
| 19 | 13 | 23 | 10011 | |||
| 20 | 14 | 24 | 10100 | |||
| 21 | 0009 90022 | 16 | 26 | 10110 | ||
| 23 | 17 | 27 | 10111 | |||
| 24 | 18 | 30 | 1 | 11000 | 11000 | 11001 |
| 26 | 1A | 32 | 11010 | |||
| 27 9000 9 | 1B | 33 | 11011 | |||
| 28 | 1C | 34 | 11100 | |||
| 29 | 1D | 35 | 9104 | 0000009 11110 | ||
| 31 | 1Ф | 37 | 11111 |
| Dec | Hex | Oct | Bin | ||
|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | ||
| 33 | 21 | 100004 | 42 | 100010 | |
| 35 | 23 | 43 | 100011 | ||
| 36 | 24 | 44 | 100100 | ||
| 37 | 0009 90038 | 26 | 46 | 100110 | |
| 39 | 27 | 47 | 100111 | ||
| 40 | 28 | 50 | 000900 | 101001 | |
| 42 | 2A | 52 | 101010 | ||
| 2B | 53 | 101011 | |||
| 44 | 2C | 54 | 101100 | ||
| 45 46 | 2D | 55104 | 0009 56101110 | ||
| 47 | 2F | 57 | 101111 |
| Dec | Hex | Oct | Bin | ||
|---|---|---|---|---|---|
| 48 | 30 | 60 | 110000 | ||
| 49 | 31 | 62 | 110010 | ||
| 51 | 33 | 63 | 110011 | ||
| 52 | 34 | 64 | 110100 | 53 | 54 | 36 | 66 | 110110 |
| 55 | 37 | 67 | 110111 | ||
| 56 | 38 | 70 | 0009111 3 | 111001 | |
| 58 | 3A | 72 | 111010 | ||
| 3B | 73 | 111011 | |||
| 60 | 3C | 74 | 111100 | ||
| 61 | 111 | 75 | 111110 | ||
| 63 | 3F | 77 | 111111 |
| Dec | Hex | Oct | Bin | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 64 | 40 | 100 | 1000000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | 41 | 1004 | 102 | 1000010 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | 43 | 103 | 1000011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | 44 | 104 | 1000100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
699 | 900970 | 46 | 106 | 1000110 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | 47 | 107 | 1000111 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | 48 | 110 |
Number Base ConverterПожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите копировать адрес ссылки и вставьте его в свой HTML-код. Преобразование базового числа образцовЗаявление об отказе от ответственностиНесмотря на то, что прилагаются все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения или за результаты, полученные в результате использования этой информации. Вся информация на этом сайте предоставляется «как есть», без каких-либо гарантий полноты, точности, своевременности или результатов, полученных в результате использования этой информации. Десятичная, шестнадцатеричная и двоичная таблица преобразованияДесятичная, шестнадцатеричная и двоичная таблица преобразования Таблица преобразования
Авторские права © 1998 DEW Associates Corporation.Все права защищены. Шестнадцатеричный калькуляторШестнадцатеричное вычисление — сложение, вычитание, умножение или делениеПреобразовать шестнадцатеричное значение в десятичное значениеПреобразовать десятичное значение в шестнадцатеричноеСвязанный двоичный калькулятор | Калькулятор IP-подсети Шестнадцатеричная система счисления (шестнадцатеричная) практически идентична десятичной и двоичной. Вместо использования базы 10 или 2 соответственно, он использует базу 16.Hex использует 16 цифр, включая 0-9, как и десятичная система, но также использует буквы A, B, C, D, E и F (эквивалентные a, b, c, d, e, f) для представления числа 10-15. Каждая шестнадцатеричная цифра представляет собой 4 двоичных числа, называемых полубайтами, что упрощает представление больших двоичных чисел. Например, двоичное значение 1010101010 может быть представлено как 2AA в шестнадцатеричном формате. Это помогает компьютерам сжимать большие двоичные значения таким образом, чтобы их можно было легко преобразовать между двумя системами. Ниже приведены некоторые типичные преобразования шестнадцатеричных, двоичных и десятичных значений: Шестнадцатеричное / десятичное преобразование
Преобразование десятичных и шестнадцатеричных значений в десятичную и шестнадцатеричную системы. .Более подробное обсуждение доступно на странице двоичного калькулятора. Обратите внимание, что преобразование между десятичным и шестнадцатеричным числами очень похоже на преобразование между десятичным и двоичным числами. Возможность выполнить преобразование одного из них должно сделать другой относительно простым. Как упоминалось ранее, шестнадцатеричные функции используют основание 16. Это означает, что для значения 2AA каждое разрядное значение представляет степень 16. Начиная справа, первая буква «A» представляет разряд «единиц», или 16 0 . Вторая буква «А» справа представляет 16 1 , а цифра 2 — 16 2 .Помните, что «A» в шестнадцатеричном формате эквивалентно 10 в десятичном. Зная эту информацию, можно преобразовать шестнадцатеричное в десятичное, как показано ниже:
Преобразование из десятичного числа в шестнадцатеричное немного сложнее, но использует те же концепции.См. Шаги и пример ниже. Чтобы понять процесс, важно проработать приведенный пример в сочетании с перечисленными шагами:
Преобразование из шестнадцатеричного в десятичное использует те же принципы, но, возможно, проще.Умножьте каждую цифру в шестнадцатеричном значении на соответствующее ей разрядное значение и найдите сумму каждого результата. Процесс одинаков, независимо от того, содержит ли шестнадцатеричное значение буквенные цифры или нет.
Шестнадцатеричное сложениеШестнадцатеричное сложение подчиняется тем же правилам, что и десятичное, с той лишь разницей, что добавляются цифры A, B, C, D, E и F.Может быть удобно иметь десятичные эквивалентные значения от A до F при выполнении шестнадцатеричных операций, если значения еще не сохранены в памяти. Ниже приведен пример шестнадцатеричного сложения. Проработайте пример и обратитесь к тексту под ним для получения дополнительных сведений. БЫВШИЙ:
Шестнадцатеричное сложение включает вычисление базового десятичного сложения при преобразовании между шестнадцатеричным и десятичным числами, когда присутствуют значения больше 9 (цифры от A до F).В приведенном выше примере B + 8 в десятичной системе счисления составляет 11 + 8 = 19. 19 в десятичной системе счисления равно 13 в шестнадцатеричной системе счисления , так как имеется 1 набор из 16, с оставшимися 3. Как и в случае с десятичным сложением, 1 переносится в следующий столбец. Следовательно, следующий столбец выглядит так: 1 + A (10) + 7 = 18 в десятичной системе счисления или 12 в шестнадцатеричной системе . Перенесите 1 в последний столбец, в результате получится 1 + 8 + B (11) = 20 в десятичной системе счисления или 14 в шестнадцатеричной системе . Это дает результат 1423 шестнадцатеричный . Шестнадцатеричное вычитаниеШестнадцатеричное вычитание можно вычислить почти так же, как шестнадцатеричное сложение; путем выполнения операции при преобразовании шестнадцатеричных значений в десятичные.Наиболее существенная разница между шестнадцатеричным и десятичным вычитанием заключается в заимствовании. При заимствовании в шестнадцатеричном формате заимствованная «1» представляет 16 десятичных , а не 10 десятичных . Это связано с тем, что заимствованный столбец в 16 раз больше, чем заимствованный столбец (по той же причине, что заимствованная 1 в десятичном представлении представляет 10). Если это отмечено и преобразование буквенных цифр A-F выполняется осторожно, шестнадцатеричное вычитание не сложнее десятичного вычитания.Проработайте пример и обратитесь к тексту под ним для получения дополнительных сведений. БЫВШИЙ:
В первом столбце справа в приведенном выше примере C или 12 в десятичной системе счисления меньше F или 15 в десятичной системе счисления .Таким образом, необходимо заимствовать из следующего столбца. Это уменьшает D до C и предоставляет 1 или 16 десятичных в первый столбец. 16 десятичное + 12 десятичное -15 десятичное = 13 десятичное , или D в первом столбце. Следующие столбцы не требуют заимствования, что упрощает вычисления. Поскольку 1 была заимствована, C — A = 12 десятичных — 10 десятичных = 2 и 5 — 3 = 2, что дает окончательный результат 22D. В случае, когда вычитаемое число больше, чем вычитаемое, просто измените позиции чисел, вычислите вычитание и добавьте к результату знак минус.Если бы в приведенном выше примере вместо 3AF — 5DC, он был бы записан как есть, за исключением того, что решение было бы -22D. Шестнадцатеричное умножениеШестнадцатеричное умножение может быть сложным, потому что преобразование между шестнадцатеричным и десятичным числом при выполнении операций требует больше усилий, поскольку числа имеют тенденцию быть больше. Может оказаться полезным наличие шестнадцатеричной таблицы умножения (она приведена ниже). В противном случае для каждого шага потребуется ручное преобразование между десятичной и шестнадцатеричной числами.Ниже приведен пример умножения шестнадцатеричного числа. Справа от примера показаны шаги умножения и сложения. Обратите внимание, что все используемые цифры шестнадцатеричные. При необходимости обратитесь к разделу «Дополнения». БЫВШИЙ:
Hex DivisionДлинное деление в шестнадцатеричном формате идентично полному делению в десятичном, за исключением того, что умножение и вычитание происходят в шестнадцатеричном формате.Также можно преобразовать в десятичное и выполнить длинное деление в десятичном, а затем преобразовать обратно после завершения. Для наглядности пример деления будет полностью рассчитан в шестнадцатеричном формате. Как и в случае с умножением, при проведении шестнадцатеричного деления было бы удобно иметь шестнадцатеричную таблицу умножения (одна из них приведена ниже). Ниже приведен пример. Обратите внимание, что все цифры в примере шестнадцатеричные. Хотя в приведенном ниже примере заимствования не происходит, помните, что заимствование в шестнадцатеричном формате приводит к заимствованию 16 десятичных , а не 10 десятичных .Обратитесь к разделу вычитания шестнадцатеричных чисел для получения дополнительной информации. Шестнадцатеричная таблица умноженияПреобразование шестнадцатеричной системы в систему с основанием 12 • Конвертер чисел • Обычные преобразователи единиц • Компактный калькулятор • Онлайн-конвертеры единицКонвертер длины и расстояния Конвертер массы Сухой объем и общие измерения при приготовлении пищи Конвертер площади Конвертер объема и общих измерений при приготовлении пищи Конвертер температуры Конвертер давления, напряжения, модуля Юнга Конвертер энергии и работыПреобразователь силы КонвертерВремяКонвертер линейной скорости и скоростиКонвертер угловой эффективности, расхода топлива и экономии топливаКонвертер единиц информации и хранения данныхКурсы валютЖенская одежда и размеры обувиМужская одежда и размеры обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер удельного ускорения Конвертер угловой силы Преобразователь крутящего момента Удельная энергия, теплота сгорания (на массу) Конвертер Удельная энергия, теплота сгорания (на объем) C Преобразователь температурного интервалаКонвертер температурного интервалаКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер теплопроводностиКонвертер удельной теплоемкостиПлотность тепла, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер коэффициента теплопередачиКонвертер абсолютного расходаПреобразователь массового расходаМолярный расход раствораПреобразователь массового расходаПреобразователь молярной концентрации Конвертер напряженияПреобразователь проницаемости, проницаемости, паропроницаемости Конвертер скорости передачи водяных паровКонвертер уровня звукаКонвертер чувствительности микрофонаКонвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с выбираемым эталонным давлениемКонвертер яркостиПреобразователь световой интенсивностиКонвертер яркостиЦифровой преобразователь разрешения изображенияПреобразователь частоты и длины волныОптическая мощность (диоптрийная мощность) Диоптрия) в Magnificati on (X) ConverterЭлектрический преобразователь зарядаЛинейный преобразователь плотности зарядаПреобразователь поверхностной плотности зарядаПреобразователь объёмной плотности зарядаПреобразователь электрического токаЛинейный преобразователь плотности токаПреобразователь плотности поверхностного токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электрической проводимости дБм, дБВ, ватт и другие единицыПреобразователь магнитодвижущей силыПреобразователь напряженности магнитного поляКонвертер магнитного потокаПреобразователь плотности магнитного потокаМощность поглощенной дозы излучения, Конвертер мощности суммарной дозы ионизирующего излученияРадиоактивность.Преобразователь радиоактивного распада Преобразователь радиационного воздействияРадиация. Конвертер поглощенной дозы Конвертер метрических префиксовКонвертер передачи данныхПреобразователь единиц типографии и цифрового изображенияКонвертер единиц измерения объема древесиныКалькулятор молярной массыПериодическая таблица ОбзорПриложение для калькулятора iPhone Число — это абстрактное математическое понятие, обозначающее количество. Используется при подсчете. Числа использовались с древних времен, сначала в виде счетных отметок — царапин на дереве или кости, а затем в виде более абстрактных систем.Есть несколько способов выражения чисел в числовых системах. Некоторые из них сегодня не используются. Различные способы представления чиселНекоторые исследователи считают, что понятие числа возникло независимо в разных регионах. Первоначально письменные представления чисел с помощью символов развивались независимо, но когда торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, а системы счисления, используемые в настоящее время, были созданы на основе коллективного знания. Индо-арабские цифрыИндо-арабская система счисления — одна из наиболее широко используемых в современном мире. Первоначально он был разработан в Индии и усовершенствован персидскими и арабскими математиками. В средние века он распространился на западный мир через торговлю, заменив римскую систему счисления. Он был дополнительно модифицирован и широко принят во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на десятичных числах и использует десять символов для представления всех чисел. Десять — это обычное число, которое используют для счета, потому что у людей десять пальцев, а исторически часто для счета использовались части тела. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать в разговоре какую-либо мысль о счете, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках. Надпись на латыни и римскими цифрами на Адмиралтейской арке в Лондоне.Он гласит: ANNO: DECIMO: EDWARDI: SEPTIMI: REGIS: VICTORIÆ: REGINÆ: CIVES: GRATISSIMI: MDCCCCX: (На десятом году правления короля Эдуарда VII королеве Виктории от самых благодарных граждан, 1910). РимскиеРимские цифры использовались в Римской империи и Европе до 14 века. Они все еще используются сегодня в некоторых контекстах, например, в часах, для обозначения часов. Римские цифры основаны на семи числах, написанных буквами латинского алфавита: Порядок важен в римской системе, потому что большее число, за которым следует меньшее, означает, что нужно сложить два, но меньшее число перед больший означает, что меньшее число вычитается из большего.Например, XI равно 11, а IX равно 9. Правило вычитания не универсальное, оно работает только для этих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, а вместо них последовательно пишутся цифры. Системы в других культурахЛюди во многих географических регионах имели системы представления чисел, похожие на римские или индуистско-арабские. Например, некоторые славяне использовали кириллический алфавит для обозначения чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами, чтобы отличать цифры от букв.В еврейской системе счисления используется еврейский алфавит для обозначения чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены в виде кратных или сумм. Греческая система счисления также похожа. В некоторых культурах используются более простые представления, такие как вавилонская система, в которой есть только два клинописных символа: один (несколько напоминающий букву «Т») и десять (немного похожий на букву «С»). Так, например, 32 будет записано (с использованием правильных символов) как CCCTT.Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы нуля, единицы и пяти, со специальными обозначениями для чисел больше девятнадцати. Унарная система счисления. Счетные метки в различных культурах УнарныйУнарная система представляет каждое число с тем же количеством символов, что и его значение.Эти символы обычно одинаковы, поэтому, если 1 представлен как A, то 5 будет представлен как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь установить связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные типы представительств. Например, при подсчете очков команд-победителей или подсчете пунктов или дней люди в западном мире и некоторых других регионах часто пишут четыре вертикальные линии, затем пересекают их пятой горизонтальной линией и повторяют процесс.Например, в части A) на картинке человек, считающий до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал ставить счетные отметки, пока не сумел до двенадцати. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части B) на картинке человек считает до пяти, завершая образ, а затем начинает новый персонаж, продолжая счет до семи.Порядок штриха задан заранее, как показано на рисунке. Унарная система также используется в информатике. Арифмометр, использующий десятичную систему, и микросхему микропроцессора, использующую двоичную систему Позиционная системаПозиционная система работает с основанием. Например, по основанию 10 мы имеем следующее:
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами, имеющими относительно большие значения, без использования большого пространства для их записи. Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰ ДвоичнаяДвоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система base-2. Числа представлены следующим образом: 0 = 0, 1 = 1, а от 2 используется принцип сложения. Добавление в основании-2 аналогично добавлению в основании-10. Чтобы увеличить число на единицу: Художественное представление двоичных чисел
Чтобы сложить два числа, они выравниваются друг относительно друга, и для каждого места 0 + 0 дает 0, 1 + 0 дает 1, а 1 + 1 дает 10, где 0 помещается в эту позицию, а 1 переносится на следующую позицию.Например: 11111 (31) В этом случае, работая справа налево:
Итак, сложив это вместе, мы получаем 101010. Вычитание работает по тому же принципу, за исключением того, что вместо переноса мы «заимствуем».Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например: 101 (5) Деление и вычисление квадратных корней также очень похоже на основание 10. Классификация номеровВсе номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются. Долг — отрицательное число Отрицательные числаОтрицательные числа — это числа, представляющие отрицательное значение.Перед ними ставится знак минус. Например, если у человека A нет денег, и он должен 5 долларов человеку B, то у человека A -5 долларов. Здесь –5 — отрицательное число. Рациональные числаРациональные числа — это числа, которые могут быть выражены в виде дробей, где знаменатель — натуральное число, не равное нулю, а числитель — целое число. Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами. Натуральные числаНатуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456. Целые числаЦелые числа включают ноль, отрицательные и положительные числа, не являющиеся дробями. Примеры включают -65 и 11 223. Комплексные числаКомплексные числа — это все числа, которые представляют собой сумму одного действительного числа и произведения другого действительного числа и квадратного корня из отрицательного числа. Простые числаПростые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11.2 57 885 161 −1 — самое большое известное простое число на зиму 2013 года. Оно состоит из 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой при безопасном онлайн-обмене данными, например, в онлайн-банкинге. Интересные факты о числахКитайские номера по борьбе с мошенничеством Цифры по борьбе с мошенничествомЧтобы предотвратить мошенничество при написании чисел в бизнесе и торговле, в китайском языке используются специальные сложные символы, которые трудно подделать, добавив лишние штрихи.Это сделано потому, что часто используемые китайские символы для чисел слишком просты, и их значение легко изменить, добавив штрихи. Современный счет в торговлеНекоторые языки в странах, где в настоящее время используется система счисления с основанием 10, по-прежнему отражают то, что другие системы счисления были распространены в прошлом. Например, в английском языке есть специальное слово для двенадцати, «дюжина» — в настоящее время оно используется в основном для подсчета яиц, выпечки, вина и цветов. В кхмерском есть особые слова, основанные на древней системе 20, для подсчета фруктов. Группировка цифрИ в Китае, и в Японии принята индийско-арабская система счисления, но большие числа сгруппированы по 10 000, и это отражено в языке. Например, в английском языке есть слово «1000», а одно указывает, сколько их тысяч, вплоть до 999 999. Затем следует слово «миллион», обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после этого приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000. Несчастливые числаЛеонардо да Винчи. Последний ужин. Церковь Пресвятой Богородицы (Санта-Мария-делле-Грацие), Милан, Италия. В западной традиции число 13 считается несчастливым. Многие считают, что это заимствовано из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время последней вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Среди викингов также существовало суеверие, что один из тринадцати собравшихся умрет в следующем году. В России и многих странах бывшего СССР все четные числа считаются несчастливыми. Возможно, эта традиция возникла из убеждения, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, не являются живыми. С другой стороны, нечетные числа представляют собой изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, дарить живым людям четное количество цветов считается невезением — эти числа обычно предназначаются для похорон. В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, потому что оно произносится так же, как «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае номер 7 тоже несчастлив, потому что он представляет духовный мир и призраков. Седьмой месяц в китайском календаре называется «месяцем призрака», когда открыта связь между мирами живых и духов.В Японии еще одно неудачное число — 9 , которое имеет то же произношение, что и «страдание». В Италии 17 — неудачное число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «Я жил». Это означает, что жизнь окончена, и относится к смерти. 666 — еще одно неудачное число, которое в Библии называется «числом зверя». Иногда считается, что это 616, но чаще встречается 666.Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, который ассоциируется с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают, что Нерон был поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками. В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или постыдным числом, связанным с проституцией.Это связано с историей о сутенере, у которого на номерном знаке и в номере квартиры был номер 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия с целью получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||