Mathcad 15/Mathcad Prime 1.0 (+Видеокурс)
419 ₽
356 ₽
# Mathcad
- Описание
- Детали
- Отзывы (0)
Описание
Книга посвящена методике решения задач высшей математики при помощи программы Mathcad. Приводятся примеры расчета типовых задач линейной алгебры, математического анализа, дифференциальных уравнений, статистики и обработки данных. Объясняется работа численных алгоритмов, заложенных во встроенных функциях и операторах системы Mathcad. Предлагаются неочевидные приемы решения актуальных задач современной вычислительной науки. Описывается интерфейс Mathcad и его основные составные части, предоставляется необходимая справочная информация. Подробно описана работа в среде Mathcad 2001/2001i/11/12/13/14/15.
Рассматриваются новые возможности и отличительные черты новой версии Mathcad Prime 1.0. На FTP-сервере издательства находятся мультимедийный видеокурс по работе с Mathcad, листинги примеров, справочник по вычислительной математике и учебник по вычислительной физике с примерами, оформленными в виде электронной книги Mathcad….
Детали
| Артикул | 2076 |
|---|---|
| ISBN | 978-5-9775-0746-2 |
| Количество страниц | 432 |
| Серия | В подлиннике |
| Переплет | Мягкая обложка |
| Печать | Черно-белая |
| Год | 2012 |
| Габариты, мм | 240 × 170 × 16 |
| Вес, кг | 0.408 |
Дополнительные файлы скачать: Зеркало1Дополнительные файлы скачать (Chrome): Зеркало2
- ✓ Новинки на 2 недели раньше магазинов
- ✓ Цены от издательства ниже до 30%
- ✓ Акции и скидки только для подписчиков
- ✓ Важные новости БХВ
ПОЛЕЗНАЯ РАССЫЛКА КНИЖНЫХ НОВОСТЕЙ
Подписываясь на рассылку, вы соглашаетесь с политикой конфиденциальности и обработкой своих персональных данных.
Рекомендуем также
-
Mathcad 14 (+Видеокурс на CD) – Бумажная книга
699₽ -
Теория вероятностей и математическая статистика. Основы, прикладные аспекты с примерами и задачами в среде Mathcad – Бумажная книга
535₽ -
Mathcad 14 для студентов и инженеров: русская версия – Бумажная книга
385₽ - Очков Валерий Федорович
Нет в наличии
Теплотехнические этюды с Excel, Mathcad и Интернет
464 ₽ -
Книга по MathCad (Книга) | Помощник студента БГУИР
Главная » Предметы » Высшая математика
Дата: Сб, 02/07/2009 — 02:13; Автор: Viking
Название:
Книга по MathCad
Тип:
Книга
Содержание:
Предисловие
Что в книге нового
Адреса для общения
О шрифтовых выделениях в книге
Предупреждения
Об использовании диска с примерами программ для MathCAD 6.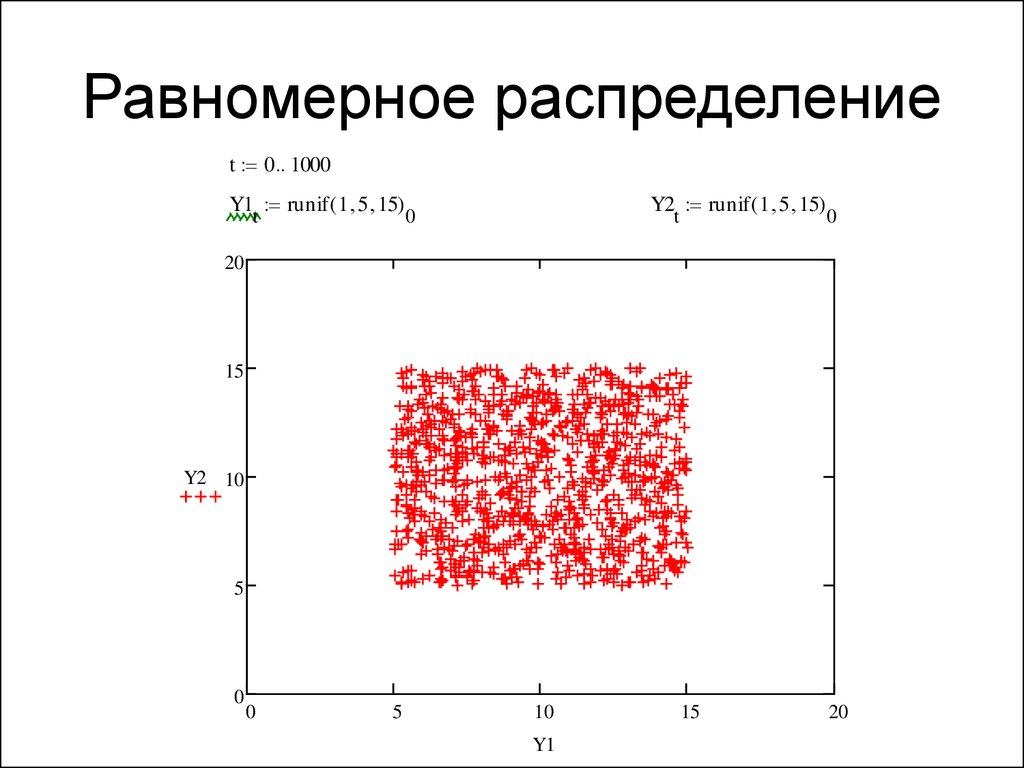
0
Глава 2 Работа с файлами
2. 1. Позиция главного меню File
2. 2. Подготовка к вводу нового документа (New)
2. 3. Ввод документа с диска (Open…)
2. 4. Запись документа на диск без переименования (Save)
2. 5. Запись документа на диск с переименованием (Save As…)
2. 7. Групповая работа над документом (Collaboratory…)
2. 8. Установка входа в сеть (Internet Setup…)
2. 9. Отправка документов по электронной почте (Send…)
2. 10. Установка параметров страницы при печати (Page Setup…)
2. 11. Предварительный просмотр страниц печати (Print Preview…)
2. 12. Печать документов (Print…)
2. 13. Выход из системы (Exit)
Глава 3 Редактирование документов
3. 1. Общие приемы редактирования документов (Edit)
3. 2. Отмена операции редактирования (Undo) и ее повтор (Redo)
3. 3. Выделение объектов и перенос их в буфер обмена (Cut)
3. 4.
Копирование объекта в буфер обмена (Copy)
3. 5. Копирование объекта из буфера обмена в окно (Paste)
3. 6. Специальная вставка (Paste Special…)
3. 8. Выделение всех объектов (Select All)
3. 9. Поиск подстроки (Find…)
3. 10. Замена подстроки (Replace…)
3. 11. Проверка орфографии (Check Speling…)
3* 12. Переход к заданной странице документа (Go to Page…)
3. 13. Связывание документов (Links…)
3. 14. Редактирование внедренных объектов (Object)
3. 15. Редактирование с применением клавиатуры
Глава 4 Управление обзором (View)
4. 1. Управление элементами интерфейса
4. 2. Выделение областей (Regions)
4. 3. Изменение масштаба документа (Zoom)
4. 4. Восстановление искажений экрана (Refresh)
4. 5. Анимация графиков (Animation)
4. 6. Вызов проигрывателя (Playback)
Глава 5 Работа со вставками
5. 1. Подменю позиции Insert (Вставка) главного меню
5.
5. 3. Установка шаблона графиков в полярной системе координат (Polar Plot)
5. 4. Установка шаблона трехмерных графиков (Surface Plot)
5. 5. Установка шаблона контурных ЗD-графиков (Contour Plot)
5. 6. Установка шаблона точечного ЗD-графика (3D Scatter Plot)
5. 7. Установка шаблона SD-графиков в виде гистограммы (3D Bar Chart)
5. 8. Установка шаблона ЗD-графиков с векторным представлением (Vector Field Plot)
5. 9. Установка шаблона матриц и векторов (Matrix…)
5. 10. Вывод функций (Choose function…)
5. 11. Установка единиц измерения размерных величин (Units…)
5. 12. Установка шаблона импортируемого рисунка (Picture)
5. 13. Вставка текстовой области (Text Region…)
5. 14. Вставка в текстовую область математических формул (Math Region…)
5. 15. Вставка линии разрыва страницы (Page Break)
5. 16. Вставка гиперссылки (Hyperlink)
5. 17. Вставка обращения к заданному файлу активизацией кнопки (Reference.
5. 18. Связь с другими компонентами системы (Component…)
5. 19. Вставка объектов (Object…)
Глава 7 Управление вычислительными процессами
7. 1. Вычисление в пределах экрана (Calculate)
7. 2. Исполнение всего документа (Calculate Worksheet)
7. 3. Вычисления в автоматическом режиме (Automatic Calculation)
7. 4. Оптимизация вычислений (Optimization)
7. 5. Установка опций (Options…)
Глава 8 Работа с символьным процессором
8. 1. Возможности символьного процессора (Symbolic)
8. 2. Выделение объектов символьных операций
8. 3. Выполнение символьных вычислений (Evaluate Symbolically)
8. 4. Упрощение выражений (Simplify)
8. 5. Расширение выражений (Expand)
8. 6. Разложение выражений (Factor)
8. 7. Комплектование по выражениям (Collect)
8. 9. Дифференцирование по заданной переменной (Differentiate)
8.
10. Интегрирование по заданной переменной (Integrate)8. 11. Решение уравнения относительно заданной переменной (Solve)
8. 12. Подстановка для заданной переменной (Substitute)
8. 13. Разложение в ряд Тейлора по заданной переменной (Expand to Series…)
8. 14. Разложение на правильные дроби (Convert to Partial Fraction)
8. 15. Транспонирование матрицы (Transpose)
8. 16. Обращение матриц (Invert)
8. 17. Функции преобразований Фурье, Лапласа и Z-преобразований
8. 18. Установка стиля эволюции символьных выражений (Evolution Style…)
8. 19. Интерпретация результатов символьных операций в буфере обмена
8. 20. Применение преобразований Лапласа для аналитического решения дифференциальных уравнений
Глава 9 Работа с окнами
9. 1. Подменю для работы с окнами (Window)
9. 2. Каскадное расположение окон (Cascade)
9. 3. Расположение окон по горизонтали (Horizontal)
9. 4. Расположение окон по вертикали (Vertical)
9.
5. Приведение в порядок пиктограмм (Arrange Icon)9. 6. Переключение окон и управление ими
Глава 10 Работа с информационными ресурсами
10. 1. Информационные ресурсы системы MathCAD 7. 0 PRO
10. 2. Работа со справочной системой (MathCAD Help)
10. 3. Построение и применение профессиональной справочной базы данных
10. 4. Работа с центром информационных ресурсов (Resource Center)
10. 5. Электронная подсказка (Tip of the Day)
10. 6. Открытие электронных книг (Open Book…)
10. 7. Использование справочной системы (Using Help…)
10. 8. Общие сведения о системе (About MathCAD)
Глава 14
14. 6. Решение задач фильтрации
14. 7. Физические расчеты
14. 8. Электро- и радиотехнические расчеты
Скачать:
Несколько способов использования runif
В языке R функция runif(n) предназначена для создания вектора длины n, каждое значение вектора представляет собой случайное число от 0 до 1.
Это один из способов получения выборок из равномерное распределение U(0, 1).
Эта функция очень полезна при моделировании, отборе проб и тестировании моделей. Позвольте мне показать вам несколько способов использования функции.
1. Отбор образцов из треугольного распределения: runif(n) — runif(n)
Для любой нормальной детерминированной функции f(x) — f(x) = 0 при любом данном x. Но для случайных или недетерминированных функций у нас будет другая случайная величина. В этом случае у нас есть случайная выборка из треугольного распределения со средним значением = 0,5-0,5 = 0 и var = 1/12 + 1/12 = 1/6 и диапазоном = (-1, 1).
https://raw.githubusercontent.com/tutrunghieu/sharing/master/runif/u1-triang-dist.R
2. Отбор образцов из нормального распределения: runif(n) + … + runif(n) — 6
Если мы нарисуем 12 случайных векторов одинаковой длины и сложим их вместе, то минус 6, мы получим выборочный вектор нормального распределения N(0, 1). Если вы посчитаете, то увидите, что E(X1 + X2 + .
.. + X12 — 6) = 0,5 + 0,5 + … + 0,5 — 6 = 0, а дисперсия Var(X1 + X2 + .. + X12 — 6) = 1/12 + 1/12 + … + 1/12 = 1. И в силу центральной предельной теоремы имеем форму нормальной кривой
https://raw.githubusercontent.com/tutrunghieu/sharing/master/runif/u2-normal-dist.R
3. Отбор образцов из категориального распределения (мешок слов)
Если мы хотим сгенерировать случайное значения, используя {красный -> 0,2, зеленый -> 0,3, синий -> 0,5}, что означает, что если мы нарисуем 1000 значений, мы увидим 200 красных значений, 300 зеленых значений и 500 синих значений в любом случайном порядке.
Образец функции можно использовать для извлечения категориальных значений из распределения с заменой. Однако мы также можем написать функцию для этого.
https://raw.githubusercontent.com/tutrunghieu/sharing/master/runif/u3-cat-dist.R
4. Отбор образцов из любой заданной функции распределения f(x) в интервале (a, b)
Если мы нарисуем x ~ U(a, b) и y ~ U(0, M) и добавим x в выходной список, если y < f(x), то мы получим случайную величину с распределением f(x)
https://raw.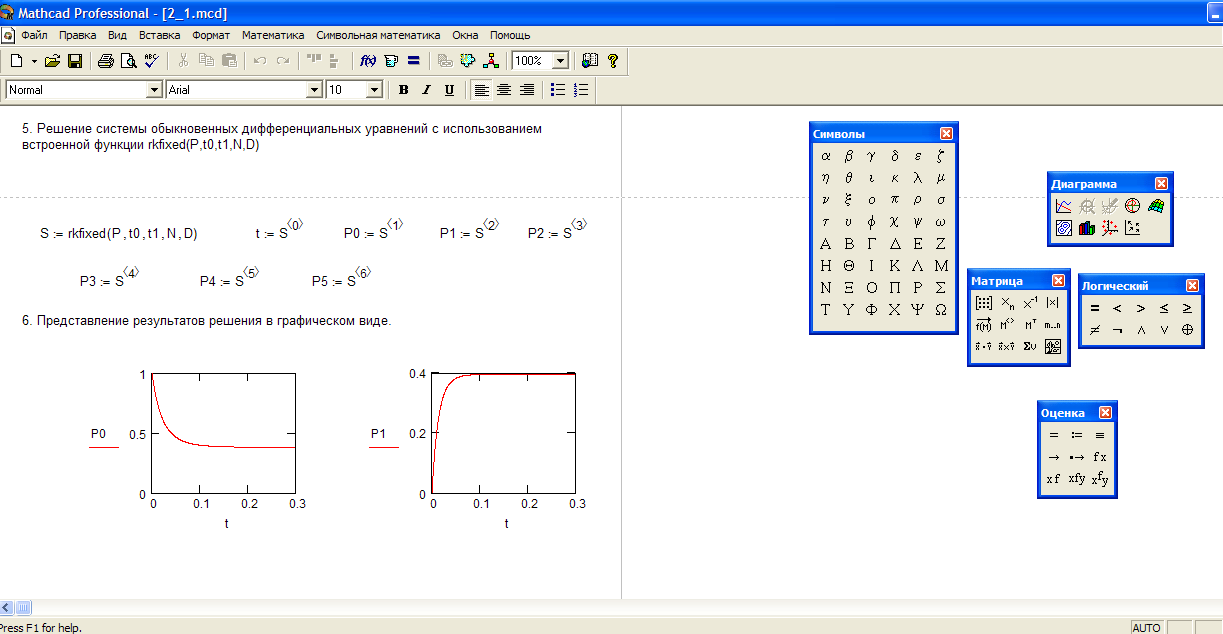
githubusercontent.com/tutrunghieu/sharing/master/runif/u4-generic-dist.R
5. Монеты из runif(n)
Мы можем сгенерировать последовательность орел/решка, аналогичную подбрасывание монеты с разной вероятностью. Если нам нужна честная монета, дайте вероятность p(орел)=p(решка)=0,5, а если мы хотим, чтобы орел выпадал чаще, дайте p(орел)=0,7 и p(решка)=1-p(орел).
https://raw.githubusercontent.com/tutrunghieu/sharing/master/runif/u5-coins.R
6. Игра в кости от runif(n)
Игра в кости используется для получения целого числа от 1 до 6 Вы можете использовать образец функции для создания категорийных значений или функцию rcat из предыдущего раздела. Для игры в кости есть простой способ комбинировать руниф и пол или потолок. Если вы используете потолок, у вас есть значения от 1 до 6, а если вы используете пол, у вас есть значения от 0 до 5
https://raw.githubusercontent.com/tutrunghieu/sharing/master/runif/u6-dice.R
Когда у нас есть одинаковые значения от 1 до 6, мы можем генерировать неоднородные значения с помощью метода преобразования или метода отклонения.
7. Игровой автомат
Игровой автомат можно смоделировать, генерируя множество независимых категориальных случайных величин (много монет, много игральных костей) и комбинируя их в таблице. Это считается наивным байесовским методом (независимый метод).
На самом деле мы не можем считать слоты независимыми. Например, когда владельцы казино не хотят, чтобы игроки выигрывали, они будут делать некоторые трюки с машиной, чтобы значение в следующем слоте не совпадало со значением в предыдущем слоте. Это байесовский игровой автомат, в котором следующий слот зависит от предыдущих слотов (байесовская сеть, сэмплер разговорной речи Шеннона).
8. Оптимизация функции f(x) на интервале (a, b)
Вместо сканирования по x от a до b можно провести выборки в пределах (a, b) и выбрать оптимальное значение x*, где f( x) <= f(x*) при любом заданном x. Чем больше у вас выборки, тем более оптимальным может быть x*.
https://raw.githubusercontent.com/tutrunghieu/sharing/master/runif/u7-optimization.
R
9. Вычисление интегрирования f(x) в интервале (a, b)
По принципу соотношения между площадью под кривой f(x) в интервале (a, b) и площадью под линией y=M в интервале (a, b) аналогично отношению между числом точек под кривой и числом точек под прямой y=M. Значение int{f(x) : x ~ a..b }/ (M*|b-a| ) = Nf / N, где Nf — количество точек под кривой, а N — общее количество точек под линией y =М
Следовательно, int{f(x) : x ~ a..b } = Nf *M*|b-a| / N можно вычислить только путем выборки с помощью runif и подсчета
https://raw.githubusercontent.com/tutrunghieu/sharing/master/runif/u8-integration.R
Заключение
Равномерное распределение является основой для общего все другие распределения, в том числе нормальное распределение, смесь Гаусса, категориальное распределение.
Используйте функцию runif творчески для решения задач оптимизации, интеграции и моделирования.
funct_r_z — Стр 3
| С этими функциями связано «начальное значение». |
| генерирует новые случайные числа на основе этого начального числа. Заданное начальное значение всегда будет генерировать | .
| та же последовательность случайных чисел. Выбор «Рассчитать» в меню «Математика» позволяет перейти к Mathcad 9.0003 |
| по этой последовательности случайных чисел. Однако изменение начального значения продвигает Mathcad по |
| совершенно другая последовательность случайных чисел. |
| Чтобы изменить начальное значение, выберите «Параметры» в меню «Математика» и измените значение «начальное значение» |
| на вкладке Встроенные переменные. Обязательно укажите целое число. |
| Чтобы сбросить генератор случайных чисел Mathcad без изменения начального значения, выберите Options |
| из меню «Математика», перейдите на вкладку «Встроенные переменные» и нажмите «ОК», чтобы принять текущий |
| семян. |
| Расчет в меню Math. Поскольку рандомизатор был сброшен, Mathcad генерирует |
| те же самые случайные числа, которые будут генерироваться при перезапуске Mathcad. |
| В Mathcad есть много других генераторов случайных величин. |
Алгоритм | Метод линейной конгруэнтности (Кнут, 1997) |
|
|
стандарт | Случайные числа |
Синтаксис | rнорм(м, мк, σ) |
Описание | Возвращает вектор из m случайных чисел, имеющих нормальное распределение. |
Аргументы | целое, м > 0 |
м | |
мк | действительное среднее |
σ | действительное стандартное отклонение, σ > 0 |
Пример |
|
Каждый раз, когда вы сбрасываете начальное значение, Mathcad
Затем щелкните уравнение, содержащее функцию генерации случайных чисел, и выберитеАлгоритм
См.
также
Примечание. Вы не сможете точно воссоздать этот пример, потому что генератор случайных чисел каждый раз выдает разные числа.
Метод соотношения форм (Деврое, 1986)
рнд
Функции | 107 |
корень | Решение |
Синтаксис root(f(var), var)
Описание Возвращает значение var, при котором выражение f(var) или функция f равно 0.
Аргументы
var вещественный или комплексный скаляр; var должно быть присвоено приблизительное значение перед использованием этой версии root.
f Действительная или комплексная функция.
Пример
Комментарии Для выражений с несколькими корнями ваше предполагаемое значение определяет, какой из корней возвращает Mathcad. В примере показана ситуация, когда корневая функция возвращает несколько разных значений, каждое из которых зависит от начального значения предположения.
Нельзя вносить числовые значения в список неизвестных; например, root(f(x), -2) или root(14, -2) не разрешены в приведенном выше примере.
Mathcad находит комплексные корни так же, как и действительные корни. Чтобы найти сложный корень, вы должны начать с комплексного значения для начального предположения.
Решение уравнения формы f(x) = g(x) эквивалентно использованию функции корня следующим образом:
root(f(x) – g(x), x)
Функция корня может решить только одно уравнение с одним неизвестным. Чтобы решить несколько уравнений одновременно, используйте Find или Minerr. Чтобы решить уравнение символически, то есть найти точный числовой ответ в терминах элементарных функций, выберите «Решить для переменной» в меню «Символика» или используйте ключевое слово «решить».
См. также polyroot для эффективного средства вычисления всех корней многочлена одновременно.
Mathcad вычисляет корневую функцию, используя метод секущих. Если этот метод не может найти корень, то используется метод Мюллера.
Предположительное значение, которое вы указываете для x, становится отправной точкой для последовательных приближений к корневому значению. Когда величина f(x), оцененная в предложенном корне, меньше значения предопределенной переменной TOL, корневая функция возвращает результат.
Если после многих приближений Mathcad все еще не может найти приемлемый ответ, он помечает корневую функцию сообщением об ошибке, указывающим на ее неспособность сходиться к результату. Эта ошибка может быть вызвана любой из следующих причин:
108 | Глава 1 Функции |
•Выражение не имеет корней.
•Корни выражения далеки от первоначального предположения.
•Выражение имеет локальные максимумы или минимумы между начальным предположением и корнями.
•Выражение имеет разрывы между начальным предположением и корнями.
•Выражение имеет комплексный корень, но первоначальная догадка была реальной (или наоборот).
Чтобы найти причину ошибки, попробуйте построить выражение. Это поможет определить, пересекает ли выражение ось X, и если да, то приблизительно где. В общем, чем ближе ваше начальное предположение к пересечению выражения с осью X, тем быстрее корневая функция сойдется к приемлемому результату.
Вот несколько советов, как максимально эффективно использовать корневую функцию:
• Чтобы изменить точность корневой функции, измените значение встроенной переменной TOL. Если увеличить TOL, корневая функция будет сходиться быстрее, но ответ будет менее точным. Если вы уменьшите TOL, корневая функция будет сходиться медленнее, но ответ будет более точным. Чтобы изменить TOL в указанной точке рабочего листа, включите такое определение, как TOL := 0.01 . Чтобы изменить TOL для всего рабочего листа, выберите «Параметры 9».0003
в меню «Математика», перейдите на вкладку «Встроенные переменные» и замените число в текстовом поле рядом с «TOL». После того, как вы нажмете «ОК», выберите «Вычислить рабочий лист» в меню «Математика», чтобы обновить весь рабочий лист, используя новое значение TOL.
• Если выражение имеет несколько корней, попробуйте найти их с помощью различных значений предположения. Построение графика функции — это хороший способ определить, сколько существует корней, где они находятся и какие первоначальные догадки могут их найти. Обратитесь к предыдущему примеру. Если два корня расположены близко друг к другу, возможно, вам придется уменьшить TOL, чтобы различать их.
• Если f(x) имеет небольшой наклон вблизи корня, то root(f(x), x) может сходиться к значению r, которое относительно далеко от фактического корня. В таких случаях, даже если f(r) < TOL, r может быть далеко от точки, где f(r) = 0. Чтобы найти более точный корень, уменьшите значение TOL.
Или попробуйте найти root(g(x),x), где g(x) | ф(х) |
= ————— . | |
| д |
| —— ф(х) |
| дх |
• Для выражения f(x) с известным корнем r поиск дополнительных корней f(x) эквивалентен
поиску корней h(x) = (f(x )) ¤ (x – р ) .
Подобное разделение известных корней полезно для разрешения двух корней, которые могут быть расположены близко друг к другу. Часто бывает проще найти корни h(x), как определено здесь, чем пытаться найти другие корни для f(x) с другими предположениями.
Алгоритм Секанта и методы Мюллера (Пресс и др., 1992; Лорчак)
раунд | Усечение и округление |
Версия с одним аргументом
Синтаксис round(x)
Описание Округляет действительное число x до ближайшего целого числа. То же, что раунд(х, 0).
Аргументы
x действительное число
Функции | 109 |
Версия с двумя аргументами
Синтаксис | круглый(x, n) |
Описание | Округляет действительное число x до n знаков после запятой. |
Аргументы |
|
х | реальный номер |
п | целое число |
См. также | потолок, пол, балка |
|
|
строки | Вектор и матрица |
Синтаксис | ряда(А) |
Описание | Возвращает количество строк в массиве A. |
Аргументы |
|
А | матрица или вектор |
См. также | столбцы например |
|
|
роль | Случайные числа |
Синтаксис | rpois(m, λ) |
Описание | Возвращает вектор из m случайных чисел с распределением Пуассона. |
Аргументы | целое, м > 0 |
м | |
λ | действительное среднее, λ > 0 |
Алгоритм | Девро, 1986 |
См. также | рнд |
|
|
ссылка | Вектор и матрица |
Синтаксис | rref(A) |
Описание | Возвращает матрицу, представляющую эшелонированную форму A с уменьшенным числом строк. |
Аргументы | реальная матрица m × n |
А | |
Алгоритм | Сокращение элементарного ряда (Антон) |
Если n < 0, x округляется слева от десятичной точки.
110 | Глава 1 Функции |
rsort
Синтаксис
Описание
Аргументы
A
i
Алгоритм
См.
также
Сортировка
rsort(A, i)
Сортирует столбцы матрицы A, размещая элементы в строке i в порядке возрастания. Результат имеет тот же размер, что и A.
m × n матрица или целое число векторов, 0 ≤ i ≤ m – 1
рт
Случайные числа
Синтаксис
рт(м, д)
Описание
Возвращает вектор из m случайных чисел с распределением Стьюдента t.
Аргументы
целое, м > 0
м
д
целые степени свободы, d > 0
Алгоритм
XG-алгоритм Беста, генератор Джонка (Деврое, 1986)
См. также
рнд
руниф | Случайные числа |
Синтаксис | руниф(м, а, б) |
Описание | Возвращает вектор из m случайных чисел с равномерным распределением |
Аргументы | целое, м > 0 |
м | |
а, б | действительные числа, a < b |
Алгоритм | Метод линейной конгруэнтности (Кнут, 1997) |
См. | рнд |
такжеФункции | 111 |
Rweibull
Синтаксис
Описание
Аргументы
M
S
Алгоритм
См. Также
Случайные числа
RWEIBUL распределение.
Целое число, m > 0
Параметр реальной формы, s > 0
Метод обратной кумулятивной плотности (Press et al., 1992)
rnd
SaveColormap |
| Доступ к файлу | |
Синтаксис | Сохранить карту цветов (файл, M) |
|
|
Описание | Создает файл карты цветов, содержащий значения матрицы M. Возвращает количество записанных строк | ||
| в файл. |
|
|
Аргументы |
|
|
|
файл | строковая переменная, соответствующая имени файла CMP |
|
|
М | целочисленная матрица с тремя столбцами, все элементы которой Mi, j удовлетворяют условию 0 ≤ Mi, j | ≤ 255 . | |
Комментарии | Файл файла — это имя карты цветов, расположенной в подкаталоге CMAPS вашего Mathcad | ||
| справочник. После использования SaveColormap цветовая карта доступна на вкладке «Дополнительно» в окне | .||
| Диалоговое окно «Формат 3D-графика». Дополнительную информацию см. в интерактивной справке. |
| |
См. | LoadColormap |
|
|
|
|
| |
сбвал | (профессиональный) | Решение дифференциальных уравнений | |
Синтаксис | sbval(v, x1, x2, D, load, score) |
|
|
Описание | Преобразует дифференциальное уравнение с граничными значениями в задачу с начальными значениями. Полезно, когда | ||
| Производныенепрерывны на всем протяжении. |
|
|
Аргументы |
|
|
|
v | действительный вектор, содержащий предположения об отсутствующих начальных значениях |
|
|
х1, х2 | реальные конечные точки интервала, на которых будет оцениваться решение ДУ |
| |
Д(х, у) | вещественная n-элементная вектор-функция, содержащая производные неизвестных функций | ||
нагрузка(x1, v) | действительная вектор-функция, n элементов которой соответствуют значениям n неизвестных функций | ||
| в х1. | ||
| неизвестно, следует использовать соответствующее предполагаемое значение из v |
| |
счет(х2, у) | действительная n-элементная векторнозначная функция, которая измеряет невязку решения при x2 | ||
также
Некоторые из этих значений будут константами, заданными вашими начальными условиями. Если значение равно112 | Глава 1 Функции |
Пример
Комментарии
Алгоритм
См. также
Решатели DE с начальным значением, такие как rkfixed, предполагают, что вы знаете значение решения и его первых n – 1 производных в начале интервала интегрирования. Решатели DE с двухточечным граничным значением, такие как sbval и bvalfit, могут использоваться, если вам не хватает этой информации о решении в начале интервала интегрирования, но вы знаете что-то о решении в другом месте интервала.
В частности:
• У вас есть дифференциальное уравнение n-го порядка.
•Вы знаете некоторые, но не все значения решения и его первых n – 1 производных в начале интервала интегрирования x1.
•Вы знаете некоторые, но не все значения решения и его первых n – 1 производных в конце интервала интегрирования x2.
• Между тем, что вы знаете о решении при x1, и тем, что вы знаете о нем при x2, у вас есть n известных значений.
Если есть разрыв в точке, промежуточной между x1 и x2, следует использовать bvalfit. Если непрерывность соблюдается повсюду, то используйте sbval для оценки тех начальных значений, которые не указаны в точке x1. sbval на самом деле не возвращает решение дифференциального уравнения; он просто вычисляет начальные значения, которые должно иметь решение, чтобы решение соответствовало заданным вами окончательным значениям. Затем вы должны взять начальные значения, возвращенные sbval, и решить получившуюся задачу с начальными значениями, используя rkfixed или любой другой более специализированный решатель DE.
Метод съемки методом Рунге-Кутта 4-го порядка (Пресс и др., 1992)
113
поиск
Синтаксис
Описание
Аргументы
(Профессиональный) | Строка |
search(S, SubS, m)
Возвращает начальную позицию подстроки SubS в S, начиная с позиции m. Возвращает -1, если подстрока не найдена.
С | строковое выражение; Mathcad предполагает, что первый символ S находится в позиции 0 | .
SubS | выражение подстроки |
м | целое, м³ 0 |
|
|
сек | Тригонометрический |
Синтаксис | sec(z), для z в радианах; |
| сек(z·град), для z в градусах |
Описание | Возвращает секанс z. |
Аргументы |
|
с | действительное или комплексное число |
|
|
сек | Гиперболический |
Синтаксис | сеч(з) |
Описание | Возвращает гиперболический секанс z. |
Аргументы |
|
с | действительное или комплексное число |
|
|
знак | Кусочно-непрерывный |
Синтаксис | знак(х) |
Описание | Возвращает 0, если x=0, 1, если x > 0, и -1 в противном случае. |
Аргументы |
|
х | реальный номер |
См. | csgn, сигнум |
также114 | Глава 1 Функции |
сигнум |
|
|
|
| Комплексные числа | |||||||||
Синтаксис | сигнум(г) | |||||||||||||
Описание | Возвращает 1, если z=0 и z ¤ |
| я |
| иначе. | |||||||||
|
| |||||||||||||
Аргументы |
|
|
|
|
| |||||||||
с | действительное или комплексное число | |||||||||||||
См. | csgn, знак | |||||||||||||
|
|
|
|
|
| |||||||||
грех |
|
|
|
| Тригонометрический | |||||||||
Синтаксис | sin(z), для z в радианах; | |||||||||||||
| sin(z·deg), для z в градусах | |||||||||||||
Описание | Возвращает синус z. | |||||||||||||
Аргументы |
|
|
|
|
| |||||||||
с | действительное или комплексное число | |||||||||||||
|
|
|
|
|
| |||||||||
синх |
|
|
|
| Гиперболический | |||||||||
Синтаксис | синх(з) | |||||||||||||
Описание | Возвращает гиперболический синус z. | |||||||||||||
Аргументы |
|
|
|
|
| |||||||||
с | действительное или комплексное число | (3)
|
|
|
|
|
|
|
|
| ||||
Возвращает асимметрию элементов A: |
|
|
|
|
| |||||||||
|
| м н | м – 1 п – 1 | æ | А | и, к | – среднее (А) | 3 | ||||||
перекос(А) | = |
|
|
|
| или | ||||||||
(——————————————мн – 1)(мн – | 2 ) | å å | —————————————————— | ø | ||||||||||
|
|
| Стдев (А) | |||||||||||
|
|
|
| i = 0 j = 0 |
|
|
|
| ||||||
также
Действительная или комплексная m ´ n матрица или вектор, m × n ³ 3
Функции | 115 |
наклон
Синтаксис
Описание
Аргументы
vx, vy
Пример
Комментарии
См.
также
Регрессия и сглаживание
наклон(vx, vy)
Возвращает наклон линии регрессии методом наименьших квадратов.
действительные векторные аргументы одинакового размера
Функции наклона и пересечения возвращают наклон и пересечение линии, которая наилучшим образом соответствует данным в смысле метода наименьших квадратов: y = наклон(vx, vy) × x + intercept(vx , вый ).
Убедитесь, что каждый элемент в массивах vx и vy содержит значение данных. Поскольку каждый элемент в массиве должен иметь значение, Mathcad присваивает 0 всем элементам, не назначенным явно.
Эти функции полезны не только тогда, когда данные линейны по своей природе, но и когда они экспоненциальны. Если x и y связаны соотношением y = Aekx, вы можете применить эти функции к логарифму значений данных и использовать тот факт, что ln (y) = ln (A) + kx, следовательно,
A = exp (отрезок (vx, ln (vy))) и k = наклон(vx, ln (vy)) .
Полученная аппроксимация взвешивает ошибки иначе, чем экспоненциальная аппроксимация методом наименьших квадратов (которую обеспечивает функция genfit), но обычно является хорошей аппроксимацией.