|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 8 из 9Следующая ⇒ Уравнения в MathCAD решаются с помощью двух встроенных функцийroot и polyroots. 3.1.2.1 Встроенная функция MathCAD – root(F(x), x) Для численного решения уравнений предназначена стандартная функция MathCAD – root(F(x), x), которая возвращает значение корня с заданной точностью. Функция root имеет два аргумента: первый – выражение, стоящее в левой части уравнения, то есть F(x), второй – переменная, относительно которой решается уравнение, то есть x. Ищется значение переменной x, при которой выражение F(x) обращается в ноль. Функция root возвращает значение переменной x, которая обращает выражение F(x) в ноль. Второй аргумент — имя переменной, которое используется в выражении. Функция реализует вычисление итерационным методом и перед её применением необходимо задать начальное значение переменной x, принадлежащее интервалу изоляции корня. В зависимости от начального приближения функция root возвращает различные значения. Решение уравнений с помощью функции root может производиться с различной точностью, которая задается значением системной переменной TOL. Пример 3.1 Решить уравнение с точностью . Процесс решения показан на рисунке 1. Выполняется следующая последовательность действий: 1.Сначала вводится функция , соответствующая левой части уравнения. 2. Задается точность. 3. Графически находится приближенное решение уравнения (можно использовать трассировку). 4. При помощи функции root выполняется нахождение решения уравнения с заданной точностью. 5. Выполняется проверка найденного решения. В зависимости от начального приближения функция root возвращает различные значения. Результат решения задачи приведён на рисунке 3.1.1 В результате найдены корни x0=-3.258, x1=0.2, x2=3.057.
Рисунок 3.1.1 – Пример решения нелинейного алгебраического уравнения
Функцию root можно записать в виде root (f(x), x, a, b) , где a, b – пределы интервала изоляции корня. При такой форме записи нет необходимости задавать начальное значение х, так как оно определено в интервале . Пример 3.2 Решить уравнение ex/5 -2(x-1)2 = 0. Результаты решения показаны на рисунке 2. Используя график функции, определяют пределы интервала изоляции каждого корня, а затем с помощью функции root (f(x), x, a, b) находят значение интересующего корня. В данном случае найдено три корня. Необходимо правильно указывать интервал изоляции, в случае ошибки значение корня не будет найдено, что показано на рисунке 3.1.2
Рисунок 3. функции root (f(x), x, a, b)
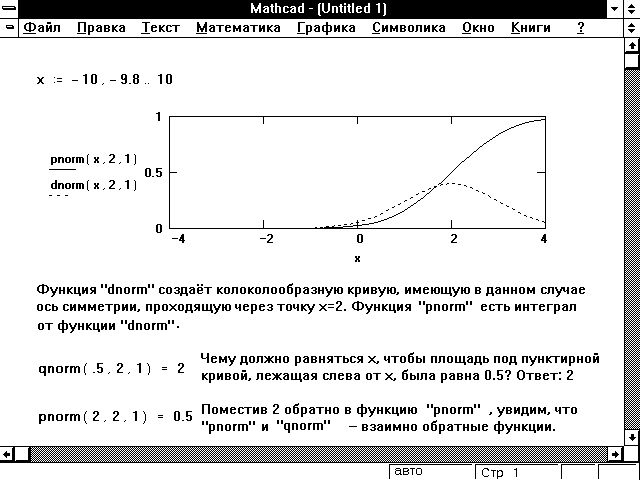
На рисунке 3.1.3 показан пример решения уравнения, имеющего комплексные корни. В таких случаях начальное приближённое значение корня также должно быть комплексным. При вводе мнимого числа надо писать 1i, а не i. В данном примере при вычислении второго корня х2 первый исключается делением f(х) на (х-х1). При нахождении третьего корня f(х) делится на (х-х1)(х-х2).
Рисунок 3.1.3 – Пример решения уравнения, имеющего действительные и комплексные корни
Необходимо отметить особенность функции root, связанную с тем, что она не всегда позволяет найти значение корня. Mathcad при поиске корня с помощью функции root использует метод итераций. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным и функция root возвращает результат. — уравнение не имеет корней; — корни уравнения располагаются далеко от начального приближения; — выражение имеет локальные максимумы или минимумы между начальным приближением и корнем; — выражение имеет разрывы между начальным приближением и корнями; — выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот). Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному решению. ⇐ Предыдущая123456789Следующая ⇒ Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 2169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Методы нахождения корней полинома в алгоритме пеленгования UCA Root Rare в пакете Mathcad
Библиографическое описание:Коробков, М. А. Методы нахождения корней полинома в алгоритме пеленгования UCA Root Rare в пакете Mathcad / М. А. Коробков. — Текст : непосредственный // Молодой ученый. — 2014. — № 14 (73). — С. 54-56. — URL: https://moluch.ru/archive/73/12348/ (дата обращения: 09.11.2022).
Рассмотрены два метода нахождения корней полинома, получаемого при выполнении алгоритма редукции ранга для пеленгования источников радиоизлучения UCA‑Root‑Rare. Продемонстрированы результаты численного моделирования. Приведён соответствующий листинг программ в пакете Mathcad.
Ключевые слова: UCA‑Root‑Rare, полином, Mathcad, polyroots, roots.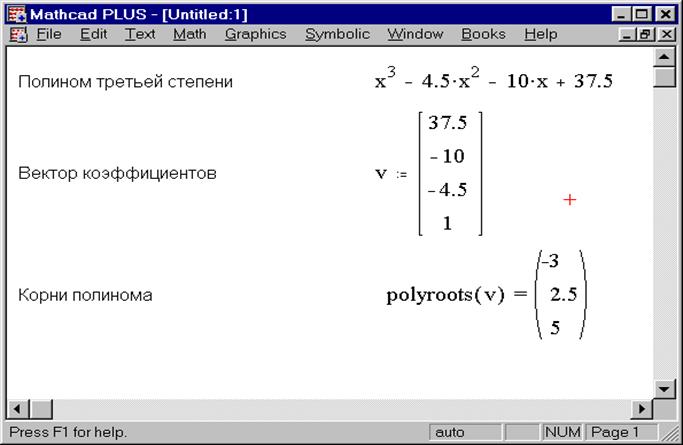
Введение. Определённый подкласс быстрых корреляционных алгоритмов оценивания координат источников излучения (ИИ), требует для своего применения выполнения поиска корней полиномов, степень, а соответственно и число корней, которых, в некоторых случаях, может быть более . В таких случаях, некоторые встроенные корни функции Mathcad не позволяют выполнить поиск решений.
Цель работы — используя свойства полинома, получаемого при выполнении алгоритма UCA‑Root‑Rare (Rare‑полином) [1], найти решения Rare‑полинома при помощи встроенных функций пакета Mathcad для произвольной степени полинома.
1.Алгоритм UCA‑Root‑Rare. Вычисление координат ИИ, в данном случае азимута, при помощи алгоритма UCA‑Root‑Rare, выполняется путём нахождения корней следующего полиномиального уравнения:
, (1)
где — определитель матрицы,
(2)
матрица размера ,
(3)
диагональная матрица размера , оператор диагонализации элементов,
. (4)
(4)
— это матрица отражений или антидиагональная единичная матрица:
. (5)
Используя (1)‑(3) и (5) матрица для будет иметь следующий вид:
. (6)
Матрица — это матрица собственных векторов, соответствующих подпространству шума корреляционной матрицы данных в пространстве лучей [2].
Исследование уравнения (1) показывает, что степень полинома будет , а следовательно уже для число корней Rare‑полинома будет равным .
2. Встроенные функции пакета Mathcad. Встроенные функции Mathcad в состоянии решить любое алгебраическое уравнение. Для решения уравнения с одним неизвестным можно использовать функции root и polyroots. Mathcad решает уравнения итерационным методом, поэтому перед решением необходимо задать начальное приближение для всех корней [3].
Mathcad решает уравнения итерационным методом, поэтому перед решением необходимо задать начальное приближение для всех корней [3].
2.А. Функция root.
Функция root используется для решения одного уравнения с одним неизвестным. Обращение к функции: root(f(x)), где — выражение, равное нулю; — аргумент, варьируя который, система ищет значение, обращающее функцию в нуль. Функция и аргумент должны быть скалярами, то есть результат вычисления функции — число, а не вектор или матрица. Функция root использует итерационный метод секущих. Корень уравнения — ближайшее к начальному приближению значение , обращающее функцию в нуль. Если корней несколько, для отыскания каждого корня необходимо задавать свое начальное приближение. Если уравнение не имеет действительных корней, то есть функция нигде не равна нулю, то Mathcad выводит комплексное число [3].
2.А. Функция polyroots
Для нахождения корней полинома можно использовать функцию polyroots(K), которая определяет все корни полинома одновременно. Здесь — вектор коэффициентов полинома, начиная со свободного члена. Нулевые коэффициенты опускать нельзя. Если полином имеет корней (с учетом кратности), то вектор включает в себя коэффициент. Начальное приближение вводить не надо. Следует обратить внимание, что вектор должен содержать от до коэффициентов.
Здесь — вектор коэффициентов полинома, начиная со свободного члена. Нулевые коэффициенты опускать нельзя. Если полином имеет корней (с учетом кратности), то вектор включает в себя коэффициент. Начальное приближение вводить не надо. Следует обратить внимание, что вектор должен содержать от до коэффициентов.
3. Получение оценок. Вэтом разделе рассматриваются оценки, получаемые при решении уравнения (1) при помощи функций polyroots и root.
3.А. Получение решений при помощи функции polyroots.
Как говорилось ранее, функция polyroots работает только с полиномами, степень которых не превышает . Накладываемое функцией polyroots ограничение позволяет применять её для решения уравнения (1) в случае, если параметр размера матрицы не превышает , что будет соответствовать корням. Для применение функции polyroots невозможно, поскольку в этом случае степень Rare‑полинома превышает значение и будет больше . Решения уравнения (1) при помощи функции polyroots показаны на рисунке 1 а), где крестиком обозначены истинные координаты азимута трех источников, кружками обозначены корни уравнения (1), пунктирной линией показана единичная окружность.
а) б)
Рис. 1. Решения Rare‑полинома при помощи функции: а) polyroots, ; б) root, . Азимут источников излучения , , .
3.А. Получение решений при помощи функции root.
Исследование уравнения (1) показывает, что истинными оценками азимута будут являться только те корни, которые максимально близко расположены к единичной окружности. Следовательно, для поиска корней полинома степени большей, чем можно применить функцию root, ограничив область поиска значениями, лежащими на единичной окружности взяв их с некоторым шагом. Для комплексной плоскости этим значениям будет соответствовать некоторый угол , косинус которого будет соответствовать действительной части числа, а синус мнимой. Ниже приведён листинг программы в пакете Mathcad реализующий поиск корней Rare‑полинома произвольной степени при помощи функции root.
Листинг 1. Нахождение корней Rare‑полинома произвольной степени
где — это соответствующий полном уравнения (1). В случае, если заданы только коэффициенты полинома, то необходимо преобразовать функцию в выражение, используя, например, следующий листинг:
Листинг 2. Преобразование коэффициентов полинома в выражение
где — это переменная полинома, — вектор столбец из действительных частей коэффициентов полинома, — вектор столбец из мнимых частей полинома. После применения листинга 2 необходимо выполнить листинг 1. Соответствующее решение уравнения (1) показаны на рисунке 1 б).
Одним из свойств корней Rare‑полинома, является то, что все его корни обладают так называемым свойством взаимной сопряжённости, которое означает, что если — это корень полинома, то также будет корнем полинома [4]. Иными словами, корни симметричны относительно единичной окружности, что можно наблюдать на рисунке 1 а). Для корней вблизи центра окружности, их парные корни находятся за пределами области построения графика, и охватывают окружность с наружи таким же плотным кольцом, как и корни вблизи центра окружности.
Поиск корней по методу, приведённому в листингах 1 и 2, даёт только один корень. Учитывать корень нет необходимости, однако при желании это возможно сделать, просто выполнив операцию для каждого найденного решения.
Следует также обратить внимание, на то, что полученные решения по листингам 1 и 2 получаются несколько искажёнными, а кольцо вблизи центра окружности на рисунке 1 б) имеет деформацию, в отличие от аналогичного кольца на рисунке 1 а). Такое различие может быть вызвано как большой дискретностью шага поиска, так и отличием методов поиска решений функций polyroots иroot.
Заключение. В статье были рассмотрены два варианта нахождения корней полинома, получаемого в результате нахождения определителя в уравнении (1). Приведён соответствующий листинг предлагаемых методов. На численном примере в графическом отображении показаны отличия, между нахождением корней полинома стандартными функциями пакета Mathcad polyroots иroot.
Литература:
1. Pesavento M., Böhme J. F. Direction of arrival estimation in uniform circular arrays composed of directional elements // Sensor Array and Multichannel Signal Processing Workshop. 2002. No 8. P. 503–507.
Pesavento M., Böhme J. F. Direction of arrival estimation in uniform circular arrays composed of directional elements // Sensor Array and Multichannel Signal Processing Workshop. 2002. No 8. P. 503–507.
2. Marple L. Digital spectral analysis with applications. New Jersey: Prentice-Hall, 1987. P. 492.
3. Макаров Е. Инженерные расчёты в Mathcad 15: Учебный курс — Спб.: Питер, 2011. — 400 с.: ил.
4. Li. H. Y., Xie J. L., He Z. S. A fast DOA estimation algorithm for uniform circular arrays in the presence of unknown mutual coupling // Progress In Electromagnetics Research C, 2011, Vol. 21, 257–271.
Основные термины (генерируются автоматически): UCA, функция, корень, полином, помощь функции, единичная окружность, начальное приближение, решение уравнения, корень полинома, центр окружности.
Расписание обучения — решения Root
Улучшите свой опыт. Нам очень жаль, но этот сайт не поддерживает Internet Explorer. Мы рекомендуем использовать другой поддерживаемый браузер, например Google Chrome или Mozilla Firefox.
Мы рекомендуем использовать другой поддерживаемый браузер, например Google Chrome или Mozilla Firefox.
Мы предлагаем широкий выбор учебных курсов по продуктам PTC и Luxion. Эти курсы варьируются от пятидневных целевых курсов до более коротких курсов на полдня, проводимых нашей командой опытных тренеров. Наши тренера также являются высококвалифицированными специалистами в своих областях и имеют за плечами многолетний профессиональный опыт.
Просмотрите наши различные учебные курсы, выбрав соответствующую категорию.
Все местоположенияCambridgeМанчестерОнлайнСтокпортВсе категорииAnsysCreo Flow AnalysisCreo IllustrateCreo ParametricCreo SimulateKeyshotMathCadWindchill Очистить фильтры
Онлайн-события в прямом эфире
(UTC-12:00) Международная линия перемены дат (UTC-11:00) Всемирное координированное время-11 (GMT-10:00) Гавайи (UTC-10:00) Алеутские острова (UTC- 09:30) Маркизские острова(GMT-09:00) Аляска(UTC-09:00) Всемирное координированное время-09(GMT-08:00) Нижняя Калифорния(GMT-08:00) Тихоокеанское время (США и Канада) (UTC-08:00) Всемирное координированное время-08(GMT-07:00) Аризона(GMT-07:00) Чиуауа, Ла-Пас, Масатлан(GMT-07:00) Горное время (США и Канада)( GMT-06:00) Центральная Америка (GMT-06:00) Центральное время (США и Канада) (GMT-06:00) Гвадалахара, Мехико, Монтеррей (GMT-06:00) Саскачеван (UTC-06:00) Остров Пасхи(GMT-05:00) Бота, Лима, Кито(GMT-05:00) Восточное время (США и Канада)(GMT-05:00) Индиана (Восток)(UTC-04:00) Теркс и Кайкос( UTC-05:00) Четумаль(UTC-05:00) Гаити(UTC-05:00) Гавана(GMT-04:00) Асунсьон(GMT-04:00) Атлантическое время (Канада)(GMT-04:00) Куяба(GMT-04:00) Джорджтаун, Ла-Пас, Манаус, Сан-Хуан(GMT-04:00) Сантия(GMT-04:30) Каракас(GMT-03:30) Ньюфаундленд(GMT-03:00) Бразилиа( GMT-03:00) Буэнос-Айрес(GMT-03:00) Кайенна, Форталеза(GMT-03:00) Гренландия(GMT-03:00) Монтевидео(UTC-03:00) Арагуаина(UTC-03:00) Пунта Аренас(UTC-03:00) Сен-Пьер и Мике lon(UTC-03:00) Сальвадор(UTC-02:00) Всемирное координированное время-02(UTC-02:00) Среднеатлантическое – старое(GMT-01:00) Азорские острова(GMT-01:00) Острова Кабо-Верде (GMT) Касабланка (GMT) Дублин, Эдинбург, Лиссабон, Лондон (GMT) Монровия, Рейкьявик (UTC) Всемирное координированное время (UTC+00:00) Сан-Томе (GMT+01:00) Амстердам, Берлин, Берн, Рим, Стокгольм, Вена (GMT+01:00) Белград, Братислава, Будапешт, Любляна, Прага (GMT+01:00) Брюссель, Копенгаген, Мадрид, Париж (GMT+01:00) Сараево, Скопье, Варшава, Загреб(GMT+01:00) Западная Центральная Африка(GMT+01:00) Виндхук(GMT+02:00) Амман(GMT+02:00) Афины, Бухарест, Стамбул(GMT+02:00) Бейрут(GMT+ 02:00) Каир(GMT+02:00) Дамаск(GMT+02:00) Хараре, Претория(GMT+02:00) Хельсинки, Киев, Рига, София, Таллинн, Вильнюс(GMT+02:00) Иерусалим( GMT+02:00) Минск(UTC+02:00) Газа, Хеврон(UTC+02:00) Калининград(UTC+02:00) Хартум(UTC+02:00) Триполи(GMT+03:00) Багдад( GMT+03:00) Кувейт, Эр-Рияд(GMT+03:00) Москва, Санкт-Петербург, Волгоград(GMT+03:00) Найроби(UTC+02:00) Стамбул(UTC+03:00) Минск(U TC+04:00) Волгоград(GMT+03:30) Тегеран(GMT+04:00) Абу-Даби, Маскат(GMT+04:00) Баку(GMT+04:00) Порт-Луи(GMT+04:00) Тбилиси(GMT+04:00) Ереван(UTC+04:00) Астрахань, Ульяновск(UTC+04:00) Ижевск, Самара(UTC+04:00) Саратов(GMT+04:30) Кабул(GMT+05: 00) Екатеринбург(GMT+05:00) Исламабад, Карачи(GMT+05:00) Ташкент(UTC+05:00) Кызылорда(GMT+05:30) Ченнаи, Калькутта, Мумбаи, Нью-Дели(GMT+05:30) ) Шри-Джаяварденепура(GMT+05:45) Катманду(GMT+06:00) Астана(GMT+06:00) Дакка(UTC+06:00) Омск(GMT+06:30) Янн (Ranon)(GMT+06) :00) Новосибирск(GMT+07:00) Бангкок, Ханой, Джакарта(GMT+07:00) Красноярск(UTC+07:00) Барнаул, Горно-Алтайск(UTC+07:00) Ховд(UTC+07:00) ) Томск(GMT+08:00) Пекин, Чунцин, Гонконг, Урумчи(GMT+08:00) Иркутск(GMT+08:00) Куала-Лумпур, Сингапур(GMT+08:00) Перт(GMT+08:00) ) Тайбэй(GMT+08:00) Улан-Батор(UTC+08:45) Eucla(GMT+09:00) Осака, Саппоро, Токио(GMT+09:00) Сеул(GMT+09:00) Якутск(UTC+08:30) Пхеньян(UTC+09:00) Чита(GMT+09:30) Аделаида(GMT +09:30) Дарвин(GMT+10:00) Брисбен(GMT+10:00) Канберра, Мельбурн, Сидней(GMT+10:00) Гуам, Порт-Морсби(GMT+10:00) Хобарт(GMT+10: 00) Владивосток(UTC+10:30) Остров Лорд-Хау(GMT+11:00) Магадан(GMT+11:00) Соломоновы острова, Новая Каледония(UTC+11:00) Остров Бугенвиль(UTC+11:00) Чокурдах(UTC+11:00) Остров Норфолк(UTC+11:00) Сахалин(GMT+12:00) Фиджи(UTC+12:00) Анадырь, Петропавловск-Камчатский(UTC+12:00) Окленд, Веллингтон(UTC) +12:00) Всемирное координированное время+12(UTC+12:00) Петропавловск-Камчатский — Старый(UTC+12:45) Острова Чатем(GMT+13:00) Нукуалофа(GMT+13:00) Самоа(UTC+13:00) Всемирное координированное время+13(UTC+14:00) Остров Киритимати
Скидка
Распроданный
Места ограничены
Обновление Mathcad Prime
Mathcad Prime Обновление Mathcad 15 для опытных пользователей Mathcad 15
PTC Mathcad | LinkedIn
О
PTC Mathcad — это стандартное в отрасли программное обеспечение для решения, анализа и обмена наиболее важными инженерными расчетами.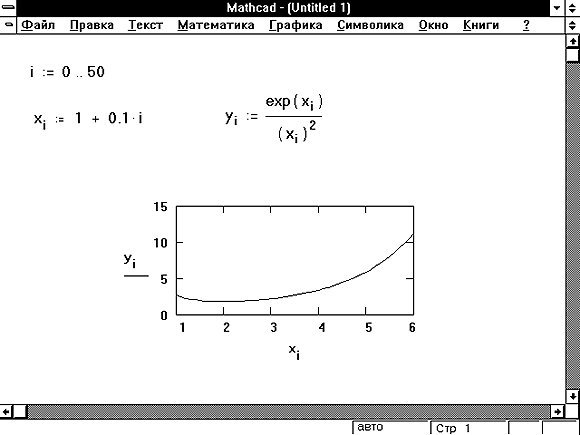
 Все правила по сольфеджио
Все правила по сольфеджио
 Это та переменная, варьируя которую Mathcad пытается обратить выражение F(x) в ноль.
Это та переменная, варьируя которую Mathcad пытается обратить выражение F(x) в ноль.
 1.2 – Пример решения уравнения с использованием
1.2 – Пример решения уравнения с использованием
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)