Решение уравнений средствами MathCad — Mathcad (мат.задачи)
Решение одного уравнения
Для простейших уравнений вида f(x) = 0 решение в Mathcad находится с помощью функции root. root( f(х1, x2, …), х1, a, b ) Возвращает значение х1, принадлежащее отрезку [a, b], при котором выражение или функция f(х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. Аргументы: f(х1, x2, …) — функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения. х1 — — имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня. a, b — необязательны, если используются, то должны быть вещественными числами, причем a < b. Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение (отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами:
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет root сходиться. Рекомендации по использованию функции root:
.
Рисунок 11.
Нахождение корней полинома Для нахождения корней выражения, имеющего вид vnxn + … + v2x2 + v1x + v0, лучше использовать функцию polyroots, нежели root. Polyroots(v) Возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n + 1. Возвращает вектор длины n, состоящий из корней полинома. Аргументы: v — вектор, содержащий коэффициенты полинома. Рисунок 11 иллюстрирует решение уравнений средствами Mathcad. |
Другой вариант заключается в замене уравнения f(x) = 0 на g(x) = 0
В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.7. РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ MATHCAD
Информатика и вычислительная техника / Программные средства / 7. РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ MATHCAD
Постановка задачи
Задача ставится следующим образом:
Пусть имеется алгебраическое уравнение с одним неизвестным х или система алгебраических уравнений
,
где f1(x1, …, xm) и fn(x1, … , xm) – некоторые функции.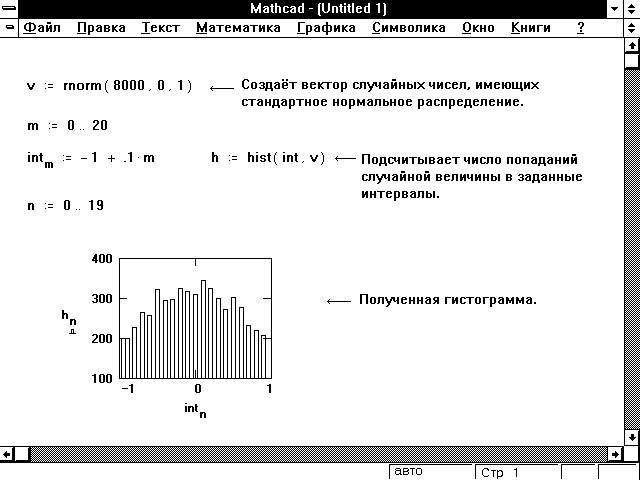
Требуется решить данное уравнение или систему уравнений, т.е. найти те значения х, в которых уравнения превращаются в верное равенство.
Отыскание корней численными методами связано с несколькими задачами:
Ø Исследование существования корней в принципе, определение их количества и примерного расположения;
Ø Отыскание корней с заданной погрешностью
Всевозможные функции MathCAD нацелены на решение второй задачи, т.е. предполагается, что корни уже приблизительно локализированы. Выбор встроенных функций для решения уравнений и систем уравнений осуществляется в зависимости от специфики уравнения.
Решение одного уравнения с одним неизвестным
Рассмотрим алгебраическое уравнение f(x)=0 с одним неизвестным х, например, sin(x)=0.
Для решения таких уравнений MathCAD имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.
Мнемоника команды выглядит следующим образом:
root (f(x), x) или root (f(x), x, a, b),
где f(х) – скалярная функция, определяющая уравнение; х – скалярная переменная, относительно которой решается уравнение; а, b – границы интервала, внутри которого происходит поиск корня.
Первый тип функции root требует дополнительного задания начального значе
ния переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.
Приведем пример решения очень простого уравнения sin(x)=0, корни которого известны заранее (рис. 38).
Обратите внимание, что, хотя уравнение имеет бесконечное количество корней MathCAD находит (с заданной точностью) только один из них, х0, лежащий наиболее близко к х = 0,5. Если задать другое начальное значение, например х = 3, то решением будет другой корень уравнения х1 = π и т.д. Таким образом, для поиска корня средствами MathCAD требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методом секущих.
Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке.
Рис. 7.1. Функция Minerr
Примечание: Для решения уравнения с одним неизвестным применимы и градиентные методы, относящиеся в MathCAD к системам уравнений.
Иногда удобнее задавать не начальное приближение к корню, а интервал [а, b], внутри которого корень заведомо находится. В этом случае следует использовать функцию root с четырьмя аргументами, а присваивать начальное значение х не нуж
но. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Явный вид функции f(x) может быть определен непосредственно в теле функции root (рис. 39).
Когда root имеет четыре аргумента, следует помнить о двух ее особенностях:
Ø внутри интервала [а, b] не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно;
Ø значения f(а) и f(b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.
Если уравнение не имеет действительных корней, но имеет мнимые, то их также можно найти. Например, уравнение х2+1=0, имеющее два чисто мнимых корня, решается два раза с разными начальными значениями (рис. 40).
При задании начального значения 0,5 численный метод отыскивает первый корень (отрицательную мнимую единицу –i), а при начальном значении –0,5 находится и второй корень i.
Для решения этого уравнения второй вид функции root (с четырьмя, а не с двумя аргументами) неприменим, поскольку f(х) является положительно определенной, и указать интервал, на границах которого она имела бы разный знак, невозможно.
Нахождение корней полинома
Если функция f(x) является полиномом, то все его корни можно определить, использую встроенную функцию polyroots(v), где v – вектор, составленный из коэффициентов полинома.
Поскольку полином n-й степени имеет ровно n корней (некоторые из них могут быть кратными), вектор v должен состоять из n+1 элемента. Результатом действия функции polyroots является вектор, составленный из n корней рассматриваемого полинома.
При этом нет надобности вводить какое-либо начальное приближение, как для функции root.
Например, найдем корни полинома четвертой степени f(x)=х4-6х3+12х2-10х+3 с
помощью функции polyroots (рис. 41).
Рис. 7.2. Функция Polyroots
Запишем коэффициенты рассматриваемого в примере полинома в виде вектора. Первым в векторе должен идти свободный член полинома, вторым – коэффициент при х 1 и т.д. Соответственно, последним n+1 элементом вектора должен быть коэффициент при старшей степени xN.
Совет: Иногда исходный полином имеется не в развернутом виде, а, например, как произведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню Symbolics (Символика) пункт Expand (Разложить). В результате символьный процессор MathCAD сам преобразует полином в нужную форму, пользователю надо будет только корректно ввести ее в аргументы функции polyroots.
Далее показано действие функции polyroots.
Обратите внимание, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня.
Для функции polyroots можно выбрать один из двух численных методов – метод полиномов Лаггера (он установлен по умолчанию) или метод парной матрицы.
Решение системы линейных алгебраических уравнений
Рассмотрим систему уравнений вида
(1)
В матричной форме СЛАУ записывается в эквивалентном виде:
А∙Х=В, (2)
где А – матрица коэффициентов СЛАУ размерности n×n; x – вектор неизвестных; В – вектор правых частей уравнений.
Рис.
7.
3. Матрица
СЛАУ имеет единственное решение, если матрица А является невырожденной, т. е. ее определитель не равен нулю. С вычислительной точки зрения, решение СЛАУ не представляет трудностей, если матрица А не очень велика.
В MathCAD СЛАУ можно решить как в более наглядной форме (1), так и в более удобной для записи форме (2). Для первого способа следует использовать вычислительный блок Given/Find, а для второго – встроенную функцию решения системы линейных уравнений lsolve. Мнемоника написания команды следующая:
lsoive (А, В),
где А – матрица коэффициентов системы; В – вектор правых частей.
Применение функции lsolve показано на рис. 42.
В некоторых случаях, для большей наглядности представления СЛАУ, его можно решить точно так же, как систему нелинейных уравнений. Не забывайте, что при численном решении всем неизвестным требуется присвоить начальные значения (это сделано в первой строке листинга) (рис. 43). Они могут быть произвольными, так как решение СЛАУ с невырожденной матрицей единственно.
Решение системы нелинейных уравнений
Рис. 7.4. Решение системы
Рассмотрим решение системы N нелинейных уравнений с m неизвестными
Здесь fi(x1, … , xm) – некоторые скалярные функции от скалярных переменных x1, x2, …, хm и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему можно формально переписать в виде f(x)=0, где х – вектор, составленный из переменных x1, x2, …, хm; f(x) – соответствующая векторная функция.
Для решения систем имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:
1) Given – ключевое слово;
2) Система, записанная логическими операторами в виде равенств и, возможно, неравенств;
3) Find (х1, …, хm
) – встроенная функция для решения системы относительно переменных х1, …, хm.
Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Если вы предпочитаете ввод с клавиатуры помните, что логический знак равенства вводится сочетанием клавиш <Ctrl> + <=>. Блок Given/Find используется для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения для всех х1, …, хm. Сделать это необходимо до ключевого слова Given. Значение функции Find есть вектор, составленный из решения по каждой переменной. Таким образом, число элементов вектора
Find равно числу аргументов.
Рис. 7.5. Система
В листинге (рис 44) приведен пример решения системы двух уравнений.
В первой строке листинга переменным х и у, относительно которых она будет решаться, присваиваются начальные значения. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find, содержащая вектор решения.
Совет: Часто бывает очень полезно проверить точность решения уравнений, вычислив значения образующих их функций в найденных вычислительным процессором корнях.
Рис. 7.6. Точность
В листинге найдено только одно из двух решений – находящееся в правой нижней части графика (рис. 45). Чтобы отыскать и второе решение, следует повторить вычисления, изменив начальные значения так, чтоб они лежали ближе к другой точке пересечения графиков, например, х=–1, y=–1.
Пока мы рассмотрели пример системы из двух уравнений и таким же числом
неизвестных, что встречается наиболее часто. Но число уравнений и неизвестных может и не совпадать. Более того, в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х (рис. 46).
Рис. 7.7. Ограничение на поиск
Обратите внимание, что, несмотря на те же начальные значения, что и в предыдущем листинге мы получили другой корень.
Это произошло именно благодаря введению дополнительного неравенства, которое определено в блоке Given в предпоследней строке.
Если предпринять попытку решить несовместную систему, MathCAD выдаст сообщение об ошибке, гласящее, что ни одного решения не найдено, и предложение попробовать поменять начальные значения или значение погрешности.
Примечание: Вычислительный блок использует константу CTOL в качестве погрешности выполнения уравнений, введенных после ключевого слова Given. Другая константа TOL определяет условие прекращения итераций численным алгоритмом. Значение CTOL может быть задано пользователем, так же как и TOL, например, CTOL:=0,01. По умолчанию принято, что CTOL=TOL=0,001, но по желанию можно переопределить их.
Рис. 7.8. Переопределение
Вычислительным блоком с функцией Find можно найти и корень уравнения с одним неизвестным. Действие Find в этом случае совершенно аналогично уже рас
смотренным в данном разделе примерам. Задача поиска корня рассматривается как решение системы, состоящей из одного уравнения.
Единственным отличием будет скалярный, а не векторный тип числа возвращаемого функцией Find (рис 47).
Символьное решение уравнений
Некоторые уравнения можно решить точно с помощью символьного процессора MathCAD. Делается это очень похоже на численное решение уравнений с применением вычислительного блока. Присваивать неизвестным начальные значения нет необходимости. Рассмотрим листинги символьного решение уравнения с одним неизвестным и системы двух уравнений с двумя неизвестными.
Как видно, вместо знака равенства после функции Find в листингах (рис. 48) следует знак символьных вычислений, который можно ввести с панели Symbolic, или, нажав клавиши <Ctrl>+<.>.
Рис. 7.9. Пример вычисления
Не забывайте, что сами уравнения должны иметь вид логических выражений, т.е. знаки равенства нужно вводить с помощью панели Booleans (Булевы операторы). Обратите внимание, что во втором листинге вычислены как два первых действительных корня, которые мы уже находили численным методом, так и два других мнимых корня.
Эти два последних корня чисто мнимые, так как множитель
Три моих любимых рабочих листа — поиск корней в Mathcad
- 03.02.2017
Большинство расчетов, с которыми мы сталкиваемся каждый день, требуют от нас нахождения корней функции. Например, чтобы минимизировать функцию, нужно найти корень ее производной. Знаете ли вы, как Mathcad может помочь вам найти корни, которые вы ищете?
В сегодняшней статье я расскажу о трех рабочих листах, демонстрирующих некоторые встроенные функции Mathcad, предназначенные для поиска корня.
Функция
Root На первом листе приведены примеры алгоритмического поиска корней с использованием функции Mathcad root . (Обратите внимание, что эта функция решает только одно уравнение с одним неизвестным.) Вы можете вызвать корневую функцию с двумя или четырьмя аргументами, в зависимости от того, хотите ли вы предоставить значение предположения для корня перед вызовом функции или значения в квадратных скобках для root внутри вызова функции.
Для функций с комплексными корнями можно также использовать комплексные приближенные значения, чтобы найти комплексный корень функции.
Пример использования функции root
Функция
Polyrootsудобнее находить все корни сразу, используя функцию polyroots . Эта функция возвращает вектор, содержащий корни многочлена. Входными данными для поликорней является один вектор действительных или комплексных чисел, содержащий коэффициенты многочлена. Коэффициенты перечислены от низшей степени к высшей, включая все 0 коэффициентов.
Пример определения вектора коэффициентов и нахождения вектора корней.
Если корни многочлена неразличимы, вы можете прочитать раздел «Повторяющиеся и парные корни» на листе, чтобы увидеть, как Mathcad справляется с этой ситуацией.
Поиск символьного корня
Я уверен, вы знаете, что Mathcad имеет два типа математических машин: числовые и символьные.
Вы можете использовать символьный процессор в Mathcad для символьного поиска корней. Это может быть более точным, чем численное нахождение корня, а также может дать больше информации о решении.
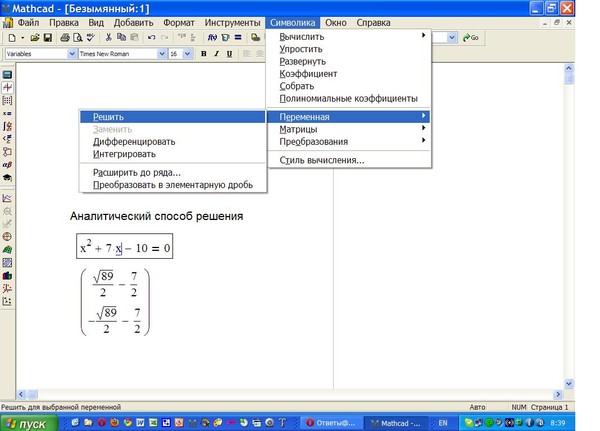
Простой пример поиска символьного корня
Вы можете присвоить символьное решение переменной или функции, сделав его доступным для использования на рабочем листе. Когда существует более одного решения, например, в приведенном выше квадратном уравнении, решение хранится в векторе, где каждый элемент представляет одну часть общего решения.
Также обратите внимание, что, поскольку выражение содержит несколько переменных, вы должны ввести запятую после «решить», а затем переменную, x , для которого вы решаете.
Вы можете найти эти три рабочих листа и множество других подробных примеров в коллекции рабочих листов PTC Mathcad — Education в интернет-магазине PTC.
Решение уравнений » MathCadHelp.
com » Номер 1 в заданиях MathCad В этой главе описывается, как решать уравнения, начиная от одного уравнения
с одним неизвестным и заканчивая системами из пятидесяти уравнений с пятьюдесятью неизвестными. Описанные здесь методы генерируют числовые решения. «Символическое вычисление» описывает различные методы символического решения уравнений.
Следующие секции составляют
Решение одного уравнения
Как использовать функцию корня Mathcad для численного решения одного уравнения с одним неизвестным.
Системы уравнений
Как использовать «блоки решения» для решения систем из n уравнений с n неизвестными.
Эффективное использование решателя
Примеры эффективного решения систем уравнений для различных значений параметра.
Решение одного уравнения
Чтобы решить одно уравнение с одним неизвестным, используйте функцию корня. Эта функция принимает выражение и одну из переменных выражения.
Затем он изменяет эту переменную до тех пор, пока выражение не станет равным нулю. После этого функция возвращает значение, при котором выражение становится равным нулю.
Возвращает значение z, при котором выражение или функцияj(z) равно 0. Оба аргумента этой функции должны быть скалярными. Функция возвращает скаляр
Первый аргумент — это либо функция, определенная в другом месте листа, либо выражение. Он должен возвращать скалярное значение.
Второй аргумент — это имя переменной, которое появляется в выражении. Именно эту переменную Mathcad будет изменять, чтобы выражение стремилось к нулю. Вы должны присвоить номер этой переменной, прежде чем использовать корневую функцию. Mathcad использует это как начальное значение при поиске решения.
Например, чтобы определить a как решение уравнения <Вставьте уравнение здесь>, выполните следующие действия: 9.0007
• Определите предполагаемое значение для x. Введите x: 3. Ваш выбор значения приближения определяет, какой корень Mathcad возвращает.
используйте корневую функцию.
• Для выражений с несколькими корнями, например, x2 – 1 = 0, ваше предполагаемое значение определяет, какой корень будет возвращен Mathcad. На рис. 15-1 показан пример, в котором корневая функция возвращает несколько разных значений, каждое из которых зависит от начального предполагаемого значения.
• Mathcad найдет комплексные корни так же, как и действительные корни. Чтобы найти сложный корень, вы должны начать с комплексного значения для начального предположения.
• Решение уравнения формы f(x) = g(x) эквивалентно использованию корневой функции следующим образом:
решение уравнения
Корневая функция может решить только одно уравнение с одним неизвестным. Чтобы решить несколько уравнений одновременно, используйте технику, описанную в следующем разделе «Системы уравнений». Чтобы решить уравнение с помощью символов или найти точный числовой ответ с точки зрения элементарных функций, выберите «Решить для переменной» в меню «Символические» или используйте ключевое слово решения.
См. главу 17, «Вычисление символов 9».0007
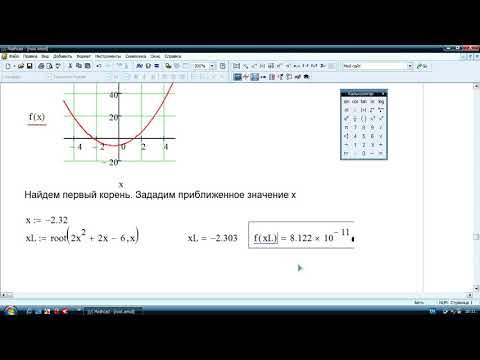
Использование графика и корневой функции для поиска корней выражения.
Что делать, если функция корня не сходится
Mathcad вычисляет функцию корня, используя метод секущих. Предположительное значение, которое вы указываете для x, становится отправной точкой для последовательных приближений к корневому значению. Когда величина j(x), оцененная в предложенном корне, меньше значения предопределенной переменной TOL, корневая функция возвращает результат.
Если после многих приближений Mathcad все еще не может найти приемлемый ответ, он помечает корневую функцию сообщением об ошибке, указывающим на ее неспособность сходиться к результату. Эта ошибка может быть вызвана любой из следующих причин:
• Выражение не имеет корней.
• Корни выражения далеки от первоначального предположения.
• Выражение имеет локальные максимумы или минимумы между начальным предположением и корнями.
• Выражение имеет разрывы между начальным предположением и корнями.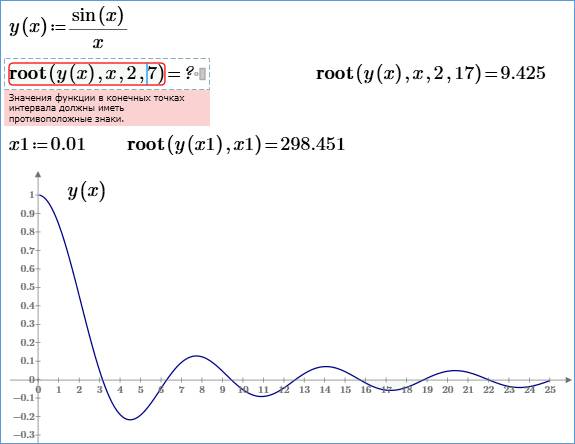
• Выражение имеет комплексный корень, но первоначальная догадка была реальной (или наоборот).
Чтобы найти причину ошибки, попробуйте построить выражение. Это поможет определить, пересекает ли выражение ось X, и если да, то примерно, где это происходит. Как правило, чем ближе ваше первоначальное предположение к точке пересечения выражения с осью X, тем быстрее корневая функция будет сходиться к приемлемому результату.
Советы по использованию корневой функции
Вот несколько советов по максимальному использованию корневой функции:
• Чтобы изменить точность корневой функции, измените значение встроенной переменной TaL. Если вы увеличите TaL, корневая функция будет сходиться быстрее, но ответ будет менее точным. Если вы уменьшите TaL, корневая функция будет сходиться медленнее, но ответ будет более точным. Чтобы изменить TaL в указанной точке рабочего листа, включите определение, например TOL := 0,01 . Чтобы изменить TaL для всего листа, выберите «Параметры» в меню «Математика», перейдите на вкладку «Встроенные переменные» и замените число в текстовом поле рядом с «TaL».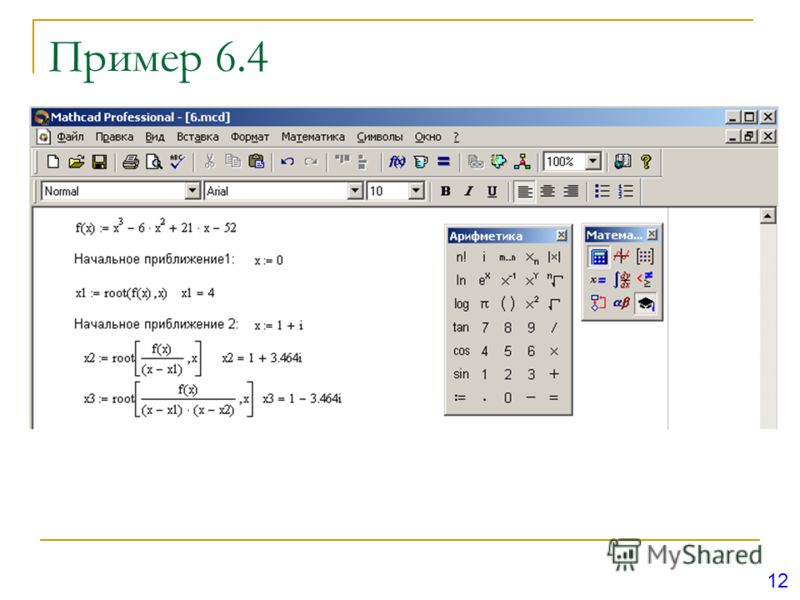
После того, как вы нажмете «ОК», выберите «Рассчитать рабочий лист» в меню «Математика», чтобы обновить весь рабочий лист, используя новое значение TaL.
• Если выражение имеет несколько корней, попробуйте найти их с разными значениями предположений. Построение графика функции – это хороший способ определить, сколько существует корней, где они находятся и какие первоначальные догадки могут их найти. На рис. 15-1 показан пример этого. Если два корня расположены близко друг к другу, возможно, вам придется сократить TaL, чтобы различить
между ними.
• Если fix) имеет небольшой наклон около корня, то root(f(x), x) может сходиться к значению r, которое относительно далеко от фактического корня. В таких случаях, даже если It( r)1 < TO L , r может быть далеко от точки, где f( r) = O. Чтобы найти более точный корень, уменьшите значение TaL. Или попробуйте найти root(g(x),x), где
Советы по использованию корневой функции
• Для выраженияfix) с известным корнем a, нахождение дополнительных корней fix) эквивалентно поиску корней hex) = (f(x))/(x – a ).
Разделение известных корней подобным образом . эффективен для разрешения двух корней, которые могут быть расположены близко друг к другу. Часто проще найти корни шестнадцатеричного числа, как определено здесь, чем пытаться найти другие корни для исправления) с различными предположениями
Многократное решение уравнения
Предположим, вы хотите решить уравнение много раз, варьируя один из параметров в уравнении. Например, предположим, что вы хотите решить уравнение eX = a · x2 для нескольких различных значений параметра a. Самый простой способ сделать это — определить функцию:
Повторное решение уравнения
Чтобы решить уравнение для определенного значения a, укажите как a, так и предполагаемое значение x в качестве аргументов для этой функции. Затем оцените помазание, набрав f (a, x) =.
На рис. 15-2 показан пример того, как такую функцию можно использовать для поиска нескольких решений корневой функции. Обратите внимание, что поскольку предполагаемое значение x передается в саму функцию, нет необходимости определять его где-либо еще на листе.