2. Решение систем дифференциальных уравнений численными методами в среде MathCad
Метод Рунге-Кутта
Решим методом Рунге-Кутта исходную систему дифференциальных уравнений, записанную в виде:
для следующих начальных условий:
,
Присвоим начальному индексу массивов значение 1.
Сформируем вектор правых частей системы дифференциальных уравнений:
Сформируем вектор начальных условий:
Вызов функции rkfixed():
Результат работы функции – матрица Xrk (таблица) значений, первый столбец которой содержит значения времени, второй искомые значения x1(t), третий – x2(t).
Для построения графика функций предварительно зададим интервал изменения индекса:
Рис.
3.2. Сравнение
численного решения методом Рунге-Кутта
(штрихи) и аналитического (сплошные
линии) решения системы дифференциальных
уравнений
Метод Рунге-Куттас адаптивным шагом
Решим ту же систему дифференциальных уравнений методом Рунге-Кутта с адаптивным шагом.
Вектор правых частей уравнения и вектор начальных условий уже сформированы выше в примере решения системы дифференциальных уравнений методом Рунге-Кутта
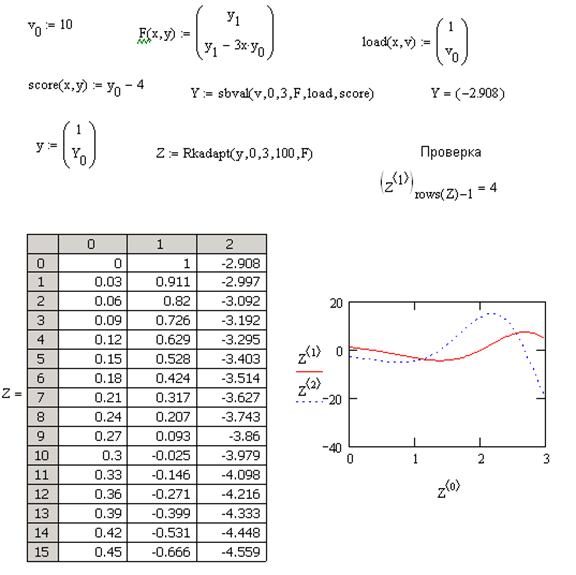
Вызов функции rkadapt():
Результат работы функции – матрица Xrkа(таблица) значений, первый столбец которой содержит значения времени, второй искомые значения x1(t), третий – x2(t).
Для построения графика функций предварительно зададим интервал изменения индекса:
Рис. 3.
Метод Булирша-Штера
Решим ту же систему дифференциальных уравнений методом Булирша-Штера. Вектор правых частей уравнения и вектор начальных условий уже сформированы выше в примере решения системы дифференциальных уравнений методом Рунге-Кутта
Вызов функции Bulstoer():
Результат работы функции – матрица Xrkb(таблица) значений, первый столбец которой содержит значения времени, второй искомые значения x1(t), третий – x2(t).
Для построения графика функций предварительно зададим интервал изменения индекса:
Рис. 3.4. Сравнение численного решения методом Булирша-Штера(штрихи) и аналитического (сплошные линии) решения системы дифференциальных уравнений
3.
Приведение дифференциальных уравнений высших порядков к нормальному видуПриведем дифференциальное уравнение к системе нормальных дифференциальных уравнений:
.
Введем замену:
x(t)=x1(t),
,
.
тогда
,
.
Приводим к нормальному виду:
,
.
В матричном виде система уравнений (44):
или
.
4. Приведение матричного уравнения к новым координатам
Решим полученное в предыдущем пункте уравнение с помощью MathCad. Задаем исходные данные:
Решение будем искать в виде:
Так как матрица А недиагональная, то решение будем искать с помощью приведения системы дифференциальных уравнений к новым координатам. Для этого определяем собственные значения матрицы А – векторlи формируем матрицуL:
находим матрицу L, обратнуюT, а затем и матрицуТ:
Выполняем проверку:
находим значения матрицы и подынтегрального выражения:
Находим функции y(t)иx(t):
Строим график:
Рис.
3.5. Решение с
помощью приведения системы дифференциальных
уравнений к новым координатам
Контрольные вопросы
Представьте дифференциальное уравнение третьего порядка, описывающее систему, в виде системы дифференциальных уравнений первого порядка в нормальном виде.
Выведите общий вид аналитического решения дифференциального матричного уравнения.
Перечислите функции Mathcadдля численного решения систем дифференциальных уравнений.
Как решить дифференциальное уравнение четвертого порядка с помощью функций rkfixed,rkadapt,bulstoer?
В чем отличия между функциями rkfixed,rkadapt,bulstoer?
Как решить дифференциальное матричное уравнение третьего порядка с помощью диагонализации матриц?
Урок 25. Дифференциальные уравнения в Mathcad
Павел Демидов 10.12.2014 Уроки Mathcad 0
Дифференциальные уравнения очень часто применяются для описания изменяющихся процессов.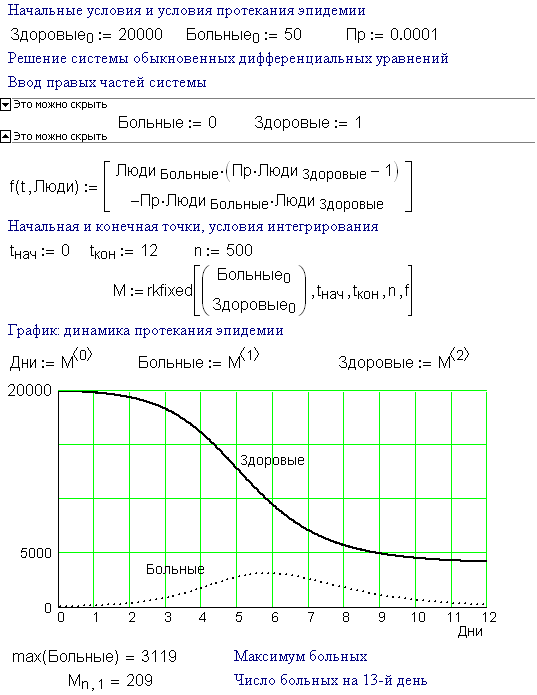
Для начала рассмотрим обыкновенное дифференциальное уравнение (ОДУ):
Аналитическое решение этого уравнения:
Аналитическое решение является точным, и оно быстро дает результат. К сожалению, многие практические дифференциальные уравнения не могут быть решены аналитически. Поэтому нам нужны численные методы.
Метод Эйлера
Наиболее простой метод решения дифференциальных уравнений – метод Эйлера. Это старый метод, легкий для понимания и программирования.
Вычисляем изменения, шаг за шагом:
Сравнение результата и точного решения:
Заметьте, что решение методом Эйлера немного отличается от точного решения, и с ростом аргумента эта разница увеличивается. Уменьшить ошибку можно, если увеличить число шагов.
Блок решения ОДУ
Mathcad содержит все главные решатели дифференциальных уравнений. Их можно найти в меню Функции –> Дифференциальные уравнения. В этом уроке мы рассмотрим самый важный из них.
Он прост в использовании и точен. Такой метод сочетает использование блока решения и функцию odesolve(). Перед решением определим:
Все вхождения зависимой переменной c в блоке решения записываются как функции независимой переменной, т.е. как
Решение этим методом и аналитическое решение близки. Этот же результат можно получить, записав производную через штрих с помощью [Ctrl+’]:
Пример: сердце и артерии
Работа сердца похожа на работу поршневого насоса: оба они расширяются и сжимаются, клапаны на входе и выходе позволяют течь только в одном направлении. Впускной клапан открывается, когда камера расширяется и позволяет крови попасть в сердце из вены. При сжатии камеры впускной клапан закрывается, и кровь выбрасывается в артерию. Выпускной клапан закрывается, когда камера начинает расширяться.
Пульсация потока уменьшается расширением и сжатием эластичных стенок артерий.
Перепады давления возле легких низки: примем, что избыточное давление в точках A и B равно нулю. Центральным элементом являются артерии, изменение объема которых определяются разницей входного и выходного потоков:
Предположим, что объем сердца изменяется во времени по синусоидальному закону, но кровь выпускается только в течение положительной полуволны:
График для восьми ударов:
Средний поток – это интеграл объема в течение одного удара, деленный на время удара:
Расширение артерий зависит от эластичности стенок и их геометрии, но мы не будем анализировать это здесь. Предположим, что объем линейно зависит от избытка давления:
Чем эластичнее стенки, тем больше значение k. Определим три значения:
Сопротивление тела:
Разность давлений следует из:
Баланс объемов артерий:
Из
получаем дифференциальное уравнение для давления:
Решим его таким же образом, как и предыдущее, с той разницей, что
Выведем решения:
Максимумы давления зависят от эластичности артерий – чем больше эластичность, тем меньше давление:
Здесь мы использовали для примера одно дифференциальное уравнение первого порядка, но Mathcad этим не ограничивается.
Резюме
- Обыкновенное дифференциальное уравнение содержит два вида переменных: зависимые (y(x)) и независимые (x).
- Решение можно получить с помощью блока решения и функции odesolve().
- Используйте оператор дифференцирования или штрих в записи дифференциального уравнения. Штрих вводится с помощью [Ctrl+’].
- Введите необходимые граничные условия (они могут содержать запись производной через штрих).
- Функция odesolve() содержит зависимую переменную и независимую переменную.
- Зависимые переменные записываются как функции от независимых.
- В завершение присвойте выходной переменной функцию odesolve(). Выходная переменная не записывается как функция от независимой переменной.
- Однако, при использовании вывода нужно записывать его как функцию независимой переменной.
About Павел Демидов
Выпускник МГТУ им.
Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.
View all posts by Павел Демидов →
Как узнать свободный объем сборки в Autodesk Inventor
Как еще можно использовать блоки в AutoCAD
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.
- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2023 Scientific Research Publishing Inc. Все права защищены.
ВершинаПочему я использую Mathcad — Debtwatch Стива Кина
- Твит
- Твит
Новый участник блога спросил: «Почему вы используете Mathcad?» в ответ на мой последний пост об использовании части средств, пожертвованных посетителями блога, для финансирования моего исследования.
Это очень хороший технический вопрос, и он заслуживает большего, чем просто ответ на комментарий.
Поэтому я попытаюсь объяснить, почему здесь.
Строю динамические модели экономики, используя системы обыкновенных дифференциальных уравнений. В наши дни существует множество программ, поддерживающих это, от общедоступных программ, таких как Scilab, до коммерческих гигантов, таких как Mathematica и Mathcad. Я пробовал большинство из них и остановился на Mathcad по двум причинам:
Его интерфейс очень естественен; и
Его сообщения об ошибках легко интерпретировать.
Я попытаюсь проиллюстрировать это моделированием одной и той же системы как в Mathcad, так и в Mathematica. Во-первых, вот успешный вывод из Mathematica моей простейшей модели эндогенных денег с ростом и кредитным кризисом:
А вот та же модель в Mathcad:
Хотя с графиками Mathematica можно сделать гораздо больше, я найдите дисплей Mathcad более интуитивным — больше похожим на то, что математик написал бы на листе бумаги, что и является философией дизайна Mathcad.
Но основное отличие заключается в следующей особенности: сообщения об ошибках, которые две программы генерируют, когда, как это часто бывает, вы допускаете ошибку в своих ранних попытках смоделировать модель. В этом случае я набрал «ss» вместо того, чтобы ввести «s» в конкретной функции. Вот реакция Mathematica на это:
А? Что означает «NDSolve::ndinnt: Начальное условие 400. ss не является числом или прямоугольным массивом чисел»? Это тривиальный пример, и, конечно, я уже знаю, но когда вы создаете сложную модель и допускаете случайную ошибку, найти ошибку может оказаться нетривиальным упражнением, даже если она на самом деле такая тривиальная, как эта. .
Вот такая же ошибка в Mathcad, и первая стадия ее реакции:
Ахах! У меня есть (пока не идентифицированная) неопределенная переменная! Я нажимаю на «отследить ошибку», и получаю следующее окно. Если бы был каскад ошибок, кнопка «Предыдущий» была бы выделена, но поскольку она только одна, когда я закрываю это окно, Mathcad помещает курсор прямо на вызывающую ошибку переменную «ss».