Mathcad

Разложение в ряд фурье mathcad: Разложение функции в гармонический ряд фурье mathcad. Ряды MathCAD

Содержание

2.7.2. Разложение в ряд Тейлора в системе Mathcad

В системе Mathcad разложение в отрезок ряда Тейлора возможно в режиме символьных вычислений, как в командном режиме, так и с помощью символьной функции series. Шаблон этой функции имеет три места ввода — для разлагаемого выражения, для имени переменной, по которой ведется разложение, и для числа возможных членов ряда n. Он также содержит оператор символьного ввода .

Пример 2.31. Вычислить разложение в отрезки ряда Маклорена (в окрестности точки x=0) следующих выражений sin(x), exp(x) и 2x:

О

.

братите внимание на то, что некоторые из возможных членов ряда могут отсутствовать, но они входят в числоn. Например, ряд для синуса содержит только члены с нечетными номерами.

.

Пример 2.32. Вычислить разложение в отрезок ряда Тейлора выражения ln(x) в окрестности точки

x=1:

Обратите внимание на то, что в этом случае вместоx надо записывать x=1, используя жирный знак равенства.

Пример 2.33. Самостоятельно постройте график функции sin(x) и графики трех разложений синуса в окрестности точки x=0 для n=3, 5 и 7. Убедитесь в том, что разложение приближается к исходной функции только при малых отклонениях от точки разложения и очень сильно отклоняется от нее вдали от нее.

К фундаментальным положениям математики относится возможность представления периодических (а при определенных условиях и непериодических) функций и сигналов совокупностью их синусоидальных (гармонических) составляющих в виде так называемого ряда Фурье. Эта возможность используется во множестве прикладных областей, достаточно отметить, что на ее основе реализуется передача через каналы связи практически любой информации, например речи или музыки, и ее эффективная

фильтрация (выделение нужной информации и отсев шумов) [16].

Рядом Фурье для интегрируемой на отрезке [-, ] функции y(x), удовлетворяющей известным условиям Дирихле (конечное число разрывов и непрерывность функции между ними), называют следующий ряд:

.

Коэффициенты Фурье этого ряда находятся по формулам Эйлера-Фурье:

.

Важными сферами применения рядов Фурье являются радиотехнические расчеты. В них периодические сигналы обычно представляют как функции времени y(t) на отрезке [0, T] с периодом T = 1/f1, где f1 — частота первой гармоники периодического сигнала. В этом случае ряд Фурье после несложных преобразований записывается в виде

.

Здесь коэффициенты выглядят следующим образом:

.

В этом случае коэффициенты ak и bk описывают косинусную и синусную составляющие k-й гармоники сигнала с периодом T и частотой повторения f1 = 1/T. Часто используется иная форма ряда Фурье, упрощающая его синтез:

.

Здесь Ak — амплитуда k-й гармоники периодического сигнала, jk — фаза k-й гармоники. Они вычисляются по формулам:

.

Разложение функции на гармонические составляющие, то есть вычисление коэффициентов Фурье, принято назвать спектральным анализом. А воссоздание приближения функции рядом Фурье, то есть получение ее тригонометрического представления, называют спектральным синтезом.

Гармонику с k = 1 называют основной

, или первой гармоникой сигнала. Она задает его частоту повторения f1. Остальные гармоники называют высшими, их частоты равны fk = k·f1, где k = 2, 3, … . Таким образом, спектр периодических сигналов дискретный — он содержит набор фиксированных частот fk, где k = 1, 2, 3, … . У непериодических сигналов спектр будет сплошным, и вместо амплитуды гармоник он характеризуется спектральной плотностью сигнала.

Ряды Тейлора и Маклорена. Ряды Фурье

Citation preview

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Оренбургский государственный университет» Кафедра математического анализа

О. Л. ТКАЧЕВА

РЯДЫ ТЕЙЛОРА И МАКЛОРЕНА. РЯДЫ ФУРЬЕ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОМУ ПРАКТИКУМУ

Рекомендовано к изданию Редакционно-издательским советом государственного образовательного учреждения высшего профессионального образования «Оренбургский государственный университет»

Оренбург 2007

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

УДК 517.518.45(076.5) ББК 22.161.5 я 7 Т 48 Рецензент кандидат технических наук И.В. Крючкова Ткачева О.Л. Ряды Тейлора и Маклорена. Ряды Фурье [Текст]: методические указания к лабораторному практикуму/О.Л. Ткачева. — Оренбург: ГОУ ОГУ, 2007. – 26с.

Т48

Лабораторный практикум по математическому анализу состоит из теоретического материала, заданий к лабораторным работам с применением программы Mathcad, контрольных вопросов для самоподготовки. Методические указания предназначены для выполнения лабораторных работ по темам, связанным с разложением функций в ряды Тейлора и Фурье для студентов всех форм обучения специальности 230104. 65 и других технических специальностей.

ББК 22.161.5 я 7

© Ткачева О.Л., 2007 © ГОУ ОГУ, 200

2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Содержание …………………………………………………………………………………………………………………….. 3 Введение………………………………………………………………………………………………………………. 4 1 Функциональные ряды………………………………………………………………………………………..5 1.1 Основные понятия……………………………………………………………………………………….. 5 1.2 Равномерная сходимость функциональных рядов…………………………………………. 5 2 Степные ряды……………………………………………………………………………………………………..6 2.1 Основные понятия ………………………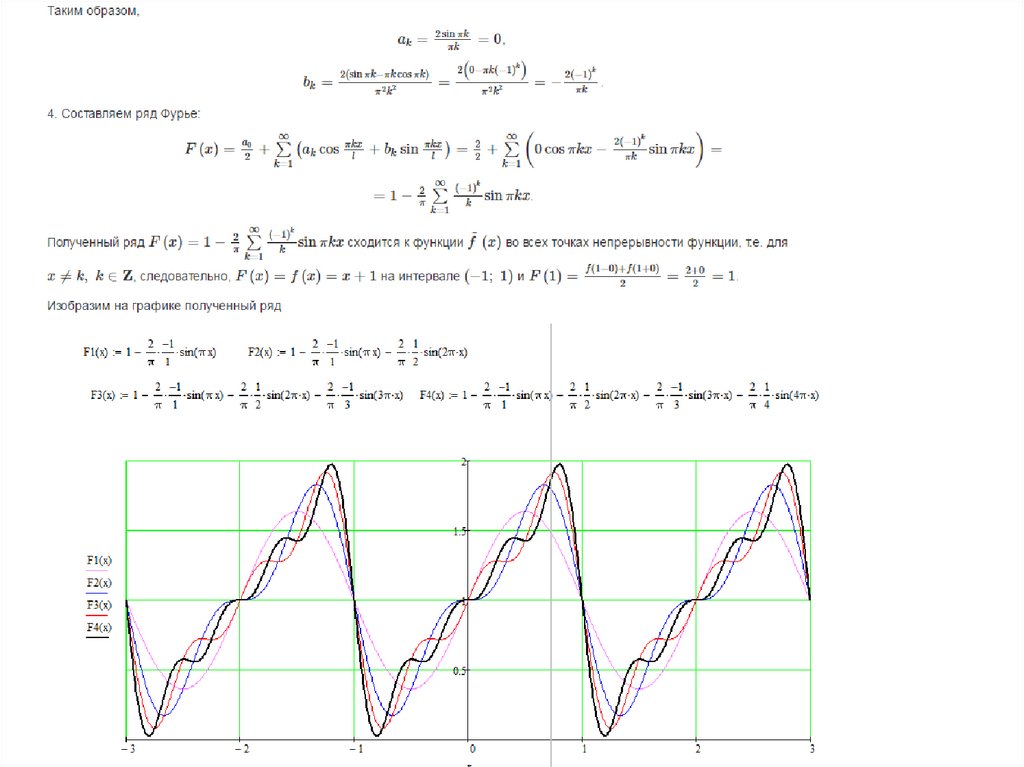 ………………………………………………………………. 6 2.2 Свойства степенного ряда……………………………………………………………………………..7 3 Ряд Тейлора……………………………………………………………………………………………………….. 8 4 Разложение функции по формуле Тейлора в программе Mathcad …………………………9 5 Ряды Фурье……………………………………………………………………………………………………….10 5.1 Основные понятия …………………………………………………………………………………….. 10 5.2 Разложение в ряд Фурье четных и нечетных функций………………………………….11 5.2.1 Разложение в ряд Фурье четных функций…………………………………………….. 11 5.2.2 Разложение в ряд Фурье нечетных функций…………………………………………. 11 5.3 Разложение в ряд Фурье функции с произвольным периодом. 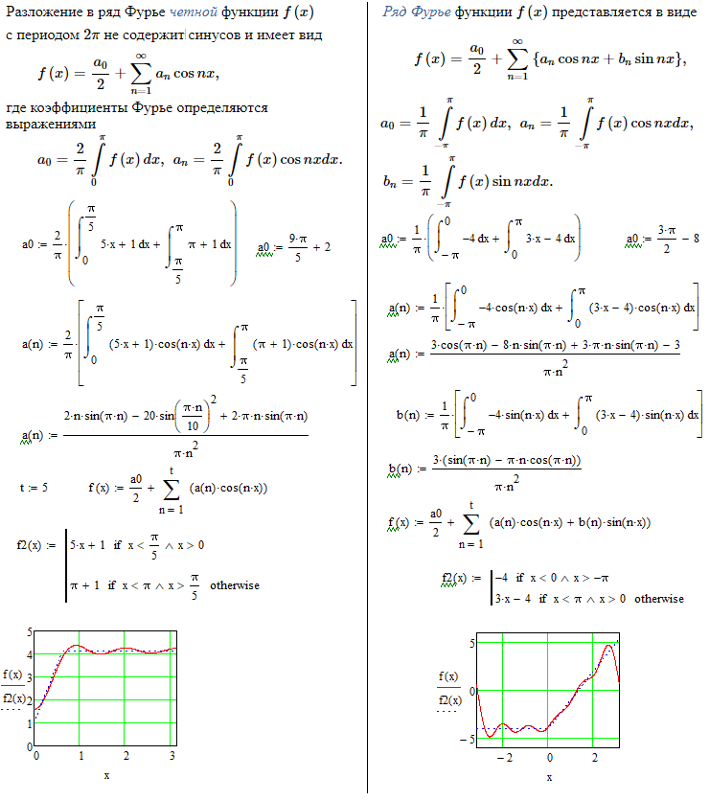…………………….. 11 5.4 Разложение функции в ряд Фурье в программе Mathcad …………………………….. 12 Список использованных источников…………………………………………………………………….15 Приложение А……………………………………………………………………………………………………..16 Приложение Б…………………………………………………………………………………………………….. 21

3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Введение Данная работа дает общий теоретический материал по темам: степенные ряды, ряды Тейлора и Маклорена, ряды Фурье. В работе рассматриваются практические примеры разложения функции в ряды Тейлора и Фурье с применение программ Mathcad. Применение программ Mathcad с большой степенью точности аппроксимировать функцию частичными суммами рядов Тейлора и Фурье, что позволяет быстро и с достаточной точностью решить многие практические вопросы.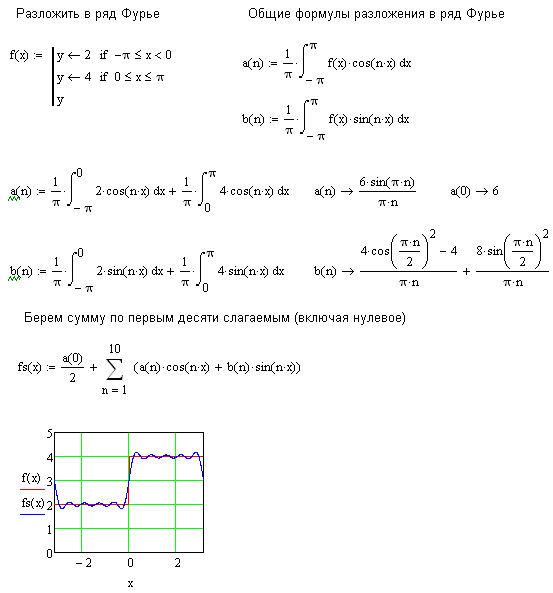

4

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 Функциональные ряды 1.1 Основные понятия Ряд, членами которого U n (x) являются функции от х, определенные на множестве D, называется функциональным: ∞

∑U n= 1

n

( x) = U1 ( x) + U 2 ( x) + … + U n ( x) + …

(1)

Придавая х определенное значение x0 ∈ D , мы получим числовой ряд ∞

∑U n= 1

n

( x0 ) = U1 ( x0 ) + U 2 ( x0 ) + … + U n ( x0 ) + …

Если полученный числовой ряд сходится, то точка x0 называется точкой сходимости ряда (1). Множество D0 ⊂ D , состоящее из всех точек сходимости ряда (1), называется областью сходимости ряда (1). Если существует lim S n ( x) = S ( x ) , x ∈ D0 n→ ∞

где Sn ( x) = U1 ( x) + U 2 ( x) + … + U n ( x) — частичная сумма ряда, то говорят, что ряд (1) сходится на множестве D0 к S (x) , т.е. ∀ ε > 0 ∃ N = N ( x, ε ) : ( n > N ) ⇒

(S

n

( x ) − S ( x )

1.2 Равномерная сходимость функциональных рядов ∞

∑

Сходящийся в некотором промежутке X функциональный ряд

n= 1

U n ( x)

называется равномерно сходящимся в этом промежутке к S (x) , если ∀ ε > 0 ∃ N = N (ε ) : (n > N ) ⇒

(S

n

( x ) − S ( x)

Признак Вейерштрасса. Если существует такой знакоположительный сходящийся числовой ряд

∞

∑

n= 1

a n , что

(∀ x ∈

X ) : U n ( x) ≤ a n ,

то ряд

∞

∑

n= 1

U n ( x ) (1)

сходится равномерно в промежутке X. В этом случае числовой ряд

∞

∑

n= 1

a n называется мажорирующим рядом или

мажорантой, а ряд (1) – мажорируемым сходящимся рядом. Терема о непрерывности суммы равномерно сходящегося ряда. Если функциональный ряд

∞

∑

n= 1

U n ( x ) сходится равномерно в промежутке X и все его члены

U n (x)

являются непрерывными на X функциями, то сумма S(x) данного функционального ряда также непрерывна на X. 5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2 Степные ряды 2.1 Основные понятия Действительными степными рядами называются функциональные ряды вида ∞

∑

n= 0

an ( x − x0 ) n ,

(2)

где x ∈ R — действительная переменная, коэффициенты ряда an n действительные числа, x0 — постоянное действительное число, un = an ( x − x0 ) общий член ряда.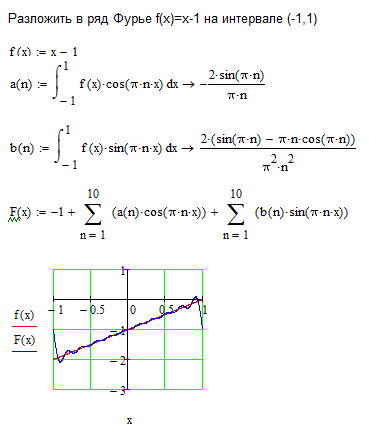 При x0 = 0 получим ряд

∞

∑

n= 0

an x n .

(3)

Теорема Абеля. Если степенной ряд (3) сходится в точке x0 ≠ 0 , то он сходится и притом абсолютно в интервале (− x0 , x0 ) Радиусом сходимости степенного ряда (3) называется такое число r, что для всех x , для которых x r , ряд расходится. Интервал (r ,− r ) называется интервалом сходимости. Для нахождения радиуса сходимости степенного ряда (3) составим ряд состоящий из модулей членов данного степенного ряда a0 + a1 x + a2 x 2 + … + an x n + …

и применим к нему признак Даламбера и при этом допустим, что существует предел lim

n→ ∞

U n+ 1 a xn+ 1 a = lim n + 1 n = x lim n + 1 ≠ 0 при x ≠ 0 n→ ∞ n→ ∞ a Un an x n

По признаку Даламбера ряд сходится, если x lim n→ ∞

an + 1

Что есть в Mathcad Prime 8? | ПТК

Написано Кэт МакКлинток

  • 10.02.2022
  • Время чтения: 4 мин.

PTC Mathcad Prime — это ведущий стандарт для решения, анализа, документирования и обмена инженерными расчетами. А с Mathcad Prime 8, который выйдет в марте 2022 года, вы получите еще больше гибкости и мощности. Посмотрите поближе, что включено и как это может вам помочь:

Предупреждения о переопределении

Благодаря функции предупреждений о переопределении в Mathcad Prime 8 предупреждения автоматически появляются при переопределениях в областях, которые их содержат. Вы можете включать и выключать предупреждения для всех или отдельных категорий идентификаторов, чтобы более точно управлять использованием своего идентификатора.

 

Показать рамку (верхний и нижний колонтитулы, тело страницы)

 

Включите границы для расчетной области верхнего и нижнего колонтитула и тела страницы на листе. Эти границы отображаются в режиме просмотра страницы, в печатных документах и ​​на листах, сохраненных в формате PDF.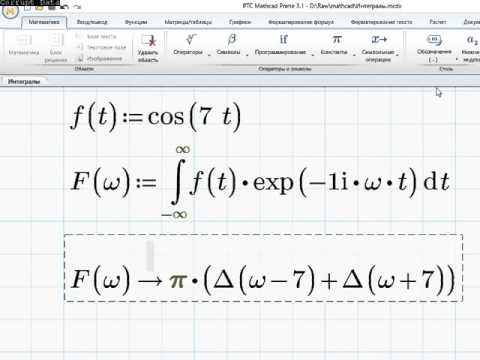

Оператор частичной производной

 

Вставьте и используйте оператор частичной производной на листе. В меню Операторы используйте новый оператор для записи выражений в терминах частных производных.

Копирование/вставка нескольких значений в поле со списком

 

Mathcad Prime 7 включает элемент управления вводом в поле со списком, чтобы вы могли управлять вычислениями на своих рабочих листах с помощью простых в создании и использовании раскрывающихся меню определений переменных. .

В Mathcad Prime 8 добавлена ​​возможность вставки нескольких значений переменных непосредственно в режим редактирования поля со списком. Скопируйте набор значений из матрицы, выберите тот же размер данных в поле со списком и вставьте. Или вы можете вставить в одно поле значения, и данные будут вставлены из этого места вниз и вправо. В обоих случаях поле со списком автоматически изменяет размер для размещения вставленных данных.

Расширения Symbolics Engine

PTC Mathcad Prime 8 продолжает расширять функциональные возможности нового механизма символов, который был представлен в PTC Mathcad Prime 6.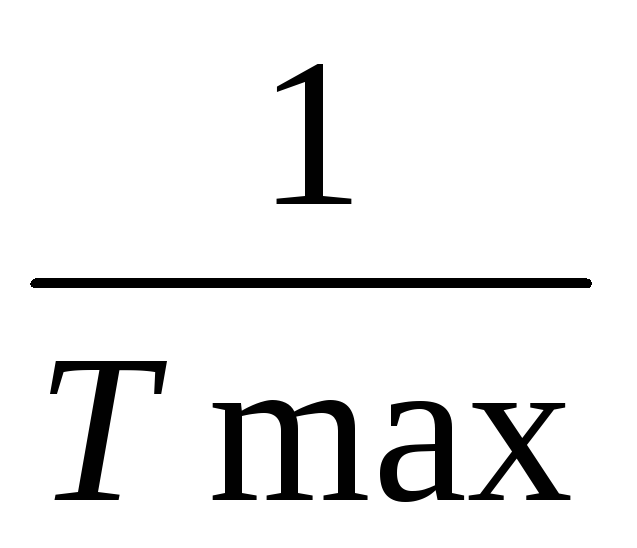 В PTC Mathcad Prime8 вы найдете:

  • Усовершенствования интегрального преобразования символов. Значительное улучшение и расширение использования и производительности, включая добавление поддерживаемых вариантов использования, были добавлены для следующих символьных интегральных преобразований:
    • фурье и фурье
    • лаплас и влаплас
    • зтранс и инвзтранс
  • Новые модификаторы nfact и ofact для использования с ключевым словом фурье , которое позволяет определять нормализационные и колебательные коэффициенты.
  • Повышена производительность и добавлены поддерживаемые варианты использования для операторов исчисления, включая ограничения, производные и интегралы.
  • Повышена производительность и добавлены поддерживаемые варианты использования для ключевых слов, в том числе решить , переписать , ряд , упростить , предположим .
  • Улучшение обработки неопределенных переменных в символьных результатах, включая улучшенную автоматическую маркировку свободных неопределенных переменных и переменных в лямбда-выражениях.

Усовершенствования Numeric Engine

В PTC Mathcad Prime 8 были внесены следующие обновления и усовершенствования числового механизма.

  • Обновлены физические константы. В соответствии с NIST и CODATA мы обновили несколько физических констант, в том числе следующие:

     

    • постоянная Планка
    • постоянная Больцмана
    • Приведенная постоянная Планка
    • Атомная единица массы
    • Номер Авогадро
    • Молярная газовая постоянная
    • Постоянная тонкой структуры
    • Элементарная зарядка
    • постоянная Стефана-Больцмана
    • Квант магнитного потока
    • постоянная Ридберга
  • Более четкие сообщения об ошибках, связанные с поведением функций statespace и odesolve при неправильной настройке.

Улучшения удобства использования


Были сделаны следующие улучшения удобства использования:

  • Масштабирование с помощью Ctrl/Wheel теперь можно использовать для увеличения и уменьшения рабочего листа.
  • Ползунок масштабирования теперь по умолчанию имеет значение 5% при использовании элементов управления + и –.
  • С помощью кнопки Закрыть на вкладках рабочих листов теперь можно закрывать рабочие листы непосредственно с вкладки рабочего листа.
  • Индикатор несохраненных рабочих листов: для рабочих листов, которые еще не сохранены, на вкладке рабочего листа появится звездочка.
  • Контекстное меню на вкладках рабочего листа: новое контекстное меню теперь доступно на всех вкладках рабочего листа, обеспечивая доступ к полезным действиям, в том числе:
    • Рассчитать
    • Закрыть (этот рабочий лист, все рабочие листы, другие рабочие листы, рабочие листы слева/справа, рабочие листы без изменений)
    • Переместить вкладку
    • Скопировать полный путь к файлу
    • Открыть папку, содержащую
    • Печать
    • Сохранить как
  • Dragandmove вкладку рабочего листа: когда открыто несколько рабочих листов, выбранную вкладку рабочего листа теперь можно перетаскивать, чтобы упорядочить вкладки рабочего листа в соответствии с предпочтениями пользователя.
  • Команда «Очистить текстовый формат»: теперь вы можете очистить форматирование текста (шрифт, размер шрифта, цвет и т. д.) для выделенного текста, вернув его к текстовому формату по умолчанию.

Разное

Наконец, вы обнаружите, что эти обновления доступны, так что ваша работа останется полезной в будущем.

Сохранение устаревших рабочих листов в формате HTML

 

Конвертер рабочих листов PTC Mathcad Prime 8.0 позволяет сохранять устаревшие рабочие листы Mathcad 15 в формате HTML.

Благодаря автономному конвертеру, представленному в PTC Mathcad Prime 7.0, вам больше не нужна устаревшая установка Mathcad для преобразования устаревших рабочих листов Mathcad 15 в формат Mathcad Prime. С Функция «Сохранить как HTML » в PTC Mathcad Prime 8.0 XMCD MCD Converter теперь позволяет создавать представление рабочего листа устаревшей версии Mathcad 15, поэтому вам больше не требуется устаревшая установка Mathcad для просмотра преобразуемого содержимого.

Используйте функцию «Сохранить как HTML » в конвертере, чтобы создать представление вашего устаревшего рабочего листа Mathcad15, прежде чем преобразовать его в формат Prime, и обратиться к нему для проверки нового рабочего листа Prime и помощи в доработке, где это необходимо.

Поддержка Windows 11

 

PTC Mathcad Prime 8.0 сертифицирован для работы в новейшей операционной системе Windows, Windows 11 (версия 21h3).

Подробнее

 

Это всего лишь первый взгляд на Mathcad Prime 8. Чтобы получить более подробную информацию, например, демонстрации и другую информацию, подпишитесь на информационный бюллетень Mathcad Minute и зарегистрируйтесь для участия в веб-семинаре «Что нового в Mathcad 8».

Веб-семинар: Новые возможности Mathcad Prime 8

Присоединяйтесь к информации, обсуждениям, демонстрациям и вопросам и ответам.

ЗАРЕГИСТРИРОВАТЬСЯ НА ВЕБИНАР

Об авторе

Кэт МакКлинток редактирует блоги Creo и Mathcad для PTC. Она была писателем и редактором более 15 лет, работая в компаниях, занимающихся разработкой программного обеспечения CAD, PDM, ERP и CRM. До этого она редактировала научные журналы для академического издательства и регулировала оптические сборки для производителя медицинского оборудования. Она имеет степени в области технической журналистики, классики и электрооптики. Ей нравится общаться с клиентами PTC и узнавать об интересной работе, которую они выполняют, и об инновационных способах использования программного обеспечения.

Что есть в Mathcad Prime 8?

PTC Mathcad Prime — это ведущий стандарт для выполнения, анализа, документирования и обмена инженерными расчетами.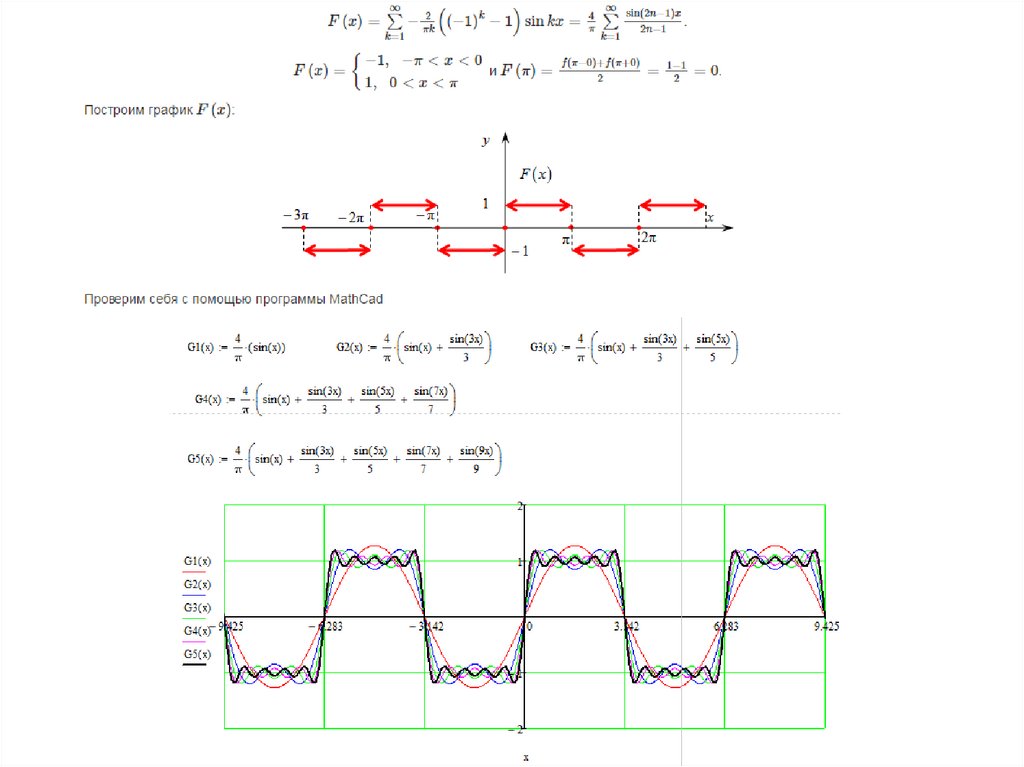 И теперь вы получаете еще больше гибкости и мощности с Mathcad Prime 8.

Новейшие вопросы по «mathcad» Задай вопрос

Mathcad — это компьютерное программное обеспечение, в первую очередь предназначенное для проверки, проверки, документирования и повторного использования инженерных расчетов. Интерфейс Mathcad позволяет пользователям объединять множество различных элементов (математику, описательный текст и вспомогательные изображения) в форму рабочего листа, который легко читается.

  • Учить больше…
  • Лучшие пользователи
  • Синонимы

45 вопросы

Новейший

Активный

Баунти

Без ответа

Фильтровать по

Нет ответов

Ответ не принят

Имеет награду

Отсортировано по

Новейший

Последние действия

Наивысший балл

Самый частый

Щедрость скоро закончится

Отмечен

Мои просматриваемые теги

Следующие теги:

0 голоса

0 ответы

33 Просмотры

Разделить на нулевую ошибку, используя сигма-нотацию

Я пытаюсь выполнить сигма-операцию, но MathCad выдает эту странную ошибку.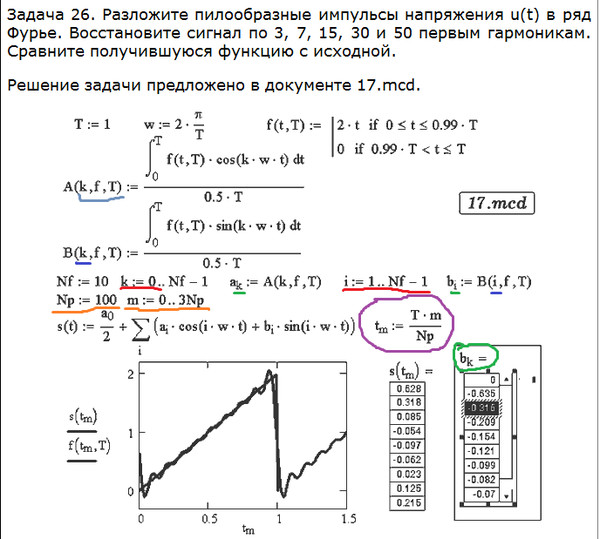 Как я могу пройти мимо этого или заменить позицию на 0? Спасибо Я пробовал цикл for, но не работает.

  • маткад

-2 голоса

1 отвечать

94 Просмотры

Перевод с Mathcad на Python

Я не могу перевести формулу из Mathcad в Python. Застрял на «а». Вот что я смог сделать: из matplotlib импортировать pyplot как plt импортировать numpy как np к1 = 1 б = 1,51 D = (1/b) * (np.sqrt(…

  • питон
  • numpy
  • matplotlib
  • математика
  • mathcad

0 голоса

0 ответы

138 Просмотры

Ошибка интервала Mathcad.

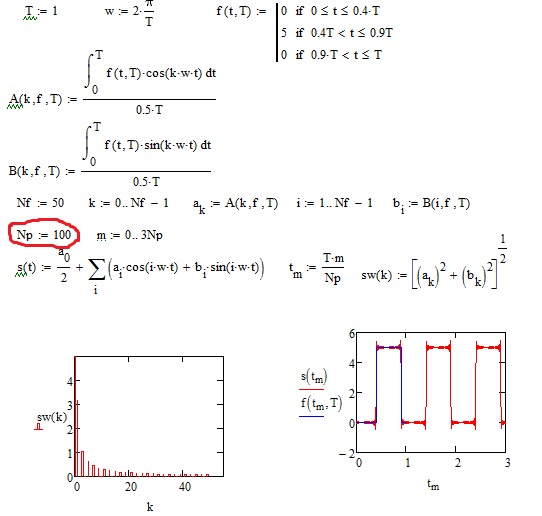Этот расчет не сходится к решению

Не могли бы вы помочь мне решить задачу в MathCAD? Программа сообщает об ошибке, но я не могу понять, что именно.

  • маткад

0 голоса

0 ответы

35 Просмотры

Реализовать алгоритм в Mathcad

Мне дали блок-схему. Я должен реализовать это в Mathcad. Не могли бы вы помочь мне понять алгоритм (на примере Python)? Где ошибки? Это алгоритм и код

  • маткад

0 голоса

1 отвечать

87 Просмотры 9-1 С:…

  • маткад

-1 голоса

1 отвечать

376 Просмотры

Логарифм Mathcad с единицами

Я изучаю, как использовать Mathcad и его символьный движок, и это довольно хорошо. Но я столкнулся с серьезным недостатком при работе с единицами измерения. ln(2)=0,693, произведя натуральный логарифм на…

  • маткад

0 голоса

1 отвечать

34 Просмотры

mathcad значения интегральной функции Лапласа

если я хочу получить табличное значение функции Лапласа, как мне его записать в mathcad? например 0.34 а мне нужно 0.1331 (мне не нужно что-то подобное)

  • маткад

0 голоса

0 ответы

55 Просмотры

Автоматизация Mathcad в Excel

Я хотел бы автоматизировать некоторые вычисления, сделанные с помощью mathcad (v15) в Excel. Первое решение (работающее) состоит в том, чтобы добавить новый пустой объект OLE (документ mathcad) и выбрать файл mathcad, который мы…

  • Excel
  • vba
  • оле
  • mathcad

0 голоса

1 отвечать

60 Просмотры

Рабочие книги в стиле Maple в MathCAD?

Я надеюсь использовать MathCAD для некоторых широких (но простых) инженерных вычислений, но, похоже, у него нет концепции рабочих книг (как у Maple). Как можно объединить рабочие листы, библиотеки, данные в …

  • проект
  • клен
  • mathcad

0 голоса

1 отвечать

129 Просмотры

Как преобразовать уравнение в переменную, используя «решить» в mathcad?

Я хотел знать (как сказано в заголовке), как преобразовать уравнение в переменную, используя «решить» в mathcad? Потому что «решить» почему-то не работает.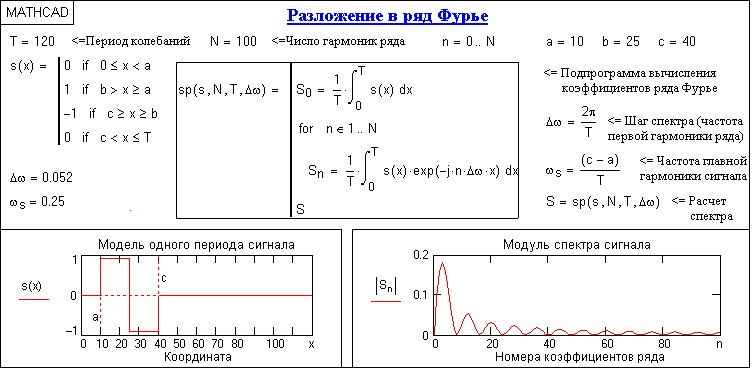 Буду признателен, если…

  • mathcad

0 голоса

1 отвечать

91 Просмотры

Как проследить стек, чтобы устранить ошибку в MathCAD?

Делая некоторые расчеты с MathCAD, я получил ошибку, например: Неизвестная ошибка: цель вызова вызвала исключение. Есть ли какая-то трассировка стека, которую я мог бы исследовать, чтобы понять ситуацию? Спасибо …

  • отладка
  • трассировка стека
  • mathcad

0 голоса

1 отвечать

105 Просмотры

Решение задачи в mathcad с помощью программирования

У меня есть средство решения проблем на первом изображении, оно возвращает значение t0: Решение проблем Этого было бы вполне достаточно, но мне нужно изменить этот «код», чтобы использовать 13 значений вместо одного t1, как во втором. ..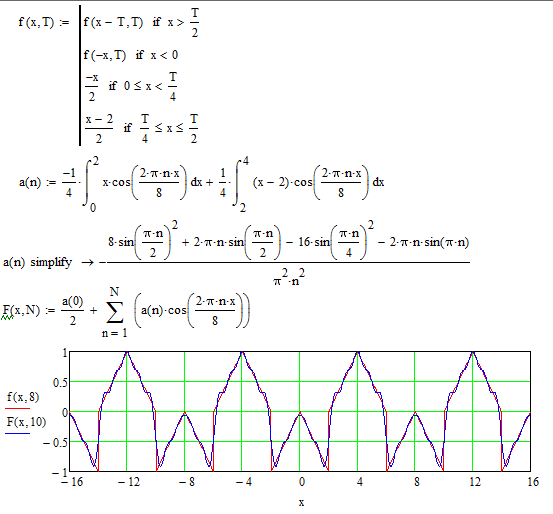

  • циклы
  • вектор
  • корень
  • интеграл
  • mathcad

0 голоса

1 отвечать

30 Просмотры

Функция с комбинаторными аргументами

Я на самом деле не знаю, как вызвать этот тип функции. Поэтому я хочу, чтобы такая функция работала. У меня много переменных Xi,j, поэтому я не хочу писать их все вручную. Как я могу выступать…

  • маткад

2 голоса

0 ответы

244 Просмотры

Первообразный интеграл

Подскажите, пожалуйста, как реализовать на питоне интеграл, показанный на рисунке 1 (или строки 18-19в коде)? Пробовал через sympy.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *