Mathcad Prime для учебного процесса — Сервисы на vc.ru
{«id»:13852,»url»:»\/distributions\/13852\/click?bit=1&hash=02f18e28c27b61d838ae83a7acfbf20b20de2f8f8cab8ca623b201894be8d52c»,»title»:»\u0410\u0440\u0435\u043d\u0434\u043e\u0434\u0430\u0442\u0435\u043b\u0438 \u043f\u0443\u0431\u043b\u0438\u043a\u0443\u044e\u0442\u0441\u044f \u043d\u0430 \u044d\u0442\u043e\u043c \u0440\u0435\u0441\u0443\u0440\u0441\u0435 \u0447\u0430\u0449\u0435, \u0447\u0435\u043c \u043d\u0430 \u0434\u0440\u0443\u0433\u0438\u0445″,»buttonText»:»\u041d\u0430 \u043a\u0430\u043a\u043e\u043c?»,»imageUuid»:»1d785562-9320-5d9c-97fe-cfc17bac150f»,»isPaidAndBannersEnabled»:false}
Mathcad, математическое программное обеспечение для решения и документирования инженерных задач, был создан Алленом Раздовым в 1986 году.
149 просмотров
Центральный интерфейс Mathcad представляет собой интерактивную записную книжку, в которой уравнения и выражения создаются и обрабатываются в том же графическом формате, в котором они представлены.
Аллен Раздов (Allen Razdow), https://razdowdotcom.wordpress.com/
Интервью Аллена Раздова можно почитать тут:
Особенности Mathcad:
- Естественная запись формул и и пересчет математических вычислений, смешанных с текстом
- Работа с физическими величинами
- Традиционные имена переменных
- Численная и символьная математика
- 2D и 3D научная графика, параметрические 2D и 3D построения и построение дискретных данных
- Пользовательские встроенные функции
- Инструменты программирования
- Многочисленные числовые функции для статистики, анализа данных, обработки изображений и обработки сигналов
- Статистические и плановые функции экспериментов и типы участков, а также оценка вероятностных распределений
- Повсеместная проверка размерности и упрощение
Промо видео PTC Mathcad:
Digital Transforms Physical at PTC, источник — официальный канал производителя данного ПО
Mathcad осуществляет полную поддержку русского языка и имеет развитую экосистему обучающих материалов:
Пример расчетов, проведенных в системе Mathcad на базе расчетного сервера НИУ МЭИ:
Mathcad Express: По состоянию на 2021 год последним выпуском PTC является Mathcad Prime 7.
0.0.0.
Этот выпуск является Freemium версией: если программное обеспечение не активировано после 30-дневной пробной версии Mathcad Prime, можно продолжать использовать PTC Mathcad Express в течение неограниченного времени в качестве бесплатного программного обеспечения для инженерных расчетов:
Материал создан в рамках бекстейджа организации онлайн-университета по экспериментальной и теоретической биофизике CRO UpgradeR&D .
Наш проект UpgradeR&D: Онлайн-курсы и исследовательский центр по спектральным методам анализа поддерживается Программой поддержки стартапов от SendPuls.
MathCAD — это просто! Часть 25. Программирование в MathCAD: практика
В прошлый раз мы с вами начали разговор о таком полезном для каждого пользователя среды MathCAD навыке, как программирование. Начать-то, начали, да вот поговорить толком о нем, в общем-то, чего уж там скрывать, практически не успели. Это не очень здорово, потому что программирование вряд ли можно отнести к тем дисциплинам, в которых для успешной работы достаточно чисто теоретических знаний.
Решение квадратного уравнения
Одна из первых программ, которую пишет человек, изучающий тот или иной язык программирования, — это программа, решающая квадратное уравнение. С одной стороны, алгоритм решения квадратных уравнений достаточно прост для того, чтобы не отвлекаться на него и сосредоточиться на особенностях изучаемого языка программирования; с другой стороны, этот алгоритм все же не сводится в тому, чтобы просто выполнить одну- единственную арифметическую операцию, которая сразу же даст нам результат.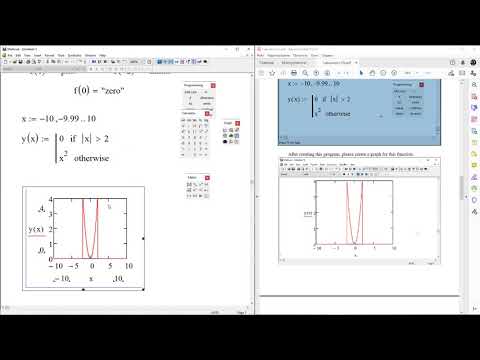
Итак, давайте будем разбираться. Как видите, для удобства коэффициенты объявлены в виде обычных переменных MathCAD’а. Такие переменные могут использоваться как в самой программе, так и вне ее — по этой причине они называются внешними.
Когда переменные объявляются в самой программе, то для нее они являются внутренними и, как несложно догадаться, за ее рамками никакой силы не имеют. В нашей программе всего две строки. Первая из них, как несложно догадаться, выполнится в том случае, если коэффициент при старшем члене в нашем уравнении будет равен нулю. Тогда оно из квадратного обратится в линейное, и решать его нужно будет уже с использованием совсем других формул. Обратите внимание, что в MathCAD’е результат выполнения условия записывается до самого условия — это, вообще говоря, совсем не характерно для большинства языков программирования, однако благодаря этому текст программы смотрится естественнее с точки зрения английского языка. Оператор return используется для того, чтобы вывести какое-либо выражение как результат выполнения нашей программы — если бы мы его не использовали, то и после знака равно ничего бы не было выведено. Вторая строка программы содержит в себе решение именно квадратного уравнения, то есть в ней рассматривается случай, когда коэффициент при старшем члене не равен нулю.
Здесь следует также заметить, что операторы необходимо вводить с помощью соответствующей панели инструментов, о которой я довольно-таки подробно рассказывал в предыдущей статье серии «MathCAD — это просто!», либо же с помощью соответствующих им горячих клавиатурных комбинаций клавиш. Дело в том, что, если вы попробуете вводить операторы в программе, просто набирая их на клавиатуре (тот же if, в принципе, набрать по буквам даже и быстрее), то MathCAD воспримет их как переменные и не будет с ними работать должным образом. Собственно говоря, как вы видите, внизу для контроля правильности написанной нами программы используется оператор solve, решающий точно такое же квадратное уравнение.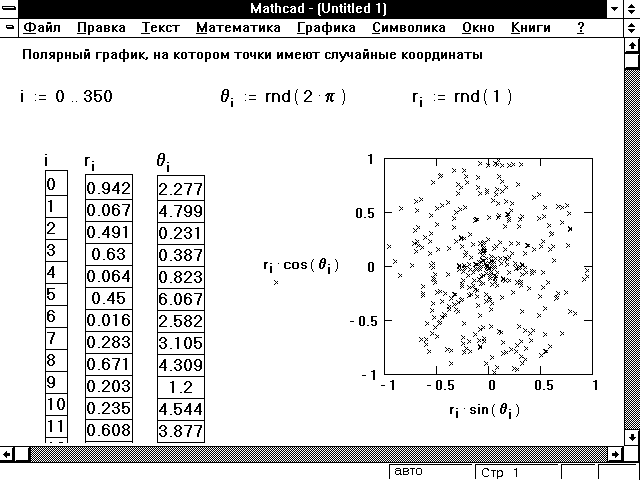
Чтобы убедиться в том, что наша мини-программа успешно справляется с уравнениями и в тех случаях, когда они вырождаются в линейные, и что все работает именно так, как первоначально и было задумано, изменим значение переменной a на нулевое и посмотрим, что из этого у нас с вами получится:
Что ж, как видите, все получилось очень даже и неплохо, и все работает именно так, как мы с вами, собственно говоря, и предполагали. Однако решение квадратных уравнений, каким бы удачным примером оно ни было, не охватывает всех операторов на панели программирования MathCAD, которые могут пригодиться вам в дальнейшем. Поэтому, пожалуй, имеет смысл заканчивать разбираться с дифференциальными уравнениями и переходить к следующим программам — таким же простым, но не менее познавательным, чем та, которую мы с вами только что успешно рассмотрели.
Транспонирование матриц
Давайте рассмотрим еще один просто-таки предельно простой пример, который также проще простого реализуется с помощью встроенных операторов MathCAD.
Что ж, как видите, уже с самого начала программный код преподносит нам некоторые сюрпризы — в нем сходу встречается доселе неизвестная нам конструкция for. Но на самом деле она очень проста и крайне часто употребляема, а потому бояться ее совсем не нужно — нужно разобраться. Что она делает? Никакого секрета, собственного говоря, из этого никто не делает. Эта конструкция используется для организации цикла с заранее заданным числом итераций (сиречь повторений). Конструкция эта очень распространена и с небольшим числом вариаций используется практически во всех более- менее распространенных языках программирования.
В общем-то, в «большом» программирование это требование вполне обоснованно, однако программирование в MathCAD, сами понимаете, имеет свою специфику, а потому тип переменной, если она не задана нигде выше, определяется автоматически. Как видите, нам не пришлось нигде и никак объяснять MathCAD’у, что K — это матрица; более того, нам даже не пришлось указывать нигде ее размеры. Разработчики этой мощной математической среды сумели сделать ее по-настоящему удобной для людей, далеких от программирования, даже тогда, когда к нему все же приходится обращаться.Стоит сказать несколько слов и по поводу того, какими особенностями обладает операция присваивания. Присвоить можно что угодно и как угодно при условии совпадения типов присваиваемого значения и той переменной, которой вы его желаете присвоить. Поэтому совершенно нормальной (и, более того, отнюдь не редкой) является ситуация, когда конструкция вида a < a + 1 кажется совершенно бессмысленной для новичка в программировании. К счастью, в MathCAD’е для обозначения присваивания не используется знак равенства, поскольку в тех языках программирования, где используется именно он, подобная конструкция выглядит поначалу совершенно дико.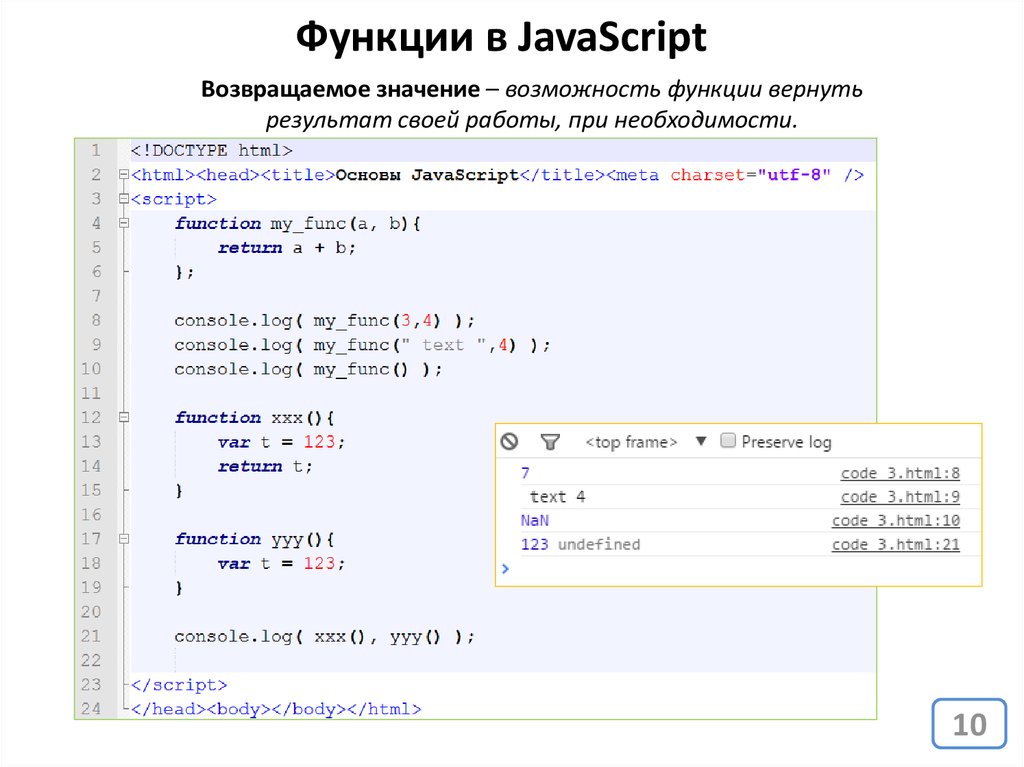
Еще одна особенность кода этой программы состоит в том, что, если вы попробуете использовать переменную K после самой программы, то результат будет не вполне ожидаемым: вы можете наблюдать его на соответствующей иллюстрации. Так происходит по той причине, что переменная K является внутренней переменной для той программы, о которой мы сейчас ведем разговор, а потому вне программы мы и не можем никак ее использовать — фактически K в программе и K вне ее являются с точки зрения MathCAD’а в данном случае разными переменными.
Выводы
Давайте подытожим то, о чем мы сегодня говорили. Как видите, MathCAD — настолько мощная среда, что в ней даже такие простые операции, как транспонирование матриц и решение квадратных уравнений, можно выполнить несколькими способами. Конечно, в этих случаях прибегать к программированию не совсем целесообразно, однако моей задачей было познакомить вас с основными операторами, используемыми при программировании в MathCAD’е, и именно потому я обратился к столь простым примерам.
Надеюсь, вам они тоже не показались сложными, и вы извлечете из них пользу. Программирование — замечательное занятие, и, если вы не умеете программировать, думаю, стоит найти немного свободного времени, чтобы его изучить. Пусть те простые задачи, которые мы обсуждаем, разговаривая о программировании в MathCAD’е, откроют вам дверь в удивительный мир программирования!
Компьютерная газета. Статья была опубликована в номере 39 за 2008 год в рубрике soft
Mathcad-MAE3
Программное обеспечение для анализа > Маткад
|
д.)
Доступ к подробным руководствам можно получить через вкладку «Ресурсы».Категория:Mathcad — Rosetta Code
| Эта страница незавершенная. Нужно больше информации! Вы можете помочь Rosetta Code, заполнив его! |
Веб-сайты Mathcad[править]
Веб-сайт продукта:
- https://www.mathcad.com/en
Сайт сообщества пользователей:
- https://community.ptc.com/t5/PTC-Mathcad/bd-p/PTCMathcad
Основное описание Mathcad[править]
Рабочий лист Mathcad
Mathcad — это проприетарный язык программирования, основанный на концепции написания как текста, так и математических выражений на виртуальной доске. Основное различие между реальной доской и Mathcad заключается в том, что Mathcad может оценивать выражения и отображать любые результаты на виртуальной доске. белая доска».
Рабочий лист может быть любой длины и ширины по желанию пользователя. Mathcad делит доску на виртуальные страницы (размер выбирается пользователем) с ограничением Mathcad Prime, согласно которому можно печатать только левые страницы (отличие от более ранних версий).
Уравнения и текст вводятся в «Области», которые можно произвольно перемещать в соответствии с потребностями пользователя. Однако порядок диапазонов важен, так как Mathcad оценивает рабочие листы от верхнего левого угла к нижнему правому.
Типы Mathcad
Основными типами данных Mathcad являются строки, комплексные скаляры, вложенные двумерные массивы, функции и диапазоны. Он также имеет базовые средства программирования, ограниченные циклами for и while, if-else if-else и try-catch с возвратом, прерыванием и продолжением. Переменным могут быть присвоены значения и выражения. Учитывая порядок оценки рабочего листа в Mathcad, определение действует только в том месте, где оно определено. Любое последующее переопределение имени переменной действует только с момента переопределения; это не влияет на значения переменной до этого, и добавление нового выражения перед переопределением будет использовать старые значения переменных.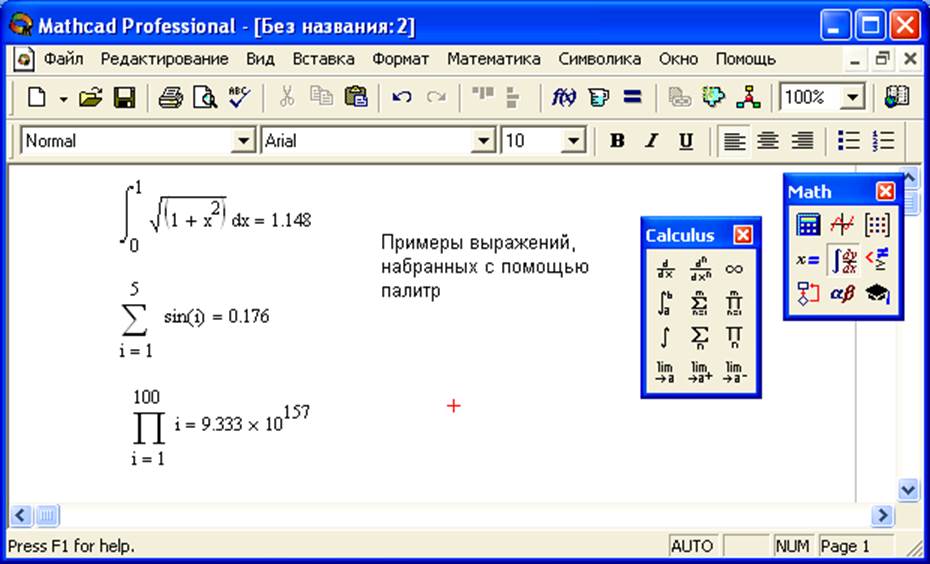
Массивы Mathcad
Элементы массива могут быть любого типа Mathcad, включая массивы и функции. К элементам массива обращаются с помощью оператора индекса, который можно использовать вне программы.
Mathcad обрабатывает одностолбцовые числовые массивы как векторы, а двумерные плоские числовые массивы — как матрицы. Термин «вектор» перегружен и означает любой тип массива из одного столбца, независимо от типов элементов. Важно понимать разницу между переменной диапазона и переменной, содержащей вектор, поскольку их поведение совершенно различно.
Диапазоны и переменные диапазонов
Тип диапазона позволяет выполнять итерацию по диапазону числовых значений и задается с помощью оператора диапазона, затем вводятся значения для первого числа в последовательности, второго числа и последнего числа; второе число является необязательным и по умолчанию равно первому числу + 1. Например, 1.0, 1.1 .. 2.0 при вычислении генерирует числа 1.0, 1.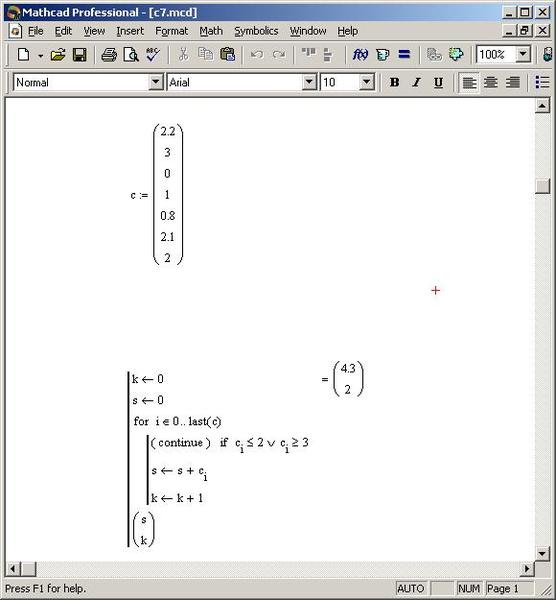
1.2, 1.4, 1.6, 1.8, 20, а 1.0 .. 2.0 генерирует 1.0 , 2.0. Диапазоны обычно используются путем присвоения их переменной, которая затем называется переменной диапазона, которую Mathcad будет автоматически перебирать.
Функции и операторы
Функции Mathcad рассматриваются как объекты первого класса и могут передаваться другим функциям в качестве аргументов и возвращаться из функций. Программирование Mathcad поддерживает локальные определения функций. Mathcad поддерживает определения рекурсивных функций как посредством программирования, так и посредством функциональной композиции и передачи аргументов. Однако одной из возможностей Mathcad 15, которой нет в Mathcad Prime, является рекурсия локальных функций.
Многие функции реализованы в виде операторов, и большинство из них можно ввести с помощью комбинации клавиш или из палитры операторов на панели инструментов (лента в Mathcad Prime). Например, нажатие клавиши «+» автоматически создает оператор добавления инфикса, который имеет заполнители для двух аргументов.
Нажатие «=» вводит оператор Evaluation и оценивает выражение в его левом заполнителе.
Числовая и символьная обработка
Mathcad может выполнять как числовое, так и символьное вычисление выражений. Хотя существует определенная степень взаимодействия между числовой и символьной системами, обычно лучше думать о них как о двух отдельных процессорах, оценивающих один и тот же рабочий лист. Помимо способности символьного процессора оценивать числа с произвольной точностью и символически оценивать выражения, существуют также различия в том, какие функции будут обрабатываться двумя «процессорами» — см. документацию Mathcad для получения справки по этому вопросу.
Особое отличие, которое следует отметить инженерам и ученым, заключается в том, что числовой процессор поддерживает единицы измерения и будет работать с размерными величинами, выполняя любые преобразования размеров и единиц измерения, которые необходимы. Однако нелинейные функции обычно не принимают единицы измерения, и пользователь должен преобразовать размерные величины в скаляры перед их вычислением.
Версии Mathcad[править]
Mathcad существует в двух основных формах: исходная версия Mathsoft (Mathcad 15 и более ранние версии) и пересмотренный Mathcad Prime от PTC. Основное философское различие между Mathcad 15 и Mathcad Prime заключается в том, что Prime имеет более ориентированную на документы парадигму и ориентирован на работу с другими продуктами PTC. Как и в случае с большинством серьезных изменений продукта, пользователи Mathcad делятся на две основные категории: на тех, кто считает Prime шагом назад, и на тех, кто считает его лучшим; у обеих сторон есть свои аргументы, но с точки зрения обычного пользователя в Mathcad Prime по-прежнему (как и в версии Prime 6) отсутствуют некоторые ключевые функции, присутствующие в Mathcad 15. Существует также бесплатная версия Mathcad Prime, известная как Mathcad Prime Express, в котором отсутствуют некоторые расширенные функции Mathcad Prime, такие как программирование, символика и трехмерное построение, — он на удивление функционален и, что интересно, поддерживает «чистый» стиль функционального программирования.