Построение графиков в MathCad | Cl-Box
При решении задач в MathCad часто возникает необходимость построить график, будь то график функции или график по каким либо расчетным данным. В этой статье мы разберем как строятся графики в MathCad. В этой статье мы не будем рассматривать само решение задач, его Вы можете найти в других статьях, ссылка в конце статьи.
- Построение графика функции в MathCad
1.1. Рассмотрим построение на примере функции sin, для этого введем в Маткад следующее (думаю как пользоваться инструментами ввода информации подробно рассматривать не надо, а если вдруг возникнут какие-либо трудности с вводом советую почитать статью Расчаты в MathCad ):
Не забываем что необходимо ставить не знак «равно» а именно знак «определения».
1.2. Теперь нам нужно создать сам график, для этого нажимаем на пункт меню Добавить, выбираем строку Графики, и в появившемся списке выбираем X—
1. 3. Теперь, в появившемся поле графика заполняем наименование осей (в нашем варианте названиями будут f(x) и х)
3. Теперь, в появившемся поле графика заполняем наименование осей (в нашем варианте названиями будут f(x) и х)
После ввоза названий полей кликаем в любой области вне поля графика
В итоге мы получаем готовый график функции синуса:
- Построение графика в MathCad по данным
2.1. Для начала введем данные графика, для этого вводим определитель (у меня это w и r) и добавляем матрицу нужным размером (в моем случае 6х1, это 6 строк, 1 столбик) и вводим в нее свои данные для графика. Вот что получилось у меня:
2.2. Теперь повторяем действия указанные в пункте 1.2. этой статьи (т.е. добавляем график)
2.3. Как и в пункте 1.3. этой статьи заполняем название осей, только на этот раз у нас будут определители наших данных
2.4. При необходимости совместить два графика на одном делаем следующее: добавляем еще один блок данных, ставим курсор после определителя w в графике и нажимаем поставить запятую (напоминаю, что запятая на русской раскладке и на английской раскладке это разные клавиши, и так как мы работаем в Маткаде используя английскую раскладку нам нужна запятая именно английской раскладки), после этого вводим определитель во вторую (появившеюся) строку на нашем графике.
Теперь у нас получилось два пересекающихся графика (конечно же то как он будет выглядеть зависит от данных)
- Форматирование графика в MathCad
Созданный график по умолчанию очень бледный и Вам наверное захочется сделать его немого поярче.
3.1. На графике нажимаем ПКМ (правой клавишей мыши) и в контекстном меню выбираем пункт Формат…
В открывшемся диалоговом окне переходим на вкладку
Тут мы видим табличку строка трассировка 1 соответствует первой кривой нашего графика, трассировка 2 соответственно второй. Столбик Линия соответствует типу линии на нашем графике (сплошная, прерывистая, точка-тире и т.п.). Столбик Линия Вес соответствует толщине нашей линии. И Цвет соответственно цвету. Я в своем примере изменю только толщину линии, и по второму графику тип линии с точек на пунктир для этого в двух верхних строках столбика Линия Вес поставлю цифру 2 и в столбике Линия поменяю тип линии, после чего нажму Применить
Вот что получилось:
Я думаю не надо объяснять как изменять размер графика, если это необходимо.
автор: Admin
Урок 8. 2D-графики функций в Mathcad
В этом уроке мы рассмотрим варианты графиков, доступных в PTC Mathcad Prime 3.0.
Типы графиков
Чтобы изменить тип графика, нажмите на него, затем выберите на вкладке Графики –> Кривые –> Изменить тип. Ниже представлены рисунки четырех типов графиков для функции:
В списке есть еще некоторые типы осей – некоторые из них мы будем использовать позднее.
Несколько графиков на одних осях
Чтобы добавить кривую на оси, поместите курсор после обозначения легенды оси Y графика и нажмите Графики –> Кривые –> Добавить кривую. Появится еще один местозаполнитель для оси Y:
Вы можете добавить больше графиков с помощью этой же команды.
С помощью вывода нескольких графиков на одни оси мы посмотрим различные настройки из меню Графики –> Стили. Для этой цели мы создадим оси с пятью различными прямыми линиями.
Ниже этих выражений вставьте график XY, затем добавьте четыре легенды для оси Y. В местозаполнителе для оси Xвведите x[iи нажмите [Enter] – для всех пяти графиков будет использоваться одна легенда по оси X. В последний местозаполнитель для оси Y введите y[0,i и [Enter]:
Выше следует ввести y[1,i, еще выше — y[2,i и т.д. После завершения Вы увидите пять прямых линий. Свойства каждой из них можно изменить, выбрав легенды оси Y соответствующего графика и выбрав необходимые настройки на меню Графики –> Стили.
Ниже представлены получившиеся графики. Использовались различные настройки для толщины, цвета, стиля линий и символов:
Метки и их значения мы убрали с помощью меню Графики –> Оси.
Масштабирование
На графике с двумя кривыми диапазон для одной из них может быть не очень удачным для другой, например, для графиков квадрата и куба x.
Чтобы исправить это, разделите функцию куба на 5. Это называется масштабированием:
Это называется масштабированием:
Маркеры
Чтобы узнать точные значения по графику, можно использовать маркеры из меню Графики –> Маркеры. Стиль линий маркеров можно изменять таким же способом, как и для обычных графиков:
Кривая «Столбцы»
Рассмотрим тип кривой «Столбцы». Для этого используем таблицу с данными – вкладка Матрицы/таблицы –> Вставить таблицу и в появившейся сетке выберите таблицу с 2 столбцами и 10 строками:
В местозаполнителях заголовка введите x и y. Числа заполните, как на рисунке:
Вставьте график XY. Улучшите вид графика, переместив легенды по осям и отформатировав значения меток. Чтобы поменять тип графика, выберите Графики –> Кривые –> Изменить тип –> Кривая «столбцы»:
Таблица данных в Mathcadцелесообразно использовать, если данных немного. Для большого числа данных лучше совместно использовать Mathcad и Excel – об этом мы поговорим в уроке 17.
Полярный график
Построим график спирали в полярных координатах:
Вставьте полярный график с помощью Графики –> Кривые –> Вставить график –> Полярный график. В местозаполнители введите данные, как на рисунке, и нажмите [Enter]:
В местозаполнители введите данные, как на рисунке, и нажмите [Enter]:
Параметрический график
Этот график окружности построен с использованием параметра t:
Графики в логарифмическом масштабе
Логарифмический масштаб часто используется в различных областях науки и техники. Построение графиков в логарифмическом масштабе доступно в Mathcad.
Построим график функции y=x2, но с использованием параметра:
Чтобы сделать ось X логарифмической, выберите легенду оси X и нажмите Графики –> Оси –> Логарифмический масштаб. Проделайте то же самое для оси Y. В логарифмическом масштабе эта функция представляет собой прямую линию:
Резюме
В этом уроке мы показали, как можно модифицировать двумерные графики.
- Чтобы изменить тип кривой, нажмите на его легенду по оси Y и выберите Графики –> Кривые –> Изменить тип.
- Чтобы добавить кривую:
- поместите курсор на легенду оси Y;
- нажмите Графики –> Кривые –> Добавить кривую.
- Чтобы изменить символы, цвет, стиль или толщину кривой, нажмите по легенде оси Y соответствующего графика и настройте график с помощью меню Графики –> Стиль.
- Чтобы промасштабировать график, разделите легенду соответствующей оси на коэффициент масштабирования.
- Линии маркеров (горизонтальные и вертикальные) доступны в меню Графики –> Маркеры. Можно добавить любое число линий маркеров или даже сформировать из них сетку. Маркеры можно изменять так же, как и обычные графики.
- Полярный график (зависимость радиуса от угла) можно вставить так же, как и график XY – через меню Графики –> Кривые –> Вставить график –> Полярный график.
- Изменить масштаб оси на логарифмический можно с помощью команды нажмите Графики –> Оси –> Логарифмический масштаб. Выполнить ее нужно для каждой оси в отдельности (если сделать это только для одной оси, получится полулогарифмический масштаб).
Другие интересные материалы
Особенности построения графических образов в MathCAD Текст научной статьи по специальности «Компьютерные и информационные науки»
Раздел I.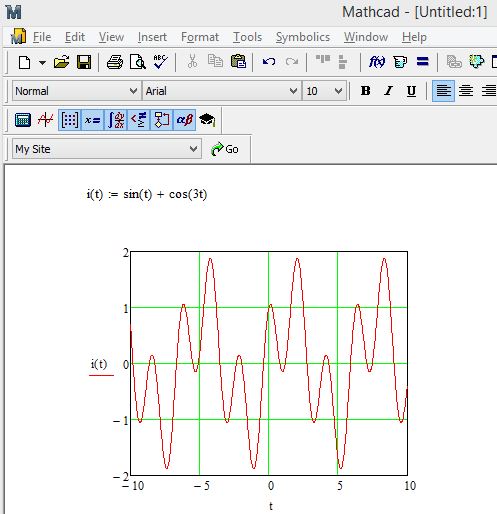 Алгебра и геометрия
Алгебра и геометрия
УДК 514.75/.77 ББК 22.151
А. В. Забеглов
ОСОБЕННОСТИ ПОСТРОЕНИЯ ГРАФИЧЕСКИХ ОБРАЗОВ В MATHCAD
Аннотация. В статье рассмотрены особенности построения графических образов в среде MathCAD. Отмечен ряд проблем, с которыми может столкнуться пользователь и пути их разрешения.
Ключевые слова: MathCAD, графики, неявные функции, метод Драгилева, точки разрыва.
A. V. Zabeglov
PECULIARITIES OF CONSTRUCTION OF GRAPHIC IMAGES IN MATHCAD
Abstract. The article considers peculiarities of graphic images construction in the MathCAD program. There is description of problems a user can face, and ways of their salvation.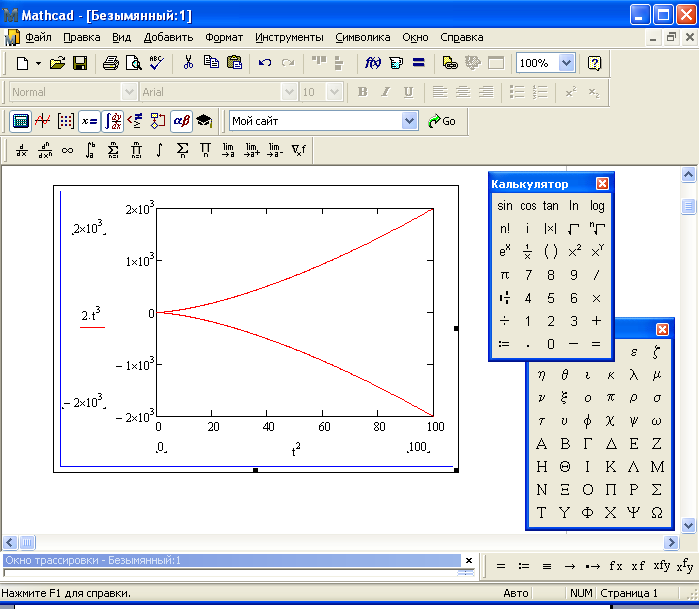
Key words: MathCAD, graphics, implicit functions, Dragilev method, breaking point.
В настоящее время широкое распространение получили пакеты математических программ (или математические системы), которые можно использовать для различных вычислений и построения графиков (Mathematica, Maple, Statistica, MathCAD, MathLAB и др.). В этих системах процесс вычислений автоматизирован, что позволяет экономить время и больше внимания уделять физическому смыслу получаемого результата. Выбор системы зависит от характера решаемых задач, от вкуса и практики. В данной статье речь пойдет о системе MathCAD — разработке фирмы MathSoft.
MathCAD — является достаточно мощным математическим пакетом, который позволяет пользователю решать огромное число самых разнообразных задач, с которыми тот может столкнуться. Одной из таких задач является графическое представление различных объектов, таких как кривые, поверхности, массивы данных и т. д. Эта задача имеет ряд особенностей на которые и хотелось бы обратить внимание.
д. Эта задача имеет ряд особенностей на которые и хотелось бы обратить внимание.
Первой особенностью является то, что в среде MathCAD нет графиков в математическом понимании этого термина. Визуальное представление графических образов происходит как отображение данных по точкам с интерполяцией. В этой связи механизм визуализации MathCAD значительно уступает таковому у Maple, где достаточно иметь только вид функции, чтобы построить график или поверхность любого уровня сложности. Данная особенность порождает ряд проблем, одной из которых является построение кривых и поверхностей, содержащих точки разрыва. В данном случае MathCAD может либо вообще не построить график (рис. 1), либо, если точка разрыва попадает между опорными точками, пропустить точку разрыва, сгладив ее (рис 2).
11 11
zl(Xy) := — + — z(x,y) :=
sin(x) sin(y) » cos(x) cos(y)
При построении графика функция представляется в виде набора точек и для построения графика перебирается определенное количество значений аргумента, для каждого из них вычисляется значение функции. При упрощенном способе построения, когда диапазон аргумента задается автоматически, по осям выбирается диапазон [-5, 5], а количество линий равно 20. Для того чтобы иметь возможность при построении графика управлять количеством точек, аргумент надо задавать
При упрощенном способе построения, когда диапазон аргумента задается автоматически, по осям выбирается диапазон [-5, 5], а количество линий равно 20. Для того чтобы иметь возможность при построении графика управлять количеством точек, аргумент надо задавать
Вестник ТГПИ
Естественные науки
как ранжированную переменную [2]. Зачастую приходится находить точки разрыва и строить график отдельно для каждых областей, что достаточно трудоемко для периодичных функций в знаменателе. Однако общего и простого решения данной проблемы не существует (рис 3).
Л Л Л Л
а := 1 к := .0 п := 0 иО := л-к—ul := л-к н—vO := л-п—vl := л-n н—
2.1
1 f cos(a-u)^
H(u,v) := — ш —
a ^cosCa-v) J
CI := CreateMesh(H,uO,ul,vO,vl)
a := lk := In := 1
C2:= CreateMesh (H,uO, и l,vO,vl)
к := 1 n := -1
C3 := CreateMesh(H,uO,иl,vO,vl) к := -1 n := -1
C4:= CreateMesh (H,uO, и l,vO,vl) к :=-ln := 1
C5 := CreateMesh(H,uO,иl,vO,vl)
Рис.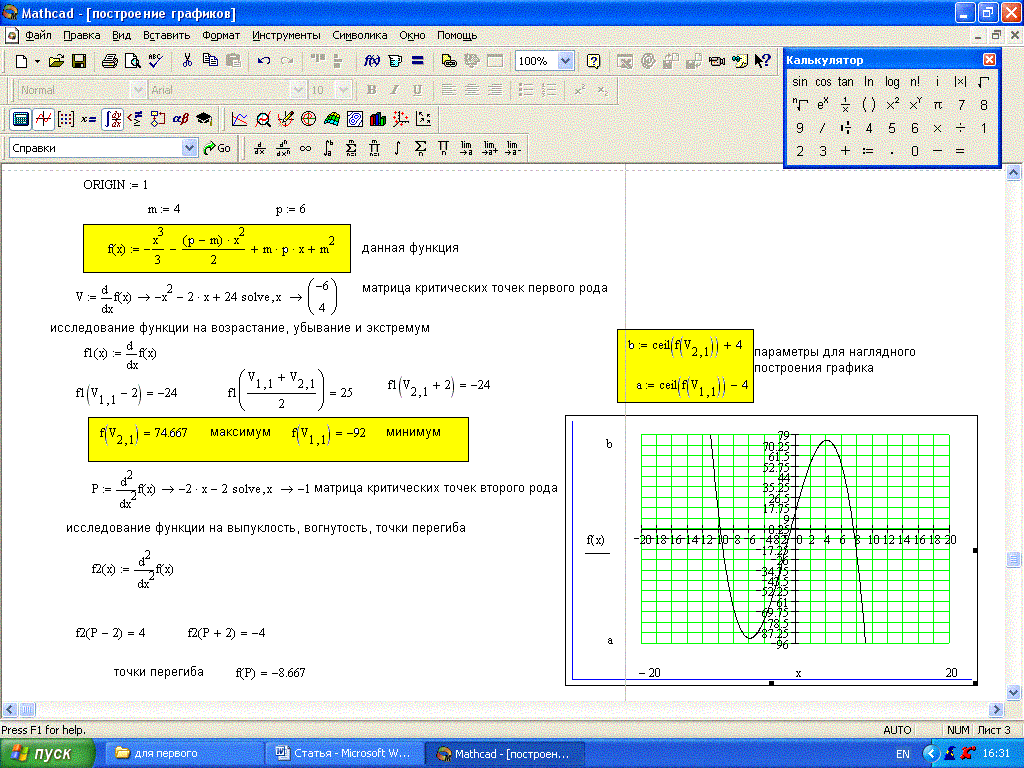 3
3
Второй особенностью системы является то, что в MathCAD невозможно встроенными средствами построить графики кривых и поверхностей заданных неявно. Это препятствие для кривых F (x, y)=0 можно обойти. Для этого строится поверхность с уравнением z=F (x, y), и форматируется с целью увеличения максимальной «разрешимости» графика (# of Grigs: 200) по обеим осям (QuickPlotData) и диапазона значений оси (Axes/Z-Axis). Измение типа графика с поверхности (Surface Plot) на контурный график (Contour Plot) дает возможность получить график искомой кривой в виде контурной линии [1] (рис. 4).
С графиками поверхностей F (x, y, z)=0 дело обстоит несколько сложнее. На сегодняшний день известны результаты по успешному построению в MathCAD неявных поверхностей методом Драгилева, который основан на возможности замены исходного уравнения дифференциальным уравнением и какой-нибудь точкой, удовлетворяющей исходному неявному уравнению.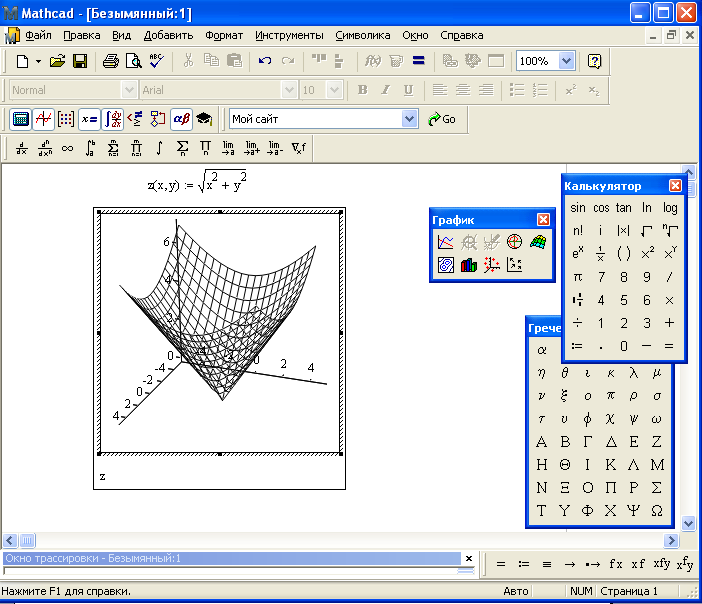 Этот приём позволяет принципиально сократить время расчёта поверхностей и расширить возможности построения. Еще одной возможностью построения неявных поверхностей послужила программная реализация метода «марширующих кубов», названная implicitplot3d [4].
Этот приём позволяет принципиально сократить время расчёта поверхностей и расширить возможности построения. Еще одной возможностью построения неявных поверхностей послужила программная реализация метода «марширующих кубов», названная implicitplot3d [4].
2.1 2.1 2.1
Cl, С2.СЗ.С4.С5
Рис. 4
Один из многочисленных примеров поверхностей построенных при помощи этой функции приведен на рис. 5 [4].
2 3 4 i~24 (х ,У := х Н- у + z — 1
xrnin := —4 ymin := —4 zmm. := —3 (nx ny nz) := (31 31 31 )
xmax := 4 ymax :— 1 zmax := 3
T
grids := (nx ny nz)
( ( 1 ^ num2str ceil — colsi’ i =
1 ‘ • v -:l1 1 1
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Гурский, Д. MаthCAD для студентов и школьников. Популярный самоучитель / Д. Гурский, Е. Турбина. — СПб.: Питер, 2005. — 400 с.
Гурский, Д. MаthCAD для студентов и школьников. Популярный самоучитель / Д. Гурский, Е. Турбина. — СПб.: Питер, 2005. — 400 с.
2. Дьяконов, В. П. Mathcad 2001. Учебный курс / В. П. Дьяконов. — СПб.: Питер. — 2001. — 624 с.
3. Компьютерная геометрия: учеб. пособие / Н. Н. Голованов и др. — М.: Академия, 2006. — 512 с.
4. Режим доступа: http//:www.exponenta.m.
УДК 512.5 ББК 22
В. М. Кривенко
ОБ ОДНОМ ВНУТРЕННЕМ АССОЦИАТИВНОМ ПРОДОЛЖЕНИИ
ЧАСТИЧНОГО МУЛЬТИПЛИКАТИВНОГО МАТРИЧНОГО ГРУППОИДА
Аннотация. В работах известного отечественного математика Е. С. Ляпина одним из центральных является вопрос о существовании ассоциативных продолжений частичных матричных группоидов. В настоящей работе установлена возможность внутреннего ассоциативного продолжения частичного мультипликативного матричного группоида.
В настоящей работе установлена возможность внутреннего ассоциативного продолжения частичного мультипликативного матричного группоида.
Ключевые слова: умножение матриц, полугруппа, продолжение.
V. M. Krivenko
ABOUT ONE INTERNAL ASSOCIATIVE EXTENSIONS OF PARTIAL MULTIPLICATE MATRICES GROUPOID
Absrtact. In works of known domestic mathematician E. S. Ljapina on the theory partial of groupoids one of central is the question on existence of associative extensions partial of groupoids. In the present work the possibility of internal associative extension of partial matrices groupoid is established.
Key words: multiplication of matrices, semigroup, extension.
1°.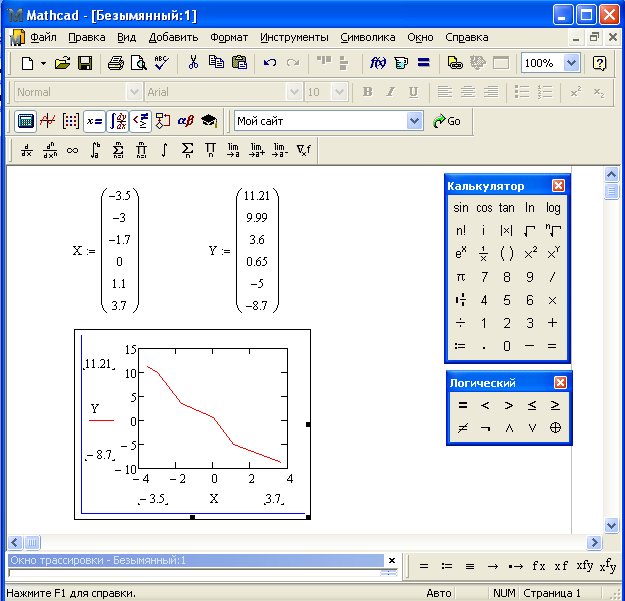 Пусть (S;) — произвольный частичный группоид [1]. В соответствии с [1] полугруппа (5;*) называется внутренним полугрупповым продолжением частичного группоида (S;), если
Пусть (S;) — произвольный частичный группоид [1]. В соответствии с [1] полугруппа (5;*) называется внутренним полугрупповым продолжением частичного группоида (S;), если
(Vx, у е S) (если х. у # 0, то х.у = х * v).
Рис. 5
ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ В СРЕДЕ MATHCAD
1 РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВ Богатова, КВ Бухенский, ИП Карасев, ГС Лукьянова ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ В СРЕДЕ MATHCAD Практикум Рязань
2 Предисловие Общий курс математики высших учебных заведений включает в себя раздел дифференциального исчисления функций одной и нескольких переменных Настоящая методическая разработка содержит краткий теоретический материал по данным темам, теоретические примеры с решениями, задания, выполненные в среде Mahca, и варианты типовых расчетов для самостоятельного решения Практикум предназначен для студентов первого курса, изучающих основы дифференциального исчисления Структура пособия позволяет использовать его как на практических занятиях, так и для самостоятельного изучения темы Разобранные примеры задач включают в себя пояснения ссылки на теоретические основы решения и последовательности операторов в среде Mahca, благодаря чему преподавателю и студентам легко контролировать вычислительные навыки студентов, анализировать появляющиеся ошибки и максимально быстро исправлять их Задания для самостоятельной работы запланированы в качестве домашних контрольных работ
3 Функции одной переменной Исследование функций с помощью первой производной Производная находит многочисленные применения к исследованию функций и построению графиков функций Рассмотрим возможные приложения производной к решению вопроса о монотонности функции на некотором промежутке Теорема (необходимые и достаточные условия монотонности функции) Если функция = f () определена и непрерывна в промежутке X и внутри него имеет конечную производную, то необходимым и достаточным условием неубывания (невозрастания) функции = f () в X является f ( ) ( f ( ) ) Определение Точка называется точкой строгого локального максимума (минимума) функции f (), если такая δ окрестность, что U (, δ ) f ( ) < ( f ( ) > ) Точки локального максимума и локального минимума функции f () называются точками локального экстремума Теорема (необходимое условие локального экстремума) Если функция f () дифференцируема в точке и в ней имеет локальный экстремум, то f ( ) = В точках локального экстремума касательная параллельна оси O Определение Точки,, K, в которых f ( ) =, называются стационарными точками, или точками возможного экстремума П р и м е р Пусть задана функция f ( ) = f ( ) =, =, = стационарная точка, но не является точкой локального экстремума Теорема (-е достаточное условие локального экстремума) Пусть функция f () дифференцируема в некоторой δ окрестности стационарной точки Тогда, если f ( ) >, ( f ( ) < ) при ( δ, ), а f ( ) < ( f ( ) > ) при (, +δ ), то в точке функция имеет локальный максимум (локальный минимум) Если f () во всей δ -окрестности точки имеет один и тот же знак, то в точке локального экстремума нет П р и м е р Найти точки экстремума функции f ( ) = ( ) 5 f ( ) =, Решение ( ) 5 f ‘( ) = 5( ) = = стационарная точка, не являющаяся точкой экстремума, так как f ‘( ) f Точек экстремума нет З а м е ч а н и е В точке экстремума производная может не существовать или обращаться в бесконечность (критическая точка!), но обязательно меняет знак в δ окрестности этой точки В этом случае
4 экстремум называют острым (в противоположность гладкому экстремуму, который имеет функция с непрерывной производной) Примером может служить функция =, у которой в точке = производная не существует, но f ( ) <, а f ( + ) > Теорема (-е достаточное условие экстремума) Пусть функция f () в стационарной точке дважды непрерывно дифференцируема Тогда функция f () имеет в точке максимум, если f »( ) < и минимум, если f »( ) > З а д а н и е Построить график функции f ( ) = * ( + ) 8 с помощью производной первого порядка Решение Для функции f () ( + ) 8 найдем производную первого порядка: p () f () + ( ) Отыскиваем критические точки решения системы уравнений Given p () + 8 p () Fin() f( ) = f( ) = Определяем: есть ли экстремумы среди точек — и — с помощью графика производной функции 5 p ( ) При переходе через точку = производная у меняет знак с на «+», значит, = точка минимума функции При переходе через точку = производная у меняет знак с «+» на «-», значит, = точка максимума функции Функция убывает на промежутках (, ) и [, + ), возрастает на промежутке (, ]
5 5 Строим график функции f( ) Выпуклость и вогнутость функций Пусть функция f () дифференцируема на интервале ( a, b) Тогда существует касательная к графику функции f () в любой точке этого интервала Определение График дифференцируемой функции f () называется выпуклым (вогнутым) на интервале ( a, b), если он расположен на ( a, b) ниже (выше) касательной, проведенной в любой его точке из ( a, b) (рис ) ( ) f( ) 5 6 Рис Теорема 5 (достаточный признак выпуклости, вогнутости) Если функция = f () имеет на интервале ( a, b) вторую производную и f ( ) < ( f ( ) > ) во всех точках интервала ( a, b), то график функции f () выпуклый (вогнутый) Определение Точка M (, f ( )) называется точкой перегиба графика непрерывной функции = f (), если точка M разделяет промежутки, в которых график выпуклый и вогнутый
6 6 Теорема 6 (необходимое условие точки перегиба) Пусть график функции = f () имеет перегиб в точке M (, f ( )) и пусть функция = f ( ) имеет в окрестности точки непрерывную вторую производную Тогда f ( ) = Теорема 7 (достаточное условие точки перегиба) Пусть функция = f () имеет вторую производную в окрестности точки Если при переходе через точку f ( ) меняет свой знак, то — точка перегиба П р и м е р Найти точки перегиба для функции f ( ) = Решение f ‘( ) = 6, f »( ) = 6 6 = 6( ), f ( ) = при = f ( ) = 6 <, f ( ) = 6 > Следовательно, точка = точка перегиба графика функции f ( ) = Асимптоты графика функции Определение 5 Прямая называется асимптотой графика функции = f (), если расстояние от точки, принадлежащей графику до этой прямой, стремится к нулю при неограниченном удалении точки по графику функции от начала координат (рис ) ( ) f() Рис Существует три типа асимптот: вертикальная, горизонтальная и наклонная Определение 6 Прямая = a называется вертикальной асимптотой графика функции = f (), если хотя бы один из односторонних пределов функции f ( ) или f ( ) равен + или (рис ) lim a lim a +
7 7 6 ( ) 6 Рис Определение 7 Прямая = k + b называется наклонной асимптотой графика функции = f () при + (или ), если lim ( f ( ) ( k + b)) = ( + ) Заметим, что при k = наклонная асимптота часто называется горизонтальной Теорема 8 Прямая = k + b является наклонной асимптотой к графику f ( ) функции = f (), если существуют пределы k = lim, b = lim + [ f ( ) k] + Если хотя бы один из этих двух пределов не существует или k + ( ), то кривая наклонных асимптот не имеет З а д а н и е Найти асимптоты и построить график функции 9 f ( ) = Решение Данная функция является четной, так как f () 9 f( ) 9 f () f( ) Найдем точки, «подозрительные» на вертикальные асимптоты Given Fin() Область определения функции — (, ) (, + ) lim + 9
8 8 Следовательно, прямые асимптотами Так как = и = являются вертикальными f () k lim 5 b lim ( f () + 5) то = 5 является наклонной асимптотой на +, а = 5 — наклонная асимптота на Найдем точки пересечения с осью O Given Fin() f () Далее строим график функции, f () Схема исследования функции Найти область определения функции, ее точки разрыва Найти точки пересечения с осями Выяснить является ли функция четной, нечетной или общего вида Найти интервалы монотонности и точки экстремума функции 5 Найти интервалы выпуклости и вогнутости графика функции и точки перегиба 6 Найти асимптоты графика функции 7 На основании полученных результатов построить график функции
9 9 З а д а н и е Провести полное исследование функции f ( ) = ( + ) ( + ) и построить ее график Решение Исследование выполним по предложенной схеме f () ( + ) ( + ) Область определения функции: õ (, + ) Найдем точки пересечения графика функции с осями координат Given Fin() f () f ( ) = 587 Проверим, является ли функция четной, нечетной или общего вида f( ) ( ) ( ) f () f( ) Функция общего вида Асимптоты графика функции (вертикальные, наклонные, горизонтальные) Вертикальных асимптот нет, так как нет точек разрыва k lim f () b lim Прямая = является горизонтальной асимптотой на + и 5 Найдем промежутки монотонности (возрастания и убывания) функции и точки экстремума Находим производную первого порядка f () p () f () p () + ( + ) + ( + ) Given p () Fin () Производная не обращается в нуль, но не существует в точках = = и
10 5 6 p( ) 5 5 При переходе через точку = производная у меняет знак с на «+», значит, = точка минимума функции При переходе через точку = производная у меняет знак с «+» на «-», значит, = точка максимума функции f( ) = f( ) = Итак, функция возрастает на промежутках (, ) и (, + ), убывает на промежутке (, ) 6 Найдем промежутки выпуклости и вогнутости графика функции и точки перегиба Для этого вычислим производную второго порядка и найдем критические точки g() f () g () ( + ) ( + ) ( + ) 5 9 ( + ) + ( + ) 5 9 ( + ) g () g( 5) = Получили, что = f( 5) =, = и = 5 7 Строим график данной функции — точки перегиба функции
Графики в маткад прайм
Категории
- 3ds Max (10)
- AutoCAD (9)
- Mathcad (7)
- Microsoft Excel (10)
- Microsoft Word (18)
- Mudbox (3)
- PHP (4)
- Windows (24)
- Главная (1)
- Железо (13)
- Компас 3D (3)
- Программы (19)
- Прочее (17)
Построение графиков в MathCad
При решении задач в MathCad часто возникает необходимость построить график, будь то график функции или график по каким либо расчетным данным.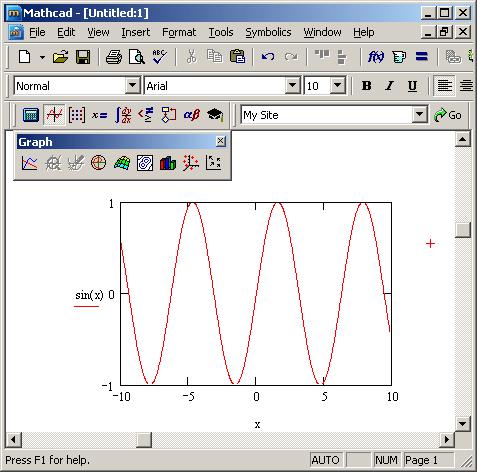 В этой статье мы разберем как строятся графики в MathCad. В этой статье мы не будем рассматривать само решение задач, его Вы можете найти в других статьях, ссылка в конце статьи.
В этой статье мы разберем как строятся графики в MathCad. В этой статье мы не будем рассматривать само решение задач, его Вы можете найти в других статьях, ссылка в конце статьи.
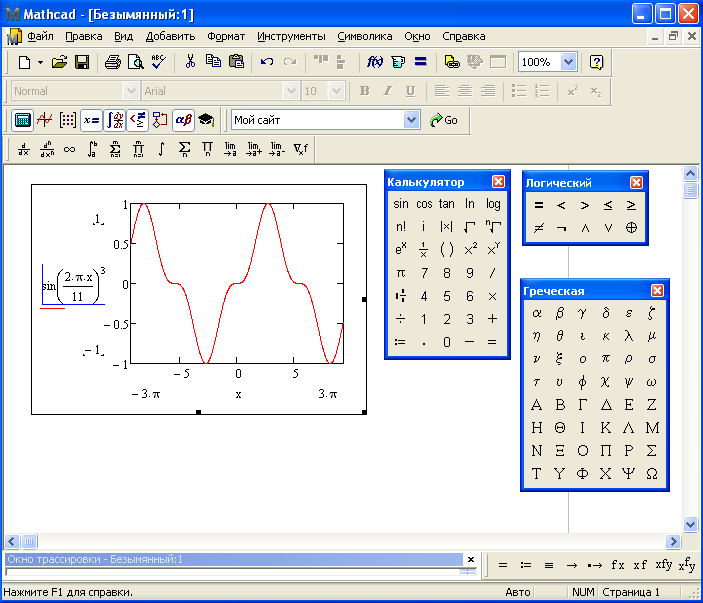
1.1. Рассмотрим построение на примере функции sin, для этого введем в Маткад следующее (думаю как пользоваться инструментами ввода информации подробно рассматривать не надо, а если вдруг возникнут какие-либо трудности с вводом советую почитать статью Расчаты в MathCad ):
Не забываем что необходимо ставить не знак «равно» а именно знак «определения».
1.2. Теперь нам нужно создать сам график, для этого нажимаем на пункт меню Добавить, выбираем строку Графики, и в появившемся списке выбираем X—Y график
1.3. Теперь, в появившемся поле графика заполняем наименование осей (в нашем варианте названиями будут f(x) и х)
После ввоза названий полей кликаем в любой области вне поля графика
В итоге мы получаем готовый график функции синуса:
Построение графика в MathCad по данным2.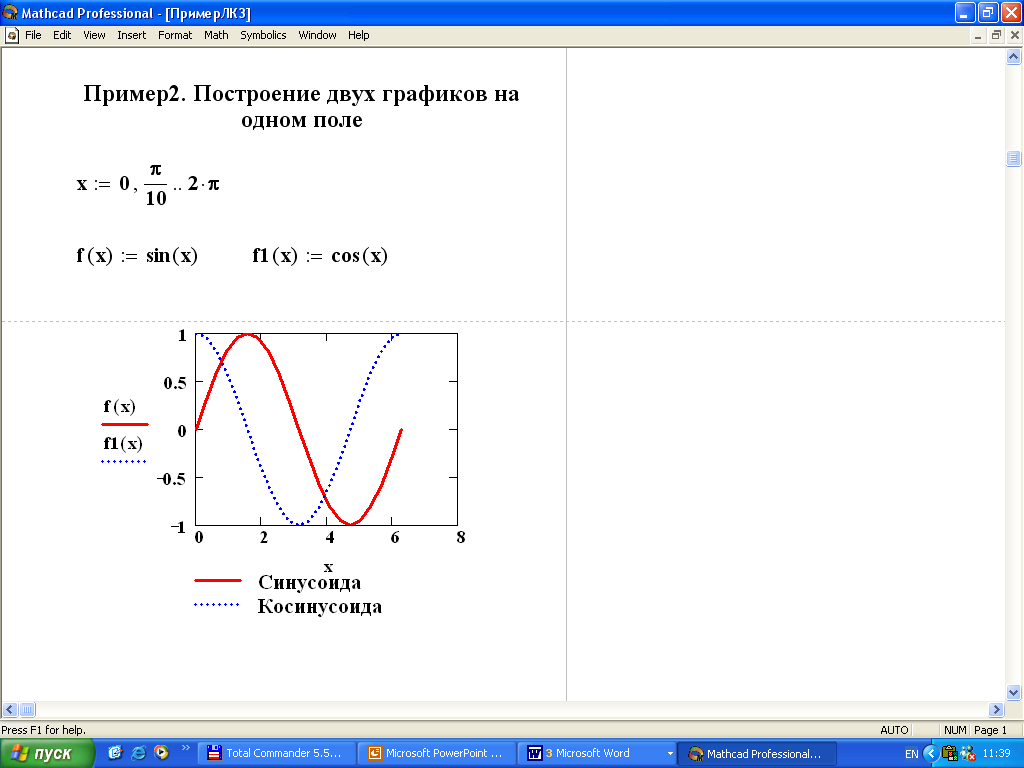 1. Для начала введем данные графика, для этого вводим определитель (у меня это w и r) и добавляем матрицу нужным размером (в моем случае 6х1, это 6 строк, 1 столбик) и вводим в нее свои данные для графика. Вот что получилось у меня:
1. Для начала введем данные графика, для этого вводим определитель (у меня это w и r) и добавляем матрицу нужным размером (в моем случае 6х1, это 6 строк, 1 столбик) и вводим в нее свои данные для графика. Вот что получилось у меня:
2.2. Теперь повторяем действия указанные в пункте 1.2. этой статьи (т.е. добавляем график)
2.3. Как и в пункте 1.3. этой статьи заполняем название осей, только на этот раз у нас будут определители наших данных
2.4. При необходимости совместить два графика на одном делаем следующее: добавляем еще один блок данных, ставим курсор после определителя w в графике и нажимаем поставить запятую (напоминаю, что запятая на русской раскладке и на английской раскладке это разные клавиши, и так как мы работаем в Маткаде используя английскую раскладку нам нужна запятая именно английской раскладки), после этого вводим определитель во вторую (появившеюся) строку на нашем графике.
Теперь у нас получилось два пересекающихся графика (конечно же то как он будет выглядеть зависит от данных)
Форматирование графика в MathCadСозданный график по умолчанию очень бледный и Вам наверное захочется сделать его немого поярче.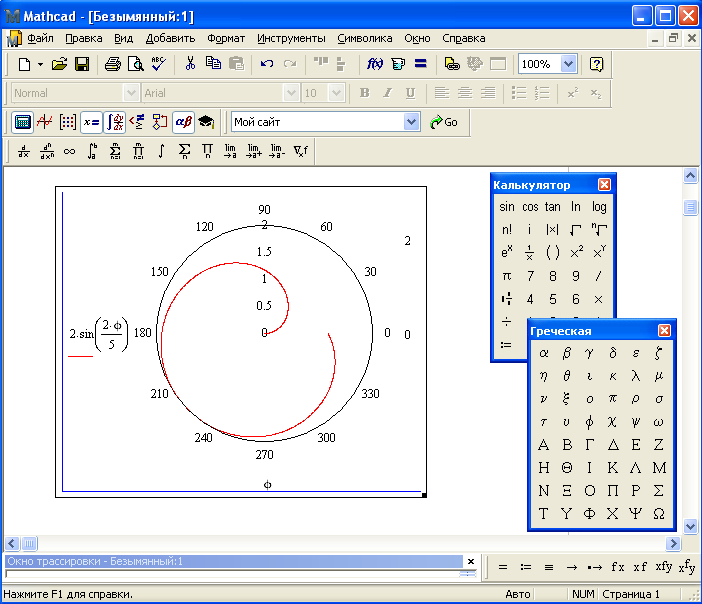
3.1. На графике нажимаем ПКМ (правой клавишей мыши) и в контекстном меню выбираем пункт Формат…
В открывшемся диалоговом окне переходим на вкладку Графики
Тут мы видим табличку строка трассировка 1 соответствует первой кривой нашего графика, трассировка 2 соответственно второй. Столбик Линия соответствует типу линии на нашем графике (сплошная, прерывистая, точка-тире и т.п.). Столбик Линия Вес соответствует толщине нашей линии. И Цвет соответственно цвету. Я в своем примере изменю только толщину линии, и по второму графику тип линии с точек на пунктир для этого в двух верхних строках столбика Линия Вес поставлю цифру 2 и в столбике Линия поменяю тип линии, после чего нажму Применить
Вот что получилось:
Я думаю не надо объяснять как изменять размер графика, если это необходимо.
Познакомьтесь с новыми возможностями последней версии PTC Mathcad
Новые возможности PTC Mathcad Prime 6.0
Визуализация ваших инженерных расчетов стала удобнее, чем когда-либо. Версия PTC Mathcad Prime 6.0 позволяет пользователям выполнять проверку орфографии в заметках на разных языках, включать гиперссылки, настраивать поля и нижние колонтитулы, в ней представлен новый символьный механизм и многое другое.
Новые возможности
- Настройка полей, включая верхние и нижние колонтитулы
- Проверка орфографии — поддержка различных языков
- Добавление гиперссылок непосредственно в документы
- Расширение функциональности, включение расширенные настройки печати и обновления функций поиска и замены
- Опции построения 2D-диаграмм, например экспорт графика в файл растрового изображения.
- Новая подсистема символьных вычислений.
Новый символьный механизм — что это означает для вас
В версии PTC Mathcad Prime 6.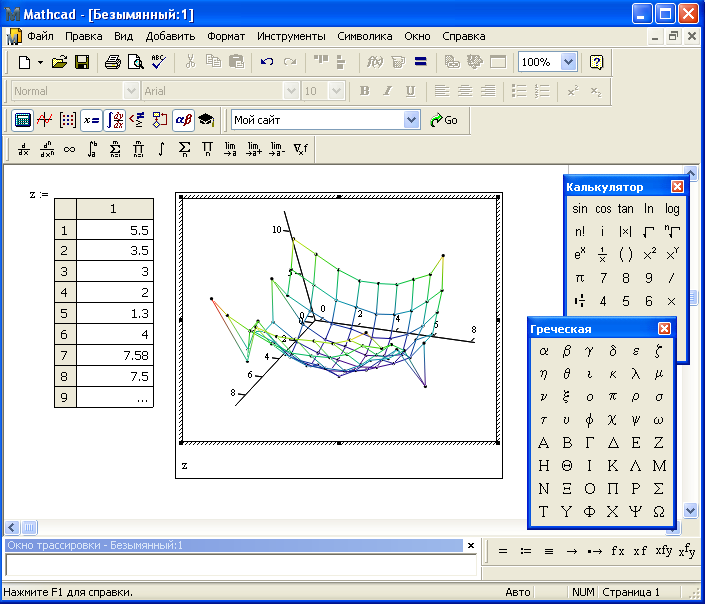 0.0.0 появился новый символьный механизм, который будет использоваться по умолчанию для выполнения символьных вычислений в вашем документе. Этот новый символьный механизм расширяет возможности управления символьными вычислениями, а также повышает гибкость в плане усовершенствований и оптимизации. Вскоре вы увидите различия в отображении символьных результатов новым символьным механизмом. Не беспокойтесь — в паре следующих версий можно переключиться обратно на старый символьный механизм, если различия будут создавать для вас проблемы, и сообщить нам о своих выводах. Мы планируем продолжить совершенствовать новый символьный механизм, чтобы обеспечить вам необходимую функциональность.
0.0.0 появился новый символьный механизм, который будет использоваться по умолчанию для выполнения символьных вычислений в вашем документе. Этот новый символьный механизм расширяет возможности управления символьными вычислениями, а также повышает гибкость в плане усовершенствований и оптимизации. Вскоре вы увидите различия в отображении символьных результатов новым символьным механизмом. Не беспокойтесь — в паре следующих версий можно переключиться обратно на старый символьный механизм, если различия будут создавать для вас проблемы, и сообщить нам о своих выводах. Мы планируем продолжить совершенствовать новый символьный механизм, чтобы обеспечить вам необходимую функциональность.
Почему стоит выбрать PTC Mathcad?
- Защищенная передача конструкторского замысла и проектных знаний.
- Интуитивно понятное построение расчетов с использованием стандартного математического представления.
- Создание документов профессионального уровня с использованием активных математических формул, графиков, текста и изображений.
- Адаптация стандартных расчетов.
- Повышение производительности за счет полной поддержки единиц измерения на всех этапах расчетов.
- Ускорение обучения и внедрения за счет мгновенного доступа к электронным обучающим материалам.
Узнайте о других новейших усовершенствованиях PTC Mathcad по сравнению с предыдущими версиями
Усовершенствуйте создание 2D-графиков
В версии PTC Mathcad Prime 6.0 предложены расширенные функции создания 2D-графиков, теперь обеспечивающие полную индивидуальную настройку вида и работы двухмерных диаграмм. Ниже указаны некоторые расширенные функции форматирования.
- Полное форматирование осей
- Заголовки и условные обозначения
- Вторая ось Y
- Сетки
- Индивидуально настраиваемый вид и работа графиков
В этом уроке мы рассмотрим варианты графиков, доступных в PTC Mathcad Prime 3.0.
Типы графиков
Чтобы изменить тип графика, нажмите на него, затем выберите на вкладке Графики –> Кривые –> Изменить тип. Ниже представлены рисунки четырех типов графиков для функции:
Ниже представлены рисунки четырех типов графиков для функции:
В списке есть еще некоторые типы осей – некоторые из них мы будем использовать позднее.
Несколько графиков на одних осях
Чтобы добавить кривую на оси, поместите курсор после обозначения легенды оси Y графика и нажмите Графики –> Кривые –> Добавить кривую. Появится еще один местозаполнитель для оси Y:
Вы можете добавить больше графиков с помощью этой же команды.
С помощью вывода нескольких графиков на одни оси мы посмотрим различные настройки из меню Графики –> Стили. Для этой цели мы создадим оси с пятью различными прямыми линиями. Каждая линия содержит 11 точек:
Ниже этих выражений вставьте график XY, затем добавьте четыре легенды для оси Y. В местозаполнителе для оси Xвведите x[iи нажмите [Enter] – для всех пяти графиков будет использоваться одна легенда по оси X. В последний местозаполнитель для оси Y введите y[0,i и [Enter]:
Выше следует ввести y[1,i, еще выше — y[2,i и т.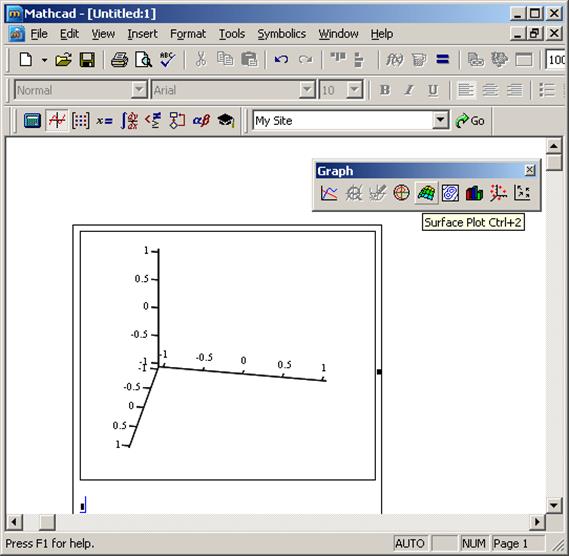 д. После завершения Вы увидите пять прямых линий. Свойства каждой из них можно изменить, выбрав легенды оси Y соответствующего графика и выбрав необходимые настройки на меню Графики –> Стили.
д. После завершения Вы увидите пять прямых линий. Свойства каждой из них можно изменить, выбрав легенды оси Y соответствующего графика и выбрав необходимые настройки на меню Графики –> Стили.
Ниже представлены получившиеся графики. Использовались различные настройки для толщины, цвета, стиля линий и символов:
Метки и их значения мы убрали с помощью меню Графики –> Оси.
Масштабирование
На графике с двумя кривыми диапазон для одной из них может быть не очень удачным для другой, например, для графиков квадрата и куба x.
Чтобы исправить это, разделите функцию куба на 5. Это называется масштабированием:
Маркеры
Чтобы узнать точные значения по графику, можно использовать маркеры из меню Графики –> Маркеры. Стиль линий маркеров можно изменять таким же способом, как и для обычных графиков:
Кривая «Столбцы»
Рассмотрим тип кривой «Столбцы». Для этого используем таблицу с данными – вкладка Матрицы/таблицы –> Вставить таблицу и в появившейся сетке выберите таблицу с 2 столбцами и 10 строками:
В местозаполнителях заголовка введите x и y. Числа заполните, как на рисунке:
Числа заполните, как на рисунке:
Вставьте график XY. Улучшите вид графика, переместив легенды по осям и отформатировав значения меток. Чтобы поменять тип графика, выберите Графики –> Кривые –> Изменить тип –> Кривая «столбцы»:
Таблица данных в Mathcadцелесообразно использовать, если данных немного. Для большого числа данных лучше совместно использовать Mathcad и Excel – об этом мы поговорим в уроке 17.
Полярный график
Построим график спирали в полярных координатах:
Вставьте полярный график с помощью Графики –> Кривые –> Вставить график –> Полярный график. В местозаполнители введите данные, как на рисунке, и нажмите [Enter]:
Параметрический график
Этот график окружности построен с использованием параметра t:
Графики в логарифмическом масштабе
Логарифмический масштаб часто используется в различных областях науки и техники. Построение графиков в логарифмическом масштабе доступно в Mathcad.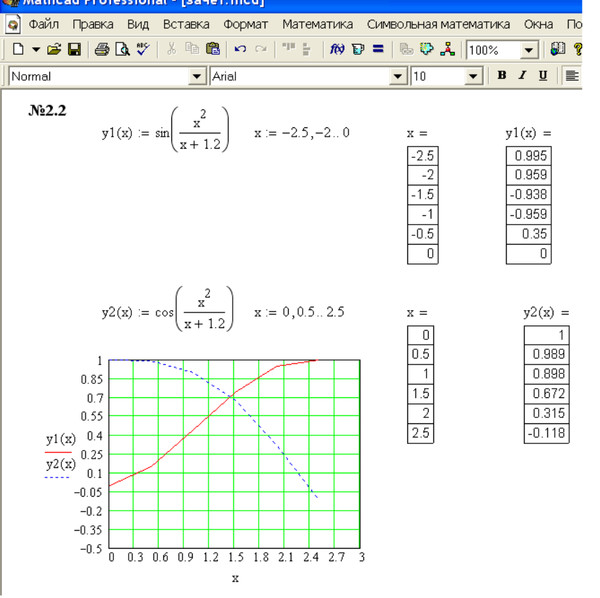
Построим график функции y=x 2 , но с использованием параметра:
Чтобы сделать ось X логарифмической, выберите легенду оси X и нажмите Графики –> Оси –> Логарифмический масштаб. Проделайте то же самое для оси Y. В логарифмическом масштабе эта функция представляет собой прямую линию:
Резюме
В этом уроке мы показали, как можно модифицировать двумерные графики.
- Чтобы изменить тип кривой, нажмите на его легенду по оси Y и выберите Графики –> Кривые –> Изменить тип.
- Чтобы добавить кривую:
- поместите курсор на легенду оси Y;
- нажмите Графики –> Кривые –> Добавить кривую.
- Чтобы изменить символы, цвет, стиль или толщину кривой, нажмите по легенде оси Y соответствующего графика и настройте график с помощью меню Графики –> Стиль.
- Чтобы промасштабировать график, разделите легенду соответствующей оси на коэффициент масштабирования.
- Линии маркеров (горизонтальные и вертикальные) доступны в меню Графики –> Маркеры.
 Можно добавить любое число линий маркеров или даже сформировать из них сетку. Маркеры можно изменять так же, как и обычные графики.
Можно добавить любое число линий маркеров или даже сформировать из них сетку. Маркеры можно изменять так же, как и обычные графики. - Полярный график (зависимость радиуса от угла) можно вставить так же, как и график XY – через меню Графики –> Кривые –> Вставить график –> Полярный график.
- Изменить масштаб оси на логарифмический можно с помощью команды нажмите Графики –> Оси –> Логарифмический масштаб. Выполнить ее нужно для каждой оси в отдельности (если сделать это только для одной оси, получится полулогарифмический масштаб).
НОУ ИНТУИТ | Лекция | Многомерные вычисления в Mathcad
Аннотация: Цель работы: знакомство с правилами организации вложенных циклов, многомерных вычислений в программе Mathcad. Построение трехмерных графиков в Mathcad.
Подготовка к работе
По указанной литературе изучить приёмы работы с вывод многомерных данных в табличной форме, построение объемной графики, контурной графики в программе Mathcad.
Контрольные вопросы
- Организация вложенных циклов.
- Правила задания многомерных функций.
- Вывод многомерных результатов в форме таблицы.
- Трехмерная графика с функциональной окраской раскраской.
- Назначение команды Surface Plot.
- Для чего используется функция CreateMesh?
- Как построить фигуру с помощью вращения во круг оси?
Задание к работе
- Построить график поверхности в системе Matcard.
Исходные данные в Таблице 8.1.
Построение поверхностей по матрице аппликат их точек.Таблица 8.1. № Функция № Функция 1 z(x,y)=3cos(x*y) 2 z(x,y)=x2*y 3 z(x,y)=sin(x*y) 4 z(x,y)=5cos(x*y) 5 z(x,y)=tg(x*y) 6 z(x,y)=2x+y2  Поскольку элементы матрицы М – переменные с целочисленными индексами, то перед созданием матрицы требуется задать индексы в виде ранжированных переменных с целочисленными значениями, а затем уже из них формировать сетку значений x и y – координат для аппликат z(x,y). Значения x и y при этом обычно должны быть вещественными числами, нередко как положительными, так и отрицательными. После выполнения указанных выше определений вводится шаблон графика (команда Surface Plot). ( Рисунок 8.1)
Поскольку элементы матрицы М – переменные с целочисленными индексами, то перед созданием матрицы требуется задать индексы в виде ранжированных переменных с целочисленными значениями, а затем уже из них формировать сетку значений x и y – координат для аппликат z(x,y). Значения x и y при этом обычно должны быть вещественными числами, нередко как положительными, так и отрицательными. После выполнения указанных выше определений вводится шаблон графика (команда Surface Plot). ( Рисунок 8.1)
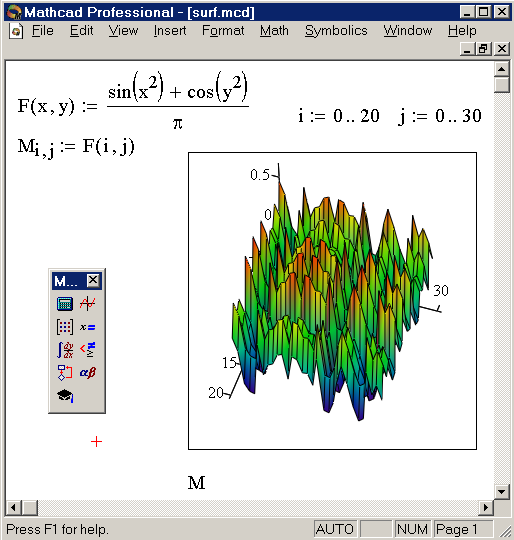
Рис. 8.1. Построение поверхности без удаления невидимых линий - Построить график поверхности в системе Matcard отформатировав его, применив алгоритм функциональной окраски и удаление невидимых линий.
На рисунке 8.2 показано, как отформатировать график, применение алгоритма функциональной окраски поверхности и удаление невидимых линий.
Рис. 8.2.
8.2. - Построить трехмерный график в системе Matcard
В программе Mathcad есть возможность построения трехмерных графиков – без задания матриц аппликат поверхностей. Единственным недостатком такого упрощенного метода построения поверхностей является неопределенность в масштабировании, поэтому графики требуют форматирования.
Рис. 8.3. Построение графика поверхности без задания матрицы - Построение графика поверхности без задания матрицы
Варианты задания в Таблице 8.2, как построить данный график показано на рисунке 8.4.
Таблица 8.2. № Функция 1 H(u,v)=3(u2*v) 2 H(u,v)=3sin(u*v) 3 H(u,v)=7cos(u*v) 4 H(u,v)=cos(u*v) 5 H(u,v)=tg(u*v) 6 H(u,v)=sin (u*v)
Рис.
 8.4. Пример построения графика поверхности с применением функции CreateMesh
8.4. Пример построения графика поверхности с применением функции CreateMeshЕще один пример применения функции CreateMesh – построение объемной фигуры, которая получается вращением кривой, заданной функцией f(x), вокруг оси X или Y.
Исходные данные в таблице 8.3.
| № | Функции | № | Функции |
|---|---|---|---|
| 1 |
| 4 |
|
| 2 |
| 5 |
|
| 3 |
|
intuit.ru/2010/edi»>На рисунке 8.5 показан пример решения данной задачи.
Рис. 8.5. Фигура полученная вращением кривой.
Презентация «Графика в системе MathCAD»
Презентация на тему: Графика в системе MathCADСкачать эту презентацию
Скачать эту презентацию
№ слайда 1 Описание слайда:Графика в системе MathCAD Лекция 5. Контрольные вопросы Перечислите хотя бы семь типов задач, которые позволяет решать пакет программ MathCAD. Различает ли MathCAD строчные и прописные буквы в именах переменных? Можно ли использовать в среде MathCAD в именах переменных русские символы? Перечислите основные возможности системы MathCAD Какие встроенные функции MathCAD Вы знаете? Каким образом «заставить» MathCAD выполнять нумерацию строк и столбцов матриц с единицы? Перечислите известные Вам матричные операторы в Mathcad? Почему система MathCAD считается универсальной массовой математической системой? Что входит в интерфейс пользователя MathCAD. Можно ли сначала набрать формулу, а затем ниже или правее этой формулы присвоить значения входящим в нее переменным?
Можно ли сначала набрать формулу, а затем ниже или правее этой формулы присвоить значения входящим в нее переменным?
Контрольные вопросы Перечислите хотя бы семь типов задач, которые позволяет решать пакет программ MathCAD. Различает ли MathCAD строчные и прописные буквы в именах переменных? Можно ли использовать в среде MathCAD в именах переменных русские символы? Перечислите основные возможности системы MathCAD Какие встроенные функции MathCAD Вы знаете? Каким образом «заставить» MathCAD выполнять нумерацию строк и столбцов матриц с единицы? Перечислите известные Вам матричные операторы в Mathcad? Почему система MathCAD считается универсальной массовой математической системой? Что входит в интерфейс пользователя MathCAD. Можно ли сначала набрать формулу, а затем ниже или правее этой формулы присвоить значения входящим в нее переменным?
№ слайда 3 Описание слайда:MathCAD позволяет легко строить двух- и трехмерные гистограммы, двухмерные графики в декартовых и полярных координатах, трехмерные графики поверхностей, линии уровня поверхностей, изображения векторных полей, пространственные кривые.
Существует три способа построения графиков в системе MathCAD: позиция Главного меню Вставка (Insert), выбрать команду График (Graph) и в раскрывающемся списке — тип графика; выбрать тип графика на наборной панели График (Graph), которая включается кнопкой на панели Math; воспользоваться быстрыми клавишами ( они предусмотрены не для всех типов графиков).
№ слайда 5 Описание слайда:X-Y Plot (X-Y Зависимость) клавиша [@] Служит доля построения графика функции y=f(x) в виде связанных друг с другом пар координат (xi,yi) при заданном промежутке изменения для i. Polar Plot (Полярные координаты)клавиши [Ctrl+7] Служит для построения графика функции r(q), заданной в полярных координатах, где полярный радиус r зависит от полярного угла q. Surface Plot (Поверхности) клавиши [Ctrl+2] Служит для представления функции z=f(x,y) в виде поверхности в трехмерном пространстве. При этом должны быть заданы векторы значений xi и yj), а также определена матрица вида Ai,j=f(xi,yj). Имя матрицы A указывается при заполнении рамки-шаблона. С помощью этой команды можно строить параметрические графики. Contour Plot (Контурный график) Строит диаграмму линий уровня функции вида z=f(x,y), т.е. отображает точки, в которых данная функция принимает фиксированное значение z=const.
При этом должны быть заданы векторы значений xi и yj), а также определена матрица вида Ai,j=f(xi,yj). Имя матрицы A указывается при заполнении рамки-шаблона. С помощью этой команды можно строить параметрические графики. Contour Plot (Контурный график) Строит диаграмму линий уровня функции вида z=f(x,y), т.е. отображает точки, в которых данная функция принимает фиксированное значение z=const.
3D Scatter Plot (3D Точечный ) Служит для точечного представления матрицы значений Ai,j или отображения значений функции z=f(x,y) в заданных точках. Эта команда может также использоваться для построения пространственных кривых. 3D Bar Plot (3D Диаграммы) Служит для представления матрицы значений Ai,j или отображения значений функции z=f(x,y) в виде трехмерной столбчатой диаграммы. Vector Field Plot (Поле векторов) Служит для представления двухмерных векторных полей V=(Vx, Vy). При этом компоненты векторного поля Vx и Vy должны быть представлены в виде матриц. При помощи этой команды можно построить поле градиента финкции f(x,y). 3D Plot Wizard (вызов мастера для быстрого построения 3-хмерного графика) При выборе этой команды возникает ряд всплывающих окон, в которых требуется выбрать параметры построения трехмерного графика (задаются тип трехмерного графика, стиль его изображения, цветовая гамма). График по умолчанию строится на промежутке от -5 до +5 (по обеим переменным).
При помощи этой команды можно построить поле градиента финкции f(x,y). 3D Plot Wizard (вызов мастера для быстрого построения 3-хмерного графика) При выборе этой команды возникает ряд всплывающих окон, в которых требуется выбрать параметры построения трехмерного графика (задаются тип трехмерного графика, стиль его изображения, цветовая гамма). График по умолчанию строится на промежутке от -5 до +5 (по обеим переменным).
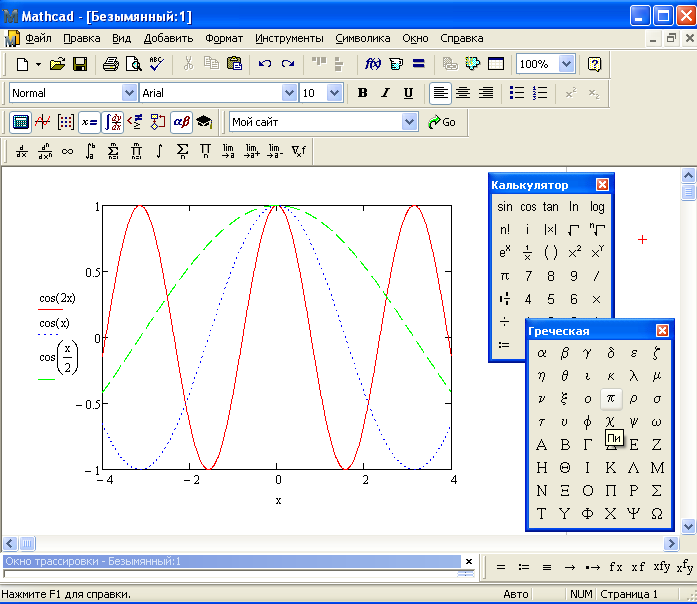
Двумерные графики в декартовой системе кординат.
№ слайда 8 Описание слайда:График функции y=f(x). В ячейке рядом с осью ординат необходимо задать функцию f(x), график которой мы хотим построить. Если эта функция была определена заранее, то в ячейку достаточно ввести f(x), в противном случае следует ввести изображаемую функцию в явном виде (например, cos(x)). После ввода x и f(x) в графической области появятся еще четыре ячейки, которые не обязательно заполнять.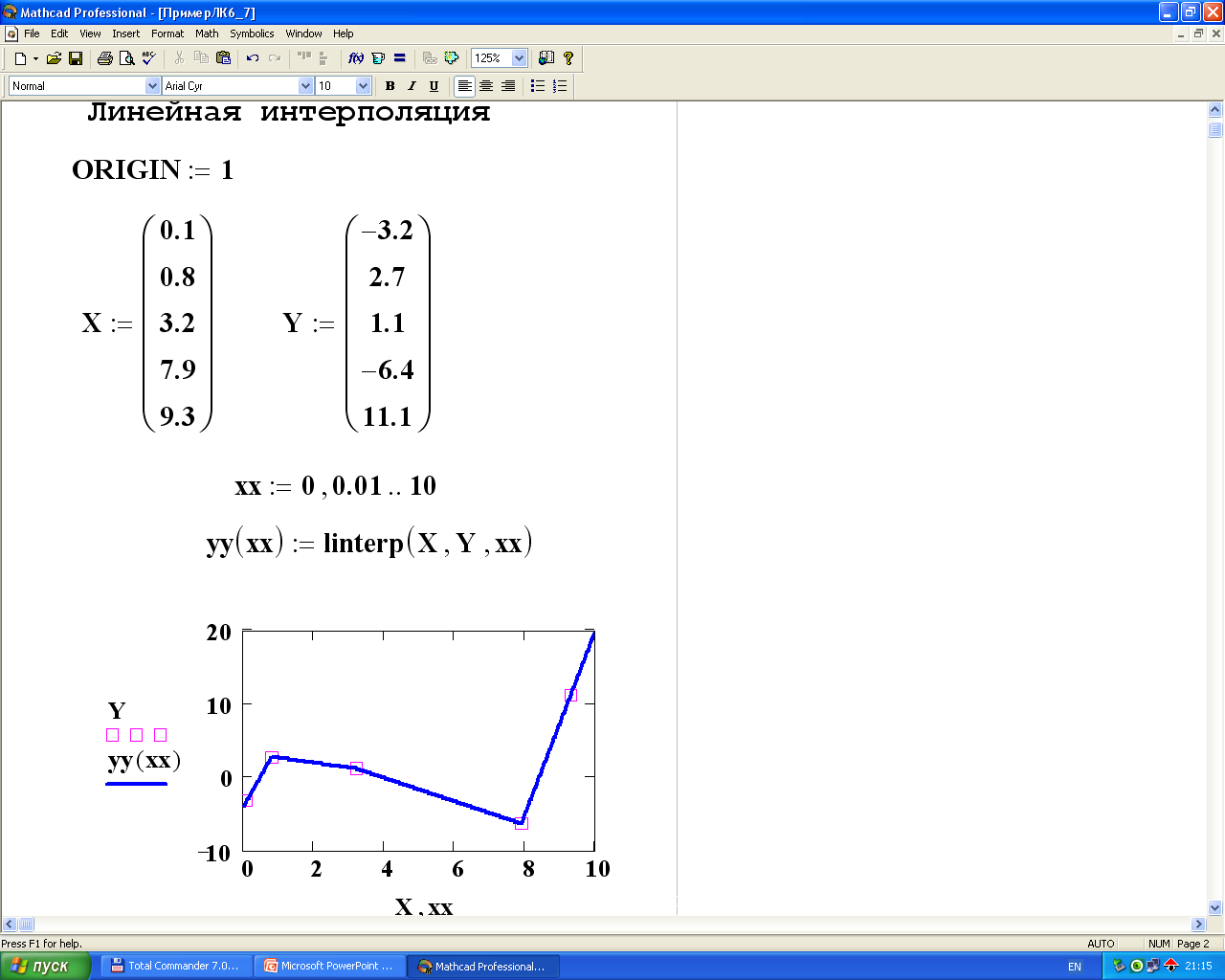 MathCAD автоматически находит подходящие значения для xmin, xmax, ymin, ymax. Если же предлагаемые MathCAD значения вас не устраивают, вы можете задать свои. В MathCAD существует возможность строить график функции, не задавая предварительно промежуток изменения независимой переменной. По умолчанию этот промежуток принимается равным [-10, 10]. Для представления на одной диаграмме графиков нескольких функций необходимо выделить ячейку рядом с осью ординат и через запятую ввести вторую функцию. По умолчанию график этой функции будет представлен пунктирной линией другого цвета.
MathCAD автоматически находит подходящие значения для xmin, xmax, ymin, ymax. Если же предлагаемые MathCAD значения вас не устраивают, вы можете задать свои. В MathCAD существует возможность строить график функции, не задавая предварительно промежуток изменения независимой переменной. По умолчанию этот промежуток принимается равным [-10, 10]. Для представления на одной диаграмме графиков нескольких функций необходимо выделить ячейку рядом с осью ординат и через запятую ввести вторую функцию. По умолчанию график этой функции будет представлен пунктирной линией другого цвета.
Кривые на плоскости, заданные параметрически В случае построения параметрически заданной кривой, вместо независимой переменной x под осью абсцисс необходимо задать индексированую переменную Xi. А рядом с осью ординат необходимо соответственно указать Yi. Для нанесения на график функции отдельных точек, их координаты указываются через запятую под осью абсцисс и слева от оси ординат.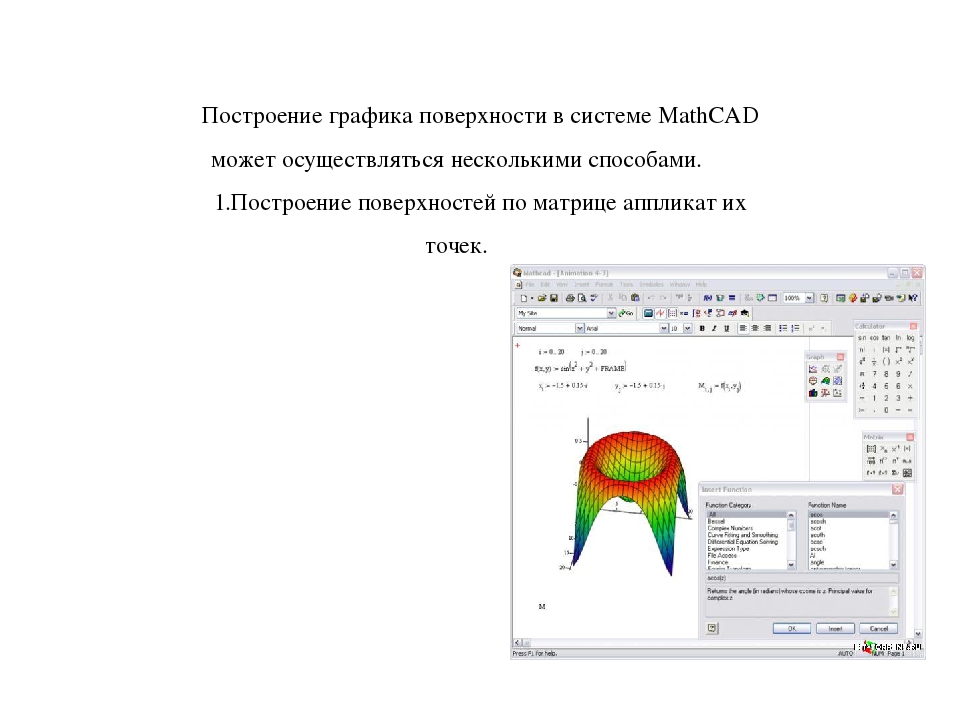 Если требуется вывести множество точек, то можно сформировать два вектора, один из которых содержит абсциссы точек, а другой — их ординаты. В этом случае на графике в соответствующих ячейках указываются только имена векторов.
Если требуется вывести множество точек, то можно сформировать два вектора, один из которых содержит абсциссы точек, а другой — их ординаты. В этом случае на графике в соответствующих ячейках указываются только имена векторов.
Редактирование графиков в декартовой системе координат Если вас не устраивает внешний вид построенных графиков, вы можете его изменить, выделив график (выполнив на нем щелчок, так, чтобы вокруг него появилась рамка) и воспользовавшись командой Format -> Graph -> X-Y Plot, или, выполнив на графике щелчок правой кнопкой мыши и выбрав команду Format из выпадающего контекстного меню. В результате на экране появится диалоговое окно, позволяющее изменить вид графика. Данное диалоговое окно содержит несколько вкладок: X-Y Axes (форматирование осей), Traces (тип линий графиков), Labels (подписи), Defaults (по умолчанию). Форматирование оси графика можно произвести, выполнив на ней двойной щелчок. Для изменения типа линий графиков необходимо активизировать вкладку Traces (След) • Line (Линия ) — тип линий dash (штриховая), solid (сплошная), dot (точечная) или dadot (штрихпунктирная). •Type (Тип) — Позволяет выбрать один из семи видов графика: в виде кривых (), в виде столбцов () и т. п. •Weight (Вес) — Позволяет задавать толщину линий графика.
Для изменения типа линий графиков необходимо активизировать вкладку Traces (След) • Line (Линия ) — тип линий dash (штриховая), solid (сплошная), dot (точечная) или dadot (штрихпунктирная). •Type (Тип) — Позволяет выбрать один из семи видов графика: в виде кривых (), в виде столбцов () и т. п. •Weight (Вес) — Позволяет задавать толщину линий графика.
Двухмерные графики в полярной системе координат.
№ слайда 12 Описание слайда:Построение полярных графиков Для построения полярного графика необходимо выполнить команду Inset -> Graph -> Polar Plot. При этом в документ помещается графическая область с двумя незаполненными ячейками для построения графика. (Клавиши [Ctrl +7]). В нижнюю ячейку вводится полярный угол q. Его следует определить заранее как переменную, принимающую значения из промежутка (ранжированная переменая). В левую ячейку вводится полярный радиус r(q) или Re(r(q)) и Im(r(q)). Функция r(q) либо задается заранее, либо ее определение вводится непосредственно в ячейку. График в полярных координатах можно построить и посредством команды X-Y Plot/ Только в этом случае необходимо дополнительно задать следующие функции: x(q)=r(q)cos(q) и y(q)=r(q)sin(q), а в ячейках для абсцисс и ординат указать соответственно x(q) и y(q) Если для некоторых углов q функция не определена (не существует радиуса с действительным значением, он принимает чисто мнимые значения), то MathCAD отображает на графике только действительные значения радиуса. Но при помощи функций Re и Im можно представить на одной круговой диаграмме графики как действительной, так и мнимой части функции r(q).
Функция r(q) либо задается заранее, либо ее определение вводится непосредственно в ячейку. График в полярных координатах можно построить и посредством команды X-Y Plot/ Только в этом случае необходимо дополнительно задать следующие функции: x(q)=r(q)cos(q) и y(q)=r(q)sin(q), а в ячейках для абсцисс и ординат указать соответственно x(q) и y(q) Если для некоторых углов q функция не определена (не существует радиуса с действительным значением, он принимает чисто мнимые значения), то MathCAD отображает на графике только действительные значения радиуса. Но при помощи функций Re и Im можно представить на одной круговой диаграмме графики как действительной, так и мнимой части функции r(q).
Форматирование полярных графиков Если вы хотите отредактировать график в полярных координатах, необходимо выделить график (щелчком левой кнопки мыши) и выполнить команду Format -> Graph -> Polar Plot или выполнить двойной щелчок на выделенном графике. При этом откроется окно Formatting Currently Selected Polar Plot (форматирование полярного графика). Это окно содержит те же вкладки, что и для графиков в декартовой системе координат.
При этом откроется окно Formatting Currently Selected Polar Plot (форматирование полярного графика). Это окно содержит те же вкладки, что и для графиков в декартовой системе координат.
Графики в трехмерном пространстве
№ слайда 15 Описание слайда:Построение графика функции z=f(x,y) в виде поверхности в декартовой системе координат. Для построения графика поверхности можно воспользоваться двумя способами: явным и неявным. Если вам надо только посмотреть общий вид поверхности, то MathCAD предоставляет возможность быстрого построения подобных графиков. Для этого достаточно определить функцию f(x,y) и выполнить команду Вставка> График> Поверхность или нажать соответствующую кнопку наборной панели График (сочетание клавиш [Ctrl+7]). В появившейся графической области под осями на месте шаблона для ввода надо указать имя (без аргументов) функции. MathCAD автоматически построит график поверхности. Независимые переменные x и y принимают значения из промежутка [-5,5].
MathCAD автоматически построит график поверхности. Независимые переменные x и y принимают значения из промежутка [-5,5].
Для построения графика поверхности в определенной области изменения независимых переменных или с конкретным шагом их изменения необходимо сначала задать узловые точки xi и yj, в которых будут определяться значения функции. После (а можно и до) этого надо определить функцию f(x,y), график которой хотите построить. После этого необходимо сформировать матрицу значений функции в виде: Ai,j=f(xi,yj). Теперь после выполнения команды Insert -> Graph -> Surface Plot в появившейся графической области достаточно ввести имя матрицы (без индексов).
№ слайда 17 Описание слайда:Для построения графика линий уровня данной функции необходимо поступать также как это было описано выше, только вместо команд Поверхности следует выбрать команду Контурный. Аналогично, при помощи команды 3D Диаграммы можно построить трехмерный столбчатый график данной функции, при помощи команды 3D Точечный — трехмерный точечный график, а при помощи команды 3D Лоскутный — трехмерный график поверхности в виде несвязанных квадратных площадок — плоскостей уровня для каждой точки данных, параллельных плоскости X-Y
Аналогично, при помощи команды 3D Диаграммы можно построить трехмерный столбчатый график данной функции, при помощи команды 3D Точечный — трехмерный точечный график, а при помощи команды 3D Лоскутный — трехмерный график поверхности в виде несвязанных квадратных площадок — плоскостей уровня для каждой точки данных, параллельных плоскости X-Y
Построение графика поверхности, заданной параметрически Если поверхность задана параметрически, это означает, что все три координаты — x и y и z — заданы как функции от двух параметров u и v. Сначала необходимо задать векторы значений параметров ui и vj. Затем необходимо определить матрицы значений функций координат x(u,v), y(u,v) и y(u,v). После выбора команды Surface Plot в MathCAD документе появится графическая область. В свободной ячейке внизу области надо указать В СКОБКАХ имена (без аргументов и индексов) трех матриц — x,y,z.
№ слайда 19 Описание слайда:Форматирование трехмерных графиков.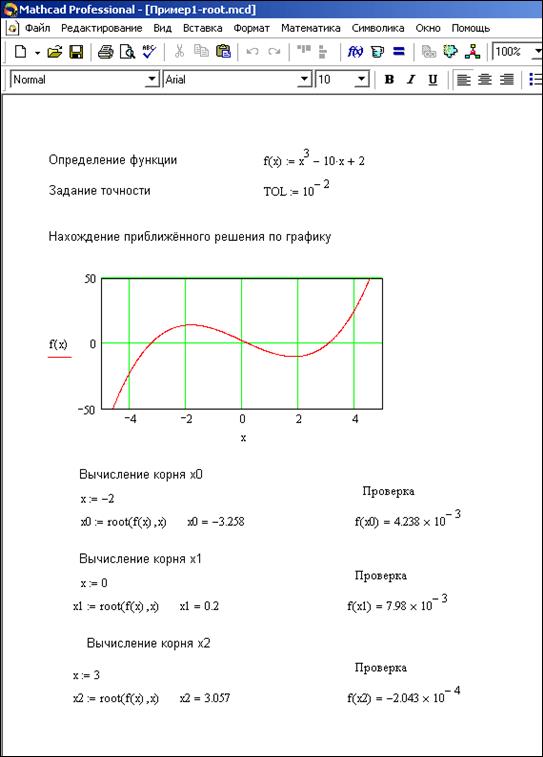 Если вас не устраивает внешний вид созданного трехмерного графика, вы можете изменитьего, выполнив команду Format -> Graph -> 3D Plot или выполнив двойной щелчок мышкой на графической области. В результате на экране появится диалоговое окно 3-D Plot Format, позволяющее изменять параметры отображения графика. Разобраться во всех тонкостях управлением видом графика вы можете самостоятельно, построив график и поэкспериментировав, выбирая те или иные опции.
Если вас не устраивает внешний вид созданного трехмерного графика, вы можете изменитьего, выполнив команду Format -> Graph -> 3D Plot или выполнив двойной щелчок мышкой на графической области. В результате на экране появится диалоговое окно 3-D Plot Format, позволяющее изменять параметры отображения графика. Разобраться во всех тонкостях управлением видом графика вы можете самостоятельно, построив график и поэкспериментировав, выбирая те или иные опции.
в Mathcad Prime | Корневые решения
Что такое компонент Mathcad Chart?
Эта функция была добавлена в Mathcad Prime 5.0 и улучшена в Mathcad Prime 6.0. График диаграммы — это усовершенствованная функция построения графика, доступная ранее. Одним из основных преимуществ этого дополнения является повышение удобства использования процесса создания диаграмм.
PTC резюмирует ключевые аспекты этого как:
- Полное форматирование осей
- Названия и легенды
- Вторая ось Y
- Сетка
- Настраиваемый внешний вид сюжета
Итак, давайте разберем некоторые из этих функций…
Компоненты диаграммы можно открыть в отдельном окне для удобного редактирования.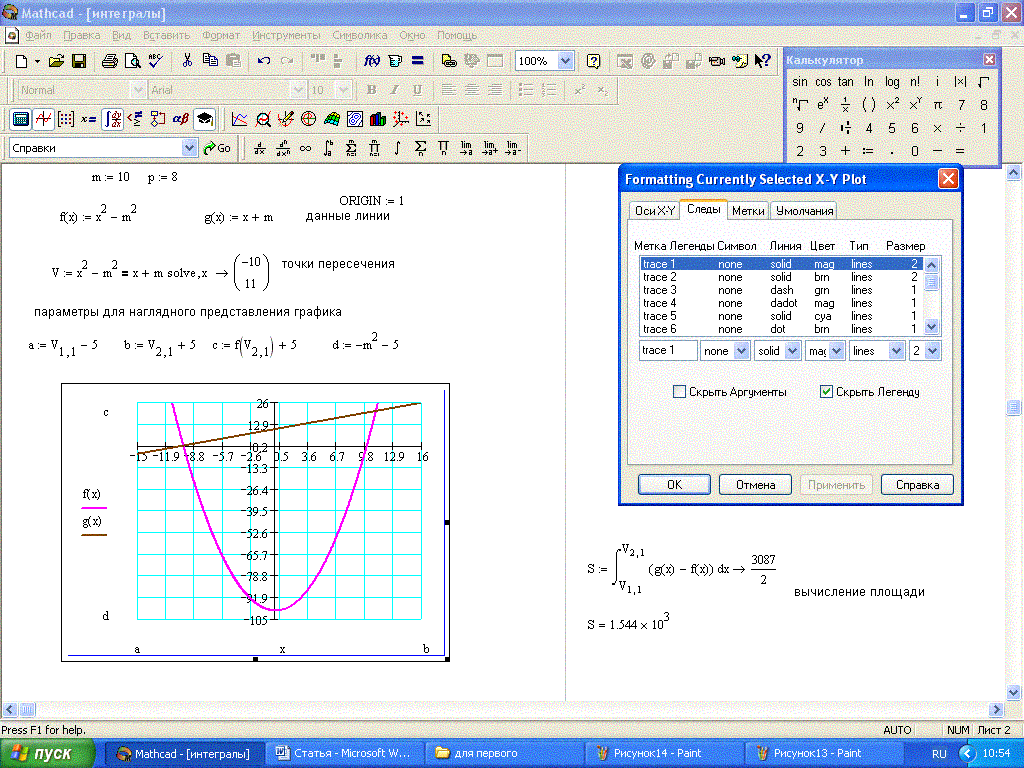 Это также дает вам дополнительную возможность увеличивать отдельные области графика в этом окне.
Это также дает вам дополнительную возможность увеличивать отдельные области графика в этом окне.
Шаблонов:
Шаблоны по умолчанию для макета диаграммы, осей и трассировок помогут вам начать работу. Посмотрите на изображение ниже, которое дает вам представление о шаблонах диаграмм, доступных в Prime 6.0
.Шаблоны осей также включают шаблоны для линий сетки, чтобы вы могли быстро настроить линейные или логарифмические линии сетки для ваших диаграмм.Затем вы можете редактировать стили линий, толщину и цвет этих линий сетки и настраивать частоту ваших второстепенных линий сетки.
Настройка:
Включайте и выключайте метки, заголовки и управление цветом фона с помощью простых флажков. Сделать ошибку? Быстро восстановите настройки по умолчанию для конкретной функции, над которой вы работали. Можно провести параллели между этим и функциональностью, присутствующей в Mathcad 15.
изображений, извлеченных из Mathcad Prime 6. 0
0
Вы можете добавить границу и заполнить многие аспекты диаграммы, такие как область построения или метки заголовков оси и графика. У вас есть 80 цветов по умолчанию на выбор с возможностью использования цветовой палитры при необходимости. Вы можете применить цвет к областям диаграммы в виде заливки или градиента с возможностью изменения непрозрачности. Сделайте свои диаграммы настолько психоделическими, насколько захотите!
График из Mathcad Prime 6.0
Быстрый пример для выделения элемента управления, который вы получаете в Mathcad Prime для форматирования ваших графиков.Вы, вероятно, не стали бы создавать такой экстравагантный график, но было бы неплохо иметь такую возможность!
Экспорт:
Mathcad Prime 6.0 дает вам возможность экспортировать диаграммы в виде изображений для использования в сторонних приложениях. Поддерживаемые форматы:
Мы рекомендуем выполнить обновление до Mathcad Prime 6. 0, чтобы воспользоваться этой полезной функцией в дополнение ко многим другим функциям, таким как доступные теперь расширенные параметры шаблонов.
0, чтобы воспользоваться этой полезной функцией в дополнение ко многим другим функциям, таким как доступные теперь расширенные параметры шаблонов.
Что делать дальше?
Если вам интересно узнать больше о Mathcad Prime 6.0 , пожалуйста, свяжитесь с нашим отделом продаж — [email protected]
Можно обсудить технические демонстрации или дополнительную информацию о более широких функциональных возможностях программного обеспечения.
Поделитесь этой страницей в социальных сетяхНовый выпуск PTC: Mathcad Prime 5.0
Mathcad Prime — это стандартная отраслевая платформа для решения, анализа и обмена наиболее важными инженерными расчетами. Он действует как единый инструмент для инженерных групп, позволяющий создавать живую математическую запись, интеллектуальные единицы измерения и мощные вычислительные возможности, и все это в простом в использовании интерфейсе.
Mathcad Prime — ведущая программа для инженерных расчетов.
В последней версии Mathcad Prime 5.0 добавлены некоторые новые функции, в том числе улучшенное приложение для построения двухмерных диаграмм, инструменты настройки двухмерных графиков и новые справочные ресурсы в Интернете. Вот все, что вам нужно знать.
Что нового в Mathcad Prime 5.0?
Выполнение сложных инженерных расчетов — это лишь один из аспектов процесса проектирования. Команды инженеров должны иметь возможность эффективно общаться и делиться своими результатами таким образом, чтобы способствовать развитию дизайна продукта.Mathcad Prime делает это возможным с новым и улучшенным:
Улучшенный 2D-график
Пользователи теперь могут полностью настраивать внешний вид 2D-диаграмм, чтобы улучшить визуализацию и коммуникацию. Расширенные функции форматирования включают:
- Полное форматирование осей, , включая возможность выбора цветов и стилей, которые наилучшим образом представляют ваши данные
- Названия и условные обозначения для предоставления контекста данных и придания графикам более профессионального вида
- Вторая ось Y, , включая возможность иметь несколько трасс и включать дополнительное форматирование для второй оси
- Линии сетки вариантов, включая добавление основных или второстепенных линий сетки с настраиваемыми параметрами цвета, стиля и толщины
Эффективно передавайте результаты инженерных расчетов с помощью полностью настраиваемых 2D-графиков.
Интерактивная справка и поддержка
PTC теперь предоставляет мгновенную онлайн-справку по всему, что вам нужно, и тогда, когда это необходимо. В новом справочном центре есть информация обо всех возможностях и функциях Mathcad Prime 5.0, включая последние обновления, примеры, учебные пособия и справочные материалы.
Расширенные функции из предыдущих выпусков
Если вы используете старую версию Mathcad Prime, вы можете упустить некоторые расширенные функции из новых выпусков, например:
- Защита содержимого: Mathcad Prime 5.0 поддерживает такую же расширенную защиту и блокировку области, поэтому пользователи могут контролировать, какой доступ и видимость есть у других пользователей при расчетах.
- Полная совместимость: Вместо того, чтобы переключаться между приложениями и координировать другую работу, Mathcad Prime может встраивать контент из других приложений в рабочие листы, а пользователи имеют возможность копировать и вставлять несколько областей рабочего листа непосредственно в MS Word.

- Повышенное удобство использования: Расширенный перенос формул означает, что вычисления не исчезают с края страницы.Пользователи могут добавить перенос формул после завершения вычислений или включить настройку переноса по мере ввода.
- Другие улучшения производительности: Предыдущие выпуски Mathcad Prime включают обновления до инженерных ноутбуков на базе PTC, средство решения триггерных уравнений, расширенные инструменты инженерной математики, преобразователь технических единиц, расширенные числовые и пользовательские функции, комплексные функции документации, программирование, символы, шаблоны , Графики XY, трехмерные графики и интеграция с Excel.
Mathcad 5.0 Цена
Так же, как PTC Creo перешел на модель ценообразования по подписке, Mathcad Prime теперь также предлагается по той же модели. Цена Mathcad Prime 5.0 составляет 600 долларов США за годовую лицензию на подписку с автоматическим продлением. Для полной функциональности доступны различные библиотеки рабочих листов для единовременной покупки на сумму от 200 до 520 долларов. Доступные библиотеки рабочих листов включают:
Для полной функциональности доступны различные библиотеки рабочих листов для единовременной покупки на сумму от 200 до 520 долларов. Доступные библиотеки рабочих листов включают:
- Библиотека рабочих листов Рорка — 6-е издание для PTC Mathcad Prime 4.0
- Библиотека таблиц PTC Mathcad — тома 1 и 2
- Библиотека таблиц PTC Mathcad — прикладная математика
- Библиотека рабочих листов PTC Mathcad — Гражданское и структурное строительство
- Библиотека таблиц PTC Mathcad — Электрооборудование
- Библиотека таблиц PTC Mathcad — Машиностроение
- Библиотека рабочих листов PTC Mathcad — Образование
Расширьте функциональные возможности Mathcad Prime с помощью разнообразных рабочих листов.
Приобретите Mathcad Prime 5.0
Mathcad Prime 5.0 — это ведущее программное обеспечение для инженерных расчетов, которое может помочь вашей организации оптимизировать процесс проектирования и расчетов. Mathcad Prime поможет вам:
Mathcad Prime поможет вам:
- Надлежащим и безопасным образом передавать проектные замыслы и инженерные знания
- Интуитивное построение вычислений с использованием стандартных математических обозначений
- Создание качественной и профессиональной документации инженерных расчетов
- Переназначить стандартные расчеты
- Повышение производительности
- Ускорение обучения и внедрения программного обеспечения с доступом к материалам электронного обучения
Готовы к покупке? Мы предлагаем специальную сделку: купи один, получи половину скидки на Mathcad 5.0 лицензий до 30 сентября 2018 г.!
Или, если вы хотите узнать больше или у вас есть вопросы о программном обеспечении, свяжитесь с нами.
(PDF) Анализ диаграмм, улучшенный с помощью Mathcad
52 · ПРИКЛАДНАЯ МИКРОВОЛНА И БЕСПРОВОДНАЯ СВЯЗЬ
y = c + ir sin (q) (2)
, где i — мнимое комплексное число, q — текущая переменная
от 0 до 2p радиан, r — радиус или величина
круга G или коэффициент отражения, а c — центральное положение
, если требуется контур круга (это будет
, необходимое для приложений, таких как графики усиления , устойчивость
плоских местоположений и контуров шума).Когда диаграмма
построена в Mathcad и границы не заданы, создаются все четыре квадрата
круговых контуров. Эта расширенная таблица
полезна для изучения конструкций с G больше
единицы. Расширенная диаграмма расширяется за пределы диаграммы Смита
единичного круга и включает отрицательное реальное сопротивление.
Случай, который обычно встречается при использовании диаграммы Smith
для пассивных сетей и не генерирующих схем, случаев
содержит только единичный круг, и все контуры реактивного сопротивления
заканчиваются на этом круге.Добавление операторов control
trol в Mathcad может ограничить контуры реактивного сопротивления
так, чтобы они заканчивались на единичной окружности. Для
в этой статье мы обрезали диаграмму, чтобы указать
для любого региона, который может представлять интерес.
Расширенная диаграмма
В Mathcad диаграмма просто ограничена и
«обрезается» до единицы, как показано в Приложении B на странице
58. Если области отрицательного сопротивления или анализ стабильности
требует расширения диаграммы, тогда «Зажим» расширяется или снимается.На рисунке 3 граница расширена до
, удвоенного радиуса единичной окружности.
Дополнительные контуры отрицательного сопротивления добавляются посредством
, расширяющего таблицу R-массива, как показано на Рисунке 4, и
, расширяющего «область зажима». Таблица массива X также увеличена для большей детализации
, а популярным набором последовательностей является
в формате 1-2-5. Или таблица может быть настроена так, чтобы она соответствовала любому дисплею
, связанному с анализатором цепей, например серии
HP8753.На рисунке 4 Γ увеличен до 10, и показаны дополнительные контуры отрицательного сопротивления
. Если
та же диаграмма закрепляется на Γ = 1, то единичный круг будет
детализирован.
Движение по кругу
Для построения окружности требуется только ввод центра —
и радиуса. Например, для расположения постоянных контуров КСВН
требуется значение Γ, которое изменяется с радиусом
, пропорциональным импедансу, и центром в исходной точке
диаграммы.Уравнения и ввод в
Mathcad показаны ниже. Эта же концепция расширена для вычисления и построения контуров шума, устойчивости
плоскостей, обратной связи и отображения n-портов, а также оценки производительности компонентов
, например Q. Это показано на примере в Приложение C, которое оценивает устройство
из раздела измеренных данных.
КСВ назначается таблице массива, состоящей из
четырех фиксированных значений.Вычисляется Γ, связанный с каждым значением КСВ
, и значения
, скоординированные с разверткой круга и координаты x, y, вводятся в диаграмму. Эта конструкция могла иметь
контур любого типа. В конкретном случае шума [7], расположение кругов будет геоцентрическим
относительно F
min
и r
n
устройства и в определенное время.
специфический угол, заданный параметрами шума, связанными с
этого устройства.
Оценка устройства на основе данных измерений
Набор Q-контуров добавляется к диаграмме путем соединения
всех равных контуров RX, как показано в Приложении C
на стр. 60. Это будет включать емкостные и индукционные контуры.
различных кругов, поскольку они пересекают соответствующие значения R.
Две окружности расположены с радиусом 1,414 и центрами
градусов при нормированном R = 1 и нормированном jX = +1 и
–1 [8]. С дугами окружности, нарисованными на диаграмме, эта структура con-
используется для оценки загруженного компонента Q.
Таблица данных рассеяния считывается из VNA
, импортируется в программу построения диаграмм, а затем строится вместе с диаграммой
в качестве наложения. Составляющая Q конфигурируемой шунтирующей катушкой индуктивности
с параллельной параллельной паразитной емкостью
определяется из уравнения ширины полосы 3 дБ.
«Квадратные» точки данных пересекают контуры Q в
, точке мощности –3 дБ, а f
0
располагается, когда Γ пересекает действительную ось
(ромбовидная отметка).Развертка контура по часовой стрелке:
CADWOLF — альтернатива MathCAD
Вступительное видео
Посмотрите 90-секундное вступительное видео и 10-минутное видео об основах
Чем занимается CADWOLF
Платформа состоит из нескольких модулей, которые можно использовать для решения простой задачи или управления всем STEM-проектом.Документы — анализ и документация
Документы — это основа CADWOLF.Они создаются и редактируются с помощью графического интерфейса пользователя и могут рассматриваться как документы Google, обладающие всеми возможностями языка программирования.
Рабочие области — создание, хранение и систематизация файлов
Рабочие области действуют как папки в CADWOLF и предоставляют место, где пользователи могут создавать и находить файлы, определять разрешения и загружать изображения.
Деревья деталей — что-то построить
Деревья деталей позволяют пользователям устанавливать схему нумерации деталей, а затем строить большие конструкции по частям.Это обеспечивает мгновенную обратную связь с моделями САПР и проектными документами, а также единое место для доступа ко всем файлам.
| Excel | MathCAD | Jupyter | CADWOLF | |
|---|---|---|---|---|
| Математический решатель | ||||
| Внешний вид документа | ||||
| На базе Интернета | ||||
| Бесплатная версия | ||||
| Организация дерева деталей | ||||
| Управление процессами | ||||
| Прямая ссылка на CAD |
Образцы документов и других предметов
Просмотр снимков экрана или открытых образцов элементов CADWOLFФункция регрессии — обзор
6.2.1 Повышенная точность
В сверхвысоком разрешении за счет закрепленной регрессии цель контролируемой задачи обучения, ведущей к функциям линейной регрессии { R i }, состоит в том, чтобы получить локально точную функцию сопоставления из участков с низким разрешением (или функции) на участки с высоким разрешением (или исправления до их грубого приближения). Для удобства чтения остальная часть текста будет относиться к заплатам с высоким разрешением, а не к их исправлению.
С более общей точки зрения предполагается, что векторы признаков с низким разрешением образуют входной коллектор M размером м , а с высоким разрешением — эквивалентный целевой коллектор N размером n . Формально для обучающих пар ( y Fi , x i ) с y F ∈ M и x 48 , мы хотим вывести отображение Ψ: M⊆Rm → N⊆Rn.
Как мы уже видели, на использование функций линейной регрессии в закрепленной регрессии влияет тот факт, что их можно легко вычислить в закрытой форме и применить как умножение матриц на этапе вывода или тестирования. Однако общее отображение Ψ очень сложное и нелинейное (Peyré, 2009). Для моделирования нелинейности отображения обучается ансамбль регрессоров { R i }, представляющий локально линейное приближение, в предположении, что оба многообразия M и N имеют одинаковые местная геометрия.Мы можем проанализировать влияние на распределение этих регрессоров по коллектору (то есть точки привязки) и важность правильного выбора N l в уравнении. (6.5), что должно интуитивно привести к усовершенствованию подхода к обучению.
Избыточное разреженное представление может быть получено из начальных обучающих патчей с низким разрешением (или векторов признаков) с использованием, например, K-SVD (Aharon et al., 2006). Этот компактный словарь D l используется в методе регрессии с привязкой к базовой линии, описанном выше, как в качестве точек привязки к коллектору, так и в качестве точек данных для контролируемого обучения (после объединения их с их высоким разрешением D h экземпляров).В экстремальной настройке с одной точкой привязки (Timofte et al., 2013) уникальный регрессор R G обучается со всеми элементами словаря, таким образом принимая более высокие ошибки восстановления из-за единственной линеаризации словаря. многообразие.
Естественно, для более точной реконструкции необходимо более плотно отобрать нижележащий коллектор. Таким образом, в более общем случае, привязанная регрессия может напрямую использовать точки словаря D1,…, Dds в качестве точек привязки A1,…, Ads и затем построить для каждого из этих атомов окрестность k -NN в том же разреженном словаре D l , следуя принципам, аналогичным принципам разреженного кодирования.
Как мы видели в предыдущей главе, выполнение разреженной декомпозиции большого количества обучающих патчей эффективно сжимает эти данные в гораздо меньший словарь, давая атомы, которые идеально представляют весь обучающий набор данных, то есть все многообразие . Это обоснование их использования в качестве опорных точек, но их природа делает их также неоптимальными для встраивания в окрестности. Причина — необходимое локальное условие для предположения линейности, которое, вероятно, будет нарушено окрестностями, разбросанными по большой площади лежащего в основе многообразия.Действительно, из-за минимального ограничения на реконструкцию — L 1 — нормы, наложенного в разреженных словарях, атомы в словаре не близки в евклидовом пространстве, как показано на рис. 6.1A.
Рис. 6.1. (A) Среднее евклидово расстояние между атомами и их окрестностями для разных размеров соседства. (B) PSNR (дБ) для реконструкции с использованием закрепленной регрессии. Для создания обеих диаграмм использовалось 1024 точки привязки. Улучшенная тренировка (темная кривая) явно превосходит базовый подход.
Это наблюдение, естественно, приводит к более подходящему подходу для обучения линейных регрессоров для SR, который был посещен C.-Y. Ян и Ян (2013), Перес-Пеллитеро и др. (2014) и Timofte et al. (2014) и др. Мы можем продолжать использовать разреженные представления в качестве точек привязки к многообразию, но мы можем улучшить локальность окрестностей с помощью необработанных обучающих выборок (то есть векторов признаков или патчей). На рис. 6.1A показано, как таким образом можно найти ближайших соседей, которые, в свою очередь, лучше соответствуют локальному условию.
Кроме того, доступно большее количество локальных независимых измерений (например, среднее расстояние для 1000 соседей в подходе raw-patch сравнимо с 40-атомным соседством в базовом или разреженном подходе), и мы можем контролировать количество k -NN выбран, то есть он не ограничен сверху размером словаря. Небольшой игрушечный пример преимуществ этой альтернативной схемы обучения показан на рис. 6.2. Обратите внимание, что доступность большего количества обучающих выборок для каждой привязки напрямую улучшает состояние контролируемого этапа обучения, что приводит к локально линейным функциям регрессии.
Рис. 6.2. Нормализованное игрушечное многообразие, иллюстрирующее эффективность выборки из плотных окрестностей по сравнению с разреженной выборкой. (A) Образцы двумерного многообразия. (B) Многообразие (линия) и разреженное представление, полученные с помощью алгоритма K-SVD (точки) всего для 8 атомов. (C) Локальные линейные регрессоры (линии, пересекающие точки), обученные с небольшими окрестностями ( k = 1 сосед для каждого якоря), полученными в разреженном словаре (базовый подход, вытекающий из разреженного кодирования).(D) Линейные регрессоры (почти идеально касательные линии), полученные с использованием улучшенного обучения с окрестностями, полученными во всех образцах многообразия ( k = 10).
На рис. 6.1B показано сравнение базовой регрессии с привязкой (Timofte et al., 2013) и улучшенной схемы обучения с точки зрения PSNR восстановленного изображения. Оба эксперимента используют один и тот же обучающий набор данных, а для плотного встраивания соседей также используются те же l 2 -нормализованные исходные функции, используемые в качестве входных данных для оптимизации разреженного словаря через K-SVD.Применение улучшенной схемы обучения позволяет заякоренной регрессии достичь существенных количественных улучшений качества, что также приводит к визуальным улучшениям.
Mathcad | GPSL | Глобальный партнер PTC — GPSL
Mathcad | GPSL | Глобальный партнер PTC — GPSL О нас Отрасли промышленности Клиенты Технологии События Новости Аэрокосмическая промышленность и оборона Производство Издательский Финансовые услуги Законодательные органы Продукты РешенияТовар
Более 250 000 инженеров по всему миру выбирают программное обеспечение PTC Mathcad, потому что оно отличается простотой использования и знакомством с их ноутбуком для инженеров — в сочетании с живыми математическими обозначениями, интеллектом единиц и мощными вычислительными возможностями
Основная информация
PTC Mathcad — это программное обеспечение для инженерной математики, которое позволяет выполнять, анализировать и публиковать наиболее важные вычисления.
Расчеты — это сердце вашей инженерной информации. Вы и ваша команда должны иметь возможность находить, повторно использовать и делиться этой важной интеллектуальной собственностью.
PTC Mathcad — это стандартное программное обеспечение для решения, анализа и обмена наиболее важными инженерными расчетами.
PTC Mathcad делает то, чего просто не могут сделать электронные таблицы, текстовый редактор, программное обеспечение для презентаций и программные приложения — он предоставляет мощные вычислительные возможности в удобочитаемой форме.
- Безопасная передача проектных замыслов и инженерных знаний
- Интуитивно понятное построение расчетов с использованием стандартной математической нотации
- Создавайте документы профессионального качества, поддерживаемые живыми математическими вычислениями, графиками, текстом и изображениями
- Повторно используйте стандартизированные вычисления для оптимизации разработки продуктов следующего поколения и избегайте повторного создания вычислений
- Повышайте продуктивность быстрее, получая мгновенный доступ к всеобъемлющим учебным материалам и руководствам из PTC Mathcad
Характеристики
- Интуитивно создавайте вычисления с использованием стандартных математических обозначений
- Создавайте документы профессионального качества с помощью математических вычислений, графиков, текста и изображений профессионального качества
- Переназначьте стандартизованные вычисления
- Повысьте продуктивность с помощью полной поддержки единиц измерения на протяжении вычислений
- Ускорьте обучение и внедрение с мгновенным доступом к электронному обучению
А теперь PTC Mathcad Prime 5.0 предлагает расширенные возможности построения 2D-графиков, позволяя вам полностью настраивать внешний вид ваших 2D-графиков.
© 2021 Global Publishing Solutions Ltd. Все права защищены.ptc mathcad — Venturo Technologies
Программное обеспечение ptc mathcad
ptc mathcad Prime 5
Решение сложных инженерных расчетов — это одно. Другое дело — передать их визуально. В ptc mathcad Prime 5.0 представлены новые простые в использовании возможности построения двухмерных графиков, которые помогут улучшить визуализацию ваших данных.
Получите необходимую помощь быстрее. Помощь теперь у вас под рукой и в режиме онлайн, что дает вам мгновенный доступ к тому, что вам нужно, когда вам это нужно.
Что нового в ptc mathcad Prime 5.0?
Визуализировать данные инженерных расчетов проще, чем когда-либо прежде. ptc mathcad Prime 5.0 предоставляет новое комплексное приложение для построения 2D-графиков, которое улучшит ваши способы комментирования и предоставления ваших инженерных данных.
Улучшение 2D-графика
ptc mathcad Prime 5.0 предлагает расширенные возможности построения 2D-графиков, позволяя вам полностью настраивать внешний вид ваших 2D-графиков. Вот некоторые из ожидаемых расширенных возможностей форматирования:
- Полное форматирование осей
- Названия и легенды
- Вторая ось Y
- Сетка
- Настраиваемый внешний вид сюжета
Почему выбирают ptc mathcad?
Безопасная передача проектных замыслов и инженерных знаний
Интуитивно понятное построение расчетов с использованием стандартных математических обозначений
Создание документов профессионального качества с использованием математических вычислений, графиков, текста и изображений профессионального качества
Многофункциональные стандартизованные вычисления
Повышение производительности за счет полной поддержки единиц измерения на протяжении вычислений
Ускорение обучения и внедрение с мгновенным доступом к электронному обучению
Защита контента
Наши инженерные расчеты — это ценные корпоративные активы.ptc mathcad Prime 5.0 предлагает защиту и блокировку области, так что вы можете контролировать степень доступа и видимость, которые должны иметь другие. ptc mathcad Prime 5.0 позволяет без проблем защищать вашу работу и делиться ею.
Полная совместимость
Тратьте меньше времени на переключение между приложениями или попытки координировать работу. Теперь вы можете встраивать содержимое из других приложений в рабочие листы ptc mathcad Prime 5.0, а также копировать и вставлять несколько областей рабочего листа в MS Word.
Повышенное удобство использования
Обтекание формулами означает, что ваши вычисления не исчезнут с края страницы. Вы даже можете обернуть его по мере ввода.
Улучшения производительности
У вас есть рабочий лист на 100 страниц или больше? В этом новом выпуске стало проще создавать, систематизировать и работать с большими и сложными таблицами.
ptc mathcad Express
Бесплатное программное обеспечение для инженерной математики
Вычисления лежат в основе инженерии.