Выделение n–го столбца матрицы M;
Vn
V [ n
Выделение n–го элемента вектора V;
Mm,n
M [(m,n)
Выделение элемента (m, n) матрицы M.
Под понятием “векторизация” подразумевается одновременное проведение математических операций в их скалярном значении над всеми элементами вектора или матрицы, помеченными векторизации. Это можно понимать и как возможность параллельных вычислений.
Если А и В – векторы, то А*В даёт скалярное произведение этих векторов. Но то же произведение под знаком векторизации создает новый вектор, каждый j-й элемент которого есть произведение j –х элементов векторов А и В. Векторизация позволяет использовать скалярные операторы и функции с массивами.
2.2 Векторные и матричные функции.
Существует также ряд встроенных векторных и матричных функций. Приведем векторные функции, входящие в систему Math CAD:
lenght (V)
возвращает длину вектора;
last (V)
возвращает индекс последнего элемента;
возвращает максимальный по значению элемент;
min (V)
возвращает минимальный по значению элемент;
Re (V)
возвращает вектор действительных частей вектора с комплексными элементами;
Im (V)
возвращает вектор мнимых частей вектора с комплексными элементами;
ε (i, j, k)
полностью асимметричный тензор размерности три.
Лаб 12. ВектМатр в MathCad
Лабораторная работа 4-5
Тема: Использование векторных и матричных операций для решения задач в системе MathCad
Задание:
Задать два вектора X и Y с пятью элементами двумя способами. Элементы первого вектора – произвольно заданные числа. Элементы 2 –го вектора вычисляются по формуле: .
Выполнить следующие преобразования: элементы вектора Х удвоить, элементы вектора Y увеличить на 1.

Получить вектор Z, равный сумме векторов X и Y. Найти скалярное произведение векторов X и Y.
Задать два вектора X и Y из трех элементов. Найти их скалярное и векторное произведения, используя соответствующие «кнопки» на панели инструментов «Matrix».
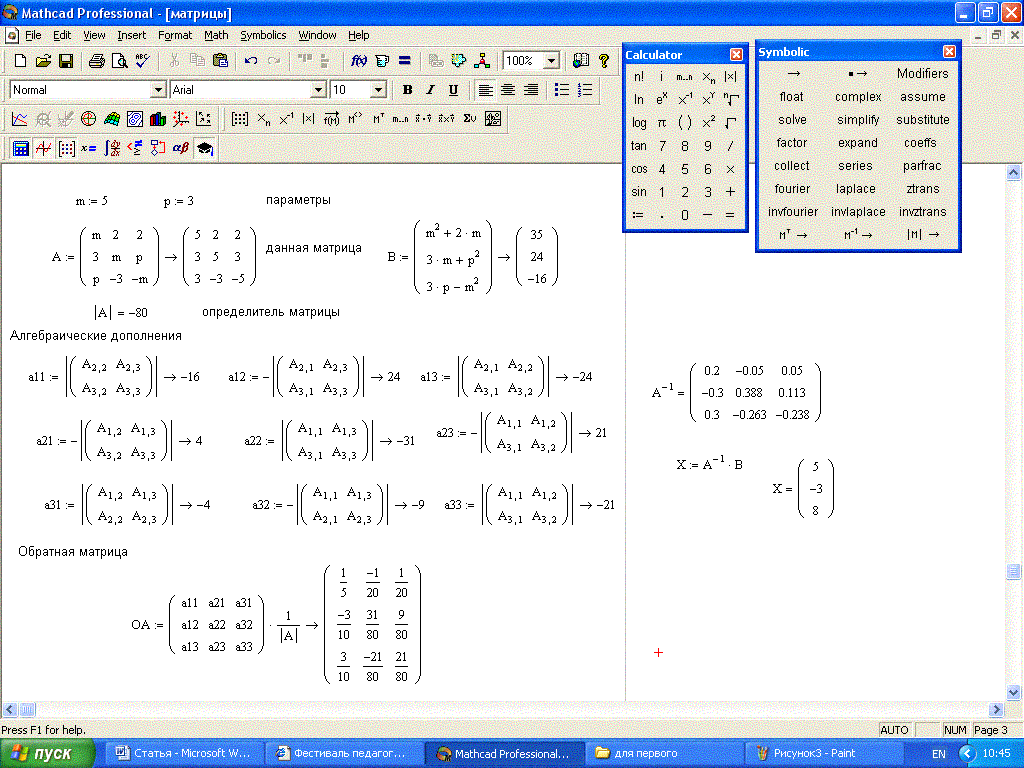
Задать две квадратные матрицы А и В одинаковых размеров (не больше 5). Получить: сумму матриц, разность матриц, произведение, определитель каждой из матриц.
Найти обратные матрицы. Произвести проверку того, что обратные матрицы вычислены верно.
Найти скалярное произведение первой строчки матрицы А на ее последний столбик.
Преобразовать матрицу А по правилу: элементы умножить на максимальный элемент этой матрицы (воспользоваться функцией мax из мастера функций).
Преобразовать матрицу В по правилу: элементы каждой строчки умножить на максимальный элемент этой строчки (воспользоваться функцией мax из мастера функций).
Найти суммы элементов в каждом из столбиков матрицы А.
Найти суммы элементов в каждом из строк матрицы А.
Найти сумму всех элементов матрицы А.
Соединить (дописывая справа) матрицы в одну матрицу D. Из второй строки матрицы D получить вектор K.
Повторить пункт 12, но соединение организовать дописыванием вниз.
Определить функцию . Определить функцию с именем — как производную от функции Fun.
Построить две матрицы, у одной матрицы элементы должны вычисляться по формуле: . У другой матрицы элементы , где t1 и t2 — переменные, принимающих значения из промежутка (каждая из своего промежутка значений).
Заметим, что размеры матрицы V зависят от выбранных промежутков и шагов.
Порядок выполнения работы
Загрузить систему Mathcad.
Познакомиться с методическим указанием.
Выполнить задание.
Подготовить отчет. В отчет включить разделы: тема, ход работы, вывод.
Сдать работу преподавателю.
Задание векторов и матриц
Векторы могут рассматриваться как матрицы, состоящие из одного столбца. Существуют две возможности задания векторов и матриц:
С помощью индексированных переменных. Любая индексированная переменная, индексами которой являются переменные, принимающие целочисленные значения из некоторого промежутка, уже представляют собой вектор или матрицу.
Пример. Требуется задать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.
Решение:
А) задать индексированный промежуток для переменной i:
i := 0..5 (знак .. появляется после набора ;)
В) присвоить элементам вектора х значения индексов (к индексу можно перейти с помощью символа
— левой квадратной скобки, либо с помощью кнопки на панели инструментов):xi := i
C) «распечатать» вектор:
С помощью использования команды Matrix. Взять эту команду можно либо из меню «Insert»(а), либо на панели инструментов «Matrix»(в), как это показано на рис.1. В открывшемся диалоговом окне «Insert Matrix» необходимо указать число строк и число столбцов.
 В нашем примере число
строк равно 6, а число столбцов равно
1. Решение предыдущего примера в этом
случае сводится к последовательности
действий:
В нашем примере число
строк равно 6, а число столбцов равно
1. Решение предыдущего примера в этом
случае сводится к последовательности
действий:
х:=
выполнить команду Matrix;
задать параметры в диалоговом окне «
заполнить шаблон, который откроется после нажатия кнопки «Ok».
P.S. Диалоговое окно «Insert Matrix» содержит кнопку «Delete». Если выделен один из элементов матрицы, эта кнопка позволяет удалить число строк (находящихся ниже выделенного элемента) и столбцов (находящихся справа от выделенного элемента), которое будет указано в полях диалогового окна. Аналогично с помощью команды «Insert» можно вставить заданное число строк и столбцов.
Рис.1. Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»
Операции с векторами и матрицами, матричные функции
С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе MathCad обозначаются так, как это принято в математике: —, +
, *, … . На рис. 2 показаны назначение некоторых команд, расположенных на панели инструментов «Matrix».Х-1 – получить обратную матрицу
|X| — вычислить детерминант
МТ – транспонировать
М< > — из матрицы взять вектор-столбец
v – получить сумму элементов
-скалярное произведение векторов
— векторное произведение векторов
Рис.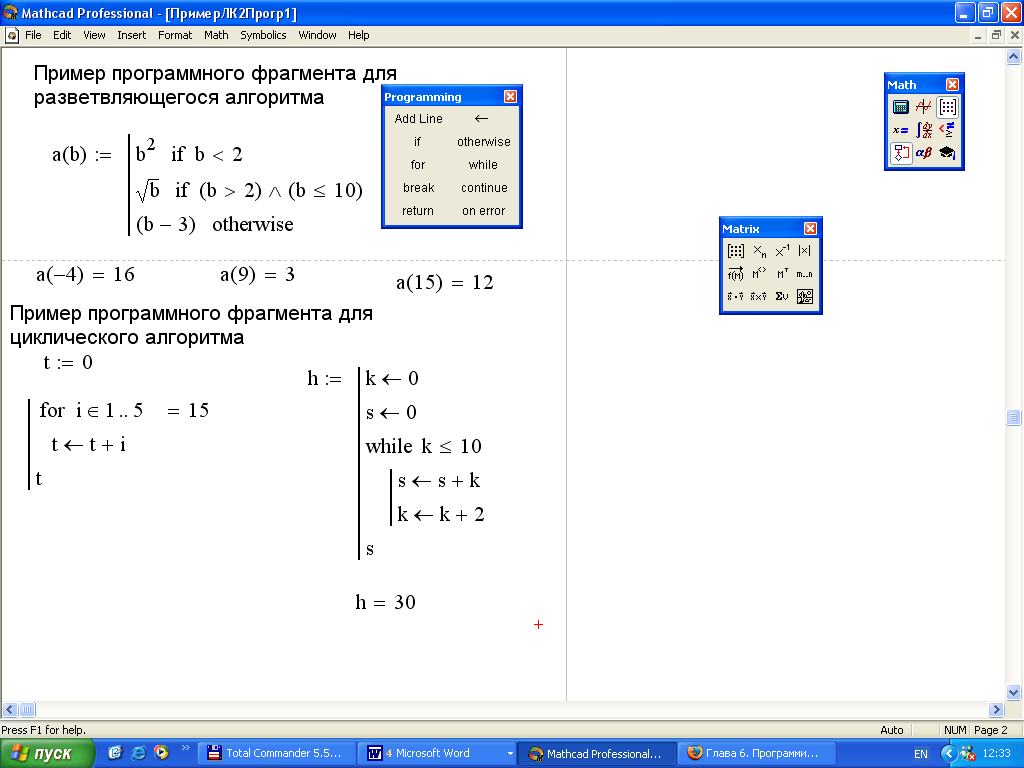 2. Назначение
некоторых команд, расположенных на
панели инструментов «Matrix».
2. Назначение
некоторых команд, расположенных на
панели инструментов «Matrix».
Рис.3. Вызов мастера функций
Вызов мастера функций открывает диалоговое окно, как это показано на рис.4. В этом окне следует открыть категорию «Vector and Matrix», как это показано на рис.4. В окне «Function Name» перечислены имена функций для выбранной категории в алфавитном порядке. А внизу комментарии по их назначению и использованию.
Рис.4. Диалоговое окно мастера функций
Формирование из вектора диагональной матрицы
Формирование матрицы заданного размера с элементами
d i,j =F(i,j),
где F – определенная функция
Соединение двух матриц в одну матрицу (рядом –функция augment, друг под другом — функция stack)
Выделение подматрицы из матрицы v
Формирование вектора из матрицы по его номеру
Преобразование прямоугольных координат в цилиндрические координаты и наоборот
Рис. 5. Примеры
использования функций и операторов для
работы с векторами и матрицами
5. Примеры
использования функций и операторов для
работы с векторами и матрицами
Контрольные вопросы
Какие операции представлены на панели инструментов «Matrix»?
Как задать вектор? Как задать матрицу?
Как задать матрицу с элементами, вычисленными по формулам?
Найти функцию еlement.и пояснить ее назначение?
Найти функцию rank.и пояснить ее назначение?
Как из матрицы получить вектор – столбец? Вектор-строчку?
Как получить обратную матрицу?
Когда обратную матрицу вычислить нельзя?
Как проверить, вычислена ли обратная матрица правильно?
Где взять функции для работы с матрицами?
Как создать единичную матрицу?
MathCAD — это просто! Часть 11. Продолжаем работать с матрицами
Матрицы — вещь важная, а потому было бы просто непростительно отводить на них всего одну статью из нашего цикла о работе в среде MathCAD. Узнав о том, как можно транспонировать матрицы, вычислять определители, обратные матрицы, а также перемножать и складывать их, сегодня мы с вами продолжим издевательства над этими важными в математике объектами. Думаю, что изложенные ниже сведения будут полезны и в практических вычислениях, производимых в среде MathCAD, ведь матрицы очень часто встречаются в реальных задачах.Еще о вспомогательных функциях
В прошлый раз мы немного поговорили о специальных MathCAD’овских функциях, позволяющих разрезать матрицы на составные части или же склеивать их. Это не единственные из вспомогательных функций, действующих над матрицами, которые могут пригодиться в практике повседневной работы. Пришло время познакомиться с некоторыми другими функциями, которые также имеют неплохой шанс оказаться весьма и весьма полезными. Особую роль в матричном исчислении играют единичные матрицы. На всякий случай напомню, что единичной называется такая матрица, у которой все недиагональные элементы равны нулю, а элементы, расположенные на главной диагонали (от верхнего левого угла к нижнему правому), равны единице. Единичные матрицы могут иметь самые разные размеры. Чтобы пользователь не тратил свое время на вбивание нулей и единиц в строки и столбцы такой матрицы, в MathCAD’е имеется специальная функция Identity, создающая единичную матрицу заданного размера. У этой функции есть единственный аргумент, задающий размерность матрицы.
Пришло время познакомиться с некоторыми другими функциями, которые также имеют неплохой шанс оказаться весьма и весьма полезными. Особую роль в матричном исчислении играют единичные матрицы. На всякий случай напомню, что единичной называется такая матрица, у которой все недиагональные элементы равны нулю, а элементы, расположенные на главной диагонали (от верхнего левого угла к нижнему правому), равны единице. Единичные матрицы могут иметь самые разные размеры. Чтобы пользователь не тратил свое время на вбивание нулей и единиц в строки и столбцы такой матрицы, в MathCAD’е имеется специальная функция Identity, создающая единичную матрицу заданного размера. У этой функции есть единственный аргумент, задающий размерность матрицы.
Для определения размера матриц можно использовать функции Rows и Cols. Каждая из них имеет один-единственный входной параметр, которым является сама матрица, а на выходе выдают значения числа строк и столбцов соответственно. Для определения размера вектора можно использовать функцию length, которая работает аналогично указанным для матриц функциям.
Интересной также является предоставляемая MathCAD’ом функция для сортировки элементов векторов. Называется она просто и незатейливо — Sort. В качестве входного параметра этой функции нужно передать вектор, сортировкой которого мы будем заниматься, и на выходе получим почти такой же вектор, только его элементы будут упорядочены по возрастанию. Для сортировки строк и столбцов матрицы можно воспользоваться соответственно функциями Rsort и Csort, которым нужно передать в качестве параметров саму матрицу и номер того столбца или строки, которые должны быть отсортированы. Правда, работают эти функции несколько загадочно, иногда сортируя не только нужный столбец (строку), но и все остальные (см. соответствующую иллюстрацию). Чтобы изменить порядок следования чисел в векторе или порядок строк в матрице на противоположный, нужно воспользоваться функцией Reverse, в качестве аргумента для которой нужно передать изменяемые матрицу или вектор.
Правда, работают эти функции несколько загадочно, иногда сортируя не только нужный столбец (строку), но и все остальные (см. соответствующую иллюстрацию). Чтобы изменить порядок следования чисел в векторе или порядок строк в матрице на противоположный, нужно воспользоваться функцией Reverse, в качестве аргумента для которой нужно передать изменяемые матрицу или вектор.Ранг и норма матрицы
Два фундаментальных понятия, играющих очень важную роль в линейной алгебре — это ранг и норма матрицы. MathCAD позволяет пользователю вычислять эти характеристики матриц без лишних усилий, и сейчас я расскажу, как именно это делается.
Минором матрицы порядка k называется определитель, вычисленный для матрицы, образованной из k столбцов и k строк данной матрицы. Главным минором называется минор, для которого номера выбранных столбцов совпадают с номерами выбранных строк. Понимаю, это определение звучит несколько громоздко, но я думаю, если вы прочитаете его внимательно еще раз, то все станет просто и понятно. Рангом матрицы называется наибольший порядок среди всех ее ненулевых миноров. Ранг матрицы характеризует число линейно независимых столбцов или строк матрицы, а потому в матричной алгебре эта характеристика используется весьма широко. Для вычисления ранга матрицы в MathCAD’е используется функция Rank, которой в качестве аргумента передается та самая матрица, ранг которой нужно вычислить.Норма матрицы — понятие более расплывчатое, чем ранг. Для полного определения нормы матрицы используется система ограничений, которым должен подчиняться строящийся по определенным правилам функционал. Вы можете найти подробное определение нормы матрицы в любом учебнике по линейной алгебре. Мы же сейчас удовлетворимся знанием того, что норма матрицы — это некоторый аналог величины, который для векторов называют длиной (норма вектора как раз и есть его длина). Впрочем, в отличие от длины вектора, где все понятно и определенно, норма матрицы может вычисляться несколькими разными способами, и в зависимости от способа вычисления ее величина может быть различной. Всем функциям для вычисления нормы матрицы, о которых здесь идет речь, требуется в качестве аргумента передавать ту матрицу, для которой будет вестись вычисление нормы. Функция Norm1 определяет норму путем складывания модулей элементов для каждого из столбцов и выбором наибольшей из получившихся для столбцов сумм. Функция Normi работает аналогичным образом, только для вычисления сумм там используются не столбцы, а строки. Функция Norme вычисляет норму матрицы по тому же алгоритму, по какому вычисляется норма вектора: квадраты всех элементов матрицы суммируются, а затем из полученного числа извлекается корень.
Всем функциям для вычисления нормы матрицы, о которых здесь идет речь, требуется в качестве аргумента передавать ту матрицу, для которой будет вестись вычисление нормы. Функция Norm1 определяет норму путем складывания модулей элементов для каждого из столбцов и выбором наибольшей из получившихся для столбцов сумм. Функция Normi работает аналогичным образом, только для вычисления сумм там используются не столбцы, а строки. Функция Norme вычисляет норму матрицы по тому же алгоритму, по какому вычисляется норма вектора: квадраты всех элементов матрицы суммируются, а затем из полученного числа извлекается корень.Собственные вектора и собственные значения матриц
Собственным вектором x и собственным значением ? матрицы X называются такие вектор и число соответственно, которые удовлетворяют соотношению xX = ?x. Обычно матрица имеет несколько собственных векторов и соответствующих им собственных значений, а потому мы будем рассматривать именно этот случай. Конечно, в MathCAD’е не слишком сложно с помощью некоторых преобразований рассчитать необходимые числа и вектора самостоятельно, однако можно еще больше упростить себе жизнь, воспользовавшись встроенными в эту среду функциями.
Функция Eigenvecs принимает в качестве входного параметра некоторую матрицу, а возвращает другую, содержащую собственные вектора исходной. При интерпретации результатов работы этой функции необходимо помнить, что в MathCAD’е вектора записываются в виде столбцов, так что и в этой матрице каждый из столбцов является собственным вектором первоначальной матрицы. Другая функция, Eigenvals, также принимает на вход некоторую матрицу, однако выдает для нее уже не собственные вектора, а собственные значения. Записываются они также в виде столбика. В этом столбце они идут в том же порядке, что и столбцы в матрице, возвращаемые первой функцией. То есть i-му столбцу матрицы, получаемой на выходе функцией Eigenvecs, соответствует i-е собственное значение в векторе. Впрочем, проследить соответствие собственных векторов и собственных значений для матрицы можно и более наглядным образом. Для этого существует специальная функция Eigenvec (не путайте с Eigenvecs), которой на вход передаются матрица и одно из ее собственных значений, а она уже вычисляет соответствующий этому собственному значению собственный вектор.
Для этого существует специальная функция Eigenvec (не путайте с Eigenvecs), которой на вход передаются матрица и одно из ее собственных значений, а она уже вычисляет соответствующий этому собственному значению собственный вектор.Скалярное и векторное произведение векторов
Напоследок поговорим о вещах довольно простых, но очень распространенных в практике решения задач, а потому особенно важных. Сейчас мы рассмотрим, как с помощью MathCAD’а вычислять скалярное и векторное произведение векторов. Напомню, что скалярным произведением x.y называется число, равное x0y0 + x1y1 + x2y2 + … + xnyn, а вот с векторным все несколько сложнее. Оно определяется только для трехмерных векторов и вычисляется как определитель матрицы, составленной из базисных векторов (i, j и k) и элементов тех векторов, для которых вычисляется векторное произведение. Традиционно в математике векторное произведение обозначают c помощью крестика, который ставится между двумя перемножаемыми векторами.
Для вычисления скалярного и векторного произведения векторов обратимся снова к панели матричных вычислений, неоднократно выручавшей нас в наших упражнениях с MathCAD’ом. Скалярное произведение называется на ней Dot Product и обозначается как точка между двумя векторами, а векторное — Cross Product и обозначается крестиком, как я уже говорил выше. Чтобы перемножить два вектора, вы можете сначала обозначить их с помощью каких- либо символьных обозначений, а можете сразу записывать произведения между столбцами чисел.Теперь, пожалуй, о матрицах самое основное и важное сказано. Как видите, в плане работы с векторами и матрицами MathCAD ничуть не менее мощный, чем во всем остальном. Поэтому использовать эту среду для матричных вычислений можно и нужно. Ну а как это делать, вы теперь уже знаете.
Компьютерная газета. Статья была опубликована в номере 24 за 2008 год в рубрике soft
Значение должно быть скаляром или матрицей маткад
Значение должно быть скаляром или матрицей маткад
Автор Alexandr Molskiy задал вопрос в разделе Другие языки и технологии
MathCAD значений должно быть скаляром и получил лучший ответ
Ответ от А[гуру]
Потому что у тебя переменная t — вектор. Нижний индекс означает элементы массива (вектора, матрицы) . Надо писать так t1, t2 — без нижнего индекса.
Нижний индекс означает элементы массива (вектора, матрицы) . Надо писать так t1, t2 — без нижнего индекса.
1.4. Техника безопасности при работе с «болгаркой»
Болгарка — довольно опасный
подробнее.
Предполагается, что стрелок удерживает пистолет в правой руке.
Главное в
подробнее.
Некоторые из операторов Mathcad имеют особые значения в применении к векторам и матрицам. Например, символ умножения означает просто умножение, когда применяется к двум числам, но он же означает скалярное произведение, когда применяется к векторам, и умножение матриц — когда применяется к матрицам.
Таблица описывает векторные и матричные операторы Mathcad. Многие из этих операторов доступны из палитры символов. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку.
Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования [Ctrl]1.
Операторы, не перечисленные в этой таблице, не будут работать для векторов и матриц. При попытке использовать такой оператор с вектором или матрицей Mathcad будет отмечать это сообщением об ошибке «неверная операция с массивом», или «нескалярная величина». Можно, однако, использовать оператор векторизации, чтобы выполнить любую скалярную операцию или функцию поэлементно на векторе или матрице. См. раздел «Выполнение параллельных вычислений» ниже в этой главе. Рисунок 9 показывает использование некоторых векторных и матричных операций.
Рисунок 9: Векторные и матричные операции.
В следующей таблице
- A
- u
- M
- и представляют отдельные элементы векторов u и v.
- z представляет скаляр.
- m и n представляют целые числа.
и B представляют массивы (векторы или матрицы).
и v представляют векторы.
представляет квадратную матрицу.
| Операция | Обозначение | Клавиши | Описание | |
| Умножение матрицы на скаляр | * | Умножает каждый элемент A на скаляр z. | ||
| Скалярное произведение | * | Возвращает скаляр: . Векторы должны иметь одинаковое число элементов. | ||
| Матричное умножение | * | Возвращает произведение матриц A и B, число столбцов в A должно соответствовать числу строк в B. | ||
| Умножение матрицы на вектор | * | Возвращает произведение матриц A и v, число столбцов в A должно соответствовать числу строк в v. | ||
| Деление | / | Делит каждый элемент массива на скаляр z. | ||
| Сложение векторов и матриц | A + B | + | Складывает соответствующие элементы A и B, массивы A и B должны иметь одинаковое число строк и столбцов. | |
| Скалярная сумма | A + z | + | Добавляет z к каждому элементу A. | |
| Векторное и матричное вычитание | A — B | — | Вычитает соответствующие элементы массива A из элементов массива B, массивы A и B должны иметь одинаковые размеры. | |
| Скалярное вычитание | A — z | — | Вычитает z из каждого элемента A.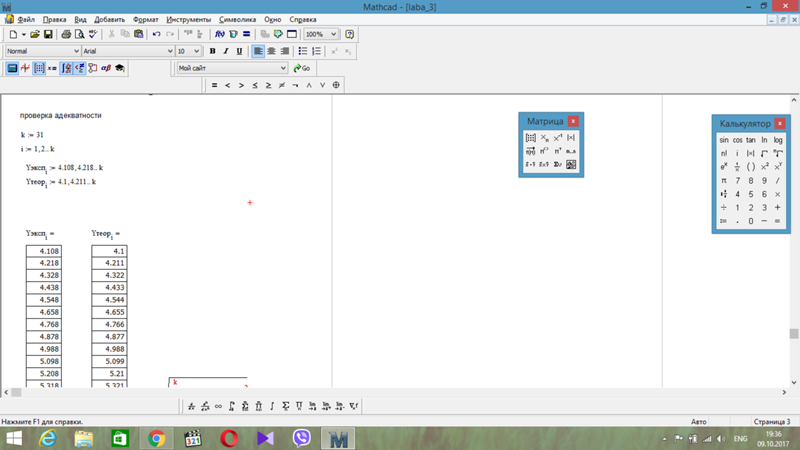 | n-ная степень квадратной матрицы M (использует умножение матриц). n должен быть целым числом. M −1 представляет матрицу, обратную к M, другие отрицательные степени — степени обратной матрицы. Возвращает матрицу. |
| Длина вектора | |v| | | | Возвращает , где — вектор, комплексно сопряженный к v. | |
| Детерминант | |M| | | | Возвращает детерминант квадратной матрицы M, результат — скаляр. | |
| Транспонирование | A T | [Ctrl]1 | Возвращает матрицу, чьи строки — столбцы А, и чьи столбцы — строки A. А может быть вектором или матрицей. | |
| Векторное произведение | u x v | [Ctrl]8 | Возвращает векторное произведение для векторов с тремя элементами u и v. | |
| Комплексное сопряжение | « | Меняет знак мнимой части каждого элемента A. | ||
| Суммирование элементов | [Ctrl]4 | Суммирует элементы вектора v; возвращает скаляр. | ||
| Векторизация | [Ctrl] — | Предписывает в выражении с A производить операции поэлементно. Полное описание дано в разделе «Выполнение параллельных вычислений» | ||
| Верхний индекс | A | [Ctrl]6 | Извлекает n-ный столбец массива A. Возвращает вектор. | |
| Нижний индекс (вектора) | vn | [ | n-ный элемент вектора. | |
| Нижние индексы матрицы | Am,n | [ | Элемент матрицы, находящийся в m-ном ряду и n-ной строке. |
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
MathCAD — это система, ориентированная на пользователя, который не обязан знать абсолютно ничего о программировании. Создатели MathCAD изначально поставили перед собой такую задачу, чтобы дать возможность профессионалам — математикам, физикам и инженерам самостоятельно проводить сложные расчеты, не обращаясь за помощью к программистам. Несмотря на блестящее воплощение этих замыслов, выяснилось, что совсем без программирования MathCAD серьезно теряет в своей силе, в основном, из-за недовольства пользователей, знакомых с техникой создания программ.
В очень ранних версиях MathCAD встроенного языка программирования не было. Чтобы применять привычные операции проверки условий и организовывать циклы, приходилось изобретать причудливую смесь из встроенных функций if и until, а также комбинаций ранжированных переменных. Но надо отметить, что использование ранжированных переменных — мощный аппарат MathCAD, похожий на применение циклов в программировании. В подавляющем большинстве случаев намного удобнее организовать циклы с помощью ранжированных, чем заниматься для этого программированием.
И тем не менее встроенный язык программирования MathCADпозволяет решать самые различные, в том числе и довольно сложные, задачи и является серьезным подспорьем для расчетов. Поэтому последние версии MathCAD имеют не очень мощный, но весьма элегантный собственный язык программирования.
Для вставки программного кода в документы MathCAD имеется специальная панель инструментов . Большинство кнопок этой панели выполнено в виде текстового представления операторов программирования, поэтому их смысл легко понятен. Операторы программирования могут быть введены только с этой панели, но никак не с клавиатуры (можно еще их вводить с помощью сочетаний клавиш, которые приведены в тексте всплывающей подсказки).Создание программного блока начинается с команды
. Нажатие этой клавиши приведет к тому, что в рабочей области документа появится вертикальная черта, а справа от нее — два пустые поля ввода . Вертикальная черта означает, что строки, находящиеся справа от нее, образуют линейную программную последовательность операций. Эта черта является особенностью программ MathCAD. В полях ввода можно ввести две первые строки программы, а если требуется большее число строк, то необходимо нажимать клавишу столько раз, сколько необходимо строк. Не стоит забывать, что программа является полноценным выражением MathCAD. Это выражение может быть использовано для присвоения значения скалярной или векторной переменной или определения функции, или даже в составе другого выражения, в том числе и другой программы.
Нажатие этой клавиши приведет к тому, что в рабочей области документа появится вертикальная черта, а справа от нее — два пустые поля ввода . Вертикальная черта означает, что строки, находящиеся справа от нее, образуют линейную программную последовательность операций. Эта черта является особенностью программ MathCAD. В полях ввода можно ввести две первые строки программы, а если требуется большее число строк, то необходимо нажимать клавишу столько раз, сколько необходимо строк. Не стоит забывать, что программа является полноценным выражением MathCAD. Это выражение может быть использовано для присвоения значения скалярной или векторной переменной или определения функции, или даже в составе другого выражения, в том числе и другой программы.Для определения функции это будет выглядеть следующим образом:
Внутри программы можно использовать глобальные переменные документа, но изменить их значение внутри программы никак нельзя. Можно создать в программе другие переменные, доступ к которым может осуществляться только из самой программы. Эти переменные называются локальными переменными. Локальные переменные «не видны» извне. Локальная переменная создается с помощью знака локального присвоения
с панели Programming. Для оператора локального присваивания, так же как и для операторов обычного и глобального присваивания, можно изменить внешний вид так, чтобы он выглядел как обычный знак равенства. Для этого достаточно вызвать контекстное меню этого оператора и в нем выбрать команду View Definition As/Equal.Последняя строка любой программы не должна содержать никаких управляющих операторов. Эта строка задает значение, возвращаемое программой. В качестве этого значения может быть скаляр (число или переменная), вектор или матрица. Таким образом, последняя строка программы может содержать имя локальной переменной либо некоторое математическое выражение, куда входят как локальные, так и глобальные переменные, либо вектор или матрицу.
Вставить строку программного кода в уже созданную программу можно в любой момент с помощью той же самой кнопки Add Line. Для этого следует поместить на нужное место внутри программы линии ввода.
Если вертикальная линия ввода находится в начале текущей строки, то нажатие кнопки
приведет к появлению новой строки перед текущей строкой, если вертикальная линия ввода находится в конце строки, то нажатие кнопки приведет к появлению новой строки после текущей. Можно выделить только часть текущей строки, что повлияет на положение новой строки в программе (например, если необходимо для некоторого условия выполнить не одно действие, а несколько). Таким образом, основной принцип создания программных модулей заключается в правильном расположении строк кода. Ориентироваться в их действии довольно легко, т.к. фрагменты кода одного уровня сгруппированы в программе с помощью вертикальных черт.Проверка условий в программах.
Программы в MathCAD могут быть не только линейными, но и разветвленными. Одним из вариантов ветвления в программах является проверка условия. Условия могут проверять значения как локальных, так и глобальных переменных, а также выражений, содержащих эти переменные.
Для проверки условий в программах MathCAD служит оператор if
. В поле ввода справа нужно ввести условие. Для ввода условий служит панель Boolean. На этой панели есть кнопки, предназначенные для проверки условий , а также кнопки, предназначенные для вставки логических операций (логическое отрицание, операция «и», операция «или», операция «исключающее или»). Вторые позволяют создавать сложные условия. В поле ввода слева нужно ввести строку программы, которая должна выполняться, если введенное условие истинно.Если для условия «истинно» необходимо выполнение нескольких строк программы, надо воспользоваться кнопкой
.Если невыполнение условия должно привести к выполнению какого-либо иного программного кода, можно в строке, следующей за оператором if, вставить оператор
. В поле ввода слева от этого оператора необходимо ввести строку программы, которая будет выполняться только в том случае, если не выполнилось условие, заданное в операторе if.
В поле ввода слева от этого оператора необходимо ввести строку программы, которая будет выполняться только в том случае, если не выполнилось условие, заданное в операторе if.Следует помнить, что если в программе введено подряд несколько строк с оператором if
, то выражение слева от оператора otherwise будет выполнено только в том случае, если не выполняются условия, заданные во всех операторах if.Другим очень важным элементом при создании нелинейных программ являются циклы. Циклы позволяют повторять несколько раз выполнение одного и того же программного блока. Для создания циклов в MathCAD предусмотрено два оператора for и while.
Цикл for — цикл со счетчиком.
В таких циклах создается некоторая переменная-счетчик, значение которой изменяется после каждого выполнения тела цикла. Выход из цикла происходит при достижении этой переменной заданного значения. Этот оператор вводится с панели Programming клавишей for
. В поле ввода после слова for следует указать имя переменной — счетчика. Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения. В поле ввода после знака следует указать диапазон значений переменной-счетчика. Вводить диапазон в данном случае следует так же, как и при создании ранжированной переменной. Вместо диапазона в данном поле ввода можно указать имя некоторого массива (вектора или матрицы). В этом случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Возможность перебора элементов массива не может быть реализована с помощью цикла while, поэтому именно в таких случаях цикл for и является незаменимым. В поле ввода под словом for следует ввести тело цикла.Пример: Заполнить вектор числами от xнач до xкон с шагом h. Затем определить сумму элементов этого вектора и найти их среднее арифметическое значение.
Цикл while — цикл, который выполняется до тех пор, пока выполняется определенное условие.
В поле ввода справа от слова while следует ввести условие. Это условие строится по тем же правилам, что и в операторе if. Оно будет проверяться после каждого выполнения тела цикла и в тот момент, когда условие перестанет выполняться, повторение тела цикла прекратится. В поле ввода ниже слова while следует ввести тело цикла (напомним, что для ввода нескольких строк в теле цикла надо воспользоваться кнопкой Add Line).Пример1: Вычислить сумму
с точностью е.Пример2: Найти первый элемент, превышающий определенный порог.
Использование операторов break и continue.
Иногда возникает необходимость повлиять на выполнение цикла некоторым образом, например, прервать его выполнение по какому-либо условию или выполнять некоторые итерации не так, как другие. Для этого и служат операторы break и continue.
Оператор break, если он расположен внутри цикла, означает немедленное прекращение выполнения текущей итерации и выход из цикла. Если есть необходимость прекратить выполнение цикла по какому-либо условию, то следует использовать конструкцию следующего вида break if (условие).
Пример: Выделить из массива все элементы от начала и до первого вхождения в него заданного числа.
Оператор continue используется для того, чтобы немедленно перейти в начало цикла и начать следующую итерацию. Этот оператор также обычно используется в составе конструкции вида continue if (условие). Оператор continue используется в случаях, когда необходимо чтобы некоторые вычисления производились для одних итераций и не производились для других.
Пример: Требуется заполнить элементы квадратной матрицы в шахматном порядке.
Оператор return (возврат значения).
Как мы уже указывали, результат выполнения программного модуля помещается, как правило, в последней его строке.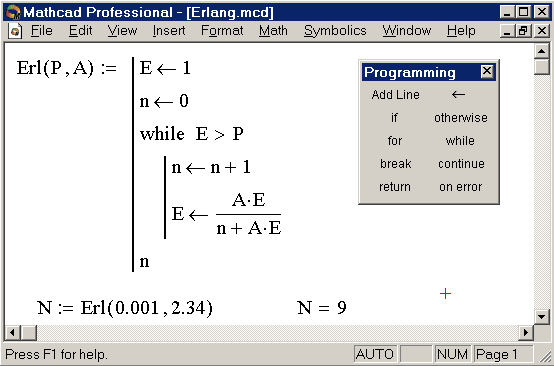 Но можно прервать выполнение программы в любой ее точке (например, с помощью условного оператора) и выдать некоторое значение, применив оператор return. В этом случае при выполнении указанного условия значение, введенное в поле ввода после return, возвращается в качестве результата, и никакой другой код больше не выполняется. Вставляется в программу оператор return с помощью одноименной кнопки панели Programming
Но можно прервать выполнение программы в любой ее точке (например, с помощью условного оператора) и выдать некоторое значение, применив оператор return. В этом случае при выполнении указанного условия значение, введенное в поле ввода после return, возвращается в качестве результата, и никакой другой код больше не выполняется. Вставляется в программу оператор return с помощью одноименной кнопки панели Programming
Система MathCAD предоставляет пользователю некоторый контроль над ошибками, которые могут возникнуть при вычислении выражений или при выполнении программ. Для этой цели служит оператор on error, который можно вставить с помощью одноименной кнопки панели Programming
. В поле ввода справа следует ввести выражение или программу, которые необходимо вычислить (известно, что это выражение может содержать ошибку при определенных значениях входных параметров). В поле ввода слева следует ввести выражение, которое будет выполнено вместо правого выражения, если при выполнении последнего возникнет ошибка. Пример: Если аргументу функции присвоено нулевое значение, то в программе возникает ошибка — деление на нуль. Но за счет оператора on error сообщение не выводится, а функции в этой точке присваивается значение, указанное слева от оператора on error — значение машинной бесконечности.В поле ввода слева может быть введено текстовое выражение, сообщающее об ошибке
Конечно, если программа содержит только простейшие математические операции, то никаких ошибок, кроме деления на нуль или превышения наибольшего допустимого числа в ней возникнуть не может. В таких программах оператор on error используется редко. Но для более сложных программ, которые содержат функции решения дифференциальных уравнений, аппроксимации или другие сложные функции MathCAD, использование on error может избавить от многих трудностей.
Иногда может возникнуть ситуация обратная той, которая была описана выше, т.е. необходимо, чтобы при определенных условиях результатом выражения было сообщение об ошибке, хотя в действительности при этом не возникает ни одной стандартной ошибки MathCAD. Для таких случаев в MathCAD предусмотрена встроенная функция error. В качестве аргумента этой функции нужно в кавычках указать текст сообщения об ошибке, который должен быть выведен. Таким образом, если необходимо, чтобы программа возвращала ошибку при определенном условии, то следует использовать конструкцию вида: error («текст ошибки») if (условие).
Для таких случаев в MathCAD предусмотрена встроенная функция error. В качестве аргумента этой функции нужно в кавычках указать текст сообщения об ошибке, который должен быть выведен. Таким образом, если необходимо, чтобы программа возвращала ошибку при определенном условии, то следует использовать конструкцию вида: error («текст ошибки») if (условие).
Для того, чтобы иметь возможность нормально вводить текст на русском языке в аргумент функции error (а также во все другие функции со строками), следует изменить шрифт, который используется во встроенном стиле Constant. Для того чтобы этот стиль правильно отображал русские буквы, установите курсор на любом числе или строковом выражении в формульном блоке. При этом в поле на панели инструментов Formatting, отображающем текущий стиль, должно быть написано — Constant. Теперь выберите из раскрывающегося списка шрифтов шрифт, поддерживающий кириллицу.
1. Вычислить функцию sin(x) с точностью е.
2. Даны массивы А(5) и В(5). Получить массив С, в который записаны сначала элементы
массива А в порядке возрастания, а затем элементы массива В порядке убывания
3. По введенным значениям коэффициентов А, В, С определить корни квадратного уравнения
4. Дан массив натуральных чисел В(10). Определить, есть ли в нем 4 последовательных числа (например, 1, 2, 3, 4, и т.п.). Напечатать такие группы чисел.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8802 —
| 7162 — или читать все.78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
НАШ САЙТ РЕКОМЕНДУЕТ:
Операции с векторами и матрицами, матричные функции в математическом пакете MathCad
Матричное исчисление играет важную роль в компьютерной математике. Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами. Вообще говоря, нельзя назвать ни одной области использования компьютера, в алгоритмах которой (в большей или меньшей степени) не использовались бы матрицы.
Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами. Вообще говоря, нельзя назвать ни одной области использования компьютера, в алгоритмах которой (в большей или меньшей степени) не использовались бы матрицы.
Понятие «вектор» обычно не отделяют от понятия «матриц». Векторы могут рассматриваться как матрицы, состоящие из одного столбца (или строки).
Матричные вычисления в MathCAD можно условно разделить на три основных типа.
К первому относятся такие элементарные действия над матрицами, как создание, извлечение из них данных, их умножение, сложение или скалярное произведение (в случае векторов). Для их реализации служат специальные операторы трех панелей семейства Math (Математические): Calculator (Калькулятор), Matrix (Матричные) иSymbolics (Символьные).
Ко второму типу можно отнести те матричные преобразования, которые требуют использования специальных функций и встроенных алгоритмов матричной алгебры, таких как, например, функции вычисления определителя, матричных норм или сортировки элементов векторов по возрастанию. Функции этой группы можно найти в категории Vector and Matrix (Векторные и матричные) у мастера функций.
И, наконец, к третьему типу матричных вычислений следует отнести те задачи, решить которые можно только используя возможности системы программирования MathCAD.
В языках программирования начальные индексы массивов обычно равняются 0. По умолчанию в MathCAD индексы строк и столбцов также отсчитываются с 0. В том случае, если такая система вам неудобна или непривычна, можно изменить точку отсчета индексов на 1, задав системную переменную ORIGIN: ORIGIN:= 1.
Доступ к элементам вектора или матрицы осуществляется с помощью индексированных переменных. Например, чтобы использовать пятый элемент вектора с именем А, нужно записать этот элемент в виде: . А для того, чтобы взять элемент матрицы В, расположенный на пересечении 3-ей строчки и 4-го столбца нужно записать: .
Для задания индексов на панели Matrix предусмотрена специальная кнопка Subscript (Индекс). Перейти к записи индекса можно также с помощью клавиши «[» ( левая квадратная скобка). Нажав ее, вы увидите, что на месте будущего индекса, чуть ниже текста имени матрицы, появится черный маркер. В него через запятую следует ввести значения индексов. На первом месте при этом должен стоять номер строки, а на втором – столбца.
3.1. Создание векторов и матриц
В системе предусмотрены различные возможности задания векторов и матриц:
Определение матрицы последовательным заданием каждого элемента.
С помощью индексированных переменных.
С помощью использования команды Insert→Matrix, либо с помощью соответствующей кнопки панели Matrix.
Задание с помощью элементов программирования.
Применение встроенных функций.
Через связь с другим приложением, например Excel.
Создание таблицы данных.
Чтение из внешнего файла.
Рассмотрим некоторые из них. Определение матрицы последовательным заданием каждого элемента очевидно и не требует пояснений. При создании матрицы или вектора с помощью индексированной переменной следует исходить из того, что любая индексированная переменная, индексами которой являются переменные, принимающие целочисленные значения из некоторого промежутка, уже представляют собой вектор или матрицу.
Пример 1. Требуется сформировать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.
Решение. Предоставим два варианта решения этой задачи:
с помощью индексированной переменной;
с помощью команды Insert→Matrix.
Вариант а
Для того, чтобы сформировать вектор, воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i), а затем будем использовать эту переменную для здания элементных значений вектора x. Формирование вектора представлено на рис. 3.1.
Рис. 3.1. Формирование вектора с использованием индексированной переменной
Вариант b
Формирование вектора х будем производить с помощью команды Matrix. Для этого сначала напишем оператор присваивания: «х:=» , а затем выполним команду Matrix. Эта команда открывает диалоговое окно«Insert Matrix», которое представлено на рис. 3.2, в котором необходимо указать число строк и число столбцов. В нашем примере число строк равно 6, а число столбцов равно 1.
После нажатия кнопки «Ok» команда предоставит шаблон с шестью ячейками, в которые следует вписать значения элементов вектора.
Рис. 3.2. Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»
Пример 2. В файле с именем «int(4_4).txt» записаны числа в виде матрицы четыре строчки по четыре элемента, разделенными пробелами. В файле с именем «int(4_1).txt» записаны числа в столбик. Требуется прочитать эти данные в матрицу Q и вектор P.
В файле с именем «int(4_1).txt» записаны числа в столбик. Требуется прочитать эти данные в матрицу Q и вектор P.
Решение. Для чтения данных из файла в матрицу/вектор можно воспользоваться функцией READPRN, которая имеет один параметр — имя файла. Фрагмент с решением представлен на рис. 3.3.
Рис. 3.3. Чтение данных из файлов
С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе MathCAD обозначаются так, как это принято в математике: —, +, *, … .
На рис. 3.4 показано назначение некоторых специализированных команд, расположенных на панели инструментов Matrix.
Помимо этого, система MathCAD представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x).
Х-1 – получить обратную матрицу
|X| – вычислить детерминант
МТ – транспонировать
М< > – из матрицы взять вектор-столбец
v – получить сумму элементов
–скалярное произведение векторов
–векторное произведение векторов
Рис. 3.4. Назначение некоторых команд, расположенных на панели инструментов «Matrix»
На рис. 3.5 представлены вычисления с использованием операций над матрицами.
Рис. 3.5. Примеры матричных вычислений в MathCAD
Пример 3. Требуется сформировать диагональную квадратную матрицу с(6×6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.
Решение. Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начнем с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рис. 3.6.
Рис. 3.6. Формирование диагональной матрицы
Пример 4. Даны две матрицы: А(4×3) и В(4×2). Требуется объединить эти матрицы в одну матрицу С(4×5), причем, первыми столбцами новой матрицы должны быть столбцы матрицы А, а справа от этих элементов следовать столбцы матрицы В (методом «дописывания справа»).
Решение. Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 7.7.
Рис. 3.7. Объединения двух матриц по правилу «дописывания справа»
Пример 5. Даны две матрицы: А(2×3) и В(3×3). Требуется объединить эти матрицы в одну матрицу С(5×3), причем, в новой матрицы в качестве первых строк должны быть строки матрицы А, а за ними должны следовать строки матрицы В.
Решение. Для соединения двух матриц в одну матрицу по правилу «друг под другом» можно использовать функцию stack, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 3.8.
Рис. 3.8. Объединения двух матриц по правилу «друг под другом»
Пример 6. Дана матрица А(6×6). Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2-го по номер 4-ый, и столбцах, начиная с номера 0-го по номер 5-ый.
Решение. Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет 5 параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рис. 3.9.
Рис. 3.9. Выделение подматрицы из заданной матрицы
Пример 7. Дана матрица А(6×6). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 4–ым столбцом матрицы А, а второй – с 3-ей строкой матрицы А.
Решение. Для получения векторных значений можно воспользоваться командой М< > (из матрицы взять вектор-столбец), которая расположена на панели «Мatrix». Для получения первого вектора эту команду нужно применить непосредственно к матрице А, а для получения второго вектора нужно сначала получить из матрицы Атранспонированную матрицу, а только потом воспользоваться командой «взять столбец». Возможное решение представлено на рис. 3.10.
Рис. 3.10. Выделение векторных значений из заданной матрицы
Пример 8. Из матрицы А(6×6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.
Решение. Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рис. 3.11.
Рис. 3.11. Выделение минора из заданной матрицы
Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i–ый элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i–ой строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементуi–ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.
Пример 9. Даны матрица: А(4×4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 0–ым столбцом матрицы А, а второй — с 3-им столбцом матрицы А.
Решение. Для получения новых векторов сформируем два вспомогательных вектора: вектор B1 – с единичным значением в строке с номером 0, а второй вектор В4 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 3.12.
Рис. 3.12. Выделение векторных значений из заданной матрицы
Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор — строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.
Пример 10. Дана матрица: А(4×4). Требуется выделить из матрицы первую строку по порядку (с номером 0).
Решение. Сначала требуется подготовить вспомогательный вектор-строку, а потом умножить эту строку слева на матрицу А. Вектор-строку можно получить из предыдущего примера транспонированием вектора-столбца В1.
Такой прием можно использовать для перестановки строк и столбцов матрицы, только для этого потребуется уже вспомогательная матрица, состоящая из векторов-столбцов (векторов-строк), место единичных элементы которых соответствуют тому порядку, который нужно иметь в результате преобразования матрицы.
Пример 11. Дана матрица: А(4×4). Требуется переставить в матрице строки с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц:
Пример 12. Дана матрица: А(4×4). Требуется переставить в матрице столбцы с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в столбцах соответствуют нужному порядку для выбора их в новую матрицу. После этого решение можно получить простым перемножением матриц:
Рассуждая, таким образом, можно с помощью вспомогательного вектора с единичными компонентами получить вектор, компоненты которого будут равны сумме строк (столбцов) матрицы, а также суммы отдельно выделенного столбика (строчки).
Пример 13. Дана матрица: А(4×4). Требуется найти сумму элементов в столбце с номером 3.
Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
Пример 14. Дана матрица: А(4×4). Требуется получить вектора, элементы которого будут представлять суммы элементов в столбцах матрицы.
Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
Для простоты решения ограничимся случаем системы из трех линейных уравнений с тремя неизвестными. Рассуждения на случай большего числа уравнений можно провести аналогичным образом. Пусть требуется найти решение система линейных алгебраических уравнений (СЛАУ) вида:
(3.1)
Введем следующие обозначения:
, (3.2)
здесь:
А – матрица коэффициентов;
В – вектор свободных членов;
х – вектор неизвестных.
В обозначениях (5.2) систему уравнений (5.1) можно записать в виде:
Ax=B. (3.3)
Из линейной алгебры известно, что система (3.3) имеет единственное решение при условии невырожденности матрицы, т.е. её детерминант должен быть отличным от нуля. Поэтому, какой бы вычислительный метод не применялся, решение системы линейных уравнений всегда нужно начинать с вычисления определителя (детерминанта) матрицы.
В разделе 6.4 мы уже рассматривали решение систем с использованием блока решения. Если применить к уравнению (3.3) аппарат матричных преобразований можно получить «матричную» формулу для вычисления x:
Помножим уравнение (3.3) слева на матрицу, обратную к матрице А:
. (3.4)
Воспользуемся свойством, что , гдеЕ – единичная матрица. Тогда уравнение (3.4) примет вид:
. (3.5)
Воспользуемся свойством, что Ex = x. Тогда уравнение (3.5) примет вид:
, (3.6)
где (3.6) – решение системы (3.3).
Пример 15. Требуется найти решение следующей системы линейных уравнений:
Решение. Решение СЛАУ матричным способом в системе MathCAD приведено на рис.3.13.
Рис. 3.13. Решение СЛАУ пакете MathCAD
Информация для студентов о прохождении военной службы по контракту Уважаемые студенты! Информируем вас о том, что 23 июня 2014 года принят Федеральный закон №159-ФЗ «О внесении изменений в отдельные законодательные акты Российской Федерации», который предоставляет гражданам, получившим высшее образование, право проходить военную службу по контракту в течении двух лет вместо одного года по призыву. Также 1 мая 2017 года принят Федеральный закон №91-ФЗ «О внесении изменений в статью 34 ФЗ «О воинской обязанности и военной службе», который предоставляет гражданам, получившим среднее профессиональное образование, право проходить военную службу по контракту в течении двух лет вместо одного года по призыву. |
Сюжет «Сибстрин ТВ» о визите Губернатора Андрея Травникова в НГАСУ (Сибстрин) 26 марта 2021 года Новосибирский государственный архитектурно-строительный университет (Сибстрин) посетил Губернатор Новосибирской области А.А. Травников. Глава региона встретился с ректором Ю.Л. Сколубовичем, познакомился с образовательной и инновационной инфраструктурой вуза и принял участие в круглом столе Министерства строительства, посвященного внедрению цифровых технологий в отрасль. Также А.А. Травников лично вручил удостоверения о получении именных стипендий Андрея Дмитриевича Крячкова семи студентам НГАСУ (Сибстрин), показавшим в 2020 году значительные достижения в учебе, научной, научно-технической и творческой деятельности. Этой чести удостоились студенты Ксения Горшкова (ИС), Татьяна Демидова (ИАГ), Ксения Дрепина (ИЭФ), Джумабек Ибрагимов (ИЭФ), Екатерина Колоколкина (ФИИТ), Егор Логачев (ИАГ) и Екатерина Минченко (ИС). |
В НГАСУ (Сибстрин) подведены итоги Регионального конкурса детских творческих работ по рисунку «Традиции академической школы рисунка, живописи и композиции» В НГАСУ (Сибстрин) подведены итоги Регионального конкурса детских творческих работ по рисунку «Традиции академической школы рисунка, живописи и композиции». Конкурс направлен на выявление и поддержку талантливых и одаренных детей, демонстрацию и пропаганду достижений подрастающего поколения в области художественного творчества, а также презентацию опыта работы образовательных учреждений по организации творческой деятельности школьников. В этом году конкурс отметил свой 5-летний юбилей и приобрел региональное значение. Стало больше участников, больше номинаций. География конкурса также расширилась: свои работы представили школьники из Новосибирска и Новосибирской области, Томска и Томской области, Новокузнецка и Кемеровской области. Всего на Региональный конкурс детских творческих работ по рисунку «Традиции академической школы рисунка, живописи и композиции» в НГАСУ (Сибстрин) было подано более 600 индивидуальных и коллективных работ от 779 участников. |
Моделирование в электроэнергетике — Определение взаимного угла в Matlab/Simulink
Определение взаимного угла в Matlab/Simulink
- Информация о материале
- Обновлено: 02.08.2018 20:40
- Категория: Общие данные
В процессе моделировании переходных процессов в Matlab/Simulink (с библиотекой SimPowerSystems) возникает необходимость в определении взаимного угла между двумя наблюдаемыми векторами (например, угол между током и напряжением или угол между двумя напряжениями). Следует отметить, что взаимным углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения второго вектора.
В статье представлены два способа моделирования отдельных пользовательских блок-элементов расчетной схемы для определения взаимного угла между двумя наблюдаемыми аналоговыми сигналами.
Рис.1. Взаимный угол между векторами
Способ №1. Определение взаимного угла из разности значений собственных углов векторов
Самым простым способом определить взаимный угол между двумя векторами является метод основанный на вычислении разности значений собственного угла первого и второго вектора:
где — собственный угол первого и второго вектора
В случае если полученное значение взаимного угла отрицательное , то второй вектор отстает от первого вектора, если полученное значение взаимного угла положительное , то второй вектор опережает первый вектор.
Следует отметить, что полученный угол имеет область значений, которая ограничивается «плавающим» интервалом с периодом изменения сигнала (в качестве примера, угол может меняться в диапазоне от -150 градусов до +220 градусов). Для решения данной проблемы необходимо дополнительно добавить два условия, которые изменяют переменную при достижении границ диапазона :
Если , то ;
Если , то .
Описанный выше алгоритм легко реализуется в программном обеспечении Matlab/Simulink.
Рис.2. Реализация в программном обеспечении Matlab/Simulink
Для преобразования аналогового сигнала в вектор используется блок «Fourier», который из периодического сигнала определяет амплитуду и фазу. В качестве блока, который позволяет выбрать необходимое значение взаимного угла используется ключ «Switch» на вход которого поступает логический сигнал «0» или «1». В зависимости от поступающего логического сигнала выбирается одно из двух значений взаимного угла.
В результате получена первая модель определения взаимного угла между аналоговыми сигналами в Matlab/Simulink область значений которой определена на интервале .
Способ №2 Определение взаимного угла из выражения для определения скалярного произведения векторов
Рассмотрим более сложный способ определения взаимного угла между векторами с использованием выражения для определения скалярного произведения векторов:
— скалярное произведение векторов можно вычислить через координаты векторов;
— модули соответствующих векторов, которые вычисляются через арифметический квадратный корень из суммы квадратов координат вектора.
В результате угол между векторами определяется через арккосинус отношения скалярного произведения к произведению модулей векторов.
Однако следует отметить, что функция арккосинус имеет область значений, которая ограничивается интервалом , поэтому невозможно определить расположение векторов в пространстве: отставание или опережение одного вектора от другого. Для решения данной проблемы необходимо к последнему выражению добавить множитель, который принимает значения «1» или «-1» в зависимости от выполнения определенных условий:
Если и или и , то коэффициент равен «1»;
Если и или и , то коэффициент равен «-1» .
В результате мы получим, что область значений будет ограничиваться интервалом .
Рассмотрим реализацию рассмотренного выше алгоритма определения взаимного угла между векторами в программном обеспечении Matlab/Simulink.
Рис.3. Реализация в программном обеспечении Matlab/Simulink
Для преобразования аналогового сигнала в вектор используется блок «Fourier», который из периодического сигнала определяет амплитуду и фазу. Также имеется возможность преобразовать вектор через вещественные и мнимые составляющие с помощью использования блока «Magnitude-Angle to Complex» и блока «Complex to Real-Imag».
Рис.4. Алгоритм определения вещественной и мнимой составляющей комплексного числа из аналогового сигнала
Взаимный угол между двумя рассматриваемыми векторами определяется с помощью использования математических блок-элементов в программном обеспечении Matlab/Simulink.
Рис.5. Математический блок.
В качестве блока, который позволяет выбрать значение между положительным и отрицательным числом, используется ключ «Switch» на вход которого поступает логический сигнал «0» или «1». В зависимости от поступающего логического сигнала выбирается одно из двух значений взаимного угла.
В результате получена вторая модель определения взаимного угла между аналоговыми сигналами в Matlab/Simulink область значений которой определена на интервале .
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
ПродуктDot — Сообщество PTC
Точечные произведения коммутативны, поэтому F · T имеет то же значение, что и T · F . Точечные продукты могут быть разработаны разными способами и имеют множество интерпретаций, в зависимости от использования.Скалярное произведение В · Вт можно рассматривать как произведение величин двух векторов, лежащих в одном направлении. Не имеет значения, рассматриваете ли вы компонент V в направлении W или компонент W в направлении V — или даже компоненты V и W в произвольном направлении. направления.Действительно, последний способ часто вычисляется скалярными произведениями, векторы представлены наборами компонентов вдоль осей системы координат, а скалярное произведение становится просто суммой произведений соответствующих компонентов.
В общем, В · Вт / Вт — это величина составляющей В в направлении Вт . И симметрично В · Вт / В — это величина составляющей Вт в направлении В .Компонент В в направлении Вт может быть записан как ( В · Вт ) Вт / Вт². Если W — единичный вектор, то W = 1, и эти выражения можно упростить, опуская его.
Если F — это сила, а T — единичный вектор, представляющий направление в пространстве, тогда F · T — это величина составляющей силы в направлении T . Если T — это единичный вектор в направлении вектора скорости (скорость объекта, к которому приложена сила), то это величина составляющей силы, которая вносит вклад в работу.Однако обычно в этом разложении нет необходимости. Если F · — это сила, а V — скорость объекта, к которому она приложена, тогда F · V — это мощность, производная работы. Обычно нет необходимости разлагать V на V T , а затем записывать ( F · T ) V для мощности.
� � � � Tom Gutman
Параллельное выполнение вычислений »MathCadHelp.com» Номер 1 в MathCad Assignments
Любые вычисления Mathcad может выполнять как с отдельными значениями, так и с векторами или матрицами значений.Это можно сделать двумя способами:
• Путем итерации по каждому элементу с использованием переменных диапазона, как описано в главе 11 «Переменные диапазона».
• С помощью оператора «векторизации», описанного в этой главе.
Оператор векторизацииMathcad позволяет ему эффективно выполнять одну и ту же операцию над каждым элементом вектора или матрицы.
Математические обозначения часто показывают повторяющиеся операции с индексами. Например, чтобы определить матрицу P путем умножения соответствующих элементов матриц M и N, вы должны написать
Параллельное выполнение расчетов
Обратите внимание, что это не матричное умножение, а поэлементное умножение.Эту операцию в Mathcad можно выполнить с помощью индексов, как описано в главе 11, «Переменные диапазона», но гораздо быстрее выполнить точно такую же операцию с векторизованным уравнением.
Как применить оператор векторизации к выражению
Вот как применить оператор векторизации к выражению типа M · N:
• Выделите все выражение, щелкнув внутри и нажав [Пробел], пока правая часть не будет удерживаться между строками редактирования.
Как применить оператор векторизации к выражению
• Нажмите [Ctrl] — чтобы применить оператор векторизации.Mathcad помещает стрелку над выбранным выражением.
Как применить оператор векторизации к выражению
Как оператор векторизации изменяет значение выражения
Оператор векторизации изменяет значение операторов и функций, к которым он применяется. Оператор векторизации сообщает Mathcad о необходимости применять операторы и функции с их скалярным значением поэлементно.
Вот несколько примеров того, как оператор векторизации изменяет значение выражений с векторами и матрицами:
• Если v — вектор, sin (v) — недопустимое выражение.Но если вы примените оператор векторизации, Mathcad применит синусоидальную функцию к каждому элементу в v. Результатом является новый вектор, элементы которого являются синусами элементов в v.
• Если M — матрица, JM — недопустимое выражение. Но если вы примените оператор векторизации, Mathcad извлечет квадратный корень из каждого элемента M и поместит результаты в новую матрицу.
• Если v и w — векторы, то v. w означает скалярное произведение v и w. Но если вы примените оператор векторизации, результатом будет новый вектор, i-й элемент которого получается умножением vi и wi ’. Это не то же самое, что скалярное произведение.
Эти свойства оператора векторизации позволяют использовать скалярные операторы и функции с операндами и аргументами массива. В данном Руководстве пользователя это называется «векторизацией» выражения. Например, предположим, что вы хотите применить квадратную формулу к трем векторам, содержащим коэффициенты a, b и c. На рис. 10-18 показано, как это сделать, если a, b и c — просто скаляры. На рис. 10-19 показано, как сделать то же самое, когда a, b и c являются векторами.
Квадратичная формула.
Квадратичная формула с векторами и оператором векторизации.
Оператор векторизации отображается в виде стрелки над формулой корней квадратного уравнения на рис. 10-19. Его использование важно в этом расчете. Без него Mathcad интерпретировал бы файл. c как скалярное произведение вектора, а также пометить квадратный корень из вектора как недопустимый. Но с оператором векторизации оба файла. c и квадратный корень выполняются поэлементно.
Вот свойства оператора векторизации:
• Оператор векторизации изменяет значение других операторов и функций, к которым он применяется.Это не меняет значения настоящих имен и номеров. Если вы примените оператор векторизации к одному имени, он просто нарисует стрелку над именем. Вы можете использовать эту стрелку только в косметических целях.
• Поскольку операции между двумя массивами выполняются поэлементно, все массивы с оператором векторизации должны быть одинакового размера. Операции между массивом и скаляром выполняются путем применения скаляра к каждому элементу массива. Например, если v — вектор, а n — скаляр, применение оператора векторизации к vn возвращает вектор, элементы которого являются n-й степенью элементов v.
• Вы не можете использовать какие-либо из следующих матричных операций с оператором векторизации: скалярное произведение, умножение матриц, степени матрицы, обратная матрица, определитель или величина вектора. Оператор векторизации преобразует эти операции в поэлементное скалярное умножение, возведение в степень или абсолютное значение, в зависимости от ситуации.
• Оператор векторизации не влияет на операторы и функции, которым требуются векторы или матрицы: транспонирование, перекрестное произведение, сумма элементов вектора и такие функции, как среднее значение.Эти операторы и функции не имеют скалярного значения.
• Оператор векторизации применяется только к последним скалярным аргументам interp и linterp. Остальные аргументы не затрагиваются. См. «Функции интерполяции» в главе 14 «Статистические функции».
векторов и матриц
Векторы и матрицыМатрицы и векторы
MathCAD широко использует матрицы и векторы. Вектор здесь определяется как матрица с одним столбцом. Матрицы могут быть созданы путем ручного ввода данных, чтения данных из текстового файла или вырезания и вставки из другой программы, такой как Excel.Чтобы ввести матрицу вручную, нажмите кнопку «Вставить матрицу» на палитре матриц. Введите желаемое количество строк и столбцов в появившемся диалоговом окне и нажмите клавишу ВВОД. Поместите курсор на первый заполнитель, введите первое значение. Нажмите вкладку, чтобы перейти к следующему заполнителю и так далее.
Ввод матрицы вручную подходит, если у вас небольшие объемы данных. Однако это довольно неэффективно, если вы вводите сотни единиц данных, например, из системы сбора данных.MathCAD предоставляет функцию READPRN () для чтения данных из файла ASCII. Аргументом этой функции является заключенная в кавычки строка, представляющая имя файла. Файл данных, содержащий данные матрицы, представляет собой чистый текстовый файл, набранный в том же формате, что и матрица, которую вы хотите отобразить. Текстовый файл должен быть чистым файлом ASCII. То есть его лучше всего создавать с помощью текстового редактора, такого как Блокнот. Если вы используете текстовый процессор, электронную таблицу или другую программу для создания файла, убедитесь, что вы используете функцию «Сохранить как», чтобы сохранить файл в формате.txt файл.
<= Читать матрицы
<= Показать матрицы
ПРИМЕЧАНИЕ. MathCAD также включает функцию READ (). Эта функция устарела и не должна использоваться. Это предусмотрено только для обратной вычислимости. Будущие версии MathCAD могут не включать функцию READ (), поэтому ее использование крайне не рекомендуется.
ПРИМЕЧАНИЕ: MathCAD также включает тринадцать других вариантов функции чтения, включая READ_IMAGE, READ_BLUE, READ_HLS и т. Д.Это специализированные функции, используемые для чтения числовых данных из растровых изображений, таких как BMP, JPEG, GIF, TGA и PCX. Эти функции будут генерировать матрицу значений данных, представляющих это изображение. Эти функции не рассматриваются в этом курсе. Чтобы узнать больше, введите «ЧИТАТЬ» на вкладке «Указатель» диалогового окна справки.
MathCAD также позволяет выводить результаты обработки матриц для дальнейшего анализа или использования другими программами. Для этого используйте функцию WRITEPRN ().
<= Точечное произведение матриц 'a' и 'b'
<= Показать результат
<= Записать результаты в файл.Если файл не существует, writeprn () создаст файл. Если файл уже существует, текущий файл будет перезаписан. Используйте Блокнот, чтобы просмотреть файл сейчас.
Если вам нужно добавить данные в существующий файл, используйте функцию APPENDPRN (). Эта функция <= НЕ будет создавать файл, если он не существует.
ПРИМЕЧАНИЕ: Обе функции будут вызваны, когда вы введете их изначально. Если вам нужно вызвать их снова, поместите курсор на функцию и пересчитайте, нажав F9 или выбрав «Рассчитать» в пункте меню «Математика».
Будьте осторожны при пересчете функции APPENDPRN (). Эта функция будет продолжать добавлять данные в указанный файл, в результате чего получается очень большая матрица с избыточными данными.
ПРИМЕЧАНИЕ. MathCAD также включает функции WRITE () и APPEND (). Эти функции устарели и не должны использоваться. Они предоставляются только для обратной вычислимости. Будущие версии MathCAD могут не включать ни одну из функций, поэтому их использование крайне не рекомендуется.
После того, как массив введен и обработан, у нас должен быть какой-то способ извлечения данных из любого заданного массива. Все элементы векторов и массивов адресуются через индексы. Подстрочный индекс массива вводится с помощью клавиши левой квадратной скобки ([). По умолчанию все векторы и массивы индексируются так, что первая строка и столбец равны нулю строки и столбца. Таким образом, первый элемент любой матрицы «M» — это M 0,0 .
Обращение к элементам вектора
Отобразить вектор ‘a’ сверху =>
<= Вы не можете использовать буквальный нижний индекс, введенный с ключом точки, для адресации элемента матрицы.
<= Введите индекс массива, используя квадратную скобку. В этом случае используйте нажатия клавиш a [1 =
<= Иногда вы можете захотеть изменить начало координат матрицы на что-нибудь другое. Сделайте это, перейдя в меню «Математика», «Параметры». Если изменить это значение в диалоговом окне, это повлияет на весь рабочий лист. В качестве альтернативы вы можете адресовать и изменять переменную ORIGIN из рабочего листа, как показано.Если вы измените источник массива таким образом, это повлияет только на область вашего рабочего листа под объявлением.
<= При установке начала координат в единицу первым элементом вектора 'a' теперь является 1 . Элемент 0 больше не существует.
<= Сбросить источник для оставшейся части лекции
Обращение к элементам матрицы
<= Отобразить матрицу 'c', как рассчитано выше
Элемент матрицы ‘c’, занимающий нулевую строку и нулевой столбец
Элемент матрицы c, занимающий седьмую строку и седьмой столбец
Если ORIGIN установлено в ноль, последняя строка матрицы ‘c’ является седьмой строкой, а не восьмой. Нет восьмой строки, поэтому это обозначение является ошибкой.
Также существуют ситуации, когда нам может потребоваться извлечь целые строки, столбцы или подматрицы данных из матрицы. Для этого мы можем использовать функцию M <> (из палитры матриц) и функцию submatrix ().
<= Прочитать матрицу из файла
<= матрица дисплея
<= извлечь второй столбец (это столбец 1, поскольку начало массива установлено в ноль). Для этого используйте M <> (ctl-6).
<= Чтобы извлечь строку, мы должны сначала транспонировать матрицу с помощью функции M T (ctl-1) из палитры матриц.
<= Если нам нужна нулевая строка исходной матрицы, мы извлечем нулевой столбец транспонированной матрицы.Обратите внимание, что функции вложены.
<= Мы также можем извлечь целую подматрицу, используя подматрицу функции (M, r1, r2, c1, c2). Функция, показанная слева, генерирует матрицу, состоящую из нулевой и одной строк исходной матрицы 'd'. Обратите внимание, что мы можем либо объявить его для отображения, либо присвоить переменной для дальнейшего использования.
Есть много случаев, когда нам нужно изменить размер матрицы. В этом случае это означает добавление отдельных строк и / или столбцов в случайные точки по всей существующей матрице.Это также может означать увеличение или укладку двух или более существующих матриц.
<= Создать матрицу 'f'
<= Чтобы добавить столбец, поместите курсор на столбец слева от столбца, который вы хотите добавить. Нажмите CTL-M. В появившемся диалоговом окне введите ноль строк и один столбец. Нажмите на вставку. Столбец будет вставлен справа от курсора.
<= Точно так же вы можете добавить строку, поместив курсор в строку непосредственно над строкой, которую вы хотите добавить.Нажмите CTL-M. В появившемся диалоговом окне введите 1 строку и ноль столбцов. Щелкните «Вставить». Строка будет вставлена сразу под курсором.
Удаление строки или столбца аналогично. Просто поместите курсор на строку и / или столбец, которые вы хотите удалить. Нажмите CTL-M. В появившемся диалоговом окне введите количество строк и / или столбцов, которые вы хотите удалить. Указанное количество строк / столбцов непосредственно справа и ниже курсора, включая строку / столбец, в котором находится курсор, будет удалено.
Если у вас есть две или более матриц, вы можете складывать или увеличивать их. Создание матрицы с использованием Stack (a, b) означает, что вы будете «складывать» матрицу «a» поверх матрицы «b». Таким образом, матрицы ДОЛЖНЫ иметь одинаковое количество столбцов для укладки. У них может быть разное количество строк.
Точно так же создание матрицы с использованием augment (a, b) означает, что матрица «a» и матрица «b» будут размещены рядом, чтобы создать новую матрицу. Таким образом, матрицы должны иметь одинаковое количество строк.У них может быть разное количество столбцов.
<= Отобразить матрицы 'a' и 'b' как прочитанные из файла выше.
<= Поскольку матрица «a» имеет 8 строк, а матрица «b» только одна строка, их нельзя увеличить. Точно так же разное количество столбцов в каждом не позволяет их штабелировать.
<= создать матрицу 'c' путем транспонирования матрицы 'b'
создать матрицу ‘d’ путем транспонирования матрицы ‘a’
<= Показать матрицы 'j' и 'k'.
<= Поскольку матрицы 'a' и 'j' теперь имеют одинаковое количество строк, мы можем увеличить их.
<= Аналогично, матрицы 'b' и 'k' имеют одинаковое количество столбцов и могут быть сложены друг с другом.
Большинство предыдущих функций используются для управления внешним видом и порядком матрицы или вектора. Теперь нам нужно взглянуть на некоторые матричные функции, которые мы можем использовать для расчетов и анализа.
<= Отобразить матрицу 'd', как рассчитано выше
<= Функции, показанные слева, обращаются к массиву для определения различных свойств массива.Функции min () и max () находят числовые минимальное и максимальное значения, содержащиеся в матрице.
Функции row () и cols () определяют количество строк и столбцов, составляющих матрицу. Обратите внимание, что произведением будет количество элементов в матрице.
Все эти функции действительны для матриц и векторов.
<= Функции length (), last () и S () (векторная сумма) действительны только для векторов.Длина определяет количество элементов в векторе, а последний возвращает значение индекса последнего элемента, содержащегося в векторе. Применение этих функций к матрице приведет к ошибке.
Обратите внимание, что мы можем вложить функцию извлечения столбца с любой из векторных функций, чтобы имитировать вектор и выполнить соответствующую операцию.
<= Обратите внимание, что одним из применений этих матричных функций является статистика.Например, мы можем взять векторную сумму нулевого столбца матрицы «d» и разделить ее на длину нулевого столбца матрицы «d», чтобы определить среднее значение этого столбца чисел.
Еще одна полезная матричная функция матрицы — это возможность сортировать элементы массива на основе некоторых критериев. Для этого в MathCAD доступны функции sort (), reverse (), csort () и rsort (). Первые два применимы только к векторам. Последние два предназначены для множественных массивов столбцов.
<= Отобразить матрицу 'd', как рассчитано выше
<= Поскольку функция сортировки применяется только к векторам, мы сгенерируем вектор, извлекая столбец из матрицы 'd'.
<= Функция сортировки сортирует элементы вектора 'e' от меньшего к большему
<= Если вы хотите отсортировать вектор по убыванию, примените обратную функцию, как показано.
Мы также можем отсортировать элементы матрицы ‘d’, используя функции csort (v, n) и rsort (v, n), сортировку столбцов и сортировку строк соответственно.Аргументами этих функций являются вектор «v» и столбец или строка «n», на которых основана сортировка. Например:
В трех примерах, показанных слева, мы отсортируем матрицу d по столбцам 0, 1 и 2 соответственно.
Первая функция преобразует матрицу d, упорядочивая нулевой столбец от младшего к большему. Остальные элементы каждой строки сохраняют свое относительное положение.
Вторая функция сортирует матрицу ‘d’, упорядочивая первый столбец от меньшего к большему.Остальные элементы каждой строки сохраняют свое относительное положение.
Третья функция сортирует матрицу ‘d’, располагая столбец два от младшего к большему. Остальные элементы каждой строки сохраняют свое относительное положение.
Функция rsort () делает то же самое, но только по строкам. Рассмотрение трех примеров слева показывает матрицу «d», отсортированную по нулевой, первой и второй строкам соответственно.
Обычно матрицы используются при решении одновременных уравнений.Для этого нам нужно иметь возможность инвертировать матрицу. Обратной к любой матрице «a» является матрица «b», так что скалярное произведение a и b даст единичную матрицу.
Пример: найти обратную матрицу ‘a’
<= Первый шаг - дополнить матрицу «а» единичной матрицей. MathCAD предоставляет функцию identity (), позволяющую легко создавать единичную матрицу.
<= Создайте матрицу «ai», увеличив матрицу «a» и «I».
<= Теперь выполните ряд операций со строками так, чтобы левая половина матрицы 'ai' была заменена единичной матрицей, а правая половина - обратной. После выполнения этих операций у вас должна получиться матрица, показанная слева.
<= Сначала установите для первого элемента матрицы 'ai' значение единицы, умножив строку 1 матрицы 'ai' на 1/2.
<= Затем установите первый элемент второй строки в ноль, умножив вторую строку на выражение -1R 1 + R 2 , где R 1 и R 2 — элементы первой и второй строки матрицы.
<= Затем установите второй элемент второй строки в единицу, умножив вторую строку на 2.
<= Наконец, установите второй элемент первой строки в ноль, используя выражение -7 / 2R 1 + R 2 , где R 1 и R 2 — первая и вторая строки матрицы.
<= Используйте функцию подматрицы, чтобы извлечь правую половину матрицы 'ai'.Это будет обратная матрица 'a'
<= Проверьте свою работу, взяв скалярное произведение матриц «a» и «b». Это должно дать единичную матрицу.
Конечно, MathCAD позволяет нам сделать то же самое намного проще, используя обратную функцию из палитры матриц.
MathCAD также позволяет вычислять определитель матрицы. Определитель матрицы можно использовать для решения одновременных уравнений (правило Крамера).Он также используется для определения того, имеет ли система одновременных линейных уравнений единственное решение. Ненулевой определитель указывает на то, что существует единственное решение. Матричную функцию можно выбрать из палитры матриц или ввести, нажав ‘|’ ключ. Хотя MathCAD вычисляет определитель для любой матрицы порядка, определитель наиболее полезен, когда имеется квадратная матрица.
<= Определитель матрицы 'a'
Пример использования определителя и обратной матрицы — решение одновременных уравнений.
Найдите решение следующей системы уравнений, используя матричные методы
Боковое примечание:
Уравнения слева отображаются со знаком равенства жирным шрифтом. Это логическое равенство. Мы обсудим это в следующей лекции. На данный момент я использую его исключительно для демонстрации. Чтобы не создавать вычислительных проблем, эти уравнения были «отключены», как показано поднятым черным квадратом.
Определите матрицы коэффициентов, переменных и решений
Во-первых, давайте определим, имеет ли эта система уравнений единственное решение.Для этого найдем определитель матрицы коэффициентов.
Поскольку определитель отличен от нуля, эта система уравнений имеет единственное решение. В матричной форме эта система уравнений записывается как a * b = c. Мы можем определить содержание матрицы ‘b’, матрицы решения, умножив обе части уравнения на обратную матрицу ‘a’
Поскольку a * a -1 является единичной матрицей, матрица решения ‘b’ находится просто умножением матрицы ‘c’ на матрицу, обратную матрице ‘a’.
Проверьте правильность этой матрицы решений, записав каждую функцию следующим образом:
Другой метод — использовать функцию MathCAD lsolve ().
Точечный продукт vs.кросс-продукт против векторизации
Скалярное произведение относится к умножению матриц. Как и в случае с большинством матричных операций, это интенсивный
процесс, когда выполняется вручную. В отличие от скалярного умножения, скалярное произведение матриц не равно
.
коммутативный. Другими словами, V * U не равно U * V. Скалярное произведение может быть взято только в том случае, если
количество столбцов в первой матрице равно количеству строк во второй матрице. Прочие
слов, V mxn * U nxp допустимо, поскольку матрица V имеет n столбцов, а матрица U имеет n строк.В результате
матрица будет иметь m строк и p столбцов. Однако U nxp * V mxn не является допустимым скалярным произведением, поскольку матрица
U имеет p столбцов, а матрица V имеет m столбцов.
Скалярное произведение двух матриц определяется следующим образом:
<= Показать матрицы 'a', 'b' и 'c', как определено выше
Например, скалярное произведение матриц «a» и «b» будет три строки на один вектор-столбец. Модель
Первый элемент — это произведение нулевой строки матрицы «a» и столбца «0» матрицы «b».Рассчитано
как (1 * -1) + (0 * 2) + (7 * 3) = 20. Второй элемент является произведением первой строки матрицы ‘a’ и
нулевой столбец матрицы ‘b’. Он рассчитывается как (2 * -1) + (1 * 2) + (- 1 * 3) = -3. Последний элемент находится
умножением второй строки матрицы ‘a’ и нулевого столбца матрицы ‘b’. Рассчитывается как
(7 * -1) + (3 * 2) + (1 * 3) = 2. MathCAD упрощает эту задачу с возможностью выбора функции скалярного произведения
из палитры матриц или вводится с помощью клавиши звездочки (Shift-8).
Примеры, показанные слева, представляют собой множество скалярных произведений трех матриц «a», «b» и «c». Почему скалярное произведение b * a и c * недействительно по сравнению с скалярным произведением a * b и a * c?
Почему скалярные произведения b * c и c * b действительны? Почему они равны?
Хотя ряд методов анализа требует истинного умножения матриц, бывают случаи, когда мы предпочитаем выполнять умножение элементов на элементы.MathCAD позволяет нам делать это с помощью функции векторизации (CTL — -).
Умножение элементов на элементы, очевидно, дает вектор 3×1 с элементами -20, -6 и 6.
<= Используйте функцию векторизации MathCAD, как показано слева, выполнит этот расчет за вас.
Последняя матричная функция — это функция перекрестного произведения. Перекрестное произведение можно брать только с векторами, состоящими из трех элементов. Элементы этих векторов представляют координаты в пространстве, таким образом, направление и величину вектора.Перекрестное произведение двух векторов дается выражением c = a * b * sin (a), где a — угол между векторами a и b. Эта концепция широко используется в статике для определения сил, действующих на конструкцию. Он также широко используется в электронике.
<= Предположим, векторы 'x' и 'y', как показано. Перекрестным произведением этих векторов является некоторый вектор 'c' такой, что элементы вектора 'c' определены как:
<= Отображение векторов 'b' и 'c', как было вычислено ранее
<= Перекрестное произведение b x c вычисляется MathCAD, как показано.Ниже показано поэлементное построение.
<= Обратите внимание, что перекрестное произведение c x b - это перекрестное произведение b x c, умноженное на -1.
% PDF-1.3 % 35 0 объект > эндобдж xref 35 68 0000000016 00000 н. 0000001708 00000 н. 0000001931 00000 н. 0000001960 00000 н. 0000002015 00000 н. 0000002461 00000 н. 0000002683 00000 н. 0000002746 00000 н. 0000002862 00000 н. 0000002943 00000 н. 0000003033 00000 н. 0000003122 00000 п. 0000003452 00000 н. 0000003680 00000 н. 0000004030 00000 н. 0000004229 00000 п. 0000004445 00000 н. 0000004887 00000 н. 0000005107 00000 н. 0000005324 00000 н. 0000005746 00000 н. 0000005969 00000 н. 0000006203 00000 н. 0000006786 00000 н. 0000007010 00000 п. 0000007447 00000 н. 0000007959 00000 н. 0000007998 00000 н. 0000008045 00000 н. 0000008066 00000 н. 0000009067 00000 н. 0000009677 00000 н. 0000009830 00000 н. 0000010581 00000 п. 0000010797 00000 п. 0000010819 00000 п. 0000012049 00000 п. 0000012071 00000 п. 0000013290 00000 н. 0000013312 00000 п. 0000014466 00000 п. 0000014488 00000 н. 0000015844 00000 п. 0000015865 00000 п. 0000016679 00000 п. 0000016701 00000 п. 0000017783 00000 п. 0000017804 00000 п. 0000018761 00000 п. 0000018819 00000 п. 0000041336 00000 п. 0000073455 00000 п. 0000085238 00000 п. 0000085377 00000 п. 0000101854 00000 н. 0000104531 00000 н. 0000104736 00000 н. 0000116057 00000 н. 0000137921 00000 н. 0000138612 00000 н. 0000146249 00000 н. 0000158690 00000 н. 0000165606 00000 н. 0000165798 00000 н. 0000165982 00000 н. 0000166166 00000 н. 0000002054 00000 н. 0000002439 00000 н. трейлер ] >> startxref 0 %% EOF 36 0 объект > эндобдж 37 0 объект [ 38 0 руб. ] эндобдж 38 0 объект > / Ж 44 0 Р >> эндобдж 39 0 объект > эндобдж 101 0 объект > транслировать Hb«a«c`c`fb @
(by-Brent-Maxfield- (Auth)) — Essential-PTC-Mathcad-2278342- (z-lib org) (1) — Cálculo Numérico
где инкремент не останавливается на конечном значении РИСУНОК 6.10 Расчет приращений 136 ГЛАВА 6 Массивы, векторы и матрицы угол. Эти точки называются Matrix Navigator и указывают на то, что матрица больше, чем отображается. Отображение и изменение размера большой матрицы По умолчанию PTC Mathcad отображает матрицу размером до 12x12. Когда в матрице больше чем 12 строк или столбцов, PTC Mathcad по умолчанию отображает только 12 строк и 12 столбцы, а затем отобразите Матричный навигатор в правом нижнем углу. Когда ты щелкните в этой области, PTC Mathcad отобразит номера индексов для строк и цветов. умнс.См. Рисунок 6.11. Матричный навигатор позволяет просматривать скрытые части матрицы. Когда ты щелкните на Matrix Navigator, появится небольшое окно Matrix Navigator. Окно имеет светло-серое окно, которое представляет полный размер матрицы. Темно-серый window представляет отображаемую часть матрицы относительно полного размера матрица. Ваш курсор изменится на четырехконечную стрелку, когда он будет помещен на темно-серое окно. Если вы нажмете и удерживаете мышь, вы можете переместить дисплей окно в светло-сером окне, и различные части матрицы будут отображается.В светло-сером окне дисплея также отображаются два числа, которые представляют начальная строка и столбец отображаемой матрицы. Это показано в рисунок ниже. Вы также можете использовать серые полосы изменения размера, чтобы увеличить размер дисплея до размера матричный дисплей по умолчанию. Расширенная отображаемая матрица может быть больше, чем ширина распечатанная страница. В этом случае вы можете уменьшить математический шрифт региона. Сделать это, выберите регион, затем на вкладке Math Formatting в группе Math Font выберите шрифт меньшего размера из элемента управления «Размер шрифта» («Математическое форматирование»> «Математический шрифт»> «Размер шрифта»).Отображение массивов 137 РИСУНОК 6.11 Отображение больших матриц 138 ГЛАВА 6 Массивы, векторы и матрицы РИСУНОК 6.12 Отображение больших матриц Вы можете выбрать предустановленный размер шрифта или ввести размер шрифта в элемент управления. Видеть Рисунок 6.12. Вышеупомянутое было невозможно в Mathcad 15, потому что вы не могли изменить размер шрифта. Показать / скрыть индексы Бывают случаи, когда вы хотите увидеть порядковый номер строк и столбцов. в массиве. Отображение номеров индексов контролируется элементом управления Показать индексы в группа Формат результата на вкладке Матрицы / Таблицы (Матрицы / Таблицы> Формат результата> Показать индексы).Это переключатель включения / выключения. По умолчанию PTC Mathcad отключен. Этот элемент управления можно применить ко всем регионам на листе, но вы также можете выбрать и применить элемент управления к отдельному региону. После того, как элемент управления будет применен к отдельного региона, он переопределяет настройку рабочего листа. Отображение массивов 139 Этот элемент управления в PTC Mathcad Prime 3.0 имеет неожиданное поведение. Ты можно было бы ожидать, что если элемент управления включен, вы всегда будете видеть индексы, и когда он выключен, вы не увидите индексов.Первое, что нужно понять, это что этот элемент управления включает или выключает отображение индексов, когда регион неактивен. vated. См. Рисунок 6.13. Второе, что нужно понять, это то, что индексы никогда не отображаются, когда полный отображается матрица. Это относится к регионам, которые активированы или не активированы, и нет неважно, насколько велика матрица. Третье, что нужно понять, это то, что когда полная матрица не отображается, индекс числа всегда появляются, когда область активирована, даже если элемент управления Показать индексы выключен.См. Рисунок 6.14. РИСУНОК 6.13 Показать или скрыть индексы 140 ГЛАВА 6 Массивы, векторы и матрицы Использование единиц с массивами PTC Mathcad Prime теперь допускает смешанные измерения единиц в векторе и матрице. ☺ Единицы измерения так же важны для векторов и матриц, как и для других PTC. Переменные Mathcad. Единицы измерения необходимы в технических расчетах. PTC Mathcad позволяет теперь использовать смешанные единичные измерения в векторах и матрицах. Этот было невозможно с предыдущими версиями PTC Mathcad. Это отличный РИСУНОК 6.14 Отображение индексов при выборе региона Использование единиц измерения с массивами 141 улучшение. Если все значения в массиве имеют одинаковые единицы измерения, то вы можете умножить целую матрицу на единицу, а не на привязку единицы к каждому значению. Если вход значения имеют разные единицы, затем умножьте каждое отдельное значение на единицу. Видеть Рисунок 6.15. По умолчанию PTC Mathcad не позволяет управлять отображением индивидуальных результатов. Другими словами, внутри диска нет заполнителя. воспроизведенный массив, чтобы изменить отображаемые единицы.Заполнитель единиц измерения находится за пределами array, и вы застряли с отображением по умолчанию. См. Рисунок 6.16. Несмотря на то, что внутри отображаемого массива нет заполнителя единиц измерения, есть способ чтобы вы могли отображать значения в желаемых единицах. Вы можете добавить массив единиц в заполнитель единицы. См. Рисунок 6.17. РИСУНОК 6.15 Использование модулей с массивами 142 ГЛАВА 6 Массивы, векторы и матрицы РИСУНОК 6.16 Отображение смешанных единиц в массивах РИСУНОК 6.17 Управление отображением смешанных единиц с помощью массива в заполнителе единиц Использование единиц измерения с массивами 143 Расчет с помощью массивов PTC Mathcad позволяет использовать множество математических операторов с массивами точно так же, как и вы. со скалярными переменными, но вам нужно убедиться, что вы соблюдаете основные правила для матричной математики.Например, вы можете складывать и вычитать массивы так же, как и другие переменные, если массивы одинакового размера. Если они разного размера массивов, PTC Mathcad выдаст предупреждение об ошибке. Вы можете умножить скаляр и массив. Результатом будет каждый элемент массива, умноженный на скаляр. Если вы умножаете две переменные массива, PTC Mathcad предполагает, что вам нужна матрица скалярное произведение и дает результат (при условии, что два массива совместимы с правила скалярного произведения). Есть способ сообщить PTC Mathcad, что вам нужна матрица перекрестное произведение.Также есть способ сообщить PTC Mathcad, что вы хотите умножить два массива на поэлементной основе и возвращают массив аналогичного размера. Эти будет обсуждаться в ближайшее время. Сложение и вычитание Если векторы и матрицы одинакового размера, вы можете складывать или вычитать их как вы бы использовали любую переменную PTC Mathcad. Сложение и вычитание поэлементная основа. См. Рисунок 6.18. Умножение Теперь мы обсудим несколько различных способов умножения массивов. Скалярное умножение Вы можете умножить любой вектор или матрицу на скалярное число.PTC Mathcad умножает каждый элемент в массиве скаляром и возвращает результаты. Скаляр может быть до или после массива. См. Рисунок 6.19. Умножение скалярных произведений Когда вы умножаете два массива, PTC Mathcad предполагает, что вам нужна матричная точка произведение двух массивов. (Скалярное произведение рассчитывается путем умножения каждого элемент первого вектора на соответствующий элемент комплексно сопряженного второго вектора, а затем суммируем результат. См. Текст по математике матриц для обсуждения матричного скалярного произведения.) Чтобы точечный продукт работал, количество столбцов в первой матрице должно соответствовать количеству строк во второй онд матрица. Другими словами, матрицы должны быть размером mxn и nxp. Результат матрица mxp. См. Рисунок 6.20. 144 ГЛАВА 6 Массивы, векторы и матрицы РИСУНОК 6.18 Сложение и вычитание РИСУНОК 6.19 Скалярное умножение Вычисления с помощью массивов 145 Векторное произведение кросс-произведения PTC Mathcad может выполнять векторное векторное произведение двух векторов-столбцов. Каждый вектор- tor должен состоять из трех элементов.В результате получается вектор, перпендикулярный плоскости первые два вектора. Направление соответствует правилу правой руки. (См. Текст на Матричная математика для обсуждения векторного векторного произведения.) Используйте элемент управления Операторы список на вкладке Математика (Математика> Операторы и символы> Операторы> Вектор и матрица> x) чтобы вставить оператор векторного произведения перекрестного произведения, или введите CTRL + 8. См. Рисунок 6.21. РИСУНОК 6.20 Умножение скалярного произведения массива 146 ГЛАВА 6 Массивы, векторы и матрицы Поэлементно
% PDF-1.4 % 3 0 obj > эндобдж 4 0 obj > эндобдж 7 0 объект (Спасибо) эндобдж 8 0 объект > эндобдж 11 0 объект (Предисловие) эндобдж 12 0 объект > эндобдж 15 0 объект (Оглавление) эндобдж 16 0 объект > эндобдж 19 0 объект (1 Matlab: Введение) эндобдж 20 0 объект > эндобдж 23 0 объект (1.1 Matlab: Введение) эндобдж 24 0 объект > эндобдж 27 0 объект (1.2 Matlab: макет) эндобдж 28 0 объект > эндобдж 31 0 объект (1.3 Matlab: примеры командного окна) эндобдж 32 0 объект > эндобдж 35 0 объект (1.4 Matlab: редактор) эндобдж 36 0 объект > эндобдж 39 0 объект (1.5 Matlab: заголовки) эндобдж 40 0 объект > эндобдж 43 0 объект (1.6 Matlab: советы редактора) эндобдж 44 0 объект > эндобдж 47 0 объект (Упражнения) эндобдж 48 0 объект > эндобдж 51 0 объект (2 Matlab: матрицы) эндобдж 52 0 объект > эндобдж 55 0 объект (2.1 Matlab: Матрицы) эндобдж 56 0 объект > эндобдж 59 0 объект (2.2 Matlab: использование матриц) эндобдж 60 0 объект > эндобдж 63 0 объект (2.3 Matlab: матричные операции) эндобдж 64 0 объект > эндобдж 67 0 объект (2.4 Matlab: общие матричные функции) эндобдж 68 0 объект > эндобдж 71 0 объект (2.5 Matlab: Системы уравнений) эндобдж 72 0 объект > эндобдж 75 0 объект (Упражнения) эндобдж 76 0 объект > эндобдж 79 0 объект (3 Matlab: Функции) эндобдж 80 0 объект > эндобдж 83 0 объект (3.1 Matlab: встроенные функции) эндобдж 84 0 объект > эндобдж 87 0 объект (Упражнения) эндобдж 88 0 объект > эндобдж 91 0 объект (4 Matlab: Графика) эндобдж 92 0 объект > эндобдж 95 0 объект (4.1 Matlab: Графика) эндобдж 96 0 объект > эндобдж 99 0 объект (Упражнения) эндобдж 100 0 объект > эндобдж 103 0 объект (5 Matlab: пользовательские функции) эндобдж 104 0 объект > эндобдж 107 0 объект (5.1 Matlab: определяемые пользователем функции) эндобдж 108 0 объект > эндобдж 111 0 объект (Упражнения) эндобдж 112 0 объект > эндобдж 115 0 объект (6 Matlab: ввод / вывод) эндобдж 116 0 объект > эндобдж 119 0 объект (6.1 Matlab: команды ввода) эндобдж 120 0 объект > эндобдж 123 0 объект (Упражнения) эндобдж 124 0 объект > эндобдж 127 0 объект (7 Matlab: структуры программирования) эндобдж 128 0 объект > эндобдж 131 0 объект (7.1 Matlab: операторы отношения) эндобдж 132 0 объект > эндобдж 135 0 объект (7.2 Matlab: логические операторы) эндобдж 136 0 объект > эндобдж 139 0 объект (7.3 Matlab: команды if и switch) эндобдж 140 0 объект > эндобдж 143 0 объект (7.4 Matlab: циклы for и while) эндобдж 144 0 объект > эндобдж 147 0 объект (Упражнения) эндобдж 148 0 объект > эндобдж 151 0 объект (8 Matlab: Приложения) эндобдж 152 0 объект > эндобдж 155 0 объект (8.1 Matlab: Численные методы) эндобдж 156 0 объект > эндобдж 159 0 объект (8.2 Коммивояжер Matlab) эндобдж 160 0 объект > эндобдж 163 0 объект (9 Matlab: аппроксимация кривой) эндобдж 164 0 объект > эндобдж 167 0 объект (9.1 Matlab: аппроксимация кривой) эндобдж 168 0 объект > эндобдж 171 0 объект (Упражнения) эндобдж 172 0 объект > эндобдж 175 0 объект (10 Mathcad: Введение) эндобдж 176 0 объект > эндобдж 179 0 объект (10.1 Mathcad: Введение) эндобдж 180 0 объект > эндобдж 183 0 объект (11 Mathcad: ввод уравнений) эндобдж 184 0 объект > эндобдж 187 0 объект (11.1 Mathcad: уравнения) эндобдж 188 0 объект > эндобдж 191 0 объект (11.2 Mathcad: редактирование уравнений) эндобдж 192 0 объект > эндобдж 195 0 объект (11.3 Mathcad: единицы измерения) эндобдж 196 0 объект > эндобдж 199 0 объект (Упражнения) эндобдж 200 0 объект > эндобдж 203 0 объект (12 Mathcad: Дано / Найти и Решить) эндобдж 204 0 объект > эндобдж 207 0 объект (12.1 Mathcad: Дано / Найти блоки) эндобдж 208 0 объект > эндобдж 211 0 объект (12.2 Mathcad: Решить блоки) эндобдж 212 0 объект > эндобдж 215 0 объект (Упражнения) эндобдж 216 0 объект > эндобдж 219 0 объект (13 Mathcad: Функции) эндобдж 220 0 объект > эндобдж 223 0 объект (13.1 Mathcad: встроенные функции) эндобдж 224 0 объект > эндобдж 227 0 объект (13.2 Mathcad: определяемые пользователем функции) эндобдж 228 0 объект > эндобдж 231 0 объект (Упражнения) эндобдж 232 0 объект > эндобдж 235 0 объект (14 Mathcad: Матрицы) эндобдж 236 0 объект > эндобдж 239 0 объект (14.1 Mathcad: определение матрицы) эндобдж 240 0 объект > эндобдж 243 0 объект (14.2 Mathcad: редактирование матриц) эндобдж 244 0 объект > эндобдж 247 0 объект (14.3 Mathcad: Ссылки на части матриц) эндобдж 248 0 объект > эндобдж 251 0 объект (14.4 Mathcad: Решение систем линейных уравнений) эндобдж 252 0 объект > эндобдж 255 0 объект (Упражнения) эндобдж 256 0 объект > эндобдж 259 0 объект (15 Mathcad: построение графиков) эндобдж 260 0 объект > эндобдж 263 0 объект (15.1 Mathcad: построение графиков) эндобдж 264 0 объект > эндобдж 267 0 объект (Упражнения) эндобдж 268 0 объект > эндобдж 271 0 объект (16 Mathcad: аппроксимация кривой) эндобдж 272 0 объект > эндобдж 275 0 объект (16.1 Mathcad: аппроксимация кривой) эндобдж 276 0 объект > эндобдж 279 0 объект (Упражнения) эндобдж 280 0 объект > эндобдж 283 0 объект (17 Mathcad: Исчисление и символика) эндобдж 284 0 объект > эндобдж 287 0 объект (17.1 Mathcad: Исчисление) эндобдж 288 0 объект > эндобдж 291 0 объект (17.2 Mathcad: Символика) эндобдж 292 0 объект > эндобдж 295 0 объект (Упражнения) эндобдж 296 0 объект > эндобдж 299 0 объект (Приложение) эндобдж 300 0 объект > эндобдж 303 0 объект (Показатель) эндобдж 304 0 объект > эндобдж 307 0 объект> транслировать x څ OO !! qf? {T & MLbO5 (mQ6܂% , o! @ ĪXRd
Как написать точку m в mathcad
Re Mathcad notation — Обсуждения на форуме по математике
июн 2006 —
Нотация Mathcad — Tech-Archive net
июн 2006 —
Сочетания клавиш PTC Mathcad Prime 3 0 — Science Software Nordic
PTC Mathcad Prime 3 0 Сочетания клавиш Шведская клавиатура Вставляет математическую область Ctrl Shift M Умножение и Точка Произведение * Отрицание и
A Mathcad Primer Содержание
г., 2006 г. —
X с точкой над точкой | Сообщество PTC
Есть способ поставить точку над переменной? Это Newton I m не хочет ничего похожего на Overdot [x, 1], только какой-то чит с rtf, возможно, Alvaro Если вы хотите копировать книги, конвертируйте в исполняемый файл Mathcad В противном случае, что Think пишет и шрифт Odeslove 10 с f, и вы ничего не видите Точка поверх нее
Re Mathcad notation — Обсуждения на форуме по математике Июнь 2006 — Лекция 2: основы Mathcad и матричные операции — essie-uf Аот 2001 — Обозначение Mathcad — Tech-Archive net Июнь 2006 — Точка по времени — PTC: Mathcad — Rus-Tips Мне удалось поставить две точки над надписью «Кажется, я не могу написать обычный, поскольку Mathcad просто добавляет круглые скобки вокруг варибала». Сочетания клавиш Mathcad Сентябрь 2011 г. —
Сочетания клавиш Mathcad Сентябрь 2011 г. — Обозначение Mathcad — Tech-Archive net Июнь 2006 — Сочетания клавиш PTC Mathcad Prime 3 0 — Science Software Nordic PTC Mathcad Prime 3 0 Сочетания клавиш Шведская клавиатура Вставка математической области Ctrl Shift M Умножение и точечное произведение * Отрицание и Mathcad Primer Содержание Dc 2006 — Точка по времени — PTC: Mathcad — Rus-Tips Мне удалось поставить две точки над надписью «Кажется, я не могу написать обычный, поскольку Mathcad просто добавляет круглые скобки вокруг варибала».
Mathcad Primer Содержание Dc 2006 — MATLAB Central — Как поставить тильду, шляпу, полосу или точку на Янв 2008 — Обозначение Mathcad — Tech-Archive net Июнь 2006 — X с точкой над точкой | Сообщество PTC Есть способ поставить точку над переменной? Это Ньютон. Я не хочу ничего похожего на Overdot [x, 1], только некоторые читы с rtf, возможно, Альваро. Если вы хотите копировать книги, конвертируйте в исполняемый файл Mathcad. В противном случае, что Подумайте, пишите и шрифт Odeslove 10 с f, и вы видите ничего не стоит над этим Сочетания клавиш PTC Mathcad Prime 3 0 — Science Software Nordic PTC Mathcad Prime 3 0 Сочетания клавиш Шведская клавиатура Вставка математической области Ctrl Shift M Умножение и точечное произведение * Отрицание и Точка по времени — PTC: Mathcad — Rus-Tips Мне удалось поставить две точки над надписью «Кажется, я не могу написать обычный, поскольку Mathcad просто добавляет круглые скобки вокруг варибала».
Лекция 2: основы Mathcad и матричные операции — essie-uf Аот 2001 — MATLAB Central — Как поставить тильду, шляпу, полосу или точку на Янв 2008 — Сочетания клавиш Mathcad Сентябрь 2011 г. — Точка по времени — PTC: Mathcad — Rus-Tips Мне удалось поставить две точки над надписью «Кажется, я не могу написать обычный, поскольку Mathcad просто добавляет круглые скобки вокруг варибала».
Сочетания клавиш PTC Mathcad Prime 3 0 — Science Software Nordic PTC Mathcad Prime 3 0 Сочетания клавиш Шведская клавиатура Вставка математической области Ctrl Shift M Умножение и точечное произведение * Отрицание и Re Mathcad notation — Обсуждения на форуме по математике Июнь 2006 — Mathcad Primer Содержание Dc 2006 — Лекция 2: основы Mathcad и матричные операции — essie-uf Аот 2001 —
Сочетания клавиш Mathcad Сентябрь 2011 г. — Re Mathcad notation — Обсуждения на форуме по математике Июнь 2006 — Сочетания клавиш PTC Mathcad Prime 3 0 — Science Software Nordic PTC Mathcad Prime 3 0 Сочетания клавиш Шведская клавиатура Вставка математической области Ctrl Shift M Умножение и точечное произведение * Отрицание и X с точкой над точкой | Сообщество PTC Есть способ поставить точку над переменной? Это Ньютон. Я не хочу ничего похожего на Overdot [x, 1], только некоторые читы с rtf, возможно, Альваро. Если вы хотите копировать книги, конвертируйте в исполняемый файл Mathcad. В противном случае, что Подумайте, пишите и шрифт Odeslove 10 с f, и вы видите ничего не стоит над этим Введение в Mathcad Клавиша и нажмите клавишу [M])) матрица с одной строкой или столбцом является вектором. Например, чтобы найти инверсию данной матрицы A, нам нужно всего лишь, чтобы на графике отображалась только точка.
Сочетания клавиш Mathcad Сентябрь 2011 г. — Лекция 2: основы Mathcad и матричные операции — essie-uf Аот 2001 — Сочетания клавиш PTC Mathcad Prime 3 0 — Science Software Nordic PTC Mathcad Prime 3 0 Сочетания клавиш Шведская клавиатура Вставка математической области Ctrl Shift M Умножение и точечное произведение * Отрицание и Re Mathcad notation — Обсуждения на форуме по математике Июнь 2006 —
Обозначение Mathcad — Tech-Archive net Июнь 2006 — MATLAB Central — Как поставить тильду, шляпу, полосу или точку на Янв 2008 — Точка по времени — PTC: Mathcad — Rus-Tips Мне удалось поставить две точки над надписью «Кажется, я не могу написать обычный, поскольку Mathcad просто добавляет круглые скобки вокруг варибала».
Сочетания клавиш PTC Mathcad Prime 3 0 — Science Software Nordic PTC Mathcad Prime 3 0 Сочетания клавиш Шведская клавиатура Вставка математической области Ctrl Shift M Умножение и точечное произведение * Отрицание и Сочетания клавиш Mathcad Сентябрь 2011 г. — X с точкой над точкой | Сообщество PTC Есть способ поставить точку над переменной? Это Ньютон. Я не хочу ничего похожего на Overdot [x, 1], только некоторые читы с rtf, возможно, Альваро. Если вы хотите копировать книги, конвертируйте в исполняемый файл Mathcad. В противном случае, что Подумайте, пишите и шрифт Odeslove 10 с f, и вы видите ничего не стоит над этим Обозначение Mathcad — Tech-Archive net Июнь 2006 — Лекция 2: основы Mathcad и матричные операции — essie-uf Аот 2001 —
Сочетания клавиш PTC Mathcad Prime 3 0 — Science Software Nordic PTC Mathcad Prime 3 0 Сочетания клавиш Шведская клавиатура Вставка математической области Ctrl Shift M Умножение и точечное произведение * Отрицание и Сочетания клавиш Mathcad Сентябрь 2011 г.