Mathcad minerr: 6.2. Приближенное решение алгебраических уравнений MathCAD 12 руководство

Решение блоков. Функции Find и Minerr

• Совместное решение уравнений и неравенств.

• Указание шага блока.

• Операции отношения применимые при создании блока.

В MathCADе используется механизм, названный SOLVE BLOCKS, для совместного решения уравнений и неравенств. При этом используются функции поиска Find и Minerr. Формат функций:

Find(список_имен_переменных)

Minerr(список_имен_переменных)

Здесь список_имен_переменных— имена переменных, относительно которых осуществляется поиск решения. Аргументы функции разделяются запятыми.

Пример MathCAD-документа:

Замечания: 1) Если решение не может быть найдено в пределах установленной точности (параметр TOL), то выводится сообщение

not converging.

Попытайтесь изменить значение параметра TOL.

2) Если при решении блока не может быть найдено решение для указанных в теле блока конструкций, то выводится сообщение

did not found solution.

В некоторых случаях удается получить приближенное решение задачи, заменив функцию Find на Minerr.

3) В блоке не должно быть условий меньше, чем число ведущих переменных. В случае необходимости блок можно пополнить фиктивными условиями.

 

При задании тела блока можно применять следующие операции отношения:

 

	[Alt]=
	>
	<
	[Alt])
	[Alt](
	[Alt]#

 

Непосредственно в теле блока последнюю операцию ( ) использовать нельзя. Условие x aможно заменить условием. Однако операцию   можно использовать во встроенной функцииif. Например,

Функция Minerr возвращает значения переменных,минимизирующие величину встроенной переменной ERR, равную сумме квадратов отклонений по всем условиям блока.

В решающем блоке используется модифицированный вариант метода Ньютона решения систем уравнений.

Интерполяция функций

• Функция линейной интерполяции.

• Функции, позволяющие осуществлять интерполяцию кубическими сплайнами.

• Этапы решения задачи интерполирования функции сплайнами.

MathCAD содержит функцию линейной интерполяции и 4 функции, позволяющие осуществить интерполяцию кубическими сплайнами.

Для всех функций индексация векторов данных, являющихся аргументами, начинается с 0. Если вы не задали значение нулевого элемента вектора, то MathCAD полагает его равным нулю, что может существенно повлиять на результат. При желании вы можете установить начальное значение индекса, задав новое определение встроенного параметра ORIGIN.

Пусть некоторая функция задается множеством точек, описываемым двумя векторами с одинаковым числом элементов:

vx -N-мерный вектор, задающий X-координаты точек в возрастающем порядке,

vy -N-мерный вектор, задающий соответствующие Y-координаты точек.

Требуется найти приближенное значение функции для произвольного значения x.

 

 

Линейная интерполяция

Функция linterp(vx,vy,x)осуществляет линейную интерполяцию на множестве данных точек.

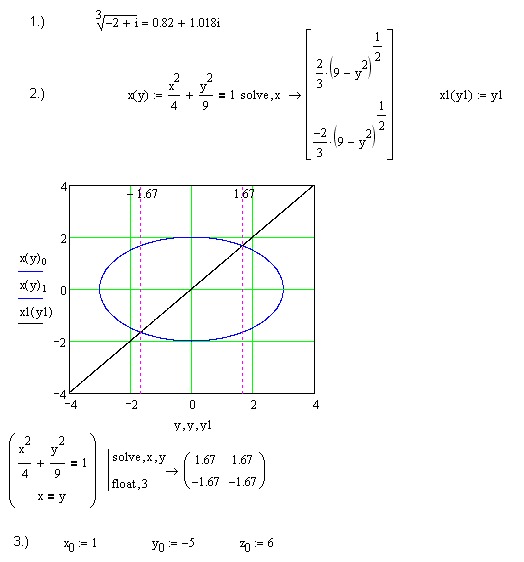
Чтобы найти значение функции для произвольного значения x, MathCAD находит два элементаvxiиvxi+1вектораvxтаких, что заданное значениеx лежит между ними. Соответствующее значение функцииyопределяется таким образом, чтобы точка(x,y)лежала на прямой, соединяющей точки(vxi,vyi)и(vxi+1,vyi+1)(см. рисунок 1) ). В случае, когда значениеx меньшеvx0или больше последнего элемента массиваvx, то интерполяция производится согласно рисункам 2) и 3).

 

Урок 24. Решение уравнений в Mathcad – использование функций

Navigation

Павел Демидов 03.12.2014 Уроки Mathcad 0

Решение уравнений является важным для решения практических задач. Поэтому уделим уравнениям еще один урок.

Блок решения в функции

Если Вы хотите исследовать изобразить на графике поведение уравнения в зависимости от значения определенного параметра, Вам, возможно, придется решить систему уравнений много раз. Вы можете сделать это, используя блок решения в функции. Покажем на примере: предположим, мы хотим исследовать поведение решения следующего уравнения в зависимости от различных значения параметра

A:

Блоку решения не нужно ни значение параметра, ни начальное приближение, поскольку решение есть функция этих двух значений. Эти значения мы будем задавать при вызове функции.

Функцию можно использовать сколько угодно раз:

Использовать функцию можно с диапазоном переменных:

Такая техника решения не самая надежная.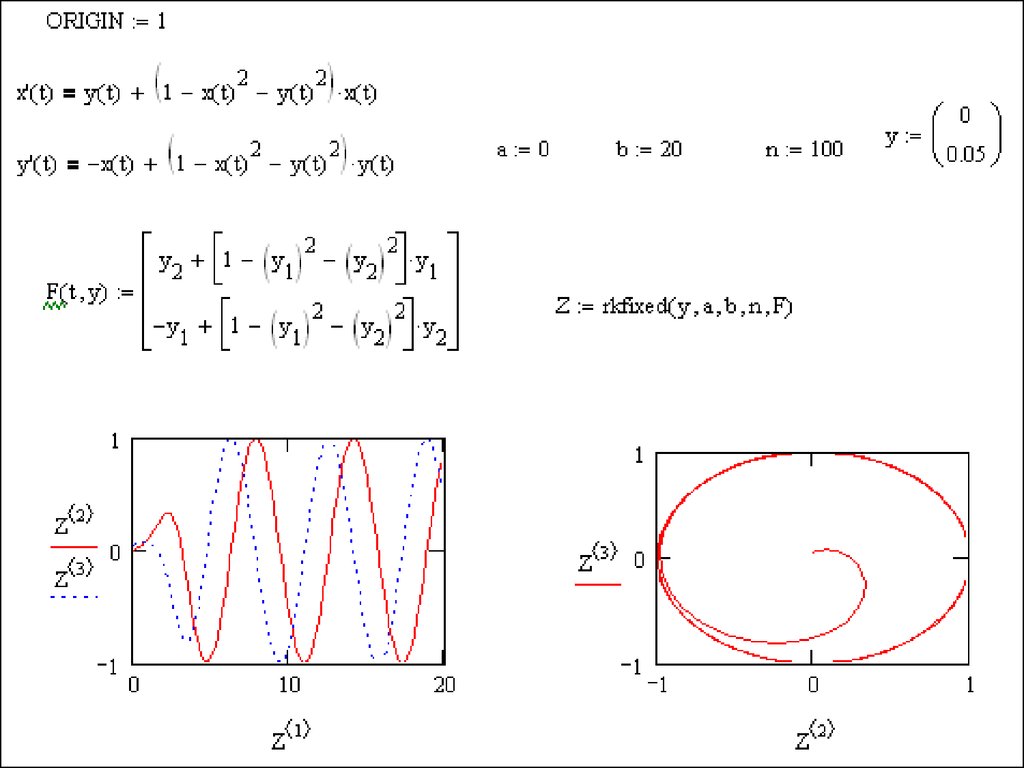 Если хотя бы одно решение не может быть найдено, Вы не получите и решений для других параметров (это произойдет, если задать A<0.7). Поэтому лучше заранее проверить свою функцию.

Сообщения об ошибке можно избежать, написав маленькую программу:

Если блок решения выдает сообщение об ошибке, на выходе получим значение

NaN (Not a Number – «Не Число»), которое просто не отображается на графике:

Построим две ветки уравнения с использованием этого приема:

Когда переменных много

Расчеты часто содержат несколько переменных, но Вам, возможно, придется использовать лишь некоторые из них. В качестве примера рассмотрим систему восьми уравнений, где нам нужно получить только значения X и Y. Начальные приближения следует задать для всех переменных:

Решение представляет собой вектор из восьми элементов, но нам нужны лишь элементы с индексами 0 и 1.

Минимизация ошибки

Find() – не единственный решатель в Mathcad.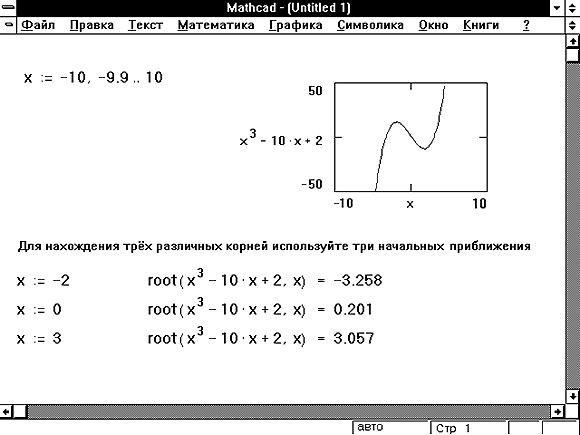 Еще один полезным решателем является Minnerr(), находящий решения, которые минимизируют ошибку в системе уравнений. Рассмотрим пример: есть набор данных, которые мы хотим аппроксимировать уравнением Бейтмена:

Мы хотим подобрать три константы в уравнении Бейтмена таким образом, чтобы ошибка приближения была минимальна. У нас есть семь уравнений (по одной для каждого эксперимента) и три константы, так что в системе избыток данных. Minerr() может обработать эту проблему:

Замечания:

1. Три константы являются переменными для этой системы.
2. Переменные не могут иметь счетных индексов.
3. У параметров (t и c) могут быть счетные индексы.

Возможно, Вам хотелось бы использовать цикл for для семи уравнений, но в блоке решений этого сделать нельзя.

Для полностью определенных систем (с одинаковым числом независимых уравнений и неизвестных) функция Minerr() дает тот же ответ, что и Find().

Резюме

В этом уроке мы определили способы расширенного использования блоков решения:

1. Вы можете определить вывод блока решения как функцию. Таким образом в блок решения можно передавать параметры и начальные приближения.
2. Если при вычислении точек для графика хотя бы одно решение не будет найдено, то график не будет построен. Этой ошибки можно избежать, написав небольшую программу с использованием “try/on error”, которая выводит NaN (Not a Number – Не Число), если результат отсутствует.
3. Для двух и более неизвестных (и уравнений) вывод блока решения является вектором. Если нужен один или два элемента этого вектора, их можно вывести, используя подстрочные индексы.
4. Вместо функции Find() можно использовать Minerr() – она минимизирует ошибку для заданного набора ограничений, в том числе, если данные избыточны. Minerr() часто может дать приближенный результат, когда Find() выдает ошибку.

About Павел Демидов

Выпускник МГТУ им. Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.

View all posts by Павел Демидов →

Урок 23. Нелинейные уравнения в Mathcad

Изображение штриховой полосы

Эффективное использование решателя » MathCadHelp.com » Номер 1 в заданиях MathCad

В этом разделе представлены некоторые идеи о том, как эффективно использовать способность Mathcad решать системы одновременных уравнений.

Многократное решение уравнения

Приведенные до сих пор методы, несмотря на то, что они эффективны для решения определенной системы уравнений, ограничены двумя факторами:

• Каждый раз, когда вы используете поиск, вы должны блок решения, чтобы пойти с ним.

• Если вы хотите изменить некоторые параметры или константы в вашей системе уравнений, чтобы увидеть, как они влияют на решение, вам нужно вернуться к блоку решения, чтобы изменить их.

Оба этих недостатка преодолеваются благодаря способности Mathcad определять функцию в терминах блока решения.

Если вы определяете функцию с помощью Find где-то справа, эта функция будет решать систему уравнений каждый раз, когда вы ее используете. Это преодолевает первую проблему.

Если эта функция имеет в качестве аргументов те же параметры, которые вы хотите изменить в блоке решения, вы можете просто изменить параметры, изменив числа, которые вы помещаете в список аргументов функции. Это преодолевает вторую проблему.

На рис. 15-14 показан конкретный пример. Коэффициент трения трубы f зависит от диаметра трубы D, ее шероховатости E и числа Рейнольдса R. Вполне возможно, что вы захотите поэкспериментировать с трубами разного размера (D), изготовленными из разных типов бетона (E). .

Уравнение на рис. 15-14 показывает взаимосвязь между этими параметрами. Уравнение слишком сложное, чтобы определить функцию R, D и E, просто найдя f через R, D и E.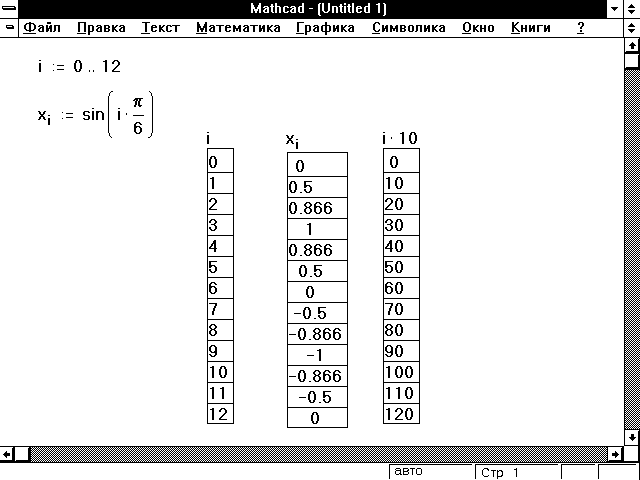 Однако вы можете определить функцию в терминах блока решения.

Всякий раз, когда вы просите Mathcad вычислить функцию FricFac(E, D, R), Mathcad берет введенные вами E, D и R, заменяет соответствующие переменные в блоке решения, вычисляет f и возвращает значение.

Решение одной и той же задачи для разных переменных

Время от времени вы будете сталкиваться с проблемой, в которой вам нужно изменить роли известных и неизвестных в уравнении. Например, рассмотрим уравнение, которое связывает процентную ставку, сумму кредита, срок кредита и платежи. Если вы знаете три из этих четырех величин, вы можете найти недостающую.

Рабочий лист на рис. 15-17 показывает, что для кредита под 12 % на 30-летнюю ипотеку и платежа в размере 1 000 долларов США в месяц самый большой возможный кредит составляет 9 долларов США.7 218,33.

Решение по кредиту в ипотеку.

С помощью нескольких простых изменений тот же рабочий лист можно использовать для расчета процентной ставки. Предположим теперь, что сумма кредита известна и составляет 120 000 долларов. Насколько должны упасть процентные ставки, прежде чем платежи упадут до 1000 долларов в месяц? На рис. 15–18 показан ответ.

Если вы сравните рисунок 15-17 и рисунок 15-18, вы увидите, что они очень похожи. Основное отличие заключается в аргументе функции Find. Чтобы изменить фиксированное и переменное в уравнении, просто измените аргументы функции поиска.

Решение процентной ставки по ипотечному кредиту.

Приблизительные решения

Mathcad предоставляет функцию Minerr, очень похожую на Find. Эта функция использует тот же алгоритм, что и поиск. Разница в том, что если решатель не может внести дальнейшие улучшения в решение, Minerr все равно возвращает значение. С другой стороны, функция «Найти» вернет сообщение об ошибке, указывающее, что не удалось найти решение. Вы используете Minerr точно так же, как и Find.

Minerr обычно возвращает ответ, который минимизирует ошибки в ограничениях.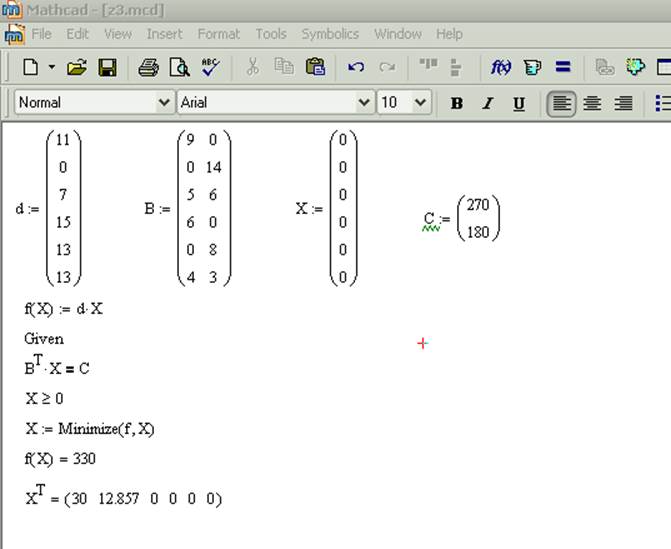 Однако Minerr не может проверить, что его ответы представляют собой абсолютный минимум ошибок в ограничениях. Если вы используете блок решения Minerrin, вы всегда должны включать дополнительные проверки на обоснованность результатов. Встроенная переменная ERR дает размер вектора ошибки для приближенного решения. Нет встроенной переменной для определения размера ошибки для отдельных решений неизвестных.

Minerr особенно полезен для решения некоторых нелинейных задач наименьших квадратов. На рис. 15-19 показан пример, в котором Minerr используется для получения неизвестных параметров в распределении Вейбулла. Функция genfit также полезна для решения нелинейных задач наименьших квадратов. Дополнительную информацию о genfit см. в разделе «Статистические функции».

Использование функции minerr для выполнения нелинейной аппроксимации методом наименьших квадратов.

Использование символьного решателя

Обычно числовые корни можно быстро и точно найти с помощью функции извлечения корня в Mathcad. Но есть некоторые обстоятельства, при которых вы можете использовать символьный решатель Mathcad для поиска точных или приблизительных корней:

• Если в уравнении, которое вы решаете, есть параметр, символьное решение может позволить вам выразить ответ напрямую через параметр. Затем вместо того, чтобы заново решать уравнение для каждого нового значения параметра, вы можете просто подставить его значение в свое символьное решение.

• Если вам нужны все комплексные корни многочлена степени 4 или меньше, символьный решатель предоставит их вам в одном векторе, точно или численно. Символьный решатель также найдет полные решения для некоторых многочленов более высокой степени.

Дополнительную информацию о символьном решении уравнений см. в разделе «Символическое решение уравнений» в главе 17. , на платформе Citrix.

Следующие приложения доступны практически всем студентам, преподавателям и сотрудникам NIU в AnywhereApps:

• CoreFTP
• Майкрософт Офис 2016
  • Доступ 2016
  • Excel 2016
  • PowerPoint 2016
  • Издатель 2016
  • Ворд 2016
• PowerBI для настольных ПК

• Замазка
• САС 9. 4
• СПСС 26
• SQL Server Management Studio 2017
• Visual Studio 2017
• ВЛК 3.0.3

Дополнительные приложения по конкретным дисциплинам доступны для студентов в зависимости от колледжа или курса. Полный список см. в разделе «Виртуальные приложения, доступные по колледжам или курсам» ниже.

Следующие дополнительные приложения доступны для использования учащимися в колледже или классе. См. Доступ к виртуальным приложениям, чтобы узнать, как получить доступ к доступным вам приложениям. В большинстве случаев преподаватели также должны иметь доступ к этим приложениям.

Колледж бизнеса

(доступно для всех студентов, изучающих бизнес)

• Crystal Reports
• Microsoft Project 2016
• Майкрософт Визио 2016
• RStudio 1.1.456

• SAP
• Анализ бизнес-объектов SAP
• Конструктор запросов SAP

Колледж инженерии и инженерных технологий

(доступно для всех студентов технических специальностей)

• Ansys
• Верстак Ansys
• Средство запуска продуктов Ansys
• Арена
• Комсол
• ИДЕЯ
• MathCAD
• Матлаб
• Microsoft Project 2016
• Майкрософт Визио 2016

• Минитаб
• PTC Creo Direct
• PTC Creo Parametric
• PTC Mathcad Prime
• Симио
• СолидВоркс
• Звезда СКК
• Звездный вид+

Химия

(доступно для всех студентов, обучающихся на курсах CHEM)

• Гауссова 16W

• GaussView

Коммуникативные расстройства

(доступно для всех студентов, обучающихся на курсах COMD)

Информатика

(доступно для всех студентов, обучающихся на курсах CSCI)

• Android Studio

Гостиничный и туристический менеджмент

(доступно для всех студентов, обучающихся на курсах гостеприимства)

• Mastercook

Математические науки

(доступно для всех студентов-математиков)

• Matlab

Управление операциями и информационные системы

(доступно для всех студентов OMIS и MSDA)

• Crystal Reports
• RStudio
• САП
• Анализ бизнес-объектов SAP
• Конструктор запросов SAP

• Руководство по SAS Enterprise
• Клиент SAS Enterprise Miner
• Рабочая станция SAS Enterprise Miner

Политология и социология

(доступно для всех студентов POLS и SOCI)

Геология и экологические науки о Земле

(доступно для всех студентов, обучающихся на курсах GEOL)

• ArcCatalog
• ArcGlobe
• АркКарта
• ArcScene
• Базовый лагерь Гармин

• Геолмапдатаэкстрактор
• Плоттер Мора
• СтереоНет
• СтереоНет 10

Геология 490 и 590

(доступно для всех студентов, зарегистрированных в GEOL 490 и 590)

• Aqtesolv Pro

Начало работы с AnywhereApps — часто задаваемые вопросы

Кто может использовать AnywhereApps?

AnywhereApps доступен для всех студентов, преподавателей и сотрудников NIU.