Mathcad генератор случайных чисел: Самоучитель MathCAD

MATHCAD 14: Основные сервисы и технологии

Главная / Математика / MATHCAD 14: Основные сервисы и технологии / Тест 5

Упражнение 1:

---

Номер 1

Стартовое значение для генератора псевдослучайных чисел задается командой меню Tools/ :

Ответ:

&nbsp(1) Optimize&nbsp

&nbsp(2) Worksheet Options&nbsp

&nbsp(3) Calculate&nbsp

&nbsp(4) Debug&nbsp

---

Номер 2

Функция seed(x) —

Ответ:

&nbsp(1) устанавливает новое начальное значение для генератора псевдослучайных чисел,&nbsp

&nbsp(2) генерирует случайное число &nbsp

&nbsp(3)

рассчитывает среднее&nbsp

&nbsp(4) рассчитывает дисперсию&nbsp

---

Номер 3

Стартовое значение для генератора псевдослучайных чисел можно задать:

Ответ:

&nbsp(1) опцией в окне Worksheet Options&nbsp

&nbsp(2) функцией seed(x)&nbsp

&nbsp(3) переменной ORIGIN&nbsp

&nbsp(4) функцией rnd(x)&nbsp

---

Упражнение 2:

---

Номер 1

Среднеквадратичное отклонение рассчитывает функция: 

Ответ:

&nbsp(1) var()&nbsp

&nbsp(2) stdev() &nbsp

&nbsp(3) mean() &nbsp

&nbsp(4) hist()&nbsp

---

Номер 2

Дисперсию  рассчитывает функция: 

Ответ:

&nbsp(1) var()&nbsp

&nbsp(2) stdev()&nbsp

&nbsp(3) mean() &nbsp

&nbsp(4) hist()&nbsp

---

Номер 3

Выборочное среднее  рассчитывает функция:

Ответ:

&nbsp(1) var()&nbsp

&nbsp(2) stdev()&nbsp

&nbsp

(3) mean() &nbsp

&nbsp(4) hist()&nbsp

---

Упражнение 3:

---

Номер 1

Функции для генерации последовательности случайных величин  находятся в категории:

Ответ:

&nbsp(1) Probaility distribution;&nbsp

&nbsp(2) Random numbers;&nbsp

&nbsp(3) Probability density&nbsp

&nbsp(4) Statistics. &nbsp

---

Номер 2

Функции для расчета числовых характеристик случайных величин  находятся в категории:

Ответ:

&nbsp(1) Probaility distribution;&nbsp

&nbsp(2) Random numbers;&nbsp

&nbsp(3) Probability density&nbsp

&nbsp(4) Statistics&nbsp

---

Номер 3

Функции для расчета функции распределения случайных величин  находятся в категории:

Ответ:

&nbsp(1) Probaility distribution;&nbsp

&nbsp(2) Random numbers&nbsp

&nbsp(3) Probability density&nbsp

&nbsp(4) Statistics&nbsp

---

Упражнение 4:

---

Номер 1

Для построения двумерной матрицы гистограммы случайных величин используется функция: 

Ответ:

&nbsp(1) hist ()&nbsp

&nbsp(2) histogram ()&nbsp

&nbsp(3) hmean( )&nbsp

&nbsp(4) gmean ()&nbsp

---

Номер 2

Гистограмма случайных величин это график:

Ответ:

&nbsp(1) значений случайных величин&nbsp

&nbsp(2) аппроксимирующий, плотность распределения случайных величин&nbsp

&nbsp(3) распределения случайных величин&nbsp

&nbsp(4) среднего значения случайных величин&nbsp

---

Номер 3

Для построения гистограммы случайных величин с произвольными интервалами разбиения используется функция :

Ответ:

&nbsp(1) hist ()&nbsp

&nbsp(2) histogram ()&nbsp

&nbsp(3) hmean( )&nbsp

&nbsp(4) gmean ()&nbsp

---

Упражнение 5:

---

Номер 1

Функция  rnd(x) генерирует :

Ответ:

&nbsp(1) вектор x случайных чисел между 0 и 1,&nbsp

&nbsp(2) равномерно распределенное случайное число между 0 и x&nbsp

&nbsp(3) экспоненциально распределенное случайное число между 0 и 1&nbsp

&nbsp(4) нормально распределенное случайное число между 0 и x&nbsp

---

Номер 2

Функция  runif()  создает вектор случайных чисел, каждое из которых имеет:

Ответ:

&nbsp(1) экспоненциальное распределение&nbsp

&nbsp(2) нормальное распределение&nbsp

&nbsp(3) равномерное распределение&nbsp

&nbsp(4) логнормальное распределение&nbsp

---

Номер 3

Функция  rt() создает вектор случайных чисел, каждое из которых имеет

Ответ:

&nbsp(1) экспоненциальное распределение&nbsp

&nbsp(2) распределение Стьюдента&nbsp

&nbsp(3) равномерное распределение&nbsp

&nbsp(4) нормальное распределение&nbsp

---

Упражнение 6:

---

Номер 1

Случайная величина распределена по нормальному закону с параметрами 
 m=10 =3, вероятность принять значение меньше 7 рассчитывается по функции: 

Ответ:

&nbsp(1) rnorm(7,m,d)&nbsp

&nbsp(2) pnorm(7,m,d)&nbsp

&nbsp(3) dnorm(7,m,d)&nbsp

&nbsp(4) 1/7•rnorm(7,m,d)&nbsp

---

Номер 2

Случайная величина  X  распределена по нормальному закону с параметрами m=10 =3, вероятность принять значение больше 5 рассчитывается по функции:

Ответ:

&nbsp(1) 1- rnorm(5,m,d)&nbsp

&nbsp(2) dnorm(5,m,d)&nbsp

&nbsp(3) 1- pnorm(5,m,d)&nbsp

&nbsp(4) - pnorm(5,m,d))&nbsp

---

Номер 3

Случайная величина  X  распределена по нормальному  закону с параметрами m=10 =3, вероятность принять значение больше 9  равна:

Ответ:

&nbsp(1) 44%&nbsp

&nbsp(2) 54%&nbsp

&nbsp(3) 64%&nbsp

&nbsp(4) 74%&nbsp

---

Упражнение 7:

---

Номер 1

Случайная величина  X  распределена по равномерному  закону на отрезке  a=20  b=40, вероятность принять значение меньше 37 рассчитывается по функции:

Ответ:

&nbsp(1) runif(37,a,b)&nbsp

&nbsp(2) punif (37, a,b)&nbsp

&nbsp(3) dunif(37, a,b)&nbsp

&nbsp(4) runif (b-a, 37)&nbsp

---

Номер 2

Случайная величина  X  распределена по равномерному  закону на отрезке  a=20 b=40, вероятность принять значение в промежутке от 24  до 32 рассчитывается по функции:

Ответ:

&nbsp(1) runif(32,a,b)- runif(24,a,b)&nbsp

&nbsp(2) punif(32,a,b)- punif(24,a,b)&nbsp

&nbsp(3) duinf(x,a,b)dx&nbsp

&nbsp(4) runif (37-24, a,b))&nbsp

---

Номер 3

Случайная величина  X  распределена по равномерному  закону с параметрами a=20 b=40, вероятность принять значение больше 31. 5 равна:

Ответ:

&nbsp(1) 0.415&nbsp

&nbsp(2) 0.425&nbsp

&nbsp(3) 0.435&nbsp

&nbsp(4) 0.445&nbsp

---

Упражнение 8:

---

Номер 1

Случайная величина  X  распределена по закону Фишера со степенями свободы  d1=5  d2=60,  математическое ожидание равно:

Ответ:

&nbsp(1) 5.11&nbsp

&nbsp(2) 3.11&nbsp

&nbsp(3) 1.03&nbsp

&nbsp(4) 2.11&nbsp

---

Номер 2

Случайная величина  X  распределена по закону Фишера со степенями свободы  d1=5  d2=60,  дисперсия  равна:

Ответ:

&nbsp(1) 0. 68&nbsp

&nbsp(2) 1.08&nbsp

&nbsp(3) 0.28&nbsp

&nbsp(4) 0.48&nbsp

---

Номер 3

Случайная величина  X  распределена по закону Фишера со степенями свободы  d1=5  d2=60,  вероятность для X принять значение  от 3 до 6 :

Ответ:

&nbsp(1) 1.7%&nbsp

&nbsp(2) 2.5%&nbsp

&nbsp(3) 5%&nbsp

&nbsp(4) 7%&nbsp

---

Упражнение 9:

---

Номер 1

Функция распределения случайной величины  имеет вид:  при  и  при , чему равно математическое ожидание?

Ответ:

&nbsp(1) 0.133&nbsp

&nbsp(2) 0. 143&nbsp

&nbsp(3) 0.153&nbsp

&nbsp(4) 0.163&nbsp

---

Номер 3

Функция распределения случайной величины  имеет вид:  при  и  при , чему равно среднее квадратическое отклонение?

Ответ:

&nbsp(1) 0.32&nbsp

&nbsp(2) 0.28&nbsp

&nbsp(3) 0.75&nbsp

&nbsp(4) 0.59&nbsp

---

Упражнение 10:

---

Номер 1

Плотность распределения случайной величины  – функция , вероятность попадания случайной величины на участок [a;b] определяется: 

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

---

Номер 2

Плотность распределения случайной величины  – функция , математическое ожидание М определяется: 

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

---

Номер 3

Плотность распределения случайной величины  – функция , дисперсия  определяется: 

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

---

Главная / Математика / MATHCAD 14: Основные сервисы и технологии / Тест 5

вычислительная генетика на Python и Mathcad (часть 1) / Хабр

Пусть в аквариуме живут рыбки двух цветов.

Начнем с визуализации. Зададим число рыбок n=100 и договоримся что каждая из них имеет случайный цвет color №0 или №1, а также находится в случайной точке (x,y). Т.е. x, y, и color — это три вектора длины n, а третью (z-) координату мы не рассматриваем.

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
n = 100
x, y = np.random.rand(n), np.random.rand(n)
color = np.random.randint(0, 2, n)
plt.scatter(x, y, c=color)

Модель аквариума

Те же три вектора в Mathcad Express можно сгенерировать так:

Генерация псевдослучайных векторов в Mathcad Express

Для векторов x,y используем генератор случайных чисел с равномерным распределением на отрезке (0, 1), а для вектора color — биномиального распределения, моделирующего, в том числе, однократное подбрасывание монеты. В данном конкретном розыгрыше в Mathcad получилось 47 рыбок №1 и 100-47=53 рыбок нулевого цвета.

Теперь перейдем к главному вопросу: почему разные рыбки обладают цветом номер 0 или 1?

Все дело здесь в генетической информации, заключенной в биологическом материале, из которого состоит тело рыбки. Грубо говоря, живые существа, даже одного вида, различаются по химическому составу, причем в «длинных» молекулах биологических полимеров, из которых состоит все живое, зашифрована определенная информация, единицу которой обычно называют геном.

Совокупность генов каждого живого существа, называемая генотипом, определяет его внешний вид. В частности, генотип каждой рыбки определяет ее цвет. В простейшем случае, модель которого мы и будем дальше программировать, цвет рыбки (0 или 1) определяет один конкретный ген («ген цвета»). Аналогичная ситуация (один ген определяет цвет) имела место в классических опытах Грегора Менделя, основоположника современной генетики, с растениями гороха, а в других случаях (например, для окраса собак-такс) на цвет отдельной особи влияет сочетание нескольких генов.

Как именно гены кодируют цвет? Прежде всего, ген цвета рыбки может существовать в двух вариантах, которые называются аллелями (я буду избегать этого и некоторых других важных для биолога терминов, чтобы сосредоточиться на информатике). В генетике их принято обозначать прописной и строчной буквами (например, А и а). Я буду чаще пользоваться цифрой А=0, а=1.

Каждое растение гороха в опытах Менделя и каждая рыбка из нашего аквариума несет в себе информацию о двух аллелях, т.е. описывается одной из трех возможных комбинаций:

Если рыбка несет ген цвета АА или Аа, то она серая, а если аа — желтая. Т.е. тип гена А полностью блокирует тип а, поэтому вариант А (0) называют доминатным, а а (1) — рецессивным.

Давайте реализуем расчет цвета рыбки по ее генетическому коду, который для i-й рыбки будем описывать вектором из двух компонентов, а генетический состав всей популяции — соответственно, матрицей, которую назовем Аа. Пусть у нас есть три рыбки, каждая из которых с равной вероятностью несет генетический код 00, 10, 01 или 11. В первых трех случаях цвет рыбки будет серым, а в четвертом — желтым.

n = 3
Aa = np.zeros((n,2))
color = np.zeros(n)
for i in range(n):
  Aa[i,0] = np.random.randint(0, 2, 1)
  Aa[i,1] = np. random.randint(0, 2, 1)
  color[i] = Aa[i,0] * Aa[i,1]
print (Aa)
print (color)

Результат работы программы вы видите на картинке:

Моделирование цвета рыбок через ее генотип

Очевидно, при такой модели, если рыбок будет много, то цветных будет около 25%. Аналогичные вычисления в Mathcad для популяции из n=1000 рыбок приведены на следующем рисунке.

Моделирование цвета рыбок через ее генотип (Mathcad)

Все эти расчеты я виду в режиме стримов на своем YouTube канале , т.е. фактически, данная статья — это краткий дайджест первых двух роликов по вычислительной генетике. А в следующих сериях я планирую организовать пересчет генотипа рыбок от поколения к поколению, причем, видимо, мне придется перейти к ООП и описывать рыбок при помощи классов в Python, а Mathcad использовать, как средство вспомогательных расчетов. В качестве опорного материала я использую Википедию и вот этот курс на Степике.

Программа для генерации простых чисел в Mathcad | ПТК

Написано Дэйв Мартин

• 16. 06.2020
• Время чтения: 5 мин.

Примечание редактора: Нахождение простых чисел в Mathcad можно выполнить всего за несколько шагов программирования. Дэйв Мартин покажет вам, как это сделать (и заверит нас, что вам не нужно большого опыта программирования, чтобы понять это).

Если число делится ровно на два числа, на единицу и на само число, оно называется простым числом.

Простые числа очаровывали математиков на протяжении тысячелетий. Около 300 г. до н.э. Евклид доказал, что существует бесконечное число простых чисел. Столетие спустя греческий математик Эрастофен (подробнее о нем позже) изобрел метод нахождения простых чисел, который сегодня носит его имя: решето Эрастофена. Великие математики, такие как Эйлер, Эскотт, Ферма и Мерсенн, работали над формулами для нахождения простых чисел.

Основная теорема арифметики утверждает, что каждое целое число можно представить как множители простых чисел. Гипотеза Гольдфарба утверждает, что каждое четное целое число можно представить в виде суммы двух простых чисел. Это не доказано для всех четных чисел, но и не опровергнуто. Так что в простых числах есть что-то особенное.

Возможно, вы этого не знаете, но простые числа каждый день влияют на вашу жизнь. Каждая отдельная финансовая транзакция, которую мы совершаем онлайн или с помощью наших банковских карт, зависит от криптосистем с открытым ключом, которые используют невероятно длинные простые числа.

Однажды я думал о простых числах и понял, что если число не делится ни на одно из чисел, меньших его квадратного корня, то это простое число.

Позже я узнал, что Эрастофен понял это более 2200 лет назад. На самом деле его сито показывает, что целое число является простым, если оно не делится на ни на одно из простых чисел , меньших его квадратного корня.

Я решил посмотреть, смогу ли я написать программу в Mathcad для простых чисел. Вместо того, чтобы определять, является число простым или нет, чтобы сделать его интересным, я хотел отправить диапазон чисел в качестве входных данных для программы, а затем заставить ее вывести вектор всех простых чисел в этом диапазоне. Вот программа:

Давайте рассмотрим некоторые аспекты этой программы:

• Зацикливание — один из самых мощных аспектов программы, а здесь используется два. Цикл for позволяет выполнять ряд действий заданное количество раз. Цикл while повторяет действия до тех пор, пока определенное условие не перестанет выполняться.
• Конструкция if-then-else оценивает условие и выполняет различные действия в зависимости от того, является ли условие истинным или ложным.
• Когда определяется, что число не является простым, оператор break позволяет программе выйти из текущего цикла и вычислить следующее целое число.
• Он использует встроенные функции, такие как ceil для округления числа до следующего целого числа и mod для вычисления модуля (остаток при делении одного числа на другое). PTC Mathcad Prime имеет более 400 встроенных функций в различных областях.
• Программа строит вектор и возвращает его в качестве результата. 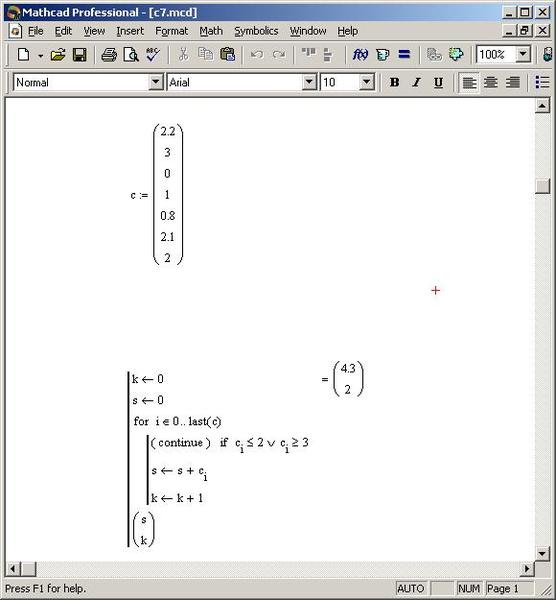Программа не знает, насколько большим будет вектор, когда он будет создан.

Неплохо для четырнадцати строк. Кроме того, я ужасен в обычном компьютерном программировании. Я прочитал книгу о Python много лет назад, но так и не продвинулся дальше, чем «Hello, World!» программа. Последний курс программирования, который я посещал, был на C — не на C++, а на обычном C — когда Буш был президентом. Первый, а не W. Я доказываю, что вам не нужно хорошо разбираться в программировании, чтобы программировать в PTC Mathcad Prime.

Вот некоторые результаты:

Программу, наверное, можно было бы сократить. Это определенно можно сделать лучше. Программы поддерживают рекурсию; программа может вызывать сама себя. Я могу сделать программу более эффективной, включив рекурсию для сравнения целого числа только с простыми числами, меньшими квадратного корня из этого целого числа. Но это проект в другой раз.

Что вы можете сделать с программами для облегчения ваших инженерных расчетов? Возможности безграничны, как и простые числа.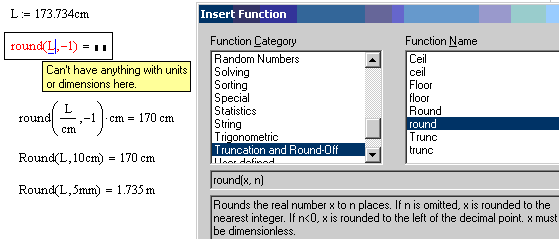

---

Дэйв Мартин — инструктор и консультант Creo, Windchill и PTC Mathcad. Он является автором книг «Проектирование сверху вниз в Creo Parametric», «Замысел проектирования в Creo Parametric» и «Настройка Creo Parametric», которые доступны на amazon.com. С ним можно связаться по адресу [email protected].

В настоящее время Дейв работает менеджером по конфигурации в компании Elroy Air, которая разрабатывает автономные летательные аппараты для доставки на средние мили. Предыдущие работодатели включают Blue Origin, Amazon Prime Air, Amazon Lab126 и PTC. Он имеет степень в области машиностроения в Массачусетском технологическом институте и является бывшим офицером бронетехники резерва армии США.

Поиск простых чисел в Mathcad можно выполнить всего за несколько шагов программирования, имея лишь небольшие знания в области кодирования.

Официальный генератор случайных чисел | Математические вкусности

Форма поиска

Поиск

Сгенерируйте мгновенное случайное число между двумя выбранными вами числами.

Пытаетесь придумать число, но ничего не можете придумать? Демонстрация вероятности для класса? Нужно вытащить случайное число из шапки для розыгрыша? Вы пришли в нужное место! Наш генератор случайных чисел даст вам именно это — случайное число.

Случайное число — это число, случайно выбранное из заданного диапазона. Прелесть случайных чисел в том, что вы не можете предсказать, какое число вы получите. Даже если вы выберете 2 в первый раз, 4 во второй и 6 в третий, любой воспринимаемый шаблон будет абсолютно случайным! В четвертый раз, когда вы выбираете, это может быть 19 или 100. Все зависит от случая.

Наш генератор предоставит случайное число между двумя выбранными вами числами. Просто введите номер нижнего предела и номер верхнего предела и нажмите ENTER. Ваше случайное число будет сгенерировано и появится в поле.

 

Почему вам следует использовать генератор случайных чисел

Теперь, если вы попытаетесь составить список случайных чисел самостоятельно, вы, вероятно, найдете шаблон. Даже подсознательно человеческий разум приучен искать и создавать вещи по шаблону или последовательности. К сожалению, это может негативно повлиять на математические задачи, над которыми вы работаете, или на запланированные действия.

Чтобы убедиться, что все зависит от случая и вы не имеете никакого влияния на этот выбор, мы создали этот удобный генератор случайных чисел, который может выбрать номер для вас. Это просто. Просто введите два числа, и генератор случайных чисел выдаст вам целое число между ними.

Как пользоваться генератором случайных чисел

Генератор случайных чисел распознает целые и отрицательные числа. Он не распознает десятичные дроби, дроби или уравнения. Если вы вставите символ процента, он не будет перенесен в поле случайного числа.

1. Начните с ввода числа по вашему выбору в поле «Нижний предел».
2. Затем введите другое число по вашему выбору в поле Верхний предел.
3. Когда у вас есть два числа, нажмите Enter.
4. Ваше случайное число появится в поле Случайное число.
5. Продолжайте нажимать Enter для ввода нового номера каждый раз.
6. Чтобы сбросить значения нижнего и верхнего пределов, выберите «Очистить».

Рабочий пример

Допустим, вам нужно вытащить случайное число для розыгрыша приза. В розыгрыше участвуют тридцать человек, и только три человека выиграют. Билеты варьируются от 1 до 150, поэтому нижний предел равен 1, а верхний предел – 150. Нажмите «Ввод», и генератор случайных чисел выдаст вам 7, 36 и 2.

Участники розыгрыша с номерами 7, 36 и 2 в билетах станут тремя победителями розыгрыша.

Проблема с десятичной дробью

Представьте, что вы пытаетесь найти число от 2,01 до 2,5. Вы вводите 2,01 в качестве нижнего предела и 2,5 в качестве верхнего предела. Вы нажимаете Enter и получаете 2? Это не входит в ваши ценности! К сожалению, в этом генераторе случайных чисел нельзя использовать десятичные дроби. Однако, пока вы работаете с десятичными знаками одного и того же целого числа, вы можете использовать другие целые числа в качестве двух ваших значений и назначать результат после десятичного числа.