Генератор случайных чисел mathcad: Сообщество Экспонента

Сообщество Экспонента

• вопрос
• 15.11.2022

Системы связи, Математика и статистика, Цифровая обработка сигналов, Радиолокация, Робототехника и беспилотники

Создать с стандартными параметрами и хорошим его рисунком, спектром, автокореляцией! Спасибо за внимание!

Создать с стандартными параметрами и хорошим его рисунком, спектром, автокореляцией! Спасибо за внимание!

1 Ответ

• вопрос
• 05.11.2022

Другое

В системе Win10 установлен MinGW64. Matlab не видит компиляторы из папки C:\mingw64 Добавил в путь матлаба и в переменные среды Windows директорию C:\mingw64\bin\, где лежит gfortran.exe, но не помога…

В системе Win10 установлен MinGW64. Matlab не видит компиляторы из папки C:\mingw64 Добавил в путь матлаба и в переменные среды Windows директорию C:\mingw64\bin\, где лежит gfortran.exe, но не помога…

• вопрос
• 05. 11.2022

Другое

Добрый день! Сегодня произошло неожиданное событие. При загрузке Матлаб он мне сообщил, что лицензия отсутствует. Я поискал ее в каталоге Матлаб, и обнаружил следующее: license_DESKTOP-NITFQJQ_4101619…

Добрый день! Сегодня произошло неожиданное событие. При загрузке Матлаб он мне сообщил, что лицензия отсутствует. Я поискал ее в каталоге Матлаб, и обнаружил следующее: license_DESKTOP-NITFQJQ_4101619…

• Публикация
• 30.10.2022

Системы связи

Мероприятие призвано собрать на одной площадке всех специалистов данной тематики для обмена знаний, опыта и технологий, чтобы вооруживший последними технологиями дать быстрый старт в развитии отечественного оборудования систем связи 5G. Подробная программа 09:…

Приглашаем разработчиков систем связи на семинар для всестороннего обсуждения вопросов построения отечественного оборудования систем связи 5G

.

Пройдет офлайн в Москве 17 ноября в 10:00.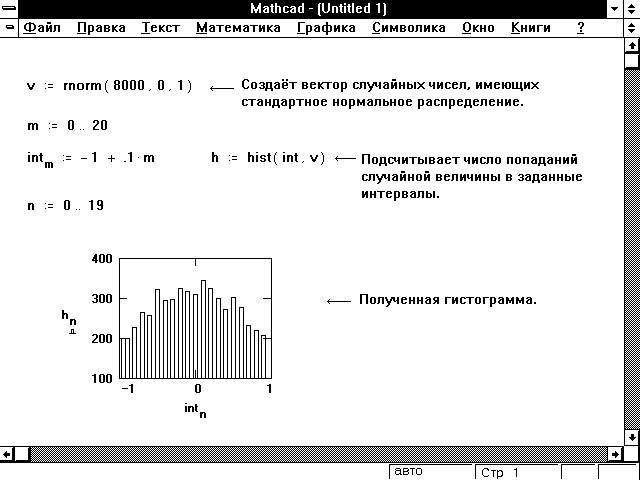

• MATLAB
• Simulink
• САУ
• ЦОС
• ПЛИС
• МОП
• 5G
• Модельно ориентированное проектирование

30.10.2022

• Публикация
• 26.10.2022

Встраиваемые системы

Эта статья написана совместно с нашими партнерами — компанией «РИТМ». Компания занимается разработкой полунатурных стендов и комплексов полунатурного моделирования «РИТМ», которые используются нашими заказчиками. Клиенты в некотор…

Уже много лет мы занимаемся продвижением модельно-ориентированного проектирования в России. Поэтому наш опыт сконцентрирован вокруг инструментов модельно-ориентированного проектирования — то есть различных сред моделирования и симуляции — и применения их в инженерных разработках.

• MATLAB
• Simulink
• САУ
• ЦОС
• ПЛИС
• МОП
• fpga
• экспонента
• Модельно ориентированное проектирование

26. 10.2022

• Публикация
• 26.10.2022

Электропривод и силовая электроника

Основа всех трех сценариев – цифровое моделирование в режиме жесткого реального времени. Наша команда инженеров показала, что КПМ РИТМ способен решать ряд сложных задач, которые стоят перед российской энергетикой. Мы благодарны всем гостям и всегда рады…

13 октября в нашем офисе прошел семинар. Всего за 5 часов мы обсудили, как использовать КПМ РИТМ для:

• Тестирования микропроцессорных реле;
• Построения систем мониторинга переходных режимов;
• Исследования кибер-инцидентов в электроэнергетике.

• экспонента
• микропроцессор
• электроэнергетика
• РИТМ
• энергетика

26.10.2022

• Публикация
• 26.10.2022

Электропривод и силовая электроника

Вас ждут: Заметки по созданию цифровых двойников; Полезные статьи и видео; Анонсы вебинаров и семинаров. Подписывайтесь: https://t.me/exponenta_energy

Наша команда инженеров электроэнергетики создала канал, где вы найдёте множество материалов про то, как используют машины реального времени в энергетике.

• MATLAB
• HIL
• РИТМ
• Hardware In the Loop
• Model In the Loop

26.10.2022

• Публикация
• 25.10.2022

Глубокое и машинное обучение(ИИ), Математика и статистика

В ходе вебинара будет рассказано о существующих подходах к организации предсказательного обслуживания. Также будет продемонстрирована экспериментальная установка, состоящая из электродвигателя, передаточного механизма, нагрузки и системы датчиков. Установка мо…

Приглашаем на вебинар «Предсказание отказов в промышленности: от теории к практике», который пройдет 8 ноября в 10:00.

Предсказание отказов промышленного оборудования достигается за счёт непрерывного мониторинга и контроля состояния оборудования.

Предсказательное обслуживание призвано существенно снизить затраты на техническое обслуживание оборудование, сократить количество поломок и время просто оборудования.

• MATLAB
• Simulink
• САУ
• ЦОС
• ПЛИС
• МОП
• ИИ
• Модельно ориентированное проектирование

25.10.2022

• вопрос
• 24.10.2022

Системы связи, ПЛИС и СнК, Радиолокация, Робототехника и беспилотники, Встраиваемые системы, Цифровая обработка сигналов

Есть модуль в Симулинк детектор приамбулы. Он считает количество бит от начала на котором находится приамбула. Выдает на выходе число. Хочу это значение использовать в модуле Си но симулинк выдает оши…

Есть модуль в Симулинк детектор приамбулы. Он считает количество бит от начала на котором находится приамбула. Выдает на выходе число. Хочу это значение использовать в модуле Си но симулинк выдает оши…

3 Ответа

• вопрос
• 19.10.2022

Математика и статистика, Цифровая обработка сигналов, Финансы

 u = (y³)/3 + 8xy — 9y — 4x² — 10 Справка

 u = (y³)/3 + 8xy — 9y — 4x² — 10 Справка

3 Ответа

12.3.1. Генерация псевдослучайных чисел MathCAD 12 руководство

• Статистика
• 12.1. Статистические распределения
  • 12.1.1. Статистические функции
  • 12.1.2. Пример: нормальное (Гауссово) распределение
• 12.2. Выборочные статистические характеристики
  • 12.2.1. Гистограммы
  • 12.2.2. Среднее и дисперсия
  • 12.2.3. Примеры: Выборочная оценка дисперсии и среднего нормальной случайной величины
  • 12.2.4. Корреляция
  • 12.2.5. Новые функции корреляционного анализа сигналов
  • 12. 2.6. Коэффициенты асимметрии и эксцесса
  • 12.2.7. Статистические функции матричного аргумента
• 12.3. Методы Монте-Карло
  • 12.3.1. Генерация псевдослучайных чисел
  • 12.3.2. Генерация коррелированных выборок
  • 12.3.3. Моделирование случайного процесса
  • 12.3.4. Пример: огибающая и фаза нормального случайного процесса

Как уже отмечалось (см. разд. 12.1.1), для генерации M-компонентного вектора независимых псевдослучайных чисел имеется ряд встроенных функций, реализующих различные типы статистических распределений и имеющих вид r*(M,раr), где * — идентификатор, a par— список параметров конкретного распределения. В частности, генератор нормальных псевдослучайных чисел был рассмотрен ранее (см. разд. 12.1.2), а для равномерного распределения предусмотрено две встроенных функции:

•  runif (M,а,b) — вектор м независимых случайных чисел, каждое из которых имеет равномерное распределение;
•  rnd(x) — случайное число, имеющее равномерную плотность распределения на интервале (0,х):

•  х — значение случайной величины;
•  Р — значение вероятности;
•  (а,b) — интервал, на котором случайная величина распределена равномерно.

Чаще всего в несложных программах применяется последняя функция, которая приводит к генерации одного псевдослучайного числа. Наличие такой встроенной функции в Mathcad — дань традиции, применяемой в большинстве сред программирования. Возможно, именно скалярный тип этой функции определяет простоту и привычность ее использования в расчетах моделей типа Монте-Карло.

Рис. 12.9. Модель сигнал/шум с равномерным законом распределения

Рис. 12.9 демонстрирует широко распространенный прием моделирования, основанный на смеси некоторого полезного сигнала f(х) и шумовой компоненты а, что характерно для типичного физического эксперимента. В качестве шума используется серия равномерно распределенных псевдослучайных чисел. Различные соотношения интенсивностей сигнала и шума определяют различные условия модельной задачи и позволяют эффективно протестировать алгоритмы, которые разработаны для ее решения.

ПРИМЕЧАНИЕ

Более сложные статистические расчеты для модели сигнал/шум приведены в листинге 12. 24 (см. разд. 12.3.4).

Параметры генераторов псевдослучайных чисел

В Mathcad применяются типичные алгоритмы генерации последовательностей псевдослучайных чисел, которые используют в качестве «отправной точки» некоторое начальное (или отправное) значение (seed value). Это начальное значение используется для того, чтобы совершить над ним определенные математические действия (к примеру, взять остаток от деления на некоторое другое число) и получить в итоге первое псевдослучайное число последовательности. Затем те же математические операции совершаются с первым числом для получения второго, и т. д.

Несложно догадаться, что если использовать все время одно и то же начальное значение генератора псевдослучайных чисел, то, открывая всякий раз новый документ со встроенной функцией получения тех или иных псевдослучайных чисел, будет выдаваться в точности одна и та же их последовательность. Сами числа внутри последовательности будут «почти» случайными (значимость этого «почти» будет зависеть только от качества алгоритма генерации), но вот сама последовательность при каждом открытии документа будет одной и той же.

ПРИМЕЧАНИЕ

Вы можете сами убедиться в идентичности выдаваемых последовательностей псевдослучайных чисел, открывая и закрывая несколько раз документ с рис. 12.9 или любой документ с иным датчиком случайных чисел, описанных в данном разделе. Любопытным также будет эксперимент по последовательному применению нескольких встроенных функций генерации псевдослучайных чисел в пределах одного документа.

Для того чтобы иметь возможность поменять саму последовательность сгенерированных случайным датчиком чисел, в Mathcad 11 (и выше) предусмотрена новая возможность явного определения используемого им начального значения. Для этого вызовите командой меню Tools/ Worksheet Options (Сервис / Опции документа) диалог Worksheet Options (Опции документа) и на вкладке Built-in Variables (Встроенные переменные) введите желаемое (целое) число в поле ввода Seed value for random Bombers (Начальное значение для генератора псевдослучайных чисел).

Альтернативный способ заключается в использовании соответствующей встроенной функции непосредственно в документе:

•  seed(x) — функция установки нового начального значения для генератора псевдослучайных чисел:

•  х — новое начальное значение для генератора псевдослучайных чисел (целое число от 1 до 2147483647).

Нравится

Твитнуть

Качество генераторов случайных чисел

Я создал этот пост после того, как тестер захотел обойти генератор случайных чисел, чтобы проверить детерминированные элементы своего кода (что было разумно). Однако они специально не проверяли, подходит ли сам генератор случайных чисел для этой цели.

Многие из поставляемых генераторов случайных чисел (в компиляторах) плохие.
Вот что говорят Пресс и др. в «Числовых рецептах на C», isbn 0-521-43108-5:
«многие, если не большинство, библиотеки ANSI C… относятся к категории «полностью испорченные».»

Даже комитет ANSI C отметил, что то, что он опубликовал, «было лишь примером» [способным быть реализованным почти на всех компьютерах, какими бы ничтожными они ни были].

Пресс и др. Продолжайте, конкретный выбор (константы в алгоритме) не особенно хороший выбор!

Продолжая, линейный конгруэнтный метод [ следующий = (предыдущий * a) mod m + c ] имеет то преимущество, что он быстр. Но у него есть недостаток, заключающийся в высокой последовательной корреляции. То есть, если вы возьмете группы из k результатов и нанесете их на график, они появятся как k-1 «плоскостей» в k-пространстве. Например, в 3D-графике и играх все триплеты будут находиться только в двух плоскостях через ваше 3D-пространство — ограничение, а!

Будет еще хуже, если вы выберете только младшие биты, они будут еще менее случайными!

Итак, убедитесь, что генератор случайных чисел («Равномерные отклонения») исправен. Далее Пресс и др. приводит множество хороших примеров для различных распределений вероятностей.

Немного о том, что существуют самолеты «k-1», показано в
http://www.math.nyu.edu/~cai/Courses/Derivatives/compfin_lecture_1.pdf

Я не понял, что плоскости закручиваются, поэтому в двух примерах k = 2 (график 2d) есть только одна линия (k-1 = 1) через все точки, но она закручивается. [По крайней мере, это то, что я думаю, что это означает] 9(1/k), где m — модуль, который может быть намного меньше.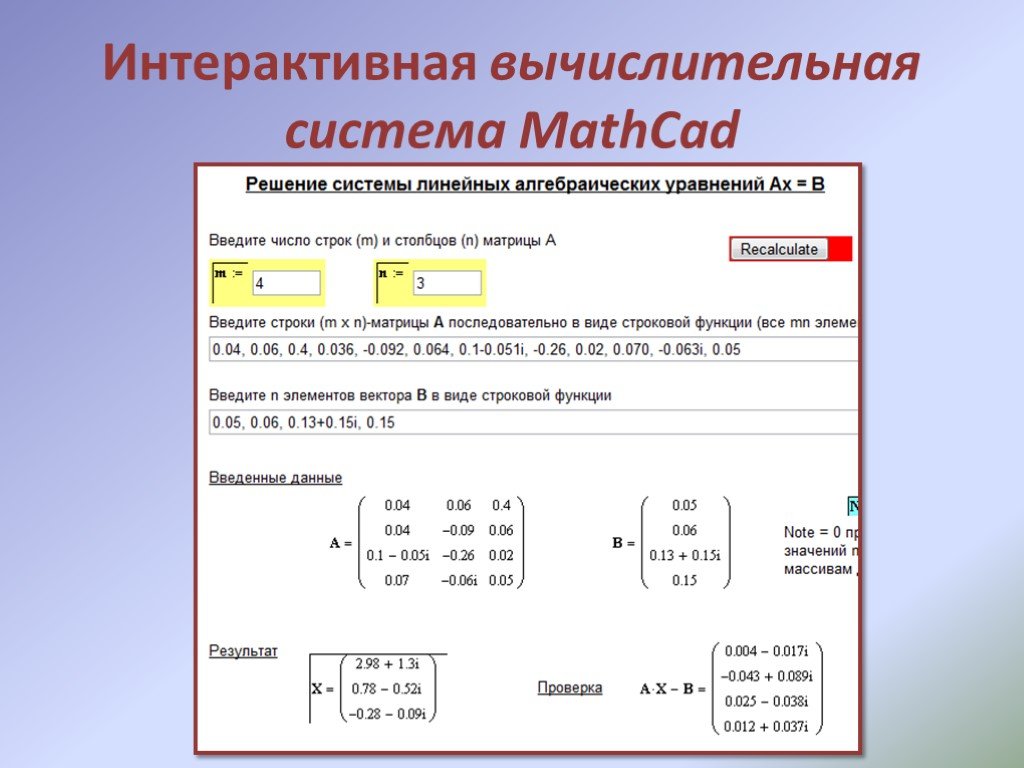

Стюарт Бруфф отмечает Вихрь Мерсенна и реализовал версию в MathCAD (к сожалению, не знаю, где сейчас находится файл). Он выбрал его, потому что он, казалось, решает многие из обозначенных проблем. Недостатком является то, что вам действительно нужно знать, сколько случайных чисел вам понадобится, чтобы сделать инициализацию и генерацию более эффективной. http://en.wikipedia.org/wiki/Mersenne_twister (веб-сайт авторов http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html)

У меня пока нет сведений об универсальном генераторе случайных чисел MathCAD (Кнут).

Я проследил одну из схем генератора случайных чисел MathCAD для других генераторов случайных чисел, и
нашел Люка Девроя (1986) в виде бесплатного полного текста http://cgm.cs.mcgill.ca/~luc/rnbookindex.html Non- Uniform Random Variate Generation (первоначально опубликовано в Springer-Verlag, New York, 1986)

Любой, кто использует генератор случайных чисел, должен всегда иметь возможность, по крайней мере, быстро проверить свой генератор.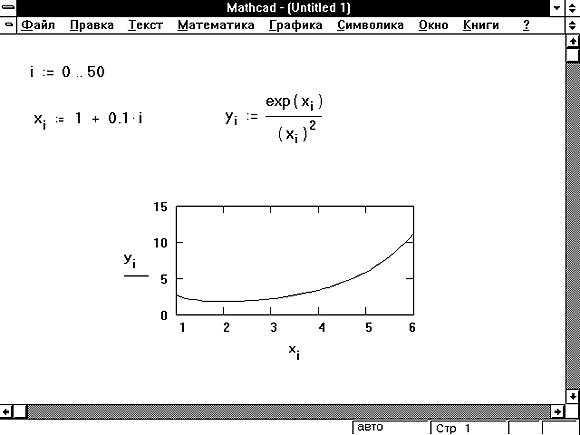

Достаточно продвинутой математики!

Philip

Функция гистограммы » MathCadHelp.com » Номер 1 в MathCad Assignments

Mathcad включает функцию hist для вычисления распределений частот для гистограмм: интервалы, представленные вектором int. Элементы как в int, так и в A должны быть реальными. Кроме того, элементы int должны быть в порядке возрастания. Результирующий вектор на один элемент короче, чем int.

Mathcad интерпретирует int как набор точек, определяющих последовательность интервалов на гистограмме. Значения в int должны быть в порядке возрастания. Результатом этой функции является вектор f, в котором Ii – это количество значений в A, удовлетворяющих условию:

Mathcad игнорирует точки данных меньше первого значения в int или больше последнего значения в int. На рис. 14-2 показано, как использовать гистограммы в Mathcad.

Гистограмма

Случайные числа

Mathcad поставляется с рядом функций для генерации случайных чисел, имеющих различные распределения вероятностей. Функциональные формы распределений, связанных со следующими функциями, приведены в разделе «Распределения вероятностей» на странице 281.

Каждый раз, когда вы пересчитываете уравнение, содержащее одну из этих функций, Mathcad генерирует новые случайные числа. Чтобы заставить Mathcad сгенерировать новые случайные числа, щелкните уравнение, содержащее функцию, и выберите «Рассчитать» в меню «Математика». На рис. 14-3 показан пример использования генератора случайных чисел Mathcad. На рис. 14-4 показано, как сгенерировать большой вектор случайных чисел с заданным распределением.

С этими функциями связано «начальное значение». Каждый раз, когда вы сбрасываете начальное значение, Mathcad генерирует новые случайные числа на основе этого начального числа. Заданное начальное значение всегда будет генерировать одну и ту же последовательность случайных чисел. Выбор параметра «Вычислить» в меню «Математика» продвигает Mathcad по этой последовательности случайных чисел. Однако изменение начального значения продвигает Mathcad по совершенно другой последовательности случайных чисел.

Чтобы изменить начальное значение, выберите «Параметры» в меню «Математика» и измените значение «начальное число» на вкладке «Встроенные переменные». Обязательно укажите целое число.

Чтобы сбросить генератор случайных чисел Mathcad без изменения начального значения, выберите «Параметры» в меню «Математика», перейдите на вкладку «Встроенные переменные» и нажмите «ОК», чтобы принять текущее начальное значение. Затем нажмите на уравнение, содержащее функцию генерации случайных чисел, и выберите «Рассчитать» в меню «Математика». Поскольку рандомизатор был сброшен, Mathcad генерирует те же случайные числа, что и при перезапуске Mathcad.

Равномерно распределенные случайные числа. Поскольку генератор случайных чисел каждый раз генерирует разные числа,

Если вы хотите несколько раз проверить тестовый набор с одними и теми же случайными числами, сбросьте генератор случайных чисел между вычислениями, как описано выше.

Чтобы увидеть новый набор случайных чисел, измените начальное значение, как описано выше.