Дифференциальные уравнения mathcad: 28. Тема 7. Решение дифференциальных уравнений и систем в MathCad. Краткие теоретические сведения

Дифференциальные уравнения. Пошаговый калькулятор

Калькулятор применяет методы для решения: разделяющихся, однородных, линейных, первого порядка, Бернулли, Риккати, с интегрирующим множителем, с группировкой под дифференциал, с понижением порядка, неоднородных, с постоянными коэффициентами, Эйлера и систем — дифференциальных уравнений. Без или с наличием начальных условий (задача Коши)

Вычислять относительно

y (x)

f (t)

▸Система

▾Система

Максимальная производная начальных условий = 4

(Ограничение калькулятора)

⌦

АвтоматическиЛинейное 1-порядкаГруппировка под дифференциалВ полных дифференциалахПодстановкаС выбором метода решения~

автозамена

Не использовать метод Бернулли
для линейных уравнений 1‑го порядка

Содержимое загружается

Заполните пропуски

Результат в LaTeX:

Копировать

Результат в виде выражения:

Копировать

Порядок производной указывается штрихами —y»’ или числом после одного штриха —y’5

Ввод распознает различные синонимы функций, как asin, arsin, arcsin

Знак умножения и скобки расставляются дополнительно — запись2sinx сходна2*sin(x)

Список математических функций и констант:

•d(x) — дифференциал

•ln(x) — натуральный логарифм

•sin(x) — синус

•cos(x) — косинус

•tg(x) — тангенс

•ctg(x) — котангенс

•arcsin(x) — арксинус

•arccos(x) — арккосинус

•arctg(x) — арктангенс

•arcctg(x) — арккотангенс

•sh(x) — гиперболический синус

•ch(x) — гиперболический косинус

•th(x) — гиперболический тангенс

•cth(x) — гиперболический котангенс

•sch(x) — гиперболический секанс

•csch(x) — гиперболический косеканс

•arsh(x) — обратный гиперболический синус

•arch(x) — обратный гиперболический косинус

•arth(x) — обратный гиперболический тангенс

•arcth(x) — обратный гиперболический котангенс

•sec(x) — секанс

•cosec(x) — косеканс

•arcsec(x) — арксеканс

•arccsc(x) — арккосеканс

•arsch(x) — обратный гиперболический секанс

•arcsch(x) — обратный гиперболический косеканс

•abs(x) — модуль

•sqrt(x) — корень

•exp(x) — экспонента в степени x

•pow(a,b) — \(a^b\)

•sqrt7(x) — \(\sqrt[7]{x}\)

•sqrt(n,x) — \(\sqrt[n]{x}\)

•lg(x) — \(\log_{10}\left(x\right)\)

•log3(x) — \(\log_3\left(x\right)\)

•log(a,x) — \(\log_a\left(x\right)\)

•pi — \(\pi\)

alpha — \(\alpha\)

beta — \(\beta\)

•sigma — \(\sigma\)

gamma — \(\gamma\)

nu — \(\nu\)

•mu — \(\mu\)

phi — \(\phi\)

psi — \(\psi\)

•tau — \(\tau\)

eta — \(\eta\)

rho — \(\rho\)

•a123 — \(a_{123}\)

x_n — \(x_{n}\)

mu11 — \(\mu_{11}\)

Добавить страницу в закладки — CTRL+D

Возможность редактировать тексты в решении (для улучшения калькулятора)

Ссылка на это решение

75% 90% 100% 110% 125% 🔍

Вычисляю решение. . Оформляю.. Перевожу.. Слишком длинное выражение! Внутренняя ошибка Ошибка соединения Калькулятор обновляется Необходимо перезагрузить страницу Ссылка скопирована! Формула скопирована Обновленный текст отправлен

Решение дифференциальных уравнений и систем в прикладной программе Mathcad.

Mathcad имеет ряд встроенных функций для решения обыкновенных дифференциальных уравнений. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений).

Каждая из встроенных функций, предназначенных для решения ОДУ, требует, чтобы было задано следующее:

Наиболее употребляемой для решения ОДУ является функция rkfixed, которая использует для поиска решения метод Рунге-Кутта четвертого порядка. В результате решения получается матрица, имеющая два столбца.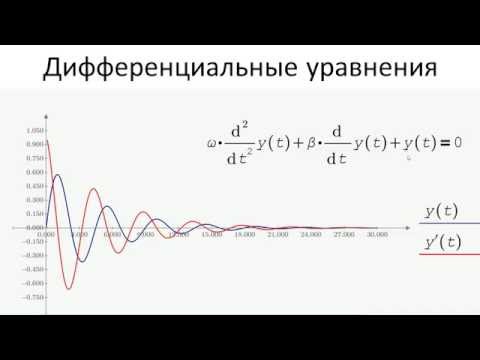 Первый столбец – точки, в которых ищется решение ОДУ. Второй – это столбец значений найденного решения в соответствующих точках. Функция rkfixed (y, x1, x2, npoints, D) имеет следующие аргументы:

у – вектор начальных условий размерности n, где n – порядок дифференциального уравнения или число уравнений в системе. Для уравнения первого порядка этот вектор вырождается в точку.

x₁, х₂ – граничные точки интервала, на котором ищется решение.

Npoints – число точек (не считая начальной), в которых ищется приближенное решение. Число строк в возвращаемой матрице решения определяется как (1+npoints).

D(

x, y) – функция, которая возвращает значение в виде вектора из n элементов, содержащих первые производные неизвестных функций.

Рассмотрим на примере, как решаются дифференциальные уравнения первого порядка.

Пример. Решить уравнениеу¢ = 2у/x + х с начальным условиему(1) = 0 на отрезке[1; 1,5]

Для решения дифференциального уравнения первого порядка

У₀: = 0 – задание начального значения

D(x, y): = – определить функцию, задающую производную

z:= rkfixed

(y,1,1.5,50,D). – находится решение в 50 точках отрезка [1, 1,5]

Дифференциальные уравнения второго порядка.

Для решения дифференциального уравнения второго порядка необходимо задать:

• вектор начальных условий состоит из двух элементов: значений функции и ее первой производной в начальной точке интеграла.

• функция D(х, у) – вектор с двумя элементами:

D(x, y) =

Матрица решения содержит три столбца: первый значения х, в которых ищется решение, второй – у(х) и третий – у¢(x)

Пример. Решить дифференциальное уравнение второго порядка со следующими начальными условиями

у(0) = 1, у¢(0) = 3 на отрезке [0; 0,5].

Системы дифференциальных уравнений.

Для решения системы обыкновенных дифференциальных уравнений первого порядка необходимо:

• определить вектор, содержащий начальные значения для каждой неизвестной функции;

• определить функцию, которая возвращает значение в виде вектора из n элементов, содержащих первые производные каждой из неизвестных функций;

• выбрать точки для поиска приближенного решения.

• задать функцию rkfixed.

Функция вернет матрицу, первый столбец которой – значения аргумента, а остальные столбцы содержат значения найденных приближенных решений в соответствующих точках.

Пример.

Решить систему двух ОДУ

с начальным условиями х₀(0) = 0, х_i(0) = 1

Примечание. Mathcad имеет ещё две встроенные функции для решения задачи Коши. Это функции Rkadapt и Bulstoer. Эти функции имеют те же самые аргументы и возвращают решения в такой же форме, что и функция rkfixed. Первая из этих функций использует метод Рунге-Кутты с переменным шагом, что позволяет повысить точность вычислений и сократить их объём, если искомое решение имеет области, где её значения меняются быстро и области плавного изменения. Функция Rkadapt будет варьировать величину шага в зависимости от скорости изменения решения.

Функция Bulstoer реализует иной численный метод – Метод Булирша-Штёра. Её следует применять, если известно, что решение является гладкой функцией.

Решение краевой задачи для дифференциального уравнения.

Пусть имеется дифференциальное уравнение второго порядка

.

Решение уравнения требуется найти на интервале [0; 1], причём известно, что у(0)=у₀, у(1)=у₁. Понятно, что произвольный интервал [a, b] заменой переменных может быть сведен к единичному.

Для решения краевой задачи обычно применяют метод стрельб, позволяющий свести решение краевой задачи к задаче Коши. Пусть k некоторый параметр, такой что y(0)=k. Для некоторого пробного значения k может быть решена задача Коши, например, методом Рунге-Кутты.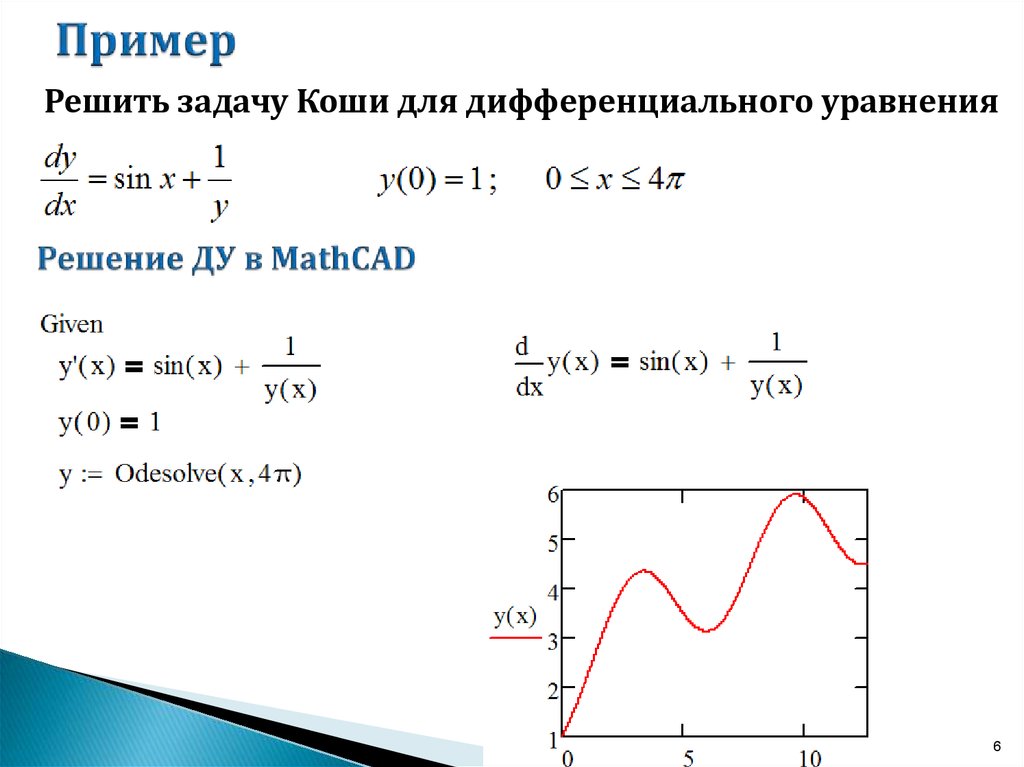

Мы хотим найти такое значение параметра, чтобы выполнялось условие y(1,k)=y₁. Фактически мы свели исходную задачу к задаче решения трансцендентного уравнения с таблично заданной функцией. Если найдены такие значения параметра k₁ и k₂, что y(1,k₁)>y₁ и y(1,k₂)<y₁, то дальнейшее уточнение значения параметра можно проводить методом деления отрезка пополам.

Пусть требуется найти решение дифференциального уравнения при условияхи.

При значениях параметров _.

Для решения краевой задачи имеется встроенная функция sbval, реализующая метод стрельб и позволяющая свести краевую задачу к задаче Коши. Функция sbval имеет следующие параметры:

• v– вектор, содержащий начальные приближения для недостающих начальных условий,

• x_min, x_max – границы интервала, на котором ищется решение,

• D(x,y) – вектор–функция, содержащий правые части системы дифференциальных уравнений первого порядка, эквивалентной исходному уравнению, размер вектора n совпадает со степенью старшей производной дифференциального уравнения

• load(xmin,v) – вектор–функция, элементы которой соответствуют n значениям функций на левой границе интервала. Часть этих значений известна, а для части заданы начальные приближения в векторе v. Их уточненные значения будут найдены в процессе вычисления

• score(xmax,y) – вектор–функция, имеющая то же число элементов, что и

  v. Каждое значение является разностью между начальными значениями в конечной точке интервала и соответствующей оценки для решения. Этот вектор показывает, на сколько близко найденное решение к истинному.

Наша задача сводится к системе двух дифференциальных уравнений первого порядка:

Поэтому функция D имеет вид

Задаем граничные условия:

Задача Коши для дифференциального уравнения второго порядка содержит два начальных условия. Нам известно только одно. Начальное приближение для недостающего значения задаем в векторе v, который в нашем случае состоит только из одного элемента. Несмотря на это, индекс о должен быть обязательно указан, чтобы подчеркнуть векторный характер этой величины:

На левой границе интервала нам известно значение и задано начальное приближение для. Это значение записано в. Задаем вектор-функцию

load. Ее нулевой элемент – начальное значение для , первый – для.

Теперь, когда нам стало известно недостающее начальное условие в задаче Коши, можно воспользоваться, например, функцией rkfixed

Обыкновенные дифференциальные уравнения — Mathcad

ФОН
	Предпосылки для обычного Дифференциальные уравнения [PDF] [ДОК] Цели обыкновенного дифференциала Уравнения [PDF] [ДОК] Что такое обыкновенные дифференциальные уравнения? [PDF] [DOC] Учебник по обыкновенным дифференциальным уравнениям [PDF] [DOC] Точное решение ОДЫ 1-го порядка [YOUTUBE 6:48] Точное решение ОДУ 1-го порядка: Другой Пример [ЮТУБ 7:37] Точное решение ОДУ 2-го порядка: Различное Корни характеристического уравнения [YOUTUBE 8:50]  Точное решение ОДУ 2-го порядка: Повторяется Корни характеристического уравнения [YOUTUBE 8:41] Точное решение ОДУ 2-го порядка: сложное Корни характеристического уравнения [YOUTUBE 9:34] Проверьте свои знания о предыстории Обыкновенное дифференциальное уравнение [HTML] [FLASH] [PDF] [ДОК]
ФИЗИЧЕСКАЯ ПРОБЛЕМА
	Сколько времени потребуется мячу, чтобы остыть? [PDF] [ДОК]
ЧИСЛЕННЫЙ МЕТОД
	МЕТОД ЭЙЛЕРА
		Предпосылки для метода Эйлера [PDF] [ДОК] Цели метода Эйлера [PDF] [ДОК] Как работает метод Эйлера? [PDF] [ДОК] Метод Эйлера решения ОДУ: Происхождение  [YOUTUBE 9:53] Метод Эйлера решения ОДУ: пример [ЮТУБ 10:57] Метод Эйлера для оценки интегралов: Теория [ЮТУБ 7:11]  Метод Эйлера для оценки интегралов: Пример [ЮТУБ 8:58] Презентация Power Point по методу Эйлера [PDF] [ППТ] Рабочий лист метода Эйлера [МКД] Рабочий лист сходимости метода Эйлера [МКД] Проверьте свои знания метода Эйлера [HTML] [FLASH] [PDF] [ДОК]
	РУНГЕ-КУТТА 2-Й ПОРЯДОК МЕТОД
		Предварительные условия для метода Рунге-Кутты 2-го порядка [PDF] [ДОК] Цели метода Рунге-Кутты 2-го порядка [PDF] [DOC] Как работает метод второго порядка Рунге-Кутты? [PDF] [ДОК] Метод Рунге-Кутты 2-го порядка: предыстория [YOUTUBE 9:46] Метод Рунге-Кутты 2-го порядка: Формулы [ЮТУБ 10:57]  Метод Рунге-Кутты 2-го порядка: Heun’s Метод  [ЮТУБ 9:27] Метод Рунге-Кутты 2-го порядка: средняя точка Метод  [ЮТУБ 10:45] Метод Рунге-Кутты 2-го порядка: Ральстон Метод Часть 1 из 2 [ ЮТУБ 7:09] Метод Рунге-Кутты 2-го порядка: Ральстон Метод Часть 2 из 2 [ ЮТУБ 5:00] Метод Рунге-Кутты 2-го порядка: вывод Часть 1 из 2 [ ЮТУБ 7:08]| Метод Рунге-Кутты 2-го порядка: вывод Часть 2 из 2 [ ЮТУБ 5:31] Презентация в Power Point по методу Рунге-Кутты 2-го порядка [PDF] [ППТ] Рабочий лист метода Рунге-Кутты 2-го порядка [МКД] Рабочий лист сходимости метода Рунге-Кутты 2-го порядка [МКД] Проверьте свои знания метода Рунге-Кутты 2-го порядка [HTML] [FLASH] [PDF] [ДОК]
	РУНГЕ-КУТТА 4-Й ПОРЯДОК МЕТОД
		Предварительные условия для метода 4-го порядка Рунге-Кутты [PDF] [ДОК] Цели метода Рунге-Кутты 4-го порядка [PDF] [DOC] Как работает метод 4-го порядка Рунге-Кутты? [PDF] [ДОК] Метод Рунге Кутта 4-го порядка: формулы [YOUTUBE 9:54] Метод Рунге Кутта 4-го порядка: Пример: Часть 1 из 2 [ЮТУБ 9:29] Метод Рунге Кутта 4-го порядка: Пример: Часть 2 из 2 [ЮТУБ 8:48] Презентация в Power Point по методу Рунге-Кутты 4-го порядка [PDF] [ППТ] Рабочий лист метода 4-го порядка Рунге-Кутты [МКД] Рабочий лист сходимости метода Рунге-Кутты 4-го порядка [МКД] Проверьте свои знания метода Рунге-Кутты 4-го порядка [HTML] [FLASH] [PDF] [ДОК]
	МЕТОД СЪЕМКИ
		Предварительные условия для метода съемки [PDF] [ДОК] Цели метода съемки [PDF] [DOC] Как работает метод съемки? [PDF] [ДОК] Презентация Power Point о методе съемки [PDF] [ППТ] Рабочий лист метода стрельбы [МКД] Проверьте свои знания метода стрельбы [HTML] [FLASH] [PDF] [ДОК]
	КОНЕЧНАЯ РАЗНИЦА МЕТОД
		Предпосылки для конечной разности Метод [PDF] [ДОК] Цели метода конечных разностей [PDF] [DOC] Как работает метод конечных разностей? [PDF] [ДОК] Метод конечных разностей решения Обыкновенные дифференциальные уравнения: история, часть 1 из 2 [YOUTUBE 3:46] Метод конечных разностей решения Обыкновенные дифференциальные уравнения: история, часть 2 из 2 [YOUTUBE 8:40] Метод конечных разностей: Пример балки: Часть 1 из 2  [ЮТУБ 6:13] Метод конечных разностей: Пример балки: Часть 2 из 2  [ЮТУБ 6:21] Метод конечных разностей: пример давления Судно: Часть 1 из 2  [YOUTUBE 9:55] Метод конечных разностей: пример давления Судно: Часть 2 из 2  [YOUTUBE 9:50] Презентация в Power Point по методу конечных разностей [PDF] [ППТ] Рабочий лист метода конечных разностей [МКД] Проверьте свои знания метода конечных разностей [HTML] [FLASH] [PDF] [ДОК]
АНЕКДОТЫ
	О решении высших порядков и связанных ординарных Дифференциальные уравнения [PDF] [DOC] [МКД] Эйлер [HTML] [PDF] [ДОК] Рунге [HTML] [PDF] [ДОК] Кутта [HTML] [PDF] [ДОК]

(PDF) Дифференциальные уравнения Mathcad Prime

Дифференциальные уравнения с

Mathcad Prime J. A. Весселинг, почетный профессор кафедры Химический инженерный университет Гронингена

Это мои заметки об обыкновенных дифференциальных уравнениях, в Mathcad Prime 2.0. Они содержат только основы — нет инженерные примеры и никаких упражнений. Не стесняйтесь использовать и улучшать их. Ханс Весселинг, Гронинген, апрель 2012 г.

Содержание 1 Введение (терминология) 2 Первый порядок, первый Уравнения степени 3 первого порядка, уравнения более высокой степени 4 второго порядка Порядок, линейные уравнения 5 Преобразование Лапласа 6 Численные методы Ссылки Ханс Весселинг и Ханс де Ваард, Расчет и Общение с Mathcad Prime, VSSD Publishers, Делфт, 2012 г. (www.vssd.nl/hlf) Эрвин Крейзиг, Advanced Engineering Mathematics, John Wiley & Sons (многие издания)

1 Введение (терминология) В этом первом уроке мы рассмотрим названия и термины в дифференциальных уравнениях.

Некоторые термины Вот простое дифференциальное уравнение:

d y( ) x) k x ( dx

Оно содержит две переменные x и y и константу k.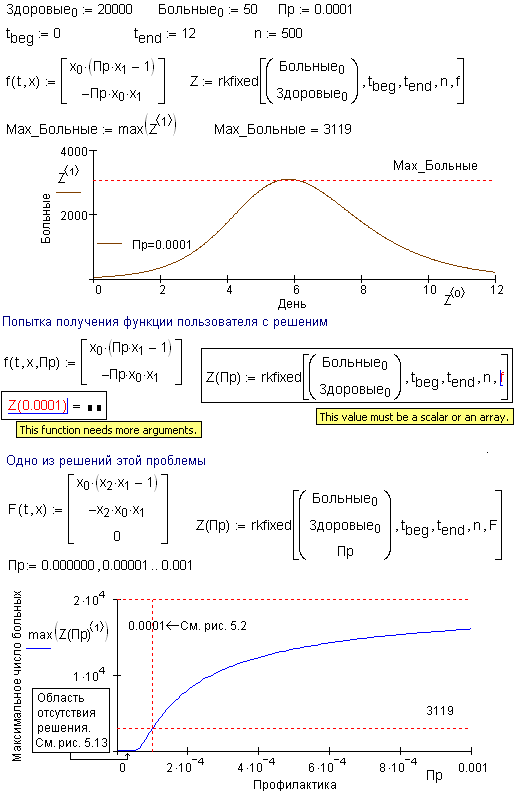 Мы будем рассматривать y как функцию x — это зависимая переменная. другая переменная x является независимой. Левая сторона уравнение содержит только первую производную: это дает первый порядок уравнение. Производную можно рассматривать как частное двух дифференциалы dx и dy. Производная часто записывается с использованием простого обозначение y'(x) и в этом предмете также с использованием символа p (параметр):d dy ( y( ) x) y (x) p ( ) dx dx

Мы будем использовать все эти обозначения, выбирая для данная проблема.

РешениеРешение нашего уравнения получить проще всего используя дифференциальную запись: dy k x dx

Мы можем проинтегрировать обе части, чтобы получить: y x2 yk + C 2

C>

x

Это решение является функцией, которая не содержит никаких производная. Он содержит постоянную интегрирования C. Это может иметь любое значение — уравнение имеет бесконечное число решений. Набор известен как общее решение. Если вы придадите C какое-то значение, у вас есть конкретное решение.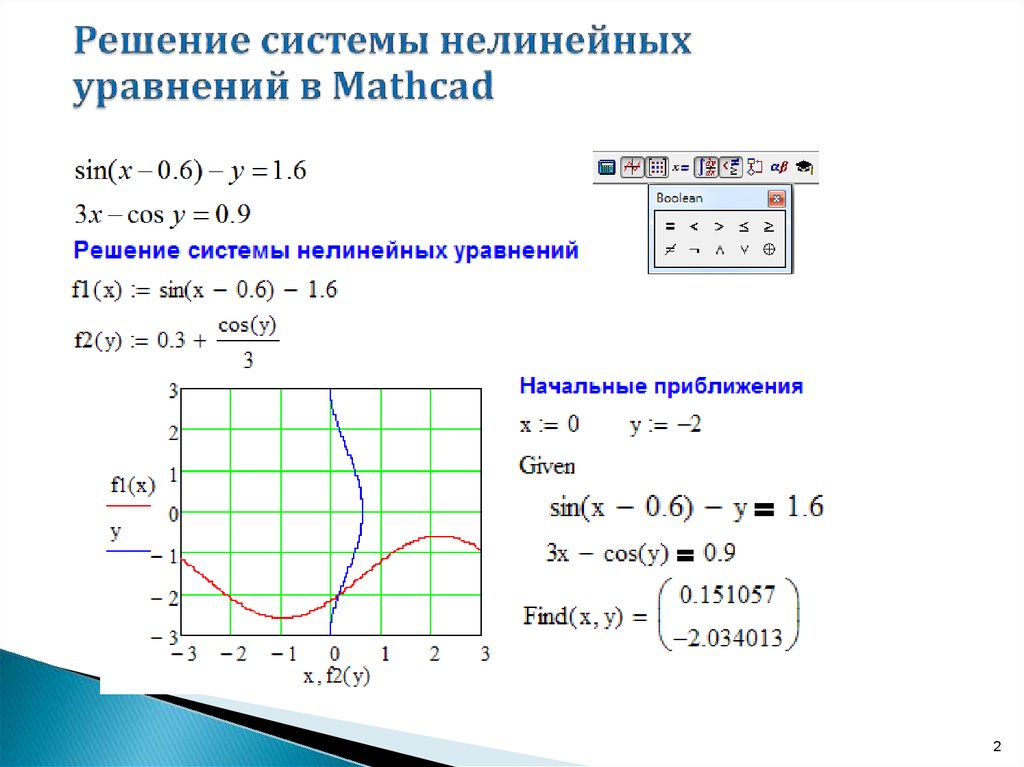

На этом графике показаны некоторые частные решения. В этом простом пример одно решение проходит через каждую точку x-y самолет.

ПорядокСледующее уравнение содержит вторую производную. Это является уравнением второго порядка. 2d y( ) x) k x ( d x2

Вы можете получить решение путем двойного интегрирования: d x2 y( ) x) k + C1 ( 2 dx x3 y (x) k + C1 x + C2 ( ) 6

y

Это уравнение имеет две константы интегрирования. Здесь две решения, проходящие через каждую точку на плоскости x, y. Перекресток черные линии – три значения первой константы; три цвета соответствуют трем значениям второй константы.

СтепеньНаше третье уравнение содержит квадрат первой производная. Это уравнение первого порядка, но второй степени.x d 2 y( ) x) x 1 ( dx 2

y

Вы можете рассматривать это как произведение двух дифференциальных уравнения: d ( y( ) x) x 1 dx d ( y( ) x) x + 1 dx

Каждое решение является произведением двух решений: x x2 (x) + x C 0 y1 ( ) 2 x2 y2 (x) x C 0 ( ) 2

Для каждого значения постоянной интегрирования получаем «двойной линия», на которой произведение равно нулю.

Категории Первые два примера представляют собой линейные уравнения. третий нелинейный. Нелинейное уравнение содержит некоторое произведение два выражения зависимой переменной y(x). Видишь ли ты понять разницу: (1) ( ) d y( ) x) k x ( dx (2) ( ) d2 y( ) x) k x ( d x22

(3) ( ) d 2 y( ) x) x 1 ( dx

Методы Существуют две основные группы методов решения дифференциальные уравнения: (а) символические методы, ведущие к уравнения (б) численные методы, приводящие к числам. в В приведенных выше примерах мы использовали символьные методы. Когда они работают, они в порядке. Они могут дать обзор, который трудно получить численно. Однако большинство дифференциальных уравнений не имеют символическое решение. Если решение существует, часто находя его требует загадок и терпения. Численные методы более гибкий. Однако и у них есть свои проблемы. Чтобы стать хорошим вам нужно будет освоить оба метода. Начнем с символических методов.

2 Уравнения первого порядка, первой степениПростейший дифференциал уравнения первого порядка и первой степени.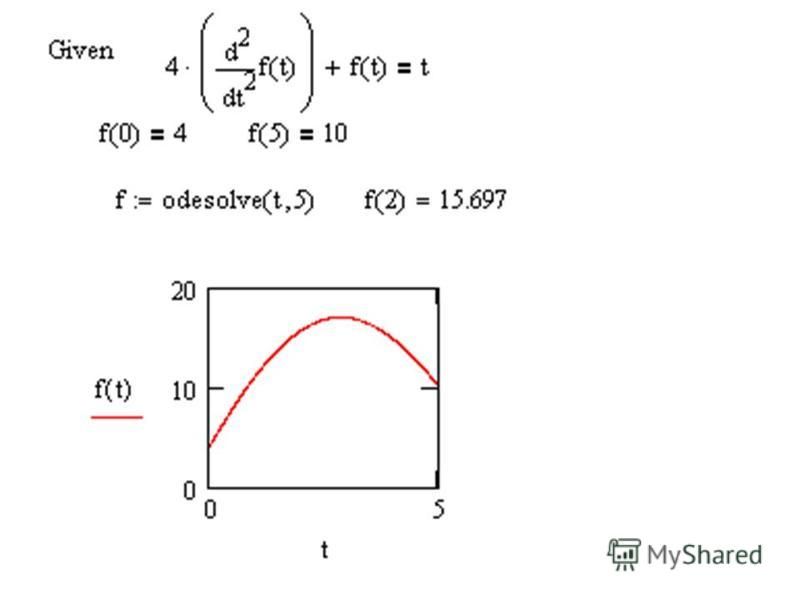 Над столетиями для их решения разрабатывалось много трюков.

Разделимое уравнениеЕсли каждое из слагаемых в дифференциале уравнение содержит только одну переменную, то члены могут быть интегрируется напрямую. В качестве примера рассмотрим: dy y x dx + y dy 0 orx x2 y2 x dx y dy 2 2 2 2 x y Включая постоянную интегрирования: + C 2 2 dx

Любое конкретное решение можно рассматривать как пересечение функция 3D:2 1,5 1 0,5 0 -0,5 -1 -1,5 -2 -2 -1,5 -1 -0,5 0 0,5 1 1,5 2

f (x , y) x 2 + y 2 ( )

с плоскостью высоты C. Это одна из прямых постоянных высота, которую вы видите на контурном графике. В данном примере это круги вокруг начала координат.

Константа интеграцииВажно включить интеграцию константа сразу после интегрирования. Этот пример показывает почему.dy 2 1 + y dx dy dx 1 + y2 atan (y) x + C ( ) y (x , C) tan (x + C) ( ) ( )

Проверяем, что это действительно решение:2 d ( y( x , C) tan (C + х) + 1 ) ( ) дх

dy 2 1 + y dx

Если мы включим константу после получения y, мы получим неверно: Y (x , C) tan (x) + C ( ) ( )

Проверка дает 2 d Y( x , C) tan (x) + 1 ( ) ( ) dx 2 dY 1 ( + (Y C) ) dx

Это не исходное уравнение.

Набор решений показан ниже. y, правильно

Y, неправильно

Уравнение отношенияВы часто можете представить уравнение первого порядка в отделимая форма с помощью замены. Одна группа уравнений, где эти работы являются уравнениями «отношений». Их можно записать в форма:y dy f dx x

(Пример «круги» представляет собой уравнение отношений, будь то очень простое один.) Если вы замените x и y в уравнении kx и ky, и k отменяется в результате, тогда у вас есть уравнение соотношения. Это привести к разделимому виду с помощью замены: y z x

или

yz x

dy x dz + z dx dy x 2 + y 2 dx xy

Возьмем уравнение отношения: Используя дифференциальную запись:

x y dy x 2 dx y 2 dx 0 dx z dz x

Замена дает 10 8 6 4 2 0 -2 -4 -6 -8 -10 1 1,5 2 2,5 3 3,5 4 4,5 5

x 2 dx + x 3 z dz

z2 ln (x) + C ( ) 2

Общее решение принимает вид( y x) ( ) ln (x) C + ( ) 22

f-20 -15 — 10 -5 0 5 10

Упростить это непросто, но контурный график показывает частные решения.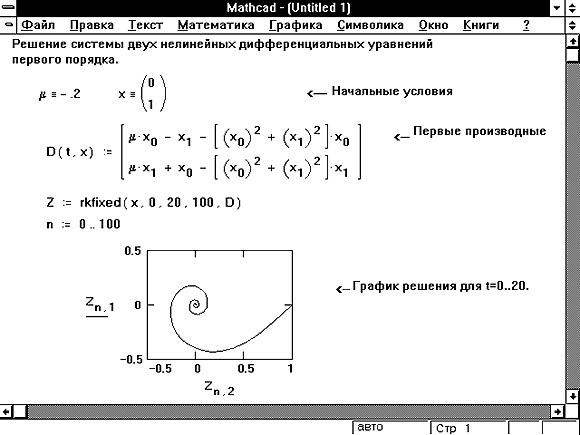 (Чтобы получить сюжет, мне пришлось уменьшить x-диапазон.)

Линейное уравнениеВ качестве примера рассмотрим

Линейное дифференциальное уравнение первого порядка:

dy + P (x) y + Q (x) 0 ( ) ( ) dx dy 2 dy x y x 2 dx x y + х 0 или dx y u (x) v (x) ( ) ( ) dy v du + u dv

Это можно решить с помощью замены: Sov du + u dv u v x 2 dx

или

v (du u dx) + u dv x 2 dx) (

Мы можем выбрать одну из двух функций u(x) и v(x). Здесь мы выбрать u таким образом, чтобы первый член в последнем уравнении стал zero:du u dx 0 du dx u ln (u) x ( ) uex

(Здесь нет необходимости включать постоянную интегрирования.) оставшееся уравнение принимает вид su dv x 2 dx dv x 2 e x dx x 2 x

dx

x

x 2 + 2 x + 2

Итак,

v

x

x 2 + 2 x + 2 + C u vx2 + 2 x + 2 + C

и общее решение

Мы увидим другие методы для линейных уравнений, когда будем рассматривать уравнения второго порядка.(x , y)) (

«Точное» уравнение Этот метод проще всего понять, начав с решением дифференциального уравнения и работает в обратном порядке.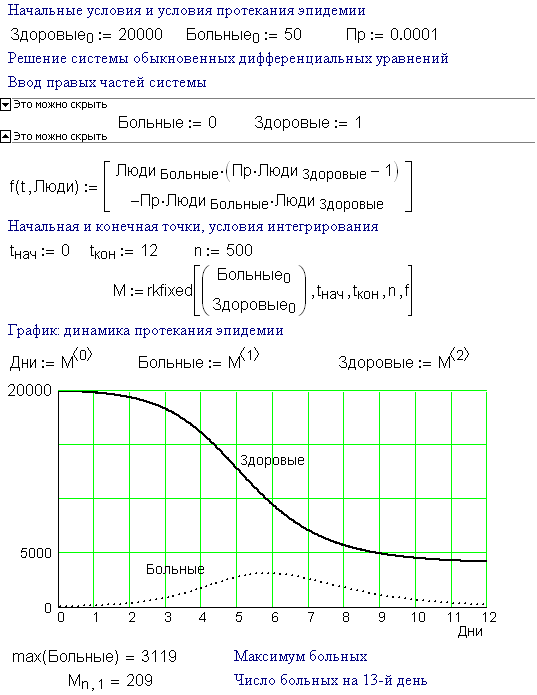 Решение, которое мы выбираем: f (x, y, C) 0) ( f (x, y, C) x + cos (x y) + C ) ) ( ( df df df dx + dy dx dy

Дифференциал этого:

(С частными дифференциальными коэффициентами. Mathcad не имеет символы для них.) Withd f( x , y , C) 1 y sin (x y) ( ) ( ) dx

получаем дифференциальное уравнение

d f( x , y , C) (x sin (x y)) ( ) ( ( )) dy

(1 y sin (x y)) dx (x sin (x y)) dy 0 )) )) ( ( ( (

Если мы начнем с этого уравнения, как мы получим решение? Сначала проверим, что это действительно дифференциал. Это так, когда: y-производная первого множителя = x-производная второго множителя (1 y sin (x y)) sin (x y) x y cos (x y) ( ( )) ( ) ( ) dy d ( x sin (x y)) sin (x y) x y cos (x y) )) ) ) ( ( ( ( dx

Они действительно равны, поэтому уравнение является дифференциальным. Мы тогда знать: df 1 y sin (x y) ( ) dx df (x sin (x y)) ( ( )) dy

Интегрирование первого должно дать члены, содержащие x, второй должен давать члены, содержащие y: 1 y sin (x y) d x x + cos (x y) ) ) ( ( (x sin (x y)) d y cos (x y) ( )) ( ) (

членов, содержащих x членов, содержащих y

Член косинуса встречается в обоих интегралах, потому что он содержит и х и у. Общее решение состоит в сочетании два результата (не сумма!). f (x, y, C) x + cos (x y) + C as ожидаемый ( ) ( ) Предупреждение: вы можете получить термы, не содержащие x, из первый интеграл, а члены не из второго. Не использовать эти. Интересно посмотреть, насколько сложны решения это простое уравнение.

3 2 1 0 -1 -2 -3 -3

-2

-1

0

1

2

3

F -3.2-2.4-1.6-0.8 0,8 1,6 2,4 3.2.

Интегрирующий коэффициентВозьмем дифференциальное уравнение из предыдущий абзац, и разделить его по какой-либо функции (здесь просто x): 1 y sin (x y) x sin (x y) ( ) ( ) dx dy 0 x x (1) ( )

Затем уравнение:( ) ( ) d 1 y sin (x y) sin (x y) + x y cos (x y) ( ) x x dy x sin (x y) d ) ( (y cos (x y)) ( ( )) x dx

Они не равны, поэтому новое уравнение больше не является точным. Однако, если мы умножим уравнение (1) на x, мы получим обратно оригинальное, точное, уравнение. Здесь x — интегрирующий множитель: a множитель, переводящий уравнение в разрешимое. Можно доказать, что все уравнения первого порядка и первой степени имеют интегрирующие факторы. Проблема найти один из них. Есть нет общего метода для этого.

3 Уравнения первого порядка высшей степениЭто уравнения содержащие производную первого порядка в степени выше единицы. Например: 2 dy + x + y 0 dx dy p dx

В последующем обсуждении мы будем часто использовать замена

Часто можно решить две группы уравнений: (1) Уравнение является произведением двух уравнений более низкой степени. (2) Одну из переменных x или y можно сделать явной, поэтому мы можем получить: (a)y f (p) ( )

или

x f (p) ( )

(b)

x f (y , p) ( )

или

y f (x , p) ( )

2

2 К ним относятся уравнения с именами Клеро и Лагранж.

Произведение уравнений. Возьмем простой пример: dy 2 y 2 0 dx x

, которое можно представить как + 0 dx

dy

y dy x dx

y x

Это уравнение состоит из двух частей: dy y + 0 dx x dy y 0 dx x y 2 x 2 + C y2 x2 + C y2 + x2 C0 y2 x2 C0

(Поскольку части принадлежат одному и тому же решению, существует только одна постоянная интегрирования. ) Общее решение:y 2 + x 2 C y 2 x 2 C 0

Попробуйте C = -1; 0; 1 и 2, чтобы увидеть эффект ниже.

C 1,4

2 1,5 1 0,5 0 -0,5 -1 -1,5 -2 -2 -1,5 -1 -0,5

Решением является линия нулевой высоты. Как видите, решение представляет собой комбинацию окружности и гиперболы. Это решения двух частей уравнения. Ниже я сделал отдельные участки двух решений. Круги исчезают для отрицательные значения постоянной интегрирования; гипербола решения переключаются с одной ветки на другую.

0

0,5

1

1,5

2

Ф-100 -80-60-40-20 0 20 40 60 80 100

2 1,5 1 0,5 0 -0,5 -1 -1,5 -2 -2 -1,5 -1 -0,5

2 2 1.5 1 0.5 0 -0.5 -1 -1.5 -2 -2 -1.5 -1 -0.5

0

0.5

1

1.5

2

0

0.5

1

1.5

2

O-4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4

H

Явный y = f(p) Здесь мы рассмотрим следующий пример: y f (п) ( ) yp2 dy p dx f (p) dp 2 p dp ( ) dx 2 dp x2 p + C xC p 2

Это дает x:

Этот параметрический график показывает, что решения представляют собой параболы, которые сдвиг по оси абсцисс при увеличении C. Есть еще один решение: y 0 Вы можете легко проверить это в исходном уравнении. Вы не можете найти его, придав C какое-то значение. это единственное число решение (которое не совпадает с частным решением). ось x касается всех частных решений

Явный x = f(p)Эти уравнения имеют те же решения, что и те же из предыдущей группы, но с поменявшимися осями x и y. Мы рассмотрим другой пример: dy 2 x dx

или

xp2 dx 2 p dp

Это дает также Sody dx p 2 p3 2 p 2 d p 3

dy p dx 2 p 2 dp 2 y p 3 + C 3 2

График использует p в качестве параметра:

x (p) p 2 ( )

2 y (p) p 3 + C ( ) 3

y

C>

Решение представляет собой сборку. Увеличение C смещает вершину вверх. Как как видите, все точки оси Y подчиняются дифференциалу уравнение. Вы не можете увидеть это в общем решении, так что это снова уникальное решение. Контурный график этого примера не интересный.

x

Уравнение КлероУравнение Клеро гласит: Я рассмотрю пример: сначала дифференцируем Usingdy p dx y p x + f (p) ( ) yp x + p2 (1) ( )

(x , y) ( )

dy p dx + x dp + 2 p dp

дает

0 x dp + 2 p dp (x + 2 p) dp 0 ( )

Есть два решения: (2) дает (1) затем дает общее раствор:

dp 0 pC

(2) ( ) (4) ( )

x + 2 p0

(3) ( )

yC x + C2

Набор прямых линий с разным началом и наклоном. Исключение p из (1) и (3) дает огибающую решения:(3) ( ) x p 2 yp x + p2 x2 y 4

Ниже я начертил несколько решений вместе с конверт:y (x , C) C x + C 2 ( ) x2 (x) Y( ) 4

y

Частные решения являются касательными к огибающей. конверт является сингулярным решением. Обратите внимание, что решений нет внутри конверта.

C>x

Уравнение ЛагранжаУравнение Лагранжа имеет вид: Буду рассмотрим в качестве примера Дифференцирование дает y x f (p) + g (p) ( ) ( ) (1) ( )

yx p2 p2

dy 2 x p dp + p 2 dx 2 p dp p dx 2 x p dp + p 2 dx 2 p dp

Первое решение Второе

p0 dx 2 x dp + p dx 2 dp

Это уравнение линейно по x. Решаем ее с помощью замена:xu v dx u dv + v du

u dv + v du p (u dv + v du) + 2 u v dp 2 dp ) ( (1 p) (u dv + v du) 2 u v dp 2 dp ( ) ( ) (dv (1 p) 2 v dp) u + 2 dp v du (p 1) 0 ) ) ) ( ( (

Выбираем v так, что 2 (п 1) ( )

Оставшееся уравнение принимает вид 2 dp v du (p 1) 0 ( )

du 2 (p 1) dp ( ) ( 2 p 2) ( ) 2 (p 1) d p ) ( 42

u ( p 1) + C ( )

2

Таким образом, решение принимает вид C 2 x u v 1 + (p 1) ( ) y ( x 1) p 2 ( )

Мы можем исключить п.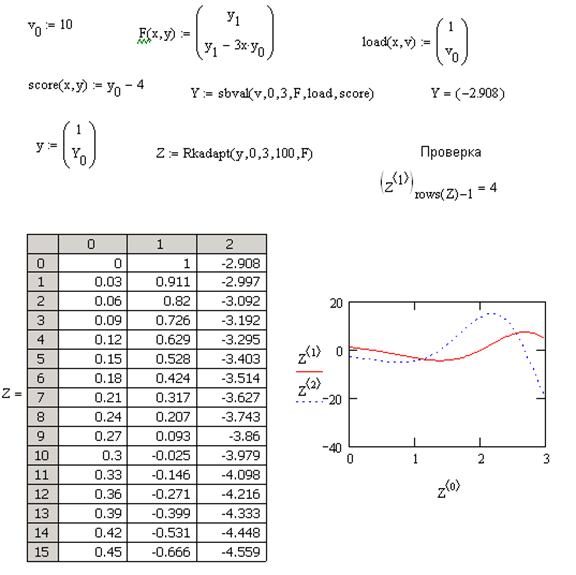 Каждое решение имеет два ветви: C p 1 + x1 y1 + C x12

C p 1 x1 y2 C x12

y

Решение для C = 0 представляет собой прямую линию. Остальные выглядят как срезанные параболы. C> Вертикальная линия x = 1 является единственной решение.

x

4 Второй порядок, линейные уравненияБольшинство уравнений с порядком выше единицы не имеют символического решения. Важный исключения составляют некоторые линейные уравнения. Здесь мы смотрим на второй линейные уравнения порядка с постоянными коэффициентами: d2 d A x) + B x) + C y (x) f (x) y( ) y( ) ( ( ( ) ( ) 2 dx dx (1) ( )

Линейные уравнения обладают важным свойством: сумма двух решения — это тоже решение. Это потому, что d2 d2 d2 (f f+ g + g) ( ) d x2 d x2 d x2

и

d d d (f f+ g + g) ( ) dx dx dx

Сначала решим «однородное» уравнение: d2 d A x) + B x) + C y (x) 0 y( ) y( ) ( ( ( ) 2 dx dx (2) ( )

Затем мы добавляем конкретное решение, чтобы учесть влияние правосторонний термин.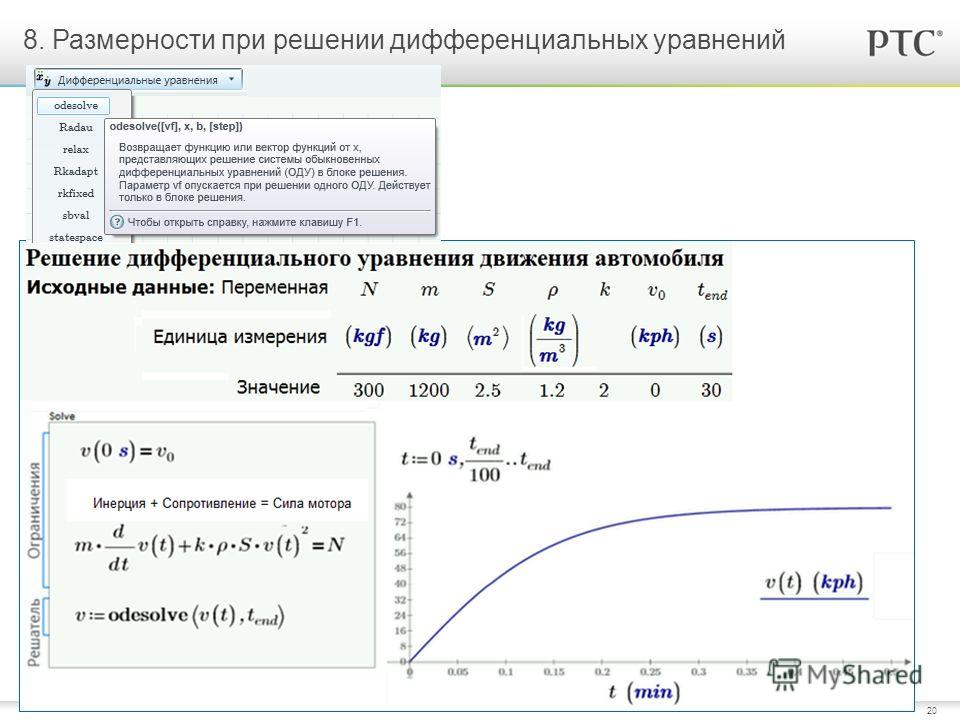 Даже наше простое уравнение не всегда может быть решено, но есть полезные частные случаи, когда решение может быть полученный.

Однородное уравнениеСледующая функция является решением уравнения однородное уравнение: y (x) e k x ( ) d ( y( ) x) k dxkx

d2 2 ( y( ) x) k 2 dx

kx

Подстановка их в однородное дифференциальное уравнение дает: e k x A k 2 + B k + C 0

Квадратное уравнение, заключенное в скобки, называется характеристическое уравнение. Он имеет два корня: B + B2 4 A C k1 2A B B2 4 A C k2 (3) ( ) 2A

Возможны три случая: (а) корни вещественные и неравные, (б) корни вещественные, но равные, и (c) корни комплексные. Корнеплоды Действительное и неравное Это когда B 2 4 A C > 0 Общее решение однородного уравнения: y C1 exp k1 x + C2 exp k2 x (4) ( )

Решение имеет две константы интегрирования, как могло бы быть ожидал.

Вещественные и равные корни Это когда B 2 4 A C 0 Два корня имеют то же значение: сокращенное уравнение теперь имеет общее решение: y C1 + C2 x exp (k x) ( )

B k 2A (5) ( )

Комплекс корней Здесь выражение квадратного корня имеет вид отрицательный: Решения теперь комплексные: withk1 a + b 1i B a 2A

B2 4 A C < 0 k2 a b 1i

B 2 4 A C b 2A

Сокращенное уравнение имеет общее решение: y C1 exp ((a + б 1i) x) + C2 exp ((a b 1i) x) (( ) ) (( ) )

Константы часто являются комплексно-сопряженными: C1 a’ + b’ 1i C2 a’ b’ 1i

Затем экспоненты можно заменить с помощью уравнения Эйлера:e i z cos (z) + i sin (z) ( ) ( )

Это дает периодические решения: y e a x C’1 cos (b x) + C’2 sin (b x) ( ) ( ) (6) ( )

Однородные примерыЛинейный дифференциал второго порядка уравнение показывает широкий спектр поведения.