Программирование В MathCad. Использование в программе функции циклических алгоритмов. Итерационные циклы и циклы с фиксированным числом повторений
Лабораторная работа № 5. Программирование В mathcad. Использование В программЕ-функциИ ЦИКЛИЧЕСКИХ алгоритмОВ. Итерационные циклы и циклы с фиксированным числом повторений.
цель работы: освоение основных приемов программирования РАЗЛИЧНЫХ циклических алгоритмов в пакете MathCad (4 часа)
Содержание
1. Программирование в программе-функции циклических алгоритмов.. 1
2. Арифметический цикл FOR (цикл с фиксированным числом повторений) 1
3. Итерационные циклы.. 2
4. Типовые алгоритмы обработки матриц. 4
4.1 Обращение к элементам главной диагонали. 5
4.2 Обращение к элементам побочной диагонали. 6
4. Дополнительные операторы программирования циклов в MathCad. 6
Порядок
выполнения лабораторной работы. . 7
. 7
Задание 1. 7
Задание 2_1. 8
Задание 2_2. 9
Задание 3. 11
Контрольные вопросы.. 13
1. Программирование в программе-функции циклических алгоритмов
Напомним, что циклические алгоритмы (или проще циклы) содержат повторяющиеся вычисления, зависящие от некоторой переменной. Такая переменная называется параметром цикла, а сами повторяющиеся вычисления составляют тело цикла.
Классификация циклов. Циклы можно условно разделить на две группы:
· · циклы с фиксированным количеством повторений, цикл типа арифметической прогрессии;
· · итерационные циклы.
Характерной чертой первой группы циклов является то, что количество повторений тела цикла можно определить до начала выполнения программы, реализующей цикл.
Для
итерационных циклов нельзя априори определить количество повторений тела цикла.
Это обусловлено тем, что окончание таких циклов определяется не выходом
параметра цикла за конечное значение, а и более сложными условиями.
2. Арифметический цикл FOR (цикл с фиксированным числом повторений)
Для программирования при помощи данного цикла, используется оператор FOR, вызов которого осуществляется одноименной кнопкой на панели Programming.
Структура оператора For:
где, в Поле 1 вводится имя параметра цикла;
в Поле 2 вводится диапазон значений параметра цикла в виде: 1. нач_знач .. кон_знач 2. нач_знач, нач_знач+шаг..кон_знач в Поле 3 вводятся операторы, составляющие тело цикла. По синтаксису оператора в цикле можно записать один оператор. Если операторов больше нужно создать дополнительные поля для ввода щелчком на кнопке “Add line” в панели программирования.
Пример 1: Вычислить значения функции
|
Результат |
Пояснение: результат расчета функции выводится в виде одномерного массива z.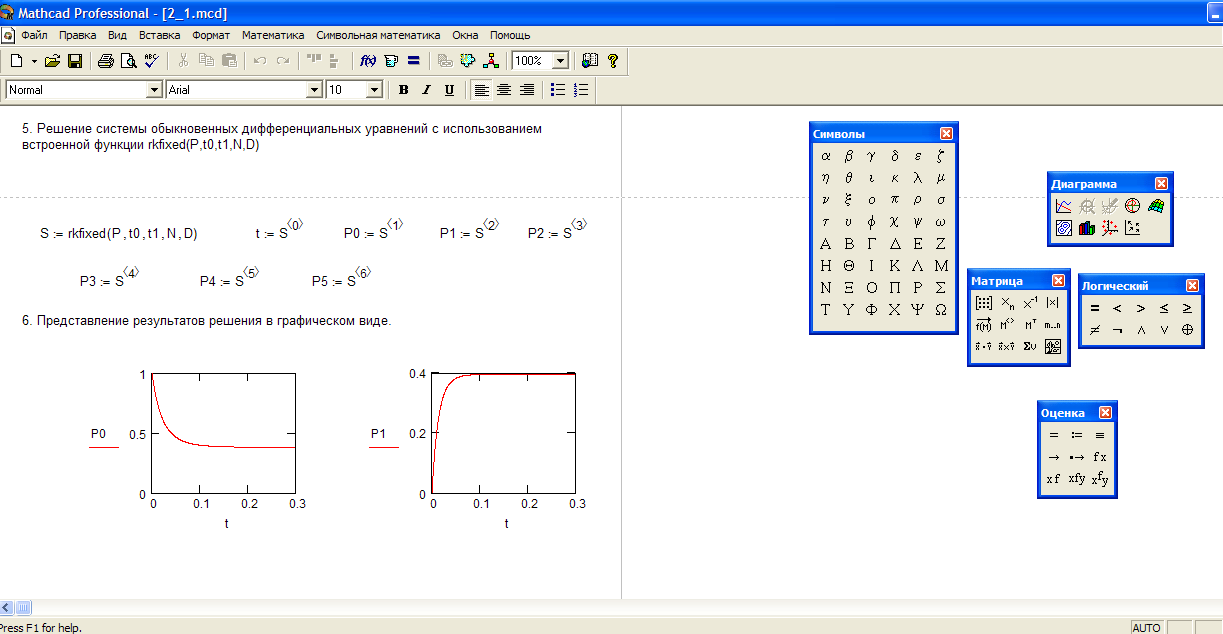 Для
того, чтобы нумерация элементов массива начиналась с 1, установите значение
функции ORIGIN=1 при помощи команды Options меню Math.
Для
того, чтобы нумерация элементов массива начиналась с 1, установите значение
функции ORIGIN=1 при помощи команды Options меню Math.
3. Итерационные циклы
Для программирования таких циклов используется оператор цикла WHILE, вызов которого осуществляется одноименной кнопкой на панели Programming.
Структура оператора While:
где, в Поле 1 вводится условие выполнение цикла;
в Поле 2 вводятся операторы, составляющие тело цикла. По синтаксису оператора в цикле можно записать один оператор. Если операторов больше нужно создать дополнительные поля для ввода щелчком на кнопке “Add line” в панели программирования.
Примечание: В теле цикла должна присутствовать переменная (параметр цикла), управляющая работой цикла и делающая, в итоге, условие цикла ложным для его завершения.
Принцип работы оператора WHILE:
1. 1. Проверяется условие, записанное в Поле 1;
2. 2.
если результатом
проверки условия является ответ “да”, то выполняются операторы, составляющие
тело цикла;
2.
если результатом
проверки условия является ответ “да”, то выполняются операторы, составляющие
тело цикла;
3. 3. если результатом проверки условия станет ответ “нет”, происходит выход из цикла.
Пример 2. Вычислить значения функции в точках , шаг равен .
|
|
Пример 3. Найти сумму положительных элементов вектора V. Вектор задавать в отдельной программе.
Примечания:
1. 1. Функция rnd(N) генерирует случайное вещественное число из диапазона [0; N-1];
2.
2. В данной программе формируется вектор с числом
элементов равных n.
Пример 4. Дан вектор V. Сформировать новый вектор V1 из элементов вектора V, значения которых больше числа d.
Примечание:
переменная с именем nomer задает нумерацию элементовMathCAD — это просто! Часть 26. Продолжаем программировать в MathCAD
Как вы уже имели возможность убедиться благодаря статьям нашей серии, программирование в этой мощнейшей математической среде доступно всем начиная от старшеклассников и заканчивая академиками. Создатели MathCAD’а специально сделали средства программирования в ней достаточно простыми для того, кто не имеет опыта программирования на современных алгоритмических языках, поскольку таким людям тоже время от времени нужно писать небольшие программки в MathCAD’е.
Как вы помните, в прошлой статье мы с вами успели рассмотреть два небольших примера: в одном мы решали путем написания соответствующей программы квадратное уравнение, а во втором занимались аналогичным, в общем-то, образом транспонированием матриц. Что ж, эти примеры, безусловно, были весьма просты и наглядны, и с их помощью действительно вполне можно понять, каким именно образом действуют некоторые из тех операторов, которые я перечислил в самом начале нашего с вами разговора о программировании в MathCAD’е. Поэтому сегодня мы с вами продолжим заниматься написанием программ в этом замечательном математическом пакете, чтобы лучше разобраться во всех операторах, используемых в процессе программирования.
Еще немного о циклах: цикл while
В прошлый раз мы с вами уже пользовались понятием цикла, когда говорили о том, как работает наша программа, предназначенная для вычисления транспонированной матрицы по какой-то заранее заданной. Напомню, что в тот раз мы использовали цикл for, который, как я уже упоминал, имеет одну существенную отличительную особенность: он используется тогда, когда мы с вами уже заранее знаем, какое число итераций (повторений операций в цикле) должны будем совершить.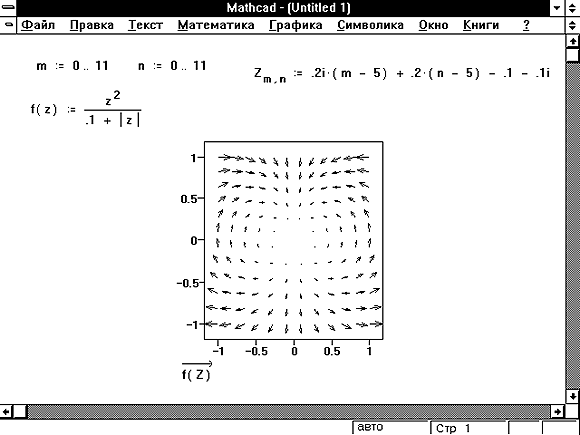
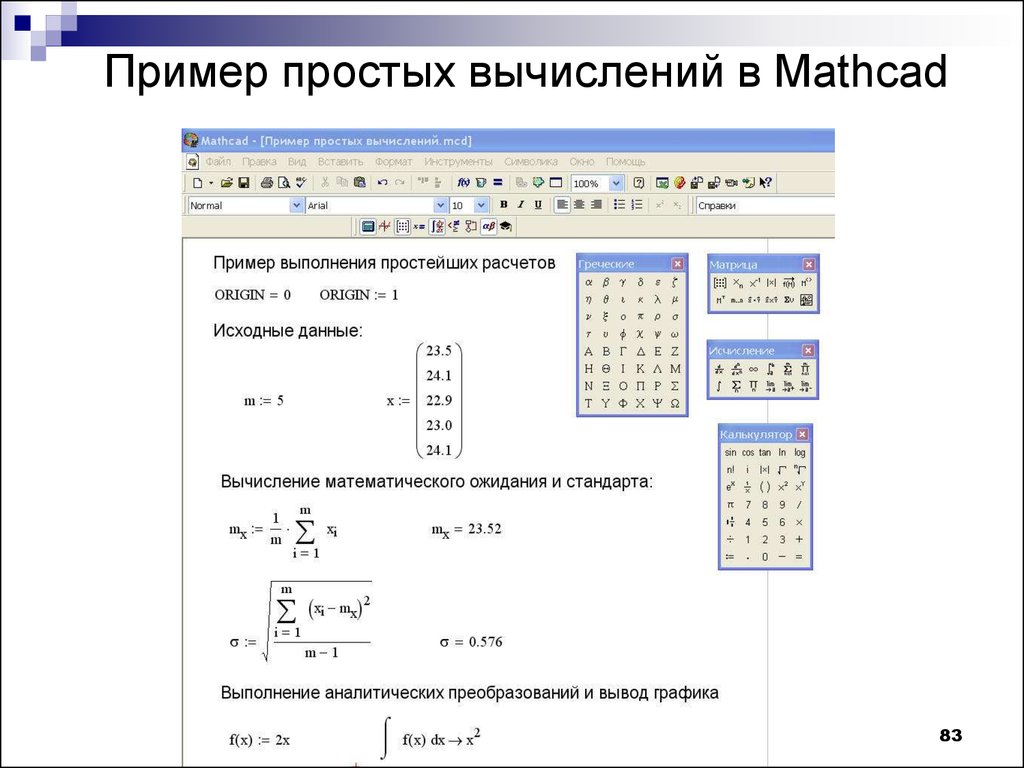

Конечно, можно было бы заранее, зная вид нашей прогрессии, сказать, когда именно член прогрессии станет настолько малым, что мы перестанем замечать его вклад в общую сумму, и исходя из этого запланировать количество итераций для цикла for. Однако этот вариант, скажем прямо, конструктивным назвать ни язык не поворачивается, ни рука не поднимается. Если воспользоваться не for, а другим видом цикла, не требующим от нас заранее указывать число итераций, то мы убьем сразу двух зайцев. Во-первых, нам не потребуется ничего заранее вычислять — MathCAD сам посчитает все, что ему будет нужно, в процессе выполнения написанной нами программы. Во-вторых, мы получим универсальную программу, которая может работать с любой бесконечно убывающей последовательностью — для этого не потребуется по-новой вычислять количество необходимых итераций; достаточно будет изменить одну-единственную формулу во всем тексте программы. Итак, давайте же посмотрим, наконец, на этот самый текст, а затем его немного обсудим.
Здесь x, как несложно, в общем-то, догадаться, та самая переменная, которая служит для обозначения номера элемента нашей прогрессии, а s содержит в себе значение суммы ее членов. x-й член нашей прогрессии вычисляется по формуле 1/x2, а суммировать такие члены наша программа должна будет до тех пор, пока их значение не станет меньше, чем 10-7. Как показывает практика, для того, чтобы вычислить сумму с точностью до трех знаков после запятой, такого ограничения вполне достаточно. Для организации цикла с заранее неизвестным числом итераций мы использовали оператор while. Он будет выполнять наш цикл до тех пор, пока условие, записанное после ключевого слова while, не станет ложным. Обратите внимание, что для того, чтобы записать внутри цикла больше одной строки программного кода, нам нужно, чтобы был отступ влево, обозначенный второй черной линией. Также здесь можно увидеть операторы присваивания, о которых я говорил в прошлый раз. Конструкция x < x +1 используется для увеличения значения переменной x на единицу в каждом шаге цикла, а s < s + 1/x2 — для увеличения значения переменной s на величину 1/x2.
Управление ходом выполнения циклов: оператор break
Когда я говорил о том, что записать программу для вычисления суммы членов бесконечно убывающей геометрической прогрессии можно только в том случае, если мы предварительно рассчитаем число итераций, я немного лукавил. «Как же так? — можете спросить вы. — Значит, цикл for вовсе не обязательно подразумевает априорное знание числа необходимых итераций?» Подразумевает, однако это вовсе не означает, что мы обязательно должны указывать именно то число, которое потребуется для достижения указанной точности. Мы можем указать заведомо большее число итераций, а при достижении некоторого минимального значения x-го члена прогрессии просто прервать выполнение цикла. MathCAD позволяет нам сделать такой финт ушами, потому что существует специальная конструкция для прерывания цикла — это оператор break. Давайте посмотрим, каким образом будет выглядеть наша программа для вычисления суммы членов бесконечно убывающей геометрической прогрессии, записанная с использованием цикла for и оператора break.
Как видите, все действительно очень просто — поскольку цикл for мы с вами уже вроде как изучили, то особенно заострять внимание на нем не буду. Оператор break прерывает выполнение цикла, и выполнение программы продолжается со строки, следующей непосредственно за циклом. Ну, или, если такой строки нет, то на этом оно, в общем-то, и заканчивается. Оператор break можно применять не только в цикле for, но и в цикле while, хотя во втором из них он, конечно же, применяется реже. Конечно, такой способ реализации вычислений в том случае, если число итераций заранее неизвестно, не отличается особым изяществом, однако, коль скоро он также существует, стало быть, его не зря придумали, и будет достаточно полезно иметь его в виду. На самом деле, конечно, в таких ситуациях лучше пользоваться циклом while, поскольку оператор break придуман для совершенно иных случаев. Каких именно? Дело в том, что иногда невозможно выбрать только одно условие завершения цикла, а потому, чтобы не загромождать заголовок цикла while, а также в цикле for, где условие и вовсе указать никак иначе попросту нельзя, используют именно оператор break. Думаю, если вы будете писать программы в MathCAD для решения каких-либо более жизненных задач, то вы рано или поздно столкнетесь с необходимостью применения этого полезного оператора.
Думаю, если вы будете писать программы в MathCAD для решения каких-либо более жизненных задач, то вы рано или поздно столкнетесь с необходимостью применения этого полезного оператора.
Управление ходом выполнения циклов: оператор continue
Есть и еще один оператор управления ходом выполнения циклов, и именно о нем мы с вами поговорим напоследок в этой статье. Дело в том, что не всегда бывает необходимым прекратить выполнение цикла вообще — иногда нужно просто перескочить с текущей итерации сразу на следующую, не прекращая при этом выполнения самого цикла. Специально для таких случаев создатели MathCAD’а предусмотрели не менее полезный оператор continue. В качестве примера давайте рассмотрим знакочередующуюся последовательность. Представим, что перед нами стоит задача найти с заданной точностью сумму только ее нечетных (отрицательных) членов. Вот как, таким образом, может выглядеть решение поставленной перед нами задачи.
Как видите, здесь вполне можно было бы обойтись и без оператора continue — например, если непосредственно перед увеличением значения суммы проверять знак слагаемого.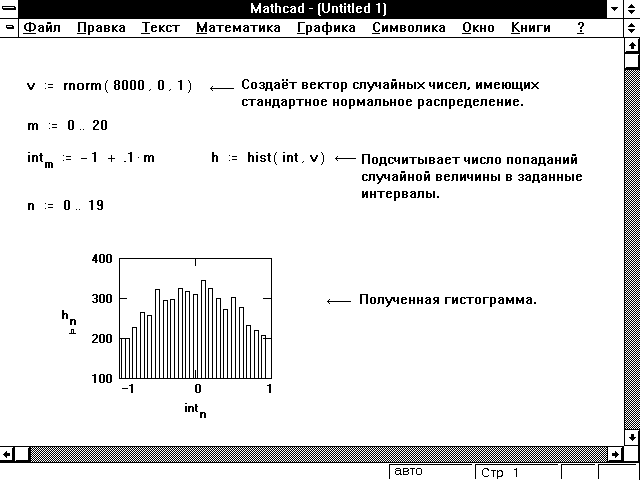 Однако, поскольку нам с вами нужно было посмотреть, как этот оператор действует на практике, я решил написать программу именно в таком варианте. Кроме оператора continue, все остальное, в принципе, вам должно быть знакомо — единственное, что стоит отметить, — это функция sign. Она возвращает -1, если знак ее аргумента меньше нуля, 1 — если больше нуля, и 0 — если равен нулю.
Однако, поскольку нам с вами нужно было посмотреть, как этот оператор действует на практике, я решил написать программу именно в таком варианте. Кроме оператора continue, все остальное, в принципе, вам должно быть знакомо — единственное, что стоит отметить, — это функция sign. Она возвращает -1, если знак ее аргумента меньше нуля, 1 — если больше нуля, и 0 — если равен нулю.
Выводы
Что ж, давайте, пожалуй, подытожим все то, что было сказано нами ранее. Как видите, в MathCAD есть очень много мощных и гибких средств построения циклов — не обязательно использовать требующую зачастую слишком многого конструкцию for, когда есть возможность использовать while. Кроме того, благодаря операторам break и continue управлять циклами можно на принципиально новом уровне, вмешиваясь в работу цикла на каждом шаге каждой итерации, если вдруг возникнет такая необходимость.
Конечно, для того, чтобы грамотно использовать все те конструкции, о которых мы с вами сейчас здесь поговорили, требуется опыт.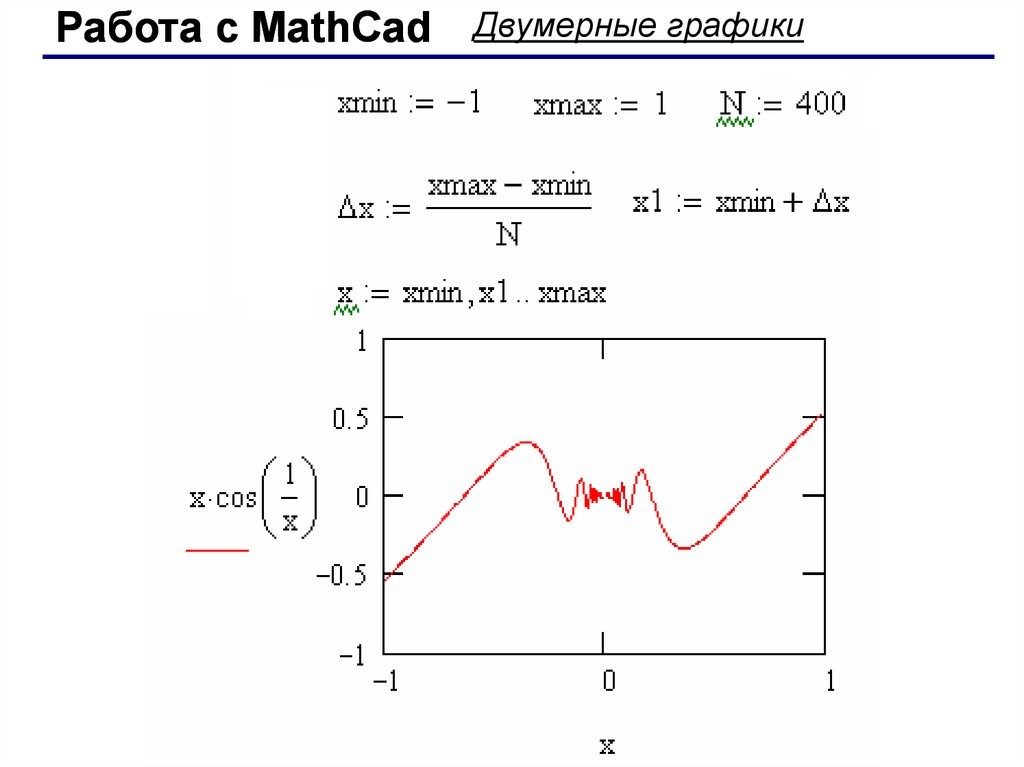 Приобрести его можно, конечно же, регулярными упражнениями в мощной математической среде MathCAD, которые доступны каждому из наших читателей. Если регулярно практиковаться, поверьте, работа в MathCAD будет не простой, а очень простой.
Приобрести его можно, конечно же, регулярными упражнениями в мощной математической среде MathCAD, которые доступны каждому из наших читателей. Если регулярно практиковаться, поверьте, работа в MathCAD будет не простой, а очень простой.
Компьютерная газета. Статья была опубликована в номере 40 за 2008 год в рубрике soft
Управление выполнением программы » MathCadHelp.com » Номер 1 в назначениях MathCad
Палитра программирования в Mathcad Professional включает три оператора для управления выполнением программы:
• Используйте оператор break в теле программы, чтобы остановить выполнение программы при возникновении определенного условия. Используйте break также внутри цикла for или while, чтобы остановить цикл и перейти к следующему оператору вне цикла, когда возникает определенное условие.
• Используйте оператор continue в цикле, чтобы прервать текущую итерацию и заставить выполнение программы продолжиться со следующей итерации цикла.
• Используйте оператор return, чтобы остановить программу и вернуть определенное значение из программы, а не из последнего вычисленного оператора.
Оператор «break»
Часто бывает полезно выйти из цикла или полностью остановить выполнение программы при возникновении некоторого условия. Например, в программе на рис. 18-6 существует вероятность неуправляемой итерации. Если каждый элемент в v меньше порогового значения, условие никогда не станет ложным, и итерация продолжится после конца вектора. В результате появится сообщение об ошибке, указывающее, что индекс указывает на несуществующий элемент массива. Чтобы этого не произошло, вы можете использовать 9Оператор 0011 break , как показано на рис. 18-7.
Программа на рис. 18-7 вернет 0, если не будет найдено ни одного элемента больше порогового значения. В противном случае он возвращает индекс и значение первого элемента, превышающего пороговое значение.
Пример на рис. 18-6 изменен для возврата как индекса, так и
Чтобы вставить оператор break, нажмите кнопку «break» в палитре программирования. Обратите внимание, что для создания программы, показанной на рис. 18.7, сначала нужно нажать кнопку «перерыв», а затем нажать «если».
Обратите внимание, что для создания программы, показанной на рис. 18.7, сначала нужно нажать кнопку «перерыв», а затем нажать «если».
Обработка ошибок
Во время выполнения программы могут возникать ошибки, из-за которых Mathcad прекращает расчет программы. Например, из-за определенного выбора входных данных программа может попытаться разделить на 0 в некотором выражении и столкнуться с ошибкой сингулярности. В этих случаях Mathcad обрабатывает программу так же, как и другие математические выражения: он помечает ошибочное выражение сообщением об ошибке и выделяет неправильное имя или оператор другим цветом, как описано в главе 7 «Уравнения и вычисления».
Mathcad Professional предоставляет две функции для улучшения обработки ошибок в программах:
• Сообщение об ошибке на палитре программирования позволяет «перехватить» числовую ошибку, которая в противном случае заставила бы Mathcad прекратить расчет программы.
• Функция строки ошибки дает вам доступ к механизму подсказок об ошибках Mathcad и позволяет настраивать сообщения об ошибках, выдаваемые вашей программой.
Заявление «при ошибке»
В некоторых случаях вы можете предвидеть входные данные программы, которые приведут к числовой ошибке (например, к сингулярности, переполнению или сбою сходимости), которая заставит Mathcad остановиться расчет программы. Как показано на рис. 18-9., оператор return в сочетании с соответствующим логическим тестом можно использовать в простых случаях для перехвата значений, которые приведут к ошибкам программы. В более сложных случаях, особенно когда ваши программы в значительной степени зависят от числовых операторов Mathcad или набора встроенных функций, вы не сможете предвидеть или перечислить все возможные числовые ошибки, которые могут возникнуть в программе. Оператор on error разработан как ловушка ошибок общего назначения для вычисления альтернативного выражения при возникновении числовой ошибки, которая в противном случае заставила бы Mathcad прекратить вычисления программы.
Пользовательские сообщения об ошибках
Подобно тому, как Mathcad автоматически выдает соответствующую «подсказку об ошибке», когда вы нажимаете на выражение, которое не может быть вычислено из-за ошибки (см. специальные сообщения об ошибках, которые появляются, когда ваши программы используются ненадлежащим образом или не могут возвращать ответы. Функция строки ошибки Mathcad Professional дает вам эту возможность. Например, вы можете создавать собственные подсказки об ошибках, которые будут появляться, когда в программу передаются неверные аргументы или когда в программе возникают определенные условия.
специальные сообщения об ошибках, которые появляются, когда ваши программы используются ненадлежащим образом или не могут возвращать ответы. Функция строки ошибки Mathcad Professional дает вам эту возможность. Например, вы можете создавать собственные подсказки об ошибках, которые будут появляться, когда в программу передаются неверные аргументы или когда в программе возникают определенные условия.
Строковая функция ошибки, описанная в разделе «Строковые функции» в вычислении, создает подсказку об ошибке, текст которой представляет собой просто строковое выражение, которое она принимает в качестве аргумента. Как правило, вы будете использовать функцию строки ошибки в заполнителе в левой части оператора программирования if или on error, чтобы функция строки ошибки генерировала соответствующую подсказку об ошибке при возникновении определенного условия.
На рис. 18.11 показано, как можно использовать собственные сообщения об ошибках даже в небольшой программе.
Выдача пользовательских подсказок об ошибках с помощью функции строки ошибок.
Точная модель контура управления для понижающих контроллеров с текущим режимом
Скачать PDF
Abstract
Разработчики источников питания предпочитают управление в режиме пикового тока, поскольку оно обеспечивает частотную характеристику первого порядка в передаточной функции управления-выход. Процедура проектирования контура управления, основанная на модели первого порядка, предсказывает запас по фазе, близкий к 90 градусов. Однако было обнаружено, что на практике полученный запас по фазе намного меньше 90 градусов в зависимости от выбора частоты кроссовера, рабочего цикла и величины используемой компенсации наклона. Это связано с эффектом дискретизации компаратора тока контура управления. В следующих указаниях по применению описана процедура проектирования контура управления для контроллера токового режима MAX1954A, которая учитывает этот эффект дискретизации и точно прогнозирует запас по фазе. Этот анализ не специфичен для MAX19.54A, и применяется к большинству продаваемых сегодня понижающих ИС текущего режима.
Этот анализ не специфичен для MAX19.54A, и применяется к большинству продаваемых сегодня понижающих ИС текущего режима.
Модель первого порядка
Типичный контур управления токовым режимом для понижающего преобразователя постоянного тока показан на рис. 1. Тактовый генератор с постоянной частотой CLK включает полевой МОП-транзистор верхнего плеча. Q1 выключается, когда масштабированный выходной ток катушки индуктивности на инвертирующем входе компаратора ШИМ превышает управляющее напряжение v c . Таким образом, vc программирует пиковый ток дросселя для поддержания выходного напряжения, v или , константа. Это приводит к поведению источника тока для выходной катушки индуктивности и, следовательно, к передаточной функции управления на выход первого порядка. Компенсирующая рампа v s подается на второй инвертирующий вход компаратора ШИМ для предотвращения субгармонической нестабильности при рабочих циклах более 0,5 и для повышения помехозащищенности. Соответствующие формы сигналов для управления по току показаны на рисунке 2.
Соответствующие формы сигналов для управления по току показаны на рисунке 2.
Рис. 1. Схема управления режимом пикового тока.
Рис. 2. Осциллограммы управления режимом тока.
Передаточная функция управления-выход, обычно используемая для разработки контроллера с режимом пикового тока, задается следующим уравнением:
Вышеупомянутое уравнение предсказывает полюс ω p из-за выходной емкости C o и сопротивления нагрузки R o . Уравнение также предсказывает ноль, ω z , из-за выходной емкости и ее эквивалентного последовательного сопротивления (ESR), R с . Усиление и фаза, предсказанные вышеприведенной моделью, отличаются от наблюдаемых на практике из-за эффекта «выборки и удержания» в компараторе ШИМ, который возникает из-за того, что текущая форма волны дискретизируется только один раз в каждом цикле. В [1] было показано, что простая модель управления режимом пикового тока в приведенном выше уравнении должна быть изменена, чтобы включить двойной полюс на половине частоты переключения, чтобы учесть эффект дискретизации.
Процедура прогнозирования запаса по фазе
Ниже приводится описание процедуры проектирования контура управления для контроллера токового режима MAX1954A, который учитывает этот высокочастотный эффект и точно прогнозирует запас по фазе. Для выполнения проекта используется схема оценочного комплекта MAX1954A. Доступны как лист данных оценочного комплекта MAX1954A, так и лист данных MAX1954A.
Точная передаточная функция управления выходом определяется следующим уравнением:
где коэффициент заполнения , добротность дискретизации , коэффициент компенсации наклона – период переключения, S e — наклон компенсирующей рампы, если она есть, R i — произведение коэффициента усиления усилителя измерения тока и сопротивления датчика тока (MOSFET верхнего плеча R ds_on для MAX1954A), R o — сопротивление нагрузки, V или — выходное напряжение, а V в — входное напряжение. Для схемы оценочного комплекта MAX1954A применяются следующие расчетные параметры:
В в = 11 В
В или = 1,5 В
D = 0,136
M C = 1
S E = 0 (компенсация уклона, применяемая в этом рабочих циклах в MAX1954A)
T S = 3,3 мкс
R C = 26 CS
R C =
C 70 707070707070707070 гг.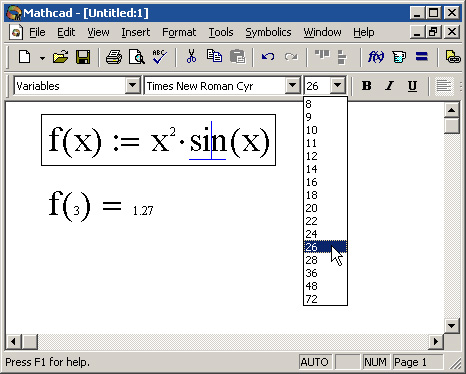
L o = 2,18 мкГн
R o = 0,3125 Ом
R i = 0,063
Компенсационная сеть спроектирована в соответствии с рекомендациями в техническом описании MAX1954A. Передаточная функция от управления к выходу и коэффициент усиления без обратной связи, предсказанные точной моделью, построены с помощью MathCad и показаны на рис. 3 и 4 соответственно. Фактические передаточные функции усиления контура управления и выхода и коэффициента усиления разомкнутого контура, измеренные на MAX19.Набор для оценки 54A показан на фиг. 5 и фиг. 6 соответственно.
Рис. 3. Графики усиления и фазы «управление-выход» из MathCad.
Рис. 4. Графики усиления и фазы без обратной связи из MathCad.
Рис. 5. Графики измеренного коэффициента усиления и фазы по отношению к выходному сигналу.
Рис. 6. Измеренные графики усиления и фазы без обратной связи.